Decision Making Under Risk Continued Bayes Theorem and Posterior

Decision Making Under Risk Continued: Bayes’Theorem and Posterior Probabilities MGS 3100 - Chapter 8 Slides 8 c

Bayesian Methods There is a continuing debate among statisticians, little known to those outside the field, over the proper definition of probability. The frequentist definition sees probability as the long-run expected frequency of occurrence. P(A) = n/N, where n is the number of times event A occurs in N opportunities. The Bayesian view of probability is related to degree of belief. It is a measure of the plausibility of an event given incomplete knowledge.

The Market Research Question P(Red/Urn 1) = 8/10 = 0. 8 8 Red (Known Population) 2 White Urn 1 Have P(A/B) Vs. What is in the urn? ? Select a sample, and then make inferences about the population Urn 2 R (Unknown Population) Want P(B/A)

How We Will Use Bayes' Theorem Prior information can be based on the results of previous experiments, or expert opinion, and can be expressed as probabilities. If it is desirable to improve on this state of knowledge, an experiment can be conducted. Bayes' Theorem is the mechanism used to update the state of knowledge with the results of the experiment to provide a posterior distribution.

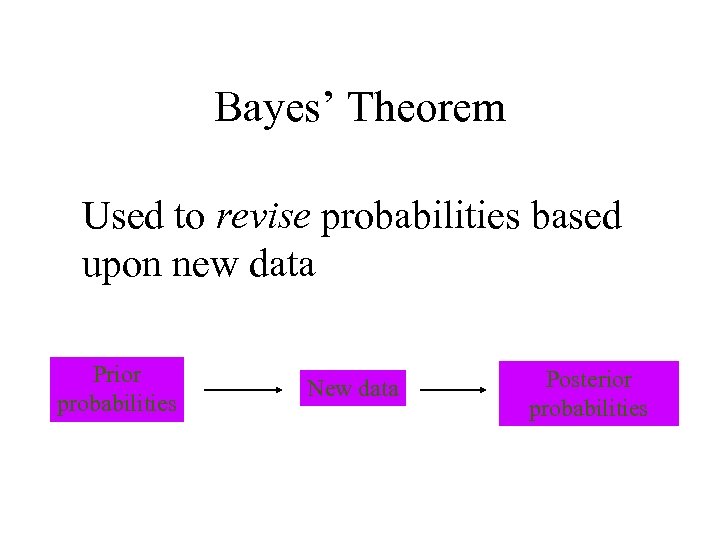
Bayes’ Theorem Used to revise probabilities based upon new data Prior probabilities New data Posterior probabilities

How Bayes' Theorem Works Let the experiment be A and the prediction be B. Let’s assume that both have occurred. The probability of both A and B together is P(A∩B), or simply P(AB). The law of conditional probability says that this probability can be found as the product of the conditional probability of one, given the other, times the probability of the other. That is: P(A|B) * P(B) = P(AB) = P(B|A) * P(A) Simple algebra shows that: P(B|A) = P(A|B) * P(B) / P(A) This is Bayes' Theorem.

Example Problem: Thompson Lumber Company is trying to decide whether to expand its product line by manufacturing and marketing a new product which is “backyard storage sheds. ” The courses of action that may be chosen include: (1) large plant to manufacture storage sheds, (2) small plant to manufacture storage sheds, or (3) build no plant at all.

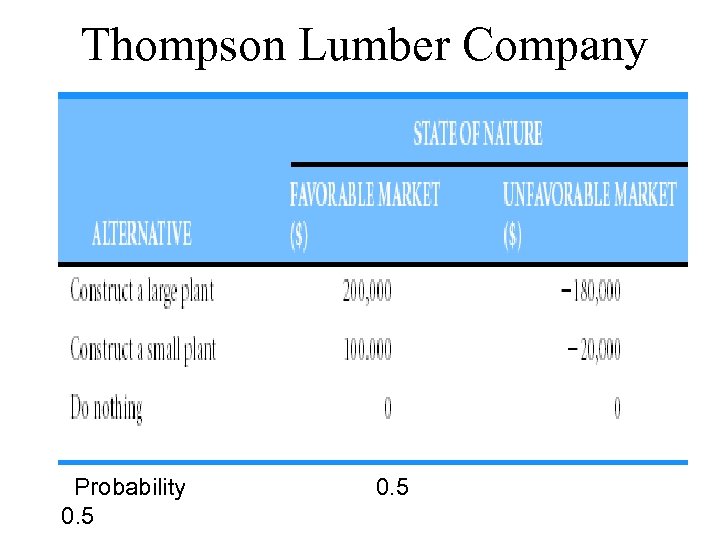
Thompson Lumber Company Probability 0. 5

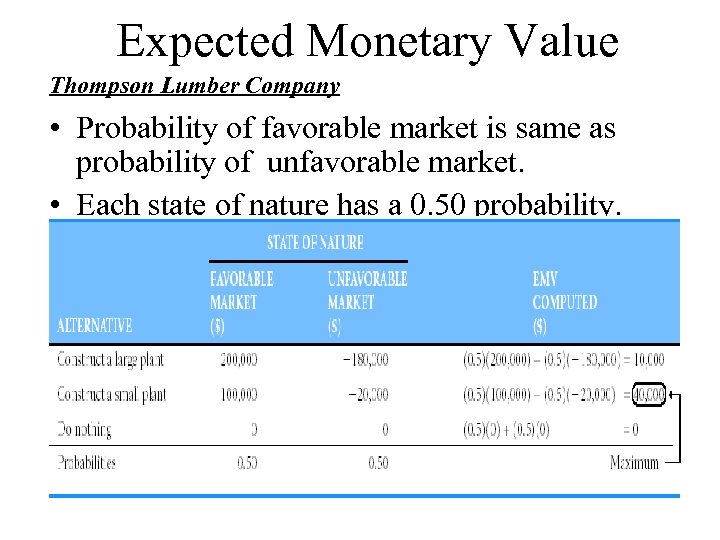
Expected Monetary Value Thompson Lumber Company • Probability of favorable market is same as probability of unfavorable market. • Each state of nature has a 0. 50 probability.

Calculating the EVPI • Best outcome for state of nature "favorable market" is "build a large plant" with a payoff of $200, 000. • Best outcome for state of nature "unfavorable market" is "do nothing, " with payoff of $0. • Therefore, Expected value with perfect information EVw. PI = ($200, 000)(0. 50) + ($0)(0. 50) = $ 100, 000 • If one had perfect information, an average payoff of $100, 000 could be achieved in the long run. • However, the maximum EMV (EVBEST) or expected value without perfect information, is $40, 000. • Therefore, EVPI = $100, 000 - $40, 000 = $60, 000.

To Test or Not to Test • Often, companies have the option to perform market tests/surveys, usually at a price, to get additional information prior to making decisions. • However, some interesting questions need to be answered before this decision is made: – How will the test results be combined with prior information? – How much should you be willing to pay to test? • The good news is that Bayes’ Theorem can be used to combine the information, and we can use our decision tree to find EVSI, the Expected Value of Sample Information. • In order to perform these calculations, we first need to know how reliable the potential test may be.

Market Survey Reliability in Predicting Actual States of Nature Assuming that the above information is available, we can combine these conditional probabilities with our prior probabilities using Bayes’ Theorem.

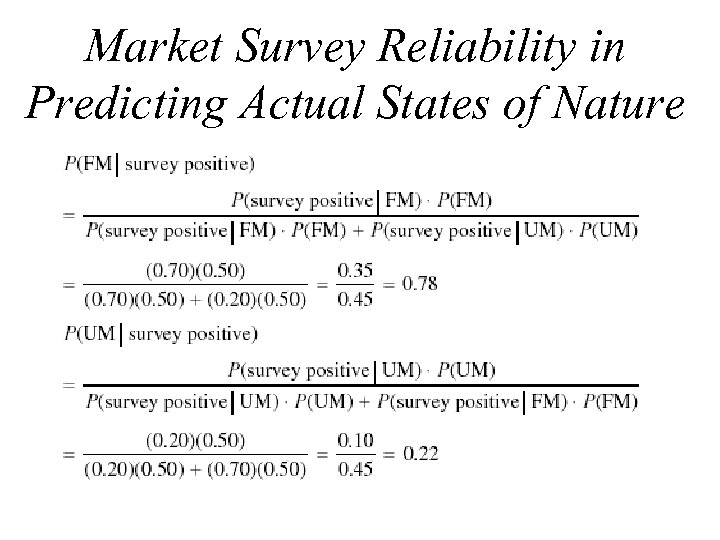
Market Survey Reliability in Predicting Actual States of Nature

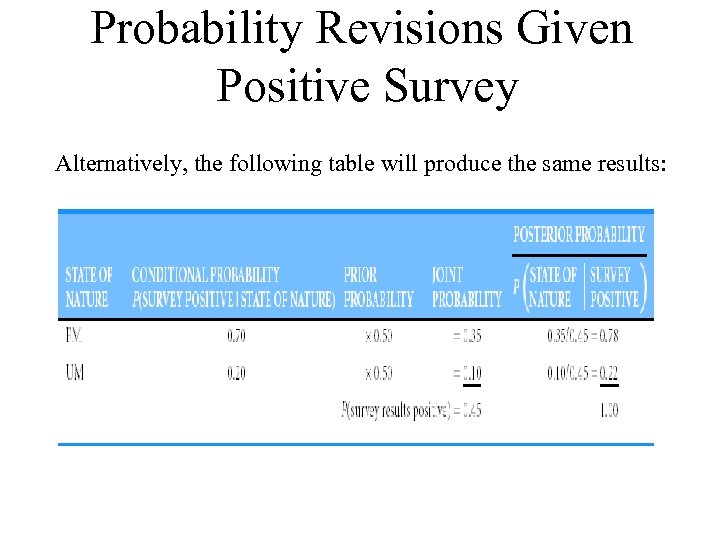
Probability Revisions Given Positive Survey Alternatively, the following table will produce the same results:

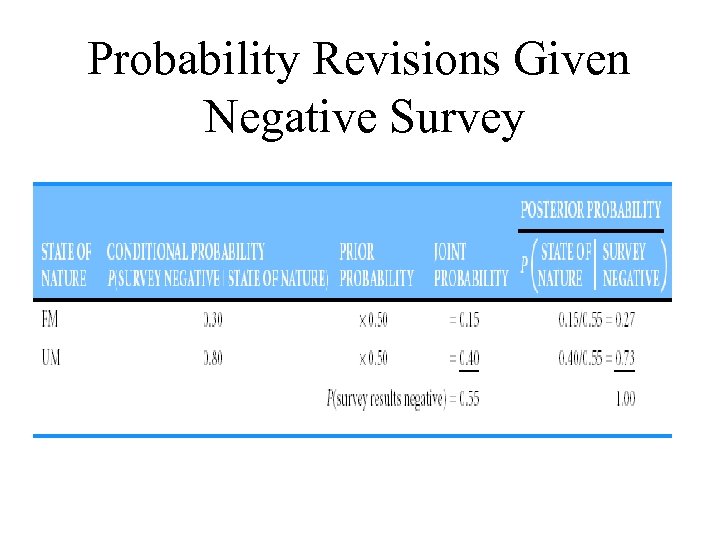
Probability Revisions Given Negative Survey

Placing Posterior Probabilities on the Decision Tree • The bottom of the tree is the “no test” part of the analysis; therefore, the prior probabilities are assigned to these events. P(favorable market) = P(FM) = 0. 5 P(unfavorable market) = P(UM) = 0. 5 The calculations here will be identical to the EMV calculations performed without a decision tree. • The top of the tree is the “test” part of the analysis; therefore, the posterior probabilities are assigned to these events.

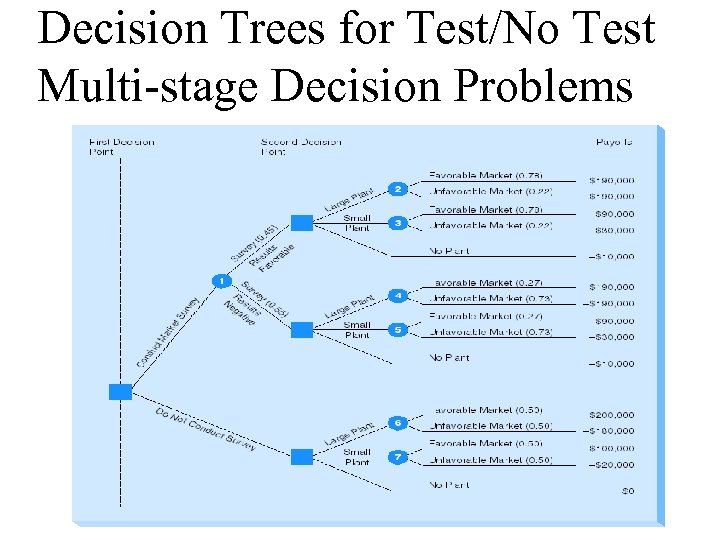
Decision Trees for Test/No Test Multi-stage Decision Problems

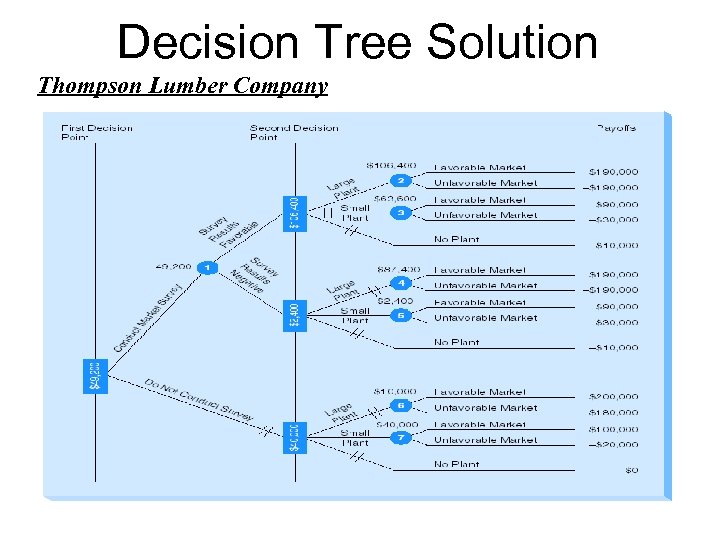
Decision Tree Solution Thompson Lumber Company

Expected Value of Sample Information = EV of the top of the tree - EV of the bottom of the tree This calculation ignores the cost of the test. Once you compute the EVSI, you can compare it to the cost of the test to determine the desirability to test. The ratio of the EVSI to the EVPI times 100 will also give you a measure of “efficiency” of the proposed test, expressed as a percentage.

Expected Value of Sample Information For Thompson Lumber Company, EVSI = $49, 200 - $40, 000 = $9, 200 And since the EVPI was previously calculated to be $60, 000, Thompson would be willing to pay up to $9, 200 for this test information, with an efficiency of (9200/60000)*100 = 15. 3%

Decision Tree Class Exercise: Jenny Lind, Part 2 (see text, #8 -16 and 8 -37) Jenny Lind may hire a market research firm to conduct a survey at a cost of $100, 000. The result of the survey would be either a favorable (F) or unfavorable (U) public response to the movie. The firm’s ability to assess the market is: P(F/S) = 0. 3 P(U/S) = 0. 7 P(F/M) = 0. 6 P(U/M) = 0. 4 P(F/L) = 0. 8 P(U/L) = 0. 2 • Should Jenny conduct the survey? • What is the most she should be willing to pay for the survey? What is the efficiency of this survey?