Decision Making Supplement A 2007 Pearson Education

Decision Making Supplement A © 2007 Pearson Education

Break-Even Analysis Ø Break-even analysis is used to compare processes by finding the volume at which two different processes have equal total costs. Ø Break-even point is the volume at which total revenues equal total costs. Ø Variable costs (c) are costs that vary directly with the volume of output. Ø Fixed costs (F) are those costs that remain constant with changes in output level. © 2007 Pearson Education

Break-Even Analysis Ø “Q” is the volume of customers or units, “c” is the unit variable cost, F is fixed costs and p is the revenue per unit Ø c. Q is the total variable cost. Ø Total cost = F + c. Q Ø Total revenue = p. Q Ø Break-even is where p. Q = F + c. Q © 2007 Pearson Education (Total revenue = Total cost)

Break-Even Analysis can tell you… Ø If a forecast sales volume is sufficient to break even (no profit or no loss) Ø How low variable cost per unit must be to break even given current prices and sales forecast. Ø How low the fixed cost need to be to break even. Ø How price levels affect the break-even volume. © 2007 Pearson Education

Hospital Example A. 1 A hospital is considering a new procedure to be offered at $200 per patient. The fixed cost per year would be $100, 000, with total variable costs of $100 per patient. What is the break-even quantity for this service? Q = F / (p - c) = 100, 000 / (200 -100) = 1, 000 patients © 2007 Pearson Education

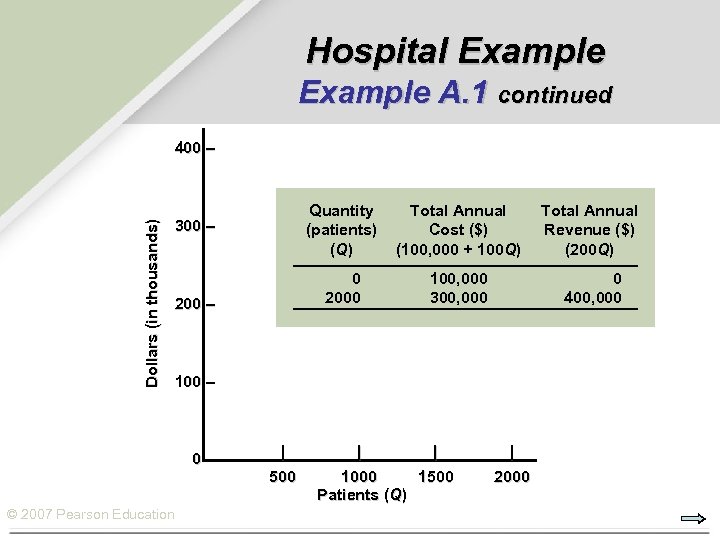Hospital Example A. 1 continued Dollars (in thousands) 400 – Quantity (patients) (Q) 200 – Total Annual Cost ($) (100, 000 + 100 Q) Total Annual Revenue ($) (200 Q) 0 2000 300 – 100, 000 300, 000 0 400, 000 100 – © 2007 Pearson Education | 500 | | 1000 1500 Patients (Q) | 2000

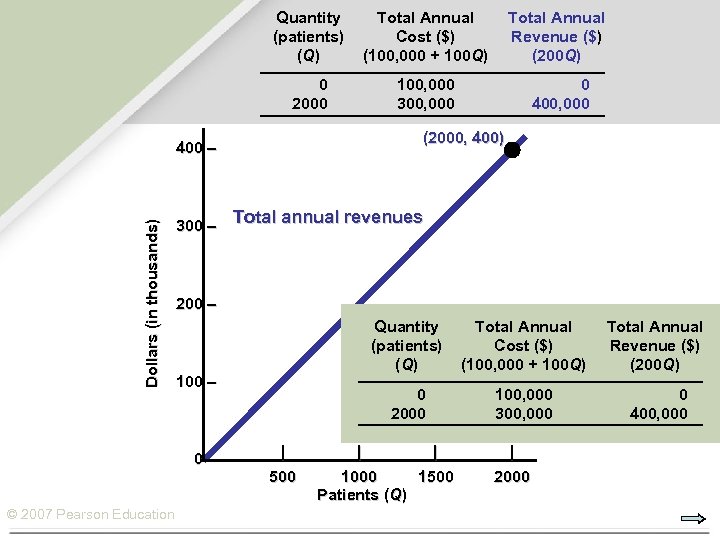Quantity (patients) (Q) Total Annual Cost ($) (100, 000 + 100 Q) Total Annual Revenue ($) (200 Q) 0 2000 100, 000 300, 000 0 400, 000 (2000, 400) Dollars (in thousands) 400 – 300 – 200 – Quantity (patients) (Q) | 500 | Total Annual Cost ($) (100, 000 + 100 Q) Total Annual Revenue ($) (200 Q) 0 2000 100 – © 2007 Pearson Education Total annual revenues 100, 000 300, 000 0 400, 000 | 1000 1500 Patients (Q) | 2000

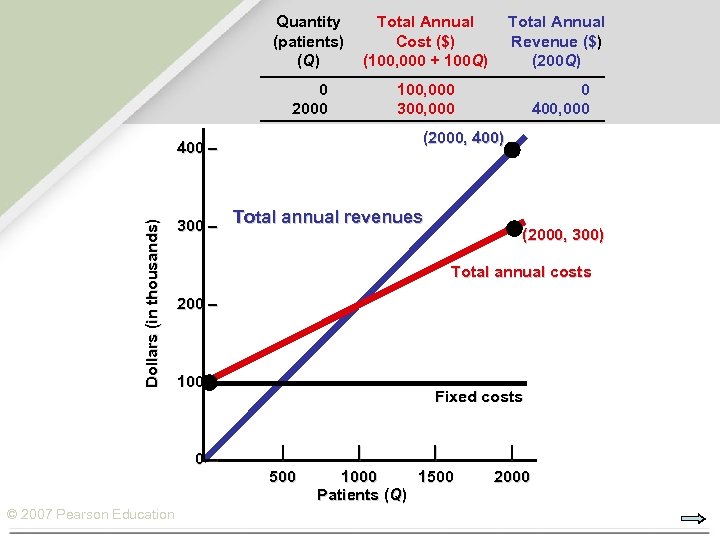Quantity (patients) (Q) Total Annual Cost ($) (100, 000 + 100 Q) Total Annual Revenue ($) (200 Q) 0 2000 100, 000 300, 000 0 400, 000 (2000, 400) Dollars (in thousands) 400 – 300 – Total annual revenues Total annual costs 200 – 100 – © 2007 Pearson Education (2000, 300) Fixed costs | 500 | | 1000 1500 Patients (Q) | 2000

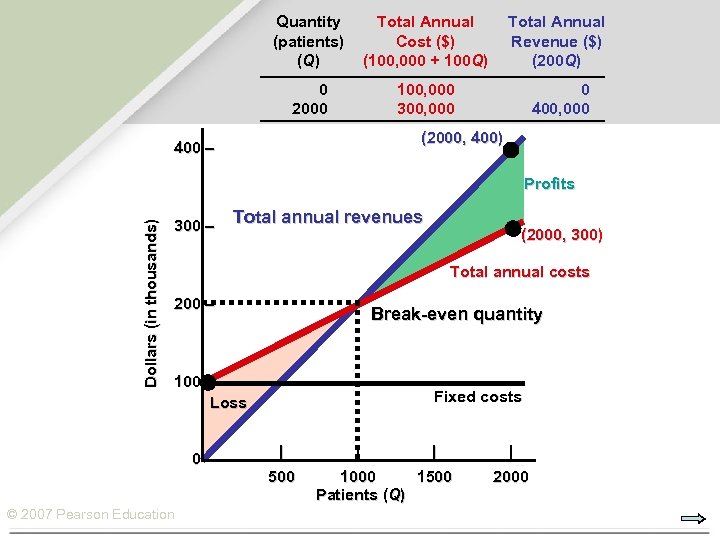Quantity (patients) (Q) Total Annual Cost ($) (100, 000 + 100 Q) Total Annual Revenue ($) (200 Q) 0 2000 100, 000 300, 000 0 400, 000 (2000, 400) 400 – Dollars (in thousands) Profits 300 – Total annual revenues (2000, 300) Total annual costs 200 – Break-even quantity 100 – Loss 0 – © 2007 Pearson Education Fixed costs | 500 | | 1000 1500 Patients (Q) | 2000

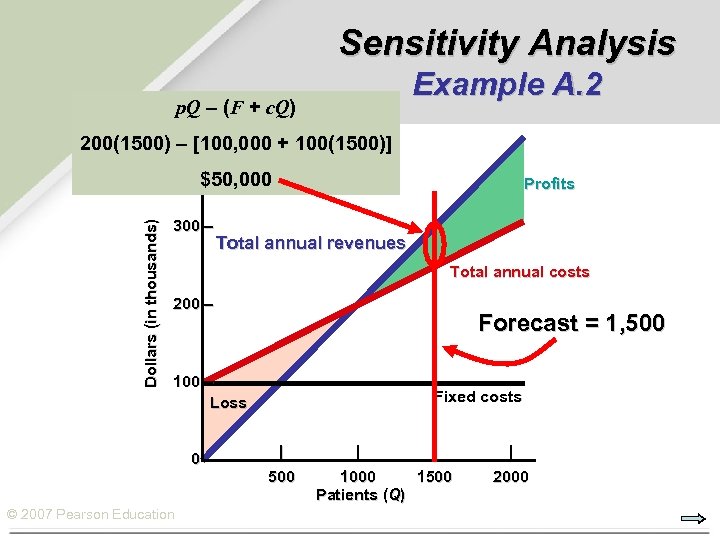Sensitivity Analysis Example A. 2 p. Q – (F + c. Q) 200(1500) – [100, 000 + 100(1500)] 400 – Dollars (in thousands) $50, 000 300 – Profits Total annual revenues Total annual costs 200 – Forecast = 1, 500 100 – Loss 0 – © 2007 Pearson Education Fixed costs | 500 | | 1000 1500 Patients (Q) | 2000

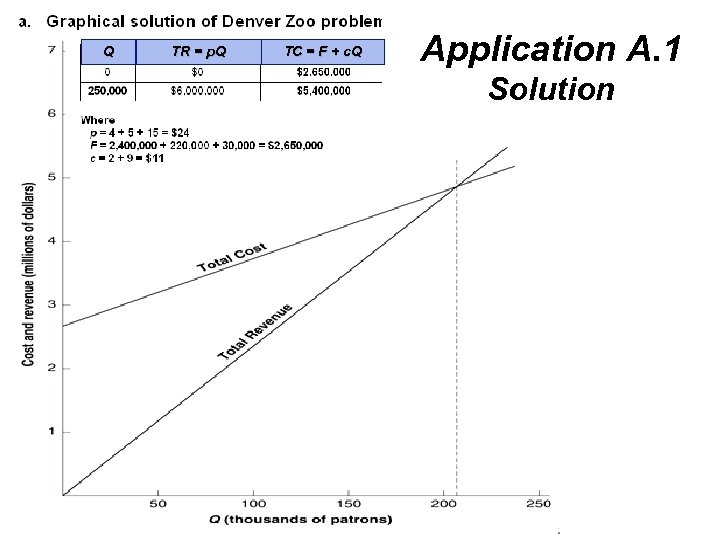
Application A. 1 © 2007 Pearson Education

Application A. 1 Solution Q © 2007 Pearson Education TR = p. Q TC = F + c. Q

Q TR = p. Q TC = F + c. Q Application A. 1 Solution © 2007 Pearson Education

Application A. 1 Solution p. Q = F + c. Q Q © 2007 Pearson Education TR = p. Q TC = F + p. Q

Two Processes and Make-or-Buy Decisions Ø Breakeven analysis can be used to choose between two processes or between an internal process and buying those services or materials. Ø The solution finds the point at which the total costs of each of the two alternatives are equal. Ø The forecast volume is then applied to see which alternative has the lowest cost for that volume. © 2007 Pearson Education

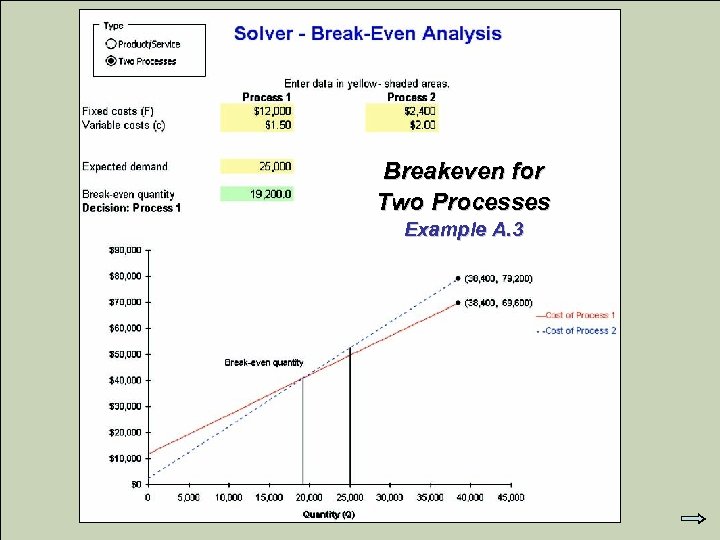Breakeven for Two Processes Example A. 3 © 2007 Pearson Education

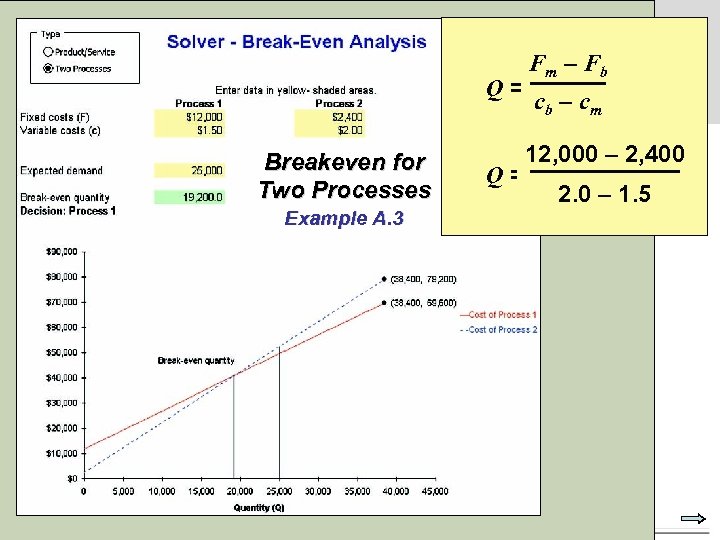Q = Breakeven for Two Processes Example A. 3 © 2007 Pearson Education Q = Fm – Fb cb – cm 12, 000 – 2, 400 2. 0 – 1. 5

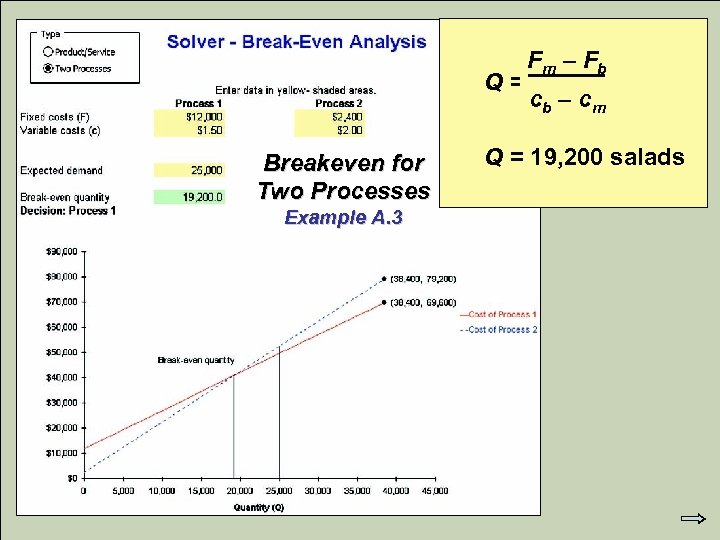Q = Breakeven for Two Processes Example A. 3 © 2007 Pearson Education Fm – Fb cb – cm Q = 19, 200 salads

Application A. 2 Q = Fm – Fb cb – c m © 2007 Pearson Education = $300, 000 – $0 $9 – $7 = $150, 000

Preference Matrix ØA Preference Matrix is a table that allows you to rate an alternative according to several performance criteria. ØThe criteria can be scored on any scale as long as the same scale is applied to all the alternatives being compared. ØEach score is weighted according to its perceived importance, with the total weights typically equaling 100. ØThe total score is the sum of the weighted scores (weight × score) for all the criteria. The manager can compare the scores for alternatives against one another or against a predetermined threshold. © 2007 Pearson Education

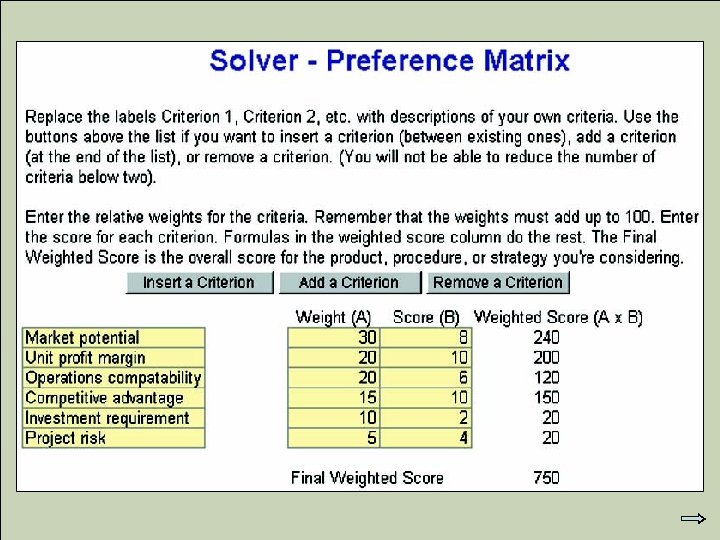
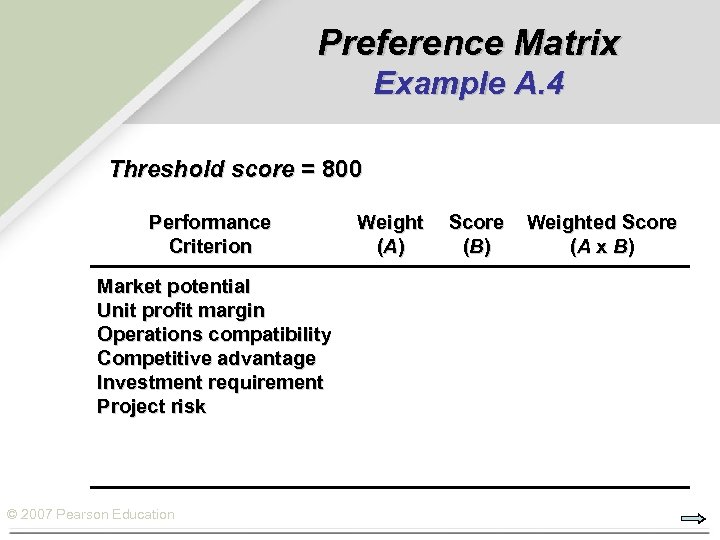Preference Matrix Example A. 4 Threshold score = 800 Performance Criterion Weight (A ) Market potential Unit profit margin Operations compatibility Competitive advantage Investment requirement Project risk © 2007 Pearson Education Score (B ) Weighted Score (A x B)

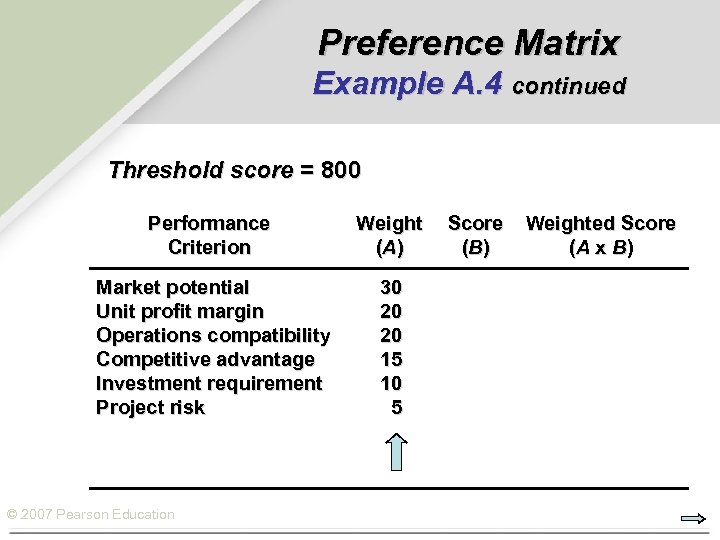Preference Matrix Example A. 4 continued Threshold score = 800 Performance Criterion Weight (A ) Market potential Unit profit margin Operations compatibility Competitive advantage Investment requirement Project risk 30 20 20 15 10 5 © 2007 Pearson Education Score (B ) Weighted Score (A x B)

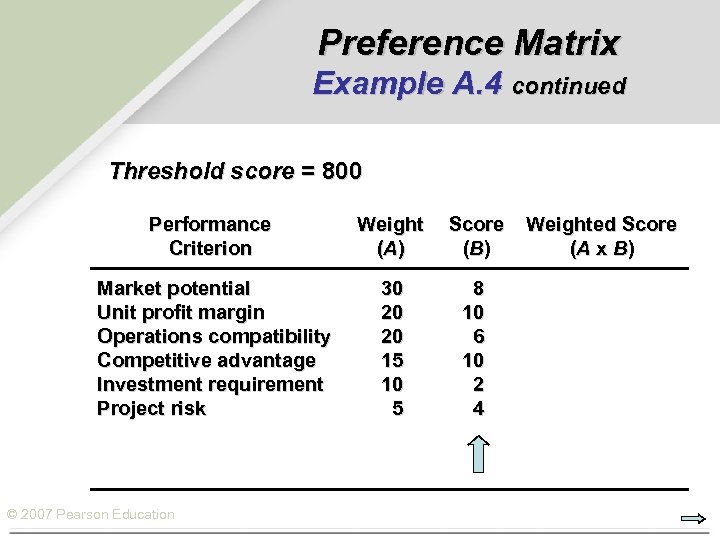Preference Matrix Example A. 4 continued Threshold score = 800 Performance Criterion Weight (A ) Score (B ) Market potential Unit profit margin Operations compatibility Competitive advantage Investment requirement Project risk 30 20 20 15 10 5 8 10 6 10 2 4 © 2007 Pearson Education Weighted Score (A x B)

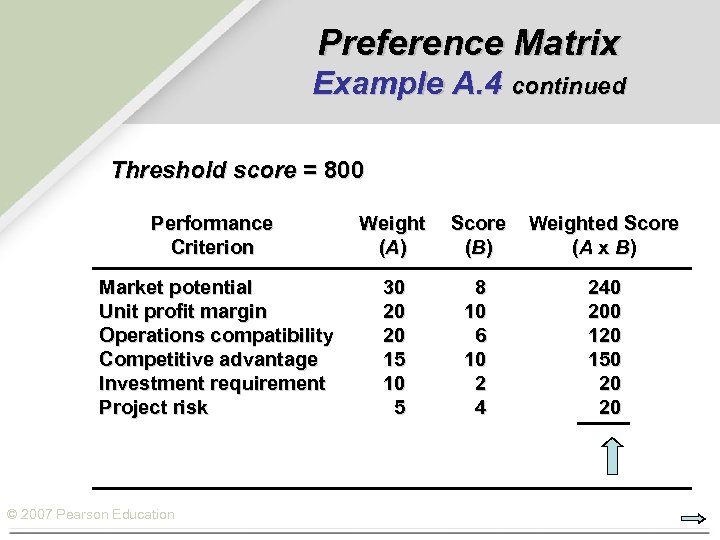Preference Matrix Example A. 4 continued Threshold score = 800 Performance Criterion Weight (A ) Score (B ) Weighted Score (A x B) Market potential Unit profit margin Operations compatibility Competitive advantage Investment requirement Project risk 30 20 20 15 10 5 8 10 6 10 2 4 240 200 120 150 20 20 © 2007 Pearson Education

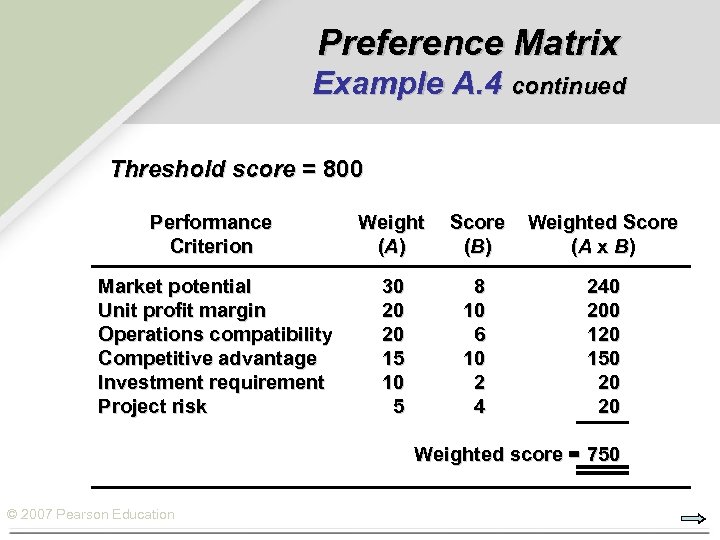Preference Matrix Example A. 4 continued Threshold score = 800 Performance Criterion Weight (A ) Score (B ) Weighted Score (A x B) Market potential Unit profit margin Operations compatibility Competitive advantage Investment requirement Project risk 30 20 20 15 10 5 8 10 6 10 2 4 240 200 120 150 20 20 Weighted score = 750 © 2007 Pearson Education

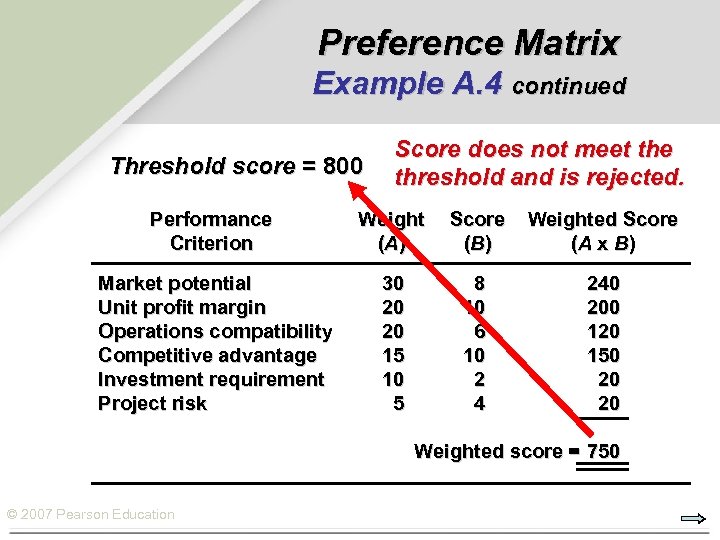Preference Matrix Example A. 4 continued Threshold score = 800 Score does not meet the threshold and is rejected. Performance Criterion Weight (A ) Score (B ) Weighted Score (A x B) Market potential Unit profit margin Operations compatibility Competitive advantage Investment requirement Project risk 30 20 20 15 10 5 8 10 6 10 2 4 240 200 120 150 20 20 Weighted score = 750 © 2007 Pearson Education

© 2007 Pearson Education

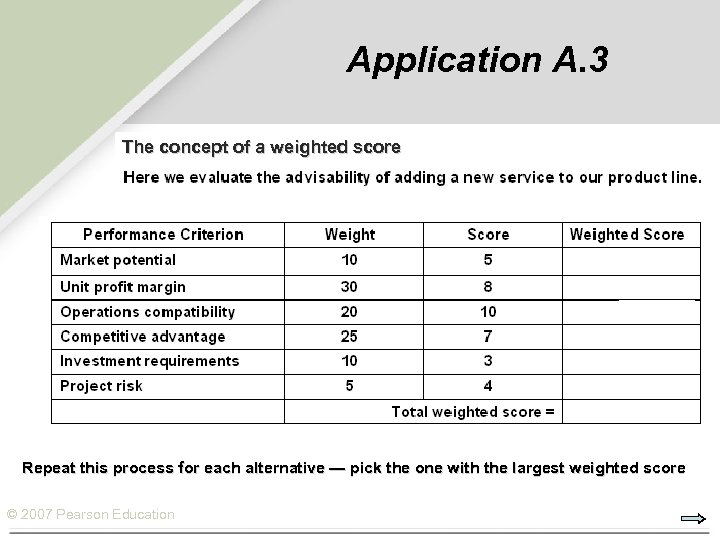Application A. 3 The concept of a weighted score Repeat this process for each alternative — pick the one with the largest weighted score © 2007 Pearson Education

Decision Theory Ø Decision theory is a general approach to decision making when the outcomes associated with alternatives are often in doubt. Ø A manager makes choices using the following process: 1. List the feasible alternatives 2. List the chance events (states of nature). 3. Calculate the payoff for each alternative in each event. 4. Estimate the probability of each event. (The total probabilities must add up to 1. ) 5. Select the decision rule to evaluate the alternatives. © 2007 Pearson Education

Decision Rules Ø Decision Making Under Uncertainty is when you are unable to estimate the probabilities of events. Ø Ø Maximin: The best of the worst. A pessimistic approach. Maximax: The best of the best. An optimistic approach. Minimax Regret: Minimizing your regret (also pessimistic) Laplace: The alternative with the best weighted payoff using assumed probabilities. Ø Decision Making Under Risk is when one is able to estimate the probabilities of the events. Ø Expected Value: The alternative with the highest weighted payoff using predicted probabilities. © 2007 Pearson Education

Maxi. Min Decision Example A. 6 a. Events (Uncertain Demand) Alternatives Low High Small facility Large facility Do nothing 200 160 0 270 800 0 1. Look at the payoffs for each alternative and identify the lowest payoff for each. 2. Choose the alternative that has the highest of these. (the maximum of the minimums) © 2007 Pearson Education

Maxi. Max Decision Example A. 6 b. Events (Uncertain Demand) Alternatives Low High Small facility Large facility Do nothing 200 160 0 270 800 0 1. Look at the payoffs for each alternative and identify the “highest” payoff for each. 2. Choose the alternative that has the highest of these. (the maximum of the maximums) © 2007 Pearson Education

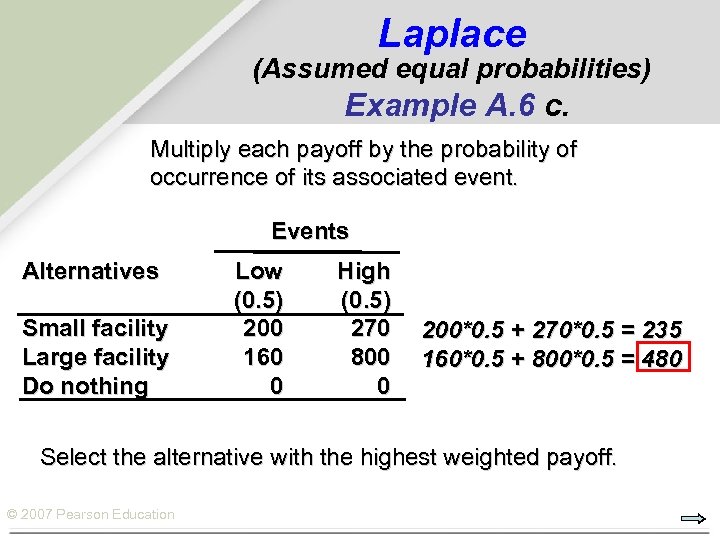Laplace (Assumed equal probabilities) Example A. 6 c. Multiply each payoff by the probability of occurrence of its associated event. Events Alternatives Small facility Large facility Do nothing Low (0. 5) 200 160 0 High (0. 5) 270 800 0 200*0. 5 + 270*0. 5 = 235 160*0. 5 + 800*0. 5 = 480 Select the alternative with the highest weighted payoff. © 2007 Pearson Education

Mini. Max Regret Example A. 6 d. Events (Uncertain Demand) Alternatives Low High Small facility Large facility Do nothing 200 160 0 270 800 0 Look at each payoff and ask yourself, “If I end up here, do I have any regrets? ” Your regret, if any, is the difference between that payoff and what you could have had by choosing a different alternative, given the same state of nature (event). © 2007 Pearson Education

Mini. Max Regret Example A. 6 d. continued Events (Uncertain Demand) Alternatives Low High Small facility Large facility Do nothing 200 160 0 270 800 0 If you chose a small facility and demand is low, you have zero regret. © 2007 Pearson Education If you chose a large facility and demand is low, you have a regret of 40. (The difference between the 160 you got and the 200 you could have had. )

Mini. Max Regret Example A. 6 d. continued Events (Uncertain Demand) Alternatives Low High Small facility Large facility Do nothing 200 160 0 270 800 0 Regret Matrix Building a large facility offers the least regret. © 2007 Pearson Education Events Alternatives Low High Small facility 0 Large facility 40 Do nothing 200 530 0 800 Max. Regret 530 40 800

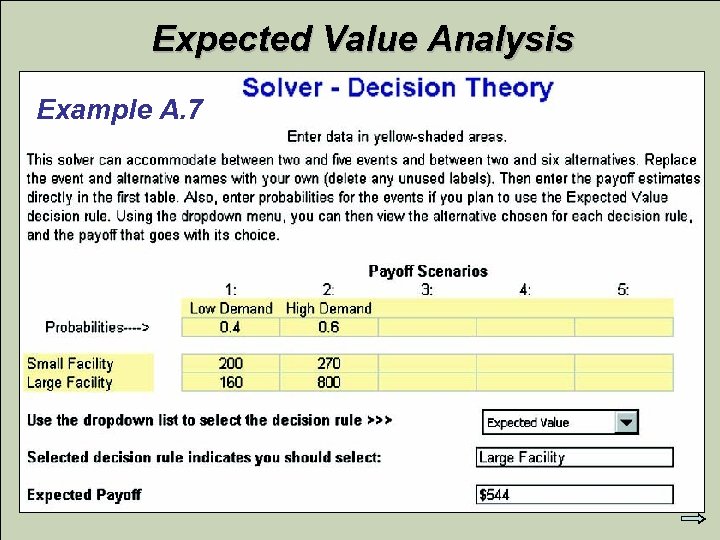
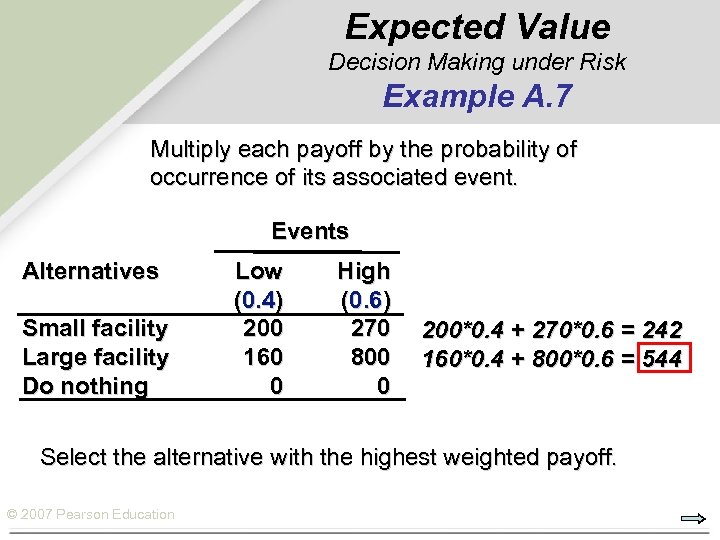Expected Value Decision Making under Risk Example A. 7 Multiply each payoff by the probability of occurrence of its associated event. Events Alternatives Small facility Large facility Do nothing Low (0. 4) 200 160 0 High (0. 6) 270 800 0 200*0. 4 + 270*0. 6 = 242 160*0. 4 + 800*0. 6 = 544 Select the alternative with the highest weighted payoff. © 2007 Pearson Education

Expected Value Analysis Example A. 7 © 2007 Pearson Education

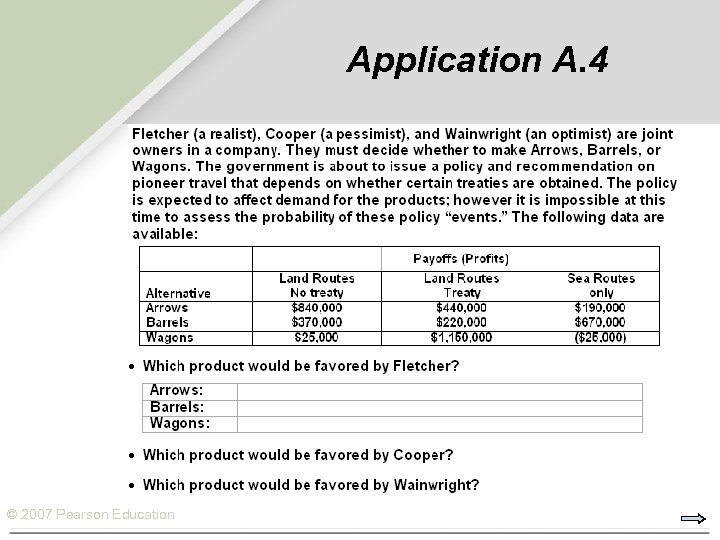Application A. 4 © 2007 Pearson Education

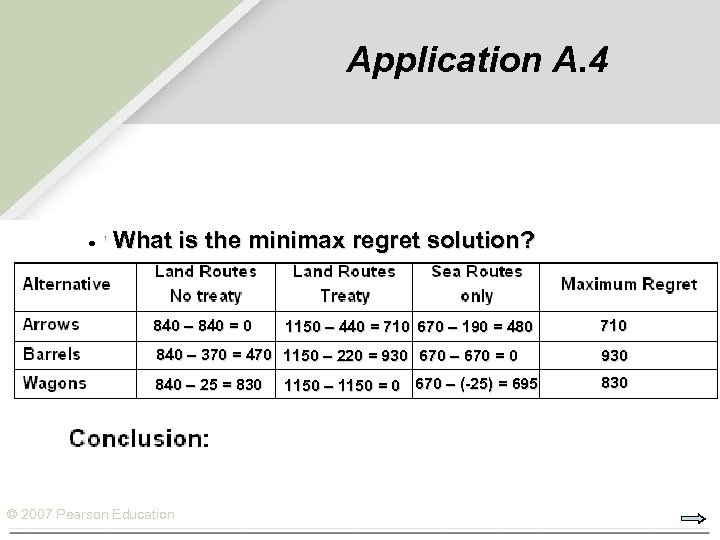Application A. 4 What is the minimax regret solution? 840 – 840 = 0 1150 – 440 = 710 670 – 190 = 480 840 – 370 = 470 1150 – 220 = 930 670 – 670 = 0 840 – 25 = 830 © 2007 Pearson Education 1150 – 1150 = 0 670 – (-25) = 695 710 930 830

Application A. 5 © 2007 Pearson Education

Decision Trees Ø Decision Trees are schematic models of alternatives available along with their possible consequences. Ø They are used in sequential decision situations. Ø Decision points are represented by squares. Ø Event points are represented by circles. © 2007 Pearson Education

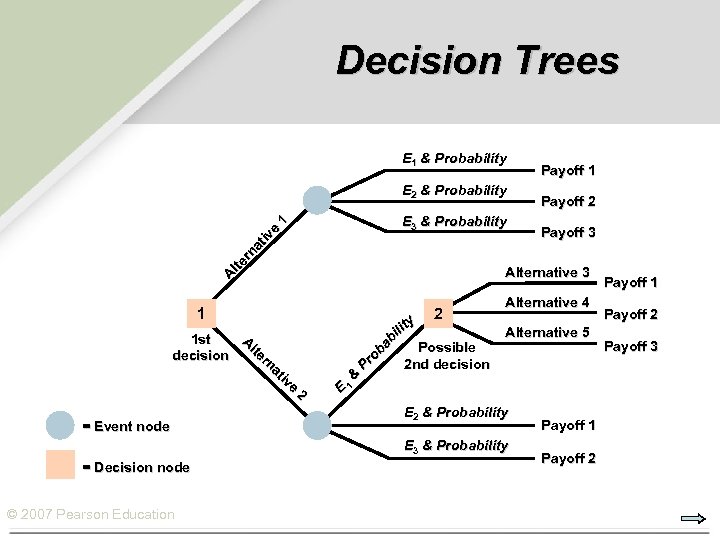Decision Trees E 1 & Probability E 2 & Probability A lte rn at iv e 1 E 3 & Probability = Event node P ro ba bi lit y 2 © 2007 Pearson Education Payoff 3 Alternative 5 E 1 & Possible 2 nd decision Alternative 4 E 2 & Probability E 3 & Probability = Decision node Payoff 2 Alternative 3 1 A 1 st lte decision rn at iv e 2 Payoff 1 Payoff 2 Payoff 3

Decision Trees Ø After drawing a decision tree, we solve it by working from right to left, starting with decisions farthest to the right, and calculating the expected payoff for each of its possible paths. Ø We pick the alternative for that decision that has the best expected payoff. ØWe “saw off, ” or “prune, ” the branches not chosen by marking two short lines through them. ØThe decision node’s expected payoff is the one associated with the single remaining branch. © 2007 Pearson Education

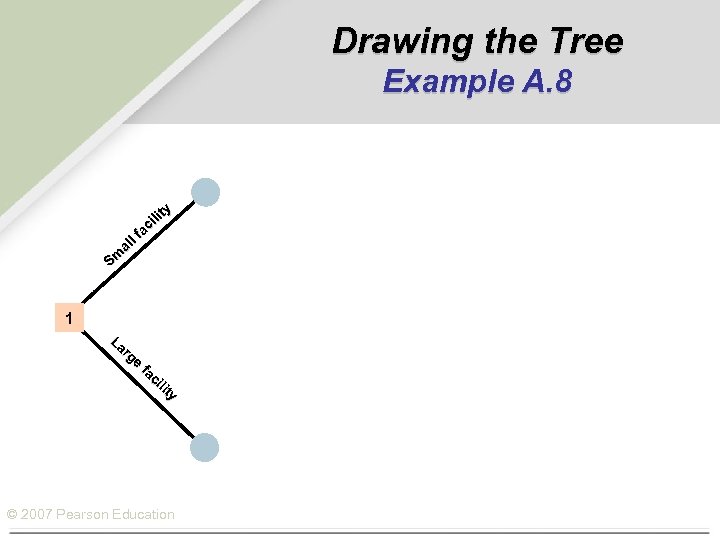Drawing the Tree Example A. 8 ty ili c fa l al Sm 1 La rg e fa ci lit y © 2007 Pearson Education

Drawing the Tree Example A. 8 continued Low demand [0. 4] ty ili c fa l al Sm 1 La rg e fa ci lit y © 2007 Pearson Education H ig h d [0 em. 6 an ] d 2 Don’t expand Expand $200 $223 $270

Completed Drawing Example A. 8 Low demand [0. 4] ty ili ac l f al m S Hi gh d [ 0 em. 6 ] an d 2 1 La rg e fa ci lit y Don’t expand Expand Do nothing d an m de. 4] ow [0 L 3 $223 $270 $40 Modest response [0. 3] Advertise Sizable response [0. 7] High demand [0. 6] © 2007 Pearson Education $200 $800 $220

Solving Decision #3 Example A. 8 Low demand [0. 4] ty ili ac l f al m S Hi gh d [0 em. 6 an ] d 2 1 La rg e fa ci lit y Don’t expand Expand Do nothing d an m de. 4] ow [0 L 3 $200 $223 $270 $40 0. 3 x $20 = $6 Modest response [0. 3] Advertise Sizable response [0. 7] $6 + $154 = $160 $220 0. 7 x $220 = $154 High demand [0. 6] © 2007 Pearson Education $800

Solving Decision #3 Example A. 8 Low demand [0. 4] ty ili ac l f al m S Hi gh d [0 em. 6 an ] d Don’t expand 2 Expand 1 La rg e fa ci lit y Do nothing d 3 an m e d. 4] w 0 $160 Lo [ $223 $270 $40 Modest response [0. 3] Advertise High demand [0. 6] © 2007 Pearson Education $200 $160 $800 Sizable response [0. 7] $20 $220

Solving Decision #2 Example A. 8 Low demand [0. 4] ty ili ac l f al m S Hi gh d [0 em. 6 an ] d 2 $270 1 La rg e fa ci lit y Don’t expand Expand $40 Expanding has a higher value. Modest response [0. 3] Advertise $160 High demand [0. 6] © 2007 Pearson Education $223 $270 Do nothing d 3 an m e d. 4] $160 w 0 Lo [ $200 $800 Sizable response [0. 7] $20 $220

Solving Decision #1 Example A. 8 Low demand [0. 4] $200 x 0. 4 = $80 $242 ty ili c fa l al Sm Hi gh d [0 em. 6 an ] d 2 $270 1 La rg e fa ci lit y Don’t expand Expand $40 Modest response [0. 3] Advertise $160 High demand [0. 6] © 2007 Pearson Education $223 $270 x 0. 6 = $162 Do nothing d 3 an m e d. 4] $160 w 0 Lo [ $470 $800 Sizable response [0. 7] $20 $220

Solving Decision #1 Example A. 8 Low demand [0. 4] $200 $242 Hi gh d [0 em. 6 an ] d ty ili c fa l al Sm 2 $270 1 La rg e fa ci lit y Don’t expand Expand $544 $40 Modest response [0. 3] Advertise 0. 4 x $160 = $64 © 2007 Pearson Education $270 Do nothing d 3 an m e d. 4] $160 w 0 Lo [ $223 $160 High demand [0. 6] Sizable response [0. 7] $800 x 0. 6 = $480 $220

Solving Decision #1 Example A. 8 Low demand [0. 4] ty ili $242 c fa l al Sm Hi gh d [0 em. 6 an ] d 2 $270 1 $544 La rg e fa ci lit y Expand d 3 an m e d. 4] $160 w 0 Lo [ $223 $270 Do nothing $544 © 2007 Pearson Education Don’t expand $200 $40 Modest response [0. 3] Advertise $160 High demand [0. 6] $800 Sizable response [0. 7] $20 $220

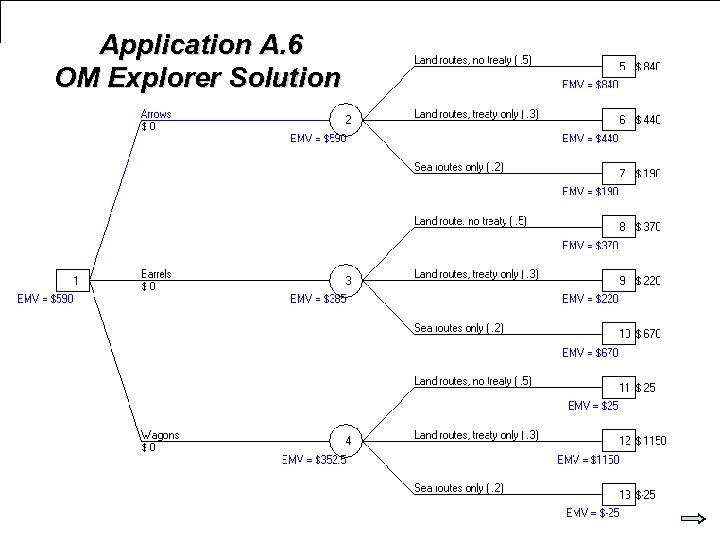Application A. 6 OM Explorer Solution © 2007 Pearson Education

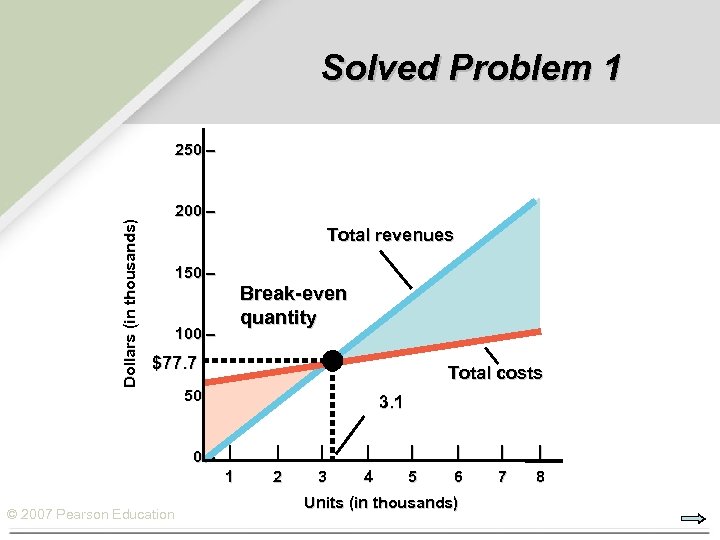Solved Problem 1 Dollars (in thousands) 250 – 200 – Total revenues 150 – 100 – Break-even quantity $77. 7 50 – | 1 © 2007 Pearson Education Total costs 3. 1 | | | | 2 3 4 5 6 7 8 Units (in thousands)

Solved Problem 4 Bad times [0. 3] Normal times [0. 5] One lift $225. 3 $256. 0 Good times [0. 2] Bad times [0. 3] Two lifts Normal times [0. 5] $256. 0 © 2007 Pearson Education Good times [0. 2] $191 $240 $151 $245 $441