346125ea835a055baa165a6426167f4f.ppt
- Количество слайдов: 45
 Decision Making ECE 457 Applied Artificial Intelligence Spring 2008 Lecture #10
Decision Making ECE 457 Applied Artificial Intelligence Spring 2008 Lecture #10
 Outline n n n Maximum Expected Utility (MEU) Decision network Making decisions n Russell & Norvig, chapter 16 ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 2
Outline n n n Maximum Expected Utility (MEU) Decision network Making decisions n Russell & Norvig, chapter 16 ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 2
 Acting Under Uncertainty n With no uncertainty, rational decision is to pick action with “best” outcome n Two actions n n n #1 leads to great outcome #2 leads to good outcome It’s only rational to pick #1 Assumes outcome is 100% certain With uncertainty, it’s a little harder n Two actions n n n #1 has 1% probability to lead to great outcome #2 has 90% probability to lead to good outcome What is the rational decision? ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 3
Acting Under Uncertainty n With no uncertainty, rational decision is to pick action with “best” outcome n Two actions n n n #1 leads to great outcome #2 leads to good outcome It’s only rational to pick #1 Assumes outcome is 100% certain With uncertainty, it’s a little harder n Two actions n n n #1 has 1% probability to lead to great outcome #2 has 90% probability to lead to good outcome What is the rational decision? ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 3
 Acting Under Uncertainty n Maximum Expected Utility (MEU) n n Pick action that leads to best outcome averaged over all possible outcomes of the action How do we compute the MEU? n Easy once we know the probability of each outcome and their utility ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 4
Acting Under Uncertainty n Maximum Expected Utility (MEU) n n Pick action that leads to best outcome averaged over all possible outcomes of the action How do we compute the MEU? n Easy once we know the probability of each outcome and their utility ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 4
 Utility n n Value of a state or outcome Computed by utility function n n U(S) = utility of state S U(S) [0, 1] if normalized ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 5
Utility n n Value of a state or outcome Computed by utility function n n U(S) = utility of state S U(S) [0, 1] if normalized ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 5
 Expected Utility n Sum of utility of each possible outcome times probability of that outcome n n n Known evidence E about the world Action A has i possible outcomes, with probability P(Resulti(A)|Do(A), E) Utility of each outcome is U(Resulti(A)) n n Evaluation function of the state of the world given Resulti(A) EU(A|E)= i P(Resulti(A)|Do(A), E) U(Resulti(A)) ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 6
Expected Utility n Sum of utility of each possible outcome times probability of that outcome n n n Known evidence E about the world Action A has i possible outcomes, with probability P(Resulti(A)|Do(A), E) Utility of each outcome is U(Resulti(A)) n n Evaluation function of the state of the world given Resulti(A) EU(A|E)= i P(Resulti(A)|Do(A), E) U(Resulti(A)) ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 6
 Maximum Expected Utility n n List all possible actions Aj For each action, list all possible outcomes Resulti(Aj) Compute EU(Aj|E) Pick action that maximises EU ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 7
Maximum Expected Utility n n List all possible actions Aj For each action, list all possible outcomes Resulti(Aj) Compute EU(Aj|E) Pick action that maximises EU ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 7
 Utility of Money n n Use money as measure of utility? Example n n A 1 = 100% chance of $1 M A 2 = 50% chance of $3 M or nothing EU(A 2) = $1. 5 M > $1 M = EU(A 1) Is that rational? ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 8
Utility of Money n n Use money as measure of utility? Example n n A 1 = 100% chance of $1 M A 2 = 50% chance of $3 M or nothing EU(A 2) = $1. 5 M > $1 M = EU(A 1) Is that rational? ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 8
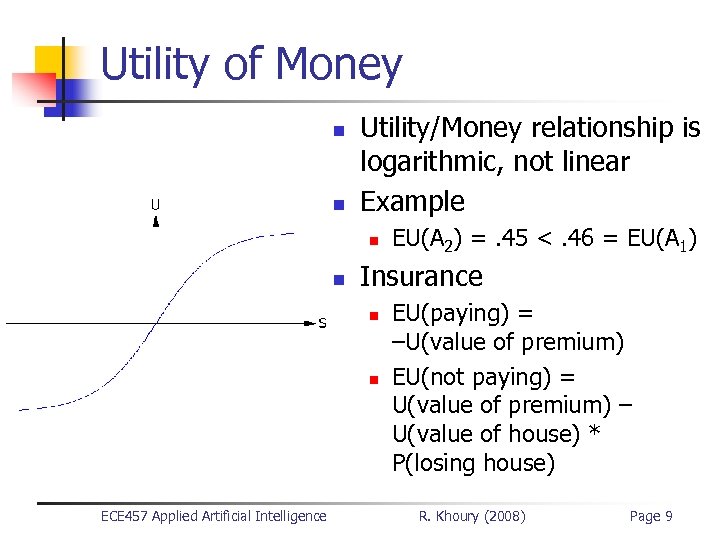 Utility of Money n n Utility/Money relationship is logarithmic, not linear Example n n Insurance n n ECE 457 Applied Artificial Intelligence EU(A 2) =. 45 <. 46 = EU(A 1) EU(paying) = –U(value of premium) EU(not paying) = U(value of premium) – U(value of house) * P(losing house) R. Khoury (2008) Page 9
Utility of Money n n Utility/Money relationship is logarithmic, not linear Example n n Insurance n n ECE 457 Applied Artificial Intelligence EU(A 2) =. 45 <. 46 = EU(A 1) EU(paying) = –U(value of premium) EU(not paying) = U(value of premium) – U(value of house) * P(losing house) R. Khoury (2008) Page 9
 Axioms n n Given three states A, B, C A B n n A~B n n The agent is indifferent between A and B A B n n The agent prefers A to B or is indifferent between A and B [p 1, A; p 2, B; p 3, C] n A can occur with probability p 1, B can occur with probability p 2, C can occur with probability p 3 ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 10
Axioms n n Given three states A, B, C A B n n A~B n n The agent is indifferent between A and B A B n n The agent prefers A to B or is indifferent between A and B [p 1, A; p 2, B; p 3, C] n A can occur with probability p 1, B can occur with probability p 2, C can occur with probability p 3 ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 10
 Axioms n Orderability n n Transitivity n n A ~ B [p, A; 1 -p, C] ~ [p, B; 1 -p, C] Monotonicity n n A B C p [p, A; 1 -p, C] ~ B Substituability n n (A B) (B C) (A C) Continuity n n (A B) (B A) (A ~ B) A B ( p q [p, A; 1 -p, B] [q, A; 1 -q, B] ) Decomposability n [p, A; 1 -p, [q, B; 1 -q, C]] ~ [p, A; (1 -p)q, B; (1 -p)(1 -q), C] ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 11
Axioms n Orderability n n Transitivity n n A ~ B [p, A; 1 -p, C] ~ [p, B; 1 -p, C] Monotonicity n n A B C p [p, A; 1 -p, C] ~ B Substituability n n (A B) (B C) (A C) Continuity n n (A B) (B A) (A ~ B) A B ( p q [p, A; 1 -p, B] [q, A; 1 -q, B] ) Decomposability n [p, A; 1 -p, [q, B; 1 -q, C]] ~ [p, A; (1 -p)q, B; (1 -p)(1 -q), C] ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 11
 Axioms n Utility principle n n n Maximum utility principle n n U(A) > U(B) A B U(A) = U(B) A ~ B U([p 1, A 1; … ; pn, An]) = i pi. U(Ai) Given these axioms, MEU is rational! ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 12
Axioms n Utility principle n n n Maximum utility principle n n U(A) > U(B) A B U(A) = U(B) A ~ B U([p 1, A 1; … ; pn, An]) = i pi. U(Ai) Given these axioms, MEU is rational! ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 12
 Decision Network n Our agent makes decisions given evidence n n Similar to conditional probability n n n Observed variables and conditional probability tables of hidden variables Probability of variables given other variables Relationships represented graphically in Bayesian network Could we make a similar graph here? ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 13
Decision Network n Our agent makes decisions given evidence n n Similar to conditional probability n n n Observed variables and conditional probability tables of hidden variables Probability of variables given other variables Relationships represented graphically in Bayesian network Could we make a similar graph here? ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 13
 Decision Network n n Sometimes called influence diagram Like a Bayesian Network for decision making n n n Start with variables of problem Add decision variables that the agent controls Add utility variable that specify how good each state is ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 14
Decision Network n n Sometimes called influence diagram Like a Bayesian Network for decision making n n n Start with variables of problem Add decision variables that the agent controls Add utility variable that specify how good each state is ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 14
 Decision Network n Chance node (oval) n n n Decision node (rectangle) n n Uncertain variable Like in Bayesian network Choice of action Parents: variables affecting decision, evidence Children: variables affected by decision Utility node (diamond) n n n Utility function Parents: variables affecting utility Typically one in network ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 15
Decision Network n Chance node (oval) n n n Decision node (rectangle) n n Uncertain variable Like in Bayesian network Choice of action Parents: variables affecting decision, evidence Children: variables affected by decision Utility node (diamond) n n n Utility function Parents: variables affecting utility Typically one in network ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 15
 Decision Network Example Lucky S F F T P(E) 0. 01 0. 5 0. 9 W F T F E F F T H 0. 2 0. 6 0. 8 T Study L F T 0. 99 T T 0. 99 Pass. Exam P(L) = 0. 75 ECE 457 Applied Artificial Intelligence Win Happiness L P(W) F T 0. 01 0. 4 R. Khoury (2008) Page 16
Decision Network Example Lucky S F F T P(E) 0. 01 0. 5 0. 9 W F T F E F F T H 0. 2 0. 6 0. 8 T Study L F T 0. 99 T T 0. 99 Pass. Exam P(L) = 0. 75 ECE 457 Applied Artificial Intelligence Win Happiness L P(W) F T 0. 01 0. 4 R. Khoury (2008) Page 16
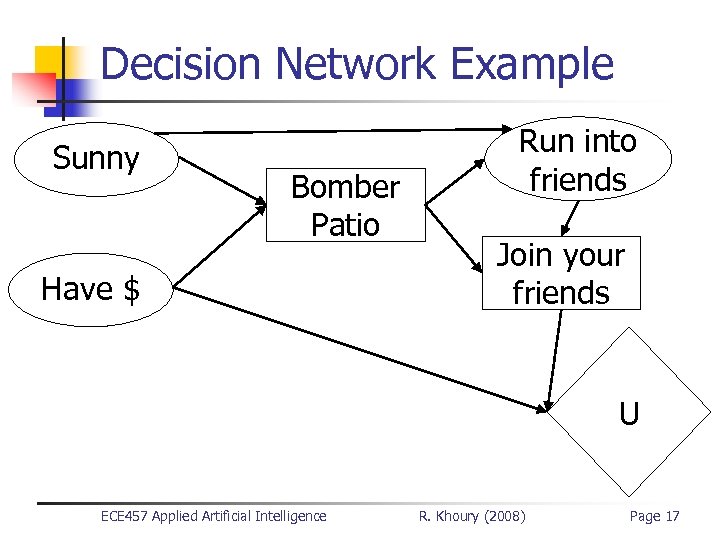 Decision Network Example Sunny Bomber Patio Have $ Run into friends Join your friends U ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 17
Decision Network Example Sunny Bomber Patio Have $ Run into friends Join your friends U ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 17
 Making a Rational Decision n n At a decision node Given a combination of values of evidence variables, and each possible action given this evidence n n n Compute the EU of each action you can decide to do Decide to do the action with the maximum EU Policy: choice of action (not necessarily the best) for each possible combination of values of evidence variables ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 18
Making a Rational Decision n n At a decision node Given a combination of values of evidence variables, and each possible action given this evidence n n n Compute the EU of each action you can decide to do Decide to do the action with the maximum EU Policy: choice of action (not necessarily the best) for each possible combination of values of evidence variables ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 18
 Policy n Decision node Di n n n Can take values in domain dom(Di) Has set of parents Pi that take values in domain dom(Pi) Policy is a set of mappings i of dom(Pi) to dom(Di) n n i associates a decision to each state the parents of Di can be in associates a series of decisions to each state the network can be in ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 19
Policy n Decision node Di n n n Can take values in domain dom(Di) Has set of parents Pi that take values in domain dom(Pi) Policy is a set of mappings i of dom(Pi) to dom(Di) n n i associates a decision to each state the parents of Di can be in associates a series of decisions to each state the network can be in ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 19
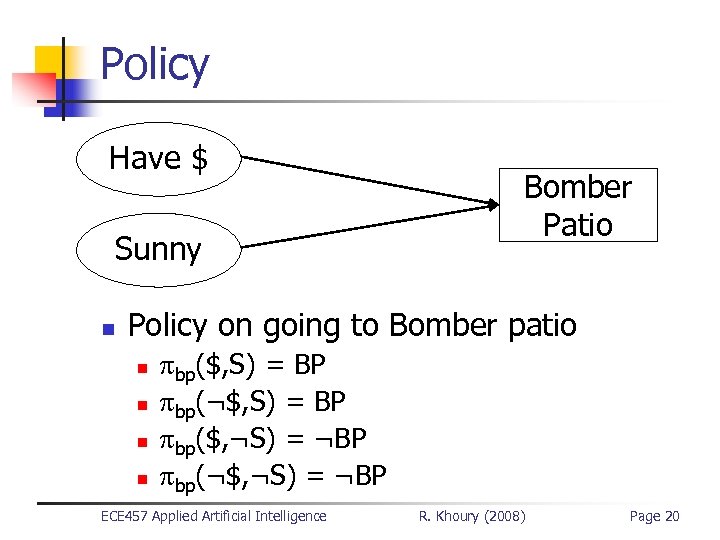 Policy Have $ Sunny n Bomber Patio Policy on going to Bomber patio n n bp($, S) = BP bp(¬$, S) = BP bp($, ¬S) = ¬BP bp(¬$, ¬S) = ¬BP ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 20
Policy Have $ Sunny n Bomber Patio Policy on going to Bomber patio n n bp($, S) = BP bp(¬$, S) = BP bp($, ¬S) = ¬BP bp(¬$, ¬S) = ¬BP ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 20
 Value of a Policy n n Expected utility if decisions are taken according to the policy EU( ) = x P(x) U(x, (x)) n n EU( bp) = $, s P($, S) U($, S, bp($, S)) Optimal policy * is the one with the highest expected utility n EU( *) EU( ) for all policies ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 21
Value of a Policy n n Expected utility if decisions are taken according to the policy EU( ) = x P(x) U(x, (x)) n n EU( bp) = $, s P($, S) U($, S, bp($, S)) Optimal policy * is the one with the highest expected utility n EU( *) EU( ) for all policies ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 21
 Computing the Optimal Policy n n Start from last decision node before utility For each combination of values of a node’s parents n n n Compute the expected utility of each decision Set policy as decision that maximises utility Work backward to the first decision in the network ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 22
Computing the Optimal Policy n n Start from last decision node before utility For each combination of values of a node’s parents n n n Compute the expected utility of each decision Set policy as decision that maximises utility Work backward to the first decision in the network ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 22
 Computing the Optimal Policy Sunny Bomber Patio Have $ n Compute the optimal policy for JF n n Run into friends Join your friends U For each combination of BP, RF and $, make a decision JF and compute U(JF, $) Set the policy as the max utility decision for each combination of BP and RF ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 23
Computing the Optimal Policy Sunny Bomber Patio Have $ n Compute the optimal policy for JF n n Run into friends Join your friends U For each combination of BP, RF and $, make a decision JF and compute U(JF, $) Set the policy as the max utility decision for each combination of BP and RF ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 23
 Computing the Optimal Policy Sunny Run into friends Bomber Patio Have $ n Compute the optimal policy for BP given JF(BP, RF) n n n Join your friends For each combination of S and $, make a decision BP, which will affect RF and JF JF is decided by optimal policy So we can compute U(JF, $) ECE 457 Applied Artificial Intelligence R. Khoury (2008) U Page 24
Computing the Optimal Policy Sunny Run into friends Bomber Patio Have $ n Compute the optimal policy for BP given JF(BP, RF) n n n Join your friends For each combination of S and $, make a decision BP, which will affect RF and JF JF is decided by optimal policy So we can compute U(JF, $) ECE 457 Applied Artificial Intelligence R. Khoury (2008) U Page 24
 Decision Network Example n n Bob wants to buy a used car. Unfortunately, the car he’s considering has a 50% chance of being a lemon. Before buying, he can decide to take the car to a mechanic to have it inspected. The mechanic will report if the car is good or bad, but he can make mistakes, and the inspection is expensive. Bob prefers owning a good car to not owning a car, and prefers that to owning a lemon. Should Bob have the car inspected first or not? ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 25
Decision Network Example n n Bob wants to buy a used car. Unfortunately, the car he’s considering has a 50% chance of being a lemon. Before buying, he can decide to take the car to a mechanic to have it inspected. The mechanic will report if the car is good or bad, but he can make mistakes, and the inspection is expensive. Bob prefers owning a good car to not owning a car, and prefers that to owning a lemon. Should Bob have the car inspected first or not? ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 25
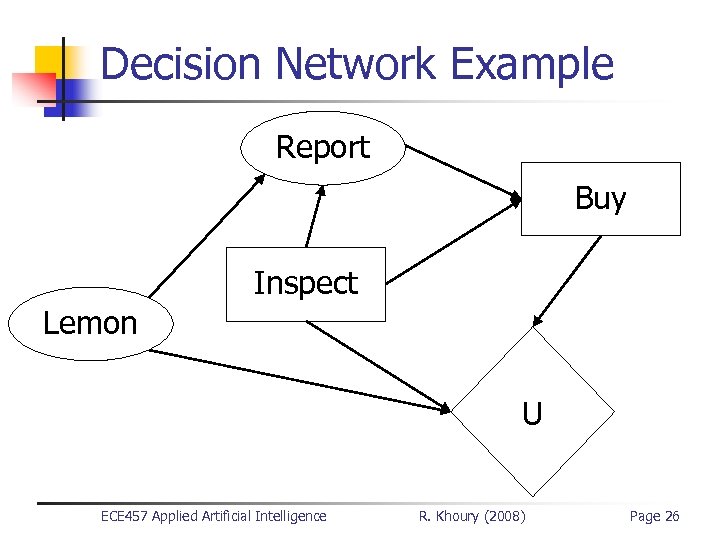 Decision Network Example Report Buy Inspect Lemon U ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 26
Decision Network Example Report Buy Inspect Lemon U ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 26
 Decision Network Example l F T F i F F T P(G) 0 0 0. 9 P(¬G) 0 0 0. 1 P(N) Utility cost of inspection = -50 1 1 l b 0 F F T T 0. 2 0. 8 0 Report Lemon Buy Inspect P(L) = 0. 5 ECE 457 Applied Artificial Intelligence U R. Khoury (2008) T F F T i F F F T F T T U -300 1000 -600 -350 950 -650 Page 27
Decision Network Example l F T F i F F T P(G) 0 0 0. 9 P(¬G) 0 0 0. 1 P(N) Utility cost of inspection = -50 1 1 l b 0 F F T T 0. 2 0. 8 0 Report Lemon Buy Inspect P(L) = 0. 5 ECE 457 Applied Artificial Intelligence U R. Khoury (2008) T F F T i F F F T F T T U -300 1000 -600 -350 950 -650 Page 27
 Decision Network Example n Compute EU of Buy and Not Buy given all combinations of evidence n n Select action with MEU given each case Compute EU of Inspect and Not Inspect given all combinations of evidence and then select Buy/Not Buy action n Decide on Inspect or Not Inspect, depending on MEU ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 28
Decision Network Example n Compute EU of Buy and Not Buy given all combinations of evidence n n Select action with MEU given each case Compute EU of Inspect and Not Inspect given all combinations of evidence and then select Buy/Not Buy action n Decide on Inspect or Not Inspect, depending on MEU ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 28
 Decision Network Example n Compute the expected utility of buying and not buying the car given the evidence n n The evidence is whether or not Bob got the car inspected, and what the result of the inspection is EU(b|i, r) = l P(l|b, i, r)U(b, i, l) ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 29
Decision Network Example n Compute the expected utility of buying and not buying the car given the evidence n n The evidence is whether or not Bob got the car inspected, and what the result of the inspection is EU(b|i, r) = l P(l|b, i, r)U(b, i, l) ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 29
 Decision Network Example n n n EU(B|¬I, N) = l P(l|B, ¬I, N)U(B, ¬I, l) EU(B|¬I, N) = P(L)U(B, L, ¬I) + P(¬L)U(B, ¬L, ¬I) EU(B|¬I, N) = 0. 5 * -600 + 0. 5 * 1000 EU(B|¬I, N) = 200 EU(¬B|¬I, N) = l P(l|¬B, ¬I, N)U(¬B, ¬I, l) EU(¬B|¬I, N) = P(L)U(¬B, L, ¬I) + P(¬L)U(¬B, ¬L, ¬I) EU(¬B|¬I, N) = 0. 5 * -300 + 0. 5 * -300 EU(¬B|¬I, N) = -300 Rational decision, if Bob doesn’t get the car inspected, is to buy it ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 30
Decision Network Example n n n EU(B|¬I, N) = l P(l|B, ¬I, N)U(B, ¬I, l) EU(B|¬I, N) = P(L)U(B, L, ¬I) + P(¬L)U(B, ¬L, ¬I) EU(B|¬I, N) = 0. 5 * -600 + 0. 5 * 1000 EU(B|¬I, N) = 200 EU(¬B|¬I, N) = l P(l|¬B, ¬I, N)U(¬B, ¬I, l) EU(¬B|¬I, N) = P(L)U(¬B, L, ¬I) + P(¬L)U(¬B, ¬L, ¬I) EU(¬B|¬I, N) = 0. 5 * -300 + 0. 5 * -300 EU(¬B|¬I, N) = -300 Rational decision, if Bob doesn’t get the car inspected, is to buy it ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 30
 Decision Network Example n n EU(B|I, G) = l P(l|B, I, G)U(B, I, l) We’re missing some information! n n From the network, we know P(L) and P(G|L), but not P(L|G) nor P(G) Compute P(G) using marginalization n n P(G) = P(G|L)P(L) + P(G|¬L)P(¬L) = 0. 55 Compute P(L|G) using Bayes’ Theorem n n P(L|G) = P(G|L)P(L)/P(G) = 0. 18 P(¬L|G) = P(G|¬L)P(¬L)/P(G) = 0. 82 ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 31
Decision Network Example n n EU(B|I, G) = l P(l|B, I, G)U(B, I, l) We’re missing some information! n n From the network, we know P(L) and P(G|L), but not P(L|G) nor P(G) Compute P(G) using marginalization n n P(G) = P(G|L)P(L) + P(G|¬L)P(¬L) = 0. 55 Compute P(L|G) using Bayes’ Theorem n n P(L|G) = P(G|L)P(L)/P(G) = 0. 18 P(¬L|G) = P(G|¬L)P(¬L)/P(G) = 0. 82 ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 31
 Decision Network Example n n n EU(B|I, G) = l P(l|B, I, G)U(B, I, l) EU(B|I, G) = P(L|G)U(B, L, I) + P(¬L|G)U(B, ¬L, I) EU(B|I, G) = 0. 18 * -650 + 0. 82 * 950 EU(B|I, G) = 662 EU(¬B|I, G) = l P(l|¬B, I, G)U(¬B, I, l) EU(¬B|I, G) = P(L|G)U(¬B, L, I) + P(¬L|G)U(¬B, ¬L, I) EU(¬B|I, G) = 0. 18 * -350 + 0. 82 * -350 EU(¬B|I, G) = -350 Rational decision, if Bob gets the car inspected and the report says it’s good, is to buy it ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 32
Decision Network Example n n n EU(B|I, G) = l P(l|B, I, G)U(B, I, l) EU(B|I, G) = P(L|G)U(B, L, I) + P(¬L|G)U(B, ¬L, I) EU(B|I, G) = 0. 18 * -650 + 0. 82 * 950 EU(B|I, G) = 662 EU(¬B|I, G) = l P(l|¬B, I, G)U(¬B, I, l) EU(¬B|I, G) = P(L|G)U(¬B, L, I) + P(¬L|G)U(¬B, ¬L, I) EU(¬B|I, G) = 0. 18 * -350 + 0. 82 * -350 EU(¬B|I, G) = -350 Rational decision, if Bob gets the car inspected and the report says it’s good, is to buy it ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 32
 Decision Network Example n n n EU(B|I, ¬G) = l P(l|B, I, G)U(B, I, l) EU(B|I, ¬G) = P(L| G)U(B, L, I) + P(¬L| G)U(B, ¬L, I) EU(B|I, ¬G) = 0. 89 * -650 + 0. 11 * 950 EU(B|I, ¬G) = -474 EU(¬B|I, ¬G) = l P(l|¬B, I, ¬G)U(¬B, I, l) EU(¬B|I, ¬G) = P(L|¬G)U(¬B, L, I) + P(¬L|¬G)U(¬B, ¬L, I) EU(¬B|I, ¬G) = 0. 89 * -350 + 0. 11 * -350 EU(¬B|I, ¬G) = -350 Rational decision, if Bob gets the car inspected and the report says it’s not good, is to not buy it ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 33
Decision Network Example n n n EU(B|I, ¬G) = l P(l|B, I, G)U(B, I, l) EU(B|I, ¬G) = P(L| G)U(B, L, I) + P(¬L| G)U(B, ¬L, I) EU(B|I, ¬G) = 0. 89 * -650 + 0. 11 * 950 EU(B|I, ¬G) = -474 EU(¬B|I, ¬G) = l P(l|¬B, I, ¬G)U(¬B, I, l) EU(¬B|I, ¬G) = P(L|¬G)U(¬B, L, I) + P(¬L|¬G)U(¬B, ¬L, I) EU(¬B|I, ¬G) = 0. 89 * -350 + 0. 11 * -350 EU(¬B|I, ¬G) = -350 Rational decision, if Bob gets the car inspected and the report says it’s not good, is to not buy it ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 33
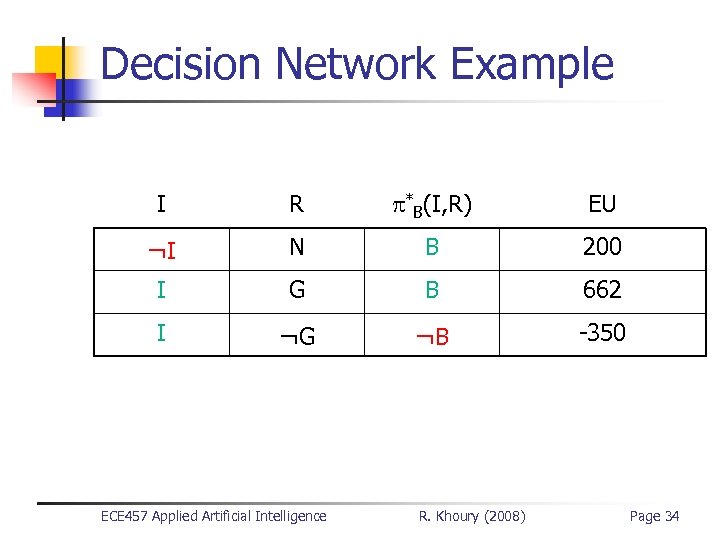 Decision Network Example I R *B(I, R) EU ¬I N B 200 I G B 662 I ¬G ¬B -350 ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 34
Decision Network Example I R *B(I, R) EU ¬I N B 200 I G B 662 I ¬G ¬B -350 ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 34
 Decision Network Example n n Should Bob get the car inspected? EU(i) = l, r P(l, r|i)U(l, i, b) P(l, r|i) = P(r|l, i)P(l) EU(i) = l, r P(r|l, i)P(l)U(l, i, b) ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 35
Decision Network Example n n Should Bob get the car inspected? EU(i) = l, r P(l, r|i)U(l, i, b) P(l, r|i) = P(r|l, i)P(l) EU(i) = l, r P(r|l, i)P(l)U(l, i, b) ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 35
 Decision Network Example n n EU(i) = l, r P(r|l, i)P(l)U(l, i, b) EU(¬I) = P(N|L, ¬I)P(L)U(L, ¬I, B) + P(N|¬L, ¬I)P(¬L)U(¬L, ¬I, B) EU(¬I) = 1 * 0. 5 * -600 + 1 * 0. 5 * 1000 EU(¬I) = 200 ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 36
Decision Network Example n n EU(i) = l, r P(r|l, i)P(l)U(l, i, b) EU(¬I) = P(N|L, ¬I)P(L)U(L, ¬I, B) + P(N|¬L, ¬I)P(¬L)U(¬L, ¬I, B) EU(¬I) = 1 * 0. 5 * -600 + 1 * 0. 5 * 1000 EU(¬I) = 200 ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 36
 Decision Network Example n n EU(i) = l, r P(r|l, i)P(l)U(l, i, b) EU(I) = P(G|L, I)P(L)U(L, I, B) + P(G|¬L, I)P(¬L)U(¬L, I, B) + P(¬G|L, I)P(L)U(L, I, ¬B) + P(¬G|¬L, I)P(¬L)U(¬L, I, ¬B) EU(I) = 0. 2 * 0. 5 * -650 + 0. 9 * 0. 5 * 950 + 0. 8 * 0. 5 * -350 + 0. 1 * 0. 5 * -350 EU(I) = 205 ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 37
Decision Network Example n n EU(i) = l, r P(r|l, i)P(l)U(l, i, b) EU(I) = P(G|L, I)P(L)U(L, I, B) + P(G|¬L, I)P(¬L)U(¬L, I, B) + P(¬G|L, I)P(L)U(L, I, ¬B) + P(¬G|¬L, I)P(¬L)U(¬L, I, ¬B) EU(I) = 0. 2 * 0. 5 * -650 + 0. 9 * 0. 5 * 950 + 0. 8 * 0. 5 * -350 + 0. 1 * 0. 5 * -350 EU(I) = 205 ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 37
 Decision Network Example n n n EU(I) = 205 > EU(¬I) = 200 Therefore, Bob should get the car inspected * = { *B(I, R) , *I } *I EU I R *B(I, R) EU I 205 ¬I N B 200 I I G B ¬G ¬B 662 -350 ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 38
Decision Network Example n n n EU(I) = 205 > EU(¬I) = 200 Therefore, Bob should get the car inspected * = { *B(I, R) , *I } *I EU I R *B(I, R) EU I 205 ¬I N B 200 I I G B ¬G ¬B 662 -350 ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 38
 Value of Information n n Utility of decision without inspection is 200 Utility of decision with inspection is 205, utility of the decision minus the utility cost of the inspection n n Utility of decision is 255 At what point is the utility cost of the inspection too high? n n 255 – Utility Cost < 200 Value of the information gained from the inspection is 55 ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 39
Value of Information n n Utility of decision without inspection is 200 Utility of decision with inspection is 205, utility of the decision minus the utility cost of the inspection n n Utility of decision is 255 At what point is the utility cost of the inspection too high? n n 255 – Utility Cost < 200 Value of the information gained from the inspection is 55 ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 39
 Value of Information n Information has value if n n n It causes a change in the decision The new decision has higher utility than the old one The value is n n n Non-negative Zero for irrelevant facts Zero for information already known ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 40
Value of Information n Information has value if n n n It causes a change in the decision The new decision has higher utility than the old one The value is n n n Non-negative Zero for irrelevant facts Zero for information already known ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 40
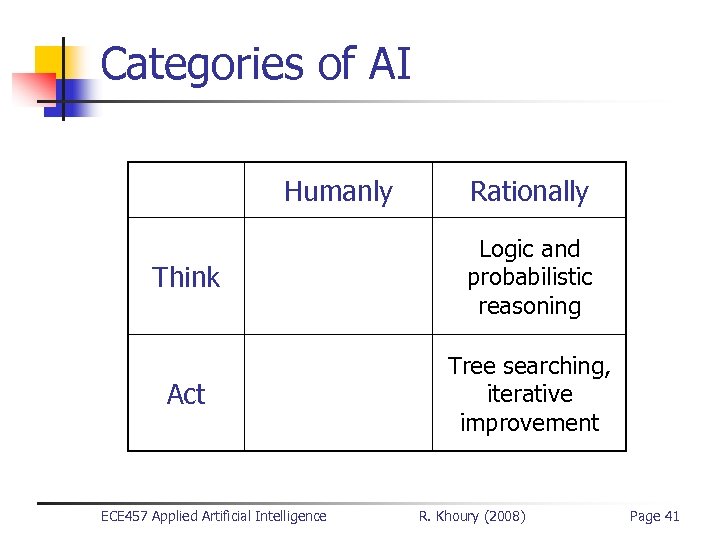 Categories of AI Humanly Rationally Think Logic and probabilistic reasoning Act Tree searching, iterative improvement ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 41
Categories of AI Humanly Rationally Think Logic and probabilistic reasoning Act Tree searching, iterative improvement ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 41
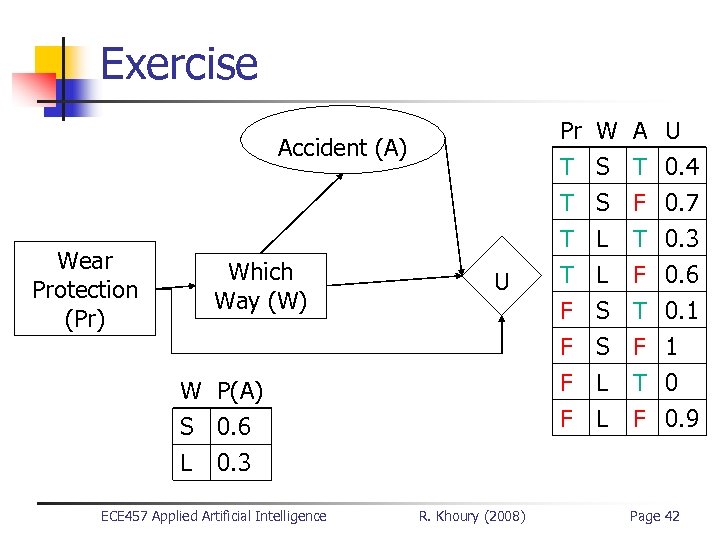 Exercise Pr T T T Accident (A) Wear Protection (Pr) Which Way (W) U W P(A) S 0. 6 L 0. 3 ECE 457 Applied Artificial Intelligence R. Khoury (2008) W S S L A T F T U 0. 4 0. 7 0. 3 T F F L S S L L F T F 0. 6 0. 1 1 0 0. 9 Page 42
Exercise Pr T T T Accident (A) Wear Protection (Pr) Which Way (W) U W P(A) S 0. 6 L 0. 3 ECE 457 Applied Artificial Intelligence R. Khoury (2008) W S S L A T F T U 0. 4 0. 7 0. 3 T F F L S S L L F T F 0. 6 0. 1 1 0 0. 9 Page 42
 Exercise n Which way to go if you wear protection? n n n EU( S | Pr ) = P(A|S) * U(Pr, S, A) + P(~A|S) * U(Pr, S, ~A) EU( S | Pr ) = 0. 6 * 0. 4 + 0. 4 * 0. 7 EU( S | Pr ) = 0. 52 EU( L | Pr ) = P(A|L) * U(Pr, L, A) + P(~A|L) * U(Pr, L, ~A) EU( L | Pr ) = 0. 3 * 0. 3 + 0. 7 * 0. 6 EU( L | Pr ) = 0. 51 Rational decision, if you wear protection, is to go the short way ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 43
Exercise n Which way to go if you wear protection? n n n EU( S | Pr ) = P(A|S) * U(Pr, S, A) + P(~A|S) * U(Pr, S, ~A) EU( S | Pr ) = 0. 6 * 0. 4 + 0. 4 * 0. 7 EU( S | Pr ) = 0. 52 EU( L | Pr ) = P(A|L) * U(Pr, L, A) + P(~A|L) * U(Pr, L, ~A) EU( L | Pr ) = 0. 3 * 0. 3 + 0. 7 * 0. 6 EU( L | Pr ) = 0. 51 Rational decision, if you wear protection, is to go the short way ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 43
 Exercise n Which way to go if you don’t wear protection? n n n EU( S | ~Pr ) = P(A|S) * U(~Pr, S, A) + P(~A|S) * U(~Pr, S, ~A) EU( S | ~Pr ) = 0. 6 * 0. 1 + 0. 4 * 1 EU( S | ~Pr ) = 0. 46 EU( L | ~Pr ) = P(A|L) * U(~Pr, L, A) + P(~A|L) * U(~Pr, L, ~A) EU( L | ~Pr ) = 0. 3 * 0 + 0. 7 * 0. 9 EU( L | ~Pr ) = 0. 63 Rational decision, if you don’t wear protection, is to go the long way ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 44
Exercise n Which way to go if you don’t wear protection? n n n EU( S | ~Pr ) = P(A|S) * U(~Pr, S, A) + P(~A|S) * U(~Pr, S, ~A) EU( S | ~Pr ) = 0. 6 * 0. 1 + 0. 4 * 1 EU( S | ~Pr ) = 0. 46 EU( L | ~Pr ) = P(A|L) * U(~Pr, L, A) + P(~A|L) * U(~Pr, L, ~A) EU( L | ~Pr ) = 0. 3 * 0 + 0. 7 * 0. 9 EU( L | ~Pr ) = 0. 63 Rational decision, if you don’t wear protection, is to go the long way ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 44
 Exercise n Given the decision on which way to go, should we wear protection? n n n EU( Pr ) = P(A|S) * U(Pr, S, A) + P(~A|S) * U(Pr, S, ~A) EU( Pr ) = 0. 6 * 0. 4 + 0. 4 * 0. 7 EU( Pr ) = 0. 52 EU( ~Pr ) = P(A|L) * U(~Pr, L, A) + P(~A|L) * U(~Pr, L, ~A) EU( ~Pr ) = 0. 3 * 0 + 0. 7 * 0. 9 EU( ~Pr ) = 0. 63 Rational decision is to not wear protection n And therefore go the long way ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 45
Exercise n Given the decision on which way to go, should we wear protection? n n n EU( Pr ) = P(A|S) * U(Pr, S, A) + P(~A|S) * U(Pr, S, ~A) EU( Pr ) = 0. 6 * 0. 4 + 0. 4 * 0. 7 EU( Pr ) = 0. 52 EU( ~Pr ) = P(A|L) * U(~Pr, L, A) + P(~A|L) * U(~Pr, L, ~A) EU( ~Pr ) = 0. 3 * 0 + 0. 7 * 0. 9 EU( ~Pr ) = 0. 63 Rational decision is to not wear protection n And therefore go the long way ECE 457 Applied Artificial Intelligence R. Khoury (2008) Page 45


