Deciding Primality is in P M Agrawal N

Deciding Primality is in P M. Agrawal, N. Kayal, N. Saxena Slides by Adi Akavia

Background • Sieve of Eratosthenes 240 BC - (n) • Fermat’s Little Theorem (17 th century): p is prime, a 0 (mod p) ap-1 1 (mod p) (The converse does not hold – Carmichael numbers) • Polynomial-time algorithms: – [Miller 76] deterministic, assuming Extended Riemann Hypothesis. – [Solovay, Strassen 77; Rabin 80] unconditional, but randomized. – [Goldwasser, Kilian 86] randomized produces certificate for primality! (expected poly time for almost all inputs) – [Adelman Huang 92] primality certificate for all numbers. • [Adelman, Pomerance, Rumely 83] deterministic (log n)O(log log n)-time.

This Paper Algo for deciding primality which is: • unconditional, • deterministic, • polynomial-time

Special Numbers • Def: r is special with respect to n if: 1. r is prime, 2. r-1 has a large prime factor q = (r 2/3) , and Def: order n mod r, denoted Or(n), is the smallest power t s. t. nt 1 (mod r). 3. q|Or(n). • Tools: – simple algebra – High density Thm for numbers with properties (1) and (2). [Fou 85, BH 96]

Basic Idea • Fact: For any a s. t (a, n) =1: – n is prime (x-a)n xn-a (mod n) – n is composite (x-a)n xn-a (mod n) Proof: Develop (x-a)n according to Newton-binomial. n Assume n is prime, then n Assume n is composite, then let q|n, let qk||n, then and , hence xq has non zero coefficient (mod n). • Naive algo: Pick an arbitrary a, check if (x-a)n xn-a (mod n) • Problem: time complexity - (n).

Basic Idea • Idea: Pick an arbitrary a, and some polynomial xr-1, with r = poly (log n), check if (x-a)n xn-a (mod xr-1, n) – time complexity – poly(r) – n is prime (x-a)n xn-a (mod xr-1, n) – n is composite ? ? (x-a)n xn-a (mod xr-1, n) Not true for some (few) values of a, r !

Improved Idea • Improved Idea: Pick many (poly log n) a’s, check for all of them if: (x-a)n xn-a (mod xr-1, n) Accept if equality holds for all a’s

Some Algebra Reminders Def: Fp (p is prime) denotes the finite field of p elements {0, 1, …, p-1}. Def: Fp[x] denotes the ring of polynomials over Fp. Let f(x) be a k-degree polynomial. Def: Fp[x]/f(x) denotes the set of k-1 -degree polynomials over Fp, with addition and multiplication modulo f(x). Thm: If f(x) is irreducible over Fp, then Fp[x]/f(x) GF(pk) (the unique field with pk elements. )

Fp[x]/f(x) - Addition • Let the polynomial f(x) over F 2 be: • Represent polynomials as vectors (k-1 degree polynomial vector of k coefficient): • Addition:

Fp[x]/f(x) - Multiplication: • First, multiply ‘mod p’: • Next, apply ’mod f(x)’:

Fp[x]/f(x) - mod f(x) • Example: • In general for f(x) = xr-1:

Irreducible Factors of (xr-1)/(x-1) • Fact: Consider the polynomial (xr-1)/(x 1) over Fp. All its irreducible factors are of degree Or(p)

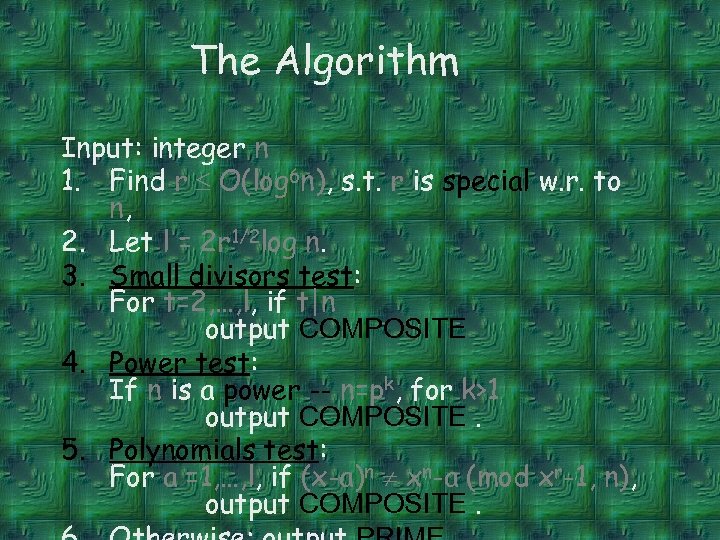The Algorithm Input: integer n 1. Find r O(log 6 n), s. t. r is special w. r. to n, 2. Let l = 2 r 1/2 log n. 3. Small divisors test: For t=2, …, l, if t|n output COMPOSITE 4. Power test: If n is a power -- n=pk, for k>1 output COMPOSITE. 5. Polynomials test: For a =1, …, l, if (x-a)n xn-a (mod xr-1, n), output COMPOSITE.

1. 2. 3. Saw: algorithm 4. 5. 6. Find r O(log 6 n), s. t. r is special, Let l = 2 r 1/2 log n. If exists a small ( < l+1) divisor, output COMPOSITE If n is a power, output COMPOSITE. For a = 1, …, l, if (x-a)n xn-a (mod xr-1, n), output COMPOSITE. Otherwise output PRIME. Yet to be seen: • Special r O(log 6 n) exists (later) • If n is composite then one of the tests returns COMPOSITE.

Algo’s Correctness 1. 2. 3. Thm: n is composite 4. algo returns ‘composite’. 5. That is, • If n is composite, and – n has no divisor t l, and 6. – n is not a (prime) power Find r O(log 6 n), s. t. r is special, Let l = 2 r 1/2 log n. If exists a small ( < l+1) divisor, output COMPOSITE If n is a power, output COMPOSITE. For a = 1, …, l, if (x-a)n xn-a (mod xr-1, n), output COMPOSITE. Otherwise output PRIME. • then a [1. . l] s. t. (x-a)n xn-a (mod xr-1, n)

For Proof Purpose – Use p and h(x) • Let p be a prime factor of n, and let h(x) be an irreducible factor of xr-1, • Suffices to show inequality (mod h(x), p) instead of: (mod xr-1, n), i. e. a [1. . l] s. t. (x-a)n xn-a (mod h(x), p) • Choose p and h(x) s. t. – q|Or(p), and Such p exists: r(p) – deg(h(x)) = O q|Or(n) and Or(n) | lcm{Or(pi)}, where n=p 1 p 2…pk. Such h(x) exists: by previous fact.

Proof • Assume by contradiction that n is composite, and passes all the tests, i. e. – n has no small factor, and – n is not a (prime) power, and – a [1. . l] (x-a)n xn-a (mod h(x), p), • For any f(x), which is a multiple of polynomials (x-a) (where a [1. . l]), f(x)n=f(xn). – Example: f(x)=(x-a 1)(x-a 2) [(x-a 1)(x-a 2)]n = (xn-a 1) (xn-a 2)

Find small special r Small divisors test – composite 3. Power test – composite f(x) G, test Therefore, consider 4. if. Polynomialsf(x)n – f(xn) the group generated composite 5. Otherwise - PRIME. by {(x-a)} : Variation on Polynomials test • 1. 2. a [1. . l] • Prop: n passes the polynomials test f(x) G, f(x)n f(xn) • Proof: Recall, the polynomials test was: a=1, …, l, check if (x-a)n xn-a r

Defining I • Are there other integers m s. t. f(x) G, f(x)m f(xm) ? • Yes! For example: p, 1. • Any others? • Let I = { m | f G, f(x)m f(xm) }. • What’s Ahead: – We first prove that I [|G|] is small. – However, we show that if n is composite which passes all the tests then I [|G|] must be large. – Thus obtaining a contradiction.

I [|G|] is small • Lemma: Let m 1, m 2 I, then m 1 m 2 (mod |G|) m 1 m 2 (mod r) • Proof: Let g(x) be a generator of G. Let m 2=m 1+kr. • (*) m 1 m 2 (mod r), then xm 1 xm 2 (mod h(x)) (as xr 1 (mod h(x))) • Therefore:

I [|G|] is large • First note that |G| is large. • Lemma: • Proof: Let d=deg(h(x)). Consider all polynomials in G of degree

I [|G|] is large – cont. • Recall: – p, 1 I and – n passes the polynomials test n I • Lemma: I is multiplicative, i. e. u, v I uv I. • Hence, in particular {nipj : 0 ≤ i, j ≤ r 1/2} I. • Therefore, • Hence (since )

Proof Summary • We saw that I [|G|] is small (unconditionally, using properties of xr-1), • However, if n is composite, has no small divisors, and it is not a prime power, then passing the polynomials test (i. e. n I) implies that I [|G|] is large. (using properties of the special r and of xr 1) • Therefore, the polynomials test must

Back to Special Numbers • Recall: r is special with respect to n if: 1. r is prime, 2. r-1 has a large prime factor q = (r 2/3) 3. q|Or(n).

Finding Special r Elaborating on step (1): 1. while r < c log 6 n 1. 2. 3. 4. 5. Find r O(log 6 n), s. t. r is special, Let l = 2 r 1/2 log n. If exists a small ( < l+1) divisor, output COMPOSITE If n is a power, output COMPOSITE. For a = 1, …, l, if (x-a)n xn-a (mod xr-1, n), output COMPOSITE. Otherwise output PRIME. 1. if r is prime 2. let q be the largest 6. prime factor of r-1 3. if (q 4 r 1/2 log n) and (n(r-1)/q 1 (mod r)) • when ‘break’ is reached: break; r is prime, q is large, and 4. r r+1 q|O (n) r Complexity: O(log 6 n) iterations, each taking: O(r 1/2 poly log r), hence total poly log n.

Special r O(log 6 n) exists • Consider interval [. . ], , =O(log 6 n). Recall: r is special with respect to n if: 1. r is prime, 2. q = (r 2/3) prime factor of r-1, 3. q|Or(n). • Numbers with properties (1) and (2) are dense in [. . ] – immediate from density bounds for numbers with these properties and for primes. • For many primes r [. . ], property (3) holds. – For many r’s Or(n) > 1/3: Or(n) < 1/3 r | =(n-1)(n 2 -1). . . (n^ 1/3 -1). However, has no more than 2/3 log n prime divisors. – Moreover, Or(n) > 1/3 q | Or(n): if q doesn’t divide Or(n), then n(r-1)/q 1, therefore Or(n) (r-1)/q. However (r-1)/q < 1/3 -- a contradiction. (here we utilize again the fact that q is large). • Hence, by counting argument, exists a special r [. . ].

The End

Title

Slide Title