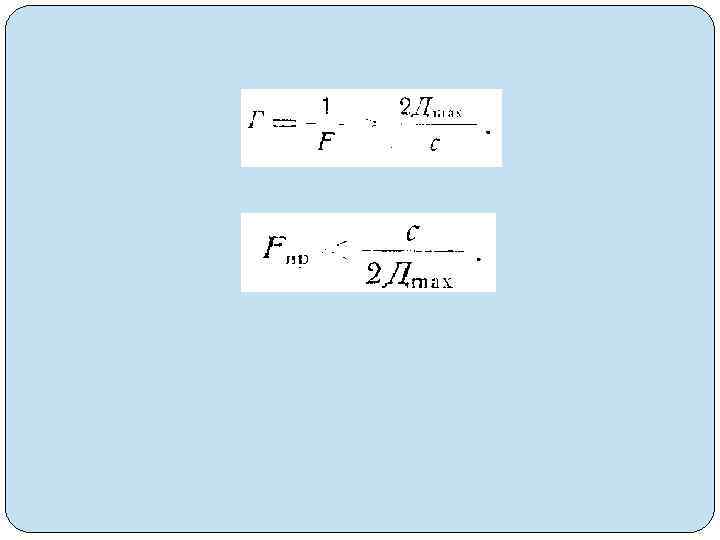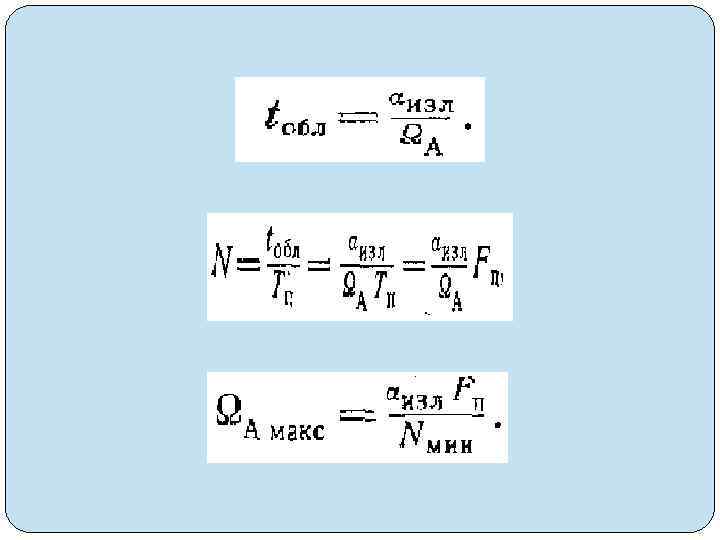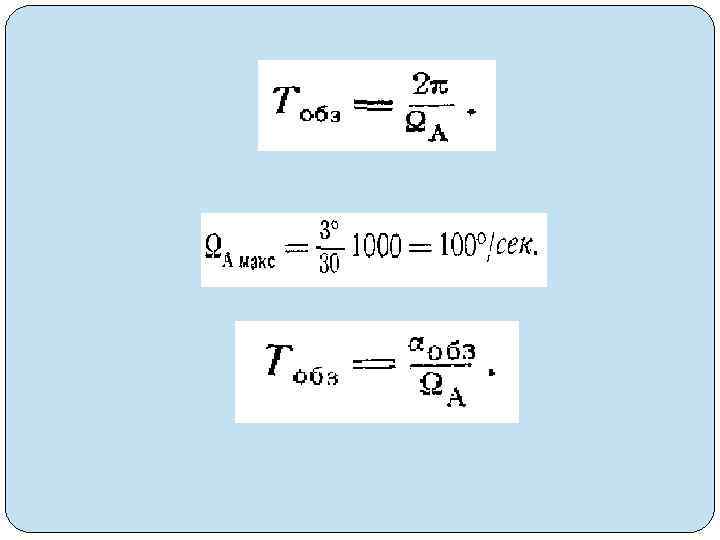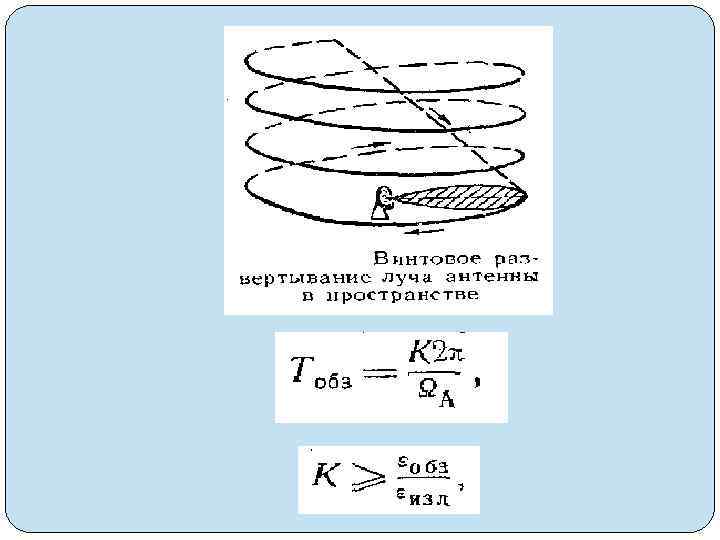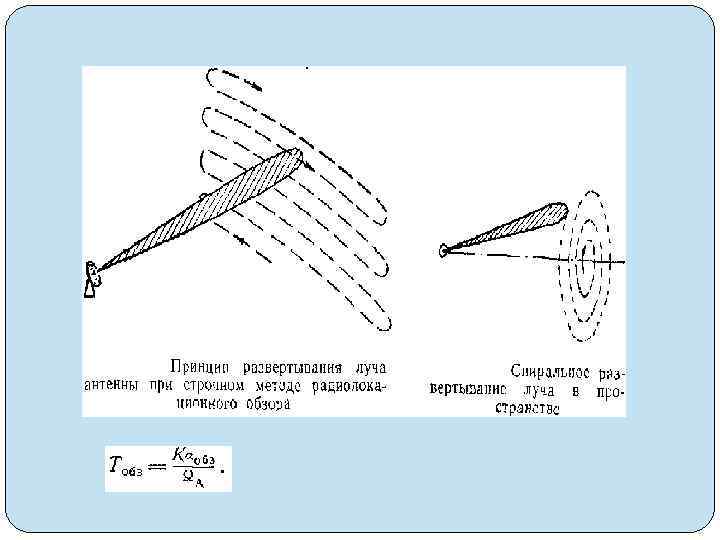
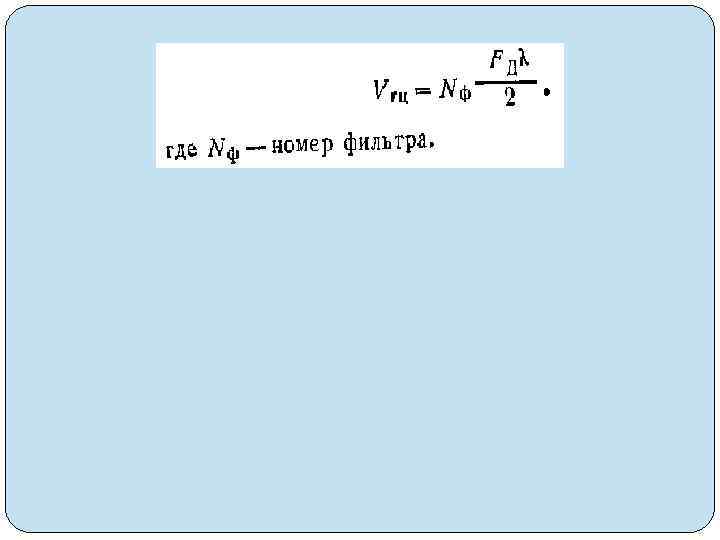
Dц. макс = =с. Тп/2
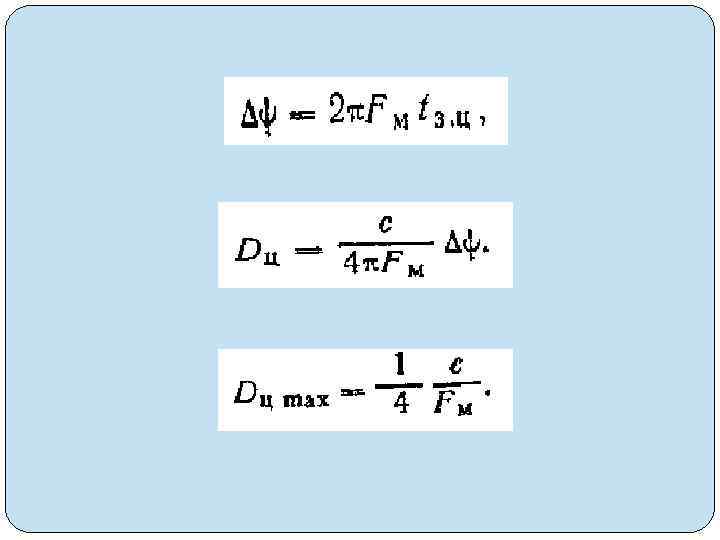
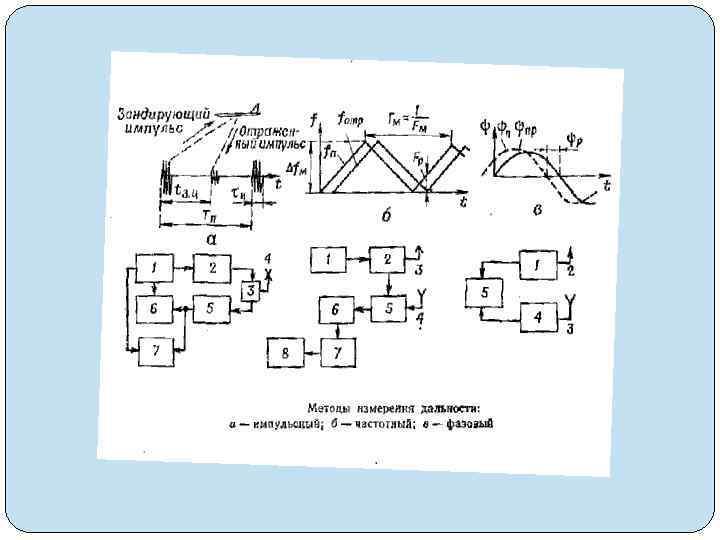
Uco = KΔt Uco = F(Δt) S=d. Uco/dt
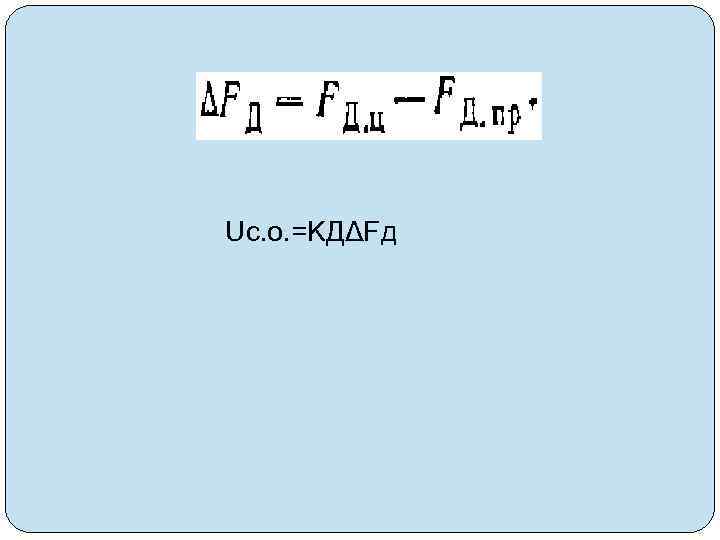Uc. o. =KДΔFд
Направленные свойства антенны позволяют установить связь между амплитудой выходного напряжения приемника Uт и направлением приема радиоволн (азимутом ά и углом места β). Выявить эту связь можно измерением амплитуд или фаз сигналов, принимаемых с раз личных направлений. Соответственно методы радиопеленгации разде ляются на амплитудные и фазовые. Из них к амплитудным относятся методы максимума, минимума и сравнения. Радиопеленгаторы, подобно радиодальномерам, классифицируют ся следующим образом: а) одноканальные или многоканальные; б) с неследящим или следящим измерителем; в) с аналоговой или цифровой системой измерителя. Для радиопеленгации вид модуляции не имеет существенного значения, так как от этого не зависит направленность антенны.
1. Метод максимума. В процессе обзора пространства силовой привод вращает антенну (рис. 3. 22, а), а угол поворота ее диаграммы направленности (ДН) контролируется указателем. Принимаемые ан тенной сигналы поступают в приемник, выход которого подключен к измерителю, например к ЭЛТ. По показаниям измерительного при бора можно построить характеристику (рис. 3. 22, б): Um = Umm. F(a) (3. 31) где Umm максимальная амплитуда выходного напряжения приемника; F (а)— нормированная диаграмма направленности антенны, которая показывает, какую часть от Umm составляет амплитуда вы ходного напряжения приемника Um при данном направлении ά мак симума диаграммы.
Если одна и та же антенна используется для передачи и приема, то амплитуда сигнала дважды умножается на функцию направлен ности антенны и в уравнение характеристики вводится F 2 (а) вместо F (а). Ширина этой характеристики имеет большое практическое зна чение, так как она определяет потенциальные (предельные) возможности метода пеленгации. Луч антенны, вращаясь, набегает на цель, затем удаляется от нее. Амплитуда отметки цели на экране ЭЛТ соответственно возрастает и понижается (рис. 3. 22, в). Наибольшая высота отметки Uтт получается при совпадении максимума диаграммы с направлением на цель, и тогда оператор считывает угловую координату цели ац по шкале указателя угла а (см. рис. 3. 22, а, б). Как видно из рис. 3. 22, б, приращения угловой координаты вызывают тем меньшие приращения амплитуды принимаемого сигнала, чем ближе направление на цель к направлению максимума функции направленности антенны. Например, изменение амплитуды ΔU'm у вершины характеристики намного меньше, чем ΔU''m (на скате характеристики), несмотря на то, что они вызваны одинаковыми приращениями угла (Δά' = Δά"). В таких условиях, даже при отчетливом различении сигнала и помех, среднеквадратическая потенциальная погрешность пеленга σάп составляет довольно значительную величину —(0, 1— 0, 25) ширины диаграммы направленности антенны на уровне половинной мощности 2φ0, 5: σάп = (0, 1— 0, 25) 2φ0, 5 (3. 32)
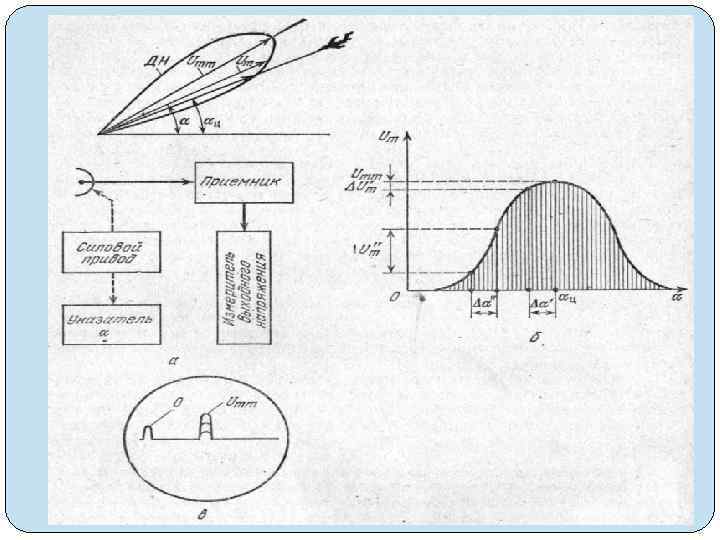
Ширина ДН 2φ0, 5 определяет потенциальную разрешающую способность по угловой координате Δάмин п , так как раздельная пеленгация двух целей возможна, если только одна цель облучается значительно, а другая в это время весьма незначительно или совсем не облучается: Δάмин п = 2φ0, 5 (3. 33) Метод максимума отличается простотой измерений пеленга и максимально возможным уровнем сигнала, в связи с чем он нашел применение в РЛС, рассчитанных на большую дальность обнаружения целей при низкой точности измерения координат, а также в РЛС с остронаправленными антеннами.
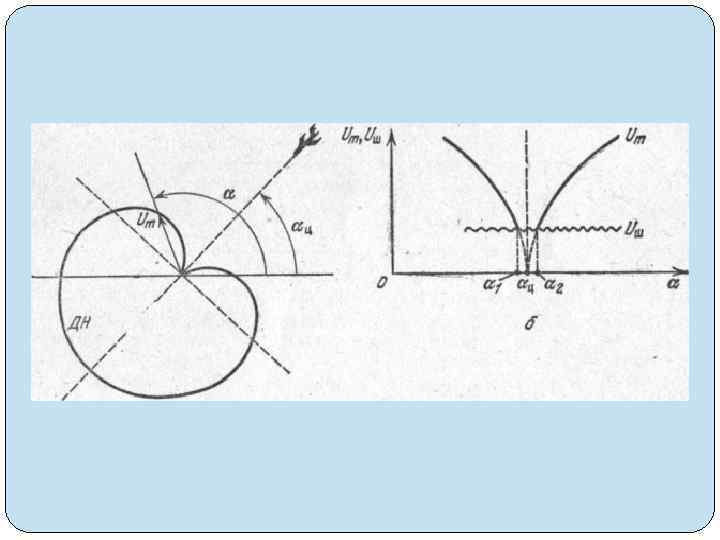
2. Метод минимума Метод означает, что пеленг цели считывается тогда, когда с направлением на цель совпадает минимум ДН антенны (рис. 3. 23, а). Для этого пригодны антенны с ярко выраженным минимумом диаг раммы направленности, например с показанной на рисунке диаграммой в форме кардиоиды. Так как на выходе приемника всегда имеется напряжение помех UШ то выявить нулевой сигнал невозможно (рис. 3. 23, б). В таких условиях пеленг вычисляют как среднее арифметическое двух ближайших углов ά 1, ά 2, при которых сигнал выделяется на фоне помех: άц= (ά 1+ ά 2)/2.
