93eed532090791d4fb723853ad6c6f46.ppt
- Количество слайдов: 77

DB Seminar Schedule n Seminar Schedule ================================= Chui Chun Kit 30/11/07 Gong Jian Jim 7/12/07 Loo Kin Kong 14/12/07 Ngai Wang Kay Jackie 21/12/07 Siu Wing Yan Angela 4/1/08 Tam Ming Wai 11/1/08 Tsang Pui Kwan Smith 18/1/08 U Leong Hou Kamiru 25/1/08 Wong Wai Kit 1/2/08 Cui Yingjie Jason 15/2/08 LEE King For 22/2/08 Lin Zhifeng Arthur 7/3/08 Yuan Wenjun Clement 14/3/08 Zhang Shiming Simon 28/3/08 Zhang Yiwei Kelvin 11/4/08 LEE Yau Tat 18/4/08 Pan Guodong Delvin 25/4/08 n Please send the abstract to dbgroup@cs. hku. hk one week before your talk

Refreshing the Sky: The Compressed Skycube with Efficient Support for Frequent Updates Authors : Tian Xia, Donghui Zhang Northeastern University Published in : SIGMOD 2006 Presenter : Chun-Kit Chui (Kit)

Presentation Outline n Introduction ¨ What is skylines? ¨ Motivation for subspace ¨ Skycube. n n n skyline queries. Compressed skycube (CSC) How to use the compressed skycube to answer skyline queries? How to handle object updates in compressed skycube? Experimental evaluation Conclusion

Introduction What is skyline?

What is skyline? n Skyline query: Find the hotels with both low price and close to the beach. Hotels in Hawaii t 1 Price 3 Dist. To Beach 2 t 3 4 9 7 5 t 4 t 5 t 6 t 7 9 2 6 1 1 3 1 4 Ranked the price of the hotels (the smaller the cheaper). Ranked the distance of the hotel to the beach (the smaller the closer).
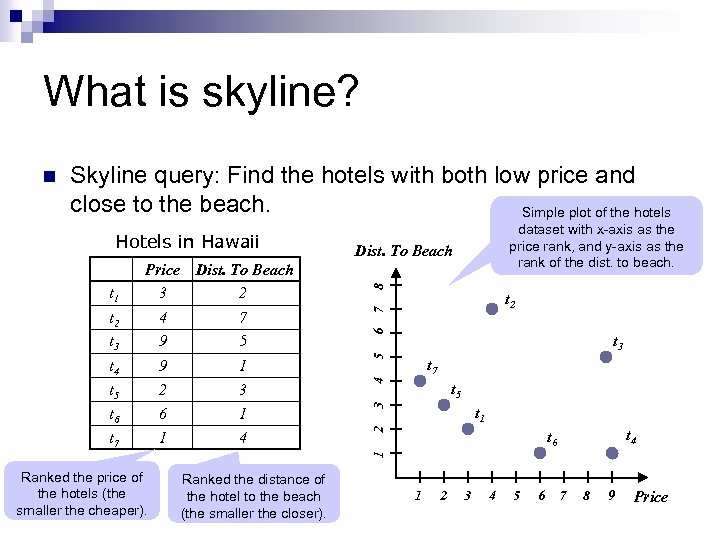
What is skyline? n Skyline query: Find the hotels with both low price and close to the beach. Simple plot of the hotels Dist. To Beach 2 t 3 4 9 7 5 t 4 t 5 t 6 t 7 9 2 6 1 1 3 1 4 t 2 7 t 1 Price 3 8 Dist. To Beach 6 Hotels in Hawaii dataset with x-axis as the price rank, and y-axis as the rank of the dist. to beach. 5 t 3 4 t 7 3 t 5 2 t 1 t 4 1 t 6 Ranked the price of the hotels (the smaller the cheaper). Ranked the distance of the hotel to the beach (the smaller the closer). 1 2 3 4 5 6 7 8 9 Price
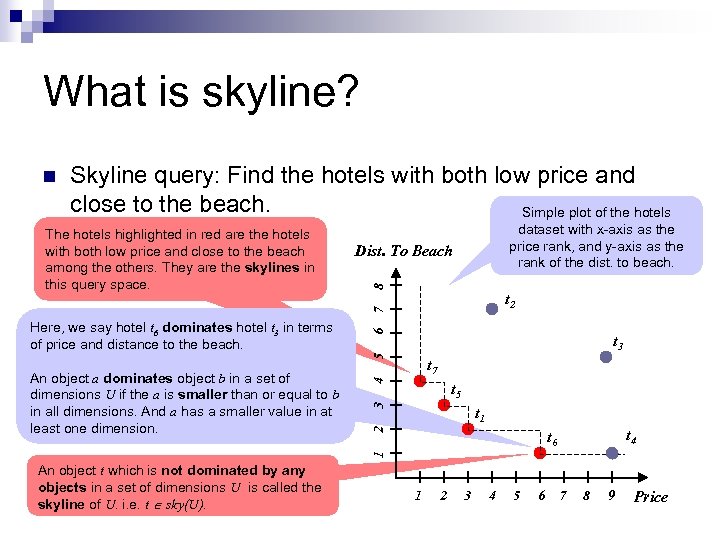
What is skyline? Skyline query: Find the hotels with both low price and close to the beach. Simple plot of the hotels dataset with x-axis as the price rank, and y-axis as the rank of the dist. to beach. Dist. To Beach t 2 t 3 5 Here, we say hotel t 6 dominates hotel t 3 in terms of price and distance to the beach. 6 7 The hotels highlighted in red are the hotels with both low price and close to the beach among the others. They are the skylines in this query space. 8 n 4 t 7 3 t 5 2 t 1 t 4 t 6 1 An object a dominates object b in a set of dimensions U if the a is smaller than or equal to b in all dimensions. And a has a smaller value in at least one dimension. An object t which is not dominated by any objects in a set of dimensions U is called the skyline of U. i. e. t sky(U). 1 2 3 4 5 6 7 8 9 Price
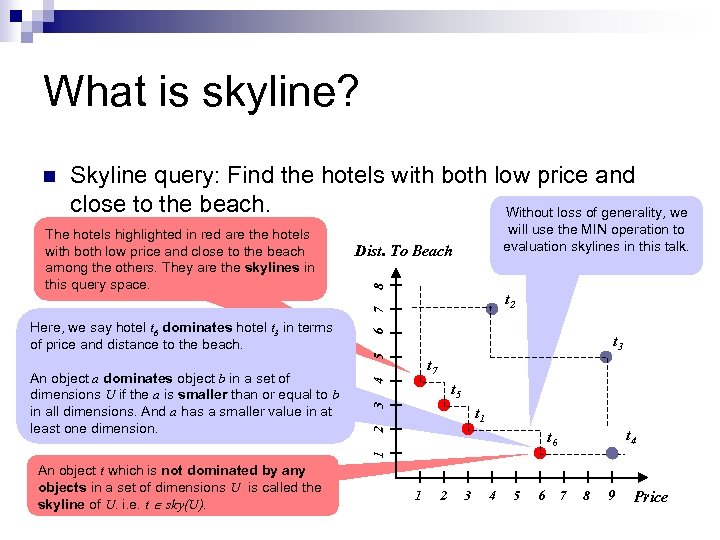
What is skyline? Skyline query: Find the hotels with both low price and close to the beach. Without loss of generality, we will use the MIN operation to evaluation skylines in this talk. Dist. To Beach t 2 t 3 5 Here, we say hotel t 6 dominates hotel t 3 in terms of price and distance to the beach. 6 7 The hotels highlighted in red are the hotels with both low price and close to the beach among the others. They are the skylines in this query space. 8 n 4 t 7 3 t 5 2 t 1 t 4 t 6 1 An object a dominates object b in a set of dimensions U if the a is smaller than or equal to b in all dimensions. And a has a smaller value in at least one dimension. An object t which is not dominated by any objects in a set of dimensions U is called the skyline of U. i. e. t sky(U). 1 2 3 4 5 6 7 8 9 Price
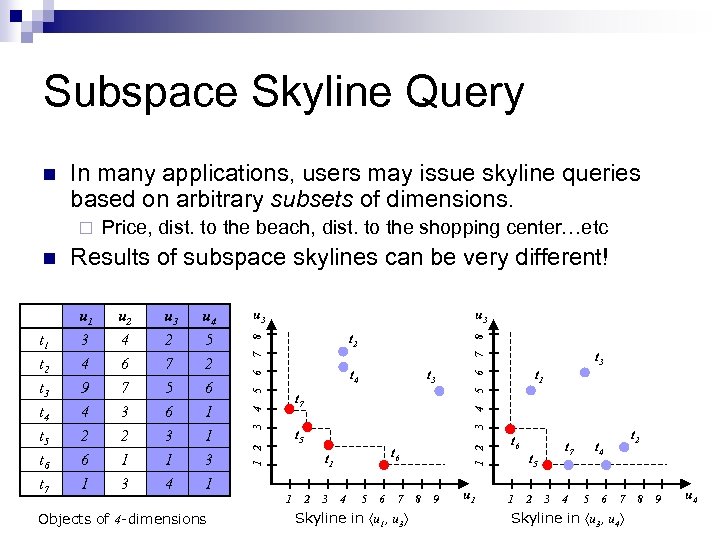
Subspace Skyline Query In many applications, users may issue skyline queries based on arbitrary subsets of dimensions. ¨ Results of subspace skylines can be very different! Objects of 4 -dimensions 8 7 t 5 t 6 t 1 1 t 1 6 t 3 5 1 t 4 4 4 t 3 3 3 t 2 2 3 4 5 6 7 Skyline in u 1, u 3 1 2 1 u 3 8 t 7 u 3 7 u 4 5 2 6 1 1 3 6 u 3 2 7 5 6 3 1 5 u 2 4 6 7 3 2 1 4 t 1 t 2 t 3 t 4 t 5 t 6 u 1 3 4 9 4 2 6 3 n Price, dist. to the beach, dist. to the shopping center…etc 1 2 n 8 9 u 1 t 6 t 7 t 5 1 2 3 4 t 2 t 4 5 6 7 Skyline in u 3, u 4 8 9 u 4
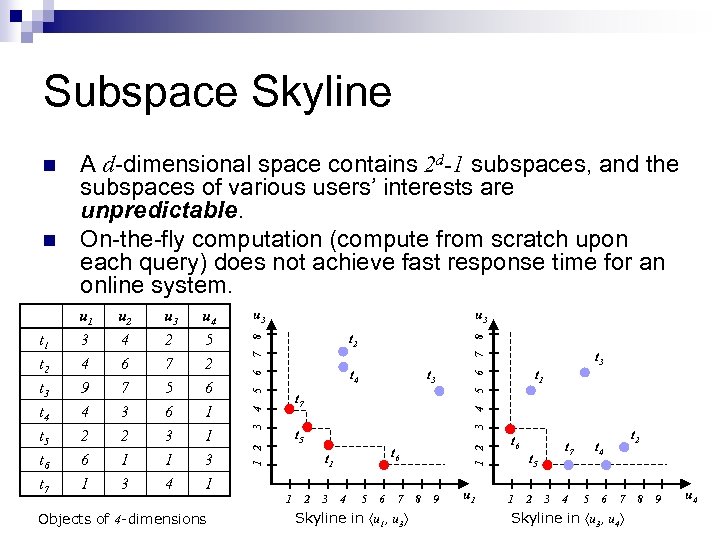
Subspace Skyline Objects of 4 -dimensions 8 7 t 5 t 6 t 1 1 t 1 6 t 3 5 1 t 4 4 4 t 3 3 3 t 2 2 3 4 5 6 7 Skyline in u 1, u 3 1 2 1 u 3 8 t 7 u 3 7 u 4 5 2 6 1 1 3 6 u 3 2 7 5 6 3 1 5 u 2 4 6 7 3 2 1 4 t 1 t 2 t 3 t 4 t 5 t 6 u 1 3 4 9 4 2 6 3 n A d-dimensional space contains 2 d-1 subspaces, and the subspaces of various users’ interests are unpredictable. On-the-fly computation (compute from scratch upon each query) does not achieve fast response time for an online system. 1 2 n 8 9 u 1 t 6 t 7 t 5 1 2 3 4 t 2 t 4 5 6 7 Skyline in u 3, u 4 8 9 u 4
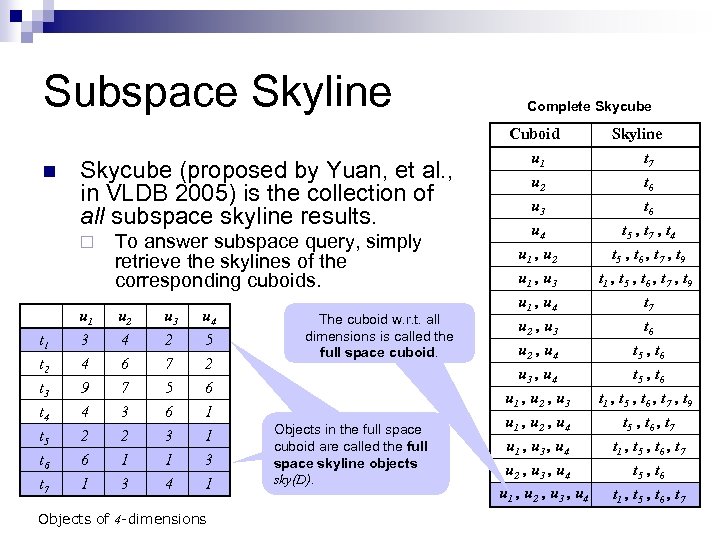
Subspace Skyline n Skycube (proposed by Yuan, et al. , in VLDB 2005) is the collection of all subspace skyline results. ¨ To answer subspace query, simply retrieve the skylines of the corresponding cuboids. t 1 t 2 t 3 t 4 t 5 t 6 u 1 3 4 9 4 2 6 u 2 4 6 7 3 2 1 u 3 2 7 5 6 3 1 u 4 5 2 6 1 1 3 t 7 1 3 4 1 Objects of 4 -dimensions The cuboid w. r. t. all dimensions is called the full space cuboid. Objects in the full space cuboid are called the full space skyline objects sky(D). Complete Skycube Cuboid u 1 u 2 u 3 u 4 u 1 , u 2 Skyline t 7 t 6 t 5 , t 7 , t 4 t 5 , t 6 , t 7 , t 9 u 1 , u 3 u 1 , u 4 u 2 , u 3 u 2 , u 4 u 3 , u 4 u 1 , u 2 , u 3 t 1 , t 5 , t 6 , t 7 , t 9 t 7 t 6 t 5 , t 6 t 1 , t 5 , t 6 , t 7 , t 9 u 1 , u 2 , u 4 u 1 , u 3 , u 4 u 2 , u 3 , u 4 u 1 , u 2 , u 3 , u 4 t 5 , t 6 , t 7 t 1 , t 5 , t 6 , t 7 t 5 , t 6 t 1 , t 5 , t 6 , t 7

Subspace Skyline n n Skycube (proposed by Yuan, et al. , in VLDB 2005) is the collection of all subspace skyline results. A skycube can be viewed as a lattice of cuboids. u 1 u 2 u 3 u 4 u 1 u 2 u 3 u 1 u 2 u 4 u 1 u 3 u 1 u 4 u 1 u 2 The cuboid w. r. t. all dimensions is called the full space cuboid. u 1 u 3 u 4 u 2 u 3 u 4 u 2 u 4 Skycube of 4 -dimensions u 3 u 4 Complete Skycube Cuboid u 1 u 2 u 3 u 4 u 1 , u 2 Skyline t 7 t 6 t 5 , t 7 , t 4 t 5 , t 6 , t 7 , t 9 u 1 , u 3 u 1 , u 4 u 2 , u 3 u 2 , u 4 u 3 , u 4 u 1 , u 2 , u 3 t 1 , t 5 , t 6 , t 7 , t 9 t 7 t 6 t 5 , t 6 t 1 , t 5 , t 6 , t 7 , t 9 u 1 , u 2 , u 4 u 1 , u 3 , u 4 u 2 , u 3 , u 4 u 1 , u 2 , u 3 , u 4 t 5 , t 6 , t 7 t 1 , t 5 , t 6 , t 7 t 5 , t 6 t 1 , t 5 , t 6 , t 7

Motivations n In many scenarios of the subspace skyline applications, the data are changing constantly. ¨ n In an online hotel-booking system, room prices change due to the availability. On-the-fly computation Low update cost. ¨ Slow query response time. ¨ n Complete Skycube Fast query response time. ¨ High update cost ¨ n The skycube contains a huge number of duplicates. Complete Skycube Cuboid u 1 u 2 u 3 u 4 u 1 , u 2 Skyline t 7 t 6 t 5 , t 7 , t 4 t 5 , t 6 , t 7 , t 9 u 1 , u 3 u 1 , u 4 u 2 , u 3 u 2 , u 4 u 3 , u 4 u 1 , u 2 , u 3 t 1 , t 5 , t 6 , t 7 , t 9 t 7 t 6 t 5 , t 6 t 1 , t 5 , t 6 , t 7 , t 9 u 1 , u 2 , u 4 u 1 , u 3 , u 4 u 2 , u 3 , u 4 u 1 , u 2 , u 3 , u 4 t 5 , t 6 , t 7 t 1 , t 5 , t 6 , t 7 t 5 , t 6 t 1 , t 5 , t 6 , t 7

Motivations n For example, object t 6 appears in 12 cuboids. Whenever t 6 is updated, at least 12 cuboids have to be updated. In addition, all affected cuboids have to be recomputed to reflect the correct result. Both waste of storage and difficult to maintain. In many scenarios of the subspace skyline applications, the data are changing constantly. ¨ n In an online hotel-booking system, room prices change due to the availability. On-the-fly computation Low update cost. ¨ Slow query response time. ¨ n Complete Skycube Fast query response time. ¨ High update cost ¨ n The skycube contains a huge number of duplicates. Complete Skycube Cuboid u 1 u 2 u 3 u 4 u 1 , u 2 Skyline t 7 t 6 t 5 , t 7 , t 4 t 5 , t 6 , t 7 , t 9 u 1 , u 3 u 1 , u 4 u 2 , u 3 u 2 , u 4 u 3 , u 4 u 1 , u 2 , u 3 t 1 , t 5 , t 6 , t 7 , t 9 t 7 t 6 t 5 , t 6 t 1 , t 5 , t 6 , t 7 , t 9 u 1 , u 2 , u 4 u 1 , u 3 , u 4 u 2 , u 3 , u 4 u 1 , u 2 , u 3 , u 4 t 5 , t 6 , t 7 t 1 , t 5 , t 6 , t 7 t 5 , t 6 t 1 , t 5 , t 6 , t 7

Motivations n For example, object t 6 appears in 12 cuboids. Whenever t 6 is updated, at least 12 cuboids have to be updated. In addition, all affected cuboids have to be recomputed to reflect the correct result. Both waste of storage and difficult to maintain. In many scenarios of the subspace skyline applications, the data are changing constantly. ¨ n In an online hotel-booking system, room prices change due to the availability. On-the-fly computation Low update cost. ¨ Slow query response time. ¨ n Complete Skycube Fast query response time. ¨ High update cost ¨ n The skycube contains a huge number of duplicates. Complete Skycube Cuboid u 1 u 2 u 3 u 4 u 1 , u 2 Skyline t 7 t 6 t 5 , t 7 , t 4 t 5 , t 6 , t 7 , t 9 u 1 , u 3 u 1 , u 4 u 2 , u 3 u 2 , u 4 u 3 , u 4 u 1 , u 2 , u 3 t 1 , t 5 , t 6 , t 7 , t 9 t 7 t 6 t 5 , t 6 t 1 , t 5 , t 6 , t 7 , t 9 u 1 , u 2 , u 4 u 1 , u 3 , u 4 u 2 , u 3 , u 4 u 1 , u 2 , u 3 , u 4 t 5 , t 6 , t 7 t 1 , t 5 , t 6 , t 7 t 5 , t 6 t 1 , t 5 , t 6 , t 7

The Compressed Skycube

The Compressed Skycube n In the paper, the authors proposed: A new compressed model for the Skycube, which greatly reduces the storage. ¨ A new object-aware update scheme, which avoids unnecessary disk access and cuboids' computation. ¨ n By taking advantages of the compact structure and the update scheme, the Compressed Skycube achieves both fast query response and efficient update.

Minimum Subspace n DEFINITION: Given an object t, the minimum subspaces of t, denoted as mss(t), satisfies the following two conditions: For any subspace U in mss(t), t is in the skyline of U; 2. For any subspace V U, t is not in the skyline of V. 1.
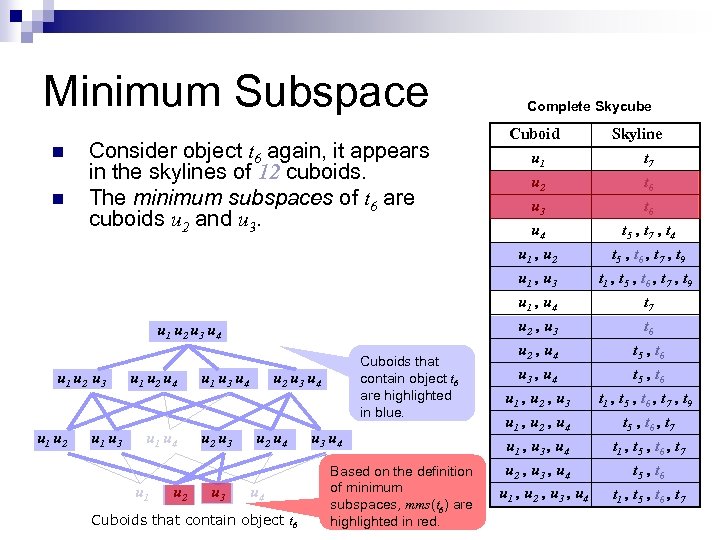
Minimum Subspace n n Consider object t 6 again, it appears in the skylines of 12 cuboids. The minimum subspaces of t 6 are cuboids u 2 and u 3. u 1 u 2 u 3 u 4 u 1 u 2 u 3 u 1 u 2 u 1 u 3 u 1 u 2 u 4 u 1 u 2 u 1 u 3 u 4 u 2 u 3 Cuboids that contain object t 6 are highlighted in blue. u 2 u 3 u 4 u 2 u 4 Cuboids that contain object t 6 u 3 u 4 Based on the definition of minimum subspaces, mms(t 6) are highlighted in red. Complete Skycube Cuboid u 1 u 2 u 3 u 4 u 1 , u 2 Skyline t 7 t 6 t 5 , t 7 , t 4 t 5 , t 6 , t 7 , t 9 u 1 , u 3 u 1 , u 4 u 2 , u 3 u 2 , u 4 u 3 , u 4 u 1 , u 2 , u 3 t 1 , t 5 , t 6 , t 7 , t 9 t 7 t 6 t 5 , t 6 t 1 , t 5 , t 6 , t 7 , t 9 u 1 , u 2 , u 4 u 1 , u 3 , u 4 u 2 , u 3 , u 4 u 1 , u 2 , u 3 , u 4 t 5 , t 6 , t 7 t 1 , t 5 , t 6 , t 7 t 5 , t 6 t 1 , t 5 , t 6 , t 7
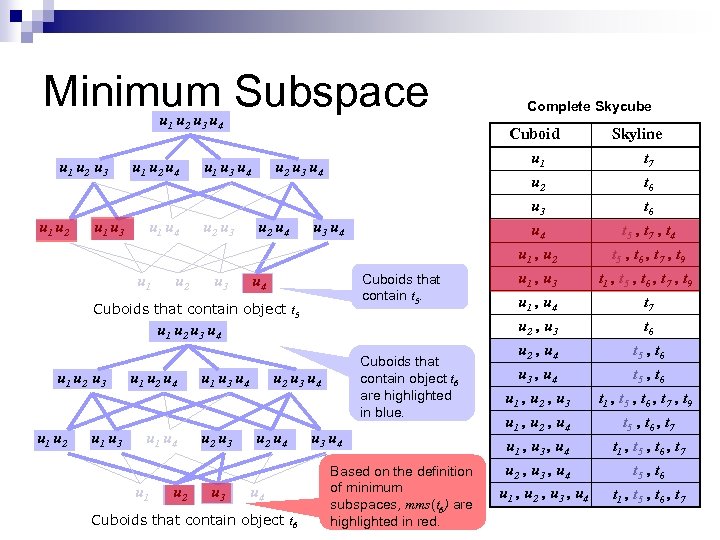
Minimum Subspace u 1 u 2 u 3 u 4 u 1 u 2 u 3 u 1 u 2 u 1 u 3 u 1 u 2 u 4 u 1 u 2 u 1 u 3 u 4 u 2 u 3 Cuboid u 1 u 2 u 3 u 4 u 1 , u 2 u 3 u 4 u 2 u 4 u 3 u 4 Cuboids that contain t 5. u 4 Cuboids that contain object t 5 u 1 u 2 u 3 u 4 u 1 u 2 u 3 u 1 u 2 u 1 u 3 u 1 u 2 u 4 u 1 u 2 u 1 u 3 u 4 u 2 u 3 Cuboids that contain object t 6 are highlighted in blue. u 2 u 3 u 4 u 2 u 4 Cuboids that contain object t 6 Complete Skycube u 3 u 4 Based on the definition of minimum subspaces, mms(t 6) are highlighted in red. Skyline t 7 t 6 t 5 , t 7 , t 4 t 5 , t 6 , t 7 , t 9 u 1 , u 3 u 1 , u 4 u 2 , u 3 u 2 , u 4 u 3 , u 4 u 1 , u 2 , u 3 t 1 , t 5 , t 6 , t 7 , t 9 t 7 t 6 t 5 , t 6 t 1 , t 5 , t 6 , t 7 , t 9 u 1 , u 2 , u 4 u 1 , u 3 , u 4 u 2 , u 3 , u 4 u 1 , u 2 , u 3 , u 4 t 5 , t 6 , t 7 t 1 , t 5 , t 6 , t 7 t 5 , t 6 t 1 , t 5 , t 6 , t 7

Minimum Subspace u 1 u 2 u 3 u 4 u 1 u 2 u 3 u 1 u 2 u 4 u 1 u 3 u 1 u 4 u 1 u 3 u 4 u 2 u 3 u 3 u 4 Cuboids that contain object t 5 Minimum Subspaces t 1 t 5 u 1, u 3 u 4 , u 1, u 2 , u 1, u 3 t 6 u 2 , u 3 t 7 t 4 u 1 , u 4 t 9 u 1, u 2 , u 1, u 3 Cuboid u 1 u 2 u 3 u 4 u 1 , u 2 u 3 u 4 u 2 u 4 Complete Skycube Cuboids that contain t 5. Similar for all other skyline objects, we store the minimum subspaces of all skyline objects in a table. For easy processing in the later sections, we organize the full-space skyline objects together in the front. Skyline t 7 t 6 t 5 , t 7 , t 4 t 5 , t 6 , t 7 , t 9 u 1 , u 3 u 1 , u 4 u 2 , u 3 u 2 , u 4 u 3 , u 4 u 1 , u 2 , u 3 t 1 , t 5 , t 6 , t 7 , t 9 t 7 t 6 t 5 , t 6 t 1 , t 5 , t 6 , t 7 , t 9 u 1 , u 2 , u 4 u 1 , u 3 , u 4 u 2 , u 3 , u 4 u 1 , u 2 , u 3 , u 4 t 5 , t 6 , t 7 t 1 , t 5 , t 6 , t 7 t 5 , t 6 t 1 , t 5 , t 6 , t 7

Compressed Skycube n The compressed skycube (CSC) consists of non-empty cuboids such that an object t is stored in a cuboid iff the cuboid is the minimum subspace of t. Compare with the complete skycube, CSC has fewer number of duplicates. Compressed Skycube Minimum Subspaces t 1 t 5 u 1, u 3 u 4 , u 1, u 2 , u 1, u 3 Cuboid u 1 Skyline t 7 u 2 t 6 t 6 u 2 , u 3 t 7 t 4 u 1 , u 4 t 5 , t 7 , t 4 u 1 , u 2 t 5 , t 9 u 1, u 2 , u 1, u 3 u 1 , u 3 t 1 , t 5 , t 9 Complete Skycube Cuboid u 1 u 2 u 3 u 4 u 1 , u 2 Skyline t 7 t 6 t 5 , t 7 , t 4 t 5 , t 6 , t 7 , t 9 u 1 , u 3 u 1 , u 4 u 2 , u 3 u 2 , u 4 u 3 , u 4 u 1 , u 2 , u 3 t 1 , t 5 , t 6 , t 7 , t 9 t 7 t 6 t 5 , t 6 t 1 , t 5 , t 6 , t 7 , t 9 u 1 , u 2 , u 4 u 1 , u 3 , u 4 u 2 , u 3 , u 4 u 1 , u 2 , u 3 , u 4 t 5 , t 6 , t 7 t 1 , t 5 , t 6 , t 7 t 5 , t 6 t 1 , t 5 , t 6 , t 7

Querying the Compressed Skycube

Querying CSC Raw dataset n Overview example: query space Uq = u 2, u 3 , u 4 To find the skylines in Uq i. e. sky(Uq), we only need to: ¨ LEMMA 1. search within the cuboids of the compressed skycube which are the subsets of Uq. u 2 u 3 u 4 t 1 n u 1 3 4 2 5 t 5 2 2 3 1 t 6 6 1 1 3 t 7 1 3 4 1 t 4 4 3 6 1 t 9 2 2 3 7 Compressed Skycube Cuboid Skyline u 1 t 7 u 2 t 6 u 3 t 6 u 4 t 5 , t 7, t 4 u 1, u 2 t 5 , t 9 u 1 , u 3 t 1 , t 5 , t 9
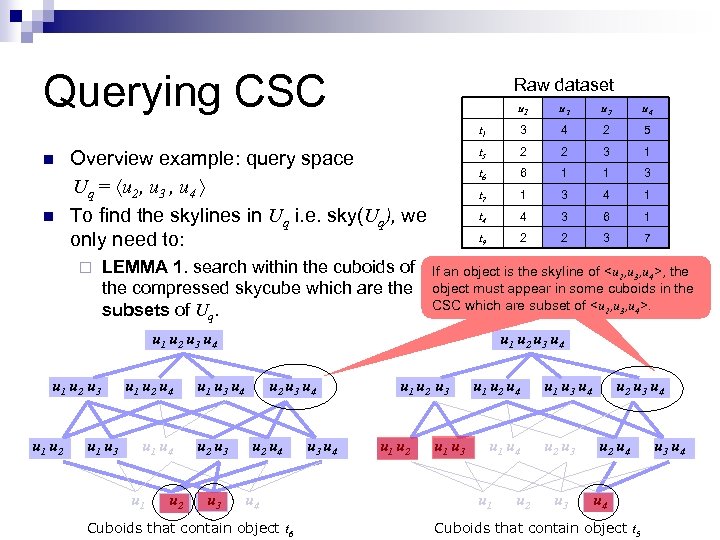
Querying CSC Raw dataset n ¨ LEMMA 1. search within the cuboids of the compressed skycube which are the subsets of Uq. u 3 u 4 3 4 2 5 t 5 2 2 3 1 t 6 6 1 1 3 t 7 1 3 4 1 t 4 4 3 6 1 t 9 Overview example: query space Uq = u 2, u 3 , u 4 To find the skylines in Uq i. e. sky(Uq), we only need to: u 2 t 1 n u 1 2 2 3 7 If an object is the skyline of <u 2, u 3, u 4>, the object must appear in some cuboids in the CSC which are subset of <u 2, u 3, u 4>. u 1 u 2 u 3 u 4 u 1 u 2 u 3 u 1 u 2 u 1 u 3 u 1 u 2 u 4 u 1 u 2 u 3 u 4 u 1 u 3 u 4 u 2 u 3 u 4 u 2 u 4 Cuboids that contain object t 6 u 3 u 4 u 1 u 2 u 3 u 1 u 2 u 1 u 3 u 1 u 2 u 4 u 1 u 2 u 1 u 3 u 4 u 2 u 3 u 4 u 2 u 4 Cuboids that contain object t 5 u 3 u 4

Querying CSC Raw dataset n Overview example: query space Uq = u 2, u 3 , u 4 To find the skylines in Uq i. e. sky(Uq), we only need to: LEMMA 1. search within the cuboids of the compressed skycube which are the subsets of Uq. ¨ LEMMA 2. If an object t in a cuboid V (V is subset of Uq) is not dominated in Uq by other objects in the same cuboid, then t is a full space skyline object. u 2 u 3 u 4 t 1 n u 1 3 4 2 5 t 5 2 2 3 1 t 6 6 1 1 3 t 7 1 3 4 1 t 4 4 3 6 1 t 9 2 2 3 7 ¨ Compressed Skycube Cuboid Skyline t 7 u 2 t 6 u 3 t 6 u 4 t 5 , t 7, t 4 u 1, u 2 t 5 , t 9 u 1 , u 3 No comparison is needed for t 6. u 1 t 1 , t 5 , t 9 t 5, t 7, t 4 are only locally compared to each other. Why ?

Querying CSC Raw dataset LEMMA 2. If an object t in a cuboid V (V is subset of Uq) is not dominated in Uq by other objects in the same cuboid, then t is a full space skyline object. There are NO objects in this area. Otherwise, t 5, t 7, and t 4 will not be the skylines of u 4. u 3 t 7 t 5 u 3 u 4 3 4 2 5 t 5 2 2 3 1 t 6 6 1 1 3 t 7 1 3 4 1 t 4 4 3 6 1 t 9 2 2 3 7 Compressed Skycube Therefore, no other objects can dominate t 5, t 7 and t 4 in the superset of u 4. e. g. If t 4 is not dominated by t 7 and t 8 in full space, no other objects can dominate t 4 u 2 t 1 n u 1 Cuboid Skyline u 4 No comparison is needed for t 6. t 7 u 2 t 6 u 3 t 6 u 4 Plot of objects t 5, t 7 and t 4 in u 4. Since they have the smallest values in u 4, they are skylines of u 4. u 1 t 5 , t 7, t 4 u 1, u 2 t 5 , t 9 u 1 , u 3 t 1 , t 5 , t 9 t 5, t 7, t 4 are only locally compared to each other. Why ?

The query system based on CSC
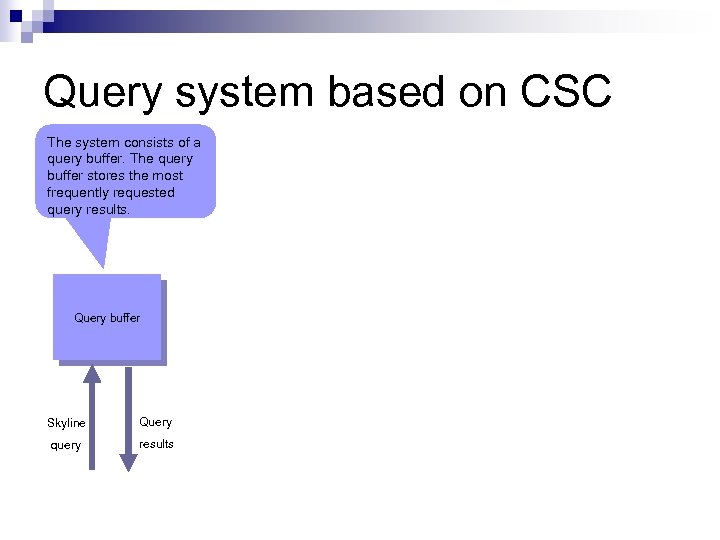
Query system based on CSC The system consists of a query buffer. The query buffer stores the most frequently requested query results. Query buffer Skyline Query query results
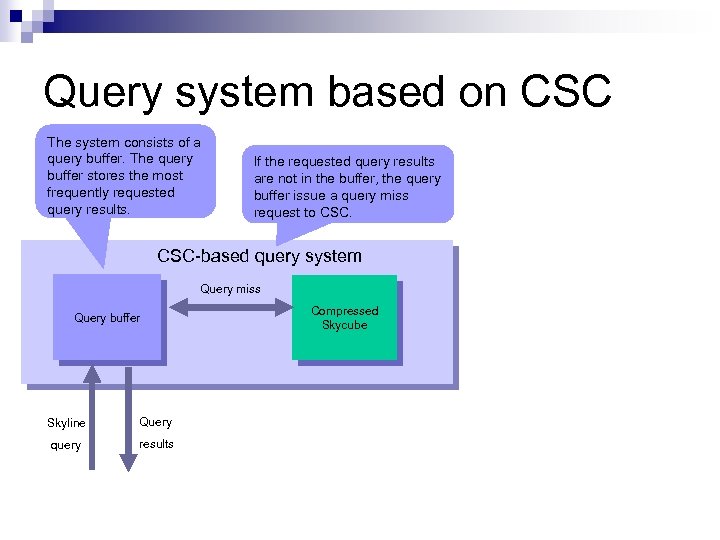
Query system based on CSC The system consists of a query buffer. The query buffer stores the most frequently requested query results. If the requested query results are not in the buffer, the query buffer issue a query miss request to CSC-based query system Query miss Query buffer Skyline Query query results Compressed Skycube
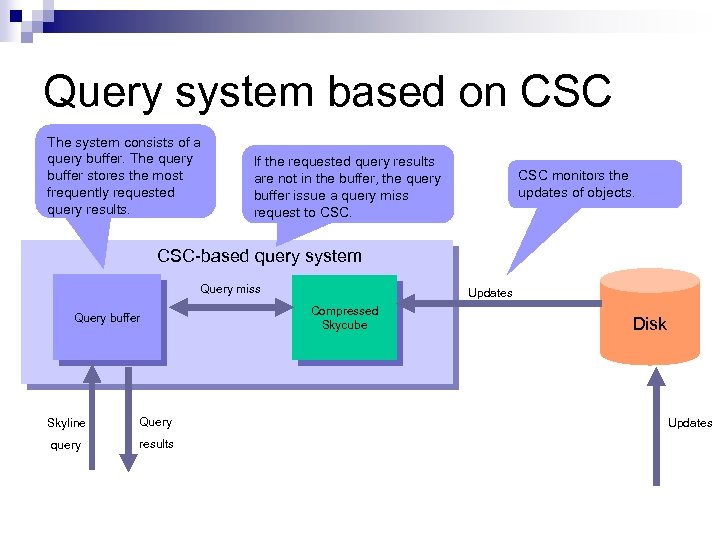
Query system based on CSC The system consists of a query buffer. The query buffer stores the most frequently requested query results. If the requested query results are not in the buffer, the query buffer issue a query miss request to CSC monitors the updates of objects. CSC-based query system Query miss Query buffer Skyline Query query results Updates Compressed Skycube Disk Updates
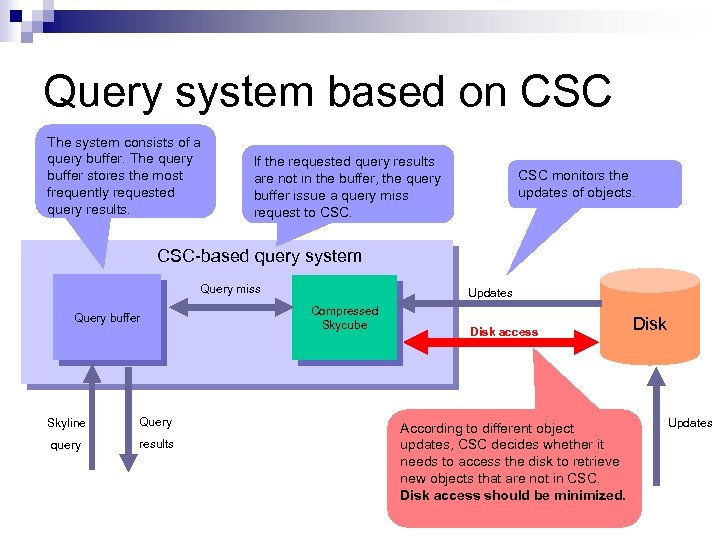
Query system based on CSC The system consists of a query buffer. The query buffer stores the most frequently requested query results. If the requested query results are not in the buffer, the query buffer issue a query miss request to CSC monitors the updates of objects. CSC-based query system Query miss Query buffer Skyline Query query results Updates Compressed Skycube Disk access According to different object updates, CSC decides whether it needs to access the disk to retrieve new objects that are not in CSC. Disk access should be minimized. Disk Updates
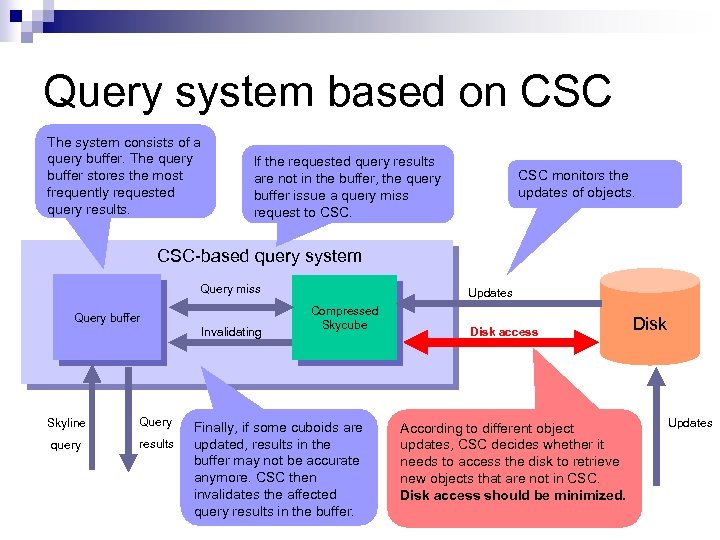
Query system based on CSC The system consists of a query buffer. The query buffer stores the most frequently requested query results. If the requested query results are not in the buffer, the query buffer issue a query miss request to CSC monitors the updates of objects. CSC-based query system Query miss Query buffer Invalidating Skyline Query query results Updates Compressed Skycube Finally, if some cuboids are updated, results in the buffer may not be accurate anymore. CSC then invalidates the affected query results in the buffer. Disk access According to different object updates, CSC decides whether it needs to access the disk to retrieve new objects that are not in CSC. Disk access should be minimized. Disk Updates

Updating the Compressed Skycube

Updating CSC n Intuitions: ¨ ¨ Not all updates of objects need to access the disk. Not all updates of objects need to re-compute the skyline of a cuboid. n These intuitions are supported by theorems in the paper. n D: full-space; sky(D): full-space skyline. t: object before update; tnew: object after update. n t sky(D) No dataset (disk) access tnew sky(D) Considering the proportion Insert new of full-space May access t sky(D) objects in the whole dataset, the skyline objects dataset (disk) above covers most cases of the updates n
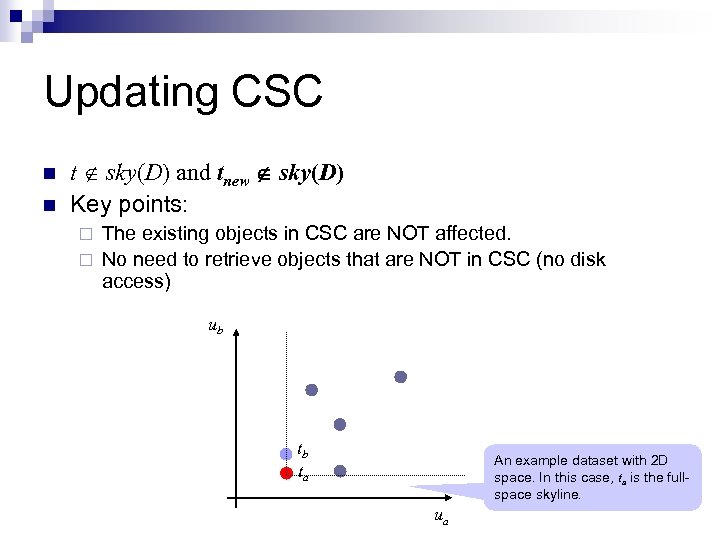
Updating CSC n n t sky(D) and tnew sky(D) Key points: The existing objects in CSC are NOT affected. ¨ No need to retrieve objects that are NOT in CSC (no disk access) ¨ ub tb ta An example dataset with 2 D space. In this case, ta is the fullspace skyline. ua
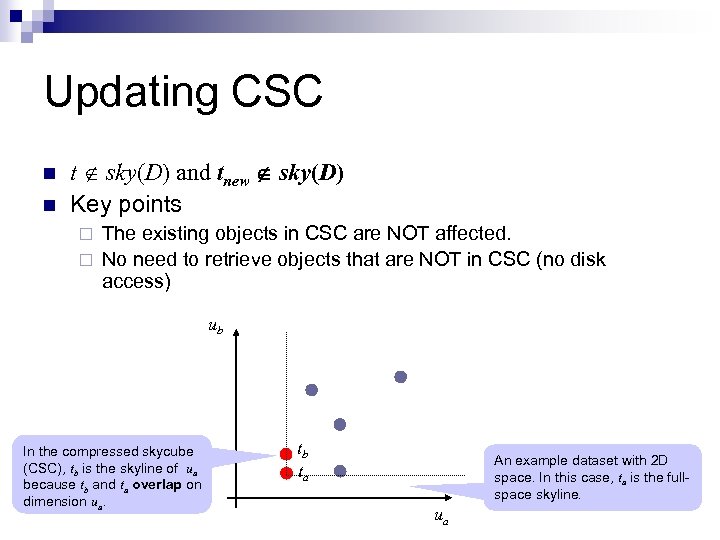
Updating CSC n n t sky(D) and tnew sky(D) Key points The existing objects in CSC are NOT affected. ¨ No need to retrieve objects that are NOT in CSC (no disk access) ¨ ub In the compressed skycube (CSC), tb is the skyline of ua because tb and ta overlap on dimension ua. tb ta An example dataset with 2 D space. In this case, ta is the fullspace skyline. ua

Updating CSC n n t sky(D) and tnew sky(D) Key points The existing objects in CSC are NOT affected. ¨ No need to retrieve objects that are NOT in CSC (no disk access) ¨ If t sky(D) and tnew sky(D), tnew will fall within this area, which will NOT affect the existing skyline objects. As a result, the objects in CSC are NOT affected. In the compressed skycube (CSC), tb is the skyline of ua because tb and ta overlap on dimension ua. ub t sky(D) and tnew sky(D) t tb ta An example dataset with 2 D space. In this case, ta is the fullspace skyline. ua

Updating CSC n n t sky(D) and tnew sky(D) Key points The existing objects in CSC are NOT affected. ¨ No need to retrieve objects that are NOT in CSC (no disk access) ¨ If t sky(D) and tnew sky(D), tnew will fall within this area, which will NOT affect the existing skyline objects. As a result, the objects in CSC are NOT affected. In the compressed skycube (CSC), tb is the skyline of ua because tb and ta overlap on dimension ua. ub t sky(D) and tnew sky(D) tnew tb ta t tnew ua Only when tnew overlaps with some subspace (e. g. ua or ub), tnew will becomes the skyline of the corresponding cuboids. In this case, tnew is added into CSC. An example dataset with 2 D space. In this case, ta is the fullspace skyline.

Updating CSC n n t sky(D) and tnew sky(D) Two steps approach to update CSC ¨ ¨ Compare tnew with existing full-space skyline objects (sky(D)). Determine the minimum subspaces of tnew n Can be determined by ANY dominating object in sky(D) (Why? ). If t sky(D) and tnew sky(D), tnew will fall within this area, which will NOT affect the existing skyline objects. As a result, the objects in CSC are NOT affected. In the compressed skycube (CSC), tb is the skyline of ua because tb and ta overlap on dimension ua. ub t sky(D) and tnew sky(D) tnew tb ta t tnew ua Only when tnew overlaps with some subspace (e. g. ua or ub), tnew will becomes the skyline of the corresponding cuboids. In this case, tnew is added into CSC. An example dataset with 2 D space. In this case, ta is the fullspace skyline.

Updating CSC n n t sky(D) and tnew sky(D) Two steps approach to update CSC ¨ ¨ Compare tnew with existing full-space skyline objects (sky(D)). Determine the minimum subspaces of tnew n Can be determined by ANY dominating object in sky(D) (Why? ). ub t Another example with ta and tb as the full-space skylines. tb ta ua

Updating CSC n n t sky(D) and tnew sky(D) Two steps approach to update CSC ¨ ¨ Compare tnew with existing full-space skyline objects (sky(D)). Determine the minimum subspaces of tnew n Can be determined by ANY dominating object in sky(D) (Why? ). ub tnew Another example with ta and tb as the full-space skylines. t tb ta tnew ua tnew will be the skyline of a subspace (e. g. ub) only when tnew overlaps with a fullspace skyline in that subspace (e. g. overlaps with ta in ub ). That is, tnew lies on the red lines.

Updating CSC n n t sky(D) and tnew sky(D) Two steps approach to update CSC ¨ ¨ Compare tnew with existing full-space skyline objects (sky(D)). Determine the minimum subspaces of tnew n Can be determined by ANY dominating object in sky(D) (Why? ). ub tnew If tnew is dominated by tb, the minimum subspaces of tnew must be the minimum subspaces of tb. E. g. If tnew is the skyline of ua, tb is also the skyline of ua as tb is a full-space skyline and is dominating tnew will be the skyline of a subspace (e. g. ub) only when tnew overlaps with a fullspace skyline in that subspace (e. g. overlaps with ta in ub ). That is, tnew lies on the red lines. t tb ta ua

Updating CSC n n t sky(D) and tnew sky(D) Two steps approach to update CSC ¨ ¨ Compare tnew with existing full-space skyline objects (sky(D)). Determine the minimum subspaces of tnew n Can be determined by ANY dominating object in sky(D) (Why? ). ub t If tnew is dominated by tb, the minimum subspaces of tnew must be the minimum subspaces of tb. E. g. If tnew is the skyline of ua, tb is also the skyline of ua as tb is a full-space skyline and is dominating tnew. tb ta tnew ua Similarly, if tnew is the skyline of ub, ta is also the skyline of ub because ta is a full-space skyline and is dominating tnew.

Updating CSC n n t sky(D) and tnew sky(D) Two steps approach to update CSC ¨ ¨ Compare tnew with existing full-space skyline objects (sky(D)). Determine the minimum subspaces of tnew n Can be determined by ANY dominating object in sky(D) (Why? ). Therefore, to determine the minimum subspaces of tnew , we only need to consider the minimum subspaces of any full -space skylines that dominates tnew. ub tnew If tnew is dominated by tb, the minimum subspaces of tnew must be the minimum subspaces of tb. E. g. If tnew is the skyline of ua, tb is also the skyline of ua as tb is a full-space skyline and is dominating tnew. t tb ta tnew ua Similarly, if tnew is the skyline of ub, ta is also the skyline of ub because ta is a full-space skyline and is dominating tnew.

Updating CSC t sky(D) and tnew sky(D) Two steps approach to update CSC n n Compare tnew with existing full-space skyline objects (sky(D)). Determine the minimum subspaces of tnew ¨ ¨ n Can be determined by ANY dominating object in sky(D). Objects in the Compressed Skycube u 1 u 2 u 3 u 4 t 1 3 4 2 5 t 5 2 2 3 1 t 6 6 1 1 3 t 7 1 3 4 1 t 4 4 3 6 1 t 9 2 2 3 7 Object t 9 is not a fullspace skyline object. Full-space skylines Update object

Updating CSC t sky(D) and tnew sky(D) Two steps approach to update CSC n n Compare tnew with existing full-space skyline objects (sky(D)). Determine the minimum subspaces of tnew ¨ ¨ n Can be determined by ANY dominating object in sky(D). Objects in the Compressed Skycube u 1 u 2 u 3 t 1 3 4 2 5 t 5 2 2 3 1 t 6 6 1 1 3 t 7 1 3 4 1 t 4 4 3 6 1 t 9 2 2 3 7 We first compare object t 9 with existing full-space skyline objects. u 4 Object t 9 is not a fullspace skyline object. Full-space skylines Update object

Updating CSC t sky(D) and tnew sky(D) Two steps approach to update CSC n n Compare tnew with existing full-space skyline objects (sky(D)). Determine the minimum subspaces of tnew ¨ ¨ n Can be determined by ANY dominating object in sky(D). Objects in the Compressed Skycube u 1 u 2 u 3 t 1 3 4 2 5 t 5 2 2 3 1 t 6 6 1 1 3 t 7 1 3 4 1 t 4 4 3 6 1 t 9 2 2 3 7 We first compare object t 9 with existing full-space skyline objects. u 4 Object t 9 is not a fullspace skyline object. Full-space skylines Update object The full-space skyline object t 1 does NOT dominate object t 9, continue to compare the next full-space skyline object.

Updating CSC t sky(D) and tnew sky(D) Two steps approach to update CSC n n Compare tnew with existing full-space skyline objects (sky(D)). Determine the minimum subspaces of tnew ¨ ¨ n Can be determined by ANY dominating object in sky(D). Objects in the Compressed Skycube u 1 u 2 u 3 t 1 3 4 2 5 t 5 2 2 3 1 t 6 6 1 1 3 t 7 1 3 4 1 t 4 4 3 6 1 t 9 2 2 3 7 We first compare object t 9 with existing full-space skyline objects. u 4 Object t 9 is not a fullspace skyline object. Full-space skylines Update object The full-space skyline object t 1 does NOT dominate object t 9, continue to compare the next full-space skyline object. The full-space skyline object t 5 dominates object t 9, we then retrieve the minimum subspaces of t 5. The retrieved subspaces are the candidates for the minimum subspaces of object t 9.

Updating CSC t sky(D) and tnew sky(D) Two steps approach to update CSC n n Compare tnew with existing full-space skyline objects (sky(D)). Determine the minimum subspaces of tnew ¨ ¨ n Can be determined by ANY dominating object in sky(D). Objects in the Compressed Skycube Minimum subspace u 1 u 2 u 3 u 4 t 1 3 4 2 5 t 1 u 1, u 3 t 5 2 2 3 1 t 5 u 4 , u 1, u 2 , u 1, u 3 t 6 6 1 1 3 t 6 u 2 , u 3 t 7 1 3 4 1 t 7 u 1 , u 4 t 4 4 3 6 1 t 4 u 4 t 9 2 2 3 7 t 9 u 1, u 2 , u 1, u 3 Object t 9 is not a fullspace skyline object. Minimum subspaces of t 9 are u 1, u 2 , u 1, u 3 . . u 4 , u 1, u 2 , u 1, u 3 are the candidates of the minimum subspaces of Object t 9. The full-space skyline object t 5 dominates object t 9, we then retrieve the minimum subspaces of t 5. The retrieved subspaces are the candidates for the minimum subspaces of object t 9.

Updating CSC t sky(D) and tnew sky(D) Two steps approach to update CSC n n Compare tnew with existing full-space skyline objects (sky(D)). Determine the minimum subspaces of tnew ¨ ¨ n Can be determined by ANY dominating object in sky(D). Objects in the Compressed Skycube Minimum subspace u 1 t 1 u 2 u 3 u 4 3 4 2 5 t 1 u 1, u 3 u 4 , u 1, u 2 , u 1, u 3 t 5 2 2 3 1 t 5 t 6 6 1 1 3 t 6 u 2 , u 3 t 7 1 3 4 1 t 7 u 1 , u 4 t 4 4 3 6 1 t 4 u 4 t 9 2 2 3 7 t 9 u 1, u 2 , u 1, u 3 Object t 9 is not a fullspace skyline object. Minimum subspaces of t 9 are u 1, u 2 , u 1, u 3 . . Compressed Skycube Cuboid Skyline u 1 t 7 u 2 t 6 u 3 t 6 u 4 t 5 , t 7, t 4 u 1, u 2 t 5 , t 9 u 1 , u 3 t 1 , t 5 , t 9 Finally, we update the compressed skycube and insert object t 9 into the corresponding cuboids.

Updating CSC t sky(D) and tnew sky(D) Two steps approach to update CSC n n Compare tnew with existing full-space skyline objects (sky(D)). Determine the minimum subspaces of tnew ¨ ¨ n Can be determined by ANY dominating object in sky(D). Objects in the Compressed Skycube Minimum subspace u 1 t 1 u 2 u 3 u 4 3 4 2 5 t 1 u 1, u 3 u 4 , u 1, u 2 , u 1, u 3 t 5 2 2 3 1 t 5 t 6 6 1 1 3 t 6 u 2 , u 3 t 7 1 3 4 1 t 7 u 1 , u 4 t 4 4 3 6 1 t 4 u 4 t 9 2 2 3 7 t 9 u 1, u 2 , u 1, u 3 Object t 9 is not a fullspace skyline object. Minimum subspaces of t 9 are u 1, u 2 , u 1, u 3 . . Compressed Skycube Cuboid Skyline u 1 t 7 u 2 t 6 u 3 t 6 u 4 t 5 , t 7, t 4 u 1, u 2 t 5 , t 9 u 1 , u 3 t 1 , t 5 , t 9 Finally, we update the compressed skycube and insert object t 9 into the corresponding cuboids. We don’t need to retrieve the objects that are NOT in the compressed skycube throughout the whole update process. i. e. No disk access in this case.
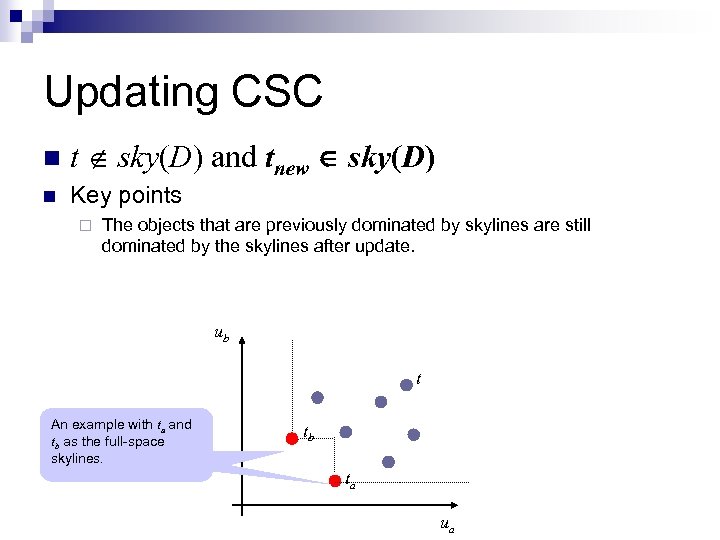
Updating CSC n t sky(D) and tnew sky(D) n Key points ¨ The objects that are previously dominated by skylines are still dominated by the skylines after update. ub t An example with ta and tb as the full-space skylines. tb ta ua
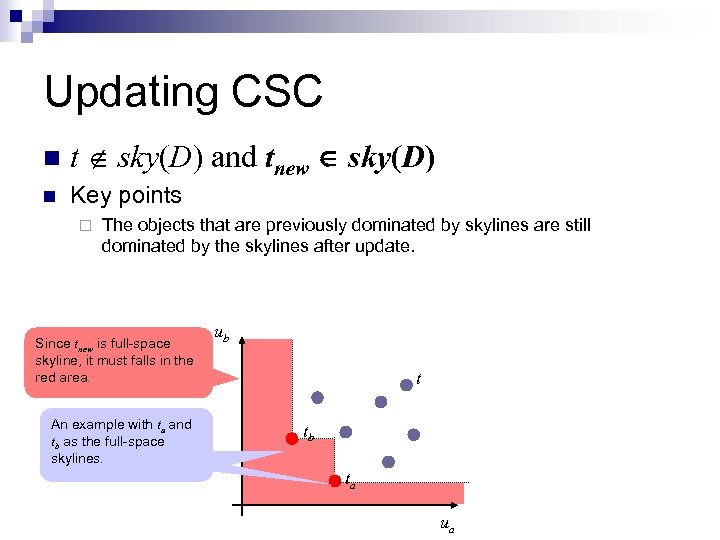
Updating CSC n t sky(D) and tnew sky(D) n Key points ¨ The objects that are previously dominated by skylines are still dominated by the skylines after update. Since tnew is full-space skyline, it must falls in the red area. An example with ta and tb as the full-space skylines. ub t tb ta ua
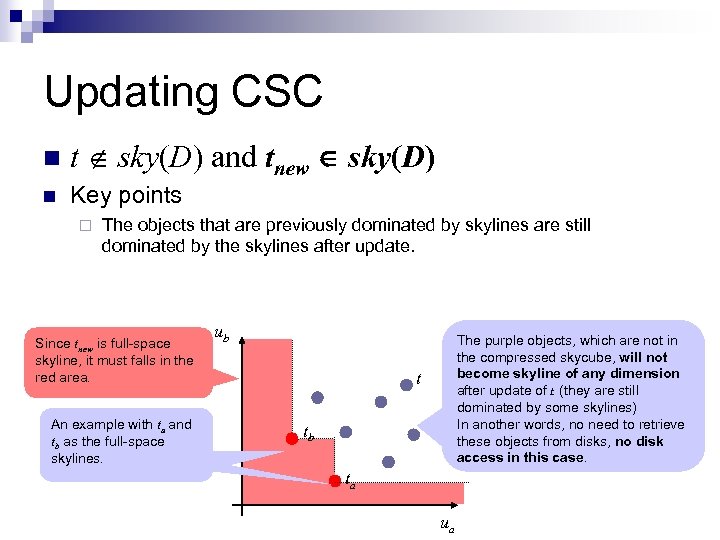
Updating CSC n t sky(D) and tnew sky(D) n Key points ¨ The objects that are previously dominated by skylines are still dominated by the skylines after update. Since tnew is full-space skyline, it must falls in the red area. An example with ta and tb as the full-space skylines. ub The purple objects, which are not in the compressed skycube, will not become skyline of any dimension after update of t. (they are still dominated by some skylines) In another words, no need to retrieve these objects from disks, no disk access in this case. t tb ta ua

Updating CSC n t sky(D) and tnew sky(D) n Key points The objects that are previously dominated by skylines are still dominated by the skylines after update. ¨ Existing skylines may be dominated by tnew. ¨ Since tnew is full-space skyline, it must falls in the red area. If tnew is updated to here, tb will be dominated by tnew, tb is then removed from the cuboid of full-space skylines, and the minimum subspaces of tb need to be updated. ub The purple objects, which are not in the compressed skycube, will not become skyline of any dimension after update of t. (they are still dominated by some skylines) In another words, no need to retrieve these objects from disks, no disk access in this case. t tnew tb ta ua

Updating CSC n t sky(D) and tnew sky(D) n Key points The objects that are previously dominated by skylines are still dominated by the skylines after update. ¨ Existing skylines may be dominated by tnew. ¨ Objects in the Compressed Skycube u 1 u 2 u 3 u 4 t 1 3 4 2 5 t 5 2 2 3 1 t 6 6 1 1 3 t 7 1 3 4 1 t 4 4 3 6 1 t 9 2 2 3 7 t 10 1 3 Object t 10 is updated. It was not a full-space skyline.

Updating CSC n t sky(D) and tnew sky(D) n Key points The objects that are previously dominated by skylines are still dominated by the skylines after update. ¨ Existing skylines may be dominated by tnew. ¨ Objects in the Compressed Skycube u 1 u 2 u 3 u 4 t 1 3 4 2 5 t 5 2 2 3 1 t 6 6 1 1 3 t 7 1 3 4 1 t 4 4 3 6 1 t 9 2 2 3 7 t 10 1 3 Object t 10 is updated. It was not a full-space skyline. Minimum subspace t 1 u 1, u 3 t 5 u 4 , u 1, u 2 , u 1, u 3 t 6 u 2 , u 3 t 7 u 1 , u 4 t 4 u 4 t 9 u 1, u 2 u 1, u 3 We first compare t 1 with t 10. Since object t 10 dominates t 1 in the fullspace, t 1 is no longer the skyline of <u 1, u 3>. The minimum subspace <u 1, u 3> of t 1 is removed.

Updating CSC n t sky(D) and tnew sky(D) n Key points The objects that are previously dominated by skylines are still dominated by the skylines after update. We then compare t 5 with t 10. Since object t 10 dominates t 5 in ¨ Existing skylines may be dominated by tnew. ¨ Objects in the Compressed Skycube u 1 u 2 u 3 u 4 t 1 3 4 2 5 t 5 2 2 3 1 t 6 6 1 1 3 t 7 1 3 4 1 t 4 4 3 6 1 t 9 2 2 3 7 t 10 1 3 Object t 10 is updated. It was not a full-space skyline. Minimum subspace t 1 u 1, u 3 t 5 u 4 , u 1, u 2 , u 1, u 3 t 6 u 2 , u 3 t 7 u 1 , u 4 t 4 u 4 t 9 u 1, u 2 u 1, u 3 <u 1, u 3> only, we need to update the minimum subspaces of t 5.

Updating CSC n t sky(D) and tnew sky(D) n Key points The objects that are previously dominated by skylines are still dominated by the skylines after update. We then compare t 5 with t 10. Since object t 10 dominates t 5 in ¨ Existing skylines may be dominated by tnew. ¨ Objects in the Compressed Skycube u 1 u 2 u 3 u 4 t 1 3 4 2 5 t 5 2 2 3 1 t 6 6 1 1 3 t 7 1 3 4 1 t 4 4 3 6 1 t 9 2 2 3 7 t 10 1 3 1 <u 1, u 3> only, we need to update the minimum subspaces of t 5. Minimum subspace 3 Object t 10 is updated. It was not a full-space skyline. t 1 t 5 u 4 , u 1, u 2 , u 1, u 3 t 6 u 2 , u 3 t 7 u 1 , u 4 t 4 u 4 t 9 u 1, u 2 u 1, u 3 u 1 u 2 u 3 u 4 u 1, u 3 u 1 u 2 u 3 u 1 u 2 Remove <u 1, u 3> as t 5 is no longer skyline of this subspace. u 1 u 3 u 1 u 2 u 4 u 1 u 2 u 1 u 3 u 4 u 2 u 3 u 4 u 2 u 4 Cuboids that contain object t 5 u 3 u 4
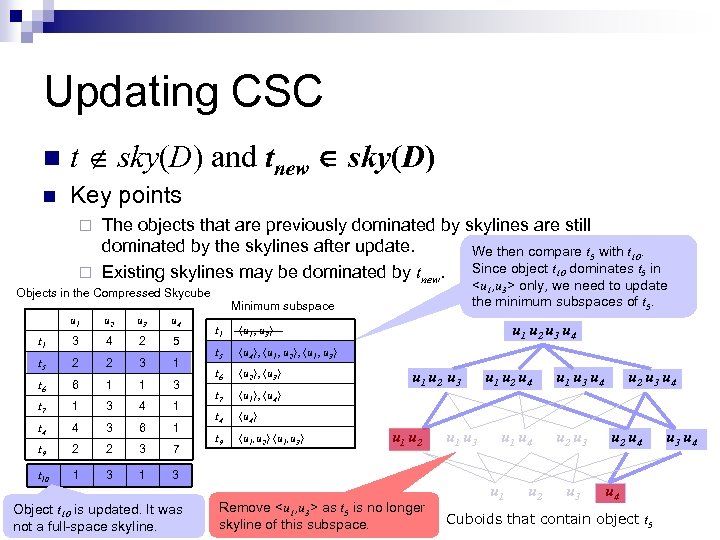
Updating CSC n t sky(D) and tnew sky(D) n Key points The objects that are previously dominated by skylines are still dominated by the skylines after update. We then compare t 5 with t 10. Since object t 10 dominates t 5 in ¨ Existing skylines may be dominated by tnew. ¨ Objects in the Compressed Skycube u 1 u 2 u 3 u 4 t 1 3 4 2 5 t 5 2 2 3 1 t 6 6 1 1 3 t 7 1 3 4 1 t 4 4 3 6 1 t 9 2 2 3 7 t 10 1 3 1 <u 1, u 3> only, we need to update the minimum subspaces of t 5. Minimum subspace 3 Object t 10 is updated. It was not a full-space skyline. t 1 t 5 u 4 , u 1, u 2 , u 1, u 3 t 6 u 2 , u 3 t 7 u 1 , u 4 t 4 u 4 t 9 u 1, u 2 u 1, u 3 u 1 u 2 u 3 u 4 u 1, u 3 u 1 u 2 u 3 u 1 u 2 Remove <u 1, u 3> as t 5 is no longer skyline of this subspace. u 1 u 3 u 1 u 2 u 4 u 1 u 2 u 1 u 3 u 4 u 2 u 3 u 4 u 2 u 4 Cuboids that contain object t 5 u 3 u 4
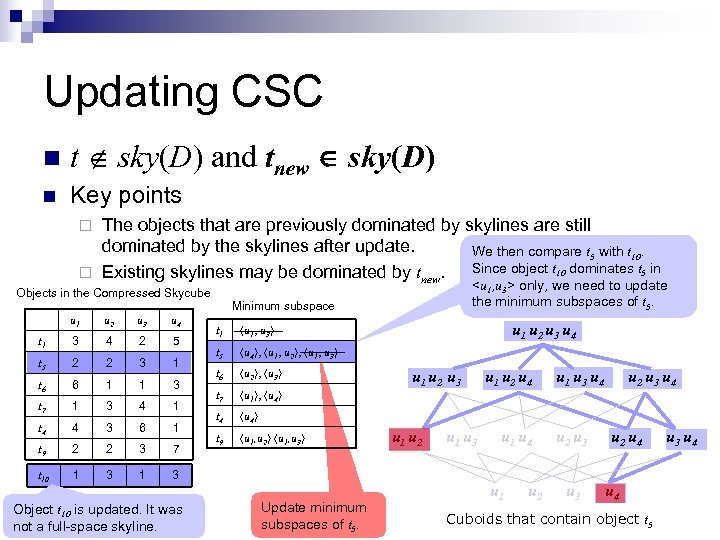
Updating CSC n t sky(D) and tnew sky(D) n Key points The objects that are previously dominated by skylines are still dominated by the skylines after update. We then compare t 5 with t 10. Since object t 10 dominates t 5 in ¨ Existing skylines may be dominated by tnew. ¨ Objects in the Compressed Skycube u 1 u 2 u 3 u 4 t 1 3 4 2 5 t 5 2 2 3 1 t 6 6 1 1 3 t 7 1 3 4 1 t 4 4 3 6 1 t 9 2 2 3 7 t 10 1 3 1 Minimum subspace 3 Object t 10 is updated. It was not a full-space skyline. <u 1, u 3> only, we need to update the minimum subspaces of t 5. t 1 t 5 u 4 , u 1, u 2 , u 1, u 3 t 6 u 2 , u 3 t 7 u 1 , u 4 t 4 u 4 t 9 u 1, u 2 u 1, u 3 u 1 u 2 u 3 u 4 u 1, u 3 Update minimum subspaces of t 5. u 1 u 2 u 3 u 1 u 2 u 1 u 3 u 1 u 2 u 4 u 1 u 2 u 1 u 3 u 4 u 2 u 3 u 4 u 2 u 4 Cuboids that contain object t 5 u 3 u 4

Updating CSC n t sky(D) and tnew sky(D) n Key points The objects that are previously dominated by skylines are still dominated by the skylines after update. ¨ Existing skylines may be dominated by tnew. ¨ Objects in the Compressed Skycube u 1 u 2 u 3 u 4 t 1 3 4 2 5 t 5 2 2 3 1 t 6 6 1 1 3 t 7 1 3 4 1 t 4 4 3 6 1 t 9 2 2 3 7 t 10 1 3 Object t 10 is updated. It was not a full-space skyline. Minimum subspace t 1 u 1, u 3 t 5 u 4 , u 1, u 2 , u 1, u 3 t 6 u 2 , u 3 t 7 u 1 , u 4 t 4 u 4 t 9 u 1, u 2 u 1, u 3 t 10 u 1 , u 3 Minimum subspaces of t 10 are u 1 , and u 3 . Similar for other objects, we update the skylines that are dominated by tnew. Then we find the minimum subspaces of tnew. The paper describes an algorithm to deduce the minimum subspaces of tnew from the previous skylines.

Updating CSC n t sky(D) and tnew sky(D) n Key points The objects that are previously dominated by skylines are still dominated by the skylines after update. ¨ Existing skylines may be dominated by tnew. ¨ Objects in the Compressed Skycube u 1 u 2 u 3 u 4 t 1 3 4 2 5 t 5 2 2 3 1 t 6 6 1 1 3 t 7 1 3 4 1 t 4 4 3 6 1 t 9 2 2 3 7 t 10 1 3 Object t 10 is updated. It was not a full-space skyline. Minimum subspace Compressed Skycube t 1 u 1, u 3 Cuboid Skyline t 5 u 4 , u 1, u 2 , u 1, u 3 u 1 t 7 , t 10 t 6 u 2 , u 3 u 2 t 6 t 7 u 1 , u 4 u 3 t 6 , t 10 t 4 u 4 t 5 , t 7, t 4 t 9 u 1, u 2 u 1, u 3 u 1, u 2 t 5 , t 9 u 1 , u 3 t 1 , t 5 , t 9 t 10 u 1 , u 3 Minimum subspaces of t 10 are u 1 , and u 3 . Finally, we update the compressed skycube. Insert object t 10 into the corresponding cuboids and remove the dominated objects.

Experimental Evaluation
![Storage Comparison n Settings: ¨ Dimensionality (Full-space) – [4, 8]; default = 6. ¨ Storage Comparison n Settings: ¨ Dimensionality (Full-space) – [4, 8]; default = 6. ¨](https://present5.com/presentation/93eed532090791d4fb723853ad6c6f46/image-66.jpg)
Storage Comparison n Settings: ¨ Dimensionality (Full-space) – [4, 8]; default = 6. ¨ Cardinality – [100 K, 500 K]; default = 300 K. ¨ Distribution: Independent, Corr, Anti-Corr.
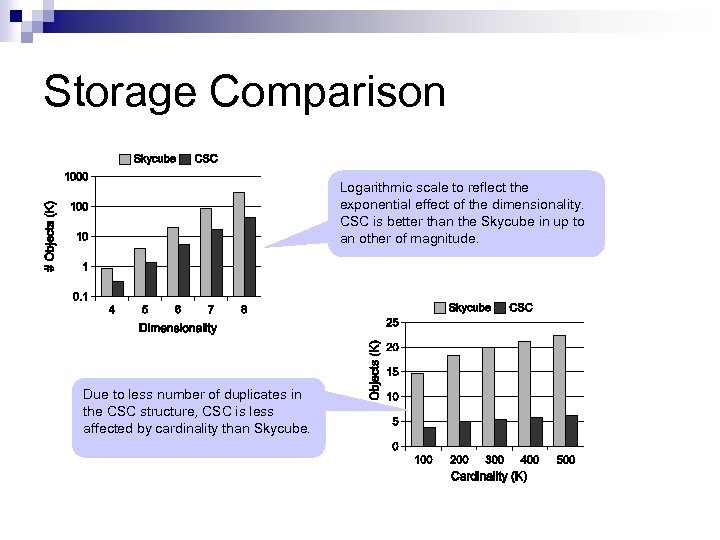
Storage Comparison Logarithmic scale to reflect the exponential effect of the dimensionality. CSC is better than the Skycube in up to an other of magnitude. Due to less number of duplicates in the CSC structure, CSC is less affected by cardinality than Skycube.
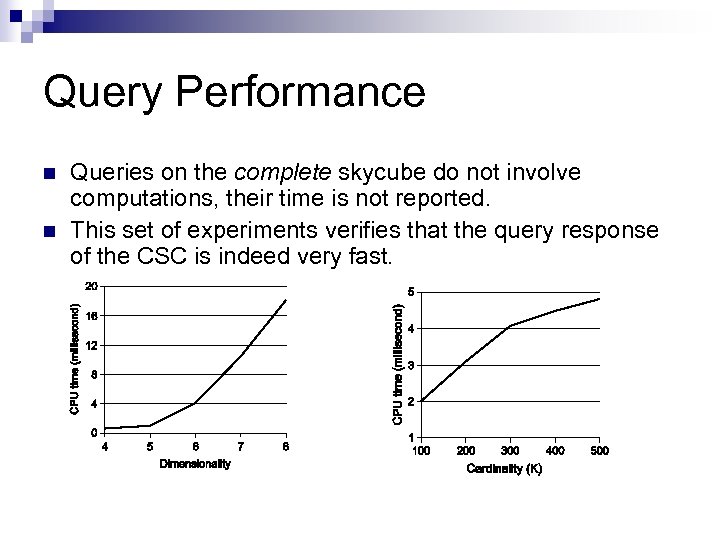
Query Performance n n Queries on the complete skycube do not involve computations, their time is not reported. This set of experiments verifies that the query response of the CSC is indeed very fast.
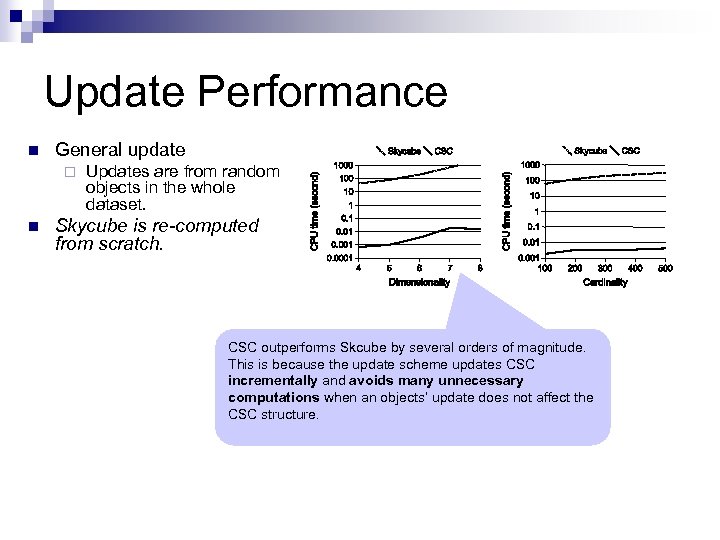
Update Performance n General update ¨ n Updates are from random objects in the whole dataset. Skycube is re-computed from scratch. CSC outperforms Skcube by several orders of magnitude. This is because the update scheme updates CSC incrementally and avoids many unnecessary computations when an objects’ update does not affect the CSC structure.
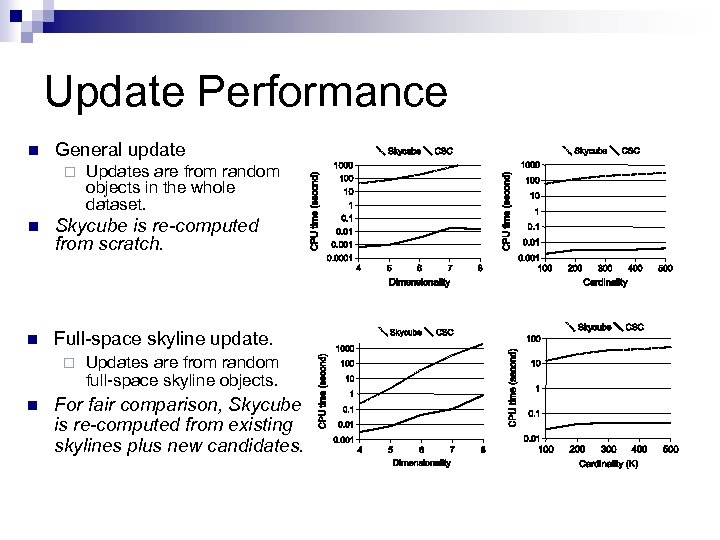
Update Performance n General update ¨ Updates are from random objects in the whole dataset. n Skycube is re-computed from scratch. n Full-space skyline update. ¨ n Updates are from random full-space skyline objects. For fair comparison, Skycube is re-computed from existing skylines plus new candidates.

Conclusion

Conclusions n In the paper, the authours ¨ addressed the update support of the skycube in dynamic environment, and provided an efficient and scalable solution for online skyline query system. ¨ proposed a compact structure, the Compressed Skycube (CSC), with about 10% disk space of the Complete Skycube and fast query response. ¨ proposed an object-aware update scheme, such that different updates trigger different amount of computation. The Compressed Skycube outperforms the Skycube in update by several orders of magnitude.

Thank you! Tian Xia and Donghui Zhang. Refreshing the Sky: the Compressed Skycube with Efficient Support for Frequent Updates. SIGMOD 2006.

DB Seminar Schedule n Seminar Schedule ================================= Chui Chun Kit 30/11/07 Gong Jian Jim 7/12/07 Loo Kin Kong 14/12/07 Ngai Wang Kay Jackie 21/12/07 Siu Wing Yan Angela 4/1/08 Tam Ming Wai 11/1/08 Tsang Pui Kwan Smith 18/1/08 U Leong Hou Kamiru 25/1/08 Wong Wai Kit 1/2/08 Cui Yingjie Jason 15/2/08 LEE King For 22/2/08 Lin Zhifeng Arthur 7/3/08 Yuan Wenjun Clement 14/3/08 Zhang Shiming Simon 28/3/08 Zhang Yiwei Kelvin 11/4/08 LEE Yau Tat 18/4/08 Pan Guodong Delvin 25/4/08 n Please send the abstract to dbgroup@cs. hku. hk one week before your talk
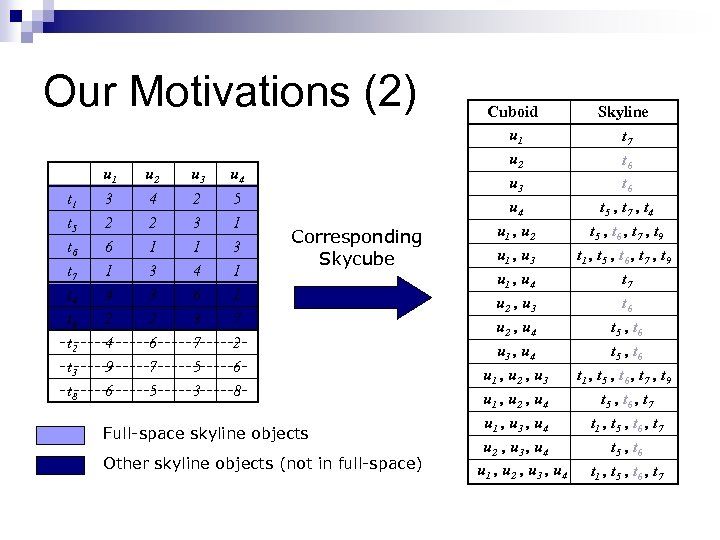
Our Motivations (2) u 1 u 2 u 3 u 4 t 1 t 5 t 6 3 2 6 4 2 1 2 3 1 5 1 3 t 7 t 4 t 9 t 2 t 3 t 8 1 4 2 4 9 6 3 3 2 6 7 5 4 6 3 7 5 3 1 1 7 2 6 8 Corresponding Skycube Full-space skyline objects Other skyline objects (not in full-space) Cuboid u 1 Skyline t 7 u 2 t 6 u 3 t 6 u 4 t 5 , t 7 , t 4 u 1 , u 2 t 5 , t 6 , t 7 , t 9 u 1 , u 3 t 1 , t 5 , t 6 , t 7 , t 9 u 1 , u 4 t 7 u 2 , u 3 t 6 u 2 , u 4 t 5 , t 6 u 3 , u 4 t 5 , t 6 u 1 , u 2 , u 3 t 1 , t 5 , t 6 , t 7 , t 9 u 1 , u 2 , u 4 t 5 , t 6 , t 7 u 1 , u 3 , u 4 t 1 , t 5 , t 6 , t 7 u 2 , u 3 , u 4 t 5 , t 6 u 1 , u 2 , u 3 , u 4 t 1 , t 5 , t 6 , t 7

Querying CSC n n LEMMA 1: Given a query space Uq and an object t, if for any subspace Ui in mss(t), Ui Uq, then t is not in the skyline of Uq. Lemma 1 implies two important facts: 1) 2) n Only the existing cuboids that Uq need to be searched. No other cuboids need to be accessed or computed in the query process. Example: Uq = u 2, u 3 , u 4 , and t 9 can be safely pruned. u 1 u 2 u 3 u 4 t 1 t 5 t 6 3 2 6 4 2 1 2 3 1 5 1 3 t 7 t 4 t 9 1 4 2 3 3 2 4 6 3 1 1 7 Cuboid u 1 u 2 u 3 Skyline u 4 u 1 , u 2 t 5 , t 7 , t 4 t 5 , t 9 u 1 , u 3 t 1 , t 5 , t 9 t 7 t 6

Some properties of CSC n The number of non-empty cuboids is solely decided by sky(D). ¨ In other words, there does not exist a cuboid which only contains objects not in sky(D). ¨ Each non-empty cuboid in CSC contains at least one object in sky(D). ¨ Therefore, as long as the full-space skyline is unchanged, no new cuboid will be added to CSC.
93eed532090791d4fb723853ad6c6f46.ppt