Data Mining Concepts and Techniques Slides for

Data Mining: Concepts and Techniques — Slides for Textbook — — Chapter 10 — ©Jiawei Han and Micheline Kamber Intelligent Database Systems Research Lab School of Computing Science Simon Fraser University, Canada http: //www. cs. sfu. ca 16 March 2018 Data Mining: Concepts and Techniques 1

Chapter 8. Cluster Analysis n What is Cluster Analysis? n Types of Data in Cluster Analysis n A Categorization of Major Clustering Methods n Partitioning Methods n Hierarchical Methods n Density-Based Methods n Grid-Based Methods n Model-Based Clustering Methods n Outlier Analysis n Summary 16 March 2018 Data Mining: Concepts and Techniques 2

Clustering Problem Formally n n n Given a database D={t 1, t 2, …, tn} of tuples and an integer value k, the Clustering Problem is to define a mapping f: D {1, . . , k} where each ti is assigned to one cluster Kj, 1<=j<=k. A cluster, Kj, contains precisely those tuples mapped to it. Unlike classification problem, clusters are not known a priori. 16 March 2018 Data Mining: Concepts and Techniques 4

General Applications of Clustering n n n Pattern Recognition Spatial Data Analysis n create thematic maps in GIS by clustering feature spaces n detect spatial clusters and explain them in spatial data mining Image Processing Economic Science (especially market research) WWW n Document classification n Cluster Weblog data to discover groups of similar access patterns 16 March 2018 Data Mining: Concepts and Techniques 5

Examples of Clustering Applications n n n Marketing: Help marketers discover distinct groups in their customer bases, and then use this knowledge to develop targeted marketing programs Land use: Identification of areas of similar land use in an earth observation database Insurance: Identifying groups of motor insurance policy holders with a high average claim cost City-planning: Identifying groups of houses according to their house type, value, and geographical location Earth-quake studies: Observed earth quake epicenters should be clustered along continent faults 16 March 2018 Data Mining: Concepts and Techniques 6

Clustering as a Preprocessing Tool (Utility) n Summarization: n n Compression: n n Image processing: vector quantization Finding K-nearest Neighbors n n Preprocessing for regression, PCA, classification, and association analysis Localizing search to one or a small number of clusters Outlier detection n Outliers are often viewed as those “far away” from any cluster 7

Clustering Issues – The appropriate number of clusters for each data set. – How to define similarity or the criterion used to group data together. – Outlier handling is difficult. Should they be a part of an existing cluster, or another cluster? – Dynamic database, how to update the clusters when there are changes in data. – The semantic meaning of each cluster. (Contrast with classes in classification process, each has a definitive meaning. ) – Type of attributes that the clustering algorithm can handle. – Scalability to large datasets. 16 March 2018 Data Mining: Concepts and Techniques 8

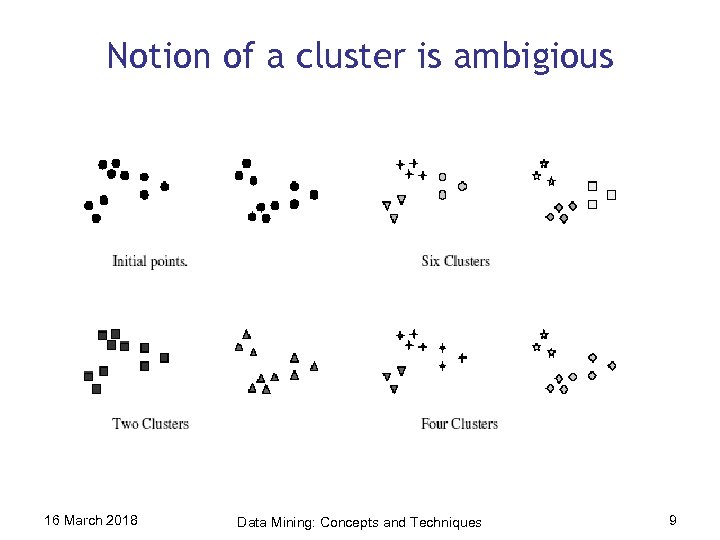Notion of a cluster is ambigious 16 March 2018 Data Mining: Concepts and Techniques 9

Different types of clusters Cluster 1 Cluster 2 Cluster 3 16 March 2018 Cluster 4 Data Mining: Concepts and Techniques 10

Quality: What Is Good Clustering? • A good clustering method will produce high quality clusters – high intra-class similarity: cohesive within clusters – low inter-class similarity: distinctive between clusters • The quality of a clustering method depends on – the similarity measure used by the method – its implementation, and – Its ability to discover some or all of the hidden patterns 11

Requirements of Clustering in Data Mining n Scalability n Ability to deal with different types of attributes n Discovery of clusters with arbitrary shape n Minimal requirements for domain knowledge to determine input parameters n Able to deal with noise and outliers n Insensitive to order of input records n High dimensionality n Incorporation of user-specified constraints n Interpretability and usability 16 March 2018 Data Mining: Concepts and Techniques 12

Measure the Quality of Clustering n n Dissimilarity/Similarity metric n Similarity is expressed in terms of a distance function, typically metric: d(i, j) n The definitions of distance functions are usually rather different for interval-scaled, boolean, categorical, ordinal ratio, and vector variables n Weights should be associated with different variables based on applications and data semantics Quality of clustering: n There is usually a separate “quality” function that measures the “goodness” of a cluster. n It is hard to define “similar enough” or “good enough” n The answer is typically highly subjective 13

Similarity and Dissimilarity Metric • Similarity - Numerical measure of how alike two data objects are. - Is higher when objects are more alike. - Often falls in the range [0, 1] • Dissimilarity - Numerical measure of how different two data objects are. - Is lower when objects are more alike. - Minimum dissimilarity is often 0. - Upper limit varies • Proximity refers to a similarity or dissimilarity 16 March 2018 Data Mining: Concepts and Techniques 14

Data Structures n Data matrix n n n This represents n objects, such as persons, with p variables (also called measurements or attributes), such as age, height, gender, race, and so on. Called “two modes” : since rows and columns represent different entities Dissimilarity matrix n n n Stores a collection of proximities that are available for all pairs of n objects. (n by n matrix) Called “one mode” : since it reprsents the same entity d(i, j) is the measured difference or dissimilarity between objects i and j. 16 March 2018 Data Mining: Concepts and Techniques 15

Measure the Quality of Clustering n n n Dissimilarity/Similarity metric: Similarity is expressed in terms of a distance function, which is typically metric: d(i, j) There is a separate “quality” function that measures the “goodness” of a cluster. The definitions of distance functions are usually very different for interval-scaled, boolean, categorical, ordinal and ratio variables. Weights should be associated with different variables based on applications and data semantics. It is hard to define “similar enough” or “good enough” n the answer is typically highly subjective. 16 March 2018 Data Mining: Concepts and Techniques 16

Type of data in clustering analysis n Interval-scaled variables: n Binary variables: n Nominal, ordinal, and ratio variables: n Variables of mixed types: 16 March 2018 Data Mining: Concepts and Techniques 17

Interval-valued variables n Interval-scaled (based) variables are continuous measurements of a roughly linear scale (such as weight, height, weather). n The measurement unit used can affect the clustering analysis. Using inches or meters for a measurement may lead to a very different clustering structure. To avoid dependence on on the choice of measurement units, the data should be standardized. n How to Standardize data n Calculate the mean absolute deviation: where n n Calculate the standardized measurement (z-score) Using mean absolute deviation is more robust than using standard deviation 16 March 2018 Data Mining: Concepts and Techniques 18

Similarity and Dissimilarity Between Objects n n Distances are normally used to measure the similarity or dissimilarity between two data objects Some popular ones include: Minkowski distance: where i = (xi 1, xi 2, …, xip) and j = (xj 1, xj 2, …, xjp) are two pdimensional data objects, and q is a positive integer n If q = 1, d is Manhattan distance 16 March 2018 Data Mining: Concepts and Techniques 19

Similarity and Dissimilarity Between Objects (Cont. ) n If q = 2, d is Euclidean distance: n Properties n n n d(i, j) 0 d(i, i) = 0 d(i, j) = d(j, i) d(i, j) d(i, k) + d(k, j) Also one can use weighted distance, parametric Pearson product moment correlation, or other disimilarity measures. 16 March 2018 Data Mining: Concepts and Techniques 20

Euclidean Distance Source : S. Ranka 16 March 2018 Data Mining: Concepts and Techniques 21

Similarity and Dissimilarity Between Objects (Cont. ) n Determine similarity between two objects. Definition: Similarity characteristics: Source : Dunham 16 March 2018 Data Mining: Concepts and Techniques 22

Similarity and Dissimilarity Between Objects (Cont. ) 16 March 2018 Data Mining: Concepts and Techniques 23

Similarity and Dissimilarity Between Objects (Cont. ) n Measure dissimilarity between objects 16 March 2018 Data Mining: Concepts and Techniques 24

Binary Variables n How can we compute the dissimilaty between objects descired by by either symmetic or asymmetic binary variables. A binary variable has only two states 0 and 1. n Symetric : both states are equally valuable and carry the same weight. n n Example: gender having states male and female Asymmetric : the outcome states are not equally important, such as the positive and negative outcomes of a disease test. n Example : n HIV positive - represented by 1 (rarest) n HIV negative – represented by 0 16 March 2018 Data Mining: Concepts and Techniques 25

Binary Variables n A contingency table for binary data Object j Object i • Simple matching coefficient (invariant, if the binary variable is symmetric): • Jaccard coefficient (noninvariant if the binary variable is asymmetric): 16 March 2018 Data Mining: Concepts and Techniques 26

Dissimilarity between Binary Variables n Example n n n gender is a symmetric attribute the remaining attributes are asymmetric binary let the values Y and P be set to 1, and the value N be set to 0 16 March 2018 Data Mining: Concepts and Techniques 27

Nominal Variables n n A nominal variable is a generalization of the binary variable in that it can take more than 2 states, e. g. , red, yellow, blue, green Method 1: Simple matching n n m: # of matches, p: total # of variables Method 2: use a large number of binary variables n creating a new binary variable for each of the M nominal states 16 March 2018 Data Mining: Concepts and Techniques 28

Ordinal Variables n order is important, e. g. , rank n An ordinal variable can be discrete or continuous n n A discrete ordinal variable resebles a nominal variable, except that M states of the ordinal value are ordered in a meaningful sequence (e. g. Projesional ranks : Assistant, Associate, Full professor) A continuous ordinal variable looks like a set of continous data of of an unkwon scale; that is, the realtive ordering of values is essential but their actual size is not. (e. g. The relative ranking in a particular sport: gold, silver, and bronze) 16 March 2018 Data Mining: Concepts and Techniques 29

Ordinal Variables n They can be treated like interval-scaled Suppose f is a variable from a set of ordinal variables descibing n objects n n The value of f for the ith object is xif f has Mf ordered states 1, . . , Mf n. Replace each xif by its rank corresponding rank n n map the range of each variable onto [0, 1] by replacing i-th object in the f-th variable by n n compute the dissimilarity using methods for interval-scaled variables 16 March 2018 Data Mining: Concepts and Techniques 30

Ratio-Scaled Variables n n Ratio-scaled variable: A ratio scale variable makes a positive measurement on a nonlinear scale, approximately at exponential scale, such as Ae. Bt or Ae-Bt Methods: n treat them like interval-scaled variables — not a good choice! (why? ) it is likely that the scale may be distorted. n apply logarithmic transformation yif = log(xif) n treat them as continuous ordinal data treat their rank as intervalscaled. 16 March 2018 Data Mining: Concepts and Techniques 31

Variables of Mixed Types n n A database may contain all the six types of variables n symmetric binary, asymmetric binary, nominal, ordinal, interval and ratio. One may use a weighted formula to combine their effects. n n n f is binary or nominal: dij(f) = 0 if xif = xjf , or dij(f) = 1 otherwise f is interval-based: use the normalized distance f is ordinal or ratio-scaled n compute ranks rif and n and treat zif as interval-scaled 16 March 2018 Data Mining: Concepts and Techniques 32

Considerations for Cluster Analysis n Partitioning criteria n n Separation of clusters n n Exclusive (e. g. , one customer belongs to only one region) vs. non -exclusive (e. g. , one document may belong to more than one class) Similarity measure n n Single level vs. hierarchical partitioning (often, multi-level hierarchical partitioning is desirable) Distance-based (e. g. , Euclidian, road network, vector) vs. connectivity-based (e. g. , density or contiguity) Clustering space n Full space (often when low dimensional) vs. subspaces (often in high-dimensional clustering) 33

Requirements and Challenges n n n Scalability n Clustering all the data instead of only on samples Ability to deal with different types of attributes n Numerical, binary, categorical, ordinal, linked, and mixture of these Constraint-based clustering n User may give inputs on constraints n Use domain knowledge to determine input parameters Interpretability and usability Others n Discovery of clusters with arbitrary shape n Ability to deal with noisy data n Incremental clustering and insensitivity to input order n High dimensionality 34

Chapter 8. Cluster Analysis n What is Cluster Analysis? n Types of Data in Cluster Analysis n A Categorization of Major Clustering Methods n Partitioning Methods n Hierarchical Methods n Density-Based Methods n Grid-Based Methods n Model-Based Clustering Methods n Outlier Analysis n Summary 16 March 2018 Data Mining: Concepts and Techniques 35

Major Clustering Approaches (Han) n Partitioning algorithms: Construct various partitions and then evaluate them by some criterion n Hierarchy algorithms: Create a hierarchical decomposition of the set of data (or objects) using some criterion n Density-based: based on connectivity and density functions n Grid-based: based on a multiple-level granularity structure n Model-based: A model is hypothesized for each of the clusters and the idea is to find the best fit of that model to each other 16 March 2018 Data Mining: Concepts and Techniques 36

Major Clustering Approaches (I) n n Partitioning approach: n Construct various partitions and then evaluate them by some criterion, e. g. , minimizing the sum of square errors n Typical methods: k-means, k-medoids, CLARANS Hierarchical approach: n Create a hierarchical decomposition of the set of data (or objects) using some criterion n Typical methods: Diana, Agnes, BIRCH, CAMELEON Density-based approach: n Based on connectivity and density functions n Typical methods: DBSACN, OPTICS, Den. Clue Grid-based approach: n based on a multiple-level granularity structure n Typical methods: STING, Wave. Cluster, CLIQUE 37

Major Clustering Approaches (II) n n Model-based: n A model is hypothesized for each of the clusters and tries to find the best fit of that model to each other n Typical methods: EM, SOM, COBWEB Frequent pattern-based: n Based on the analysis of frequent patterns n Typical methods: p-Cluster User-guided or constraint-based: n Clustering by considering user-specified or application-specific constraints n Typical methods: COD (obstacles), constrained clustering Link-based clustering: n Objects are often linked together in various ways n Massive links can be used to cluster objects: Sim. Rank, Link. Clus 38

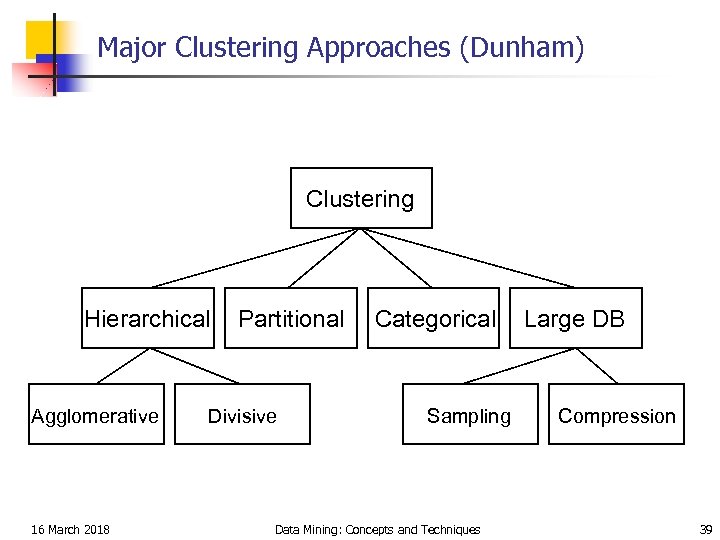Major Clustering Approaches (Dunham) Clustering Hierarchical Agglomerative 16 March 2018 Partitional Divisive Categorical Sampling Data Mining: Concepts and Techniques Large DB Compression 39