Скачать презентацию Data Mining Concepts and Techniques Chapter 8
3438dc797ef887960217f41f3a3fb151.ppt
- Количество слайдов: 42
Data Mining: Concepts and Techniques — Chapter 8 — 8. 3 Mining sequence patterns in non-biological databases Jiawei Han and Micheline Kamber Department of Computer Science University of Illinois at Urbana-Champaign www. cs. uiuc. edu/~hanj © 2009 Jiawei Han and Micheline Kamber. All rights reserved. 1
16 March 2018 Data Mining: Concepts and Techniques 2
Sequence Databases & Sequential Patterns n n n Transaction databases, time-series databases vs. sequence databases Frequent patterns vs. (frequent) sequential patterns Applications of sequential pattern mining n Customer shopping sequences: n First buy computer, then CD-ROM, and then digital camera, within 3 months. n Medical treatments, natural disasters (e. g. , earthquakes), science & eng. processes, stocks and markets, etc. n Telephone calling patterns, Weblog click streams n Program execution sequence data sets n DNA sequences and gene structures 3
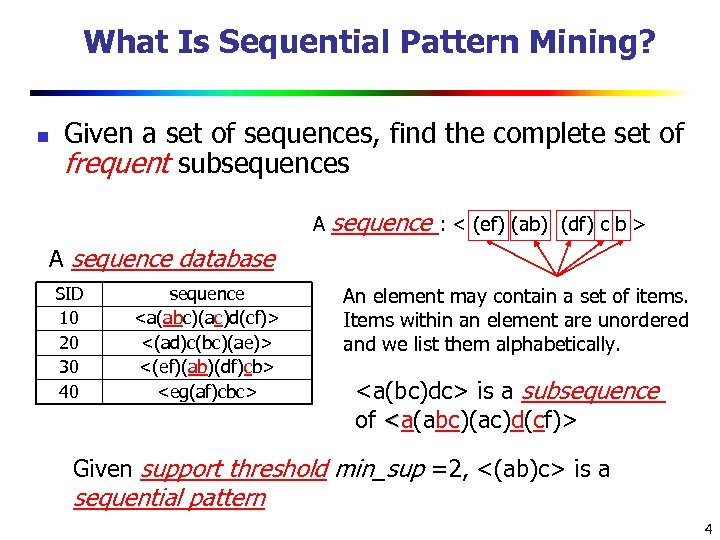What Is Sequential Pattern Mining? n Given a set of sequences, find the complete set of frequent subsequences A sequence : < (ef) (ab) (df) c b > A sequence database SID 10 20 30 40 sequence
Challenges on Sequential Pattern Mining n n A huge number of possible sequential patterns are hidden in databases A mining algorithm should n n n find the complete set of patterns, when possible, satisfying the minimum support (frequency) threshold be highly efficient, scalable, involving only a small number of database scans be able to incorporate various kinds of user-specific constraints 5
Sequential Pattern Mining Algorithms n Concept introduction and an initial Apriori-like algorithm n n Agrawal & Srikant. Mining sequential patterns, ICDE’ 95 Apriori-based method: GSP (Generalized Sequential Patterns: Srikant & Agrawal @ EDBT’ 96) n Pattern-growth methods: Free. Span & Prefix. Span (Han et al. @KDD’ 00; Pei, et al. @ICDE’ 01) n Vertical format-based mining: SPADE (Zaki@Machine Leanining’ 00) n Constraint-based sequential pattern mining (SPIRIT: Garofalakis, Rastogi, Shim@VLDB’ 99; Pei, Han, Wang @ CIKM’ 02) n Mining closed sequential patterns: Clo. Span (Yan, Han & Afshar @SDM’ 03) 6
The Apriori Property of Sequential Patterns n A basic property: Apriori (Agrawal & Sirkant’ 94) n If a sequence S is not frequent n Then none of the super-sequences of S is frequent n E. g,
GSP—Generalized Sequential Pattern Mining n n n GSP (Generalized Sequential Pattern) mining algorithm n proposed by Agrawal and Srikant, EDBT’ 96 Outline of the method n Initially, every item in DB is a candidate of length-1 n for each level (i. e. , sequences of length-k) do n scan database to collect support count for each candidate sequence n generate candidate length-(k+1) sequences from length-k frequent sequences using Apriori n repeat until no frequent sequence or no candidate can be found Major strength: Candidate pruning by Apriori 8
Finding Length-1 Sequential Patterns n n n Examine GSP using an example Initial candidates: all singleton sequences n , ,
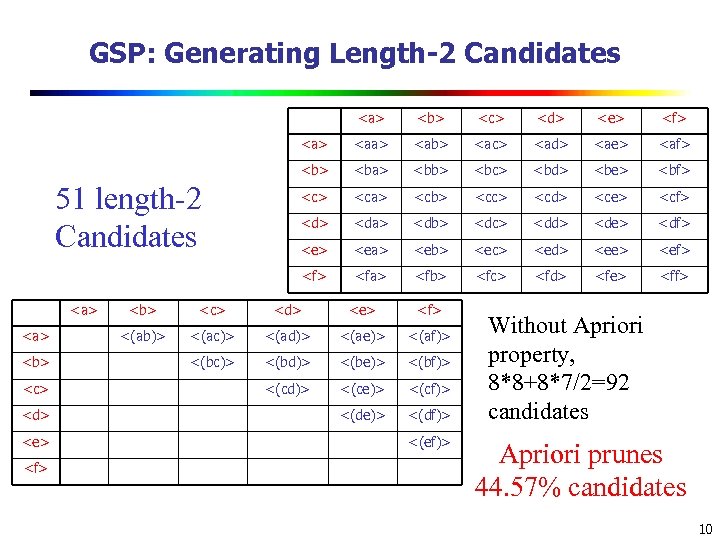GSP: Generating Length-2 Candidates
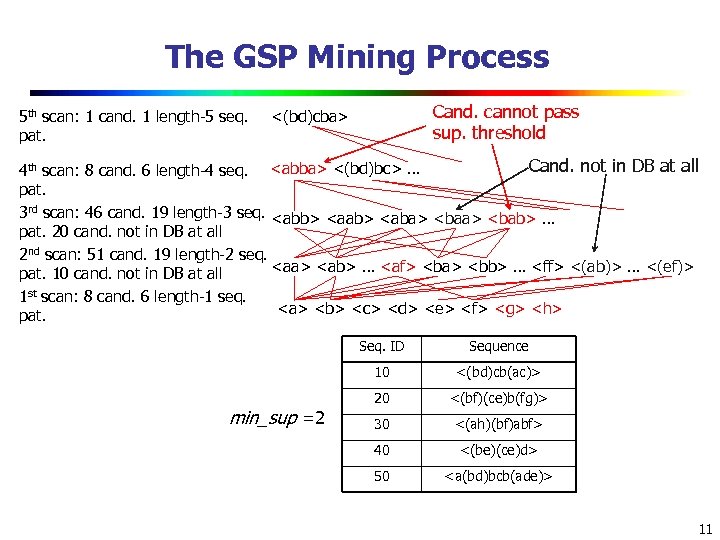The GSP Mining Process 5 th scan: 1 cand. 1 length-5 seq. pat. Cand. cannot pass sup. threshold <(bd)cba> Cand. not in DB at all 4 th scan: 8 cand. 6 length-4 seq.
Candidate Generate-and-test: Drawbacks n A huge set of candidate sequences generated n n Especially 2 -item candidate sequence Multiple Scans of database needed n The length of each candidate grows by one at each database scan n Inefficient for mining long sequential patterns n A long pattern grow up from short patterns n The number of short patterns is exponential to the length of mined patterns 12
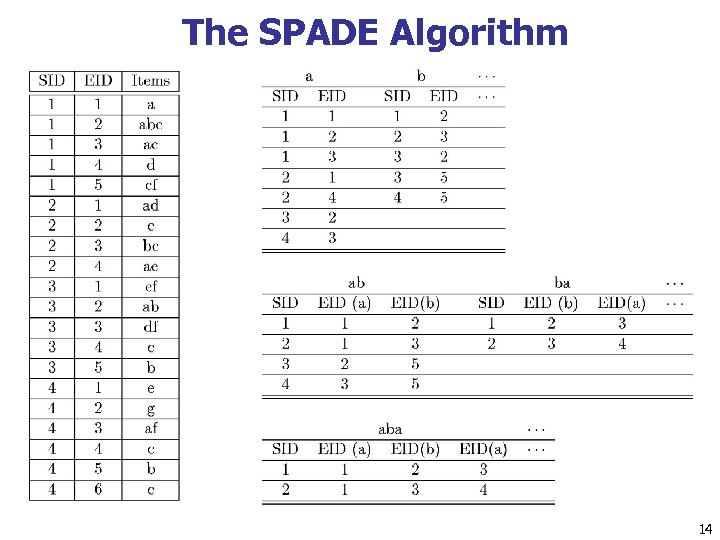
The SPADE Algorithm n SPADE (Sequential PAttern Discovery using Equivalent Class) developed by Zaki 2001 n A vertical format sequential pattern mining method n A sequence database is mapped to a large set of n n Item:
The SPADE Algorithm 14
Bottlenecks of GSP and SPADE n A huge set of candidates could be generated n 1, 000 frequent length-1 sequences generate s huge number of length-2 candidates! n Multiple scans of database in mining n Breadth-first search n Mining long sequential patterns n Needs an exponential number of short candidates n A length-100 sequential pattern needs 1030 candidate sequences! 15
Prefix and Suffix (Projection) n ,
Mining Sequential Patterns by Prefix Projections n n Step 1: find length-1 sequential patterns n , ,
Finding Seq. Patterns with Prefix n Only need to consider projections w. r. t. n -projected database: n <(abc)(ac)d(cf)> n <(_d)c(bc)(ae)> n n n <(_b)(df)cb> <(_f)cbc> SID 10 20 30 40 sequence
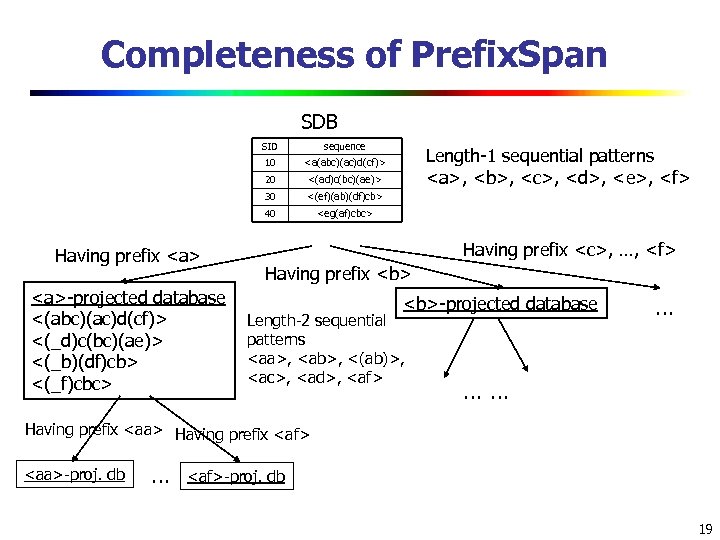Completeness of Prefix. Span SDB SID 10 <(ad)c(bc)(ae)> 30 <(ef)(ab)(df)cb> 40 -projected database <(abc)(ac)d(cf)> <(_d)c(bc)(ae)> <(_b)(df)cb> <(_f)cbc>
Efficiency of Prefix. Span n No candidate sequence needs to be generated n Projected databases keep shrinking n Major cost of Prefix. Span: Constructing projected databases n Can be improved by pseudo-projections 20
Speed-up by Pseudo-projection n Major cost of Prefix. Span: projection n Postfixes of sequences often appear repeatedly in recursive projected databases n When (projected) database can be held in main memory, use pointers to form projections n Pointer to the sequence n Offset of the postfix s=
Pseudo-Projection vs. Physical Projection n Pseudo-projection avoids physically copying postfixes n n However, it is not efficient when database cannot fit in main memory n n Efficient in running time and space when database can be held in main memory Disk-based random accessing is very costly Suggested Approach: n n Integration of physical and pseudo-projection Swapping to pseudo-projection when the data set fits in memory 22
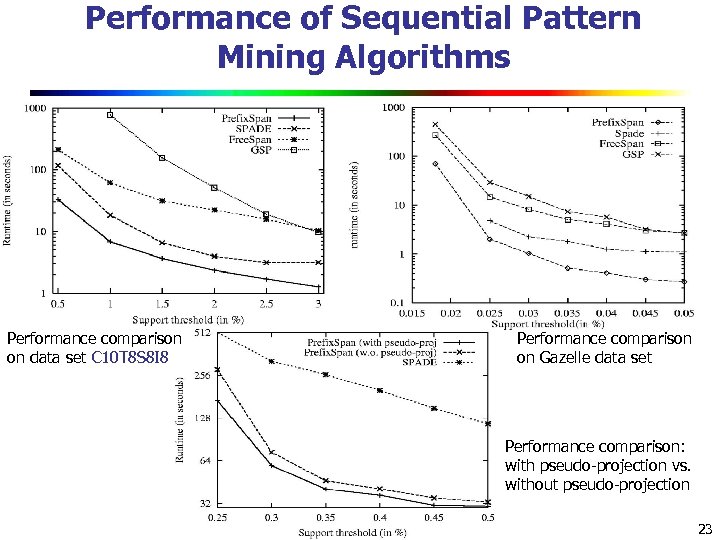Performance of Sequential Pattern Mining Algorithms Performance comparison on data set C 10 T 8 S 8 I 8 Performance comparison on Gazelle data set Performance comparison: with pseudo-projection vs. without pseudo-projection 23
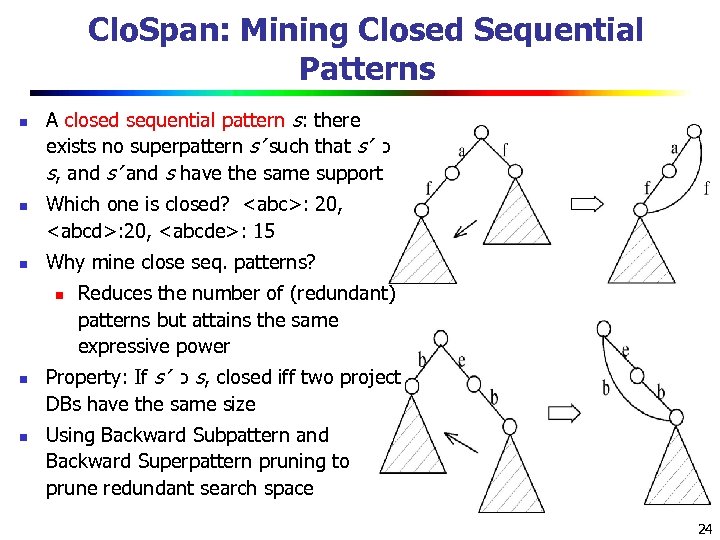Clo. Span: Mining Closed Sequential Patterns n n n A closed sequential pattern s: there exists no superpattern s’ such that s’ כ s, and s’ and s have the same support Which one is closed?
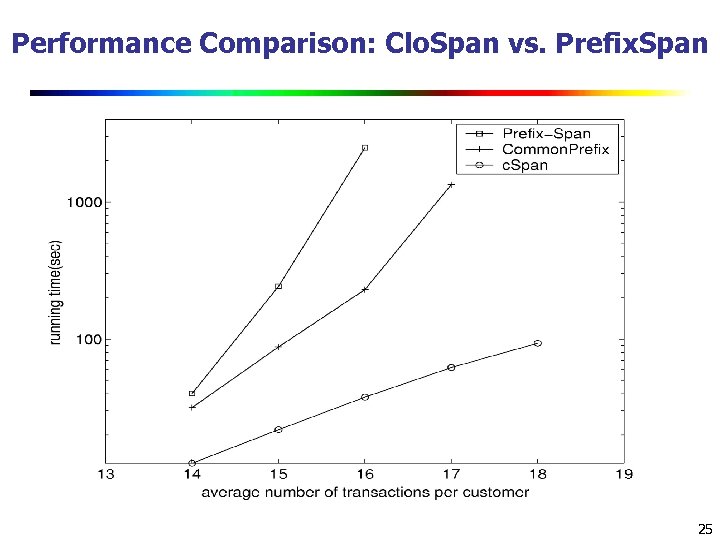Performance Comparison: Clo. Span vs. Prefix. Span 25
Constraint-Based Seq. -Pattern Mining n n Constraint-based sequential pattern mining n Constraints: User-specified, for focused mining of desired patterns n How to explore efficient mining with constraints? — Optimization Classification of constraints n Anti-monotone: E. g. , value_sum(S) < 150, min(S) > 10 n Monotone: E. g. , count (S) > 5, S {PC, digital_camera} n Succinct: E. g. , length(S) 10, S {Pentium, MS/Office, MS/Money} n Convertible: E. g. , value_avg(S) < 25, profit_sum (S) > 160, max(S)/avg(S) < 2, median(S) – min(S) > 5 n Inconvertible: E. g. , avg(S) – median(S) = 0 26
From Sequential Patterns to Structured Patterns n n Sets, sequences, trees, graphs, and other structures n Transaction DB: Sets of items n {{i 1, i 2, …, im}, …} n Seq. DB: Sequences of sets: n {<{i 1, i 2}, …, {im, in, ik}>, …} n Sets of Sequences: n {{, …,
Alternative I: Episodes and Episode Pattern Mining n Alternative patterns: Episodes and regular expressions n n Parallel episodes: A & B n n Serial episodes: A B Regular expressions: (A|B)C*(D E) Methods for episode pattern mining n Method 1: Variations of Apriori/GSP-like algorithms n Method 2: Projection-based pattern growth n n Can you work out the details? Question: What is the difference between mining episodes and constraint-based pattern mining? 28
Alternative 2: Periodicity Analysis n n Periodicity is everywhere: tides, seasons, daily power consumption, etc. Full periodicity n Every point in time contributes (precisely or approximately) to the periodicity Partial periodicity: n Only some segments contribute to the periodicity n Jim reads NY Times 7: 00 -7: 30 am every week day Methods n Full periodicity: FFT, other statistical analysis methods n Partial and cyclic periodicity: pattern mining methods 29
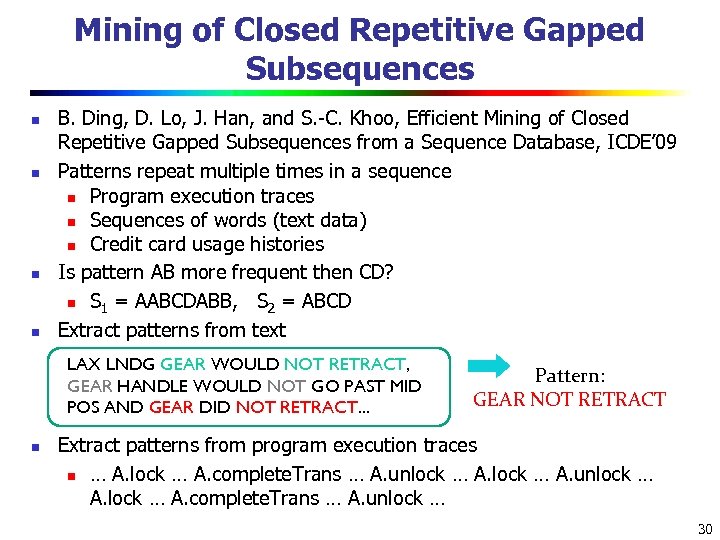Mining of Closed Repetitive Gapped Subsequences n n B. Ding, D. Lo, J. Han, and S. -C. Khoo, Efficient Mining of Closed Repetitive Gapped Subsequences from a Sequence Database, ICDE’ 09 Patterns repeat multiple times in a sequence n Program execution traces n Sequences of words (text data) n Credit card usage histories Is pattern AB more frequent then CD? n S 1 = AABCDABB, S 2 = ABCD Extract patterns from text LAX LNDG GEAR WOULD NOT RETRACT, GEAR HANDLE WOULD NOT GO PAST MID POS AND GEAR DID NOT RETRACT. . . n Pattern: GEAR NOT RETRACT Extract patterns from program execution traces n … A. lock … A. complete. Trans … A. unlock … 30
Repetitive Gapped Subsequence: Support n Repetitive instances of a pattern within each sequence n sup(P): the maximum NON-overlapping instances set sup(P) = max{|INS|: INS is a set of non-overlapping instances of P} n Why non-overlapping n Avoid over-estimating the frequency: in AAAABBBBCCCC, 43 instances of ABC, and 4 non-overlapping ones n Maximize the size of the non-overlapping instance set n n n Measure how frequent a pattern is A unified definition for all patterns Example n sup(AB) = 4 4 non-overlapping instances S 1 = A A B C D A B B, S 2 = A B CD 3 non-overlapping instances 31
Properties of Repetitive Support n n n Monotonicity n If P’ is a super-pattern of P, then sup(P’) ≤ sup(P) n Each INS’ = a set of non-overlapping instances of P’ n Construct from INS’: INS = a set of non-overlapping instances of P |INS| = |INS’| n sup(P’) = max{ |INS’| } ≤ max{ |INS’| } = sup(P) n Example: n ABA in ABAABA n AB in ABAABA Apriori Property Closed patterns have the same monotonicity 32
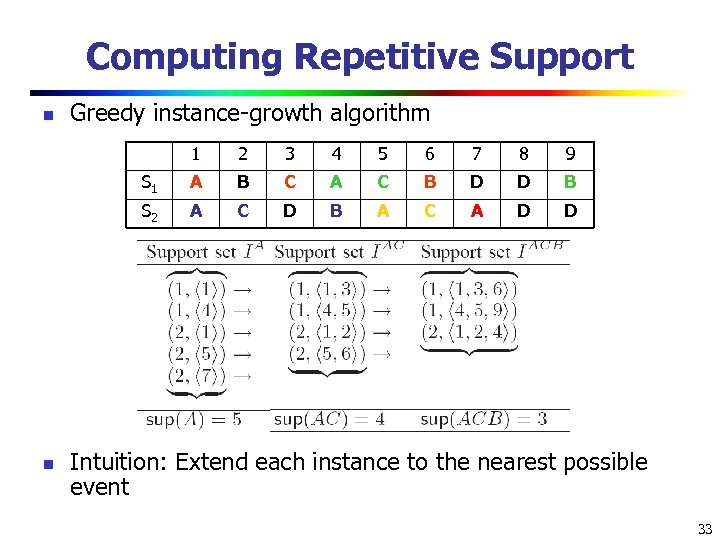Computing Repetitive Support n Greedy instance-growth algorithm 1 3 4 5 6 7 8 9 S 1 A B C A C B D D B S 2 n 2 A C D B A C A D D Intuition: Extend each instance to the nearest possible event 33
Computing Repetitive Support n Correctness of greedy instance-growth algorithm n Optimality: sup(P) = max{ |INS| } n Leftmost support set INS of P → Leftmost support set INS+ of pattern P○e n Instance-growth routine INSgrow(P, INS, e): n Given a support set INS of P, with |INS| = sup(P), and event e n Extend each instance in INS to the nearest possible event e + of n INSgrow(P, INS, e) returns a support set INS pattern P○e 34
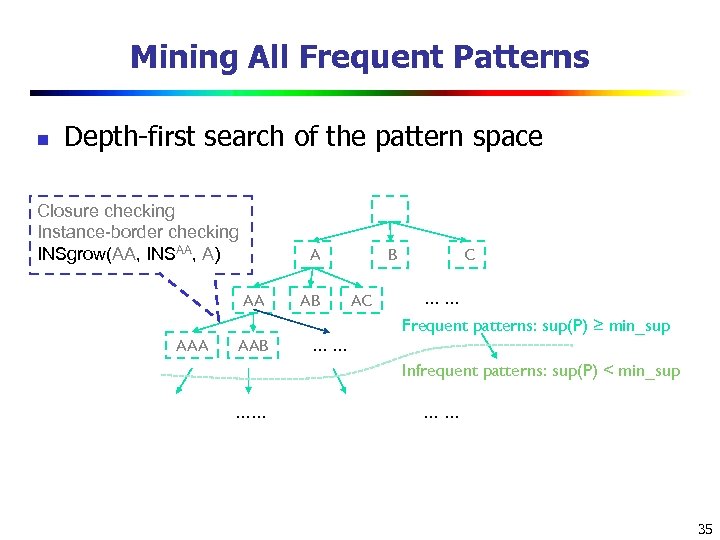Mining All Frequent Patterns n Depth-first search of the pattern space Closure checking Instance-border checking INSgrow(AA, INSAA, A) A AA AB B AC C …… Frequent patterns: sup(P) ≥ min_sup AAA AAB …… Infrequent patterns: sup(P) < min_sup …… …… 35
Mining Closed Patterns n n Pattern extension n Patterns with one more event in P = e 1 e 2 … em n Extension(P, e) = {ee 1 e 2…em, e 1 ee 2…em, …, e 1 e 2…eme} Closure checking n Pattern P is NOT closed iff sup(P) = sup(Q) for some Q ∈ Extension(P, e) n Unable to prune the search space n It is possible that AB is NOT closed but ABAC is closed Instance-border checking: Prune the search space n Pattern P is prunable if there exists Q ∈ Extension(P, e) for some e s. t. n sup(P) = sup(Q) (P is NOT closed) P Q n (leftmost) support set INS and (lesfmost) support set INS : for each (i,
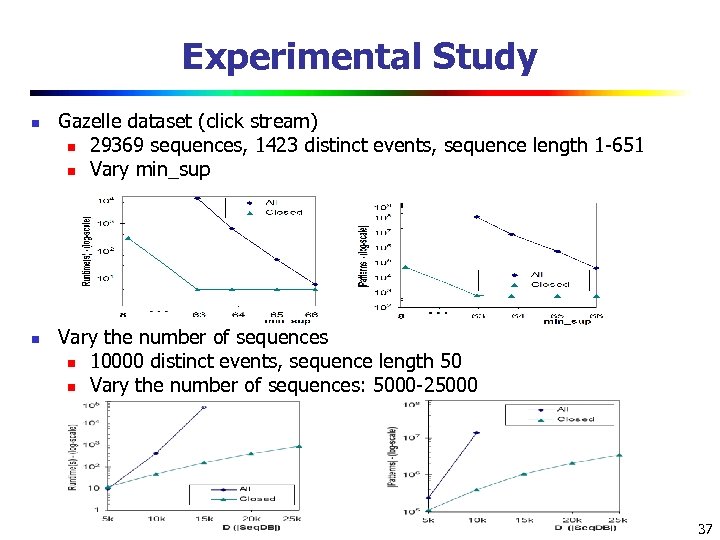Experimental Study n n Gazelle dataset (click stream) n 29369 sequences, 1423 distinct events, sequence length 1 -651 n Vary min_sup Vary the number of sequences n 10000 distinct events, sequence length 50 n Vary the number of sequences: 5000 -25000 37
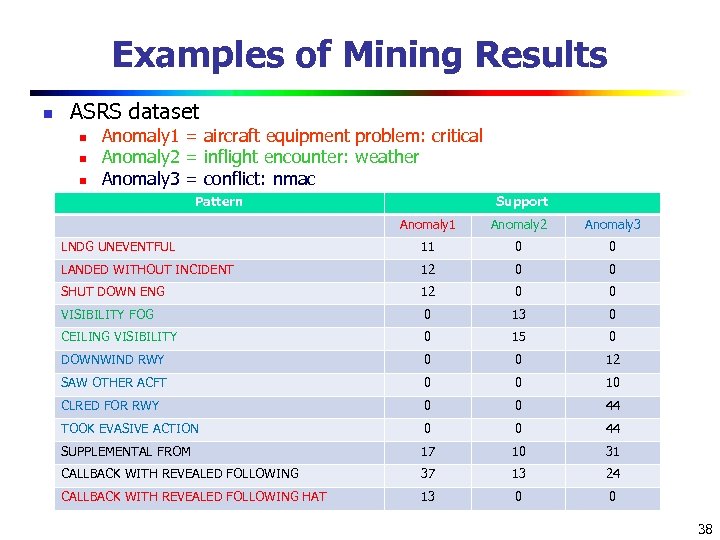Examples of Mining Results n ASRS dataset n n n Anomaly 1 = aircraft equipment problem: critical Anomaly 2 = inflight encounter: weather Anomaly 3 = conflict: nmac Pattern Support Anomaly 1 Anomaly 2 Anomaly 3 LNDG UNEVENTFUL 11 0 0 LANDED WITHOUT INCIDENT 12 0 0 SHUT DOWN ENG 12 0 0 VISIBILITY FOG 0 13 0 CEILING VISIBILITY 0 15 0 DOWNWIND RWY 0 0 12 SAW OTHER ACFT 0 0 10 CLRED FOR RWY 0 0 44 TOOK EVASIVE ACTION 0 0 44 SUPPLEMENTAL FROM 17 10 31 CALLBACK WITH REVEALED FOLLOWING 37 13 24 CALLBACK WITH REVEALED FOLLOWING HAT 13 0 0 38
Examples: Program Execution Traces n JBoss Application Server: Longest repetitive gapped subsequence (of length 66) Mined from JBoss Transaction Component 39
Ref: Mining Sequential Patterns n n n n n R. Srikant and R. Agrawal. Mining sequential patterns: Generalizations and performance improvements. EDBT’ 96. H. Mannila, H Toivonen, and A. I. Verkamo. Discovery of frequent episodes in event sequences. DAMI: 97. M. Zaki. SPADE: An Efficient Algorithm for Mining Frequent Sequences. Machine Learning, 2001. J. Pei, J. Han, H. Pinto, Q. Chen, U. Dayal, and M. -C. Hsu. Prefix. Span: Mining Sequential Patterns Efficiently by Prefix-Projected Pattern Growth. ICDE'01 (TKDE’ 04). J. Pei, J. Han and W. Wang, Constraint-Based Sequential Pattern Mining in Large Databases, CIKM'02. X. Yan, J. Han, and R. Afshar. Clo. Span: Mining Closed Sequential Patterns in Large Datasets. SDM'03. J. Wang and J. Han, BIDE: Efficient Mining of Frequent Closed Sequences, ICDE'04. H. Cheng, X. Yan, and J. Han, Inc. Span: Incremental Mining of Sequential Patterns in Large Database, KDD'04. J. Han, G. Dong and Y. Yin, Efficient Mining of Partial Periodic Patterns in Time Series Database, ICDE'99. J. Yang, W. Wang, and P. S. Yu, Mining asynchronous periodic patterns in time series data, KDD'00. 40
Research Problems n Mining repetitive sequential patterns in Seq. DBs with mixed long and short sequences n n Ding et al. ’s ICDE’ 09 paper Exploring applications of sequential pattern mining n Mining sequential patterns in text documents? Will sequential pattern be more powerful than n-grams? n Efficient mining of colossal sequential patterns? n Mining approximate sequential patterns? n Classification using sequential patterns? n Clustering with sequential patterns? n Exploring sequential pattern mining for biological data analysis 41
16 March 2018 Data Mining: Concepts and Techniques 42