d7ef55457286cfd471a98d514304f0d3.ppt
- Количество слайдов: 68
 Data Mining: Concepts and Techniques (3 rd ed. ) — Chapter 6 — 1
Data Mining: Concepts and Techniques (3 rd ed. ) — Chapter 6 — 1
 Chapter 5: Mining Frequent Patterns, Association and Correlations: Basic Concepts and Methods n Basic Concepts n Frequent Itemset Mining Methods n Which Patterns Are Interesting? —Pattern Evaluation Methods n Summary 2
Chapter 5: Mining Frequent Patterns, Association and Correlations: Basic Concepts and Methods n Basic Concepts n Frequent Itemset Mining Methods n Which Patterns Are Interesting? —Pattern Evaluation Methods n Summary 2
 What Is Frequent Pattern Analysis? n Frequent pattern: a pattern (a set of items, subsequences, substructures, etc. ) that occurs frequently in a data set n First proposed by Agrawal, Imielinski, and Swami [AIS 93] in the context of frequent itemsets and association rule mining n Motivation: Finding inherent regularities in data n What products were often purchased together? — Beer and diapers? ! n What are the subsequent purchases after buying a PC? (sequential pattern) n n What kinds of DNA are sensitive to this new drug? Applications n Basket data analysis, cross-marketing, catalog design, sale campaign analysis, Web log (click stream) analysis, and DNA sequence analysis. 3
What Is Frequent Pattern Analysis? n Frequent pattern: a pattern (a set of items, subsequences, substructures, etc. ) that occurs frequently in a data set n First proposed by Agrawal, Imielinski, and Swami [AIS 93] in the context of frequent itemsets and association rule mining n Motivation: Finding inherent regularities in data n What products were often purchased together? — Beer and diapers? ! n What are the subsequent purchases after buying a PC? (sequential pattern) n n What kinds of DNA are sensitive to this new drug? Applications n Basket data analysis, cross-marketing, catalog design, sale campaign analysis, Web log (click stream) analysis, and DNA sequence analysis. 3
 Why Is Freq. Pattern Mining Important? n n Freq. pattern: An intrinsic and important property of datasets Foundation for many essential data mining tasks n Association, correlation, and causality analysis n Sequential, structural (e. g. , sub-graph) patterns n Pattern analysis in spatiotemporal, multimedia, timeseries, and stream data n Classification: discriminative, frequent pattern analysis n Cluster analysis: frequent pattern-based clustering n Data warehousing: iceberg cube and cube-gradient n Semantic data compression: fascicles n Broad applications 4
Why Is Freq. Pattern Mining Important? n n Freq. pattern: An intrinsic and important property of datasets Foundation for many essential data mining tasks n Association, correlation, and causality analysis n Sequential, structural (e. g. , sub-graph) patterns n Pattern analysis in spatiotemporal, multimedia, timeseries, and stream data n Classification: discriminative, frequent pattern analysis n Cluster analysis: frequent pattern-based clustering n Data warehousing: iceberg cube and cube-gradient n Semantic data compression: fascicles n Broad applications 4
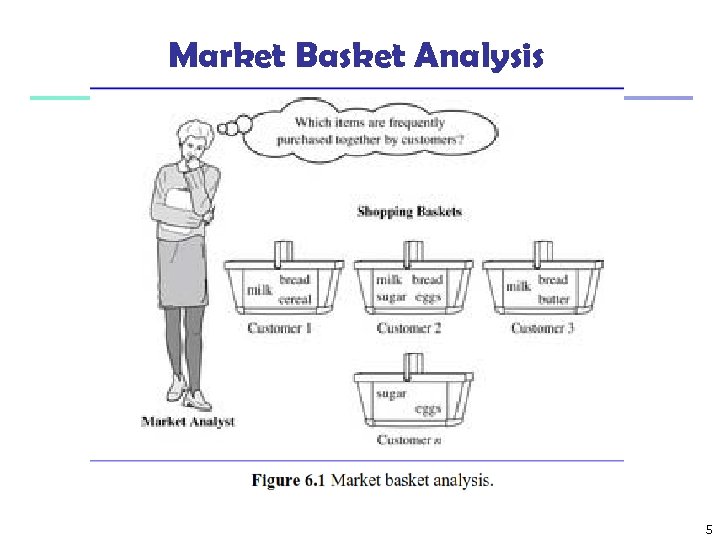 Market Basket Analysis 5
Market Basket Analysis 5
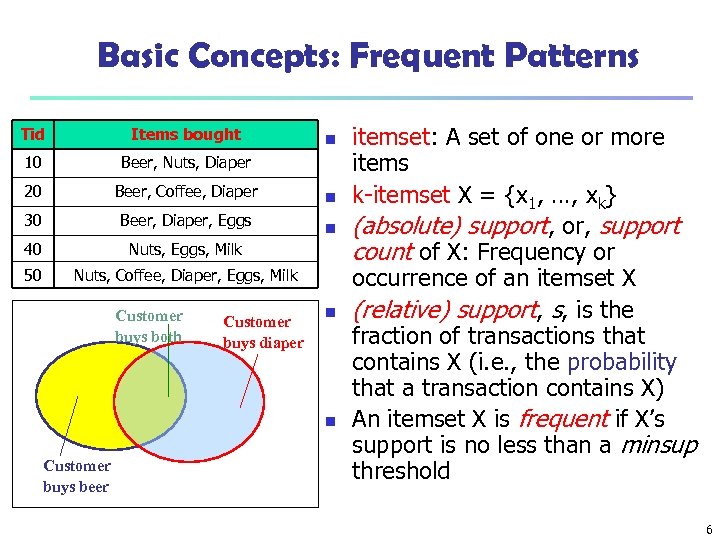 Basic Concepts: Frequent Patterns Tid Items bought 10 Beer, Nuts, Diaper 20 Beer, Coffee, Diaper 30 Beer, Diaper, Eggs 40 Nuts, Eggs, Milk 50 Nuts, Coffee, Diaper, Eggs, Milk Customer buys both Customer buys diaper n n n Customer buys beer itemset: A set of one or more items k-itemset X = {x 1, …, xk} (absolute) support, or, support count of X: Frequency or occurrence of an itemset X (relative) support, s, is the fraction of transactions that contains X (i. e. , the probability that a transaction contains X) An itemset X is frequent if X’s support is no less than a minsup threshold 6
Basic Concepts: Frequent Patterns Tid Items bought 10 Beer, Nuts, Diaper 20 Beer, Coffee, Diaper 30 Beer, Diaper, Eggs 40 Nuts, Eggs, Milk 50 Nuts, Coffee, Diaper, Eggs, Milk Customer buys both Customer buys diaper n n n Customer buys beer itemset: A set of one or more items k-itemset X = {x 1, …, xk} (absolute) support, or, support count of X: Frequency or occurrence of an itemset X (relative) support, s, is the fraction of transactions that contains X (i. e. , the probability that a transaction contains X) An itemset X is frequent if X’s support is no less than a minsup threshold 6
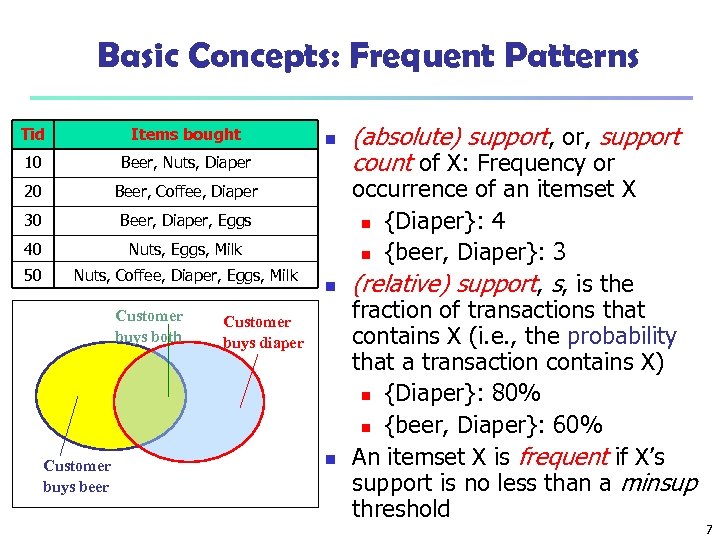 Basic Concepts: Frequent Patterns Tid Items bought 10 Beer, Nuts, Diaper 20 Beer, Coffee, Diaper 30 Beer, Diaper, Eggs 40 Nuts, Eggs, Milk 50 Nuts, Coffee, Diaper, Eggs, Milk Customer buys both Customer buys beer n n Customer buys diaper n (absolute) support, or, support count of X: Frequency or occurrence of an itemset X n {Diaper}: 4 n {beer, Diaper}: 3 (relative) support, s, is the fraction of transactions that contains X (i. e. , the probability that a transaction contains X) n {Diaper}: 80% n {beer, Diaper}: 60% An itemset X is frequent if X’s support is no less than a minsup threshold 7
Basic Concepts: Frequent Patterns Tid Items bought 10 Beer, Nuts, Diaper 20 Beer, Coffee, Diaper 30 Beer, Diaper, Eggs 40 Nuts, Eggs, Milk 50 Nuts, Coffee, Diaper, Eggs, Milk Customer buys both Customer buys beer n n Customer buys diaper n (absolute) support, or, support count of X: Frequency or occurrence of an itemset X n {Diaper}: 4 n {beer, Diaper}: 3 (relative) support, s, is the fraction of transactions that contains X (i. e. , the probability that a transaction contains X) n {Diaper}: 80% n {beer, Diaper}: 60% An itemset X is frequent if X’s support is no less than a minsup threshold 7
 Basic Concepts: Association Rules Tid Items bought 10 Beer, Nuts, Diaper 20 Beer, Coffee, Diaper 30 Beer, Diaper, Eggs 40 50 Nuts, Eggs, Milk n Nuts, Coffee, Diaper, Eggs, Milk Customer buys both Customer buys beer Customer buys diaper Find all the rules X Y with minimum support and confidence n support, s, probability that a transaction contains X Y n confidence, c, conditional probability that a transaction having X also contains Y Let minsup = 50%, minconf = 50% Freq. Pat. : Beer: 3, Nuts: 3, Diaper: 4, Eggs: 3, {Beer, Diaper}: 3 n Association rules: (many more!) n Beer Diaper (60%, 100%) n Diaper Beer (60%, 75%) 8
Basic Concepts: Association Rules Tid Items bought 10 Beer, Nuts, Diaper 20 Beer, Coffee, Diaper 30 Beer, Diaper, Eggs 40 50 Nuts, Eggs, Milk n Nuts, Coffee, Diaper, Eggs, Milk Customer buys both Customer buys beer Customer buys diaper Find all the rules X Y with minimum support and confidence n support, s, probability that a transaction contains X Y n confidence, c, conditional probability that a transaction having X also contains Y Let minsup = 50%, minconf = 50% Freq. Pat. : Beer: 3, Nuts: 3, Diaper: 4, Eggs: 3, {Beer, Diaper}: 3 n Association rules: (many more!) n Beer Diaper (60%, 100%) n Diaper Beer (60%, 75%) 8
 Closed Patterns and Max-Patterns n n n A long pattern contains a combinatorial number of subpatterns, e. g. , {a 1, …, a 100} contains (1001) + (1002) + … + (110000) = 2100 – 1 = 1. 27*1030 sub-patterns! Solution: Mine closed patterns and max-patterns instead An itemset X is closed if X is frequent and there exists no super-pattern Y כ X, with the same support as X (proposed by Pasquier, et al. @ ICDT’ 99) An itemset X is a max-pattern if X is frequent and there exists no frequent super-pattern Y כ X (proposed by Bayardo @ SIGMOD’ 98) Closed pattern is a lossless compression of freq. patterns n Reducing the # of patterns and rules 9
Closed Patterns and Max-Patterns n n n A long pattern contains a combinatorial number of subpatterns, e. g. , {a 1, …, a 100} contains (1001) + (1002) + … + (110000) = 2100 – 1 = 1. 27*1030 sub-patterns! Solution: Mine closed patterns and max-patterns instead An itemset X is closed if X is frequent and there exists no super-pattern Y כ X, with the same support as X (proposed by Pasquier, et al. @ ICDT’ 99) An itemset X is a max-pattern if X is frequent and there exists no frequent super-pattern Y כ X (proposed by Bayardo @ SIGMOD’ 98) Closed pattern is a lossless compression of freq. patterns n Reducing the # of patterns and rules 9
 Closed Patterns and Max-Patterns n Exercise. DB = {, < a 1, …, a 50>} n n Min_sup = 1. What is the set of closed itemset? n n n : 1 < a 1, …, a 50>: 2 What is the set of max-pattern? n n : 1 What is the set of all patterns? n !! 10
Closed Patterns and Max-Patterns n Exercise. DB = {, < a 1, …, a 50>} n n Min_sup = 1. What is the set of closed itemset? n n n : 1 < a 1, …, a 50>: 2 What is the set of max-pattern? n n : 1 What is the set of all patterns? n !! 10
 Chapter 5: Mining Frequent Patterns, Association and Correlations: Basic Concepts and Methods n Basic Concepts n Frequent Itemset Mining Methods n Which Patterns Are Interesting? —Pattern Evaluation Methods n Summary 11
Chapter 5: Mining Frequent Patterns, Association and Correlations: Basic Concepts and Methods n Basic Concepts n Frequent Itemset Mining Methods n Which Patterns Are Interesting? —Pattern Evaluation Methods n Summary 11
 Scalable Frequent Itemset Mining Methods n Apriori: A Candidate Generation-and-Test Approach n Improving the Efficiency of Apriori n FPGrowth: A Frequent Pattern-Growth Approach n ECLAT: Frequent Pattern Mining with Vertical Data Format 12
Scalable Frequent Itemset Mining Methods n Apriori: A Candidate Generation-and-Test Approach n Improving the Efficiency of Apriori n FPGrowth: A Frequent Pattern-Growth Approach n ECLAT: Frequent Pattern Mining with Vertical Data Format 12
 The Downward Closure Property and Scalable Mining Methods n n The downward closure property of frequent patterns n Any subset of a frequent itemset must be frequent n If {beer, diaper, nuts} is frequent, so is {beer, diaper} n i. e. , every transaction having {beer, diaper, nuts} also contains {beer, diaper} Scalable mining methods: Three major approaches n Apriori (Agrawal & Srikant@VLDB’ 94) n Freq. pattern growth (FPgrowth—Han, Pei & Yin @SIGMOD’ 00) n Vertical data format approach (Charm—Zaki & Hsiao @SDM’ 02) 13
The Downward Closure Property and Scalable Mining Methods n n The downward closure property of frequent patterns n Any subset of a frequent itemset must be frequent n If {beer, diaper, nuts} is frequent, so is {beer, diaper} n i. e. , every transaction having {beer, diaper, nuts} also contains {beer, diaper} Scalable mining methods: Three major approaches n Apriori (Agrawal & Srikant@VLDB’ 94) n Freq. pattern growth (FPgrowth—Han, Pei & Yin @SIGMOD’ 00) n Vertical data format approach (Charm—Zaki & Hsiao @SDM’ 02) 13
 Apriori: A Candidate Generation & Test Approach n n Apriori pruning principle: If there is any itemset which is infrequent, its superset should not be generated/tested! (Agrawal & Srikant @VLDB’ 94, Mannila, et al. @ KDD’ 94) Method: n n Initially, scan DB once to get frequent 1 -itemset Generate length (k+1) candidate itemsets from length k frequent itemsets Test the candidates against DB Terminate when no frequent or candidate set can be generated 14
Apriori: A Candidate Generation & Test Approach n n Apriori pruning principle: If there is any itemset which is infrequent, its superset should not be generated/tested! (Agrawal & Srikant @VLDB’ 94, Mannila, et al. @ KDD’ 94) Method: n n Initially, scan DB once to get frequent 1 -itemset Generate length (k+1) candidate itemsets from length k frequent itemsets Test the candidates against DB Terminate when no frequent or candidate set can be generated 14
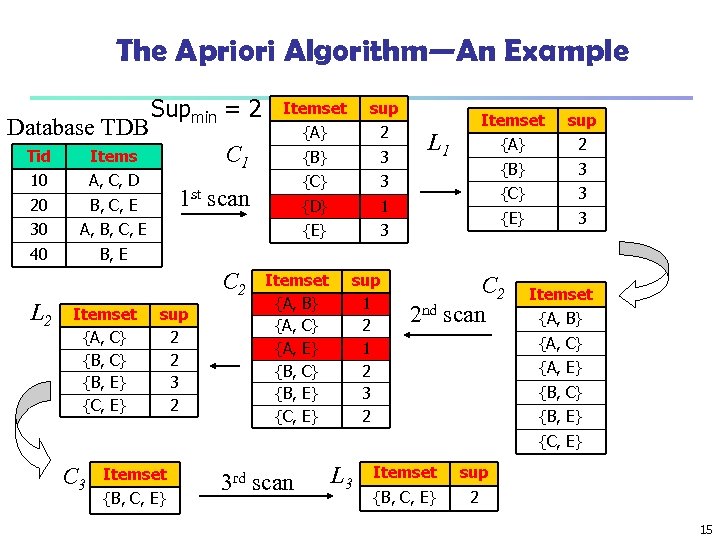 The Apriori Algorithm—An Example Database TDB Tid B, C, E 30 {A} 2 {B} 3 {C} 3 {D} 1 3 A, B, C, E 40 sup {E} A, C, D 20 Itemset C 1 Items 10 Supmin = 2 Itemset {A} 2 {B} 3 {C} 3 {E} L 1 sup 3 B, E 1 st scan C 2 L 2 Itemset {A, C} {B, E} {C, E} sup 2 2 3 2 Itemset {A, B} {A, C} {A, E} {B, C} {B, E} {C, E} sup 1 2 3 2 C 2 2 nd scan Itemset {A, B} {A, C} {A, E} {B, C} {B, E} {C, E} C 3 Itemset {B, C, E} 3 rd scan L 3 Itemset sup {B, C, E} 2 15
The Apriori Algorithm—An Example Database TDB Tid B, C, E 30 {A} 2 {B} 3 {C} 3 {D} 1 3 A, B, C, E 40 sup {E} A, C, D 20 Itemset C 1 Items 10 Supmin = 2 Itemset {A} 2 {B} 3 {C} 3 {E} L 1 sup 3 B, E 1 st scan C 2 L 2 Itemset {A, C} {B, E} {C, E} sup 2 2 3 2 Itemset {A, B} {A, C} {A, E} {B, C} {B, E} {C, E} sup 1 2 3 2 C 2 2 nd scan Itemset {A, B} {A, C} {A, E} {B, C} {B, E} {C, E} C 3 Itemset {B, C, E} 3 rd scan L 3 Itemset sup {B, C, E} 2 15
 The Apriori Algorithm (Pseudo-Code) Ck: Candidate itemset of size k Lk : frequent itemset of size k L 1 = {frequent items}; for (k = 1; Lk != ; k++) do begin Ck+1 = candidates generated from Lk; for each transaction t in database do increment the count of all candidates in Ck+1 that are contained in t Lk+1 = candidates in Ck+1 with min_support end return k Lk; 16
The Apriori Algorithm (Pseudo-Code) Ck: Candidate itemset of size k Lk : frequent itemset of size k L 1 = {frequent items}; for (k = 1; Lk != ; k++) do begin Ck+1 = candidates generated from Lk; for each transaction t in database do increment the count of all candidates in Ck+1 that are contained in t Lk+1 = candidates in Ck+1 with min_support end return k Lk; 16
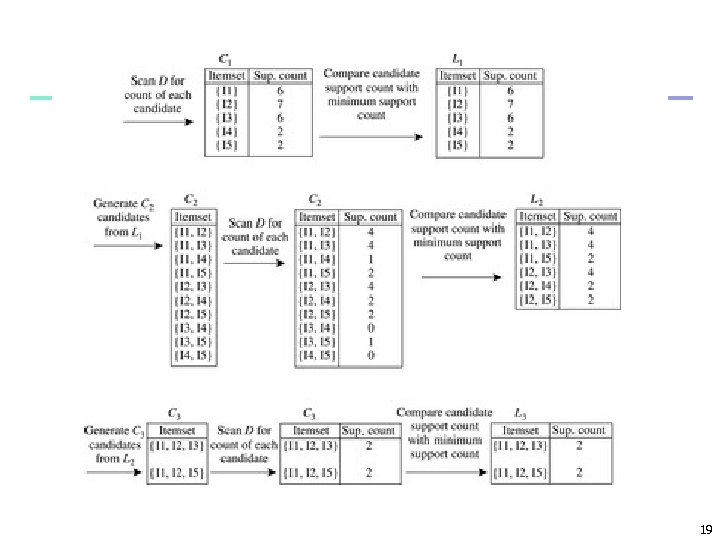
 Example minimum support = 2 18
Example minimum support = 2 18
 19
19
 Scalable Frequent Itemset Mining Methods n Apriori: A Candidate Generation-and-Test Approach n Improving the Efficiency of Apriori n FPGrowth: A Frequent Pattern-Growth Approach n ECLAT: Frequent Pattern Mining with Vertical Data Format n Mining Close Frequent Patterns and Maxpatterns 23
Scalable Frequent Itemset Mining Methods n Apriori: A Candidate Generation-and-Test Approach n Improving the Efficiency of Apriori n FPGrowth: A Frequent Pattern-Growth Approach n ECLAT: Frequent Pattern Mining with Vertical Data Format n Mining Close Frequent Patterns and Maxpatterns 23
 Further Improvement of the Apriori Method n Major computational challenges n n Huge number of candidates n n Multiple scans of transaction database Tedious workload of support counting for candidates Improving Apriori: general ideas n Reduce passes of transaction database scans n Shrink number of candidates n Facilitate support counting of candidates 24
Further Improvement of the Apriori Method n Major computational challenges n n Huge number of candidates n n Multiple scans of transaction database Tedious workload of support counting for candidates Improving Apriori: general ideas n Reduce passes of transaction database scans n Shrink number of candidates n Facilitate support counting of candidates 24
 Partition: Scan Database Only Twice n n Any itemset that is potentially frequent in DB must be frequent in at least one of the partitions of DB n Scan 1: partition database and find local frequent patterns n Scan 2: consolidate global frequent patterns A. Savasere, E. Omiecinski and S. Navathe, VLDB’ 95 DB 1 sup 1(i) < σDB 1 + DB 2 sup 2(i) < σDB 2 + + DBk supk(i) < σDBk = DB sup(i) < σDB
Partition: Scan Database Only Twice n n Any itemset that is potentially frequent in DB must be frequent in at least one of the partitions of DB n Scan 1: partition database and find local frequent patterns n Scan 2: consolidate global frequent patterns A. Savasere, E. Omiecinski and S. Navathe, VLDB’ 95 DB 1 sup 1(i) < σDB 1 + DB 2 sup 2(i) < σDB 2 + + DBk supk(i) < σDBk = DB sup(i) < σDB
 DHP: Reduce the Number of Candidates A k-itemset whose corresponding hashing bucket count is below the n Candidates: a, b, c, d, e n Hash entries n {ab, ad, ae} n {bd, be, de} n … count itemsets 35 88 {ab, ad, ae} {bd, be, de} . . . threshold cannot be frequent 102 . . . n {yz, qs, wt} Hash Table n Frequent 1 -itemset: a, b, d, e n ab is not a candidate 2 -itemset if the sum of count of {ab, ad, ae} is below support threshold n J. Park, M. Chen, and P. Yu. An effective hash-based algorithm for mining association rules. SIGMOD’ 95 26
DHP: Reduce the Number of Candidates A k-itemset whose corresponding hashing bucket count is below the n Candidates: a, b, c, d, e n Hash entries n {ab, ad, ae} n {bd, be, de} n … count itemsets 35 88 {ab, ad, ae} {bd, be, de} . . . threshold cannot be frequent 102 . . . n {yz, qs, wt} Hash Table n Frequent 1 -itemset: a, b, d, e n ab is not a candidate 2 -itemset if the sum of count of {ab, ad, ae} is below support threshold n J. Park, M. Chen, and P. Yu. An effective hash-based algorithm for mining association rules. SIGMOD’ 95 26
 Sampling for Frequent Patterns n Select a sample of original database, mine frequent patterns within sample using Apriori n Scan database once to verify frequent itemsets found in sample, only borders of closure of frequent patterns are checked n Example: check abcd instead of ab, ac, …, etc. n Scan database again to find missed frequent patterns n H. Toivonen. Sampling large databases for association rules. In VLDB’ 96 27
Sampling for Frequent Patterns n Select a sample of original database, mine frequent patterns within sample using Apriori n Scan database once to verify frequent itemsets found in sample, only borders of closure of frequent patterns are checked n Example: check abcd instead of ab, ac, …, etc. n Scan database again to find missed frequent patterns n H. Toivonen. Sampling large databases for association rules. In VLDB’ 96 27
 Scalable Frequent Itemset Mining Methods n Apriori: A Candidate Generation-and-Test Approach n Improving the Efficiency of Apriori n FPGrowth: A Frequent Pattern-Growth Approach n ECLAT: Frequent Pattern Mining with Vertical Data Format n Mining Close Frequent Patterns and Maxpatterns 29
Scalable Frequent Itemset Mining Methods n Apriori: A Candidate Generation-and-Test Approach n Improving the Efficiency of Apriori n FPGrowth: A Frequent Pattern-Growth Approach n ECLAT: Frequent Pattern Mining with Vertical Data Format n Mining Close Frequent Patterns and Maxpatterns 29
 Pattern-Growth Approach: Mining Frequent Patterns Without Candidate Generation n Bottlenecks of the Apriori approach n Breadth-first (i. e. , level-wise) search n Candidate generation and test n n Often generates a huge number of candidates The FPGrowth Approach (J. Han, J. Pei, and Y. Yin, SIGMOD’ 00) n n n Depth-first search Avoid explicit candidate generation Major philosophy: Grow long patterns from short ones using local frequent items only n “abc” is a frequent pattern n Get all transactions having “abc”, i. e. , project DB on abc: DB|abc n “d” is a local frequent item in DB|abc abcd is a frequent pattern 30
Pattern-Growth Approach: Mining Frequent Patterns Without Candidate Generation n Bottlenecks of the Apriori approach n Breadth-first (i. e. , level-wise) search n Candidate generation and test n n Often generates a huge number of candidates The FPGrowth Approach (J. Han, J. Pei, and Y. Yin, SIGMOD’ 00) n n n Depth-first search Avoid explicit candidate generation Major philosophy: Grow long patterns from short ones using local frequent items only n “abc” is a frequent pattern n Get all transactions having “abc”, i. e. , project DB on abc: DB|abc n “d” is a local frequent item in DB|abc abcd is a frequent pattern 30
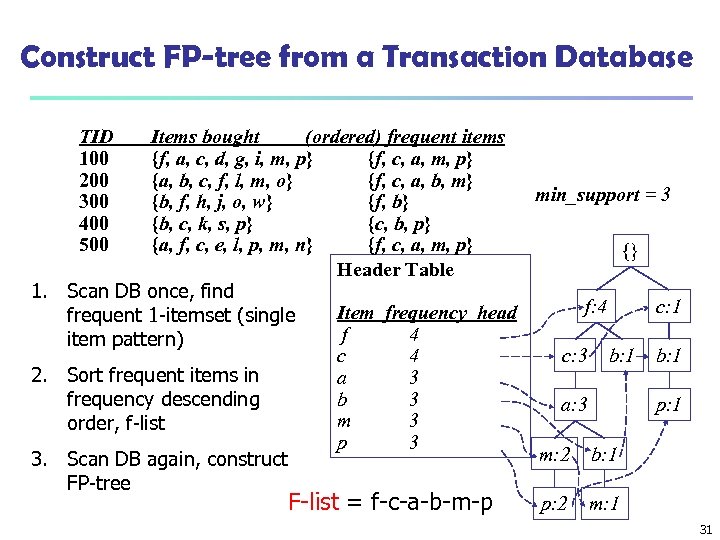 Construct FP-tree from a Transaction Database TID 100 200 300 400 500 Items bought (ordered) frequent items {f, a, c, d, g, i, m, p} {f, c, a, m, p} {a, b, c, f, l, m, o} {f, c, a, b, m} min_support = 3 {b, f, h, j, o, w} {f, b} {b, c, k, s, p} {c, b, p} {a, f, c, e, l, p, m, n} {f, c, a, m, p} {} Header Table 1. Scan DB once, find f: 4 c: 1 Item frequency head frequent 1 -itemset (single f 4 item pattern) c: 3 b: 1 c 4 2. Sort frequent items in a 3 b 3 frequency descending a: 3 p: 1 m 3 order, f-list p 3 m: 2 b: 1 3. Scan DB again, construct FP-tree p: 2 m: 1 F-list = f-c-a-b-m-p 31
Construct FP-tree from a Transaction Database TID 100 200 300 400 500 Items bought (ordered) frequent items {f, a, c, d, g, i, m, p} {f, c, a, m, p} {a, b, c, f, l, m, o} {f, c, a, b, m} min_support = 3 {b, f, h, j, o, w} {f, b} {b, c, k, s, p} {c, b, p} {a, f, c, e, l, p, m, n} {f, c, a, m, p} {} Header Table 1. Scan DB once, find f: 4 c: 1 Item frequency head frequent 1 -itemset (single f 4 item pattern) c: 3 b: 1 c 4 2. Sort frequent items in a 3 b 3 frequency descending a: 3 p: 1 m 3 order, f-list p 3 m: 2 b: 1 3. Scan DB again, construct FP-tree p: 2 m: 1 F-list = f-c-a-b-m-p 31
 Partition Patterns and Databases n n Frequent patterns can be partitioned into subsets according to f-list n F-list = f-c-a-b-m-p n Patterns containing p n Patterns having m but no p n … n Patterns having c but no a nor b, m, p n Pattern f Completeness and non-redundency 32
Partition Patterns and Databases n n Frequent patterns can be partitioned into subsets according to f-list n F-list = f-c-a-b-m-p n Patterns containing p n Patterns having m but no p n … n Patterns having c but no a nor b, m, p n Pattern f Completeness and non-redundency 32
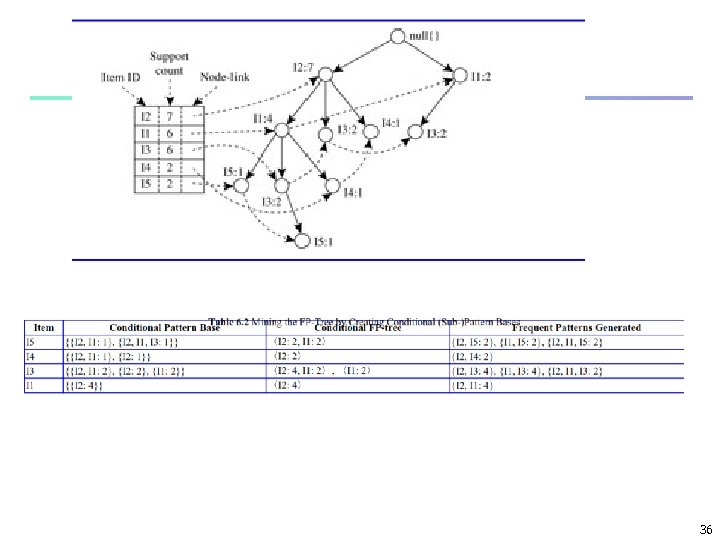
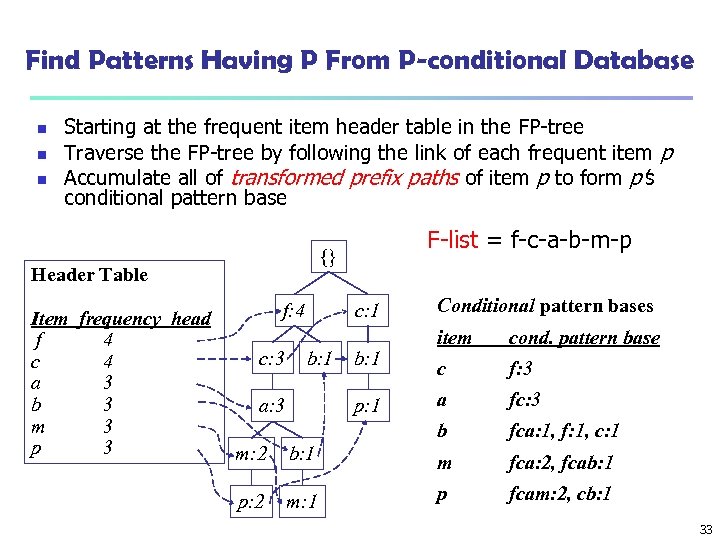 Find Patterns Having P From P-conditional Database n n n Starting at the frequent item header table in the FP-tree Traverse the FP-tree by following the link of each frequent item p Accumulate all of transformed prefix paths of item p to form p’s conditional pattern base {} Header Table Item frequency head f 4 c 4 a 3 b 3 m 3 p 3 F-list = f-c-a-b-m-p f: 4 c: 1 Conditional pattern bases b: 1 a: 3 b: 1 p: 1 cond. pattern base c f: 3 a fc: 3 b c: 3 item fca: 1, f: 1, c: 1 m: 2 b: 1 m fca: 2, fcab: 1 p: 2 m: 1 p fcam: 2, cb: 1 33
Find Patterns Having P From P-conditional Database n n n Starting at the frequent item header table in the FP-tree Traverse the FP-tree by following the link of each frequent item p Accumulate all of transformed prefix paths of item p to form p’s conditional pattern base {} Header Table Item frequency head f 4 c 4 a 3 b 3 m 3 p 3 F-list = f-c-a-b-m-p f: 4 c: 1 Conditional pattern bases b: 1 a: 3 b: 1 p: 1 cond. pattern base c f: 3 a fc: 3 b c: 3 item fca: 1, f: 1, c: 1 m: 2 b: 1 m fca: 2, fcab: 1 p: 2 m: 1 p fcam: 2, cb: 1 33
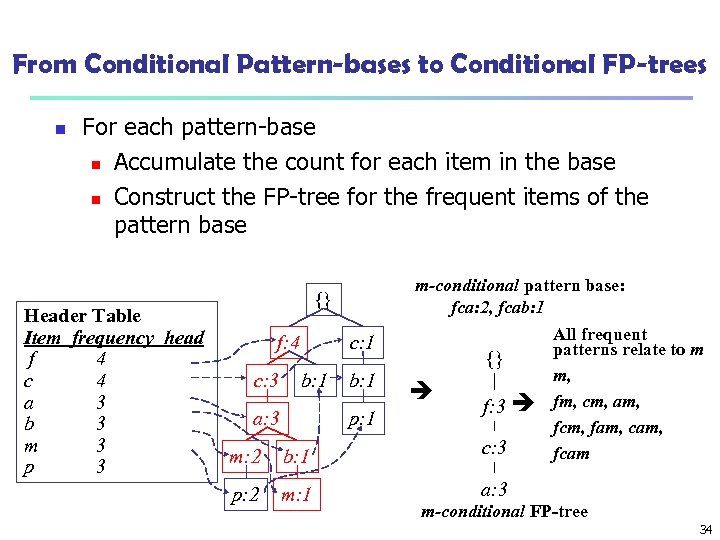 From Conditional Pattern-bases to Conditional FP-trees n For each pattern-base n Accumulate the count for each item in the base n Construct the FP-tree for the frequent items of the pattern base Header Table Item frequency head f 4 c 4 a 3 b 3 m 3 p 3 m-conditional pattern base: fca: 2, fcab: 1 {} f: 4 c: 3 c: 1 b: 1 a: 3 b: 1 p: 1 {} f: 3 m: 2 b: 1 c: 3 p: 2 m: 1 All frequent patterns relate to m m, fm, cm, am, fcm, fam, cam, fcam a: 3 m-conditional FP-tree 34
From Conditional Pattern-bases to Conditional FP-trees n For each pattern-base n Accumulate the count for each item in the base n Construct the FP-tree for the frequent items of the pattern base Header Table Item frequency head f 4 c 4 a 3 b 3 m 3 p 3 m-conditional pattern base: fca: 2, fcab: 1 {} f: 4 c: 3 c: 1 b: 1 a: 3 b: 1 p: 1 {} f: 3 m: 2 b: 1 c: 3 p: 2 m: 1 All frequent patterns relate to m m, fm, cm, am, fcm, fam, cam, fcam a: 3 m-conditional FP-tree 34
 Example minimum support = 2 35
Example minimum support = 2 35
 36
36
 Benefits of the FP-tree Structure n Completeness n n n Preserve complete information for frequent pattern mining Never break a long pattern of any transaction Compactness n n n Reduce irrelevant info—infrequent items are gone Items in frequency descending order: the more frequently occurring, the more likely to be shared Never be larger than the original database (not count node-links and the count field) 39
Benefits of the FP-tree Structure n Completeness n n n Preserve complete information for frequent pattern mining Never break a long pattern of any transaction Compactness n n n Reduce irrelevant info—infrequent items are gone Items in frequency descending order: the more frequently occurring, the more likely to be shared Never be larger than the original database (not count node-links and the count field) 39
 The Frequent Pattern Growth Mining Method n n Idea: Frequent pattern growth n Recursively grow frequent patterns by pattern and database partition Method n For each frequent item, construct its conditional pattern -base, and then its conditional FP-tree n Repeat the process on each newly created conditional FP-tree n Until the resulting FP-tree is empty, or it contains only one path—single path will generate all the combinations of its sub-paths, each of which is a frequent pattern 40
The Frequent Pattern Growth Mining Method n n Idea: Frequent pattern growth n Recursively grow frequent patterns by pattern and database partition Method n For each frequent item, construct its conditional pattern -base, and then its conditional FP-tree n Repeat the process on each newly created conditional FP-tree n Until the resulting FP-tree is empty, or it contains only one path—single path will generate all the combinations of its sub-paths, each of which is a frequent pattern 40
 Advantages of the Pattern Growth Approach n Divide-and-conquer: n n n Decompose both the mining task and DB according to the frequent patterns obtained so far Lead to focused search of smaller databases Other factors n No candidate generation, no candidate test n Compressed database: FP-tree structure n No repeated scan of entire database n n Basic ops: counting local freq items and building sub FP-tree, no pattern search and matching A good open-source implementation and refinement of FPGrowth n FPGrowth+ (Grahne and J. Zhu, FIMI'03) 44
Advantages of the Pattern Growth Approach n Divide-and-conquer: n n n Decompose both the mining task and DB according to the frequent patterns obtained so far Lead to focused search of smaller databases Other factors n No candidate generation, no candidate test n Compressed database: FP-tree structure n No repeated scan of entire database n n Basic ops: counting local freq items and building sub FP-tree, no pattern search and matching A good open-source implementation and refinement of FPGrowth n FPGrowth+ (Grahne and J. Zhu, FIMI'03) 44
 Further Improvements of Mining Methods n AFOPT (Liu, et al. @ KDD’ 03) n A “push-right” method for mining condensed frequent pattern (CFP) tree n Carpenter (Pan, et al. @ KDD’ 03) n n n Mine data sets with small rows but numerous columns Construct a row-enumeration tree for efficient mining FPgrowth+ (Grahne and Zhu, FIMI’ 03) n Efficiently Using Prefix-Trees in Mining Frequent Itemsets, Proc. ICDM'03 Int. Workshop on Frequent Itemset Mining Implementations (FIMI'03), Melbourne, FL, Nov. 2003 n TD-Close (Liu, et al, SDM’ 06) 45
Further Improvements of Mining Methods n AFOPT (Liu, et al. @ KDD’ 03) n A “push-right” method for mining condensed frequent pattern (CFP) tree n Carpenter (Pan, et al. @ KDD’ 03) n n n Mine data sets with small rows but numerous columns Construct a row-enumeration tree for efficient mining FPgrowth+ (Grahne and Zhu, FIMI’ 03) n Efficiently Using Prefix-Trees in Mining Frequent Itemsets, Proc. ICDM'03 Int. Workshop on Frequent Itemset Mining Implementations (FIMI'03), Melbourne, FL, Nov. 2003 n TD-Close (Liu, et al, SDM’ 06) 45
 Extension of Pattern Growth Mining Methodology n n n n Mining closed frequent itemsets and max-patterns n CLOSET (DMKD’ 00), FPclose, and FPMax (Grahne & Zhu, Fimi’ 03) Mining sequential patterns n Prefix. Span (ICDE’ 01), Clo. Span (SDM’ 03), BIDE (ICDE’ 04) Mining graph patterns n g. Span (ICDM’ 02), Close. Graph (KDD’ 03) Constraint-based mining of frequent patterns n Convertible constraints (ICDE’ 01), g. Prune (PAKDD’ 03) Computing iceberg data cubes with complex measures n H-tree, H-cubing, and Star-cubing (SIGMOD’ 01, VLDB’ 03) Pattern-growth-based Clustering n Ma. Ple (Pei, et al. , ICDM’ 03) Pattern-Growth-Based Classification n Mining frequent and discriminative patterns (Cheng, et al, ICDE’ 07) 46
Extension of Pattern Growth Mining Methodology n n n n Mining closed frequent itemsets and max-patterns n CLOSET (DMKD’ 00), FPclose, and FPMax (Grahne & Zhu, Fimi’ 03) Mining sequential patterns n Prefix. Span (ICDE’ 01), Clo. Span (SDM’ 03), BIDE (ICDE’ 04) Mining graph patterns n g. Span (ICDM’ 02), Close. Graph (KDD’ 03) Constraint-based mining of frequent patterns n Convertible constraints (ICDE’ 01), g. Prune (PAKDD’ 03) Computing iceberg data cubes with complex measures n H-tree, H-cubing, and Star-cubing (SIGMOD’ 01, VLDB’ 03) Pattern-growth-based Clustering n Ma. Ple (Pei, et al. , ICDM’ 03) Pattern-Growth-Based Classification n Mining frequent and discriminative patterns (Cheng, et al, ICDE’ 07) 46
 Homework n P 273: Exercise 6. 6 47
Homework n P 273: Exercise 6. 6 47
 Weka 48
Weka 48
 Scalable Frequent Itemset Mining Methods n Apriori: A Candidate Generation-and-Test Approach n Improving the Efficiency of Apriori n FPGrowth: A Frequent Pattern-Growth Approach n ECLAT: Frequent Pattern Mining with Vertical Data Format n Mining Close Frequent Patterns and Maxpatterns 49
Scalable Frequent Itemset Mining Methods n Apriori: A Candidate Generation-and-Test Approach n Improving the Efficiency of Apriori n FPGrowth: A Frequent Pattern-Growth Approach n ECLAT: Frequent Pattern Mining with Vertical Data Format n Mining Close Frequent Patterns and Maxpatterns 49
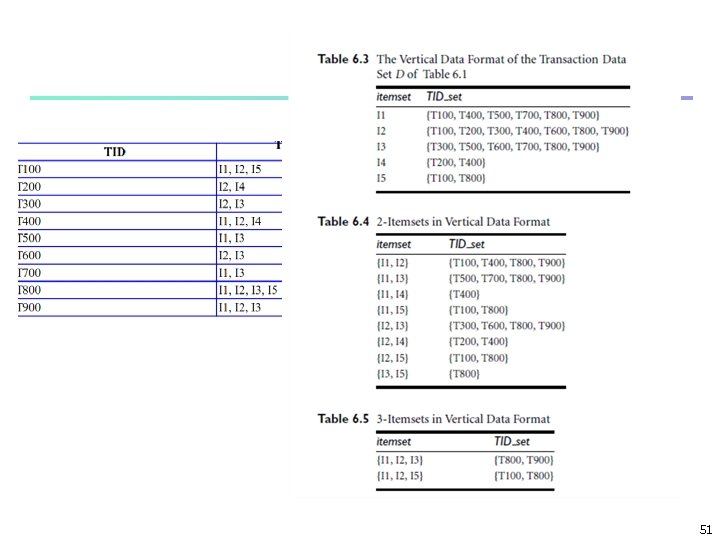
 ECLAT: Mining by Exploring Vertical Data Format n Vertical format: t(AB) = {T 11, T 25, …} n n tid-list: list of trans. -ids containing an itemset Deriving frequent patterns based on vertical intersections n n n t(X) = t(Y): X and Y always happen together t(X) t(Y): transaction having X always has Y Using diffset to accelerate mining n n n t(X) = {T 1, T 2, T 3}, t(XY) = {T 1, T 3} n n Only keep track of differences of tids Diffset (XY, X) = {T 2} Eclat (Zaki et al. @KDD’ 97) Mining Closed patterns using vertical format: CHARM (Zaki & Hsiao@SDM’ 02) 50
ECLAT: Mining by Exploring Vertical Data Format n Vertical format: t(AB) = {T 11, T 25, …} n n tid-list: list of trans. -ids containing an itemset Deriving frequent patterns based on vertical intersections n n n t(X) = t(Y): X and Y always happen together t(X) t(Y): transaction having X always has Y Using diffset to accelerate mining n n n t(X) = {T 1, T 2, T 3}, t(XY) = {T 1, T 3} n n Only keep track of differences of tids Diffset (XY, X) = {T 2} Eclat (Zaki et al. @KDD’ 97) Mining Closed patterns using vertical format: CHARM (Zaki & Hsiao@SDM’ 02) 50
 51
51
 Scalable Frequent Itemset Mining Methods n Apriori: A Candidate Generation-and-Test Approach n Improving the Efficiency of Apriori n FPGrowth: A Frequent Pattern-Growth Approach n ECLAT: Frequent Pattern Mining with Vertical Data Format n Mining Close Frequent Patterns and Maxpatterns 52
Scalable Frequent Itemset Mining Methods n Apriori: A Candidate Generation-and-Test Approach n Improving the Efficiency of Apriori n FPGrowth: A Frequent Pattern-Growth Approach n ECLAT: Frequent Pattern Mining with Vertical Data Format n Mining Close Frequent Patterns and Maxpatterns 52
 Mining Association Rule n Frequent Pattern {A, B} n Possible Association Rule A B, B A n Support and confidence of the rule: n Strong association rule with minimum thresholds. n No enough! 16 March 2018 Data Mining: Concepts and Techniques 53
Mining Association Rule n Frequent Pattern {A, B} n Possible Association Rule A B, B A n Support and confidence of the rule: n Strong association rule with minimum thresholds. n No enough! 16 March 2018 Data Mining: Concepts and Techniques 53
 Misleading “strong” association rule n n Suppose we are interested in analyzing transactions at All. Electronics with respect to the purchase of computer games and videos. Let game refer to the transactions containing computer games, and video refer to those containing videos. Of the 10, 000 transactions analyzed, the data show that 6000 of the customer transactions included computer games, while 7500 included videos, and 4000 included both computer games and videos. Suppose that a data mining program for discovering association rules is run on the data, using a minimum support of, say, 30% and a minimum confidence of 60%. The following association rule is discovered: P(videos) = 75% > P(videos | computer games) = 66% 54
Misleading “strong” association rule n n Suppose we are interested in analyzing transactions at All. Electronics with respect to the purchase of computer games and videos. Let game refer to the transactions containing computer games, and video refer to those containing videos. Of the 10, 000 transactions analyzed, the data show that 6000 of the customer transactions included computer games, while 7500 included videos, and 4000 included both computer games and videos. Suppose that a data mining program for discovering association rules is run on the data, using a minimum support of, say, 30% and a minimum confidence of 60%. The following association rule is discovered: P(videos) = 75% > P(videos | computer games) = 66% 54
 From Association Rule to Correlation Rule n n n Life=1: independent Life>1: positive correlated Life<1: negetive correlated 55
From Association Rule to Correlation Rule n n n Life=1: independent Life>1: positive correlated Life<1: negetive correlated 55
 n n n P(V)=. 75 P(G)=. 6 P(VG) =. 40 Life(VG) =. 40/(. 75*. 6)<1 Negative correlated 56
n n n P(V)=. 75 P(G)=. 6 P(VG) =. 40 Life(VG) =. 40/(. 75*. 6)<1 Negative correlated 56
 Interestingness Measure: Correlations ( 2) n Χ 2 (chi-square) test 16 March 2018 57
Interestingness Measure: Correlations ( 2) n Χ 2 (chi-square) test 16 March 2018 57
 Interestingness Measure: Correlations ( 2) n n n The larger the Χ 2 value, the more likely the variables are related The cells that contribute the most to the Χ 2 value are those whose actual count is very different from the expected count Correlation does not imply causality n # of hospitals and # of car-theft in a city are correlated n Both are causally linked to the third variable: population 58
Interestingness Measure: Correlations ( 2) n n n The larger the Χ 2 value, the more likely the variables are related The cells that contribute the most to the Χ 2 value are those whose actual count is very different from the expected count Correlation does not imply causality n # of hospitals and # of car-theft in a city are correlated n Both are causally linked to the third variable: population 58
 Interestingness Measure: Correlations (all_confidence) n All_confidence(g, v)=0. 53 16 March 2018 Data Mining: Concepts and Techniques 59
Interestingness Measure: Correlations (all_confidence) n All_confidence(g, v)=0. 53 16 March 2018 Data Mining: Concepts and Techniques 59
 Interestingness Measure: Correlations (max confidence) 16 March 2018 Data Mining: Concepts and Techniques 60
Interestingness Measure: Correlations (max confidence) 16 March 2018 Data Mining: Concepts and Techniques 60
 Interestingness Measure: Correlations (cosine) n cosine(g, v)=0. 6 61
Interestingness Measure: Correlations (cosine) n cosine(g, v)=0. 6 61
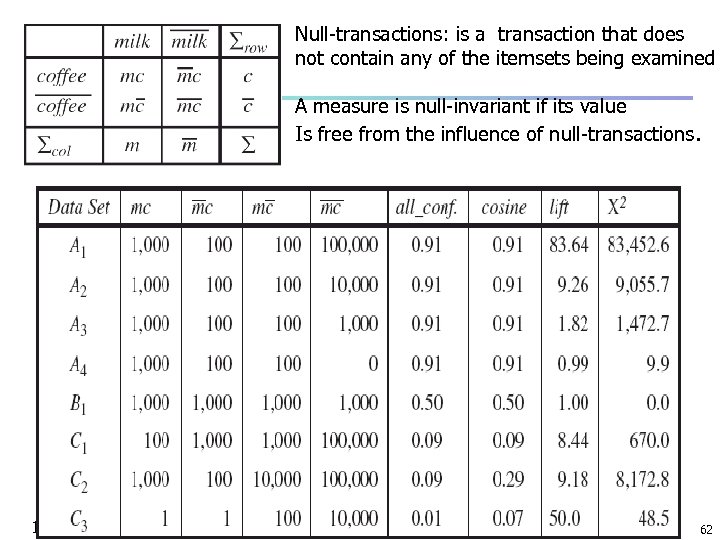 Null-transactions: is a transaction that does not contain any of the itemsets being examined A measure is null-invariant if its value Is free from the influence of null-transactions. 16 March 2018 Data Mining: Concepts and Techniques 62
Null-transactions: is a transaction that does not contain any of the itemsets being examined A measure is null-invariant if its value Is free from the influence of null-transactions. 16 March 2018 Data Mining: Concepts and Techniques 62
 Which Measures Should Be Used? n n lift and 2 are not good measures for correlations in large transactional DBs all-conf or coherence could be good measures (Omiecinski@TKDE’ 03) n n Both all-conf and coherence have the downward closure property Efficient algorithms can be derived for mining (Lee et al. @ICDM’ 03 sub) 16 March 2018 Data Mining: Concepts and Techniques 63
Which Measures Should Be Used? n n lift and 2 are not good measures for correlations in large transactional DBs all-conf or coherence could be good measures (Omiecinski@TKDE’ 03) n n Both all-conf and coherence have the downward closure property Efficient algorithms can be derived for mining (Lee et al. @ICDM’ 03 sub) 16 March 2018 Data Mining: Concepts and Techniques 63
 Chapter 5: Mining Frequent Patterns, Association and Correlations: Basic Concepts and Methods n Basic Concepts n Frequent Itemset Mining Methods n Which Patterns Are Interesting? —Pattern Evaluation Methods n Summary 70
Chapter 5: Mining Frequent Patterns, Association and Correlations: Basic Concepts and Methods n Basic Concepts n Frequent Itemset Mining Methods n Which Patterns Are Interesting? —Pattern Evaluation Methods n Summary 70
![Interestingness Measure: Correlations (Lift) n play basketball eat cereal [40%, 66. 7%] is misleading Interestingness Measure: Correlations (Lift) n play basketball eat cereal [40%, 66. 7%] is misleading](https://present5.com/presentation/d7ef55457286cfd471a98d514304f0d3/image-55.jpg) Interestingness Measure: Correlations (Lift) n play basketball eat cereal [40%, 66. 7%] is misleading n n The overall % of students eating cereal is 75% > 66. 7%. play basketball not eat cereal [20%, 33. 3%] is more accurate, although with lower support and confidence n Measure of dependent/correlated events: lift Basketball Not basketball Sum (row) Cereal 2000 1750 3750 Not cereal 1000 250 1250 Sum(col. ) 3000 2000 5000 71
Interestingness Measure: Correlations (Lift) n play basketball eat cereal [40%, 66. 7%] is misleading n n The overall % of students eating cereal is 75% > 66. 7%. play basketball not eat cereal [20%, 33. 3%] is more accurate, although with lower support and confidence n Measure of dependent/correlated events: lift Basketball Not basketball Sum (row) Cereal 2000 1750 3750 Not cereal 1000 250 1250 Sum(col. ) 3000 2000 5000 71
 Are lift and 2 Good Measures of Correlation? n “Buy walnuts buy milk [1%, 80%]” is misleading if 85% of customers buy milk n Support and confidence are not good to indicate correlations n Over 20 interestingness measures have been proposed (see Tan, Kumar, Sritastava @KDD’ 02) n Which are good ones? 72
Are lift and 2 Good Measures of Correlation? n “Buy walnuts buy milk [1%, 80%]” is misleading if 85% of customers buy milk n Support and confidence are not good to indicate correlations n Over 20 interestingness measures have been proposed (see Tan, Kumar, Sritastava @KDD’ 02) n Which are good ones? 72
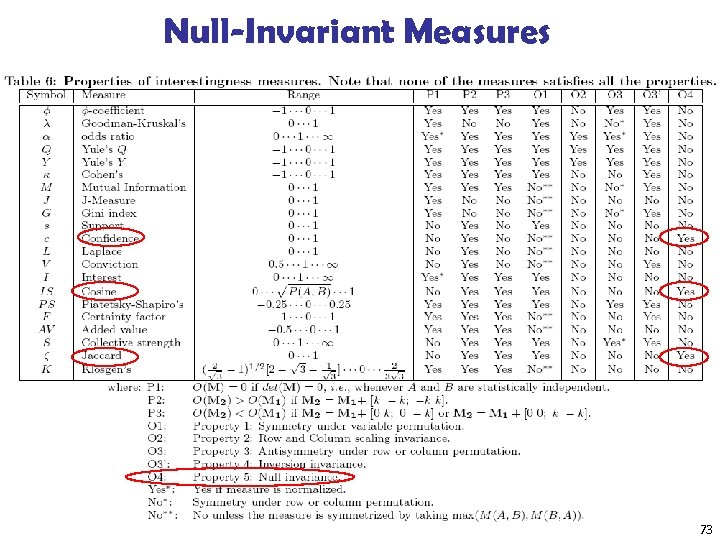 Null-Invariant Measures 73
Null-Invariant Measures 73
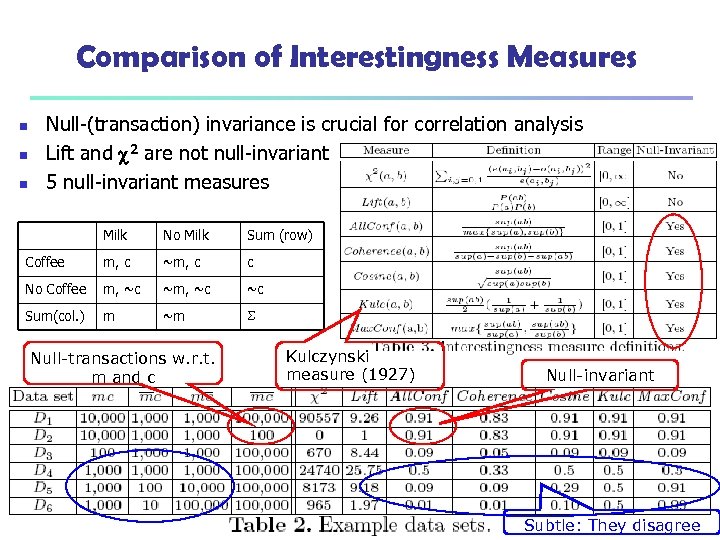 Comparison of Interestingness Measures n n n Null-(transaction) invariance is crucial for correlation analysis Lift and 2 are not null-invariant 5 null-invariant measures Milk No Milk Sum (row) Coffee m, c ~m, c c No Coffee m, ~c ~c Sum(col. ) m ~m Null-transactions w. r. t. m and c 16 March 2018 Kulczynski measure (1927) Data Mining: Concepts and Techniques Null-invariant Subtle: They disagree 74
Comparison of Interestingness Measures n n n Null-(transaction) invariance is crucial for correlation analysis Lift and 2 are not null-invariant 5 null-invariant measures Milk No Milk Sum (row) Coffee m, c ~m, c c No Coffee m, ~c ~c Sum(col. ) m ~m Null-transactions w. r. t. m and c 16 March 2018 Kulczynski measure (1927) Data Mining: Concepts and Techniques Null-invariant Subtle: They disagree 74
 Analysis of DBLP Coauthor Relationships Recent DB conferences, removing balanced associations, low sup, etc. Advisor-advisee relation: Kulc: high, coherence: low, cosine: middle n Tianyi Wu, Yuguo Chen and Jiawei Han, “Association Mining in Large Databases: A Re-Examination of Its Measures”, Proc. 2007 Int. Conf. Principles and Practice of Knowledge Discovery in Databases (PKDD'07), Sept. 2007 75
Analysis of DBLP Coauthor Relationships Recent DB conferences, removing balanced associations, low sup, etc. Advisor-advisee relation: Kulc: high, coherence: low, cosine: middle n Tianyi Wu, Yuguo Chen and Jiawei Han, “Association Mining in Large Databases: A Re-Examination of Its Measures”, Proc. 2007 Int. Conf. Principles and Practice of Knowledge Discovery in Databases (PKDD'07), Sept. 2007 75
 Which Null-Invariant Measure Is Better? n n IR (Imbalance Ratio): measure the imbalance of two itemsets A and B in rule implications Kulczynski and Imbalance Ratio (IR) together present a clear picture for all the three datasets D 4 through D 6 n D 4 is balanced & neutral n D 5 is imbalanced & neutral n D 6 is very imbalanced & neutral
Which Null-Invariant Measure Is Better? n n IR (Imbalance Ratio): measure the imbalance of two itemsets A and B in rule implications Kulczynski and Imbalance Ratio (IR) together present a clear picture for all the three datasets D 4 through D 6 n D 4 is balanced & neutral n D 5 is imbalanced & neutral n D 6 is very imbalanced & neutral
 Chapter 5: Mining Frequent Patterns, Association and Correlations: Basic Concepts and Methods n Basic Concepts n Frequent Itemset Mining Methods n Which Patterns Are Interesting? —Pattern Evaluation Methods n Summary 77
Chapter 5: Mining Frequent Patterns, Association and Correlations: Basic Concepts and Methods n Basic Concepts n Frequent Itemset Mining Methods n Which Patterns Are Interesting? —Pattern Evaluation Methods n Summary 77
 Summary n n Basic concepts: association rules, supportconfident framework, closed and max-patterns Scalable frequent pattern mining methods n n Projection-based (FPgrowth, CLOSET+, . . . ) n § Apriori (Candidate generation & test) Vertical format approach (ECLAT, CHARM, . . . ) Which patterns are interesting? § Pattern evaluation methods 78
Summary n n Basic concepts: association rules, supportconfident framework, closed and max-patterns Scalable frequent pattern mining methods n n Projection-based (FPgrowth, CLOSET+, . . . ) n § Apriori (Candidate generation & test) Vertical format approach (ECLAT, CHARM, . . . ) Which patterns are interesting? § Pattern evaluation methods 78
 Ref: Basic Concepts of Frequent Pattern Mining n n (Association Rules) R. Agrawal, T. Imielinski, and A. Swami. Mining association rules between sets of items in large databases. SIGMOD'93 (Max-pattern) R. J. Bayardo. Efficiently mining long patterns from databases. SIGMOD'98 (Closed-pattern) N. Pasquier, Y. Bastide, R. Taouil, and L. Lakhal. Discovering frequent closed itemsets for association rules. ICDT'99 (Sequential pattern) R. Agrawal and R. Srikant. Mining sequential patterns. ICDE'95 79
Ref: Basic Concepts of Frequent Pattern Mining n n (Association Rules) R. Agrawal, T. Imielinski, and A. Swami. Mining association rules between sets of items in large databases. SIGMOD'93 (Max-pattern) R. J. Bayardo. Efficiently mining long patterns from databases. SIGMOD'98 (Closed-pattern) N. Pasquier, Y. Bastide, R. Taouil, and L. Lakhal. Discovering frequent closed itemsets for association rules. ICDT'99 (Sequential pattern) R. Agrawal and R. Srikant. Mining sequential patterns. ICDE'95 79
 Ref: Apriori and Its Improvements n n n n R. Agrawal and R. Srikant. Fast algorithms for mining association rules. VLDB'94 H. Mannila, H. Toivonen, and A. I. Verkamo. Efficient algorithms for discovering association rules. KDD'94 A. Savasere, E. Omiecinski, and S. Navathe. An efficient algorithm for mining association rules in large databases. VLDB'95 J. S. Park, M. S. Chen, and P. S. Yu. An effective hash-based algorithm for mining association rules. SIGMOD'95 H. Toivonen. Sampling large databases for association rules. VLDB'96 S. Brin, R. Motwani, J. D. Ullman, and S. Tsur. Dynamic itemset counting and implication rules for market basket analysis. SIGMOD'97 S. Sarawagi, S. Thomas, and R. Agrawal. Integrating association rule mining with relational database systems: Alternatives and implications. SIGMOD'98 80
Ref: Apriori and Its Improvements n n n n R. Agrawal and R. Srikant. Fast algorithms for mining association rules. VLDB'94 H. Mannila, H. Toivonen, and A. I. Verkamo. Efficient algorithms for discovering association rules. KDD'94 A. Savasere, E. Omiecinski, and S. Navathe. An efficient algorithm for mining association rules in large databases. VLDB'95 J. S. Park, M. S. Chen, and P. S. Yu. An effective hash-based algorithm for mining association rules. SIGMOD'95 H. Toivonen. Sampling large databases for association rules. VLDB'96 S. Brin, R. Motwani, J. D. Ullman, and S. Tsur. Dynamic itemset counting and implication rules for market basket analysis. SIGMOD'97 S. Sarawagi, S. Thomas, and R. Agrawal. Integrating association rule mining with relational database systems: Alternatives and implications. SIGMOD'98 80
 Ref: Depth-First, Projection-Based FP Mining n n n n R. Agarwal, C. Aggarwal, and V. V. V. Prasad. A tree projection algorithm for generation of frequent itemsets. J. Parallel and Distributed Computing, 2002. G. Grahne and J. Zhu, Efficiently Using Prefix-Trees in Mining Frequent Itemsets, Proc. FIMI'03 B. Goethals and M. Zaki. An introduction to workshop on frequent itemset mining implementations. Proc. ICDM’ 03 Int. Workshop on Frequent Itemset Mining Implementations (FIMI’ 03), Melbourne, FL, Nov. 2003 J. Han, J. Pei, and Y. Yin. Mining frequent patterns without candidate generation. SIGMOD’ 00 J. Liu, Y. Pan, K. Wang, and J. Han. Mining Frequent Item Sets by Opportunistic Projection. KDD'02 J. Han, J. Wang, Y. Lu, and P. Tzvetkov. Mining Top-K Frequent Closed Patterns without Minimum Support. ICDM'02 J. Wang, J. Han, and J. Pei. CLOSET+: Searching for the Best Strategies for Mining Frequent Closed Itemsets. KDD'03 81
Ref: Depth-First, Projection-Based FP Mining n n n n R. Agarwal, C. Aggarwal, and V. V. V. Prasad. A tree projection algorithm for generation of frequent itemsets. J. Parallel and Distributed Computing, 2002. G. Grahne and J. Zhu, Efficiently Using Prefix-Trees in Mining Frequent Itemsets, Proc. FIMI'03 B. Goethals and M. Zaki. An introduction to workshop on frequent itemset mining implementations. Proc. ICDM’ 03 Int. Workshop on Frequent Itemset Mining Implementations (FIMI’ 03), Melbourne, FL, Nov. 2003 J. Han, J. Pei, and Y. Yin. Mining frequent patterns without candidate generation. SIGMOD’ 00 J. Liu, Y. Pan, K. Wang, and J. Han. Mining Frequent Item Sets by Opportunistic Projection. KDD'02 J. Han, J. Wang, Y. Lu, and P. Tzvetkov. Mining Top-K Frequent Closed Patterns without Minimum Support. ICDM'02 J. Wang, J. Han, and J. Pei. CLOSET+: Searching for the Best Strategies for Mining Frequent Closed Itemsets. KDD'03 81
 Ref: Vertical Format and Row Enumeration Methods n M. J. Zaki, S. Parthasarathy, M. Ogihara, and W. Li. Parallel algorithm for discovery of association rules. DAMI: 97. n M. J. Zaki and C. J. Hsiao. CHARM: An Efficient Algorithm for Closed Itemset Mining, SDM'02. n C. Bucila, J. Gehrke, D. Kifer, and W. White. Dual. Miner: A Dual-Pruning Algorithm for Itemsets with Constraints. KDD’ 02. n F. Pan, G. Cong, A. K. H. Tung, J. Yang, and M. Zaki , CARPENTER: Finding Closed Patterns in Long Biological Datasets. KDD'03. n H. Liu, J. Han, D. Xin, and Z. Shao, Mining Interesting Patterns from Very High Dimensional Data: A Top-Down Row Enumeration Approach, SDM'06. 82
Ref: Vertical Format and Row Enumeration Methods n M. J. Zaki, S. Parthasarathy, M. Ogihara, and W. Li. Parallel algorithm for discovery of association rules. DAMI: 97. n M. J. Zaki and C. J. Hsiao. CHARM: An Efficient Algorithm for Closed Itemset Mining, SDM'02. n C. Bucila, J. Gehrke, D. Kifer, and W. White. Dual. Miner: A Dual-Pruning Algorithm for Itemsets with Constraints. KDD’ 02. n F. Pan, G. Cong, A. K. H. Tung, J. Yang, and M. Zaki , CARPENTER: Finding Closed Patterns in Long Biological Datasets. KDD'03. n H. Liu, J. Han, D. Xin, and Z. Shao, Mining Interesting Patterns from Very High Dimensional Data: A Top-Down Row Enumeration Approach, SDM'06. 82
 Ref: Mining Correlations and Interesting Rules n n n n S. Brin, R. Motwani, and C. Silverstein. Beyond market basket: Generalizing association rules to correlations. SIGMOD'97. M. Klemettinen, H. Mannila, P. Ronkainen, H. Toivonen, and A. I. Verkamo. Finding interesting rules from large sets of discovered association rules. CIKM'94. R. J. Hilderman and H. J. Hamilton. Knowledge Discovery and Measures of Interest. Kluwer Academic, 2001. C. Silverstein, S. Brin, R. Motwani, and J. Ullman. Scalable techniques for mining causal structures. VLDB'98. P. -N. Tan, V. Kumar, and J. Srivastava. Selecting the Right Interestingness Measure for Association Patterns. KDD'02. E. Omiecinski. Alternative Interest Measures for Mining Associations. TKDE’ 03. T. Wu, Y. Chen, and J. Han, “Re-Examination of Interestingness Measures in Pattern Mining: A Unified Framework", Data Mining and Knowledge Discovery, 21(3): 371397, 2010 83
Ref: Mining Correlations and Interesting Rules n n n n S. Brin, R. Motwani, and C. Silverstein. Beyond market basket: Generalizing association rules to correlations. SIGMOD'97. M. Klemettinen, H. Mannila, P. Ronkainen, H. Toivonen, and A. I. Verkamo. Finding interesting rules from large sets of discovered association rules. CIKM'94. R. J. Hilderman and H. J. Hamilton. Knowledge Discovery and Measures of Interest. Kluwer Academic, 2001. C. Silverstein, S. Brin, R. Motwani, and J. Ullman. Scalable techniques for mining causal structures. VLDB'98. P. -N. Tan, V. Kumar, and J. Srivastava. Selecting the Right Interestingness Measure for Association Patterns. KDD'02. E. Omiecinski. Alternative Interest Measures for Mining Associations. TKDE’ 03. T. Wu, Y. Chen, and J. Han, “Re-Examination of Interestingness Measures in Pattern Mining: A Unified Framework", Data Mining and Knowledge Discovery, 21(3): 371397, 2010 83
 WEKA 84
WEKA 84


