Data Mining Concepts and Techniques 3 rd ed

Data Mining: Concepts and Techniques (3 rd ed. ) — Chapter 8 — Jiawei Han, Micheline Kamber, and Jian Pei University of Illinois at Urbana-Champaign & Simon Fraser University © 2011 Han, Kamber & Pei. All rights reserved. 1

Chapter 8. Classification: Basic Concepts n Decision Tree Induction n Bayes Classification Methods n Rule-Based Classification n Model Evaluation and Selection n Summary 2

Supervised vs. Unsupervised Learning n Classification: A form of data analysis that extracts model describing important data classes n Supervised learning (classification) n n n Class label of each training tuple is provided New data is classified based on the training set Unsupervised learning (clustering) n The class labels of training data is unknown n Number of classes to be learned may not be known in advance 3

Prediction Problems: Classification vs. Numeric Prediction n Classification n predicts categorical class labels (discrete or nominal) n classifies data (constructs a model) based on the training set and the values (class labels) in a classifying attribute and uses it in classifying new data n Typical applications n n n Credit/loan approval: Medical diagnosis: if a tumor is cancerous or benign Fraud detection: if a transaction is fraudulent Web page categorization: which category it is Numeric Prediction n models continuous-valued functions, i. e. , predicts unknown or missing values. n Example, how much will a given customer spend during a sale? 4

Classification—A Two-Step Process n n Model construction: describing a set of predetermined classes n Each tuple/sample is assumed to belong to a predefined class, as determined by the class label attribute n The set of tuples used for model construction is training set n The model is represented as classification rules, decision trees, or mathematical formulae Model usage: for classifying future or unknown objects n Estimate accuracy of the model n The known label of test sample is compared with the classified result from the model n Accuracy rate is the percentage of test set samples that are correctly classified by the model n Test set is independent of training set (otherwise overfitting) n If the accuracy is acceptable, use the model to classify new data 5

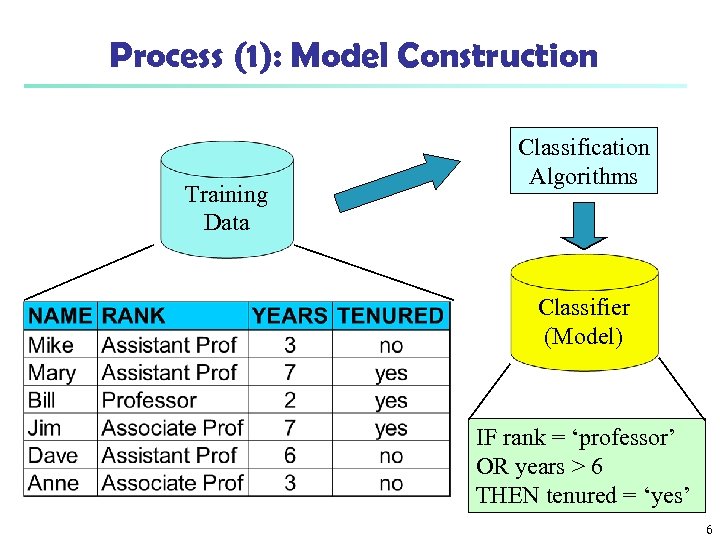Process (1): Model Construction Training Data Classification Algorithms Classifier (Model) IF rank = ‘professor’ OR years > 6 THEN tenured = ‘yes’ 6

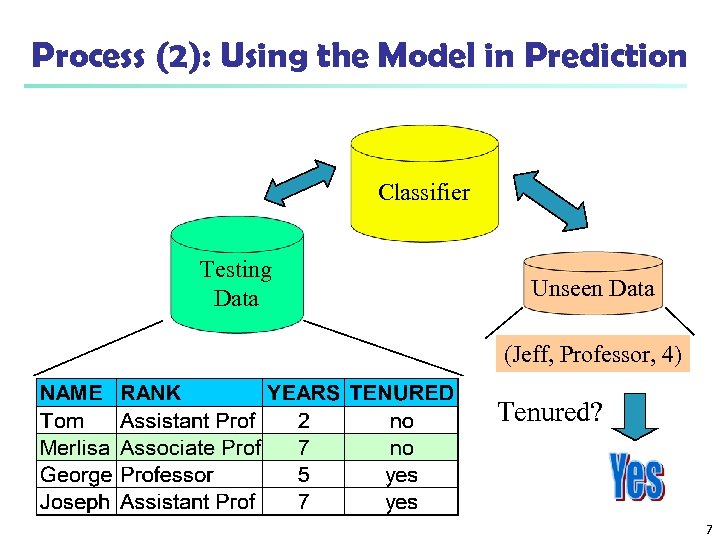Process (2): Using the Model in Prediction Classifier Testing Data Unseen Data (Jeff, Professor, 4) Tenured? 7

Chapter 8. Classification: Basic Concepts n Decision Tree Induction n Bayes Classification Methods n Rule-Based Classification n Model Evaluation and Selection n Summary 8

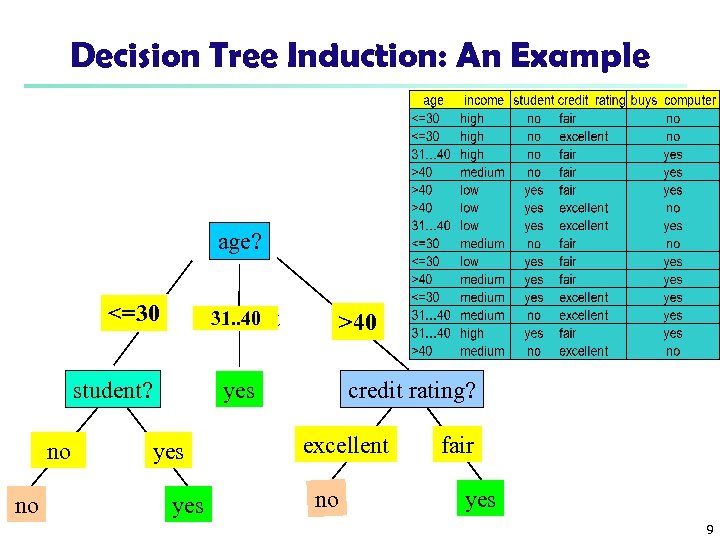Decision Tree Induction: An Example age? <=30 31. . 40 overcast student? no no >40 credit rating? yes yes excellent no fair yes 9

Algorithm for Decision Tree Induction n n Basic algorithm (a greedy algorithm) n Tree is constructed in a top-down recursive divide-and-conquer manner n At start, all the training examples are at the root n Attributes are categorical (if continuous-valued, they are discretized in advance) n Examples are partitioned recursively based on selected attributes n Test attributes are selected on the basis of a heuristic or statistical measure (e. g. , information gain) Conditions for stopping partitioning n All samples for a given node belong to the same class n There are no remaining attributes for further partitioning n There are no samples left 10

Attribute Selection Measure: Information Gain (ID 3/C 4. 5) n n n Select the attribute with the highest information gain Let pi be the probability that an arbitrary tuple in D belongs to class Ci Expected information (entropy) needed to classify a tuple in D: Information needed (after using A to split D into v partitions) to classify D: Information gained by branching on attribute A 11

Attribute Selection: Information Gain Class P: buys_computer = “yes” g Class N: buys_computer = “no” g means “age <=30” has 5 out of 14 samples, with 2 yes’es and 3 no’s. Hence Similarly, 12

Gain Ratio for Attribute Selection (C 4. 5) n n Information gain measure is biased towards attributes with a large number of values C 4. 5 (a successor of ID 3) uses gain ratio to overcome the problem (normalization to information gain) n Gain. Ratio(A) = Gain(A)/Split. Info(A) n Ex. n gain_ratio(income) = 0. 029/1. 557 = 0. 019 The attribute with the maximum gain ratio is selected as the splitting attribute n 13

Gini Index (CART, IBM Intelligent. Miner) n If a data set D contains examples from n classes, gini index, gini(D) is defined as where pj is the relative frequency of class j in D n n n If a data set D is split on A into two subsets D 1 and D 2, the gini index gini(D) is defined as Reduction in Impurity: The attribute provides the smallest ginisplit(D) (or the largest reduction in impurity) is chosen to split the node 14

Computation of Gini Index n n n Ex. D has 9 tuples in buys_computer = “yes” and 5 in “no” Suppose the attribute income partitions D into 10 in D 1: {low, medium} and 4 in D 2 Similarly, Gini{low, high} is 0. 458 and Gini{medium, high} is 0. 450. Evaluating age, we obtain {youth, senior} or {middle-aged} as the best split with Gini index of 0. 357 The attributes student and credit_rating are both binary with Gini index values of 0. 367 and 0. 429. Therefore, the attribute age and splitting subset {youth, senior} gives the minimum Gini index overall and is used as the splitting criterion. 15

Comparing Attribute Selection Measures n The three measures, in general, return good results but n Information gain: n n Gain ratio: n n biased towards multivalued attributes tends to prefer unbalanced splits in which one partition is much smaller than the others Gini index: n biased to multivalued attributes n has difficulty when # of classes is large 16

Overfitting and Tree Pruning n n Overfitting: An induced tree may overfit the training data n Too many branches, some may reflect anomalies due to noise or outliers n Poor accuracy for unseen samples Two approaches to avoid overfitting n Prepruning: Halt tree construction early do not split a node if this would result in the goodness measure falling below a threshold n Difficult to choose an appropriate threshold n Postpruning: Remove branches from a “fully grown” tree— get a sequence of progressively pruned trees n Use a set of data different from the training data to decide which is the “best pruned tree” 17

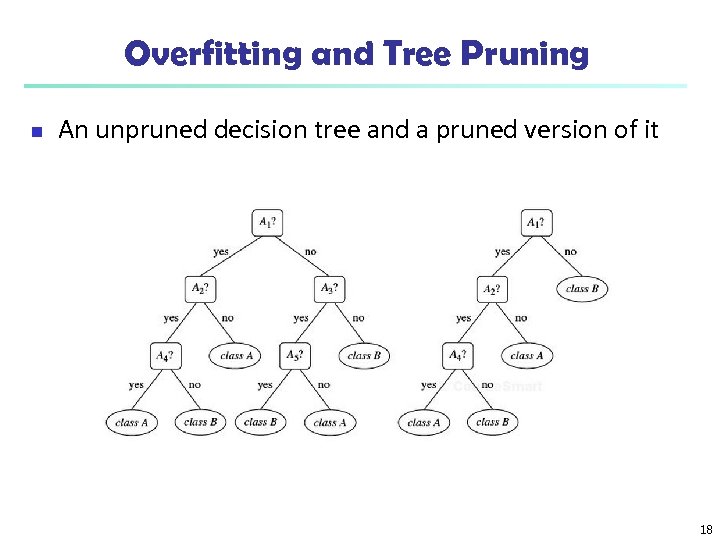Overfitting and Tree Pruning n An unpruned decision tree and a pruned version of it 18

Chapter 8. Classification: Basic Concepts n Decision Tree Induction n Bayes Classification Methods n Rule-Based Classification n Model Evaluation and Selection n Summary 19

Bayesian Classification: Why? n n n A statistical classifier: predict class membership probabilities such as the probability that a given tuple belongs to a particular class Foundation: Based on Bayes’ Theorem. Performance: A simple Bayesian classifier, naïve Bayesian classifier, has comparable performance with decision tree and selected neural network classifiers 20

Bayes’ Theorem: Basics n Bayes’ Theorem: n n n Let X be a data sample (“evidence”): class label is unknown Let H be a hypothesis that X belongs to class C Classification is to determine P(H|X), (i. e. , posteriori probability): the probability that the hypothesis holds given the observed data sample X P(H) (prior probability): the initial probability P(X): probability that sample data is observed P(X|H) (likelihood): the probability of observing the sample X, given that the hypothesis holds n E. g. , Given that X will buy computer, the prob. that X is 31. . 40, medium income 21

Bayes’ Theorem: Example n Assume that you are presented with three coins, two of them fair and the other a counterfeit that always lands heads. If you randomly pick one of the three coins, the probability that it's the counterfeit is 1 in 3. This is the prior probability of the hypothesis that the coin is counterfeit. Now after picking the coin, you flip it three times and observe that it lands heads each time. Seeing this new evidence that your chosen coin has landed heads three times in a row, you want to know the revised posterior probability that it is the counterfeit. The answer to this question, found using Bayes's theorem is 4 in 5. You thus revise your probability estimate of the coin's being counterfeit upward from 1 in 3 to 4 in 5. " 22

Bayes’ Theorem: Example 23

Classification Is to Derive the Maximum Posteriori n Let D be a training set of tuples and their associated class labels, and each tuple is represented by an n-D attribute vector X = (x 1, x 2, …, xn) Suppose there are m classes C 1, C 2, …, Cm. Classification is to derive the maximum posteriori, i. e. , the maximal P(Ci|X) This can be derived from Bayes’ theorem n Since P(X) is constant for all classes, only n needs to be maximized 24

Naïve Bayes Classifier n n A simplified assumption: attributes are conditionally independent (i. e. , no dependence relation between attributes): This greatly reduces the computation cost: Only counts the class distribution 25

Naïve Bayes Classifier: Training Dataset Class: C 1: buys_computer = ‘yes’ C 2: buys_computer = ‘no’ Data to be classified: X = (age <=30, Income = medium, Student = yes Credit_rating = Fair) 26

Naïve Bayes Classifier: An Example P(Ci): P(buys_computer = “yes”) = 9/14 = 0. 643 P(buys_computer = “no”) = 5/14= 0. 357 n Compute P(X|Ci) for each class P(age = “<=30” | buys_computer = “yes”) = 2/9 = 0. 222 P(age = “<= 30” | buys_computer = “no”) = 3/5 = 0. 6 P(income = “medium” | buys_computer = “yes”) = 4/9 = 0. 444 P(income = “medium” | buys_computer = “no”) = 2/5 = 0. 4 P(student = “yes” | buys_computer = “yes) = 6/9 = 0. 667 P(student = “yes” | buys_computer = “no”) = 1/5 = 0. 2 P(credit_rating = “fair” | buys_computer = “yes”) = 6/9 = 0. 667 P(credit_rating = “fair” | buys_computer = “no”) = 2/5 = 0. 4 n X = (age <= 30 , income = medium, student = yes, credit_rating = fair) P(X|Ci) : P(X|buys_computer = “yes”) = 0. 222 x 0. 444 x 0. 667 = 0. 044 P(X|buys_computer = “no”) = 0. 6 x 0. 4 x 0. 2 x 0. 4 = 0. 019 P(X|Ci)*P(Ci) : P(X|buys_computer = “yes”) * P(buys_computer = “yes”) = 0. 028 P(X|buys_computer = “no”) * P(buys_computer = “no”) = 0. 007 Therefore, X belongs to class (“buys_computer = yes”) n 27

Avoiding the Zero-Probability Problem n n n Naïve Bayesian prediction requires each conditional prob. be non-zero. Otherwise, the predicted prob. will be zero Ex. Suppose a dataset with 1000 tuples, income=low (0), income= medium (990), and income = high (10) Use Laplacian correction (or Laplacian estimator) n Adding 1 to each case Prob(income = low) = 1/1003 Prob(income = medium) = 991/1003 Prob(income = high) = 11/1003 n The “corrected” prob. estimates are close to their “uncorrected” counterparts 28

Naïve Bayes Classifier: Comments n n n Advantages n Easy to implement n Good results obtained in most of the cases Disadvantages n Assumption: class conditional independence, therefore loss of accuracy n Practically, dependencies exist among variables n Dependencies among these cannot be modeled by Naïve Bayes Classifier How to deal with these dependencies? Bayesian Belief Networks 29

Chapter 8. Classification: Basic Concepts n Decision Tree Induction n Bayes Classification Methods n Rule-Based Classification n Model Evaluation and Selection n Summary 30

Using IF-THEN Rules for Classification n Represent the knowledge in the form of IF-THEN rules R: IF age = youth AND student = yes THEN buys_computer = yes n Rule antecedent/precondition vs. rule consequent Assessment of a rule: coverage and accuracy n ncovers = # of tuples covered by R n ncorrect = # of tuples correctly classified by R coverage(R) = ncovers /|D| /* D: training data set */ accuracy(R) = ncorrect / ncovers If more than one rule are triggered, need conflict resolution n Size ordering: assign the highest priority to the triggering rules that has the “toughest” requirement (i. e. , with the most attribute tests) n Class-based ordering: classes are sorted in decreasing order of importance, rule that predicts the most important class gets the priority n Rule-based ordering (decision list): rules are organized into one long priority list, according to some measure of rule quality such by accuracy, coverage or by experts advice 31

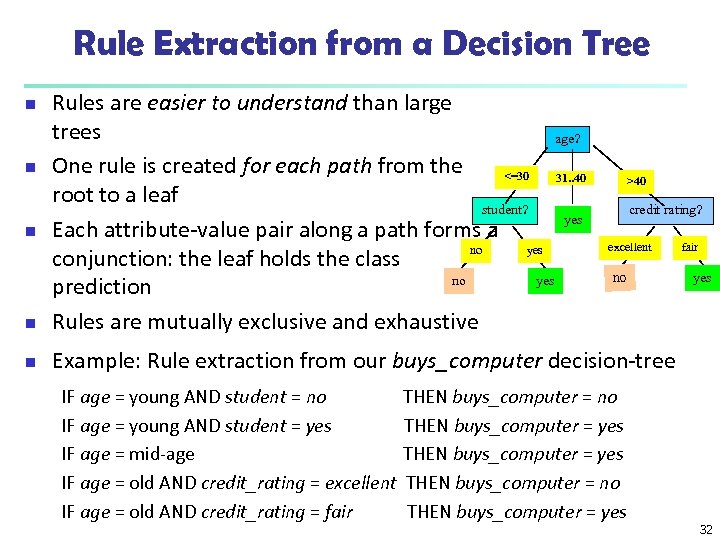Rule Extraction from a Decision Tree n Rules are easier to understand than large trees age? One rule is created for each path from the <=30 31. . 40 root to a leaf student? yes Each attribute-value pair along a path forms a no yes conjunction: the leaf holds the class no yes prediction Rules are mutually exclusive and exhaustive n Example: Rule extraction from our buys_computer decision-tree n n n IF age = young AND student = no IF age = young AND student = yes IF age = mid-age IF age = old AND credit_rating = excellent IF age = old AND credit_rating = fair >40 credit rating? excellent no THEN buys_computer = yes THEN buys_computer = no THEN buys_computer = yes fair yes 32

Rule Induction: Sequential Covering Method n n Sequential covering algorithm: Extracts rules directly from training data Typical sequential covering algorithms: FOIL, AQ, CN 2, RIPPER Rules are learned sequentially, each for a given class Ci will cover many tuples of Ci but none (or few) of the tuples of other classes Steps: n Rules are learned one at a time n Each time a rule is learned, the tuples covered by the rules are removed n Repeat the process on the remaining tuples until termination condition, e. g. , when no more training examples or when the quality of a rule returned is below a user-specified threshold 33

Chapter 8. Classification: Basic Concepts n Decision Tree Induction n Bayes Classification Methods n Rule-Based Classification n Model Evaluation and Selection n Summary 34

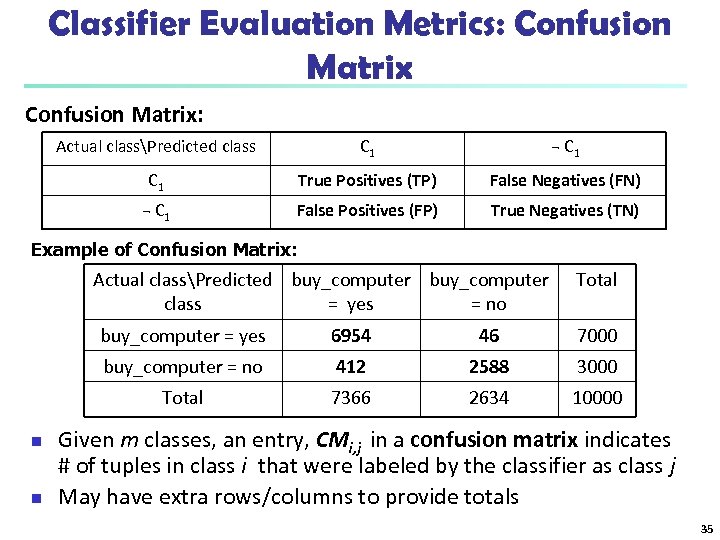Classifier Evaluation Metrics: Confusion Matrix: Actual classPredicted class C 1 ¬ C 1 True Positives (TP) False Negatives (FN) ¬ C 1 False Positives (FP) True Negatives (TN) Example of Confusion Matrix: Actual classPredicted buy_computer class = yes = no Total buy_computer = yes 7000 412 2588 3000 Total n 46 buy_computer = no n 6954 7366 2634 10000 Given m classes, an entry, CMi, j in a confusion matrix indicates # of tuples in class i that were labeled by the classifier as class j May have extra rows/columns to provide totals 35

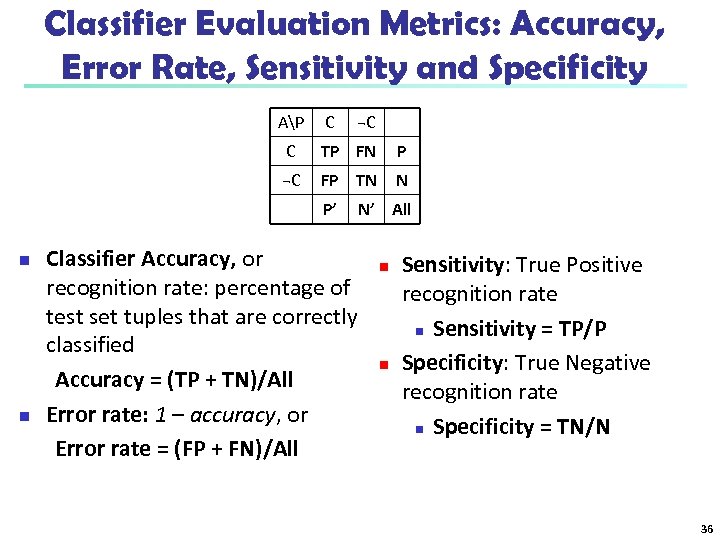Classifier Evaluation Metrics: Accuracy, Error Rate, Sensitivity and Specificity AP C ¬C C TP FN P ¬C FP TN N P’ n n N’ All Classifier Accuracy, or recognition rate: percentage of test set tuples that are correctly classified Accuracy = (TP + TN)/All Error rate: 1 – accuracy, or Error rate = (FP + FN)/All n n Sensitivity: True Positive recognition rate n Sensitivity = TP/P Specificity: True Negative recognition rate n Specificity = TN/N 36

Classifier Evaluation Metrics: Precision and Recall, and F-measures n n Precision: exactness – what % of tuples that the classifier labeled as positive are actually positive Recall: completeness – what % of positive tuples did the classifier label as positive? F measure (F 1 or F-score): harmonic mean of precision and recall, Fß: weighted measure of precision and recall 37

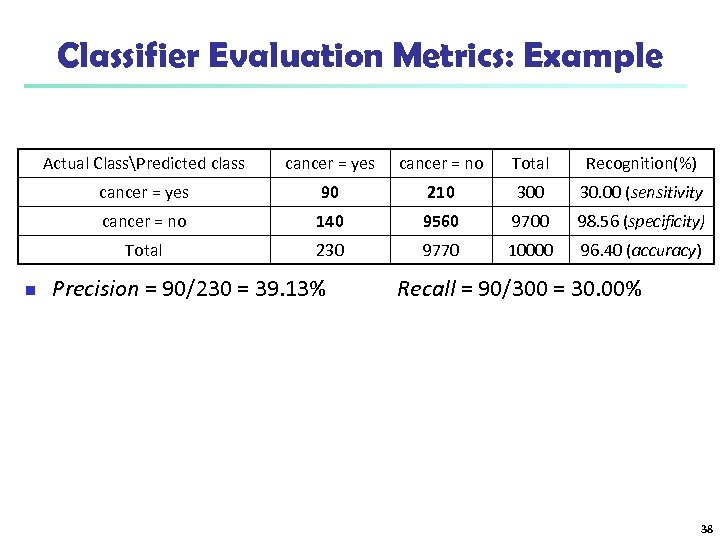Classifier Evaluation Metrics: Example Actual ClassPredicted class cancer = no Total Recognition(%) cancer = yes 90 210 30. 00 (sensitivity cancer = no 140 9560 9700 98. 56 (specificity) Total n cancer = yes 230 9770 10000 96. 40 (accuracy) Precision = 90/230 = 39. 13% Recall = 90/300 = 30. 00% 38

Chapter 8. Classification: Basic Concepts n Decision Tree Induction n Bayes Classification Methods n Rule-Based Classification n Model Evaluation and Selection n Summary 39

Summary n n n Classification is a form of data analysis that extracts models describing important data classes. Effective and scalable methods have been developed for decision tree induction, Naive Bayesian classification, rule-based classification, and many other classification methods. Evaluation metrics include: accuracy, sensitivity, specificity, precision, recall, F measure, and Fß measure. 40