Data Mining Concepts and Techniques 3 rd ed

Data Mining: Concepts and Techniques (3 rd ed. ) — Chapter 6 — Jiawei Han, Micheline Kamber, and Jian Pei University of Illinois at Urbana-Champaign & Simon Fraser University © 2011 Han, Kamber & Pei. All rights reserved. 1

17 March 2018 Data Mining: Concepts and Techniques 2

Chapter 6: Mining Frequent Patterns, Association and Correlations: Basic Concepts and Methods n Basic Concepts n Frequent Itemset Mining Methods n Which Patterns Are Interesting? —Pattern Evaluation Methods n Summary 3

What Is Association Mining? Or What Is Frequent Pattern Analysis? n Frequent pattern: a pattern (a set of items, subsequences, substructures, etc. ) that occurs frequently in a data set First proposed by Agrawal, Imielinski, and Swami [AIS 93] in the context of frequent itemsets and association rule mining n Association rule mining: n Finding frequent patterns, associations, correlations, or causal structures among sets of items or objects in transaction databases, relational databases, and other information repositories. n Applications: n Basket data analysis, cross-marketing, catalog design, loss-leader analysis, clustering, classification, etc. n Examples. n Rule form: “Body ® Head [support, confidence]”. n buys(x, “diapers”) ® buys(x, “beers”) [0. 5%, 60%] n major(x, “CS”) ^ takes(x, “DB”) ® grade(x, “A”) [1%, 75%] n 17 March 2018 Data Mining: Concepts and Techniques 4

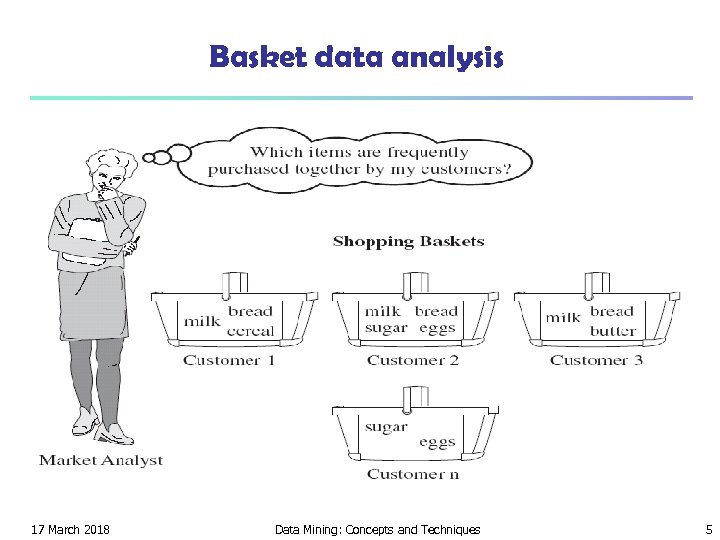Basket data analysis 17 March 2018 Data Mining: Concepts and Techniques 5

Why Is Freq. Pattern Mining Important? n n Freq. pattern: An intrinsic and important property of datasets Foundation for many essential data mining tasks n Association, correlation, and causality analysis n Sequential, structural (e. g. , sub-graph) patterns n Pattern analysis in spatiotemporal, multimedia, timeseries, and stream data n Classification: discriminative, frequent pattern analysis n Cluster analysis: frequent pattern-based clustering n Data warehousing: iceberg cube and cube-gradient n Semantic data compression: fascicles n Broad applications 6

Association Rule: Basic Concepts n n Given: (1) database of transactions, (2) each transaction is a list of items (purchased by a customer in a visit) Find: all rules that correlate the presence of one set of items with that of another set of items n E. g. , 98% of people who purchase tires and auto accessories also get automotive services done n Applications n n * Maintenance Agreement (What the store should do to boost Maintenance Agreement sales) Home Electronics * (What other products should the store stocks up? ) Attached mailing in direct marketing Detecting “ping-pong”ing of patients, faulty “collisions” 17 March 2018 Data Mining: Concepts and Techniques 7

Association Rule Mining: A Road Map Boolean vs. quantitative associations (Based on the types of values handled) n buys(x, “SQLServer”) ^ buys(x, “DMBook”) ® buys(x, “DBMiner”) [0. 2%, 60%] n age(x, “ 30. . 39”) ^ income(x, “ 42. . 48 K”) ® buys(x, “PC”) [1%, 75%] n Single dimension vs. multiple dimensional associations (see ex. Above) n buys(x, “SQLServer”)®buys(x, “DMBook”) n Single level vs. multiple-level analysis n What brands of beers are associated with what brands of diapers? n n Buys(computer) Age(X, 31. . 40) Buys(loptop_computer) Age(X, 31. . 40) Various extensions n Correlation, causality analysis n n n Association does not necessarily imply correlation or causality Maxpatterns and closed itemsets Constraints enforced n 17 March 2018 E. g. , small sales (sum < 100) trigger big buys (sum > 1, 000)? Data Mining: Concepts and Techniques 8

Rule Measures: Support and Confidence Transaction-id Items bought 10 A, B, C 20 A, C 30 A, D 40 B, E, F Customer buys both Customer buys beer Customer buys diaper n n Itemset X={x 1, …, xk} Find all the rules X Y with min confidence and support n n support, s, probability that a transaction contains X Y confidence, c, conditional probability that a transaction having X also contains Y. Let min_support = 50%, min_conf = 50%: A C (50%, 66. 7%) C A (50%, 100%) 9

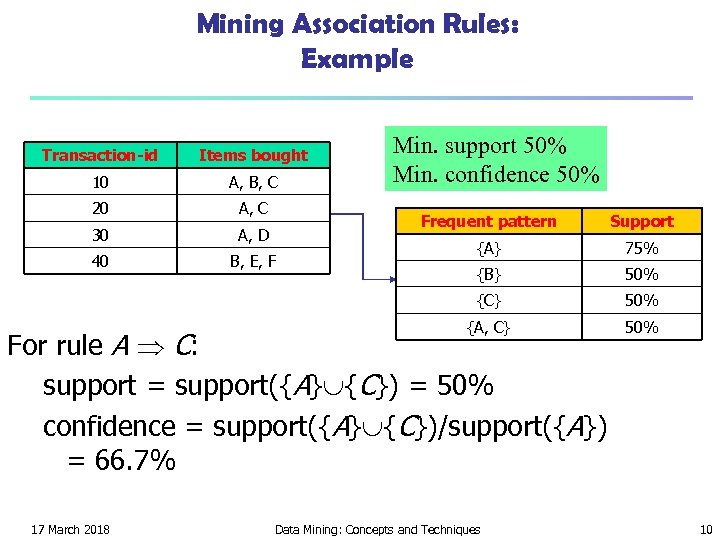Mining Association Rules: Example Transaction-id Items bought 10 A, B, C 20 A, C 30 A, D 40 B, E, F Min. support 50% Min. confidence 50% Frequent pattern Support {A} 75% {B} 50% {C} 50% {A, C} 50% For rule A C: support = support({A} {C}) = 50% confidence = support({A} {C})/support({A}) = 66. 7% 17 March 2018 Data Mining: Concepts and Techniques 10

Association Rules Example I = { Beer, Bread, Jelly, Milk, Peanut. Butter} Support of {Bread, Peanut. Butter} is 60% Support count of {Bread, Peanut. Butter} is 3 17 March 2018 Data Mining: Concepts and Techniques 11

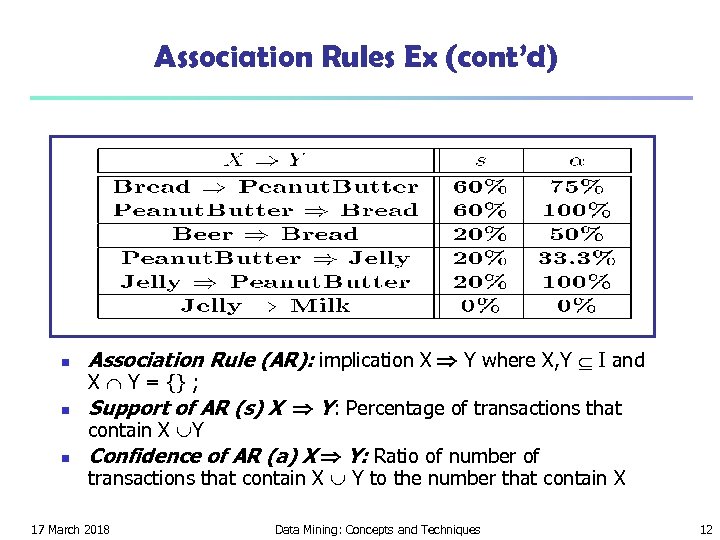Association Rules Ex (cont’d) n Association Rule (AR): implication X Y where X, Y I and n Support of AR (s) X Y: Percentage of transactions that n Confidence of AR (a) X Y: Ratio of number of X Y = {} ; contain X Y transactions that contain X Y to the number that contain X 17 March 2018 Data Mining: Concepts and Techniques 12

Chapter 6: Mining Association Rules in Large Databases n n Association rule mining Mining single-dimensional Boolean association rules from transactional databases Mining multilevel association rules from transactional databases Mining multidimensional association rules from transactional databases and data warehouse n From association mining to correlation analysis n Constraint-based association mining n Summary 17 March 2018 Data Mining: Concepts and Techniques 13

Association Rule Mining Problem n n Given: (1) database of transactions, (2) each transaction is a list of items (purchased by a customer in a visit) Find Association rules from database transcactions n n n computer ® financial management software [support = 2%; confidence = 60%] Typically, association rules are considered interesting if they satisfy both a minimum support (threshold) and a minimum confidence (threshold). Such thresholds can be set by users or domain experts. 17 March 2018 Data Mining: Concepts and Techniques 14

Basic Concepts n n Definitions: n An item: an article in a basket, or an attribute-value pair n A transaction: items purchased in a basket; it may have TID (transaction ID) n A transactional dataset: A set of transactions Example: Market basket Analysis: Basket 1: {bread, cheese, milk} Basket 2: {apple, eggs, salt, yogurt} … Basketn: {biscuit, eggs, milk} An itemset is a set of items. n E. g. , {milk, bread, cereal} is an itemset. A k-itemset is an itemset with k items. 17 March 2018 Data Mining: Concepts and Techniques 15

Basic Concepts n n n The occurrence frequency of an itemset : is the number of transactions that contain the itemset. This is also known, simply, as the frequency or support count of the itemset. Support of an itemset: Percentage of transactions which contain that itemset. An itemset satises minimum support if the occurrence frequency of the itemset is greater than or equal to the product of min_sup and the total number of transactions in D. If an itemset satises minimum support, then it is a frequent itemset. (Frequent itemset: Itemset whose number of occurrences is above a threshold). The set of frequent k-itemsets is commonly denoted by Lk 17 March 2018 Data Mining: Concepts and Techniques 16

Association Rule Mining Problem n n n Given a set of items I={I 1, I 2, …, Im} and a database of transactions D={t 1, t 2, …, tn} where ti={Ii 1, Ii 2, …, Iik} and Iij I, The Association Rule Mining Problem is to identify all association rules X Y with a minimum support and confidence. Rules that satisfy both a minimum support threshold (min_sup) and a minimum confidence threshold (min_conf) are called strong. 17 March 2018 Data Mining: Concepts and Techniques 17

Association Rule Mining Process n Association rule mining is a two-step process: n Step 1: Find all frequent itemsets. By definition, each of these itemsets will occur at least as frequently as a pre-determined minimum support count. n Step 2: Generate strong association rules from the frequent itemsets. By definition, these rules must satisfy minimum support and minimum confidence. 17 March 2018 Data Mining: Concepts and Techniques 18

The Apriori Algorithm n n n The Apriori algorithm is the most well known association rule algorithm and used in most commercial products. The name of the algorithm is based on the fact that the algorithm uses prior knowledge of frequent itemset properties. Apriori employs an iterative approach known as a level-wise search, where k-itemsets are used to explore (k+1)-itemsets. First, the set of frequent 1 -itemsets is found. This set is denoted L 1 is used to find L 2, the frequent 2 -itemsets, which is used to find L 3, and so on, until no more frequent k-itemsets can be found. The finding of each Lk requires one full scan of the database. 17 March 2018 Data Mining: Concepts and Techniques 19

Apriori property n n A frequent (large) itemset is an itemset whose support (S) is ≥ min_sup. Apriori property (downward closure): any subsets of a frequent itemset are also frequent itemsets n i. e. , if {AB} is a frequent itemset, both {A} and {B} should be a frequent itemset n Apriori property is used to reduce the search space. It improves the eficiency of the level-wise generation of frequent itemsets. ABC AB A 17 March 2018 ABD AC B AD ACD BC C BCD BD CD D Data Mining: Concepts and Techniques 20

Mining Frequent Itemsets: the Key Step n n Find the frequent itemsets: the sets of items that have minimum support Iteratively: n n Find all 1 -item frequent itemsets; then all 2 -item frequent itemsets, etc. In each iteration k, only consider itemsets that contain some k -1 frequent itemset. Candidate and frequent itemsets n C = candidates of size k: those itemsets of size k k that could be frequent, given Lk-1 n L = those itemsets that are actually frequent, L k k Ck (need to scan the database once). 17 March 2018 Data Mining: Concepts and Techniques 21

The Apriori Algorithm — Example 1 n Suppose that the minimum transaction support count required is 2 (i. e. , min_sup = 50%). Database D 17 March 2018 Data Mining: Concepts and Techniques 22

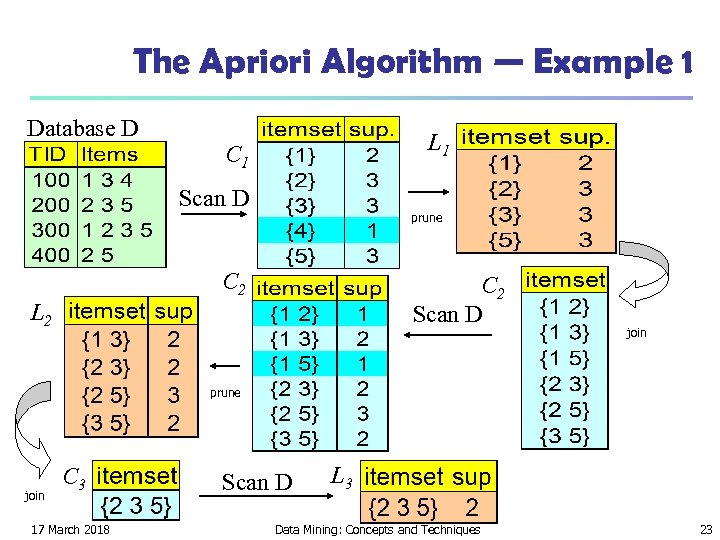The Apriori Algorithm — Example 1 Database D L 1 C 1 Scan D prune C 2 Scan D L 2 join prune join C 3 17 March 2018 Scan D L 3 Data Mining: Concepts and Techniques 23

The Apriori Algorithm — Example 2 n Suppose that the minimum transaction support count required is 2 (i. e. , min sup_count = 2, or min_sup = 2/9 = 22%) Database D 17 March 2018 Data Mining: Concepts and Techniques 24

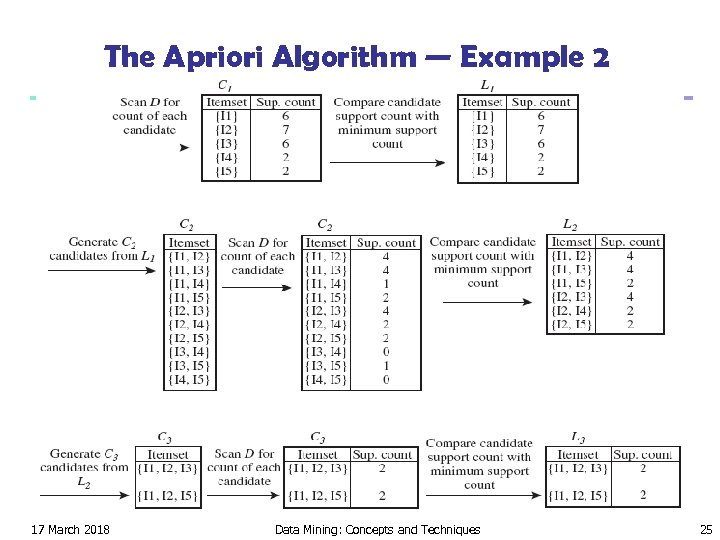The Apriori Algorithm — Example 2 17 March 2018 Data Mining: Concepts and Techniques 25

Example of Generating Candidates n By convention, Apriopri assumes that items within an itemset are sorted in lexicograhic order. The join of two k-1 itemsets is performed by comparing first k-2 items in itemsets. n L 3={abc, abd, ace, bcd} n Self-joining: L 3*L 3 n n n abcd from abc and abd acde from acd and ace Pruning: n n acde is removed because ade is not in L 3 C 4={abcd} 17 March 2018 Data Mining: Concepts and Techniques 26

An Example 17 March 2018 Data Mining: Concepts and Techniques 27

The Apriori Algorithm n n Join Step: Ck is generated by joining Lk-1 with itself Prune Step: Any (k-1)-itemset that is not frequent cannot be a subset of a frequent k-itemset n Pseudo-code: Ck: Candidate itemset of size k Lk : frequent itemset of size k L 1 = {frequent items}; for (k = 1; Lk != ; k++) do begin Ck+1 = candidates generated from Lk; for each transaction t in database do increment the count of all candidates in Ck+1 that are contained in t Lk+1 = candidates in Ck+1 with min_support end return k Lk; 17 March 2018 Data Mining: Concepts and Techniques 28

How to Generate Candidates? n Suppose the items in Lk-1 are listed in an order n Step 1: self-joining Lk-1 insert into Ck select p. item 1, p. item 2, …, p. itemk-1, q. itemk-1 from Lk-1 p, Lk-1 q where p. item 1=q. item 1, …, p. itemk-2=q. itemk-2, p. itemk-1 < q. itemk-1 n Step 2: pruning forall itemsets c in Ck do forall (k-1)-subsets s of c do if (s is not in Lk-1) then delete c from Ck 17 March 2018 Data Mining: Concepts and Techniques 29

Generating association rules from frequent itemsets n n Once the frequent itemsets from transactions in a database D have been found, it is straightforward to generate strong association rules from them (where strong association rules satisfy both minimum support and minimum condence) confidence(A B)= P(B A) = support_count(A B) / support_count(A) where support_count(A U B) is the number of transactions containing the itemsets A U B, and support_count(A) is the number of transactions containing the itemset A. n Based on this equation, association rules can be generated as follows. n n 17 March 2018 for each frequent itemset l, generate non empty sunbsets of l. For every non-empty subset s of l, output the rules s (l-s) if sup_count(l)/sup_count(s)>=min_conf Data Mining: Concepts and Techniques 30

Example 6. 2 from the Book n n the frequent item set [1 2 5] non empty subsets of l are n [1 2], [1 5], [2 5], [1], [2], [5] the resulting association rules are: n 1 2 5 conf: 2/4=50% n 1 5 2 conf: 2/2=100% n 2 5 1 conf: 2/2=100% n 1 2 5 conf: 2/6=33% n 2 1 5 conf: 2/7=29% n 5 1 2 conf: 2/2=100% if min conf=70%, then 2 nd and 3 th and last rules are strong 17 March 2018 Data Mining: Concepts and Techniques 31

How to Count Supports of Candidates? n Why counting supports of candidates a problem? n n n The total number of candidates can be very huge One transaction may contain many candidates Method: n Candidate itemsets are stored in a hash-tree n Leaf node of hash-tree contains a list of itemsets and counts n n Interior node contains a hash table Subset function: finds all the candidates contained in a transaction 17 March 2018 Data Mining: Concepts and Techniques 32

Methods to Improve Apriori’s Efficiency n Hash-based itemset counting: A k-itemset whose corresponding hashing bucket count is below the threshold cannot be frequent n Transaction reduction: A transaction that does not contain any frequent k-itemset is useless in subsequent scans n Partitioning: Any itemset that is potentially frequent in DB must be frequent in at least one of the partitions of DB n Sampling: mining on a subset of given data, lower support threshold + a method to determine the completeness n Dynamic itemset counting: add new candidate itemsets only when all of their subsets are estimated to be frequent 17 March 2018 Data Mining: Concepts and Techniques 33

Is Apriori Fast Enough? — Performance Bottlenecks n The core of the Apriori algorithm: n n n Use frequent (k – 1)-itemsets to generate candidate frequent kitemsets Use database scan and pattern matching to collect counts for the candidate itemsets The bottleneck of Apriori: candidate generation n Huge candidate sets: n n n 104 frequent 1 -itemset will generate 107 candidate 2 -itemsets To discover a frequent pattern of size 100, e. g. , {a 1, a 2, …, a 100}, one needs to generate 2100 1030 candidates. Multiple scans of database: n 17 March 2018 Needs (n +1 ) scans, n is the length of the longest pattern Data Mining: Concepts and Techniques 34

Mining Frequent Patterns Without Candidate Generation n Compress a large database into a compact, Frequent. Pattern tree (FP-tree) structure n n n highly condensed, but complete for frequent pattern mining avoid costly database scans Develop an efficient, FP-tree-based frequent pattern mining method n n A divide-and-conquer methodology: decompose mining tasks into smaller ones Avoid candidate generation: sub-database test only! 17 March 2018 Data Mining: Concepts and Techniques 35

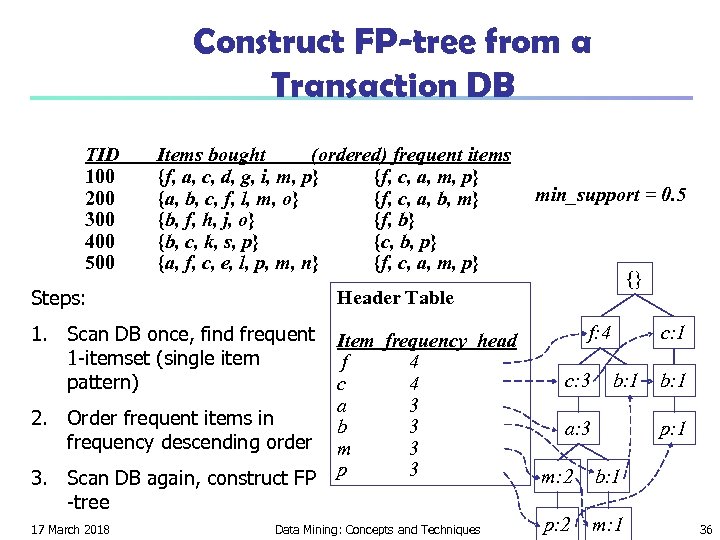Construct FP-tree from a Transaction DB TID 100 200 300 400 500 Items bought (ordered) frequent items {f, a, c, d, g, i, m, p} {f, c, a, m, p} {a, b, c, f, l, m, o} {f, c, a, b, m} {b, f, h, j, o} {f, b} {b, c, k, s, p} {c, b, p} {a, f, c, e, l, p, m, n} {f, c, a, m, p} Steps: Item frequency head f 4 c 4 a 3 b 3 m 3 p 3 {} Header Table 1. Scan DB once, find frequent 1 -itemset (single item pattern) min_support = 0. 5 2. Order frequent items in frequency descending order 3. Scan DB again, construct FP -tree 17 March 2018 Data Mining: Concepts and Techniques f: 4 c: 3 c: 1 b: 1 a: 3 b: 1 p: 1 m: 2 b: 1 p: 2 m: 1 36

Benefits of the FP-tree Structure n n Completeness: n never breaks a long pattern of any transaction n preserves complete information for frequent pattern mining Compactness n reduce irrelevant information—infrequent items are gone n frequency descending ordering: more frequent items are more likely to be shared n never be larger than the original database (if not count node-links and counts) n Example: For Connect-4 DB, compression ratio could be over 100 17 March 2018 Data Mining: Concepts and Techniques 37

Mining Frequent Patterns Using FPtree n n General idea (divide-and-conquer) n Recursively grow frequent pattern path using the FPtree Method n For each item, construct its conditional pattern-base, and then its conditional FP-tree n Repeat the process on each newly created conditional FP-tree n Until the resulting FP-tree is empty, or it contains only one path (single path will generate all the combinations of its sub-paths, each of which is a frequent pattern) 17 March 2018 Data Mining: Concepts and Techniques 38

Major Steps to Mine FP-tree Construct conditional pattern base for each node in the FP-tree 1) Construct conditional FP-tree from each conditional pattern-base 2) Recursively mine conditional FP-trees and grow frequent patterns obtained so far 3) § 17 March 2018 If the conditional FP-tree contains a single path, simply enumerate all the patterns Data Mining: Concepts and Techniques 39

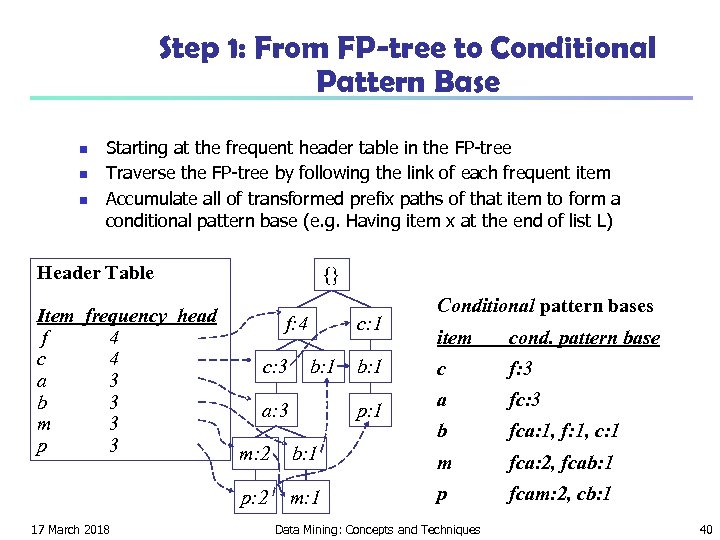Step 1: From FP-tree to Conditional Pattern Base n n n Starting at the frequent header table in the FP-tree Traverse the FP-tree by following the link of each frequent item Accumulate all of transformed prefix paths of that item to form a conditional pattern base (e. g. Having item x at the end of list L) Header Table Item frequency head f 4 c 4 a 3 b 3 m 3 p 3 {} f: 4 c: 3 c: 1 b: 1 a: 3 b: 1 p: 1 Conditional pattern bases item cond. pattern base c f: 3 a fc: 3 b fca: 1, f: 1, c: 1 b: 1 m fca: 2, fcab: 1 p: 2 17 March 2018 m: 2 m: 1 p fcam: 2, cb: 1 Data Mining: Concepts and Techniques 40

Properties of FP-tree for Conditional Pattern Base Construction n Node-link property n n For any frequent item ai, all the possible frequent patterns that contain ai can be obtained by following ai's node-links, starting from ai's head in the FP-tree header Prefix path property n 17 March 2018 To calculate the frequent patterns for a node ai in a path P, only the prefix sub-path of ai in P need to be accumulated, and its frequency count should carry the same count as node ai. Data Mining: Concepts and Techniques 41

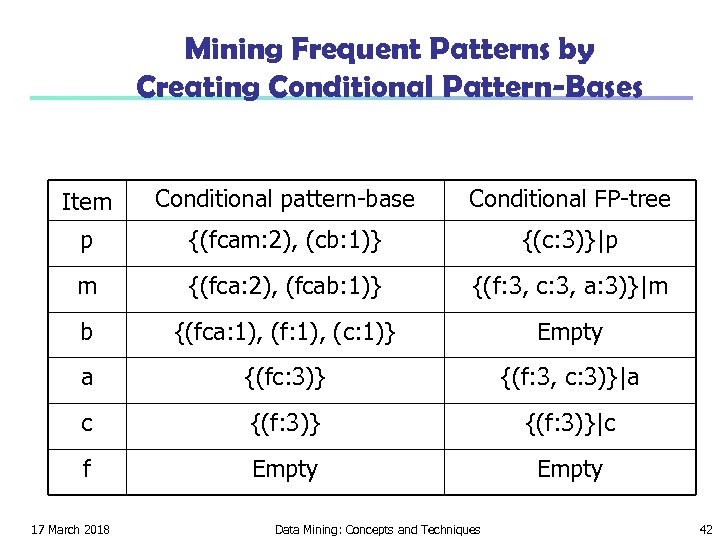Mining Frequent Patterns by Creating Conditional Pattern-Bases Item Conditional pattern-base Conditional FP-tree p {(fcam: 2), (cb: 1)} {(c: 3)}|p m {(fca: 2), (fcab: 1)} {(f: 3, c: 3, a: 3)}|m b {(fca: 1), (f: 1), (c: 1)} Empty a {(fc: 3)} {(f: 3, c: 3)}|a c {(f: 3)}|c f Empty 17 March 2018 Data Mining: Concepts and Techniques 42

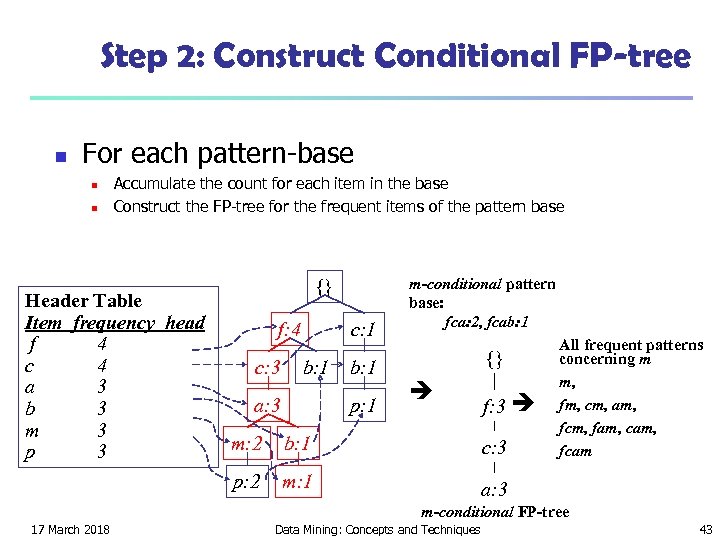Step 2: Construct Conditional FP-tree n For each pattern-base n n Accumulate the count for each item in the base Construct the FP-tree for the frequent items of the pattern base Header Table Item frequency head f 4 c 4 a 3 b 3 m 3 p 3 {} f: 4 c: 3 c: 1 b: 1 a: 3 b: 1 p: 1 m-conditional pattern base: fca: 2, fcab: 1 {} f: 3 m: 2 b: 1 c: 3 p: 2 m: 1 All frequent patterns concerning m m, fm, cm, am, fcm, fam, cam, fcam a: 3 m-conditional FP-tree 17 March 2018 Data Mining: Concepts and Techniques 43

Step 3: Recursively mine the conditional FP-tree {} {} Cond. pattern base of “am”: (fc: 3) c: 3 f: 3 am-conditional FP-tree c: 3 a: 3 f: 3 {} Cond. pattern base of “cm”: (f: 3) f: 3 m-conditional FP-tree cm-conditional FP-tree {} Cond. pattern base of “cam”: (f: 3) f: 3 cam-conditional FP-tree 17 March 2018 Data Mining: Concepts and Techniques 44

Single FP-tree Path Generation n n Suppose an FP-tree T has a single path P The complete set of frequent pattern of T can be generated by enumeration of all the combinations of the sub-paths of P {} f: 3 c: 3 a: 3 All frequent patterns concerning m m, fm, cm, am, fcm, fam, cam, fcam m-conditional FP-tree 17 March 2018 Data Mining: Concepts and Techniques 45

Principles of Frequent Pattern Growth n Pattern growth property n n Let be a frequent itemset in DB, B be 's conditional pattern base, and be an itemset in B. Then is a frequent itemset in DB iff is frequent in B. “abcdef ” is a frequent pattern, if and only if n n “abcde ” is a frequent pattern, and “f ” is frequent in the set of transactions containing “abcde ” 17 March 2018 Data Mining: Concepts and Techniques 46

Why Is Frequent Pattern Growth Fast? n Our performance study shows n FP-growth is an order of magnitude faster than Apriori, and is also faster than tree-projection n Reasoning n No candidate generation, no candidate test n Use compact data structure n Eliminate repeated database scan n Basic operation is counting and FP-tree building 17 March 2018 Data Mining: Concepts and Techniques 47

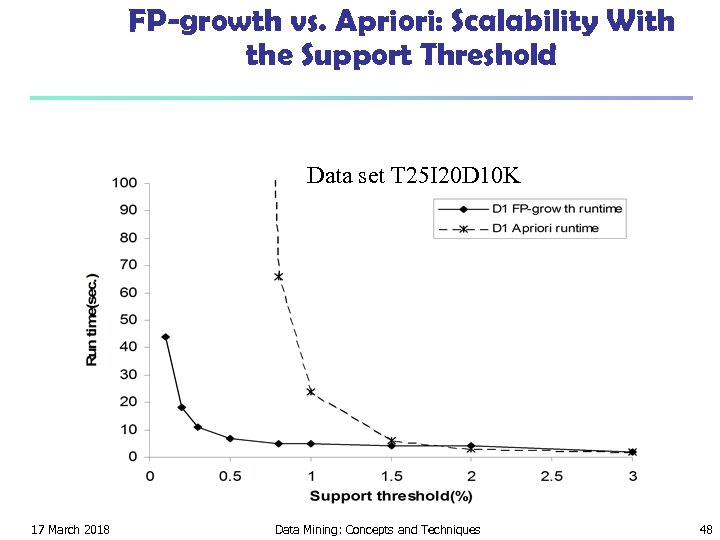FP-growth vs. Apriori: Scalability With the Support Threshold Data set T 25 I 20 D 10 K 17 March 2018 Data Mining: Concepts and Techniques 48

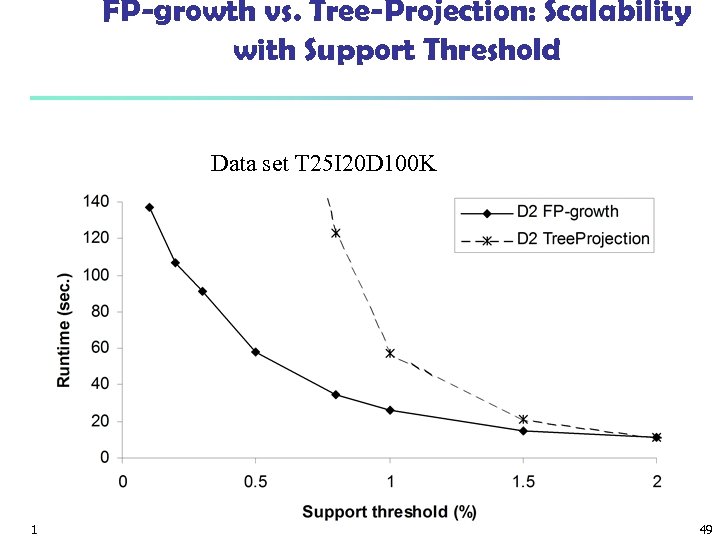FP-growth vs. Tree-Projection: Scalability with Support Threshold Data set T 25 I 20 D 100 K 17 March 2018 Data Mining: Concepts and Techniques 49

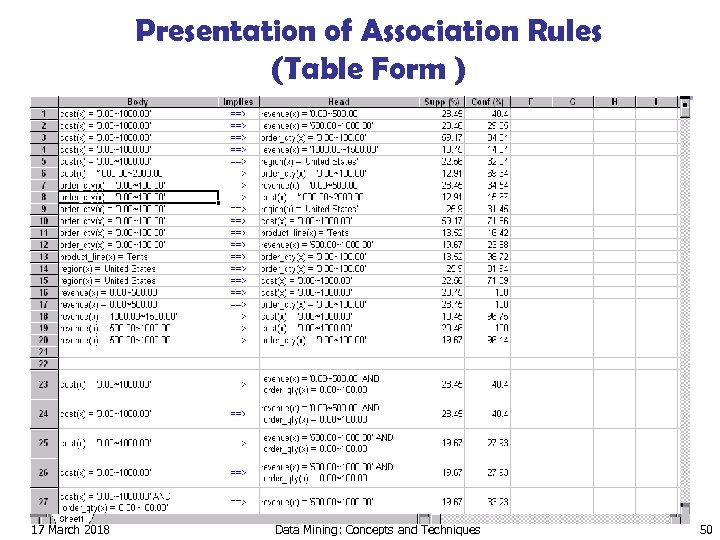Presentation of Association Rules (Table Form ) 17 March 2018 Data Mining: Concepts and Techniques 50

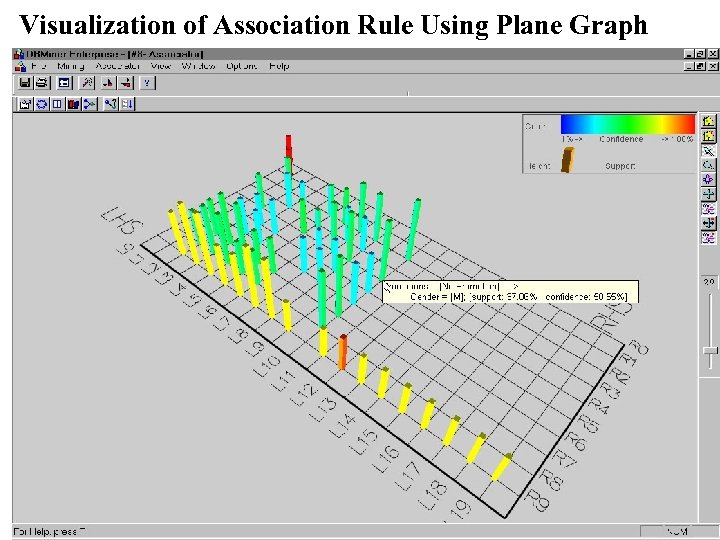Visualization of Association Rule Using Plane Graph 17 March 2018 Data Mining: Concepts and Techniques 51

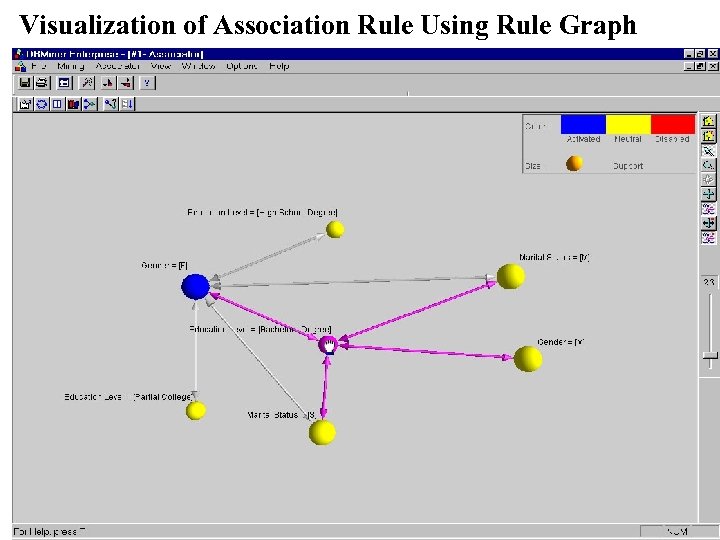Visualization of Association Rule Using Rule Graph 17 March 2018 Data Mining: Concepts and Techniques 52

Chapter 6: Mining Frequent Patterns, Association and Correlations: Basic Concepts and Methods n Basic Concepts n Frequent Itemset Mining Methods n Which Patterns Are Interesting? —Pattern Evaluation Methods n Summary 53

Interestingness Measure: Correlations (Lift) n play basketball eat cereal [40%, 66. 7%] is misleading n n The overall % of students eating cereal is 75% > 66. 7%. play basketball not eat cereal [20%, 33. 3%] is more accurate, although with lower support and confidence n Measure of dependent/correlated events: lift Basketball Not basketball Sum (row) Cereal 2000 1750 3750 Not cereal 1000 250 1250 Sum(col. ) 3000 2000 54

Are lift and 2 Good Measures of Correlation? n “Buy walnuts buy milk [1%, 80%]” is misleading if 85% of customers buy milk n Support and confidence are not good to indicate correlations n Over 20 interestingness measures have been proposed (see Tan, Kumar, Sritastava @KDD’ 02) n Which are good ones? 55

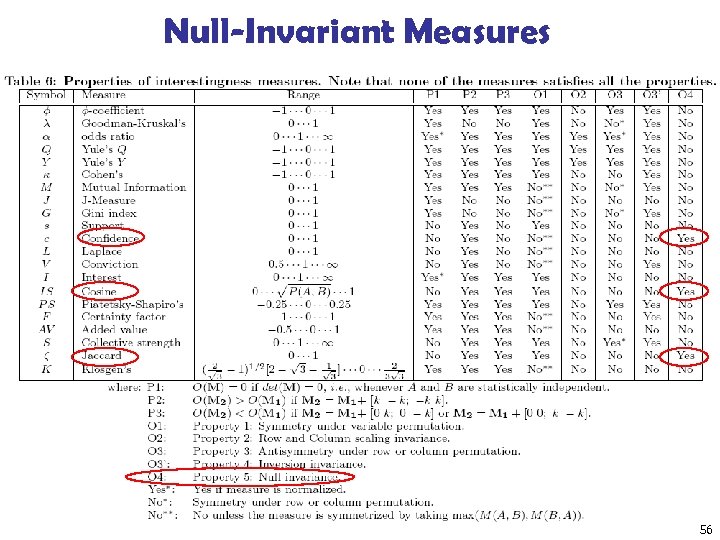Null-Invariant Measures 56

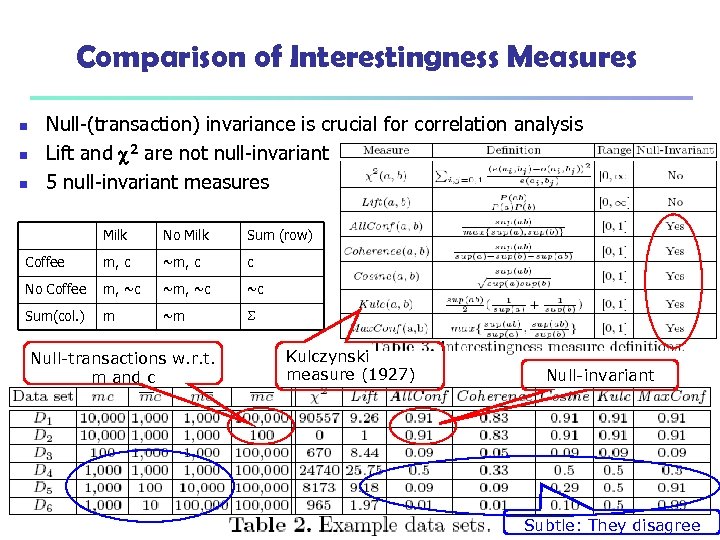Comparison of Interestingness Measures n n n Null-(transaction) invariance is crucial for correlation analysis Lift and 2 are not null-invariant 5 null-invariant measures Milk No Milk Sum (row) Coffee m, c ~m, c c No Coffee m, ~c ~c Sum(col. ) m ~m Null-transactions w. r. t. m and c 17 March 2018 Kulczynski measure (1927) Data Mining: Concepts and Techniques Null-invariant Subtle: They disagree 57

Analysis of DBLP Coauthor Relationships Recent DB conferences, removing balanced associations, low sup, etc. Advisor-advisee relation: Kulc: high, coherence: low, cosine: middle n Tianyi Wu, Yuguo Chen and Jiawei Han, “Association Mining in Large Databases: A Re-Examination of Its Measures”, Proc. 2007 Int. Conf. Principles and Practice of Knowledge Discovery in Databases (PKDD'07), Sept. 2007 58

Which Null-Invariant Measure Is Better? n n IR (Imbalance Ratio): measure the imbalance of two itemsets A and B in rule implications Kulczynski and Imbalance Ratio (IR) together present a clear picture for all the three datasets D 4 through D 6 n D 4 is balanced & neutral n D 5 is imbalanced & neutral n D 6 is very imbalanced & neutral

Summary n Association rule mining n n probably the most significant contribution from the database community in KDD A large number of papers have been published n Many interesting issues have been explored n An interesting research direction n 17 March 2018 Association analysis in other types of data: spatial data, multimedia data, time series data, etc. Data Mining: Concepts and Techniques 60

Summary n n Basic concepts: association rules, supportconfident framework, closed and max-patterns Scalable frequent pattern mining methods n n Projection-based (FPgrowth, CLOSET+, . . . ) n § Apriori (Candidate generation & test) Vertical format approach (ECLAT, CHARM, . . . ) Which patterns are interesting? § Pattern evaluation methods 61

References n n n n n R. Agarwal, C. Aggarwal, and V. V. V. Prasad. A tree projection algorithm for generation of frequent itemsets. In Journal of Parallel and Distributed Computing (Special Issue on High Performance Data Mining), 2000. R. Agrawal, T. Imielinski, and A. Swami. Mining association rules between sets of items in large databases. SIGMOD'93, 207 -216, Washington, D. C. R. Agrawal and R. Srikant. Fast algorithms for mining association rules. VLDB'94 487 -499, Santiago, Chile. R. Agrawal and R. Srikant. Mining sequential patterns. ICDE'95, 3 -14, Taipei, Taiwan. R. J. Bayardo. Efficiently mining long patterns from databases. SIGMOD'98, 85 -93, Seattle, Washington. S. Brin, R. Motwani, and C. Silverstein. Beyond market basket: Generalizing association rules to correlations. SIGMOD'97, 265 -276, Tucson, Arizona. S. Brin, R. Motwani, J. D. Ullman, and S. Tsur. Dynamic itemset counting and implication rules for market basket analysis. SIGMOD'97, 255 -264, Tucson, Arizona, May 1997. K. Beyer and R. Ramakrishnan. Bottom-up computation of sparse and iceberg cubes. SIGMOD'99, 359370, Philadelphia, PA, June 1999. D. W. Cheung, J. Han, V. Ng, and C. Y. Wong. Maintenance of discovered association rules in large databases: An incremental updating technique. ICDE'96, 106 -114, New Orleans, LA. M. Fang, N. Shivakumar, H. Garcia-Molina, R. Motwani, and J. D. Ullman. Computing iceberg queries efficiently. VLDB'98, 299 -310, New York, NY, Aug. 1998. 17 March 2018 Data Mining: Concepts and Techniques 62

References (2) n n n n n G. Grahne, L. Lakshmanan, and X. Wang. Efficient mining of constrained correlated sets. ICDE'00, 512521, San Diego, CA, Feb. 2000. Y. Fu and J. Han. Meta-rule-guided mining of association rules in relational databases. KDOOD'95, 3946, Singapore, Dec. 1995. T. Fukuda, Y. Morimoto, S. Morishita, and T. Tokuyama. Data mining using two-dimensional optimized association rules: Scheme, algorithms, and visualization. SIGMOD'96, 13 -23, Montreal, Canada. E. -H. Han, G. Karypis, and V. Kumar. Scalable parallel data mining for association rules. SIGMOD'97, 277 -288, Tucson, Arizona. J. Han, G. Dong, and Y. Yin. Efficient mining of partial periodic patterns in time series database. ICDE'99, Sydney, Australia. J. Han and Y. Fu. Discovery of multiple-level association rules from large databases. VLDB'95, 420 -431, Zurich, Switzerland. J. Han, J. Pei, and Y. Yin. Mining frequent patterns without candidate generation. SIGMOD'00, 1 -12, Dallas, TX, May 2000. T. Imielinski and H. Mannila. A database perspective on knowledge discovery. Communications of ACM, 39: 58 -64, 1996. M. Kamber, J. Han, and J. Y. Chiang. Metarule-guided mining of multi-dimensional association rules using data cubes. KDD'97, 207 -210, Newport Beach, California. M. Klemettinen, H. Mannila, P. Ronkainen, H. Toivonen, and A. I. Verkamo. Finding interesting rules from large sets of discovered association rules. CIKM'94, 401 -408, Gaithersburg, Maryland. 17 March 2018 Data Mining: Concepts and Techniques 63

References (3) n n n n n F. Korn, A. Labrinidis, Y. Kotidis, and C. Faloutsos. Ratio rules: A new paradigm for fast, quantifiable data mining. VLDB'98, 582 -593, New York, NY. B. Lent, A. Swami, and J. Widom. Clustering association rules. ICDE'97, 220 -231, Birmingham, England. H. Lu, J. Han, and L. Feng. Stock movement and n-dimensional inter-transaction association rules. SIGMOD Workshop on Research Issues on Data Mining and Knowledge Discovery (DMKD'98), 12: 112: 7, Seattle, Washington. H. Mannila, H. Toivonen, and A. I. Verkamo. Efficient algorithms for discovering association rules. KDD'94, 181 -192, Seattle, WA, July 1994. H. Mannila, H Toivonen, and A. I. Verkamo. Discovery of frequent episodes in event sequences. Data Mining and Knowledge Discovery, 1: 259 -289, 1997. R. Meo, G. Psaila, and S. Ceri. A new SQL-like operator for mining association rules. VLDB'96, 122133, Bombay, India. R. J. Miller and Y. Yang. Association rules over interval data. SIGMOD'97, 452 -461, Tucson, Arizona. R. Ng, L. V. S. Lakshmanan, J. Han, and A. Pang. Exploratory mining and pruning optimizations of constrained associations rules. SIGMOD'98, 13 -24, Seattle, Washington. N. Pasquier, Y. Bastide, R. Taouil, and L. Lakhal. Discovering frequent closed itemsets for association rules. ICDT'99, 398 -416, Jerusalem, Israel, Jan. 1999. 17 March 2018 Data Mining: Concepts and Techniques 64

References (4) n n n n n J. S. Park, M. S. Chen, and P. S. Yu. An effective hash-based algorithm for mining association rules. SIGMOD'95, 175 -186, San Jose, CA, May 1995. J. Pei, J. Han, and R. Mao. CLOSET: An Efficient Algorithm for Mining Frequent Closed Itemsets. DMKD'00, Dallas, TX, 11 -20, May 2000. J. Pei and J. Han. Can We Push More Constraints into Frequent Pattern Mining? KDD'00. Boston, MA. Aug. 2000. G. Piatetsky-Shapiro. Discovery, analysis, and presentation of strong rules. In G. Piatetsky-Shapiro and W. J. Frawley, editors, Knowledge Discovery in Databases, 229 -238. AAAI/MIT Press, 1991. B. Ozden, S. Ramaswamy, and A. Silberschatz. Cyclic association rules. ICDE'98, 412 -421, Orlando, FL. J. S. Park, M. S. Chen, and P. S. Yu. An effective hash-based algorithm for mining association rules. SIGMOD'95, 175 -186, San Jose, CA. S. Ramaswamy, S. Mahajan, and A. Silberschatz. On the discovery of interesting patterns in association rules. VLDB'98, 368 -379, New York, NY. . S. Sarawagi, S. Thomas, and R. Agrawal. Integrating association rule mining with relational database systems: Alternatives and implications. SIGMOD'98, 343 -354, Seattle, WA. A. Savasere, E. Omiecinski, and S. Navathe. An efficient algorithm for mining association rules in large databases. VLDB'95, 432 -443, Zurich, Switzerland. A. Savasere, E. Omiecinski, and S. Navathe. Mining for strong negative associations in a large database of customer transactions. ICDE'98, 494 -502, Orlando, FL, Feb. 1998. 17 March 2018 Data Mining: Concepts and Techniques 65

References (5) n n n n n C. Silverstein, S. Brin, R. Motwani, and J. Ullman. Scalable techniques for mining causal structures. VLDB'98, 594 -605, New York, NY. R. Srikant and R. Agrawal. Mining generalized association rules. VLDB'95, 407 -419, Zurich, Switzerland, Sept. 1995. R. Srikant and R. Agrawal. Mining quantitative association rules in large relational tables. SIGMOD'96, 1 -12, Montreal, Canada. R. Srikant, Q. Vu, and R. Agrawal. Mining association rules with item constraints. KDD'97, 67 -73, Newport Beach, California. H. Toivonen. Sampling large databases for association rules. VLDB'96, 134 -145, Bombay, India, Sept. 1996. D. Tsur, J. D. Ullman, S. Abitboul, C. Clifton, R. Motwani, and S. Nestorov. Query flocks: A generalization of association-rule mining. SIGMOD'98, 1 -12, Seattle, Washington. K. Yoda, T. Fukuda, Y. Morimoto, S. Morishita, and T. Tokuyama. Computing optimized rectilinear regions for association rules. KDD'97, 96 -103, Newport Beach, CA, Aug. 1997. M. J. Zaki, S. Parthasarathy, M. Ogihara, and W. Li. Parallel algorithm for discovery of association rules. Data Mining and Knowledge Discovery, 1: 343 -374, 1997. M. Zaki. Generating Non-Redundant Association Rules. KDD'00. Boston, MA. Aug. 2000. O. R. Zaiane, J. Han, and H. Zhu. Mining Recurrent Items in Multimedia with Progressive Resolution Refinement. ICDE'00, 461 -470, San Diego, CA, Feb. 2000. 17 March 2018 Data Mining: Concepts and Techniques 66

http: //www. cs. sfu. ca/~han/dmbook Thank you !!! 17 March 2018 Data Mining: Concepts and Techniques 67