Скачать презентацию Data Mining Association Rules Advanced Concepts and Algorithms Скачать презентацию Data Mining Association Rules Advanced Concepts and Algorithms

0b7a8ef844b3ef1e1937fa7864d93893.ppt

  • Количество слайдов: 67

Data Mining Association Rules: Advanced Concepts and Algorithms Lecture Notes for Chapter 7 Introduction Data Mining Association Rules: Advanced Concepts and Algorithms Lecture Notes for Chapter 7 Introduction to Data Mining by Tan, Steinbach, Kumar © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 1

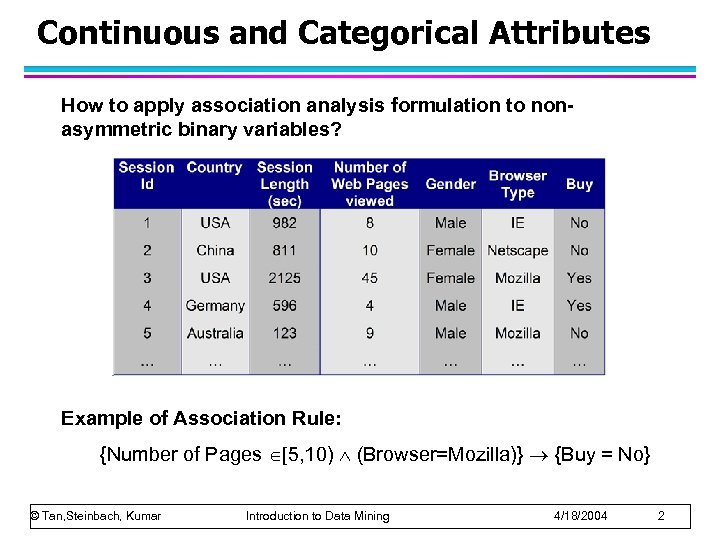Continuous and Categorical Attributes How to apply association analysis formulation to nonasymmetric binary variables? Continuous and Categorical Attributes How to apply association analysis formulation to nonasymmetric binary variables? Example of Association Rule: {Number of Pages [5, 10) (Browser=Mozilla)} {Buy = No} © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 2

Handling Categorical Attributes l Transform categorical attribute into asymmetric binary variables l Introduce a Handling Categorical Attributes l Transform categorical attribute into asymmetric binary variables l Introduce a new “item” for each distinct attributevalue pair – Example: replace Browser Type attribute with u Browser Type = Internet Explorer u Browser Type = Mozilla © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 3

Handling Categorical Attributes l Potential Issues – What if attribute has many possible values Handling Categorical Attributes l Potential Issues – What if attribute has many possible values Example: attribute country has more than 200 possible values u u Many of the attribute values may have very low support – Potential solution: Aggregate the low-support attribute values – What if distribution of attribute values is highly skewed u Example: 95% of the visitors have Buy = No u Most of the items will be associated with (Buy=No) item – Potential solution: drop the highly frequent items © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 4

Handling Continuous Attributes l Different kinds of rules: – Age [21, 35) Salary [70 Handling Continuous Attributes l Different kinds of rules: – Age [21, 35) Salary [70 k, 120 k) Buy – Salary [70 k, 120 k) Buy Age: =28, =4 l Different methods: – Discretization-based – Statistics-based – Non-discretization based u min. Apriori © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 5

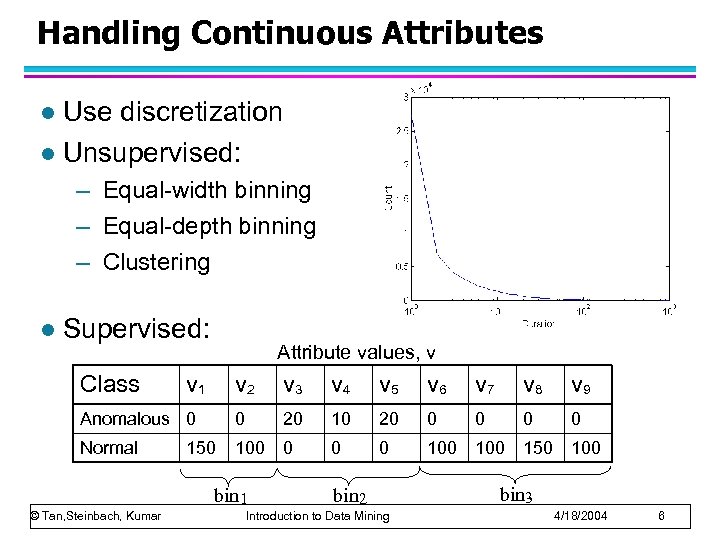Handling Continuous Attributes Use discretization l Unsupervised: l – Equal-width binning – Equal-depth binning Handling Continuous Attributes Use discretization l Unsupervised: l – Equal-width binning – Equal-depth binning – Clustering l Supervised: Class Attribute values, v v 1 v 2 v 3 v 4 v 5 v 6 v 7 v 8 v 9 Anomalous 0 0 20 10 20 0 0 Normal 100 0 100 150 bin 1 © Tan, Steinbach, Kumar bin 2 Introduction to Data Mining bin 3 4/18/2004 6

Discretization Issues l Size of the discretized intervals affect support & confidence {Refund = Discretization Issues l Size of the discretized intervals affect support & confidence {Refund = No, (Income = $51, 250)} {Cheat = No} {Refund = No, (60 K Income 80 K)} {Cheat = No} {Refund = No, (0 K Income 1 B)} {Cheat = No} – If intervals too small u may not have enough support – If intervals too large u l may not have enough confidence Potential solution: use all possible intervals © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 7

Discretization Issues l Execution time – If intervals contain n values, there are on Discretization Issues l Execution time – If intervals contain n values, there are on average O(n 2) possible ranges l Too many rules {Refund = No, (Income = $51, 250)} {Cheat = No} {Refund = No, (51 K Income 52 K)} {Cheat = No} {Refund = No, (50 K Income 60 K)} {Cheat = No} © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 8

Approach by Srikant & Agrawal l Preprocess the data – Discretize attribute using equi-depth Approach by Srikant & Agrawal l Preprocess the data – Discretize attribute using equi-depth partitioning Use partial completeness measure to determine number of partitions u Merge adjacent intervals as long as support is less than max-support u l Apply existing association rule mining algorithms l Determine © Tan, Steinbach, Kumar interesting rules in the output Introduction to Data Mining 4/18/2004 9

Approach by Srikant & Agrawal l Discretization will lose information Approximated X X – Approach by Srikant & Agrawal l Discretization will lose information Approximated X X – Use partial completeness measure to determine how much information is lost C: frequent itemsets obtained by considering all ranges of attribute values P: frequent itemsets obtained by considering all ranges over the partitions P is K-complete w. r. t C if P C, and X C, X’ P such that: 1. X’ is a generalization of X and support (X’) K support(X) 2. Y X, Y’ X’ such that support (Y’) K support(Y) (K 1) Given K (partial completeness level), can determine number of intervals (N) © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 10

Interestingness Measure {Refund = No, (Income = $51, 250)} {Cheat = No} {Refund = Interestingness Measure {Refund = No, (Income = $51, 250)} {Cheat = No} {Refund = No, (51 K Income 52 K)} {Cheat = No} {Refund = No, (50 K Income 60 K)} {Cheat = No} l Given an itemset: Z = {z 1, z 2, …, zk} and its generalization Z’ = {z 1’, z 2’, …, zk’} P(Z): support of Z EZ’(Z): expected support of Z based on Z’ – Z is R-interesting w. r. t. Z’ if P(Z) R EZ’(Z) © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 11

Interestingness Measure l For S: X Y, and its generalization S’: X’ Y’ P(Y|X): Interestingness Measure l For S: X Y, and its generalization S’: X’ Y’ P(Y|X): confidence of X Y P(Y’|X’): confidence of X’ Y’ ES’(Y|X): expected support of Z based on Z’ l Rule S is R-interesting w. r. t its ancestor rule S’ if – Support, P(S) R ES’(S) or – Confidence, P(Y|X) R ES’(Y|X) © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 12

Statistics-based Methods l Example: Browser=Mozilla Buy=Yes Age: =23 l Rule consequent consists of a Statistics-based Methods l Example: Browser=Mozilla Buy=Yes Age: =23 l Rule consequent consists of a continuous variable, characterized by their statistics – mean, median, standard deviation, etc. l Approach: – Withhold the target variable from the rest of the data – Apply existing frequent itemset generation on the rest of the data – For each frequent itemset, compute the descriptive statistics for the corresponding target variable Frequent itemset becomes a rule by introducing the target variable as rule consequent u – Apply statistical test to determine interestingness of the rule © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 13

Statistics-based Methods l How to determine whether an association rule interesting? – Compare the Statistics-based Methods l How to determine whether an association rule interesting? – Compare the statistics for segment of population covered by the rule vs segment of population not covered by the rule: A B: versus A B: ’ – Statistical hypothesis testing: u Null hypothesis: H 0: ’ = + u Alternative hypothesis: H 1: ’ > + u Z has zero mean and variance 1 under null hypothesis © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 14

Statistics-based Methods l Example: r: Browser=Mozilla Buy=Yes Age: =23 – Rule is interesting if Statistics-based Methods l Example: r: Browser=Mozilla Buy=Yes Age: =23 – Rule is interesting if difference between and ’ is greater than 5 years (i. e. , = 5) – For r, suppose n 1 = 50, s 1 = 3. 5 – For r’ (complement): n 2 = 250, s 2 = 6. 5 – For 1 -sided test at 95% confidence level, critical Z-value for rejecting null hypothesis is 1. 64. – Since Z is greater than 1. 64, r is an interesting rule © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 15

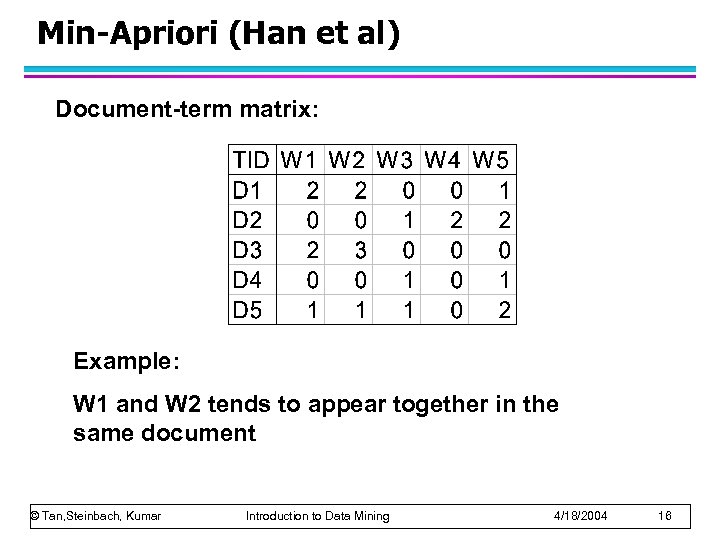Min-Apriori (Han et al) Document-term matrix: Example: W 1 and W 2 tends to Min-Apriori (Han et al) Document-term matrix: Example: W 1 and W 2 tends to appear together in the same document © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 16

Min-Apriori l Data contains only continuous attributes of the same “type” – e. g. Min-Apriori l Data contains only continuous attributes of the same “type” – e. g. , frequency of words in a document l Potential solution: – Convert into 0/1 matrix and then apply existing algorithms u lose word frequency information – Discretization does not apply as users want association among words not ranges of words © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 17

Min-Apriori l How to determine the support of a word? – If we simply Min-Apriori l How to determine the support of a word? – If we simply sum up its frequency, support count will be greater than total number of documents! u Normalize the word vectors – e. g. , using L 1 norm u Each word has a support equals to 1. 0 Normalize © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 18

Min-Apriori l New definition of support: Example: Sup(W 1, W 2, W 3) = Min-Apriori l New definition of support: Example: Sup(W 1, W 2, W 3) = 0 + 0 + 0. 17 = 0. 17 © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 19

Anti-monotone property of Support Example: Sup(W 1) = 0. 4 + 0 + 0. Anti-monotone property of Support Example: Sup(W 1) = 0. 4 + 0 + 0. 2 = 1 Sup(W 1, W 2) = 0. 33 + 0. 4 + 0. 17 = 0. 9 Sup(W 1, W 2, W 3) = 0 + 0 + 0. 17 = 0. 17 © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 20

Multi-level Association Rules © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 21 Multi-level Association Rules © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 21

Multi-level Association Rules l Why should we incorporate concept hierarchy? – Rules at lower Multi-level Association Rules l Why should we incorporate concept hierarchy? – Rules at lower levels may not have enough support to appear in any frequent itemsets – Rules at lower levels of the hierarchy are overly specific e. g. , skim milk white bread, 2% milk wheat bread, skim milk wheat bread, etc. are indicative of association between milk and bread u © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 22

Multi-level Association Rules l How do support and confidence vary as we traverse the Multi-level Association Rules l How do support and confidence vary as we traverse the concept hierarchy? – If X is the parent item for both X 1 and X 2, then (X) ≤ (X 1) + (X 2) – If and then (X 1 Y 1) ≥ minsup, X is parent of X 1, Y is parent of Y 1 (X Y 1) ≥ minsup, (X 1 Y) ≥ minsup (X Y) ≥ minsup – If then conf(X 1 Y 1) ≥ minconf, conf(X 1 Y) ≥ minconf © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 23

Multi-level Association Rules l Approach 1: – Extend current association rule formulation by augmenting Multi-level Association Rules l Approach 1: – Extend current association rule formulation by augmenting each transaction with higher level items Original Transaction: {skim milk, wheat bread} Augmented Transaction: {skim milk, wheat bread, milk, bread, food} l Issues: – Items that reside at higher levels have much higher support counts if support threshold is low, too many frequent patterns involving items from the higher levels u – Increased dimensionality of the data © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 24

Multi-level Association Rules l Approach 2: – Generate frequent patterns at highest level first Multi-level Association Rules l Approach 2: – Generate frequent patterns at highest level first – Then, generate frequent patterns at the next highest level, and so on l Issues: – I/O requirements will increase dramatically because we need to perform more passes over the data – May miss some potentially interesting cross-level association patterns © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 25

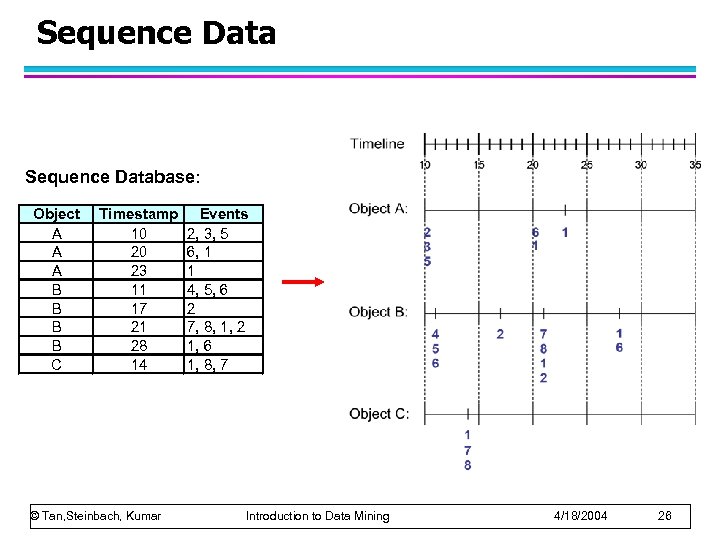Sequence Database: Object A A A B B C Timestamp 10 20 23 11 Sequence Database: Object A A A B B C Timestamp 10 20 23 11 17 21 28 14 © Tan, Steinbach, Kumar Events 2, 3, 5 6, 1 1 4, 5, 6 2 7, 8, 1, 2 1, 6 1, 8, 7 Introduction to Data Mining 4/18/2004 26

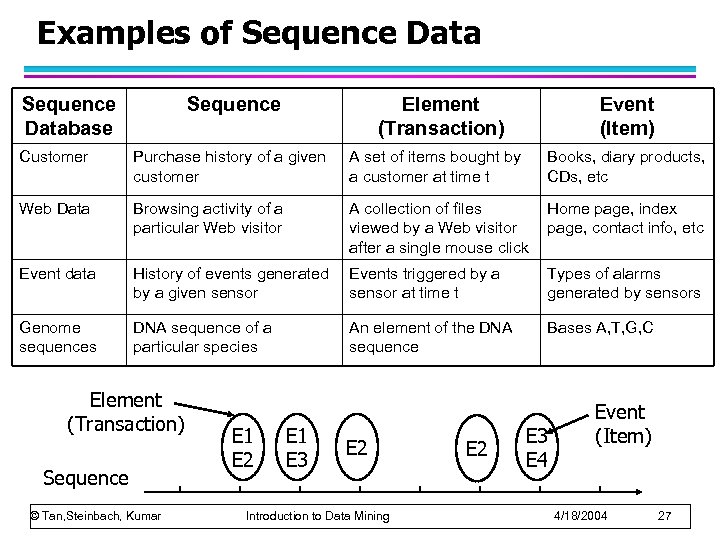Examples of Sequence Database Sequence Element (Transaction) Event (Item) Customer Purchase history of a Examples of Sequence Database Sequence Element (Transaction) Event (Item) Customer Purchase history of a given customer A set of items bought by a customer at time t Books, diary products, CDs, etc Web Data Browsing activity of a particular Web visitor A collection of files viewed by a Web visitor after a single mouse click Home page, index page, contact info, etc Event data History of events generated by a given sensor Events triggered by a sensor at time t Types of alarms generated by sensors Genome sequences DNA sequence of a particular species An element of the DNA sequence Bases A, T, G, C Element (Transaction) Sequence © Tan, Steinbach, Kumar E 1 E 2 E 1 E 3 E 2 Introduction to Data Mining E 2 E 3 E 4 Event (Item) 4/18/2004 27

Formal Definition of a Sequence l A sequence is an ordered list of elements Formal Definition of a Sequence l A sequence is an ordered list of elements (transactions) s = < e 1 e 2 e 3 … > – Each element contains a collection of events (items) ei = {i 1, i 2, …, ik} – Each element is attributed to a specific time or location l Length of a sequence, |s|, is given by the number of elements of the sequence l A k-sequence is a sequence that contains k events (items) © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 28

Examples of Sequence l Web sequence: < {Homepage} {Electronics} {Digital Cameras} {Canon Digital Camera} Examples of Sequence l Web sequence: < {Homepage} {Electronics} {Digital Cameras} {Canon Digital Camera} {Shopping Cart} {Order Confirmation} {Return to Shopping} > l Sequence of initiating events causing the nuclear accident at 3 -mile Island: (http: //stellar-one. com/nuclear/staff_reports/summary_SOE_the_initiating_event. htm) < {clogged resin} {outlet valve closure} {loss of feedwater} {condenser polisher outlet valve shut} {booster pumps trip} {main waterpump trips} {main turbine trips} {reactor pressure increases}> l Sequence of books checked out at a library: <{Fellowship of the Ring} {The Two Towers} {Return of the King}> © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 29

Formal Definition of a Subsequence l A sequence <a 1 a 2 … an> Formal Definition of a Subsequence l A sequence is contained in another sequence (m ≥ n) if there exist integers i 1 < i 2 < … < in such that a 1 bi 1 , a 2 bi 1, …, an bin Data sequence < {2} {3, 5} > Yes < {1, 2} {3, 4} > < {1} {2} > No < {2, 4} {2, 5} > l Contain? < {2, 4} {3, 5, 6} {8} > l Subsequence < {2} {4} > Yes The support of a subsequence w is defined as the fraction of data sequences that contain w A sequential pattern is a frequent subsequence (i. e. , a subsequence whose support is ≥ minsup) © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 30

Sequential Pattern Mining: Definition l Given: – a database of sequences – a user-specified Sequential Pattern Mining: Definition l Given: – a database of sequences – a user-specified minimum support threshold, minsup l Task: – Find all subsequences with support ≥ minsup © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 31

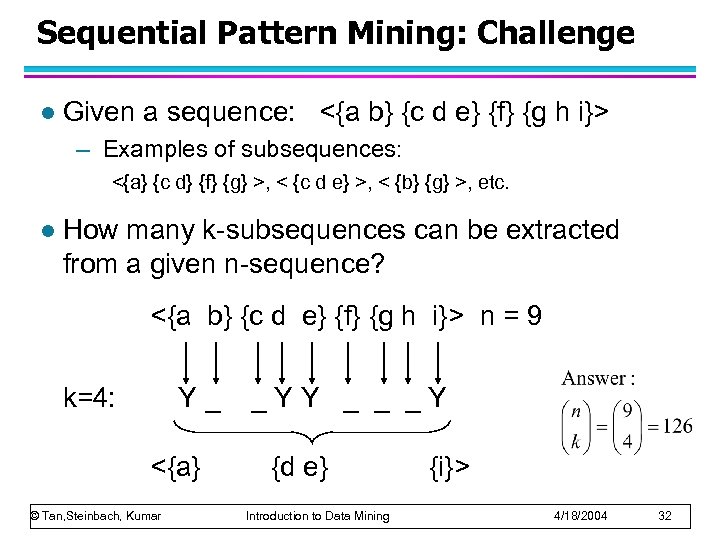Sequential Pattern Mining: Challenge l Given a sequence: <{a b} {c d e} {f} Sequential Pattern Mining: Challenge l Given a sequence: <{a b} {c d e} {f} {g h i}> – Examples of subsequences: <{a} {c d} {f} {g} >, < {c d e} >, < {b} {g} >, etc. l How many k-subsequences can be extracted from a given n-sequence? <{a b} {c d e} {f} {g h i}> n = 9 k=4: Y_ <{a} © Tan, Steinbach, Kumar _YY _ _ _Y {d e} Introduction to Data Mining {i}> 4/18/2004 32

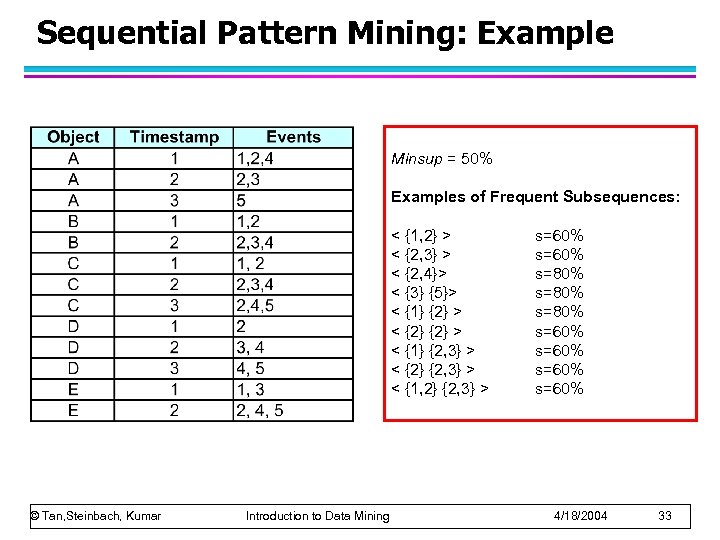Sequential Pattern Mining: Example Minsup = 50% Examples of Frequent Subsequences: < {1, 2} Sequential Pattern Mining: Example Minsup = 50% Examples of Frequent Subsequences: < {1, 2} > < {2, 3} > < {2, 4}> < {3} {5}> < {1} {2} > < {1} {2, 3} > < {2} {2, 3} > < {1, 2} {2, 3} > © Tan, Steinbach, Kumar Introduction to Data Mining s=60% s=80% s=60% 4/18/2004 33

Extracting Sequential Patterns l Given n events: i 1, i 2, i 3, …, Extracting Sequential Patterns l Given n events: i 1, i 2, i 3, …, in l Candidate 1 -subsequences: <{i 1}>, <{i 2}>, <{i 3}>, …, <{in}> l Candidate 2 -subsequences: <{i 1, i 2}>, <{i 1, i 3}>, …, <{i 1}>, <{i 1} {i 2}>, …, <{in-1} {in}> l Candidate 3 -subsequences: <{i 1, i 2 , i 3}>, <{i 1, i 2 , i 4}>, …, <{i 1, i 2} {i 1}>, <{i 1, i 2} {i 2}>, …, <{i 1} {i 1 , i 2}>, <{i 1} {i 1 , i 3}>, …, <{i 1}>, <{i 1} {i 2}>, … © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 34

Generalized Sequential Pattern (GSP) l Step 1: – Make the first pass over the Generalized Sequential Pattern (GSP) l Step 1: – Make the first pass over the sequence database D to yield all the 1 element frequent sequences l Step 2: Repeat until no new frequent sequences are found – Candidate Generation: u Merge pairs of frequent subsequences found in the (k-1)th pass to generate candidate sequences that contain k items – Candidate Pruning: u Prune candidate k-sequences that contain infrequent (k-1)-subsequences – Support Counting: u Make a new pass over the sequence database D to find the support for these candidate sequences – Candidate Elimination: u Eliminate candidate k-sequences whose actual support is less than minsup © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 35

Candidate Generation l Base case (k=2): – Merging two frequent 1 -sequences <{i 1}> Candidate Generation l Base case (k=2): – Merging two frequent 1 -sequences <{i 1}> and <{i 2}> will produce two candidate 2 -sequences: <{i 1} {i 2}> and <{i 1 i 2}> l General case (k>2): – A frequent (k-1)-sequence w 1 is merged with another frequent (k-1)-sequence w 2 to produce a candidate k-sequence if the subsequence obtained by removing the first event in w 1 is the same as the subsequence obtained by removing the last event in w 2 The resulting candidate after merging is given by the sequence w 1 extended with the last event of w 2. u – If the last two events in w 2 belong to the same element, then the last event in w 2 becomes part of the last element in w 1 – Otherwise, the last event in w 2 becomes a separate element appended to the end of w 1 © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 36

Candidate Generation Examples l Merging the sequences w 1=<{1} {2 3} {4}> and w Candidate Generation Examples l Merging the sequences w 1=<{1} {2 3} {4}> and w 2 =<{2 3} {4 5}> will produce the candidate sequence < {1} {2 3} {4 5}> because the last two events in w 2 (4 and 5) belong to the same element l Merging the sequences w 1=<{1} {2 3} {4}> and w 2 =<{2 3} {4} {5}> will produce the candidate sequence < {1} {2 3} {4} {5}> because the last two events in w 2 (4 and 5) do not belong to the same element l We do not have to merge the sequences w 1 =<{1} {2 6} {4}> and w 2 =<{1} {2} {4 5}> to produce the candidate < {1} {2 6} {4 5}> because if the latter is a viable candidate, then it can be obtained by merging w 1 with < {1} {2 6} {5}> © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 37

GSP Example © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 38 GSP Example © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 38

Timing Constraints (I) {A B} {C} <= xg {D E} xg: max-gap >ng ng: Timing Constraints (I) {A B} {C} <= xg {D E} xg: max-gap >ng ng: min-gap ms: maximum span <= ms xg = 2, ng = 0, ms= 4 Data sequence Subsequence Contain? < {2, 4} {3, 5, 6} {4, 7} {4, 5} {8} > < {6} {5} > Yes < {1} {2} {3} {4} {5}> < {1} {4} > No < {1} {2, 3} {3, 4} {4, 5}> < {2} {3} {5} > Yes < {1, 2} {3} {2, 3} {3, 4} {2, 4} {4, 5}> < {1, 2} {5} > No © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 39

Mining Sequential Patterns with Timing Constraints l Approach 1: – Mine sequential patterns without Mining Sequential Patterns with Timing Constraints l Approach 1: – Mine sequential patterns without timing constraints – Postprocess the discovered patterns l Approach 2: – Modify GSP to directly prune candidates that violate timing constraints – Question: u Does Apriori principle still hold? © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 40

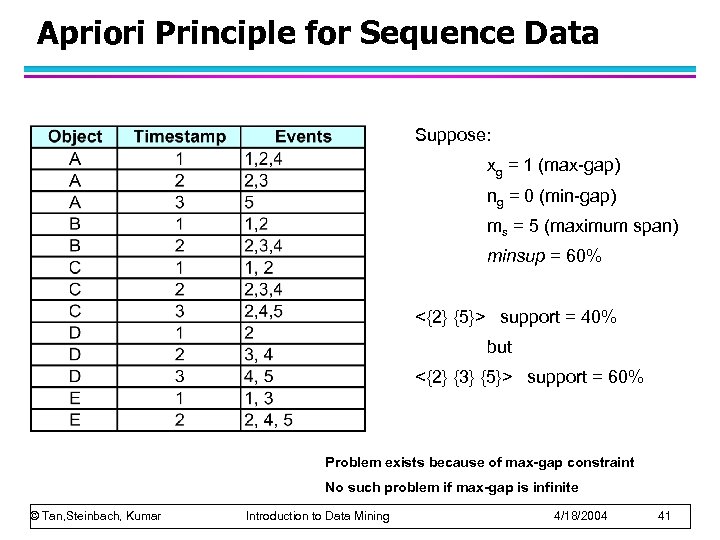Apriori Principle for Sequence Data Suppose: xg = 1 (max-gap) ng = 0 (min-gap) Apriori Principle for Sequence Data Suppose: xg = 1 (max-gap) ng = 0 (min-gap) ms = 5 (maximum span) minsup = 60% <{2} {5}> support = 40% but <{2} {3} {5}> support = 60% Problem exists because of max-gap constraint No such problem if max-gap is infinite © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 41

Contiguous Subsequences l s is a contiguous subsequence of w = <e 1>< e Contiguous Subsequences l s is a contiguous subsequence of w = < e 2>…< ek> if any of the following conditions hold: 1. s is obtained from w by deleting an item from either e 1 or ek 2. s is obtained from w by deleting an item from any element ei that contains more than 2 items 3. s is a contiguous subsequence of s’ and s’ is a contiguous subsequence of w (recursive definition) l Examples: s = < {1} {2} > – is a contiguous subsequence of < {1} {2 3}>, < {1 2} {3}>, and < {3 4} {1 2} {2 3} {4} > – is not a contiguous subsequence of < {1} {3} {2}> and < {2} {1} {3} {2}> © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 42

Modified Candidate Pruning Step l Without maxgap constraint: – A candidate k-sequence is pruned Modified Candidate Pruning Step l Without maxgap constraint: – A candidate k-sequence is pruned if at least one of its (k-1)-subsequences is infrequent l With maxgap constraint: – A candidate k-sequence is pruned if at least one of its contiguous (k-1)-subsequences is infrequent © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 43

Timing Constraints (II) {A B} {C} <= xg xg: max-gap {D E} >ng ng: Timing Constraints (II) {A B} {C} <= xg xg: max-gap {D E} >ng ng: min-gap <= ws ws: window size <= ms ms: maximum span xg = 2, ng = 0, ws = 1, ms= 5 Data sequence Subsequence Contain? < {2, 4} {3, 5, 6} {4, 7} {4, 6} {8} > < {3} {5} > No < {1} {2} {3} {4} {5}> < {1, 2} {3} > Yes < {1, 2} {2, 3} {3, 4} {4, 5}> < {1, 2} {3, 4} > Yes © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 44

Modified Support Counting Step l Given a candidate pattern: <{a, c}> – Any data Modified Support Counting Step l Given a candidate pattern: <{a, c}> – Any data sequences that contain <… {a c} … >, <… {a} … {c}…> ( where time({c}) – time({a}) ≤ ws) <…{c} … {a} …> (where time({a}) – time({c}) ≤ ws) will contribute to the support count of candidate pattern © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 45

Other Formulation l In some domains, we may have only one very long time Other Formulation l In some domains, we may have only one very long time series – Example: u u l monitoring network traffic events for attacks monitoring telecommunication alarm signals Goal is to find frequent sequences of events in the time series – This problem is also known as frequent episode mining E 1 E 3 E 1 E 2 E 4 E 2 E 3 E 5 E 1 E 2 E 3 E 1 Pattern: © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 46

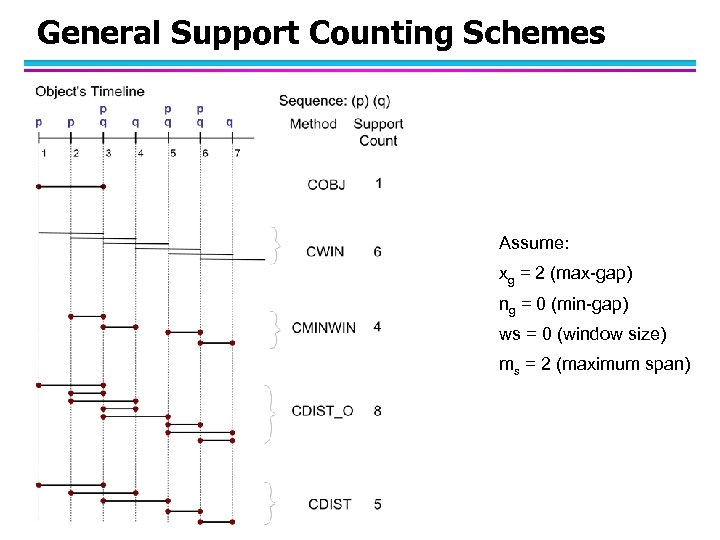General Support Counting Schemes Assume: xg = 2 (max-gap) ng = 0 (min-gap) ws General Support Counting Schemes Assume: xg = 2 (max-gap) ng = 0 (min-gap) ws = 0 (window size) ms = 2 (maximum span)

Frequent Subgraph Mining Extend association rule mining to finding frequent subgraphs l Useful for Frequent Subgraph Mining Extend association rule mining to finding frequent subgraphs l Useful for Web Mining, computational chemistry, bioinformatics, spatial data sets, etc l © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 48

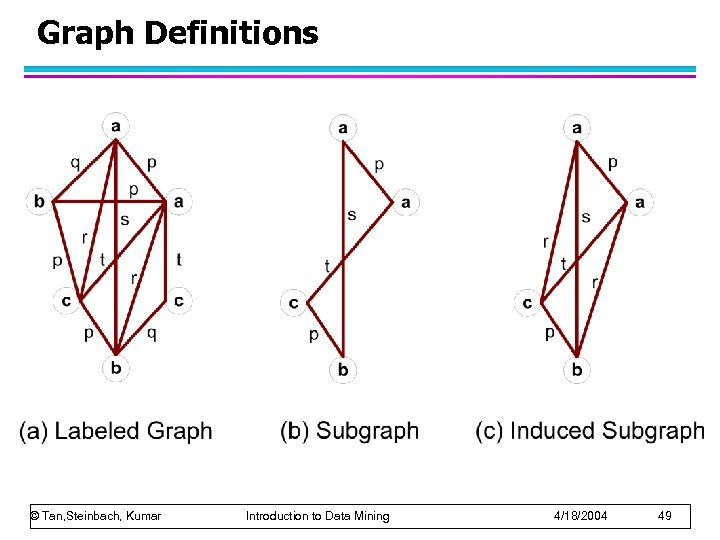Graph Definitions © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 49 Graph Definitions © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 49

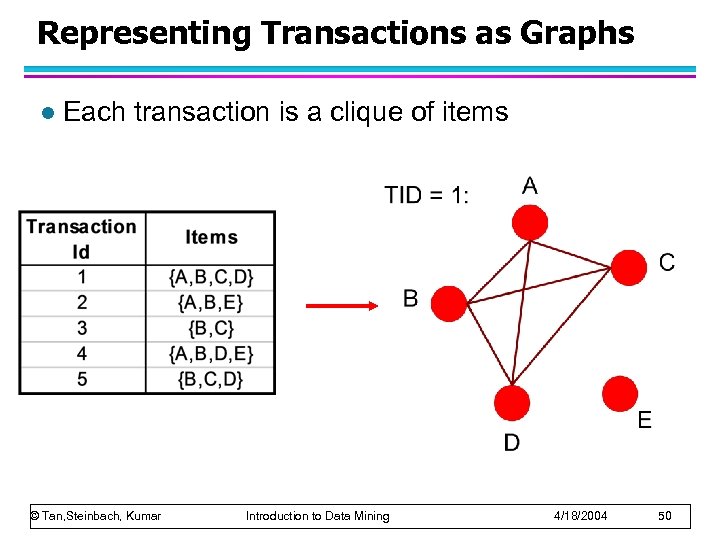Representing Transactions as Graphs l Each transaction is a clique of items © Tan, Representing Transactions as Graphs l Each transaction is a clique of items © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 50

Representing Graphs as Transactions © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 51 Representing Graphs as Transactions © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 51

Challenges Node may contain duplicate labels l Support and confidence l – How to Challenges Node may contain duplicate labels l Support and confidence l – How to define them? l Additional constraints imposed by pattern structure – Support and confidence are not the only constraints – Assumption: frequent subgraphs must be connected l Apriori-like approach: – Use frequent k-subgraphs to generate frequent (k+1) subgraphs u. What © Tan, Steinbach, Kumar is k? Introduction to Data Mining 4/18/2004 52

Challenges… l Support: – number of graphs that contain a particular subgraph l Apriori Challenges… l Support: – number of graphs that contain a particular subgraph l Apriori principle still holds l Level-wise (Apriori-like) approach: – Vertex growing: u k is the number of vertices – Edge growing: u k is the number of edges © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 53

Vertex Growing © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 54 Vertex Growing © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 54

Edge Growing © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 55 Edge Growing © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 55

Apriori-like Algorithm Find frequent 1 -subgraphs l Repeat l – Candidate generation u Use Apriori-like Algorithm Find frequent 1 -subgraphs l Repeat l – Candidate generation u Use frequent (k-1)-subgraphs to generate candidate k-subgraph – Candidate pruning Prune candidate subgraphs that contain infrequent (k-1)-subgraphs u – Support counting u Count the support of each remaining candidate – Eliminate candidate k-subgraphs that are infrequent In practice, it is not as easy. There are many other issues © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 56

Example: Dataset © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 57 Example: Dataset © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 57

Example © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 58 Example © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 58

Candidate Generation l In Apriori: – Merging two frequent k-itemsets will produce a candidate Candidate Generation l In Apriori: – Merging two frequent k-itemsets will produce a candidate (k+1)-itemset l In frequent subgraph mining (vertex/edge growing) – Merging two frequent k-subgraphs may produce more than one candidate (k+1)-subgraph © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 59

Multiplicity of Candidates (Vertex Growing) © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 Multiplicity of Candidates (Vertex Growing) © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 60

Multiplicity of Candidates (Edge growing) l Case 1: identical vertex labels © Tan, Steinbach, Multiplicity of Candidates (Edge growing) l Case 1: identical vertex labels © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 61

Multiplicity of Candidates (Edge growing) l Case 2: Core contains identical labels Core: The Multiplicity of Candidates (Edge growing) l Case 2: Core contains identical labels Core: The (k-1) subgraph that is common between the joint graphs © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 62

Multiplicity of Candidates (Edge growing) l Case 3: Core multiplicity © Tan, Steinbach, Kumar Multiplicity of Candidates (Edge growing) l Case 3: Core multiplicity © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 63

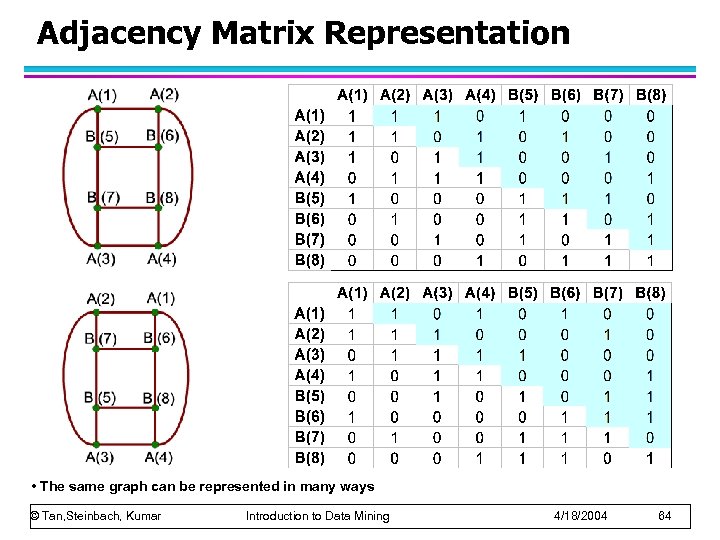Adjacency Matrix Representation • The same graph can be represented in many ways © Adjacency Matrix Representation • The same graph can be represented in many ways © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 64

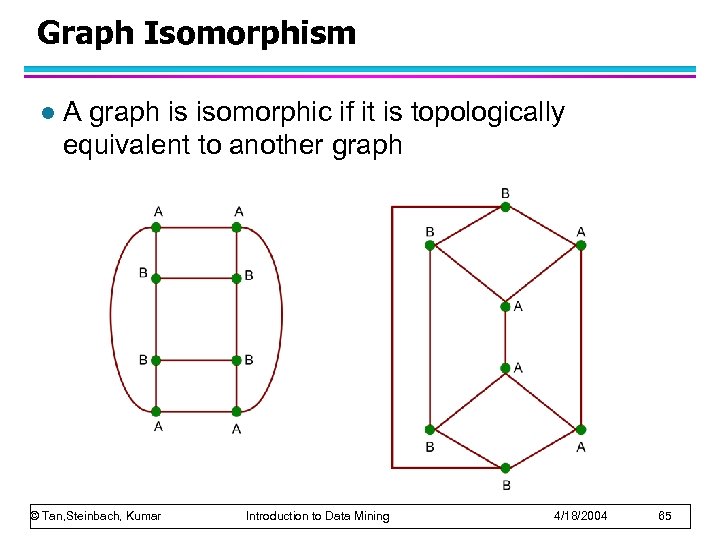Graph Isomorphism l A graph is isomorphic if it is topologically equivalent to another Graph Isomorphism l A graph is isomorphic if it is topologically equivalent to another graph © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 65

Graph Isomorphism l Test for graph isomorphism is needed: – During candidate generation step, Graph Isomorphism l Test for graph isomorphism is needed: – During candidate generation step, to determine whether a candidate has been generated – During candidate pruning step, to check whether its (k-1)-subgraphs are frequent – During candidate counting, to check whether a candidate is contained within another graph © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 66

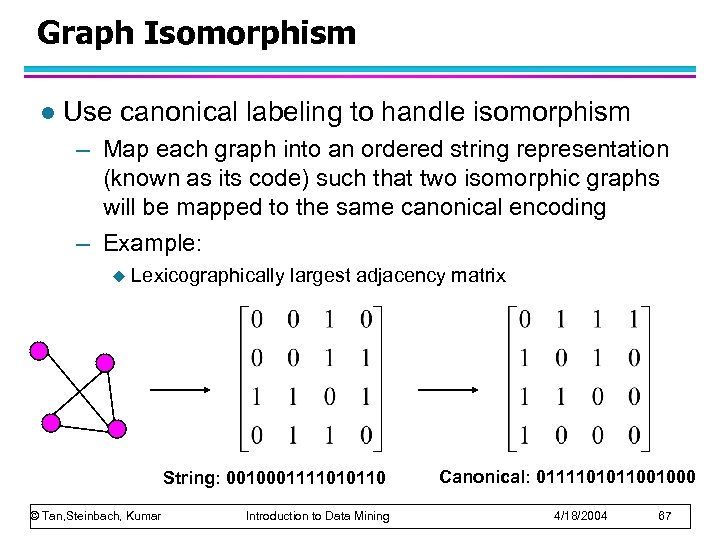Graph Isomorphism l Use canonical labeling to handle isomorphism – Map each graph into Graph Isomorphism l Use canonical labeling to handle isomorphism – Map each graph into an ordered string representation (known as its code) such that two isomorphic graphs will be mapped to the same canonical encoding – Example: u Lexicographically largest adjacency matrix String: 0010001111010110 © Tan, Steinbach, Kumar Introduction to Data Mining Canonical: 0111101011001000 4/18/2004 67