275000214218863110cda3dff070e454.ppt
- Количество слайдов: 84
 Data Mining and Knowledge Acquisition — Chapter 6 — BIS 541 2016/2017 Summer 1
Data Mining and Knowledge Acquisition — Chapter 6 — BIS 541 2016/2017 Summer 1
 Chapter 5: Mining Association Rules in Large Databases n n Association rule mining Mining single-dimensional Boolean association rules from transactional databases Mining multilevel association rules from transactional databases Mining multidimensional association rules from transactional databases and data warehouse n From association mining to correlation analysis n Constraint-based association mining n Summary 2
Chapter 5: Mining Association Rules in Large Databases n n Association rule mining Mining single-dimensional Boolean association rules from transactional databases Mining multilevel association rules from transactional databases Mining multidimensional association rules from transactional databases and data warehouse n From association mining to correlation analysis n Constraint-based association mining n Summary 2
 What Is Association Mining? Association rule mining: n Finding frequent patterns, associations, correlations, or causal structures among sets of items or objects in transaction databases, relational databases, and other information repositories. n Applications: n Market basket analysis, cross-marketing, catalog design, etc. n Examples. n Rule form: “Body Head [support, confidence]”. n buys(x, “diapers”) buys(x, “beers”) [0. 5%, 60%] n major(x, “MIS”) ^ takes(x, “DM”) grade(x, “AA”) [1%, 75%] n 3
What Is Association Mining? Association rule mining: n Finding frequent patterns, associations, correlations, or causal structures among sets of items or objects in transaction databases, relational databases, and other information repositories. n Applications: n Market basket analysis, cross-marketing, catalog design, etc. n Examples. n Rule form: “Body Head [support, confidence]”. n buys(x, “diapers”) buys(x, “beers”) [0. 5%, 60%] n major(x, “MIS”) ^ takes(x, “DM”) grade(x, “AA”) [1%, 75%] n 3
 Association Rule: Basic Concepts n n Given: n (1) database of transactions, n (2) each transaction is a list of items (purchased by a customer in a visit) Find: all rules that correlate the presence of one set of items with that of another set of items n E. g. , 98% of people who purchase tires and auto accessories also get automotive services done n The user specifies n Minimum support level n Minimum confidence level n Rules exceeding the two trasholds are listed as interesting 4
Association Rule: Basic Concepts n n Given: n (1) database of transactions, n (2) each transaction is a list of items (purchased by a customer in a visit) Find: all rules that correlate the presence of one set of items with that of another set of items n E. g. , 98% of people who purchase tires and auto accessories also get automotive services done n The user specifies n Minimum support level n Minimum confidence level n Rules exceeding the two trasholds are listed as interesting 4
 Basic Concepts cont. n n n I: {i 1, . . , im} set of all items, T any transaction A T: T contains the itemset A A T, B T A, B itemsets Examine rule like: A B where A B= , n support s: P(A B) n n frequency of transactions containing both A and B confidence c: P(B A) = P(A B)/P(A) n Conditional probability that a transaction containing A contains B 5
Basic Concepts cont. n n n I: {i 1, . . , im} set of all items, T any transaction A T: T contains the itemset A A T, B T A, B itemsets Examine rule like: A B where A B= , n support s: P(A B) n n frequency of transactions containing both A and B confidence c: P(B A) = P(A B)/P(A) n Conditional probability that a transaction containing A contains B 5
 Rule Measures: Support and Confidence Customer buys both Customer buys beer Customer n buys diaper Find all the rules X & Y Z with minimum confidence and support n support, s, probability that a transaction contains {X Y Z} n confidence, c, conditional probability that a transaction having {X Y} also contains Z Let minimum support 50%, and minimum confidence 50%, we have n A C (50%, 66. 6%) n C A (50%, 100%) 6
Rule Measures: Support and Confidence Customer buys both Customer buys beer Customer n buys diaper Find all the rules X & Y Z with minimum confidence and support n support, s, probability that a transaction contains {X Y Z} n confidence, c, conditional probability that a transaction having {X Y} also contains Z Let minimum support 50%, and minimum confidence 50%, we have n A C (50%, 66. 6%) n C A (50%, 100%) 6
 Frequent itemsets n n n n Strong association rules: n Support rule > min_support n Confidence rule > min_confidence k-item set: itemsets containing k items occurrence frequency=count=support count: Minimum support count = min_sup*#transactions in database frequent item sets: n İtemsets satisfying minimum support count The Apriori Algorithm has two steps: n (1) - Find all frequent itemsets n (2) - Genertate strong association rules from frequent itemsets 7
Frequent itemsets n n n n Strong association rules: n Support rule > min_support n Confidence rule > min_confidence k-item set: itemsets containing k items occurrence frequency=count=support count: Minimum support count = min_sup*#transactions in database frequent item sets: n İtemsets satisfying minimum support count The Apriori Algorithm has two steps: n (1) - Find all frequent itemsets n (2) - Genertate strong association rules from frequent itemsets 7
 Mining Association Rules—An Example(1) Min_support 50% Min. _confidence 50% Min_count: 0. 5*4=2 {A}. {B}. {C}. {D} are 1 -itemsets {A}. {B}. {C} are frequent 1 -itemsets as Count[{A}] = 3 >= 2 (minimum_count) or Support[{A}] = 75% >= 50% (minimum_support) {D} is not a frequent 1 -itemsets as Count[{D}] = 1 < 2 (minimum_count) or Support[{D}] = 25% < 50% (minimum_support) 8
Mining Association Rules—An Example(1) Min_support 50% Min. _confidence 50% Min_count: 0. 5*4=2 {A}. {B}. {C}. {D} are 1 -itemsets {A}. {B}. {C} are frequent 1 -itemsets as Count[{A}] = 3 >= 2 (minimum_count) or Support[{A}] = 75% >= 50% (minimum_support) {D} is not a frequent 1 -itemsets as Count[{D}] = 1 < 2 (minimum_count) or Support[{D}] = 25% < 50% (minimum_support) 8
 Mining Association Rules—An Example(2) Min_support 50% Min. _confidence 50% Min_count: 0. 5*4=2 {A. B}. {A. C}. {A. D}. {B. C} are 2 -itemsets {A. C}is frequent 2 -itemsets as Count[{A. C}] = 2 >= 2 (minimum_count) or Support[{A. C}] = 50% >= 50% (minimum_support) {A. B}. {A. D} are not frequent 2 -itemsets as Count[{A. D}] = 1 < 2 (minimum_count) or Support[{A. D}] = 25% < 50% (minimum_support) 9
Mining Association Rules—An Example(2) Min_support 50% Min. _confidence 50% Min_count: 0. 5*4=2 {A. B}. {A. C}. {A. D}. {B. C} are 2 -itemsets {A. C}is frequent 2 -itemsets as Count[{A. C}] = 2 >= 2 (minimum_count) or Support[{A. C}] = 50% >= 50% (minimum_support) {A. B}. {A. D} are not frequent 2 -itemsets as Count[{A. D}] = 1 < 2 (minimum_count) or Support[{A. D}] = 25% < 50% (minimum_support) 9
 Mining Association Rules—An Example(3) Min. support 50% Min. confidence 50% For rule A C: support = support({A C}) = 50% confidence = support({A C})/support({A}) = 66. 6% Strong rule as support >=min_support confidence >= min_confidence 10
Mining Association Rules—An Example(3) Min. support 50% Min. confidence 50% For rule A C: support = support({A C}) = 50% confidence = support({A C})/support({A}) = 66. 6% Strong rule as support >=min_support confidence >= min_confidence 10
 The Apriori Principle Min. support 50% Min. confidence 50% The Apriori principle: Any subset of a frequent itemset must be frequent {A. C} is a frequent 2 -itemset {A} and {C}: subsets of {A, C} must be frequent itemsets 1 - 11
The Apriori Principle Min. support 50% Min. confidence 50% The Apriori principle: Any subset of a frequent itemset must be frequent {A. C} is a frequent 2 -itemset {A} and {C}: subsets of {A, C} must be frequent itemsets 1 - 11
 Apriori Algorithme has two steps n (1)-Find the frequent itemsets: the sets of items that have minimum support (the key step) n A subset of a frequent itemset must also be a frequent itemset n n Iteratively find frequent itemsets with cardinality from 1 to k (kitemset) n n i. e. , if {AB} is a frequent itemset, both {A} and {B} should be a frequent itemsets Until k is an empty set (2)-Use the frequent itemsets to generate association rules. 12
Apriori Algorithme has two steps n (1)-Find the frequent itemsets: the sets of items that have minimum support (the key step) n A subset of a frequent itemset must also be a frequent itemset n n Iteratively find frequent itemsets with cardinality from 1 to k (kitemset) n n i. e. , if {AB} is a frequent itemset, both {A} and {B} should be a frequent itemsets Until k is an empty set (2)-Use the frequent itemsets to generate association rules. 12
 Generation of frequent itemsets from candidate itemsets (Step 1) n C 1 L 1 C 2 L 2 C 3 L 3 C 4 L 4… n From Ck (candidate k-itemsets) generate Lk : Ck Lk n n From candidate k itemsets generate frequent k itemsets (a)-Using the Apriori principle that: n Eliminate itemset sk in Ck if n n (b)-For candidate k itemsets in Ck n n At least one k-1 subset of sk is not in Lk-1 Make a database scan to eliminate those itemsets whose support counts are below the critical min support cout From frequent k itemsets Lk generate candidate k+1 itemsets Ck+1 : Lk Ck+1 n Self joining any Lk with Lk 13
Generation of frequent itemsets from candidate itemsets (Step 1) n C 1 L 1 C 2 L 2 C 3 L 3 C 4 L 4… n From Ck (candidate k-itemsets) generate Lk : Ck Lk n n From candidate k itemsets generate frequent k itemsets (a)-Using the Apriori principle that: n Eliminate itemset sk in Ck if n n (b)-For candidate k itemsets in Ck n n At least one k-1 subset of sk is not in Lk-1 Make a database scan to eliminate those itemsets whose support counts are below the critical min support cout From frequent k itemsets Lk generate candidate k+1 itemsets Ck+1 : Lk Ck+1 n Self joining any Lk with Lk 13
 Self Join operation n n n Sort the items in any li Lk in some lexicographic order n li[1]
Self Join operation n n n Sort the items in any li Lk in some lexicographic order n li[1]
 Example of Self Join operation n Lexigographic order: alphabetic a
Example of Self Join operation n Lexigographic order: alphabetic a
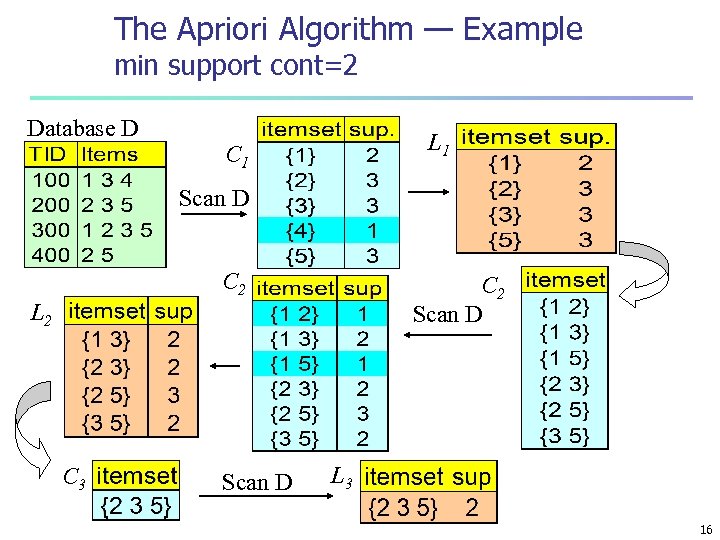 The Apriori Algorithm — Example min support cont=2 Database D L 1 C 1 Scan D C 2 Scan D L 2 C 3 Scan D L 3 16
The Apriori Algorithm — Example min support cont=2 Database D L 1 C 1 Scan D C 2 Scan D L 2 C 3 Scan D L 3 16
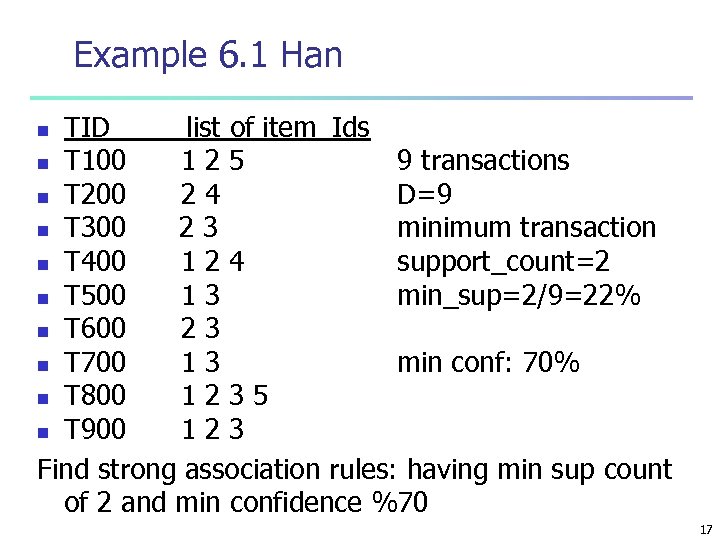 Example 6. 1 Han TID_____list of item_Ids n T 100 125 9 transactions n T 200 24 D=9 n T 300 23 minimum transaction n T 400 124 support_count=2 n T 500 13 min_sup=2/9=22% n T 600 23 n T 700 13 min conf: 70% n T 800 1235 n T 900 123 Find strong association rules: having min sup count of 2 and min confidence %70 n 17
Example 6. 1 Han TID_____list of item_Ids n T 100 125 9 transactions n T 200 24 D=9 n T 300 23 minimum transaction n T 400 124 support_count=2 n T 500 13 min_sup=2/9=22% n T 600 23 n T 700 13 min conf: 70% n T 800 1235 n T 900 123 Find strong association rules: having min sup count of 2 and min confidence %70 n 17
 Data Dictionary n n n 1: 2: 3: 4: 5: milk apple butter bread orange 18
Data Dictionary n n n 1: 2: 3: 4: 5: milk apple butter bread orange 18
 1 th iteration of algorithm n n n C 1: itemset sup_count L 1: itemset n 1 6 1 n 2 7 2 n 3 6 3 n 4 2 4 n 5 2 5 sup_count 6 7 6 2 2 C 2: L 1 join L 1, itemset sup_count 1 1 2 2 2 3 3 4 2 3 4 5 4 5 5 4 4 1 x 2 4 2 2 0 x 1 x 0 x L 2 itset supcount 12 4 13 4 15 2 23 4 24 2 25 2 frequent 2 item sets L 2 those itemsets in C 2 having minimum support Step (1 b) 19
1 th iteration of algorithm n n n C 1: itemset sup_count L 1: itemset n 1 6 1 n 2 7 2 n 3 6 3 n 4 2 4 n 5 2 5 sup_count 6 7 6 2 2 C 2: L 1 join L 1, itemset sup_count 1 1 2 2 2 3 3 4 2 3 4 5 4 5 5 4 4 1 x 2 4 2 2 0 x 1 x 0 x L 2 itset supcount 12 4 13 4 15 2 23 4 24 2 25 2 frequent 2 item sets L 2 those itemsets in C 2 having minimum support Step (1 b) 19
 3 th iteration n n n Self join to get C 3 Step (2) C 3: L 2 join L 2: [1 2 3], [1 2 5], [1 3 5], [2 3 4], [2 3 5], [2 4 5] Now Step (1 a) Apply Apriori to every itemset in C 3 2 item subsets of [1 2 3]: [1 2], [1 3], [2 3] n all 2 items sets are members of L 2 n keep [1 2 3] in C 3 2 item subsets of [1 2 5]: [1 2], [1 5], [2 5] n all 2 items sets are members of L 2 n keep [1 2 5] in C 3 2 item subsets of [1 3 5]: [1 3], [1 5], [3 5] n [3 5] is not a members of L 2 so it si not frequent n remove [1 2 5] from C 3 20
3 th iteration n n n Self join to get C 3 Step (2) C 3: L 2 join L 2: [1 2 3], [1 2 5], [1 3 5], [2 3 4], [2 3 5], [2 4 5] Now Step (1 a) Apply Apriori to every itemset in C 3 2 item subsets of [1 2 3]: [1 2], [1 3], [2 3] n all 2 items sets are members of L 2 n keep [1 2 3] in C 3 2 item subsets of [1 2 5]: [1 2], [1 5], [2 5] n all 2 items sets are members of L 2 n keep [1 2 5] in C 3 2 item subsets of [1 3 5]: [1 3], [1 5], [3 5] n [3 5] is not a members of L 2 so it si not frequent n remove [1 2 5] from C 3 20
![3 iteration cont. n n 2 item subsets of [2 3 4]: [2 3], 3 iteration cont. n n 2 item subsets of [2 3 4]: [2 3],](https://present5.com/presentation/275000214218863110cda3dff070e454/image-21.jpg) 3 iteration cont. n n 2 item subsets of [2 3 4]: [2 3], [2 4], [3 4] n [3 4] is not a members of L 2 so it si not frequent n remove [2 3 4] from C 3 2 item subsets of [2 3 5]: [2 3], [2 5], [3 5] n [3 5] is not a members of L 2 so it si not frequent n remove [2 3 5] from C 3 2 item subsets of [2 4 5]: [2 4], [2 5], [4 5] n [4 5] is not a members of L 2 so it si not frequent n remove [2 4 5] from C 3: [1 2 3], [1 2 5] after pruning 21
3 iteration cont. n n 2 item subsets of [2 3 4]: [2 3], [2 4], [3 4] n [3 4] is not a members of L 2 so it si not frequent n remove [2 3 4] from C 3 2 item subsets of [2 3 5]: [2 3], [2 5], [3 5] n [3 5] is not a members of L 2 so it si not frequent n remove [2 3 5] from C 3 2 item subsets of [2 4 5]: [2 4], [2 5], [4 5] n [4 5] is not a members of L 2 so it si not frequent n remove [2 4 5] from C 3: [1 2 3], [1 2 5] after pruning 21
 4 th iteration n n n n C 3 L 3 check min support Step (1 b) L 3: those item sets having minimum support L 3: item sets minsupcount n 1 2 3 2 n 1 2 5 2 L 3 join L 3 to generate C 4 Step (2) L 3 join L 3: 1 2 3 5 pruned since its subset [2 3 5] is not frequent C 4= the algorithm terminates 22
4 th iteration n n n n C 3 L 3 check min support Step (1 b) L 3: those item sets having minimum support L 3: item sets minsupcount n 1 2 3 2 n 1 2 5 2 L 3 join L 3 to generate C 4 Step (2) L 3 join L 3: 1 2 3 5 pruned since its subset [2 3 5] is not frequent C 4= the algorithm terminates 22
 Generating Association Rules from frequent itemsets n n Strong rules n min support and min confidence(A B)= P(B A): sup_count(A B) sup_count(A) for each frequent itemset l n generate non empty subsets of l: denoted by s n For each s l n n construct rules: s (l-s) Satısfying the condition: n n sup_count(l)/sup_count(s)>=min_conf are listed as interestıng 23
Generating Association Rules from frequent itemsets n n Strong rules n min support and min confidence(A B)= P(B A): sup_count(A B) sup_count(A) for each frequent itemset l n generate non empty subsets of l: denoted by s n For each s l n n construct rules: s (l-s) Satısfying the condition: n n sup_count(l)/sup_count(s)>=min_conf are listed as interestıng 23
 Example 6. 2 Han cont. n n the 3 -frequent item set l: [1 2 5]: transaction containing milk, apple and orange is frequent non empty subsets of l are n [1 2], [1 5], [2 5], [1], [2], [5] the resulting association rules are: n 1 2 5 conf: 2/4=50% n 1 5 2 conf: 2/2=100% n 2 5 1 conf: 2/2=100% n 1 2 5 conf: 2/6=33% n 2 1 5 conf: 2/7=29% n 5 1 2 conf: 2/2=100% if min conf: 70% 2 th 3 th and last rules are strong 24
Example 6. 2 Han cont. n n the 3 -frequent item set l: [1 2 5]: transaction containing milk, apple and orange is frequent non empty subsets of l are n [1 2], [1 5], [2 5], [1], [2], [5] the resulting association rules are: n 1 2 5 conf: 2/4=50% n 1 5 2 conf: 2/2=100% n 2 5 1 conf: 2/2=100% n 1 2 5 conf: 2/6=33% n 2 1 5 conf: 2/7=29% n 5 1 2 conf: 2/2=100% if min conf: 70% 2 th 3 th and last rules are strong 24
 Example 6. 2 cont. Detail on confidence for two rules n n n n For the rule 1 5 2 conf: s(1, 2, 5)/s(1, 5) conf: 2/2=100% >= 70% A strong rule For the rule 2 1 5 conf: s(1, 2, 5)/s(2) conf: 2/7=29% < 70% Not a strong rule 25
Example 6. 2 cont. Detail on confidence for two rules n n n n For the rule 1 5 2 conf: s(1, 2, 5)/s(1, 5) conf: 2/2=100% >= 70% A strong rule For the rule 2 1 5 conf: s(1, 2, 5)/s(2) conf: 2/7=29% < 70% Not a strong rule 25
 Exercise n Find all strong association rules in Example 6. 2 n Check minimum confindence n for 2 -frequent intemsets n n [1, 2], [1, 3], [1, 5], [2, 3], [2, 4], [2, 5] 1 2, 2 1 2 5, 5 2 exetra for 3 -frequent intemset n n n [1, 2, 5] 1 2 3 3 1 2 exetra 26
Exercise n Find all strong association rules in Example 6. 2 n Check minimum confindence n for 2 -frequent intemsets n n [1, 2], [1, 3], [1, 5], [2, 3], [2, 4], [2, 5] 1 2, 2 1 2 5, 5 2 exetra for 3 -frequent intemset n n n [1, 2, 5] 1 2 3 3 1 2 exetra 26
 Exercise n n n a) Suppose A B and B C are strong rules Dose this imply that A C is also a strong rule? b) Suppose A B and A C are strong rules Dose this imply that B C is also a strong rule? c) Suppose A C and B C are strong rules Dose this imply that A and B C is also a strong rule? 27
Exercise n n n a) Suppose A B and B C are strong rules Dose this imply that A C is also a strong rule? b) Suppose A B and A C are strong rules Dose this imply that B C is also a strong rule? c) Suppose A C and B C are strong rules Dose this imply that A and B C is also a strong rule? 27
 Bottleneck of Frequent-pattern Mining n n Multiple database scans are costly Mining long patterns needs many passes of scanning and generates lots of candidates n To find frequent itemset i 1 i 2…i 100 n n # of scans: 100 # of Candidates: (1001) + (1002) + … + (110000) = 21001 = 1. 27*1030 ! n Bottleneck: candidate-generation-and-test n Can we avoid candidate generation? 28
Bottleneck of Frequent-pattern Mining n n Multiple database scans are costly Mining long patterns needs many passes of scanning and generates lots of candidates n To find frequent itemset i 1 i 2…i 100 n n # of scans: 100 # of Candidates: (1001) + (1002) + … + (110000) = 21001 = 1. 27*1030 ! n Bottleneck: candidate-generation-and-test n Can we avoid candidate generation? 28
 Is Apriori Fast Enough? — Performance Bottlenecks n The core of the Apriori algorithm: n n n Use frequent (k – 1)-itemsets to generate candidate frequent kitemsets Use database scan and pattern matching to collect counts for the candidate itemsets The bottleneck of Apriori: candidate generation n Huge candidate sets: n n n 104 frequent 1 -itemset will generate 107 candidate 2 -itemsets To discover a frequent pattern of size 100, e. g. , {a 1, a 2, …, a 100}, one needs to generate 2100 1030 candidates. Multiple scans of database: n Needs (n +1 ) scans, n is the length of the longest pattern 29
Is Apriori Fast Enough? — Performance Bottlenecks n The core of the Apriori algorithm: n n n Use frequent (k – 1)-itemsets to generate candidate frequent kitemsets Use database scan and pattern matching to collect counts for the candidate itemsets The bottleneck of Apriori: candidate generation n Huge candidate sets: n n n 104 frequent 1 -itemset will generate 107 candidate 2 -itemsets To discover a frequent pattern of size 100, e. g. , {a 1, a 2, …, a 100}, one needs to generate 2100 1030 candidates. Multiple scans of database: n Needs (n +1 ) scans, n is the length of the longest pattern 29
 Mining Frequent Patterns Without Candidate Generation n Compress a large database into a compact, Frequent. Pattern tree (FP-tree) structure n n n highly condensed, but complete for frequent pattern mining avoid costly database scans Develop an efficient, FP-tree-based frequent pattern mining method n n A divide-and-conquer methodology: decompose mining tasks into smaller ones Avoid candidate generation: sub-database test only! 30
Mining Frequent Patterns Without Candidate Generation n Compress a large database into a compact, Frequent. Pattern tree (FP-tree) structure n n n highly condensed, but complete for frequent pattern mining avoid costly database scans Develop an efficient, FP-tree-based frequent pattern mining method n n A divide-and-conquer methodology: decompose mining tasks into smaller ones Avoid candidate generation: sub-database test only! 30
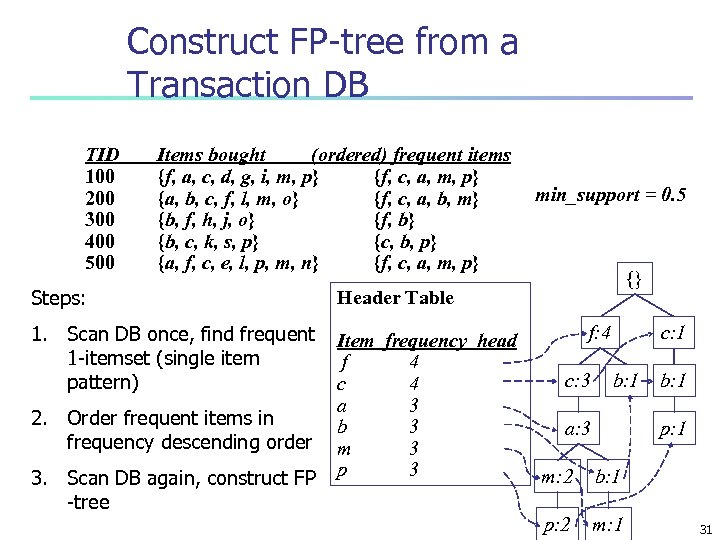 Construct FP-tree from a Transaction DB TID 100 200 300 400 500 Items bought (ordered) frequent items {f, a, c, d, g, i, m, p} {f, c, a, m, p} {a, b, c, f, l, m, o} {f, c, a, b, m} {b, f, h, j, o} {f, b} {b, c, k, s, p} {c, b, p} {a, f, c, e, l, p, m, n} {f, c, a, m, p} Steps: Item frequency head f 4 c 4 a 3 b 3 m 3 p 3 {} Header Table 1. Scan DB once, find frequent 1 -itemset (single item pattern) min_support = 0. 5 2. Order frequent items in frequency descending order 3. Scan DB again, construct FP -tree f: 4 c: 3 c: 1 b: 1 a: 3 b: 1 p: 1 m: 2 b: 1 p: 2 m: 1 31
Construct FP-tree from a Transaction DB TID 100 200 300 400 500 Items bought (ordered) frequent items {f, a, c, d, g, i, m, p} {f, c, a, m, p} {a, b, c, f, l, m, o} {f, c, a, b, m} {b, f, h, j, o} {f, b} {b, c, k, s, p} {c, b, p} {a, f, c, e, l, p, m, n} {f, c, a, m, p} Steps: Item frequency head f 4 c 4 a 3 b 3 m 3 p 3 {} Header Table 1. Scan DB once, find frequent 1 -itemset (single item pattern) min_support = 0. 5 2. Order frequent items in frequency descending order 3. Scan DB again, construct FP -tree f: 4 c: 3 c: 1 b: 1 a: 3 b: 1 p: 1 m: 2 b: 1 p: 2 m: 1 31
 Benefits of the FP-tree Structure n n Completeness: n never breaks a long pattern of any transaction n preserves complete information for frequent pattern mining Compactness n reduce irrelevant information—infrequent items are gone n frequency descending ordering: more frequent items are more likely to be shared n never be larger than the original database (if not count node-links and counts) n Example: For Connect-4 DB, compression ratio could be over 100 32
Benefits of the FP-tree Structure n n Completeness: n never breaks a long pattern of any transaction n preserves complete information for frequent pattern mining Compactness n reduce irrelevant information—infrequent items are gone n frequency descending ordering: more frequent items are more likely to be shared n never be larger than the original database (if not count node-links and counts) n Example: For Connect-4 DB, compression ratio could be over 100 32
 Chapter 5: Mining Association Rules in Large Databases n n Association rule mining Mining single-dimensional Boolean association rules from transactional databases Mining multilevel association rules from transactional databases Mining multidimensional association rules from transactional databases and data warehouse n From association mining to correlation analysis n Constraint-based association mining n Summary 33
Chapter 5: Mining Association Rules in Large Databases n n Association rule mining Mining single-dimensional Boolean association rules from transactional databases Mining multilevel association rules from transactional databases Mining multidimensional association rules from transactional databases and data warehouse n From association mining to correlation analysis n Constraint-based association mining n Summary 33
 Multiple-Level Association Rules Food n n n Items often form hierarchy. bread milk Items at the lower level are expected to have lower 2% wheat white skim support. Rules regarding itemsets at Fraser Sunset appropriate levels could be quite useful. Transaction database can be encoded based on dimensions and levels We can explore shared multilevel mining 34
Multiple-Level Association Rules Food n n n Items often form hierarchy. bread milk Items at the lower level are expected to have lower 2% wheat white skim support. Rules regarding itemsets at Fraser Sunset appropriate levels could be quite useful. Transaction database can be encoded based on dimensions and levels We can explore shared multilevel mining 34
 Mining Multi-Level Associations n A top_down, progressive deepening approach: n First find high-level strong rules: milk ® bread [20%, 60%]. n Then find their lower-level “weaker” rules: 2% milk ® wheat bread [6%, 50%]. n Variations at mining multiple-level association rules. n Level-crossed association rules: 2% milk n ® Wonder wheat bread Association rules with multiple, alternative hierarchies: 2% milk ® Wonder bread 35
Mining Multi-Level Associations n A top_down, progressive deepening approach: n First find high-level strong rules: milk ® bread [20%, 60%]. n Then find their lower-level “weaker” rules: 2% milk ® wheat bread [6%, 50%]. n Variations at mining multiple-level association rules. n Level-crossed association rules: 2% milk n ® Wonder wheat bread Association rules with multiple, alternative hierarchies: 2% milk ® Wonder bread 35
 Multi-level Association: Uniform Support vs. Reduced Support n Uniform Support: the same minimum support for all levels n + One minimum support threshold. No need to examine itemsets containing any item whose ancestors do not have minimum support. n – Lower level items do not occur as frequently. If support threshold too high miss low level associations n too low generate too many high level associations Reduced Support: reduced minimum support at lower levels n There are 4 search strategies: n n n Level-by-level independent Level-cross filtering by k-itemset Level-cross filtering by single item Controlled level-cross filtering by single item 36
Multi-level Association: Uniform Support vs. Reduced Support n Uniform Support: the same minimum support for all levels n + One minimum support threshold. No need to examine itemsets containing any item whose ancestors do not have minimum support. n – Lower level items do not occur as frequently. If support threshold too high miss low level associations n too low generate too many high level associations Reduced Support: reduced minimum support at lower levels n There are 4 search strategies: n n n Level-by-level independent Level-cross filtering by k-itemset Level-cross filtering by single item Controlled level-cross filtering by single item 36
 Uniform Support Multi-level mining with uniform support Level 1 min_sup = 5% Level 2 min_sup = 5% Milk [support = 10%] 2% Milk Skim Milk [support = 6%] [support = 4%] Back 37
Uniform Support Multi-level mining with uniform support Level 1 min_sup = 5% Level 2 min_sup = 5% Milk [support = 10%] 2% Milk Skim Milk [support = 6%] [support = 4%] Back 37
 Reduced Support Multi-level mining with reduced support Level 1 min_sup = 5% Level 2 min_sup = 3% Milk [support = 10%] 2% Milk Skim Milk [support = 6%] [support = 4%] Back 38
Reduced Support Multi-level mining with reduced support Level 1 min_sup = 5% Level 2 min_sup = 3% Milk [support = 10%] 2% Milk Skim Milk [support = 6%] [support = 4%] Back 38
 n n Controlled level-cross filtering by single item Specify a level passage treshold for each level k min_sup_T(k+1)
n n Controlled level-cross filtering by single item Specify a level passage treshold for each level k min_sup_T(k+1)
 Multi-level Association: Redundancy Filtering n n Some rules may be redundant due to “ancestor” relationships between items. Example n milk wheat bread [support = 8%, confidence = 70%] n 2% milk wheat bread [support = 2%, confidence = 72%] We say the first rule is an ancestor of the second rule. A rule is redundant if its support is close to the “expected” value, based on the rule’s ancestor. 40
Multi-level Association: Redundancy Filtering n n Some rules may be redundant due to “ancestor” relationships between items. Example n milk wheat bread [support = 8%, confidence = 70%] n 2% milk wheat bread [support = 2%, confidence = 72%] We say the first rule is an ancestor of the second rule. A rule is redundant if its support is close to the “expected” value, based on the rule’s ancestor. 40
 Multi-Level Mining: Progressive Deepening n A top-down, progressive deepening approach: n First mine high-level frequent items: milk (15%), bread (10%) n Then mine their lower-level “weaker” frequent itemsets: 2% milk (5%), wheat bread (4%) n Different min_support threshold across multi-levels lead to different algorithms: n If adopting the same min_support across multilevels then toss t if any of t’s ancestors is infrequent. n If adopting reduced min_support at lower levels then examine only those descendents whose ancestor’s support is frequent/non-negligible. 41
Multi-Level Mining: Progressive Deepening n A top-down, progressive deepening approach: n First mine high-level frequent items: milk (15%), bread (10%) n Then mine their lower-level “weaker” frequent itemsets: 2% milk (5%), wheat bread (4%) n Different min_support threshold across multi-levels lead to different algorithms: n If adopting the same min_support across multilevels then toss t if any of t’s ancestors is infrequent. n If adopting reduced min_support at lower levels then examine only those descendents whose ancestor’s support is frequent/non-negligible. 41
 Progressive Refinement of Data Mining Quality n Why progressive refinement? n n n Trade speed with quality: step-by-step refinement. Superset coverage property: n n Mining operator can be expensive or cheap, fine or rough Preserve all the positive answers—allow a positive false test but not a false negative test. Two- or multi-step mining: n n First apply rough/cheap operator (superset coverage) Then apply expensive algorithm on a substantially reduced candidate set (Koperski & Han, SSD’ 95). 42
Progressive Refinement of Data Mining Quality n Why progressive refinement? n n n Trade speed with quality: step-by-step refinement. Superset coverage property: n n Mining operator can be expensive or cheap, fine or rough Preserve all the positive answers—allow a positive false test but not a false negative test. Two- or multi-step mining: n n First apply rough/cheap operator (superset coverage) Then apply expensive algorithm on a substantially reduced candidate set (Koperski & Han, SSD’ 95). 42
 Chapter 5: Mining Association Rules in Large Databases n n Association rule mining Mining single-dimensional Boolean association rules from transactional databases Mining multilevel association rules from transactional databases Mining multidimensional association rules from transactional databases and data warehouse n From association mining to correlation analysis n Constraint-based association mining n Summary 43
Chapter 5: Mining Association Rules in Large Databases n n Association rule mining Mining single-dimensional Boolean association rules from transactional databases Mining multilevel association rules from transactional databases Mining multidimensional association rules from transactional databases and data warehouse n From association mining to correlation analysis n Constraint-based association mining n Summary 43
 Interestingness Measurements n Objective measures Two popular measurements: ¶ support; and · n confidence Subjective measures (Silberschatz & Tuzhilin, KDD 95) A rule (pattern) is interesting if ¶ it is unexpected (surprising to the user); and/or · actionable (the user can do something with it) 44
Interestingness Measurements n Objective measures Two popular measurements: ¶ support; and · n confidence Subjective measures (Silberschatz & Tuzhilin, KDD 95) A rule (pattern) is interesting if ¶ it is unexpected (surprising to the user); and/or · actionable (the user can do something with it) 44
 Criticism to Support and Confidence n Example 1: (Aggarwal & Yu, PODS 98) n Among 5000 students n 3000 play basketball n 3750 eat cereal n 2000 both play basket ball and eat cereal n play basketball eat cereal [40%, 66. 7%] is misleading because the overall percentage of students eating cereal is 75% which is higher than 66. 7%. n play basketball not eat cereal [20%, 33. 3%] is far more accurate, although with lower support and confidence 45
Criticism to Support and Confidence n Example 1: (Aggarwal & Yu, PODS 98) n Among 5000 students n 3000 play basketball n 3750 eat cereal n 2000 both play basket ball and eat cereal n play basketball eat cereal [40%, 66. 7%] is misleading because the overall percentage of students eating cereal is 75% which is higher than 66. 7%. n play basketball not eat cereal [20%, 33. 3%] is far more accurate, although with lower support and confidence 45
 Criticism to Support and Confidence (Cont. ) n n n Example 2: n X and Y: positively correlated, n X and Z, negatively related n support and confidence of X=>Z dominates We need a measure of dependent or correlated events P(B|A)/P(B) is also called the lift of rule A => B 46
Criticism to Support and Confidence (Cont. ) n n n Example 2: n X and Y: positively correlated, n X and Z, negatively related n support and confidence of X=>Z dominates We need a measure of dependent or correlated events P(B|A)/P(B) is also called the lift of rule A => B 46
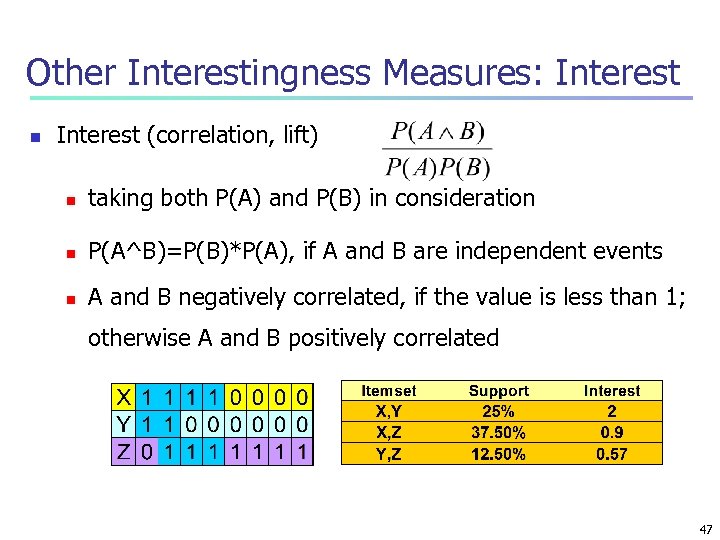 Other Interestingness Measures: Interest n Interest (correlation, lift) n taking both P(A) and P(B) in consideration n P(A^B)=P(B)*P(A), if A and B are independent events n A and B negatively correlated, if the value is less than 1; otherwise A and B positively correlated 47
Other Interestingness Measures: Interest n Interest (correlation, lift) n taking both P(A) and P(B) in consideration n P(A^B)=P(B)*P(A), if A and B are independent events n A and B negatively correlated, if the value is less than 1; otherwise A and B positively correlated 47
 Example n n n Total transactions 10, 000 İtems C: computers, V: video V: 7, 500 C: 6, 000 C and V: 4, 000 n Min_support: 0. 3 min_conf: 0, 50 Consider the rule: Buy(X: computer) buy(X: video) n Support : = 4000/10000 = 0. 4 n Confidence: P(C and V) /P(C) = 4000/6000 =%66 n Strong but n The probablity of buying a video is 0. 75 buying a comuter reduces the probablity of buying a video n From 0. 75 to 0. 66 n Computer and video are negatively correlated 48
Example n n n Total transactions 10, 000 İtems C: computers, V: video V: 7, 500 C: 6, 000 C and V: 4, 000 n Min_support: 0. 3 min_conf: 0, 50 Consider the rule: Buy(X: computer) buy(X: video) n Support : = 4000/10000 = 0. 4 n Confidence: P(C and V) /P(C) = 4000/6000 =%66 n Strong but n The probablity of buying a video is 0. 75 buying a comuter reduces the probablity of buying a video n From 0. 75 to 0. 66 n Computer and video are negatively correlated 48
 n n n Lift of A B Lift : P(A and B)/P(A)*P(B) P(A and B) = P(B|A)*P(A) then Lift = P(B|A)/P(B) Ratio of probablity of buying A and B divided by buying A and B independently Or it can be interpreted as: n Conditional probablity of buying B given that A is purchased divided by unconditional probablity of buying B 49
n n n Lift of A B Lift : P(A and B)/P(A)*P(B) P(A and B) = P(B|A)*P(A) then Lift = P(B|A)/P(B) Ratio of probablity of buying A and B divided by buying A and B independently Or it can be interpreted as: n Conditional probablity of buying B given that A is purchased divided by unconditional probablity of buying B 49
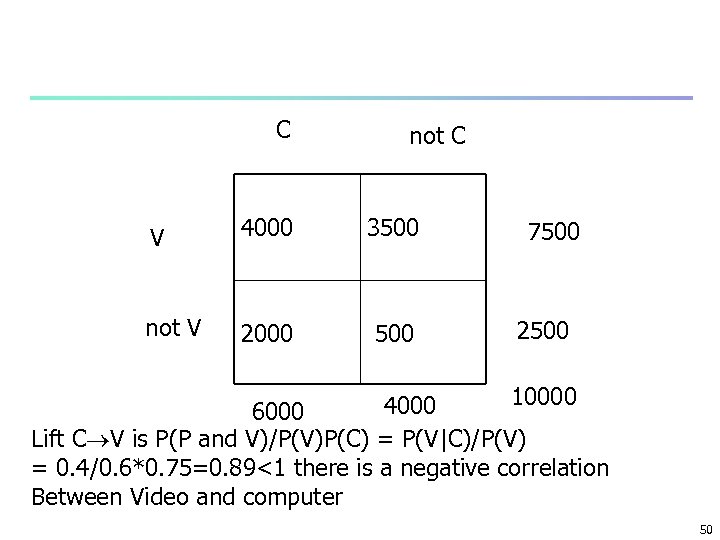 C not C V 4000 3500 not V 2000 500 7500 2500 10000 4000 6000 Lift C V is P(P and V)/P(V)P(C) = P(V|C)/P(V) = 0. 4/0. 6*0. 75=0. 89<1 there is a negative correlation Between Video and computer 50
C not C V 4000 3500 not V 2000 500 7500 2500 10000 4000 6000 Lift C V is P(P and V)/P(V)P(C) = P(V|C)/P(V) = 0. 4/0. 6*0. 75=0. 89<1 there is a negative correlation Between Video and computer 50
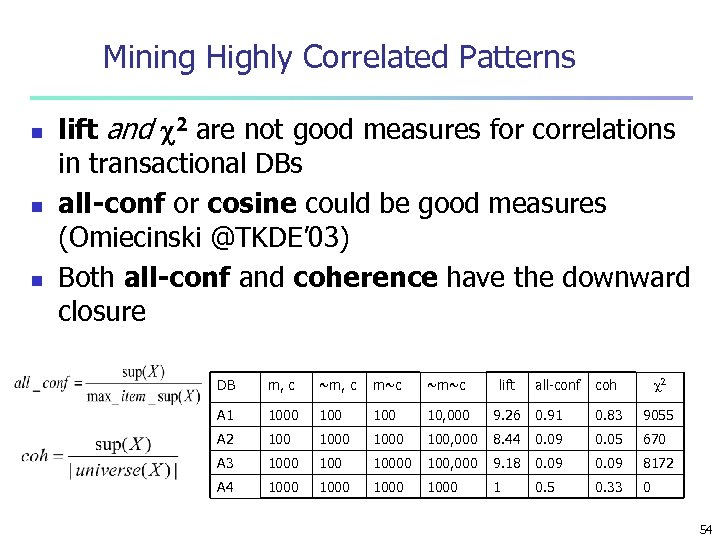
![Are All the Rules Found Interesting? n “Buy walnuts buy milk [1%, 80%]” is Are All the Rules Found Interesting? n “Buy walnuts buy milk [1%, 80%]” is](https://present5.com/presentation/275000214218863110cda3dff070e454/image-51.jpg) Are All the Rules Found Interesting? n “Buy walnuts buy milk [1%, 80%]” is misleading n if 85% of customers buy milk n Support and confidence are not good to represent correlations n So many interestingness measures? (Tan, Kumar, Sritastava @KDD’ 02) Milk No Milk Sum (row) Coffee m, c ~m, c c No Coffee m, ~c ~m, c ~c Sum(col. ) m ~m all-conf coh 2 9. 26 0. 91 0. 83 9055 100, 000 8. 44 0. 09 0. 05 670 10000 100, 000 9. 18 0. 09 8172 1000 1 0. 5 0. 33 0 DB m, c ~m, c m~c ~m~c lift A 1 1000 100 10, 000 A 2 1000 A 3 1000 100 A 4 1000 51
Are All the Rules Found Interesting? n “Buy walnuts buy milk [1%, 80%]” is misleading n if 85% of customers buy milk n Support and confidence are not good to represent correlations n So many interestingness measures? (Tan, Kumar, Sritastava @KDD’ 02) Milk No Milk Sum (row) Coffee m, c ~m, c c No Coffee m, ~c ~m, c ~c Sum(col. ) m ~m all-conf coh 2 9. 26 0. 91 0. 83 9055 100, 000 8. 44 0. 09 0. 05 670 10000 100, 000 9. 18 0. 09 8172 1000 1 0. 5 0. 33 0 DB m, c ~m, c m~c ~m~c lift A 1 1000 100 10, 000 A 2 1000 A 3 1000 100 A 4 1000 51
 All Confidence n n n n n All confidence: All_conf= sup(X)/max sup(Xi) i X: (X 1, X 2, . . . , Xk) For k = 2 Rules are X 1 X 2 and X 2 X 1 All_conf = sup(X 1, X 2)/max sup(X 1), sup(X 2) Here sup(X 1, X 2)/sup(X 1): confidence of rule X 1 X 2 Ex all conf: 0. 4/max(0. 6, 0. 75)=0. 4/0. 75=0. 53 52
All Confidence n n n n n All confidence: All_conf= sup(X)/max sup(Xi) i X: (X 1, X 2, . . . , Xk) For k = 2 Rules are X 1 X 2 and X 2 X 1 All_conf = sup(X 1, X 2)/max sup(X 1), sup(X 2) Here sup(X 1, X 2)/sup(X 1): confidence of rule X 1 X 2 Ex all conf: 0. 4/max(0. 6, 0. 75)=0. 4/0. 75=0. 53 52
 Cosine n n n Cosine : P(A, B)/sqrt(P(A), P(B)) Similar to lift but take square root of denominator Both cosine and all_conf are null inveriant n Not affected from null transactions Ex: Cosine: 0. 4/sqrt(0. 6*0. 75)=0. 27 53
Cosine n n n Cosine : P(A, B)/sqrt(P(A), P(B)) Similar to lift but take square root of denominator Both cosine and all_conf are null inveriant n Not affected from null transactions Ex: Cosine: 0. 4/sqrt(0. 6*0. 75)=0. 27 53
 Mining Highly Correlated Patterns n n n lift and 2 are not good measures for correlations in transactional DBs all-conf or cosine could be good measures (Omiecinski @TKDE’ 03) Both all-conf and coherence have the downward closure all-conf coh 2 9. 26 0. 91 0. 83 9055 100, 000 8. 44 0. 09 0. 05 670 10000 100, 000 9. 18 0. 09 8172 1000 1 0. 5 0. 33 0 DB m, c ~m, c m~c ~m~c lift A 1 1000 100 10, 000 A 2 1000 A 3 1000 100 A 4 1000 54
Mining Highly Correlated Patterns n n n lift and 2 are not good measures for correlations in transactional DBs all-conf or cosine could be good measures (Omiecinski @TKDE’ 03) Both all-conf and coherence have the downward closure all-conf coh 2 9. 26 0. 91 0. 83 9055 100, 000 8. 44 0. 09 0. 05 670 10000 100, 000 9. 18 0. 09 8172 1000 1 0. 5 0. 33 0 DB m, c ~m, c m~c ~m~c lift A 1 1000 100 10, 000 A 2 1000 A 3 1000 100 A 4 1000 54
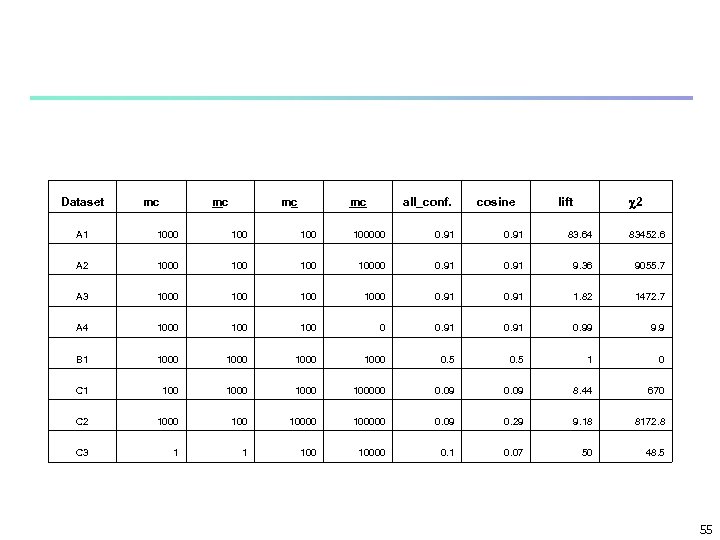 Dataset mc mc all_conf. cosine 2 lift A 1 1000 100 100000 0. 91 83. 64 83452. 6 A 2 1000 100 10000 0. 91 9. 36 9055. 7 A 3 1000 100 1000 0. 91 1. 82 1472. 7 A 4 1000 100 0 0. 91 0. 99 9. 9 B 1 1000 0. 5 1 0 C 1 100000 0. 09 8. 44 670 C 2 10000 100000 0. 09 0. 29 9. 18 8172. 8 C 3 1 1 10000 0. 1 0. 07 50 48. 5 55
Dataset mc mc all_conf. cosine 2 lift A 1 1000 100 100000 0. 91 83. 64 83452. 6 A 2 1000 100 10000 0. 91 9. 36 9055. 7 A 3 1000 100 1000 0. 91 1. 82 1472. 7 A 4 1000 100 0 0. 91 0. 99 9. 9 B 1 1000 0. 5 1 0 C 1 100000 0. 09 8. 44 670 C 2 10000 100000 0. 09 0. 29 9. 18 8172. 8 C 3 1 1 10000 0. 1 0. 07 50 48. 5 55
 Chapter 5: Mining Association Rules in Large Databases n n Association rule mining Mining single-dimensional Boolean association rules from transactional databases Mining multilevel association rules from transactional databases Mining multidimensional association rules from transactional databases and data warehouse n From association mining to correlation analysis n Constraint-based association mining n Summary 56
Chapter 5: Mining Association Rules in Large Databases n n Association rule mining Mining single-dimensional Boolean association rules from transactional databases Mining multilevel association rules from transactional databases Mining multidimensional association rules from transactional databases and data warehouse n From association mining to correlation analysis n Constraint-based association mining n Summary 56
 Constraint-based (Query-Directed) Mining n n n Finding all the patterns in a database autonomously? — unrealistic! n The patterns could be too many but not focused! Data mining should be an interactive process n User directs what to be mined using a data mining query language (or a graphical user interface) Constraint-based mining n User flexibility: provides constraints on what to be mined n System optimization: explores such constraints for efficient mining—constraint-based mining 57
Constraint-based (Query-Directed) Mining n n n Finding all the patterns in a database autonomously? — unrealistic! n The patterns could be too many but not focused! Data mining should be an interactive process n User directs what to be mined using a data mining query language (or a graphical user interface) Constraint-based mining n User flexibility: provides constraints on what to be mined n System optimization: explores such constraints for efficient mining—constraint-based mining 57
 Constraints in Data Mining n n n Knowledge type constraint: n classification, association, etc. Data constraint — using SQL-like queries n find product pairs sold together in stores in Chicago in Dec. ’ 02 Dimension/level constraint n in relevance to region, price, brand, customer category Rule (or pattern) constraint n small sales (price < $10) triggers big sales (sum > $200) Interestingness constraint n strong rules: min_support 3%, min_confidence 60% 58
Constraints in Data Mining n n n Knowledge type constraint: n classification, association, etc. Data constraint — using SQL-like queries n find product pairs sold together in stores in Chicago in Dec. ’ 02 Dimension/level constraint n in relevance to region, price, brand, customer category Rule (or pattern) constraint n small sales (price < $10) triggers big sales (sum > $200) Interestingness constraint n strong rules: min_support 3%, min_confidence 60% 58
 Example n n n bread milk butter n Strong rules but items are not that valuable TV VCD player n Support may be lower then previous rules but value of items are much higher n This rule may be more valuable 59
Example n n n bread milk butter n Strong rules but items are not that valuable TV VCD player n Support may be lower then previous rules but value of items are much higher n This rule may be more valuable 59
 n n Apriori principle stating that n All non empty subsets of a frequent itemsets must also be frequent Note that: n If a given itemset does not satisfy minimum support n None of its supersets can Other examples of anti-monotone constraints: n Min(l. price) >= 500 n Count(l) < 10 Average(l. price) < 10 : not anti-monotone 60
n n Apriori principle stating that n All non empty subsets of a frequent itemsets must also be frequent Note that: n If a given itemset does not satisfy minimum support n None of its supersets can Other examples of anti-monotone constraints: n Min(l. price) >= 500 n Count(l) < 10 Average(l. price) < 10 : not anti-monotone 60
 Anti-Monotonicity in Constraint Pushing TDB (min_sup=2) n Anti-monotonicity n n When an intemset S violates the constraint, so does any of its superset sum(S. Price) v is anti-monotone sum(S. Price) v is not anti-monotone Example. C: range(S. profit) 15 is antimonotone TID Transaction 10 a, b, c, d, f 20 b, c, d, f, g, h 30 a, c, d, e, f 40 c, e, f, g Item Profit a 40 b 0 c -20 n Itemset ab violates C d 10 n So does every superset of ab e -30 f 30 g 20 h -10 61
Anti-Monotonicity in Constraint Pushing TDB (min_sup=2) n Anti-monotonicity n n When an intemset S violates the constraint, so does any of its superset sum(S. Price) v is anti-monotone sum(S. Price) v is not anti-monotone Example. C: range(S. profit) 15 is antimonotone TID Transaction 10 a, b, c, d, f 20 b, c, d, f, g, h 30 a, c, d, e, f 40 c, e, f, g Item Profit a 40 b 0 c -20 n Itemset ab violates C d 10 n So does every superset of ab e -30 f 30 g 20 h -10 61
 Monotonicity for Constraint Pushing TDB (min_sup=2) n Monotonicity n n When an intemset S satisfies the constraint, so does any of its superset sum(S. Price) v is monotone min(S. Price) v is monotone Example. C: range(S. profit) 15 n Itemset ab satisfies C n So does every superset of ab TID Transaction 10 a, b, c, d, f 20 b, c, d, f, g, h 30 a, c, d, e, f 40 c, e, f, g Item Profit a 40 b 0 c -20 d 10 e -30 f 30 g 20 h -10 62
Monotonicity for Constraint Pushing TDB (min_sup=2) n Monotonicity n n When an intemset S satisfies the constraint, so does any of its superset sum(S. Price) v is monotone min(S. Price) v is monotone Example. C: range(S. profit) 15 n Itemset ab satisfies C n So does every superset of ab TID Transaction 10 a, b, c, d, f 20 b, c, d, f, g, h 30 a, c, d, e, f 40 c, e, f, g Item Profit a 40 b 0 c -20 d 10 e -30 f 30 g 20 h -10 62
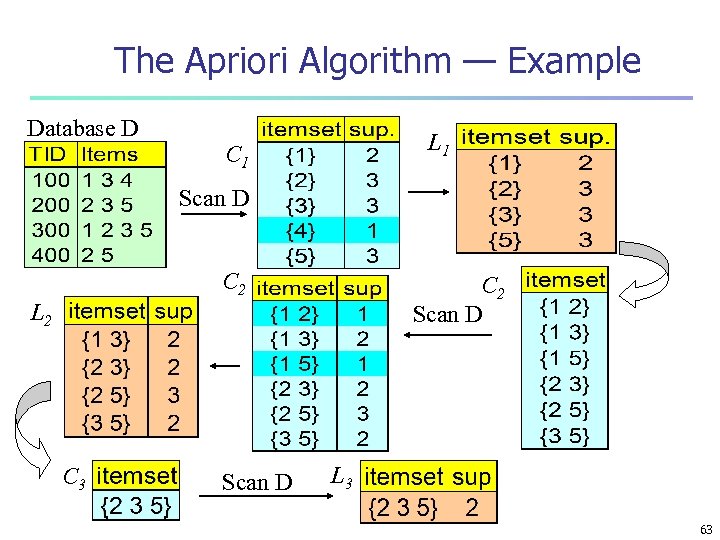 The Apriori Algorithm — Example Database D L 1 C 1 Scan D C 2 Scan D L 2 C 3 Scan D L 3 63
The Apriori Algorithm — Example Database D L 1 C 1 Scan D C 2 Scan D L 2 C 3 Scan D L 3 63
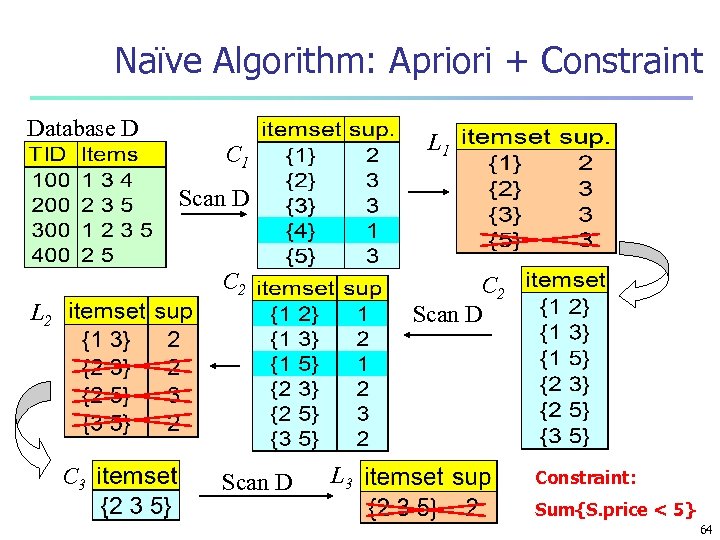 Naïve Algorithm: Apriori + Constraint Database D L 1 C 1 Scan D C 2 Scan D L 2 C 3 Scan D L 3 Constraint: Sum{S. price < 5} 64
Naïve Algorithm: Apriori + Constraint Database D L 1 C 1 Scan D C 2 Scan D L 2 C 3 Scan D L 3 Constraint: Sum{S. price < 5} 64
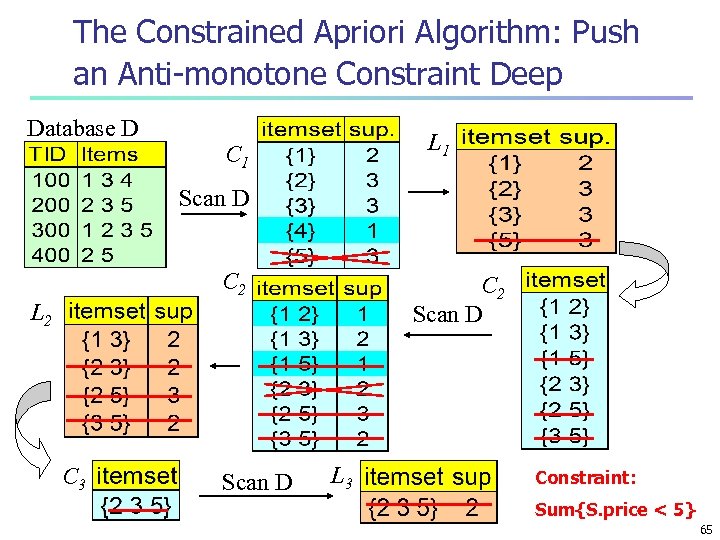 The Constrained Apriori Algorithm: Push an Anti-monotone Constraint Deep Database D L 1 C 1 Scan D C 2 Scan D L 2 C 3 Scan D L 3 Constraint: Sum{S. price < 5} 65
The Constrained Apriori Algorithm: Push an Anti-monotone Constraint Deep Database D L 1 C 1 Scan D C 2 Scan D L 2 C 3 Scan D L 3 Constraint: Sum{S. price < 5} 65
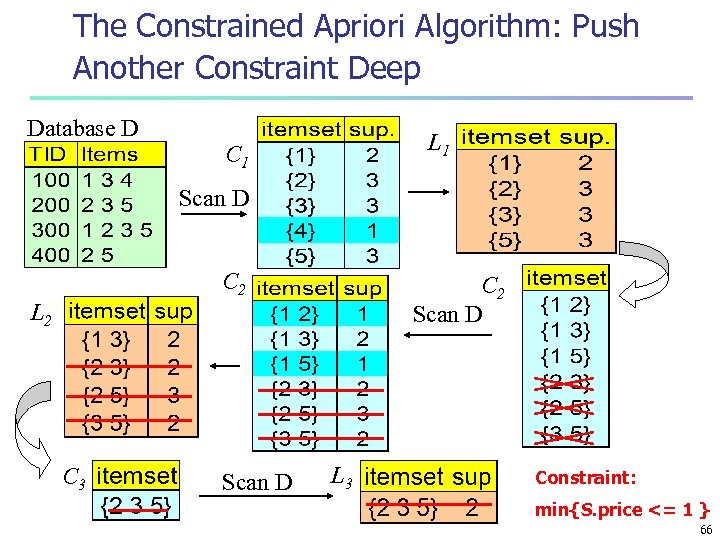 The Constrained Apriori Algorithm: Push Another Constraint Deep Database D L 1 C 1 Scan D C 2 Scan D L 2 C 3 Scan D L 3 Constraint: min{S. price <= 1 } 66
The Constrained Apriori Algorithm: Push Another Constraint Deep Database D L 1 C 1 Scan D C 2 Scan D L 2 C 3 Scan D L 3 Constraint: min{S. price <= 1 } 66
 Chapter 5: Mining Association Rules in Large Databases n Association rule mining n Algorithms for scalable mining of (single-dimensional Boolean) association rules in transactional databases n Mining various kinds of association/correlation rules n Constraint-based association mining n Sequential pattern mining n Applications/extensions of frequent pattern mining n Summary 67
Chapter 5: Mining Association Rules in Large Databases n Association rule mining n Algorithms for scalable mining of (single-dimensional Boolean) association rules in transactional databases n Mining various kinds of association/correlation rules n Constraint-based association mining n Sequential pattern mining n Applications/extensions of frequent pattern mining n Summary 67
 Sequence Databases and Sequential Pattern Analysis n Transaction databases, time-series databases vs. sequence databases n Frequent patterns vs. (frequent) sequential patterns n Applications of sequential pattern mining n Customer shopping sequences: n n First buy computer, then CD-ROM, and then digital camera, within 3 months. Medical treatment, natural disasters (e. g. , earthquakes), science & engineering processes, stocks and markets, etc. n Telephone calling patterns, Weblog click streams n DNA sequences and gene structures 68
Sequence Databases and Sequential Pattern Analysis n Transaction databases, time-series databases vs. sequence databases n Frequent patterns vs. (frequent) sequential patterns n Applications of sequential pattern mining n Customer shopping sequences: n n First buy computer, then CD-ROM, and then digital camera, within 3 months. Medical treatment, natural disasters (e. g. , earthquakes), science & engineering processes, stocks and markets, etc. n Telephone calling patterns, Weblog click streams n DNA sequences and gene structures 68
 What Is Sequential Pattern Mining? n Given a set of sequences, find the complete set of frequent subsequences A sequence : < (ef) (ab) (df) c b > A sequence database SID sequence 10
What Is Sequential Pattern Mining? n Given a set of sequences, find the complete set of frequent subsequences A sequence : < (ef) (ab) (df) c b > A sequence database SID sequence 10
 Challenges on Sequential Pattern Mining n n A huge number of possible sequential patterns are hidden in databases A mining algorithm should n n n find the complete set of patterns, when possible, satisfying the minimum support (frequency) threshold be highly efficient, scalable, involving only a small number of database scans be able to incorporate various kinds of user-specific constraints 70
Challenges on Sequential Pattern Mining n n A huge number of possible sequential patterns are hidden in databases A mining algorithm should n n n find the complete set of patterns, when possible, satisfying the minimum support (frequency) threshold be highly efficient, scalable, involving only a small number of database scans be able to incorporate various kinds of user-specific constraints 70
 Studies on Sequential Pattern Mining n n Concept introduction and an initial Apriori-like algorithm n R. Agrawal & R. Srikant. “Mining sequential patterns, ” ICDE’ 95 GSP—An Apriori-based, influential mining method (developed at IBM Almaden) n R. Srikant & R. Agrawal. “Mining sequential patterns: Generalizations and performance improvements, ” EDBT’ 96 From sequential patterns to episodes (Apriori-like + constraints) n H. Mannila, H. Toivonen & A. I. Verkamo. “Discovery of frequent episodes in event sequences, ” Data Mining and Knowledge Discovery, 1997 Mining sequential patterns with constraints n M. N. Garofalakis, R. Rastogi, K. Shim: SPIRIT: Sequential Pattern Mining with Regular Expression Constraints. VLDB 1999 71
Studies on Sequential Pattern Mining n n Concept introduction and an initial Apriori-like algorithm n R. Agrawal & R. Srikant. “Mining sequential patterns, ” ICDE’ 95 GSP—An Apriori-based, influential mining method (developed at IBM Almaden) n R. Srikant & R. Agrawal. “Mining sequential patterns: Generalizations and performance improvements, ” EDBT’ 96 From sequential patterns to episodes (Apriori-like + constraints) n H. Mannila, H. Toivonen & A. I. Verkamo. “Discovery of frequent episodes in event sequences, ” Data Mining and Knowledge Discovery, 1997 Mining sequential patterns with constraints n M. N. Garofalakis, R. Rastogi, K. Shim: SPIRIT: Sequential Pattern Mining with Regular Expression Constraints. VLDB 1999 71
 Sequential pattern mining: Cases and Parameters n n Duration of a time sequence T n Sequential pattern mining can then be confined to the data within a specified duration n Ex. Subsequence corresponding to the year of 1999 n Ex. Partitioned sequences, such as every year, or every week after stock crashes, or every two weeks before and after a volcano eruption Event folding window w n If w = T, time-insensitive frequent patterns are found n If w = 0 (no event sequence folding), sequential patterns are found where each event occurs at a distinct time instant n If 0 < w < T, sequences occurring within the same period w are folded in the analysis 72
Sequential pattern mining: Cases and Parameters n n Duration of a time sequence T n Sequential pattern mining can then be confined to the data within a specified duration n Ex. Subsequence corresponding to the year of 1999 n Ex. Partitioned sequences, such as every year, or every week after stock crashes, or every two weeks before and after a volcano eruption Event folding window w n If w = T, time-insensitive frequent patterns are found n If w = 0 (no event sequence folding), sequential patterns are found where each event occurs at a distinct time instant n If 0 < w < T, sequences occurring within the same period w are folded in the analysis 72
 Example n n When event folding window is 5 munites Purchases within 5 munits is considered to be taken together 73
Example n n When event folding window is 5 munites Purchases within 5 munits is considered to be taken together 73
 Sequential pattern mining: Cases and Parameters (2) n Time interval, int, between events in the discovered pattern n int = 0: no interval gap is allowed, i. e. , only strictly consecutive sequences are found n n min_int max_int: find patterns that are separated by at least min_int but at most max_int n n Ex. “Find frequent patterns occurring in consecutive weeks” Ex. “If a person rents movie A, it is likely she will rent movie B within 30 days” (int 30) int = c 0: find patterns carrying an exact interval n Ex. “Every time when Dow Jones drops more than 5%, what will happen exactly two days later? ” (int = 2) 74
Sequential pattern mining: Cases and Parameters (2) n Time interval, int, between events in the discovered pattern n int = 0: no interval gap is allowed, i. e. , only strictly consecutive sequences are found n n min_int max_int: find patterns that are separated by at least min_int but at most max_int n n Ex. “Find frequent patterns occurring in consecutive weeks” Ex. “If a person rents movie A, it is likely she will rent movie B within 30 days” (int 30) int = c 0: find patterns carrying an exact interval n Ex. “Every time when Dow Jones drops more than 5%, what will happen exactly two days later? ” (int = 2) 74
 A Basic Property of Sequential Patterns: Apriori n A basic property: Apriori (Agrawal & Sirkant’ 94) n If a sequence S is not frequent n Then none of the super-sequences of S is frequent n E. g,
A Basic Property of Sequential Patterns: Apriori n A basic property: Apriori (Agrawal & Sirkant’ 94) n If a sequence S is not frequent n Then none of the super-sequences of S is frequent n E. g,
 GSP—A Generalized Sequential Pattern Mining Algorithm n GSP (Generalized Sequential Pattern) mining algorithm n n Outline of the method n n proposed by Agrawal and Srikant, EDBT’ 96 Initially, every item in DB is a candidate of length-1 for each level (i. e. , sequences of length-k) do n scan database to collect support count for each candidate sequence n generate candidate length-(k+1) sequences from length-k frequent sequences using Apriori repeat until no frequent sequence or no candidate can be found Major strength: Candidate pruning by Apriori 76
GSP—A Generalized Sequential Pattern Mining Algorithm n GSP (Generalized Sequential Pattern) mining algorithm n n Outline of the method n n proposed by Agrawal and Srikant, EDBT’ 96 Initially, every item in DB is a candidate of length-1 for each level (i. e. , sequences of length-k) do n scan database to collect support count for each candidate sequence n generate candidate length-(k+1) sequences from length-k frequent sequences using Apriori repeat until no frequent sequence or no candidate can be found Major strength: Candidate pruning by Apriori 76
 Finding Length-1 Sequential Patterns n n Examine GSP using an example Initial candidates: all singleton sequences n n Scan database once, count support for candidates min_sup =2 Sup 3 5
Finding Length-1 Sequential Patterns n n Examine GSP using an example Initial candidates: all singleton sequences n n Scan database once, count support for candidates min_sup =2 Sup 3 5
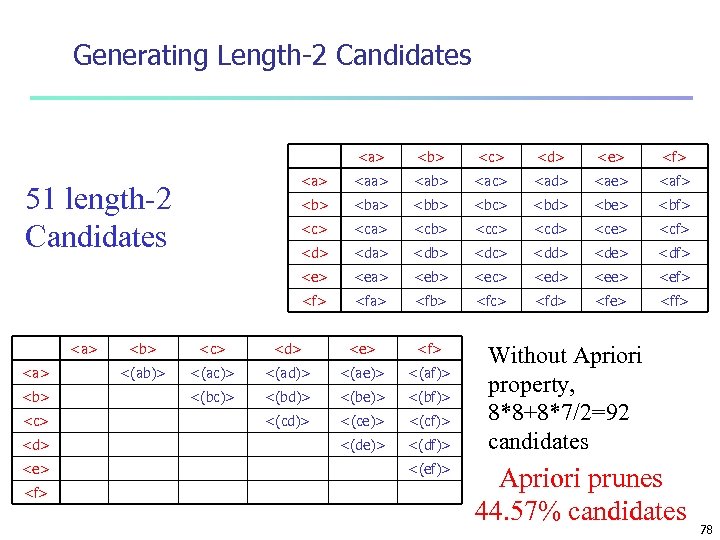 Generating Length-2 Candidates
Generating Length-2 Candidates
 Generating Length-3 Candidates and Finding Length-3 Patterns n Generate Length-3 Candidates n n n Self-join length-2 sequential patterns n Based on the Apriori property n
Generating Length-3 Candidates and Finding Length-3 Patterns n Generate Length-3 Candidates n n n Self-join length-2 sequential patterns n Based on the Apriori property n
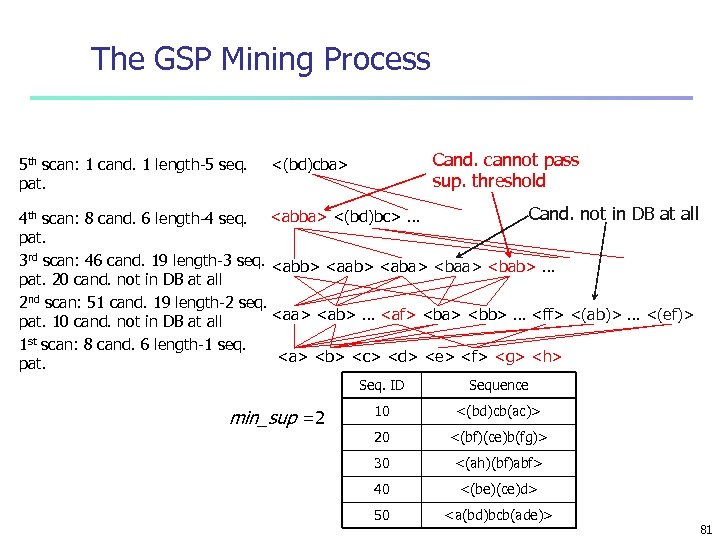 The GSP Mining Process 5 th scan: 1 cand. 1 length-5 seq. pat. Cand. cannot pass sup. threshold <(bd)cba> Cand. not in DB at all 4 th scan: 8 cand. 6 length-4 seq.
The GSP Mining Process 5 th scan: 1 cand. 1 length-5 seq. pat. Cand. cannot pass sup. threshold <(bd)cba> Cand. not in DB at all 4 th scan: 8 cand. 6 length-4 seq.
 n n Definition c is a contiguous subsequence of a sequence s: {s 1, s 2, . . . , sn} if n c is derived by dropping an item from s 1 or sn n c is derived by dropping an item from s i which has at least 2 items n c’ is a contiguous subsequence of c and c is a contiguous subsequence of s Ex: s: { (1, 2), (3, 4), 5, 6} n { 2, (3, 4), 5}, { (1, 2), 3, 5, 6}, { (3, 5} are but n { (1, 2), (3, 4), 6}, { (1, 5, 6} are not 82
n n Definition c is a contiguous subsequence of a sequence s: {s 1, s 2, . . . , sn} if n c is derived by dropping an item from s 1 or sn n c is derived by dropping an item from s i which has at least 2 items n c’ is a contiguous subsequence of c and c is a contiguous subsequence of s Ex: s: { (1, 2), (3, 4), 5, 6} n { 2, (3, 4), 5}, { (1, 2), 3, 5, 6}, { (3, 5} are but n { (1, 2), (3, 4), 6}, { (1, 5, 6} are not 82
 Candidate genration n n Step 1: Join Step Lk-1 join with Lk-1 to give Ck n s 1 and s 2 are joined if dropping first item of s 1 and last item of s 2 gives the same sequence n s 1 is extended by adding the last item of s 2 Step 2: Prune Step Delete candidate sequences having (k-1) contiguous subsequences whose support count is less than min_support count 83
Candidate genration n n Step 1: Join Step Lk-1 join with Lk-1 to give Ck n s 1 and s 2 are joined if dropping first item of s 1 and last item of s 2 gives the same sequence n s 1 is extended by adding the last item of s 2 Step 2: Prune Step Delete candidate sequences having (k-1) contiguous subsequences whose support count is less than min_support count 83
 n n n n L 3 {(1, 2), 3} {(1, 2), 4} {1, (3, 4)} {(1, 3), 5} {2, (3, 4)} {2, 3, 5} n n C 4 {(1, 2), (3, 4)} {(1, 2), 3, 5} L 4 {(1, 2), (3, 4)} {(1, 2), 3} joined with {2, (3, 4)} to give {(1, 2), (3, 4)} {(1, 2), 3} joined with {2, 3, 5} to give {(1, 2), 3, 5} is dropped since its 3 contiguous subseq {(1, 3, 5} not in L 3 84
n n n n L 3 {(1, 2), 3} {(1, 2), 4} {1, (3, 4)} {(1, 3), 5} {2, (3, 4)} {2, 3, 5} n n C 4 {(1, 2), (3, 4)} {(1, 2), 3, 5} L 4 {(1, 2), (3, 4)} {(1, 2), 3} joined with {2, (3, 4)} to give {(1, 2), (3, 4)} {(1, 2), 3} joined with {2, 3, 5} to give {(1, 2), 3, 5} is dropped since its 3 contiguous subseq {(1, 3, 5} not in L 3 84
 Bottlenecks of GSP n A huge set of candidates could be generated n 1, 000 frequent length-1 sequences generate length-2 candidates! n Multiple scans of database in mining n Real challenge: mining long sequential patterns n n An exponential number of short candidates A length-100 sequential pattern needs 1030 candidate sequences! 86
Bottlenecks of GSP n A huge set of candidates could be generated n 1, 000 frequent length-1 sequences generate length-2 candidates! n Multiple scans of database in mining n Real challenge: mining long sequential patterns n n An exponential number of short candidates A length-100 sequential pattern needs 1030 candidate sequences! 86


