Darcy law Figure from Hornberger et al.










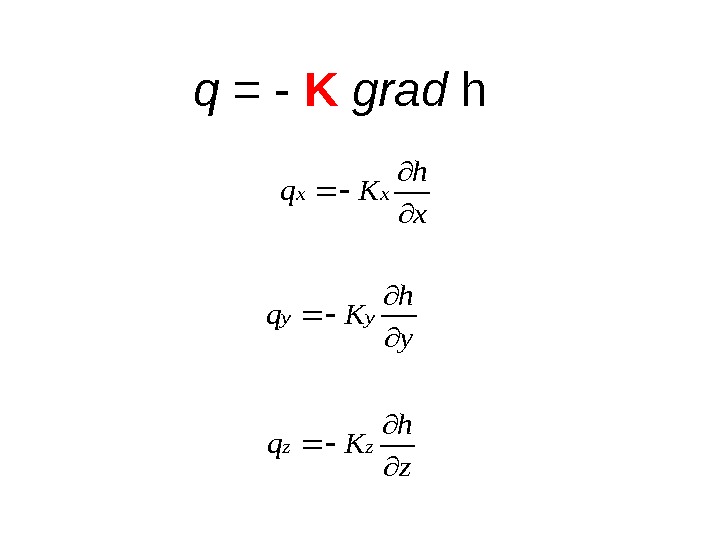















- Размер: 842 Кб
- Количество слайдов: 37
Описание презентации Darcy law Figure from Hornberger et al. по слайдам
 Darcy law
Darcy law
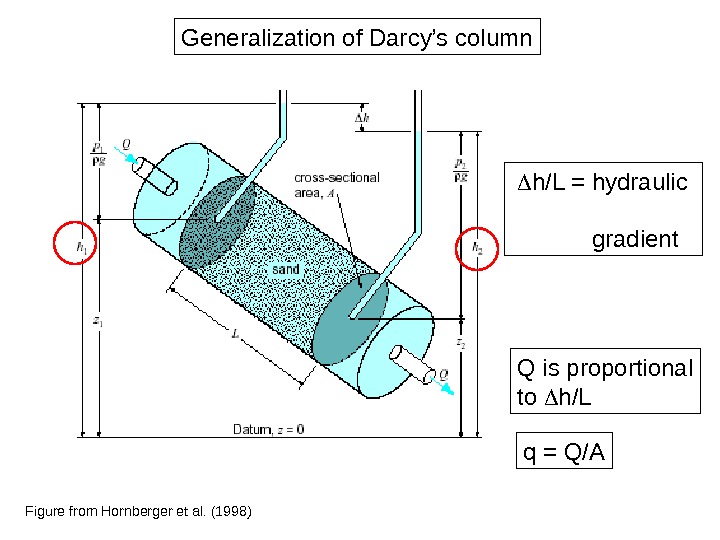
 Figure from Hornberger et al. (1998) Generalization of Darcy’s column h/L = hydraulic gradient q = Q/AQ is proportional to h/L
Figure from Hornberger et al. (1998) Generalization of Darcy’s column h/L = hydraulic gradient q = Q/AQ is proportional to h/L
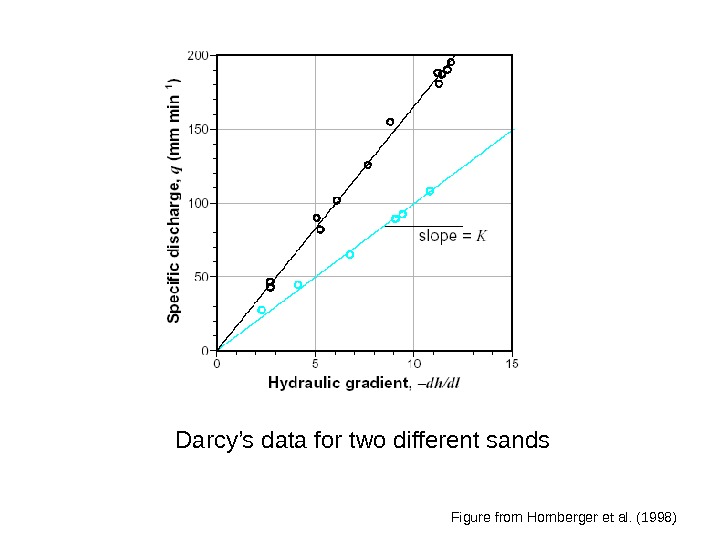
 Figure from Hornberger et al. (1998)Darcy’s data for two different sands
Figure from Hornberger et al. (1998)Darcy’s data for two different sands
 Darcy’s Law • Henri Darcy established empirically that the flux of water through a permeable formation is proportional to the distance between top and bottom of the soil column. • The constant of proportionality is called the hydraulic conductivity (K). • V = Q/A, V – ∆h, and V 1/∆L
Darcy’s Law • Henri Darcy established empirically that the flux of water through a permeable formation is proportional to the distance between top and bottom of the soil column. • The constant of proportionality is called the hydraulic conductivity (K). • V = Q/A, V – ∆h, and V 1/∆L
 V = – K (∆h/∆L) and since Q = VA (A = total area) Q = – KA (dh/d. L)Darcy’s Law
V = – K (∆h/∆L) and since Q = VA (A = total area) Q = – KA (dh/d. L)Darcy’s Law
 Hydraulic Conductivity • K represents a measure of the ability for flow through porous media: • Gravels — 0. 1 to 1 cm/sec • Sands — 10 -2 to 10 -3 cm/sec • Silts — 10 -4 to 10 -5 cm/sec • Clays — 10 -7 to 10 -9 cm/sec
Hydraulic Conductivity • K represents a measure of the ability for flow through porous media: • Gravels — 0. 1 to 1 cm/sec • Sands — 10 -2 to 10 -3 cm/sec • Silts — 10 -4 to 10 -5 cm/sec • Clays — 10 -7 to 10 -9 cm/sec
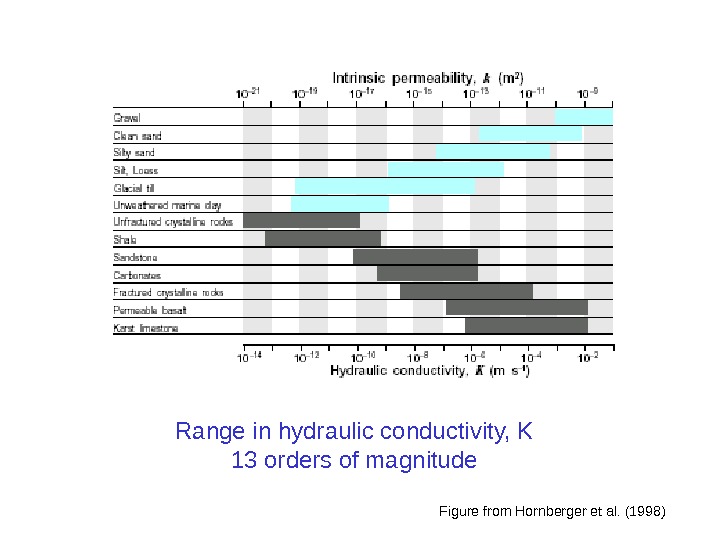
 Figure from Hornberger et al. (1998)Range in hydraulic conductivity, K 13 orders of magnitude
Figure from Hornberger et al. (1998)Range in hydraulic conductivity, K 13 orders of magnitude
 Conditions • Darcy’s Law holds for: 1. Saturated flow and unsaturated flow 2. Steady-state and transient flow 3. Flow in aquifers and aquitards 4. Flow in homogeneous and heterogeneous systems 5. Flow in isotropic or anisotropic media 6. Flow in rocks and granular media
Conditions • Darcy’s Law holds for: 1. Saturated flow and unsaturated flow 2. Steady-state and transient flow 3. Flow in aquifers and aquitards 4. Flow in homogeneous and heterogeneous systems 5. Flow in isotropic or anisotropic media 6. Flow in rocks and granular media
 Darcy Velocity • V is the specific discharge ( Darcy velocity). • (–) indicates that V occurs in the direction of the decreasing head. • Specific discharge has units of velocity. • The specific discharge is a macroscopic concept, and is easily measured. It should be noted that Darcy’s velocity is different ….
Darcy Velocity • V is the specific discharge ( Darcy velocity). • (–) indicates that V occurs in the direction of the decreasing head. • Specific discharge has units of velocity. • The specific discharge is a macroscopic concept, and is easily measured. It should be noted that Darcy’s velocity is different ….
 Darcy Velocity • . . . from the microscopic velocities associated with the actual paths if individual particles of water as they wind their way through the grains of sand. • The microscopic velocities are real, but are probably impossible to measure.
Darcy Velocity • . . . from the microscopic velocities associated with the actual paths if individual particles of water as they wind their way through the grains of sand. • The microscopic velocities are real, but are probably impossible to measure.
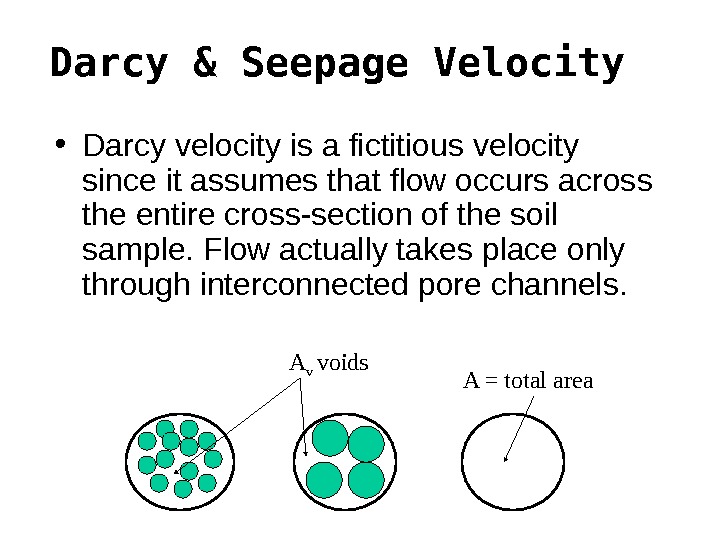
 Darcy & Seepage Velocity • Darcy velocity is a fictitious velocity since it assumes that flow occurs across the entire cross-section of the soil sample. Flow actually takes place only through interconnected pore channels. A = total area. A v voids
Darcy & Seepage Velocity • Darcy velocity is a fictitious velocity since it assumes that flow occurs across the entire cross-section of the soil sample. Flow actually takes place only through interconnected pore channels. A = total area. A v voids
 Darcy & Seepage Velocity • From the Continuity Eqn: • Q = A v D = A V V s – Where: Q = flow rate A = total cross-sectional area of material AV = area of voids V s = seepage velocity V D = Darcy velocity
Darcy & Seepage Velocity • From the Continuity Eqn: • Q = A v D = A V V s – Where: Q = flow rate A = total cross-sectional area of material AV = area of voids V s = seepage velocity V D = Darcy velocity
 Darcy & Seepage Velocity • Therefore: VS = VD ( A/AV ) • Multiplying both sides by the length of the medium ( L ) V S = VD ( AL / AV L ) = VD ( VT / VV ) • Where: V T = total volume V V = void volume • By Definition, V v / VT = n , the soil porosity • Thus V S = VD / n
Darcy & Seepage Velocity • Therefore: VS = VD ( A/AV ) • Multiplying both sides by the length of the medium ( L ) V S = VD ( AL / AV L ) = VD ( VT / VV ) • Where: V T = total volume V V = void volume • By Definition, V v / VT = n , the soil porosity • Thus V S = VD / n
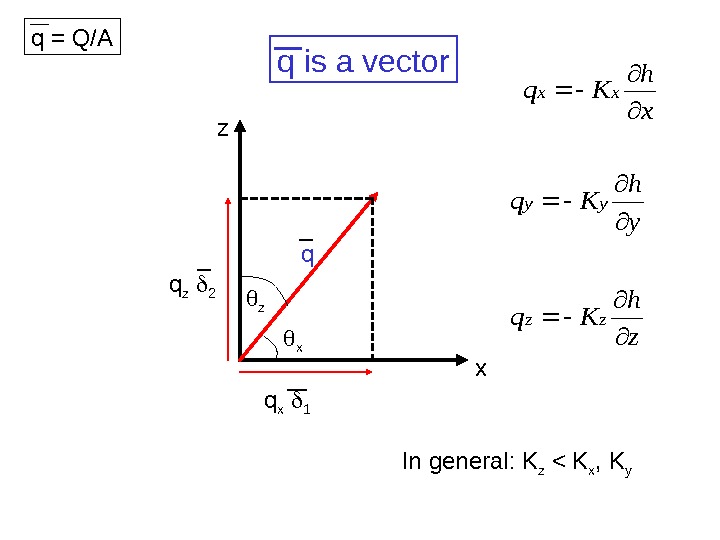
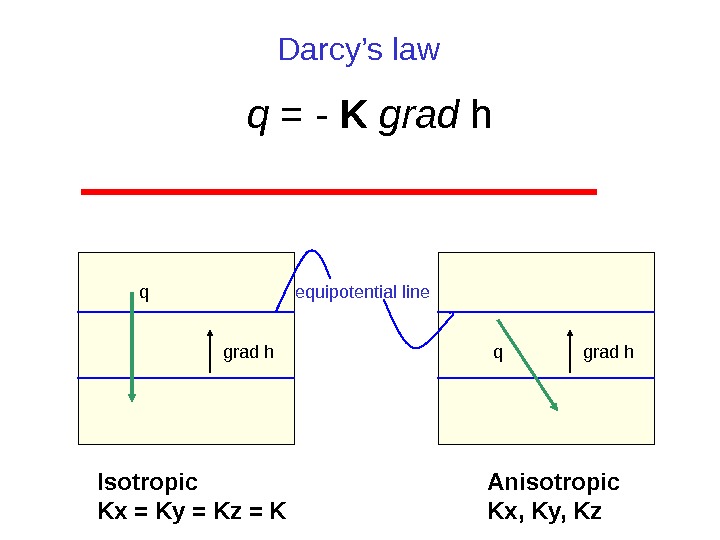
 q is a vector q xz q x 1 q z 2 z xz h Kq y h Kq x h Kq zz yy xx q = Q/A In general: K z < K x , K y
q is a vector q xz q x 1 q z 2 z xz h Kq y h Kq x h Kq zz yy xx q = Q/A In general: K z < K x , K y
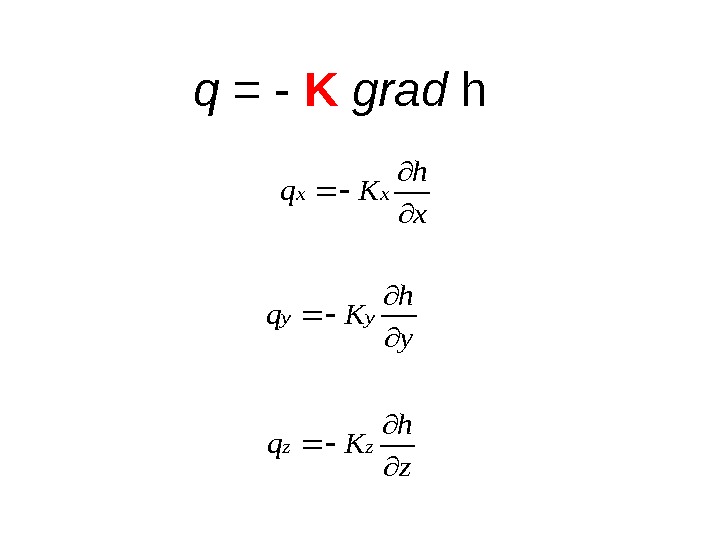 z h Kq y h Kq x h Kq zz yy xx q = — K grad h
z h Kq y h Kq x h Kq zz yy xx q = — K grad h
 Vector Form of Darcy’s Law q = — K grad h q = specific discharge (L/T) K = hydraulic conductivity (L/T) grad h = hydraulic gradient (L/L) h = head (L)
Vector Form of Darcy’s Law q = — K grad h q = specific discharge (L/T) K = hydraulic conductivity (L/T) grad h = hydraulic gradient (L/L) h = head (L)
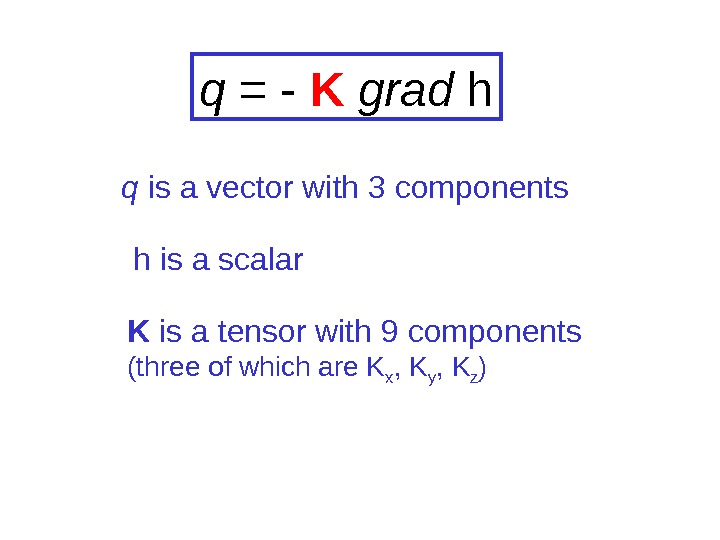
 q = — K grad h K is a tensor with 9 components (three of which are K x , K y , K z )q is a vector with 3 components h is a scalar
q = — K grad h K is a tensor with 9 components (three of which are K x , K y , K z )q is a vector with 3 components h is a scalar
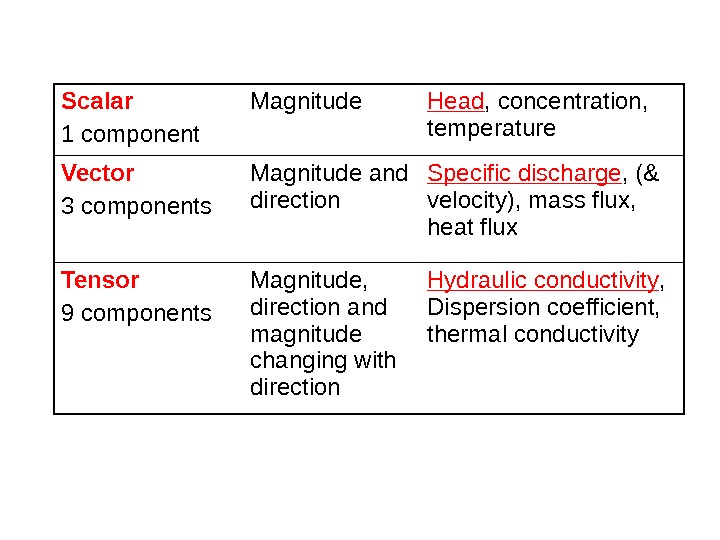
 Scalar 1 component Magnitude Head , concentration, temperature Vector 3 components Magnitude and direction Specific discharge , (& velocity), mass flux, heat flux Tensor 9 components Magnitude, direction and magnitude changing with direction Hydraulic conductivity , Dispersion coefficient, thermal conductivity
Scalar 1 component Magnitude Head , concentration, temperature Vector 3 components Magnitude and direction Specific discharge , (& velocity), mass flux, heat flux Tensor 9 components Magnitude, direction and magnitude changing with direction Hydraulic conductivity , Dispersion coefficient, thermal conductivity
 q = — K grad h. Darcy’s law grad hq equipotential line grad hq Isotropic Kx = Ky = Kz = K Anisotropic Kx, Ky, Kz
q = — K grad h. Darcy’s law grad hq equipotential line grad hq Isotropic Kx = Ky = Kz = K Anisotropic Kx, Ky, Kz


 Equations of Groundwater Flow • Description of ground water flow is based on: Darcy’s Law Continuity Equation — describes conservation of fluid mass during flow through a porous medium; results in a partial differential equation of flow. • Laplace’s Eqn — most important in math
Equations of Groundwater Flow • Description of ground water flow is based on: Darcy’s Law Continuity Equation — describes conservation of fluid mass during flow through a porous medium; results in a partial differential equation of flow. • Laplace’s Eqn — most important in math
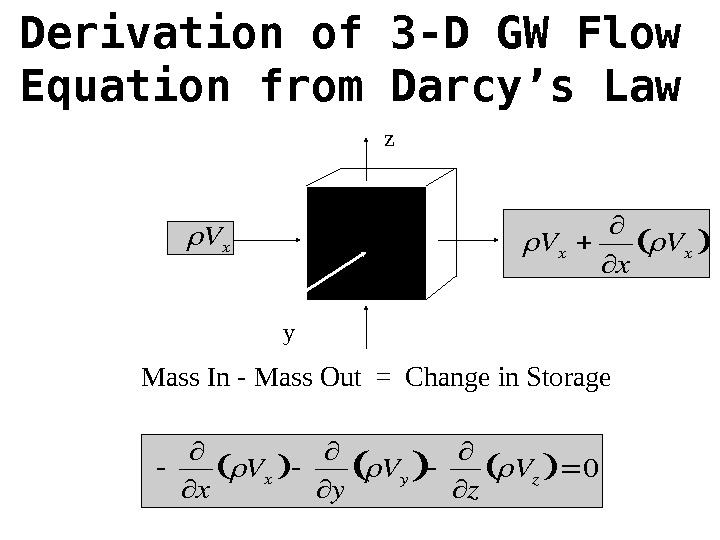
 Derivation of 3 -D GW Flow Equation from Darcy’s Law x Vx y Vy z Vz 0 Mass In — Mass Out = Change in Storage Vx x Vx Vx z y
Derivation of 3 -D GW Flow Equation from Darcy’s Law x Vx y Vy z Vz 0 Mass In — Mass Out = Change in Storage Vx x Vx Vx z y
 Derivation of 3 -D GW Flow Equation from Darcy’s Law x Kx h x y Ky h y z Kz h z 0 Replace V x , Vy , and Vz with Darcy using Kx , Ky , and Kz Divide out constant , and assume K x = K y = K z = K 2 h x 2 2 h y 2 2 h z 20 2 h 0 called. Laplace. Eqn.
Derivation of 3 -D GW Flow Equation from Darcy’s Law x Kx h x y Ky h y z Kz h z 0 Replace V x , Vy , and Vz with Darcy using Kx , Ky , and Kz Divide out constant , and assume K x = K y = K z = K 2 h x 2 2 h y 2 2 h z 20 2 h 0 called. Laplace. Eqn.
 Transient Saturated Flow x Kx h x y Ky h y z Kz h z Ss h t x Vx y Vy z Vz t n A change in h will produce change in and n, replaced with specific storage S s = g( + n ). Note, is the compressibility of aquifer and B is comp of water, therefore,
Transient Saturated Flow x Kx h x y Ky h y z Kz h z Ss h t x Vx y Vy z Vz t n A change in h will produce change in and n, replaced with specific storage S s = g( + n ). Note, is the compressibility of aquifer and B is comp of water, therefore,
 Transient Saturated Flow x h x y h y z h z Ss K h t Simplifying by assuming K = constant in all dimensions And assuming that S = S s b , and that T = Kb yields 2 h x 2 2 h y 2 2 h z 2 Ss K h t 2 h S T h t from. Jacob, Theis
Transient Saturated Flow x h x y h y z h z Ss K h t Simplifying by assuming K = constant in all dimensions And assuming that S = S s b , and that T = Kb yields 2 h x 2 2 h y 2 2 h z 2 Ss K h t 2 h S T h t from. Jacob, Theis
 Steady State Flow to Well Simplifying by assuming K = constant in all dimensions and assuming that Transmissivity T = Kb and Q = flow rate to well at point (x, y) yields 2 h x 2 2 h y 2 Qx, y T
Steady State Flow to Well Simplifying by assuming K = constant in all dimensions and assuming that Transmissivity T = Kb and Q = flow rate to well at point (x, y) yields 2 h x 2 2 h y 2 Qx, y T
 Example of Darcy’s Law • A confined aquifer has a source of recharge. • K for the aquifer is 50 m/day , and n is 0. 2. • The piezometric head in two wells 1000 m apart is 55 m and 50 m respectively, from a common datum. • The average thickness of the aquifer is 30 m , and the average width of aquifer is 5 km.
Example of Darcy’s Law • A confined aquifer has a source of recharge. • K for the aquifer is 50 m/day , and n is 0. 2. • The piezometric head in two wells 1000 m apart is 55 m and 50 m respectively, from a common datum. • The average thickness of the aquifer is 30 m , and the average width of aquifer is 5 km.
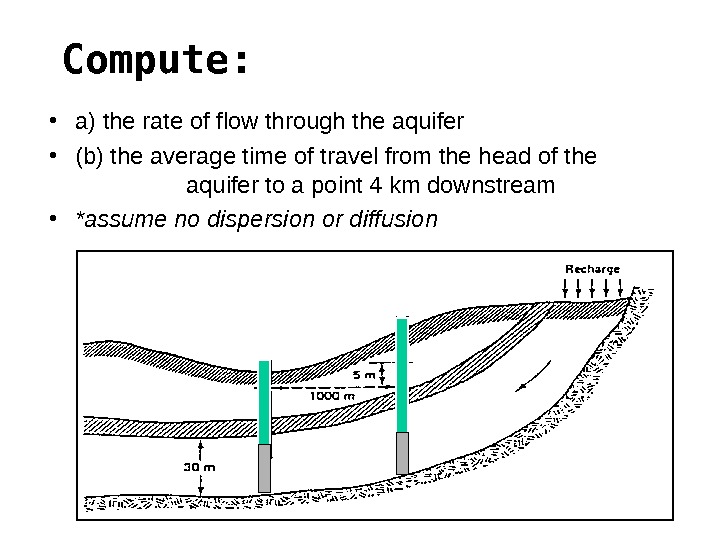
 Compute: • a) the rate of flow through the aquifer • (b) the average time of travel from the head of the aquifer to a point 4 km downstream • *assume no dispersion or diffusion
Compute: • a) the rate of flow through the aquifer • (b) the average time of travel from the head of the aquifer to a point 4 km downstream • *assume no dispersion or diffusion
 The solution • Cross-Sectional area= 30(5)(1000) = 15 x 10 4 m 2 • Hydraulic gradient = (55 -50)/1000 = 5 x 10 -3 • Rate of Flow for K = 50 m/day Q = (50 m/day) (75 x 10 1 m 2 ) = 37, 500 m 3 /day • Darcy Velocity: V = Q/A = (37, 500 m 3 /day) / (15 x 10 4 m 2 ) = 0. 25 m/day
The solution • Cross-Sectional area= 30(5)(1000) = 15 x 10 4 m 2 • Hydraulic gradient = (55 -50)/1000 = 5 x 10 -3 • Rate of Flow for K = 50 m/day Q = (50 m/day) (75 x 10 1 m 2 ) = 37, 500 m 3 /day • Darcy Velocity: V = Q/A = (37, 500 m 3 /day) / (15 x 10 4 m 2 ) = 0. 25 m/day
 And • Seepage Velocity: Vs = V/n = (0. 25) / (0. 2) = 1. 25 m/day (about 4. 1 ft/day) • Time to travel 4 km downstream: T = 4(1000 m) / (1. 25 m/day) = 3200 days or 8. 77 years • This example shows that water moves very slowly underground.
And • Seepage Velocity: Vs = V/n = (0. 25) / (0. 2) = 1. 25 m/day (about 4. 1 ft/day) • Time to travel 4 km downstream: T = 4(1000 m) / (1. 25 m/day) = 3200 days or 8. 77 years • This example shows that water moves very slowly underground.
 Limitations of the Darcian Approach 1. For Reynold’s Number, Re, > 10 or where the flow is turbulent, as in the immediate vicinity of pumped wells. 2. Where water flows through extremely fine-grained materials (colloidal clay)
Limitations of the Darcian Approach 1. For Reynold’s Number, Re, > 10 or where the flow is turbulent, as in the immediate vicinity of pumped wells. 2. Where water flows through extremely fine-grained materials (colloidal clay)
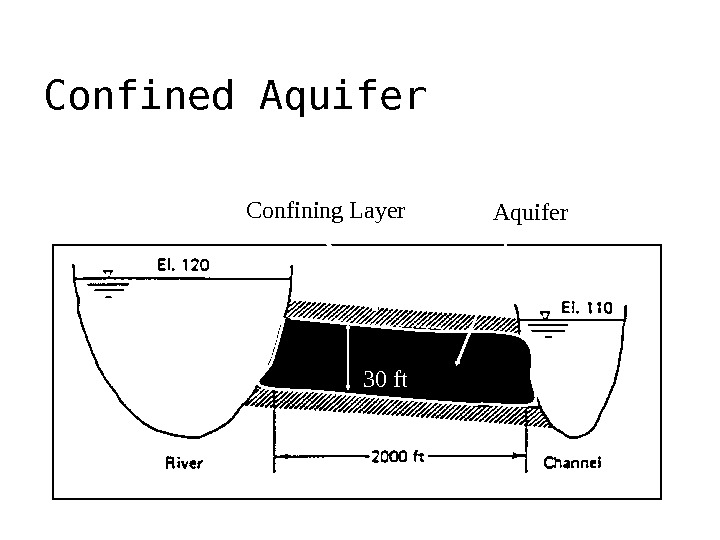
 Darcy’s Law: Example 2 • A channel runs almost parallel to a river, and they are 2000 ft apart. • The water level in the river is at an elevation of 120 ft and 110 ft in the channel. • A pervious formation averaging 30 ft thick and with K of 0. 25 ft/hr joins them. • Determine the rate of seepage or flow from the river to the channel.
Darcy’s Law: Example 2 • A channel runs almost parallel to a river, and they are 2000 ft apart. • The water level in the river is at an elevation of 120 ft and 110 ft in the channel. • A pervious formation averaging 30 ft thick and with K of 0. 25 ft/hr joins them. • Determine the rate of seepage or flow from the river to the channel.
 Confined Aquifer Confining Layer Aquifer 30 ft
Confined Aquifer Confining Layer Aquifer 30 ft
 Example 2 • Consider a 1 -ft length of river (and channel). Q = KA [(h 1 – h 2 ) / L] • Where: A = (30 x 1) = 30 ft 2 K = (0. 25 ft/hr) (24 hr/day) = 6 ft/day • Therefore, Q = [6 (30) (120 – 110)] / 2000 = 0. 9 ft 3 /day/ft length = 0. 9 ft 2 /day
Example 2 • Consider a 1 -ft length of river (and channel). Q = KA [(h 1 – h 2 ) / L] • Where: A = (30 x 1) = 30 ft 2 K = (0. 25 ft/hr) (24 hr/day) = 6 ft/day • Therefore, Q = [6 (30) (120 – 110)] / 2000 = 0. 9 ft 3 /day/ft length = 0. 9 ft 2 /day
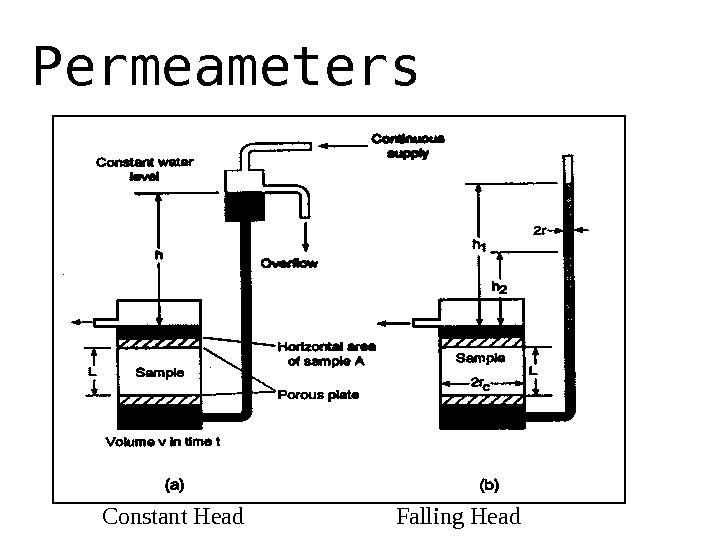
 Permeameters Constant Head Falling Head
Permeameters Constant Head Falling Head
 Constant head Permeameter • Apply Darcy’s Law to find K: V/t = Q = KA(h/L) or: K = (VL) / (Ath) • Where: V = volume flowing in time t A = cross-sectional area of the sample L = length of sample h = constant head • t = time of flow
Constant head Permeameter • Apply Darcy’s Law to find K: V/t = Q = KA(h/L) or: K = (VL) / (Ath) • Where: V = volume flowing in time t A = cross-sectional area of the sample L = length of sample h = constant head • t = time of flow

