Данная программа связана с отработкой умений вычислять несобственные

Данная программа связана с отработкой умений вычислять несобственные интегралы

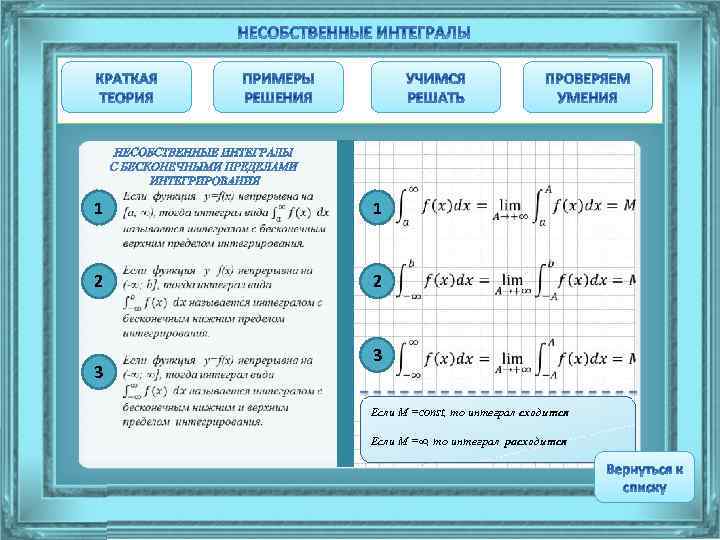
1 1 2 2 3 3 Если М =const, то интеграл сходится Если М =∞, то интеграл расходится

1 2 3 Если функция y=f(x) непрерывна на (a; b], при x=a функция f(x) терпит бесконечный разрыв. Если функция y=f(x) непрерывна на [a; b), при x=b функция f(x) терпит бесконечный разрыв. Если функция y=f(x) непрерывна на [a; b] за исключением т. c є [a; b], в которой функция терпит безграничный разрыв. 1 ( ] a 2 b x [ ) a x b 3 [ ○ ] c a b x

Пример 1. Решение Шаг 1. Установим, что данный интеграл является интегралом с бесконечным верхним пределом

Пример 1. Решение Шаг 1. = Шаг 2. Найдем первообразную от подинтегральной функции

Пример 1. Решение Шаг 1. = Шаг 2. = Шаг 3. Воспользуемся формулой Ньютона-Лейбница и вычислим предел

Пример 1. Решение Шаг 1. = Шаг 2. = Шаг 3.

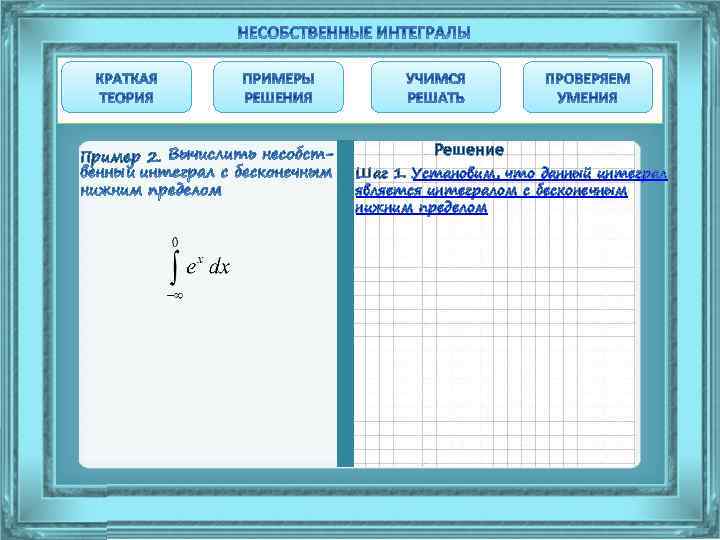
Пример 2. Решение Шаг 1. Установим, что данный интеграл является интегралом с бесконечным нижним пределом

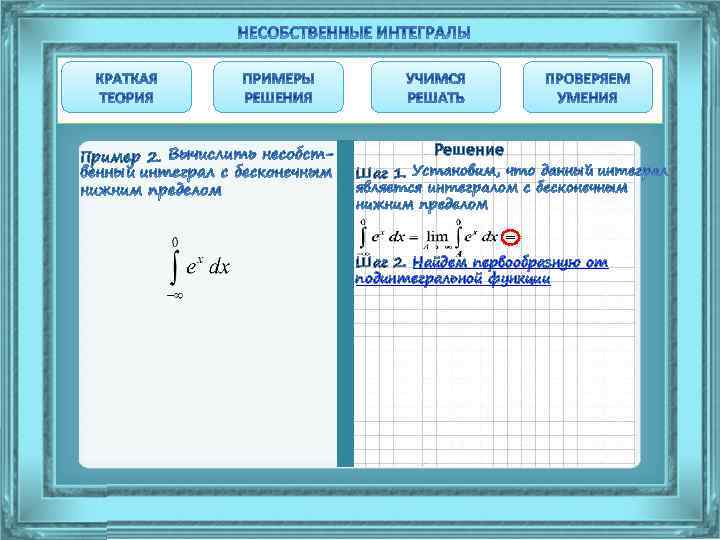
Пример 2. Решение Шаг 1. = Шаг 2. Найдем первообразную от подинтегральной функции

Пример 2. Решение Шаг 1. = Шаг 2. = Шаг 3. Воспользуемся формулой Ньютона-Лейбница и вычислим предел

Пример 2. Решение Шаг 1. = Шаг 2. = Шаг 3.

Пример 3. Решение Шаг 1. Установим, что данный интеграл является интегралом с бесконечным верхним и нижним пределом

Пример 3. Решение Шаг 1. = Шаг 2. Найдем первообразную от подинтегральной функции

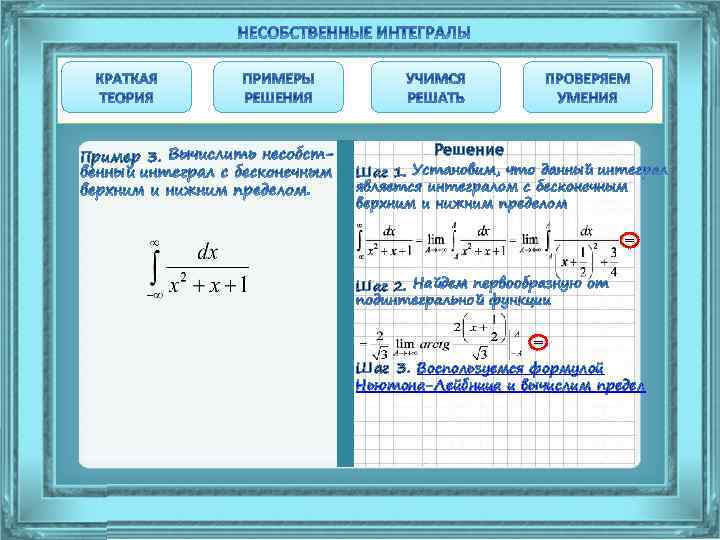
Пример 3. Решение Шаг 1. = Шаг 2. = Шаг 3. Воспользуемся формулой Ньютона-Лейбница и вычислим предел

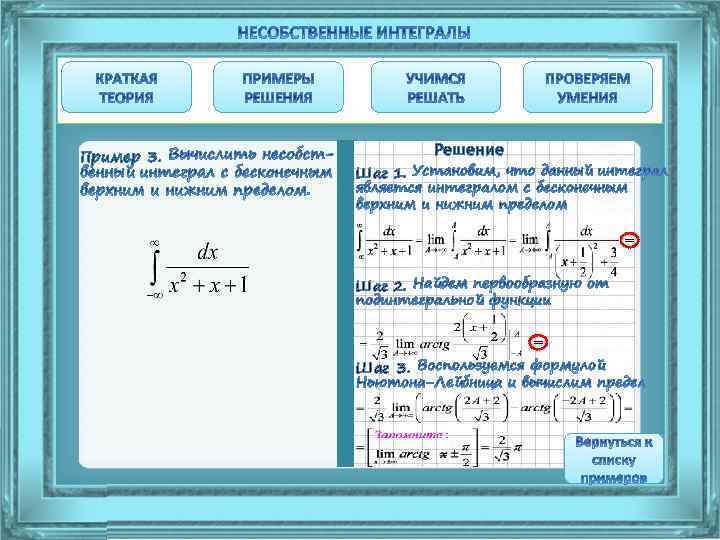
Пример 3. Решение Шаг 1. = Шаг 2. = Шаг 3.

Пример 4. Решение Шаг 1. Установим, что данный интеграл является интегралом от неограниченной функции (х=3 – точка разрыва)

Пример 4. Решение Шаг 1. [ ) 0 3 x Шаг 2. Найдем первообразную от подинтегральной функции =

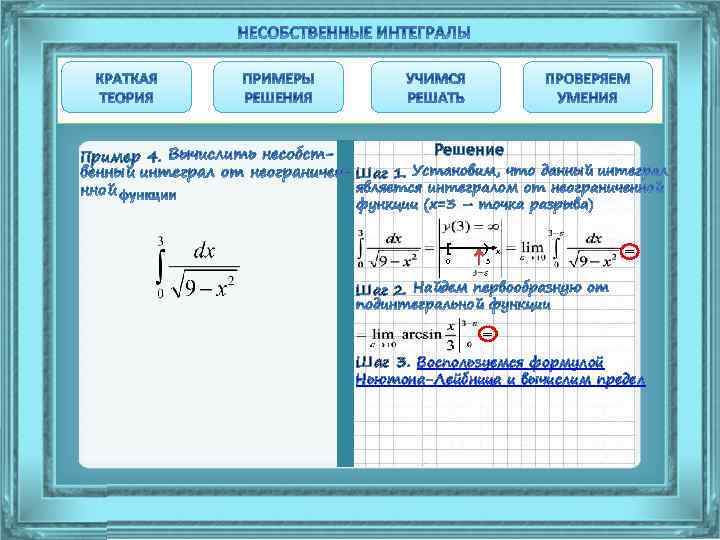
Пример 4. Решение Шаг 1. [ Шаг 2. ) 0 3 x = = Шаг 3. Воспользуемся формулой Ньютона-Лейбница и вычислим предел

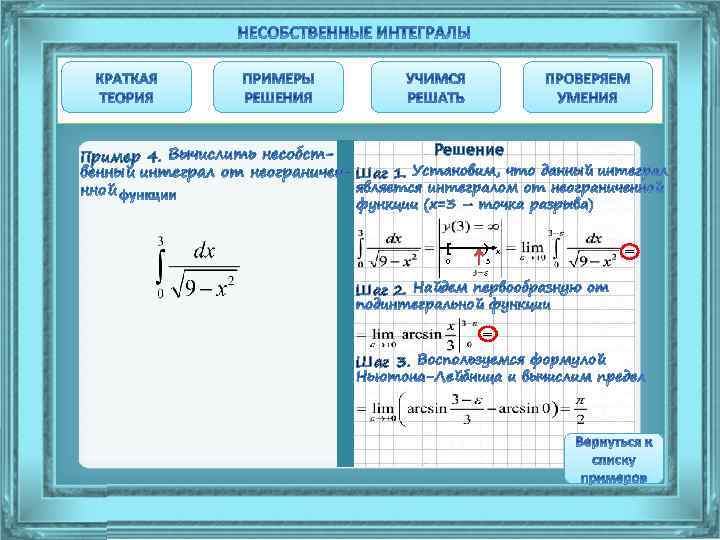
Пример 4. Решение Шаг 1. [ Шаг 2. ) 0 3 = Шаг 3. x =

Пример 5. Решение Шаг 1. Установим, что данный интеграл является интегралом от неограниченной функции (х=0 – точка разрыва)

Пример 5. Решение Шаг 1. 0 [ ) 1 x Шаг 2. Найдем первообразную от подинтегральной функции =

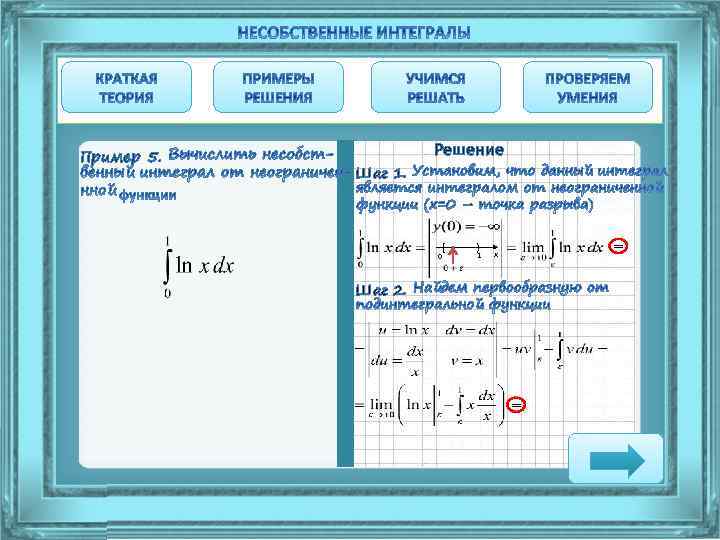
Пример 5. Решение Шаг 1. 0 Шаг 2. [ ) 1 = x =

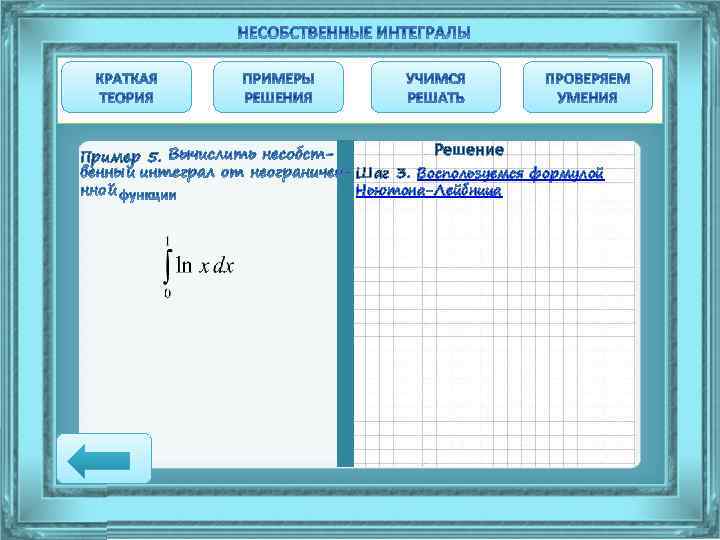
Пример 5. Решение Шаг 3. Воспользуемся формулой Ньютона-Лейбница

Пример 5. Шаг 3. Решение =

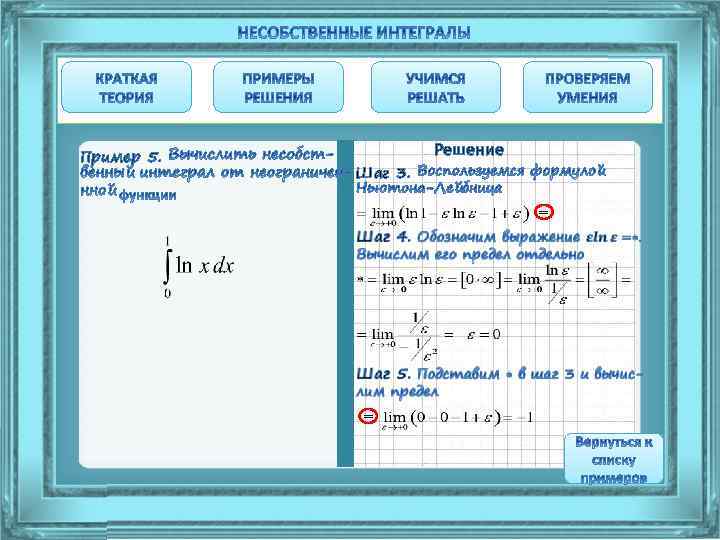
Пример 5. Шаг 3. Решение = =

Пример 6. Решение Шаг 1. Установим, что данный интеграл является интегралом от неограниченной функции (х=4 – точка разрыва)

Пример 6. Решение Шаг 1. [ ○ ] 4 2 6 x = Шаг 2. Найдем первообразную от подинтегральной функции

Пример 6. Решение Шаг 1. [ ○ ] 4 2 6 x = Шаг 2. =

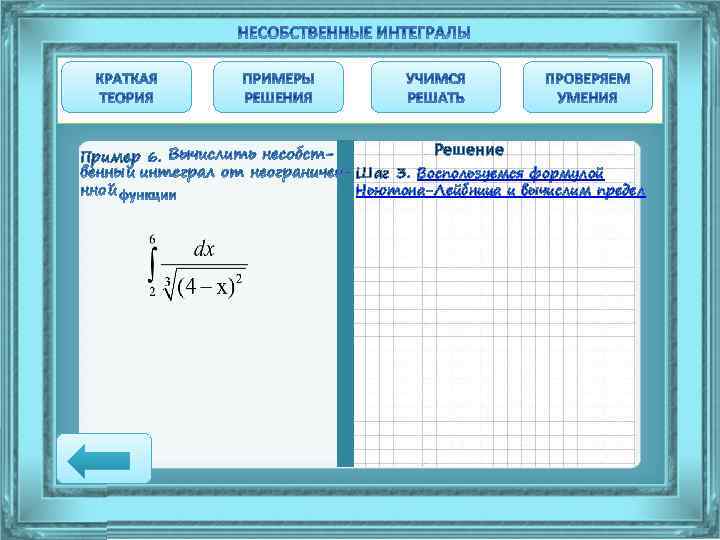
Пример 6. Решение Шаг 3. Воспользуемся формулой Ньютона-Лейбница и вычислим предел

Пример 6. Шаг 3. Решение

Пример 1. Каждый следующий шаг решения интеграла появляется при нажатии на предыдущий шаг Решение

Пример 1. Решение

Пример 2. Каждый следующий шаг решения интеграла появляется при нажатии на предыдущий шаг Решение

Пример 2. Решение

Пример 3. Каждый следующий шаг решения интеграла появляется при нажатии на предыдущий шаг Решение

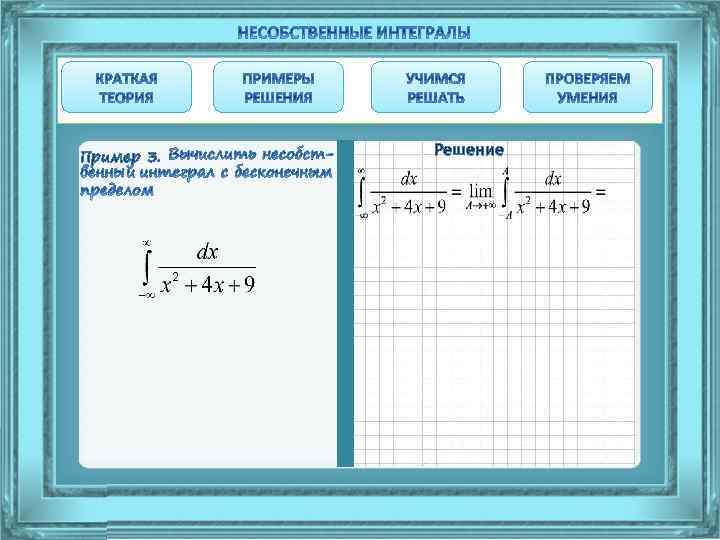
Пример 3. Решение

Пример 4. Каждый следующий шаг решения интеграла появляется при нажатии на предыдущий шаг Решение

Пример 4. Решение X -1 2 t 0 15

Решение Пример 4. X ( ] 15 x 2 t 0 -1 0 15

Пример 5. Каждый следующий шаг решения интеграла появляется при нажатии на предыдущий шаг Решение

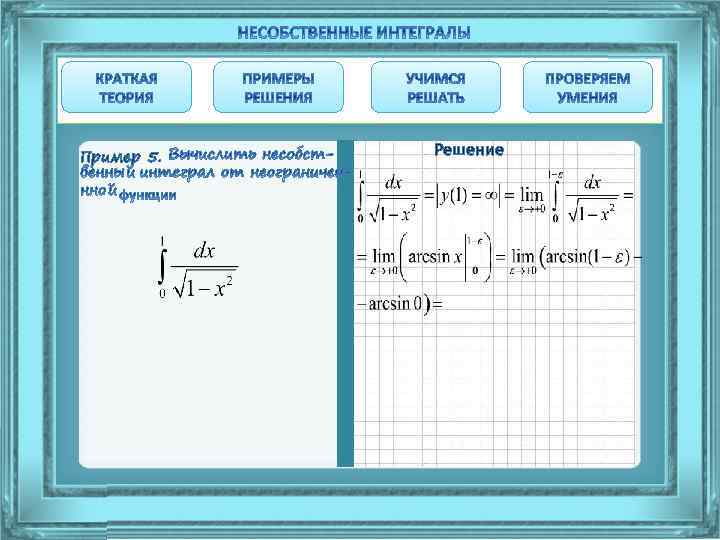
Пример 5. Решение

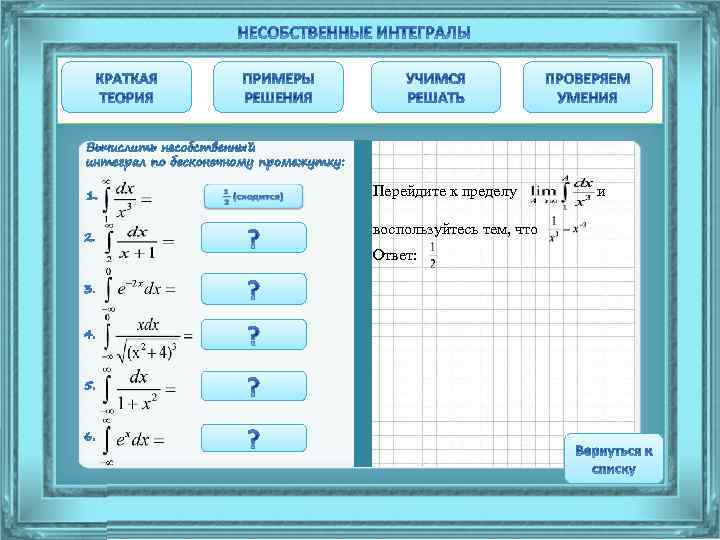
Перейдите к пределу воспользуйтесь тем, что Ответ: и

Перейдите к пределу и воспользуйтесь тем, что Ответ:

Перейдите к пределу и сделайте замену Ответ:

Перейдите к пределу и воспользуйтесь тем, что Ответ:

Перейдите к пределу и сделайте замену Ответ:

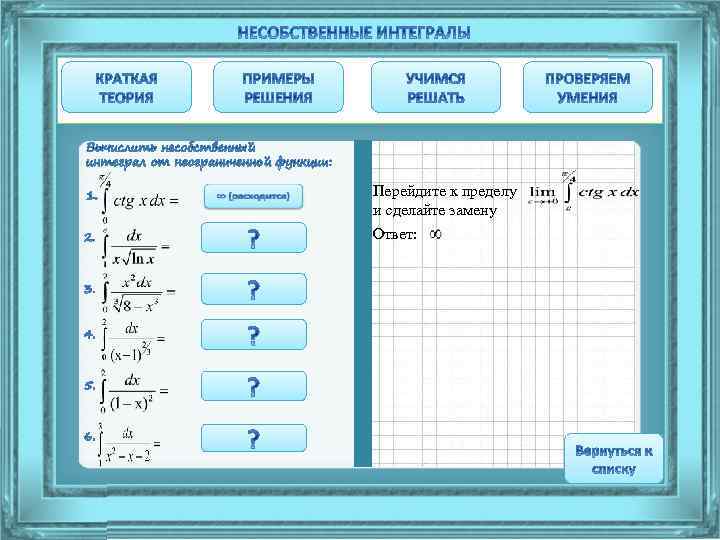
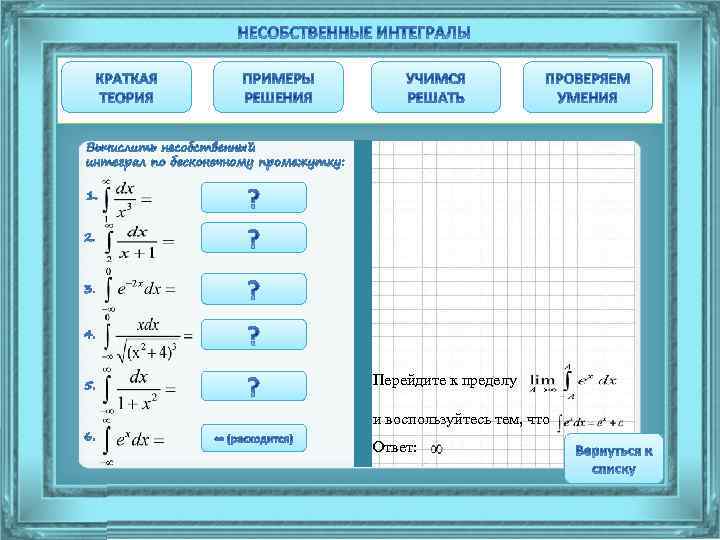
Перейдите к пределу и воспользуйтесь тем, что Ответ:

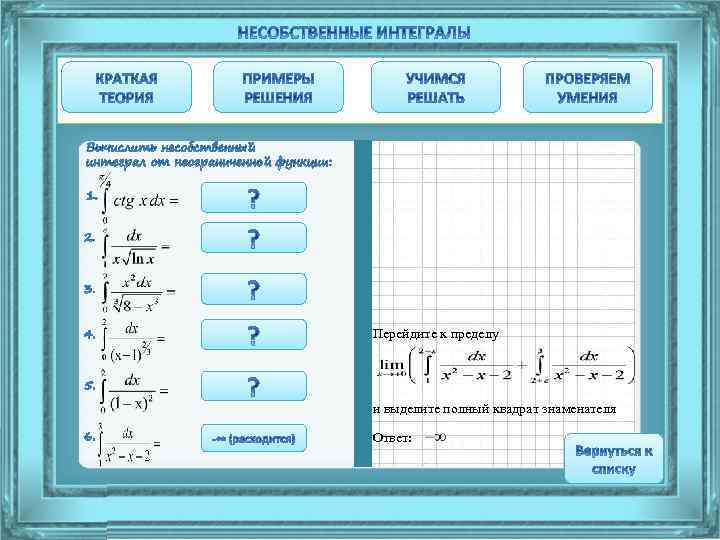
Перейдите к пределу и выделите полный квадрат знаменателя Ответ:

Пример 6. Каждый следующий шаг решения интеграла появляется при нажатии на предыдущий шаг Решение

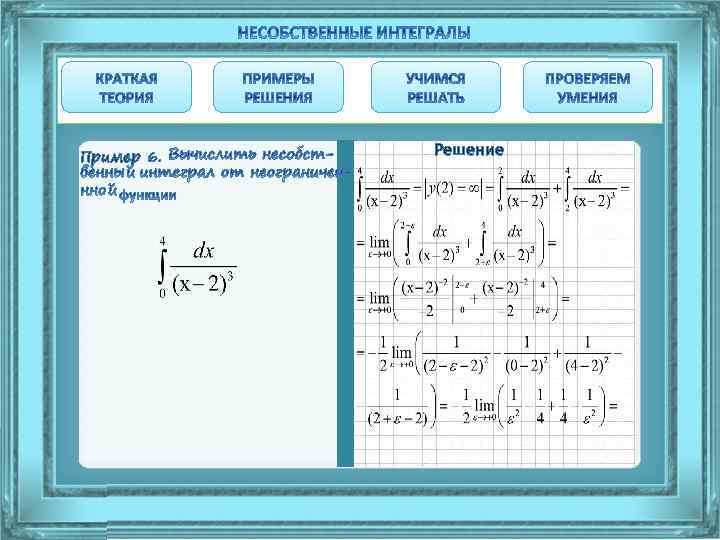
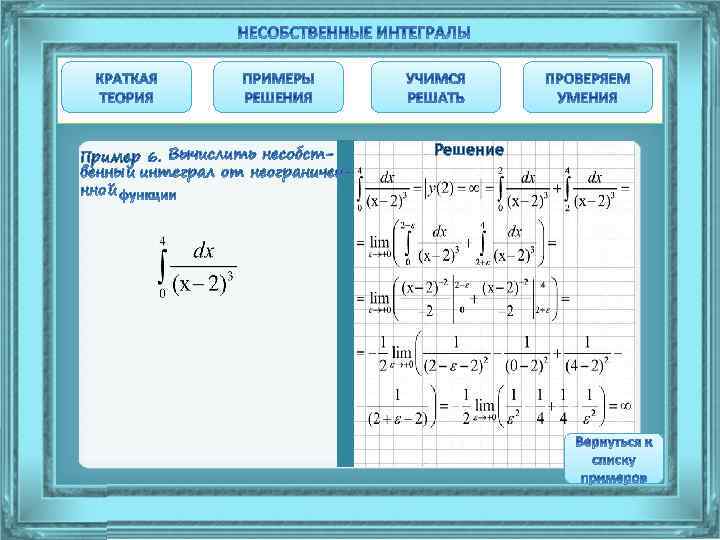
Пример 6. Решение

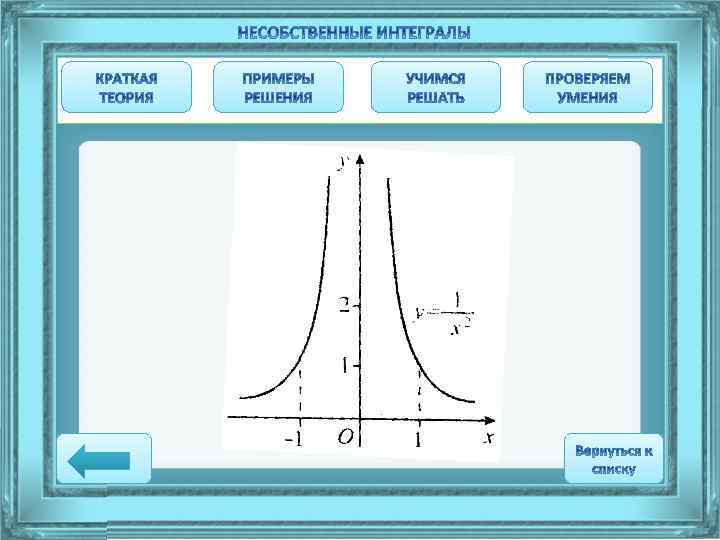
Доказать, что: а) площадь области, расположенная между кривой и прямыми х=± 1, конечная и равняется 6; б) площадь области, расположенная между кривой и прямыми х=± 1, бесконечная. , осью абсцисс

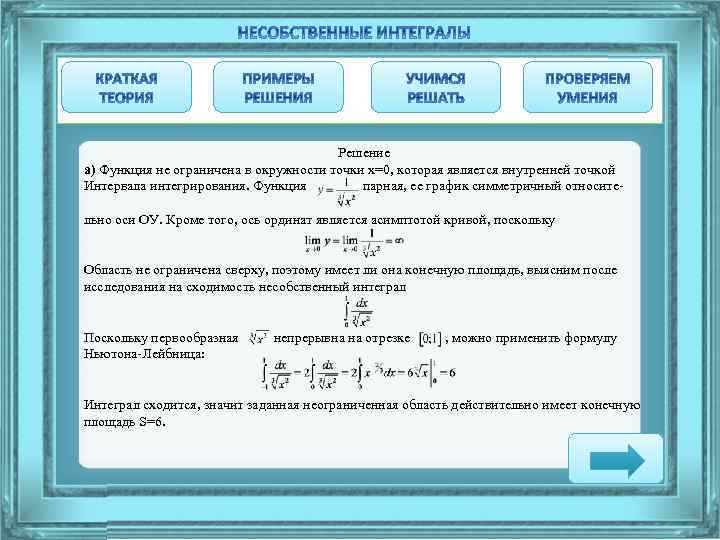
Решение а) Функция не ограничена в окружности точки х=0, которая является внутренней точкой Интервала интегрирования. Функция парная, ее график симметричный относительно оси ОУ. Кроме того, ось ординат является асимптотой кривой, поскольку Область не ограничена сверху, поэтому имеет ли она конечную площадь, выясним после исследования на сходимость несобственный интеграл Поскольку первообразная Ньютона-Лейбница: непрерывна на отрезке , можно применить формулу Интеграл сходится, значит заданная неограниченная область действительно имеет конечную площадь S=6.

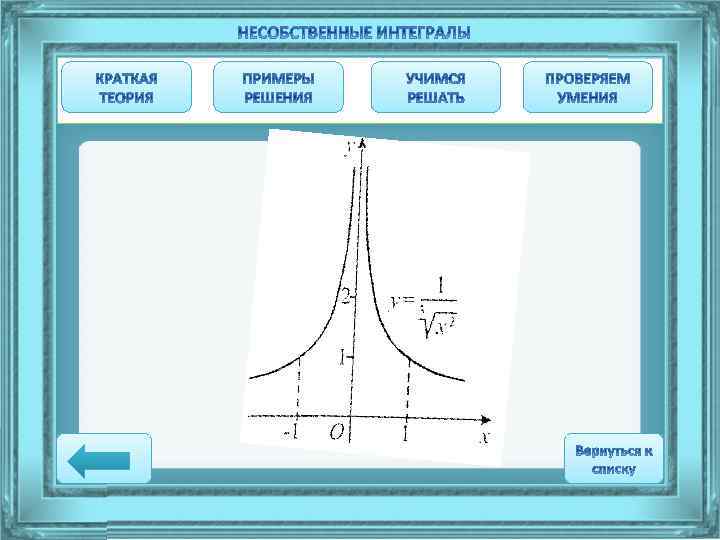
Решение б) Функция парная и имеет точку разрыва х=0. Ее асимптотой также служит ось ординат. Как и в случае а), имеем область, ограниченную снизу осью абсцисс, с боков прямыми х=-1 и х=1 и не ограниченную сверху. Но в отличии от случая а) эта область не имеет конечной площади, поскольку т. е. интеграл расходится. Если бы мы «не заметили» особенность данной функции в точке х=0 и формально вычислили заданный интеграл как определенный, то получили бы неправильный результат: Действительно, интеграл от положительной функции не может быть отрицательным.