7568dbae6cae2c784b3ab77f12d65c8a.ppt
- Количество слайдов: 134

Daniel Webster College, Nashua, NH, March 24, 2012 July 10— 15, 2010 ~ Asilomar Conference Grounds ~ Pacific Grove, California, USA RAREFACTION EFFECTS IN HYPERSONIC AERODYNAMICS Vladimir V. Riabov, Ph. D. Professor of Computer Science & Math Rivier College Nashua, New Hampshire vriabov@rivier. edu http: //www. rivier. edu/faculty/vriabov/

Topics for Discussing • Experimental and numerical simulation of hypersonic rarefied-gas flows in air, nitrogen, carbon dioxide, argon, and helium; • Study of aerodynamics of simple-shape bodies (plate, wedge, cone, disk, sphere, side-by-side plates and cylinders, torus, and rotating cylinder); • Analysis of the role of various similarity parameters in low-density aerothermodynamics; • Evaluation of various rarefaction and kinetic effects on drag, lift, pitching moment, and heat transfer. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 2

Techniques & Tools • Experiments in hypersonic vacuum chamber; • Direct Simulation Monte-Carlo technique: – DS 2 G (version 3. 2) code of Dr. Graeme A. Bird – Knudsen numbers Kn∞, L from 0. 01 to 10 – (Reynolds numbers Re 0, L from 200 to 0. 2); • Solutions of the Navier-Stokes 2 -D equations; • Solutions of the Thin-Viscous-Shock-Layer equations; • Similarity principles applied to hypersonic rarefied-gas flows. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 3
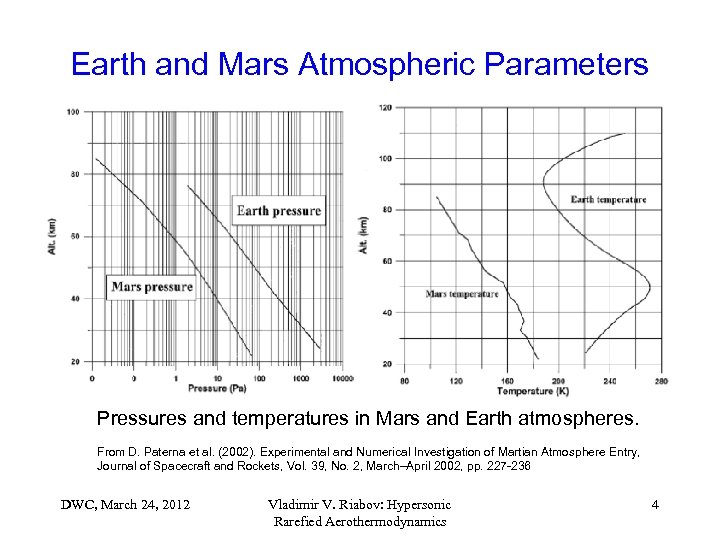
Earth and Mars Atmospheric Parameters Pressures and temperatures in Mars and Earth atmospheres. From D. Paterna et al. (2002). Experimental and Numerical Investigation of Martian Atmosphere Entry, Journal of Spacecraft and Rockets, Vol. 39, No. 2, March–April 2002, pp. 227 -236 DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 4
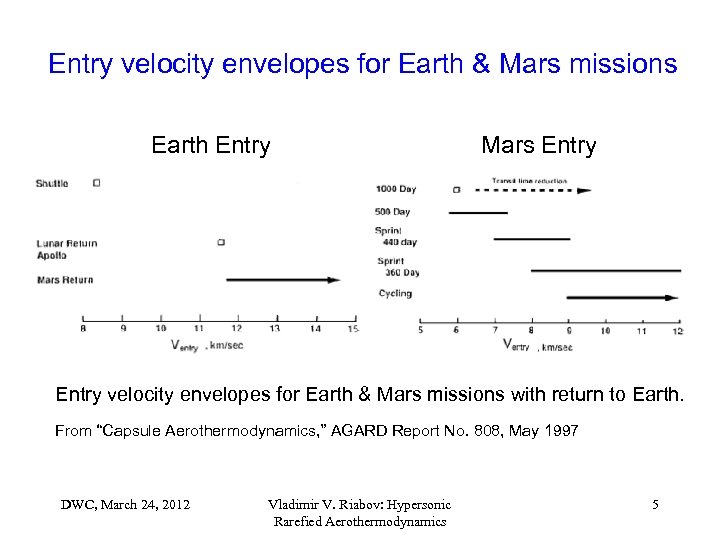
Entry velocity envelopes for Earth & Mars missions Earth Entry Mars Entry velocity envelopes for Earth & Mars missions with return to Earth. From “Capsule Aerothermodynamics, ” AGARD Report No. 808, May 1997 DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 5
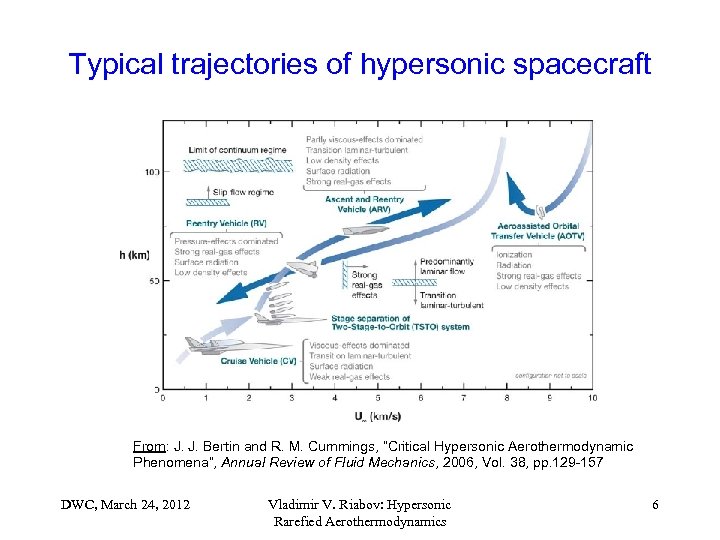
Typical trajectories of hypersonic spacecraft From: J. J. Bertin and R. M. Cummings, “Critical Hypersonic Aerothermodynamic Phenomena”, Annual Review of Fluid Mechanics, 2006, Vol. 38, pp. 129 -157 DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 6

European Space Agency Projects DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 7

Flow regimes and thermochemical phenomena in the stagnation region of a 30. 5 cm radius sphere flying in air. From R. N. Gupta et al. NASA-RP-1232, 1990. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 8
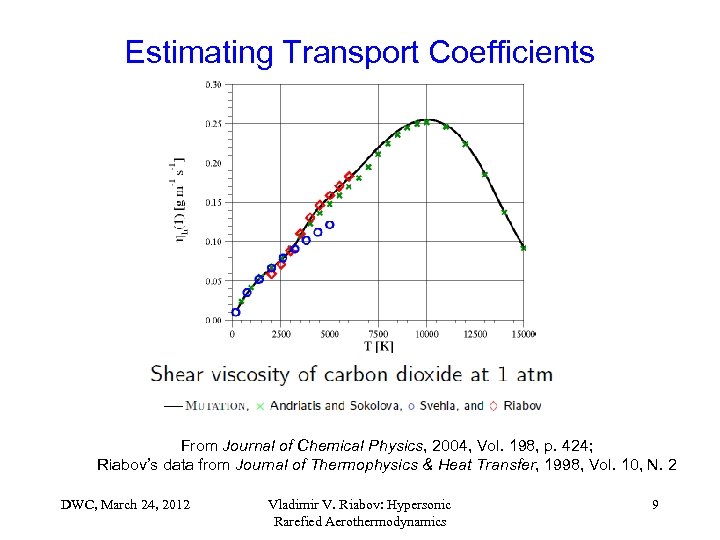
Estimating Transport Coefficients From Journal of Chemical Physics, 2004, Vol. 198, p. 424; Riabov’s data from Journal of Thermophysics & Heat Transfer, 1998, Vol. 10, N. 2 DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 9

Similarity parameters • Knudsen number, Kn , L = λ /L • or equivalent Reynolds number, Re 0, L = ρ U∞L/μ(T 0) ~ 1/Kn , L • Interaction parameter χ for pressure approximation: • Viscous-interaction parameter V for skin-friction approximation: • • • Temperature factor, tw = Tw/T 0 Specific heat ratio, γ = cp/cv Viscosity parameter, n: μ Tn Upstream Mach number, M∞ Hypersonic similarity parameter, K∞ = M∞ × sinθ Spin rate, W = ΩD/2 U∞ DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 10
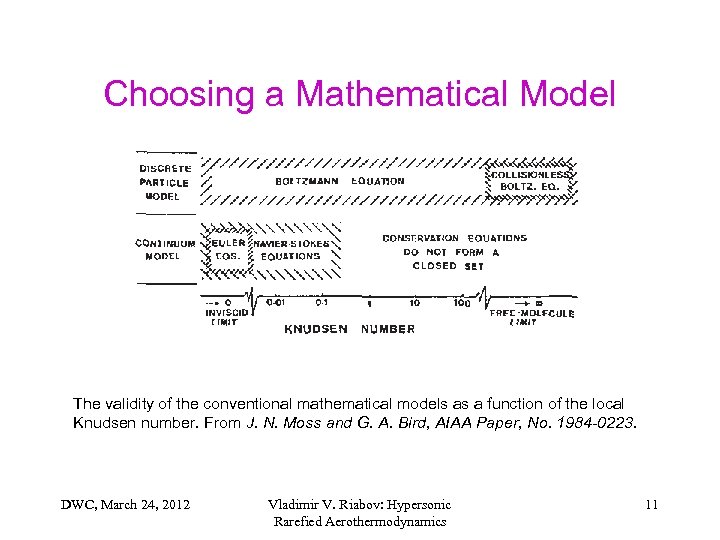
Choosing a Mathematical Model The validity of the conventional mathematical models as a function of the local Knudsen number. From J. N. Moss and G. A. Bird, AIAA Paper, No. 1984 -0223. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 11
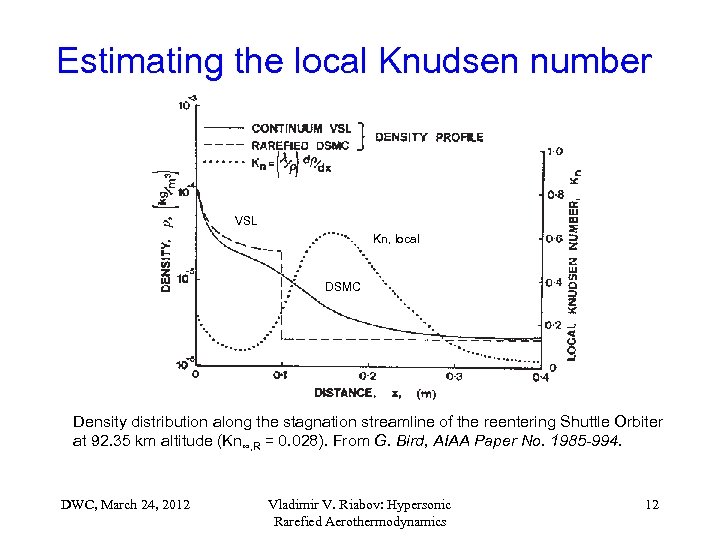
Estimating the local Knudsen number VSL Kn, local DSMC Density distribution along the stagnation streamline of the reentering Shuttle Orbiter at 92. 35 km altitude (Kn∞, R = 0. 028). From G. Bird, AIAA Paper No. 1985 -994. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 12

Modeling of Hypersonic Flight Regimes in Wind Tunnels The catalogs “Wind Tunnels in the Western and Eastern Hemispheres” (U. S. Congress, 2008) profiles 65 hypersonic wind tunnels used for aeronautical testing. The countries represented in the catalogs include those in America (Brazil [1] and USA [12]), Asia (Australia [7], China [5], and Japan [4]), Europe (Belgium [2], France [5], Germany [2], Italy [1], the Netherlands [1], and Russia [21]), and the Middle East and Central and South Asia (India [3] and Israel [1]). Aerial view of the Thermal Protection Laboratory at NASA Ames, California DWC, March 24, 2012 Nozzle and test chamber of the H 2 K hypersonic wind tunnel, Germany Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics T-117 hypersonic wind tunnel, Ts. AGI, Moscow region, Russia 13

DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 14

Research on Hypersonics in Ts. AGI (Moscow region, Russia) DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 15
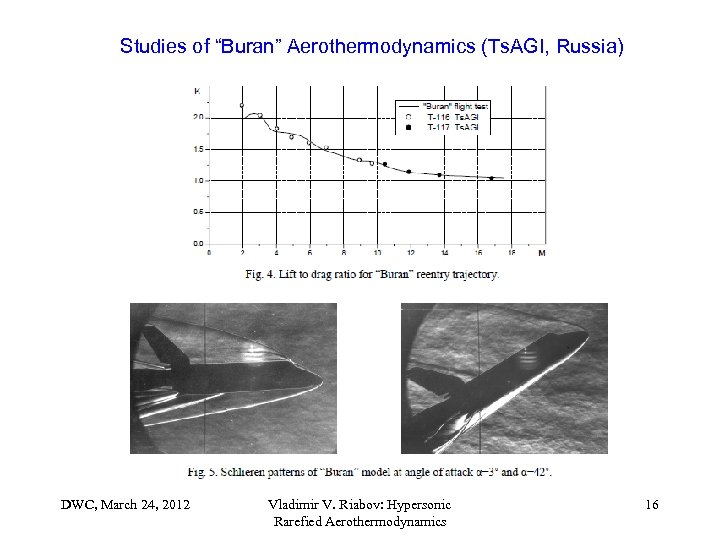
Studies of “Buran” Aerothermodynamics (Ts. AGI, Russia) DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 16

International Cooperation: Space Projects British HOTOL and Mriya-225 Launcher tested in T-128 Ts. AGI Wind Tunnel, Moscow region, Russia DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 17

Ground based testing in Germany DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 18

Ground based testing in Germany DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 19
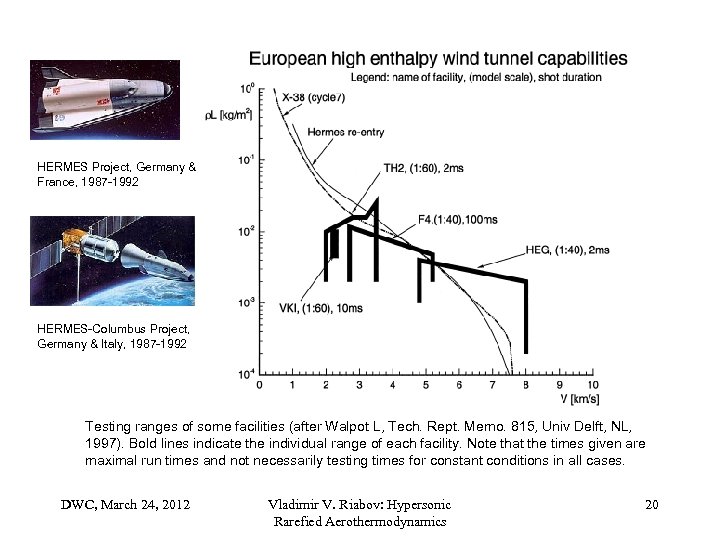
HERMES Project, Germany & France, 1987 -1992 HERMES-Columbus Project, Germany & Italy, 1987 -1992 Testing ranges of some facilities (after Walpot L, Tech. Rept. Memo. 815, Univ Delft, NL, 1997). Bold lines indicate the individual range of each facility. Note that the times given are maximal run times and not necessarily testing times for constant conditions in all cases. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 20

The International Space Station Mission The ISS effort involves more than 100, 000 people in space agencies and at 500 contractor facilities in 37 U. S. states and in 16 countries. http: //www. boeing. com/defense-space/spacestation/gallery/ DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 21

The International Space Station Mission World ISS Team: USA, Canada, ESA (Belgium, Denmark, France, Germany, Italy, the Netherlands, Norway, Spain, Sweden, Switzerland, the United Kingdom), Japan, Russia, Italy, and Brazil http: //science. nationalgeographic. com/science/space-exploration/ DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 22
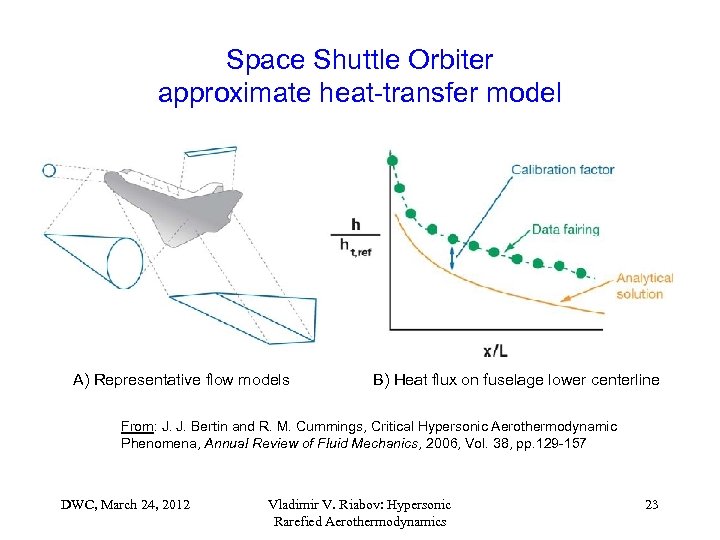
Space Shuttle Orbiter approximate heat-transfer model A) Representative flow models B) Heat flux on fuselage lower centerline From: J. J. Bertin and R. M. Cummings, Critical Hypersonic Aerothermodynamic Phenomena, Annual Review of Fluid Mechanics, 2006, Vol. 38, pp. 129 -157 DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 23

Applications of Underexpanded Jets in Hypersonic Aerothermodynamic Research • A method of underexpanded hypersonic viscous jets has been developed to acquire experimental aerodynamic data for simpleshape bodies (plates, wedges, cones, spheres and cylinders) in the transitional regime between free-molecular and continuum regimes. • The kinetic, viscous, and rotational nonequilibrium quantum processes in the jets of He, Ar, N 2, and CO 2 under various experimental conditions have been analyzed by asymptotic methods and numerical techniques. • Fundamental laws for the characteristics and similarity parameters are revealed. • In the case of hypersonic stabilization, the Reynolds number Re 0 (or Knudsen number Kn) and temperature factor are the main similarity parameters. • The acquired data could be used for research and prediction of aerodynamic characteristics of hypersonic vehicles during their flights under atmospheric conditions of Earth, Mars, and other planets. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 24

Underexpanded Hypersonic Viscous Jet DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 25
![Inviscid Gas Jets • Ashkenas and Sherman [1964], Muntz [1970], and Gusev and Klimova Inviscid Gas Jets • Ashkenas and Sherman [1964], Muntz [1970], and Gusev and Klimova](https://present5.com/presentation/7568dbae6cae2c784b3ab77f12d65c8a/image-26.jpg)
Inviscid Gas Jets • Ashkenas and Sherman [1964], Muntz [1970], and Gusev and Klimova [1968] analyzed the structure of inviscid gas jets in detail. • The flow inside the jet bounded by shock waves becomes significantly overexpanded relative to the outside pressure pa. • If the pressure pj » pa , the overexpansion value is determined by the location of the front shock wave ("Mach disk") on the jet axis rd [Muntz, 1970]: rd/rj = 1. 34 (ps/pa)½ DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics (1) 26
![The asymptotic solution [Riabov, 1995] of the Euler equations in a hypersonic jet region: The asymptotic solution [Riabov, 1995] of the Euler equations in a hypersonic jet region:](https://present5.com/presentation/7568dbae6cae2c784b3ab77f12d65c8a/image-27.jpg)
The asymptotic solution [Riabov, 1995] of the Euler equations in a hypersonic jet region: u'=u 0+u 1×z 2(γ-1) +. . . ; z=r*'(φ)/r' (2) u 0=[(γ+1)/(γ-1)]½ (7) v'=v 1×z 2(γ-1)×d/dφ[lnr*'(φ)] +. . . (3) u 1=-θ 1/(γ 2 -1)½ (8) ρ'=1/u 0×z 2 +. . . (4) v 1=-2θ 1/{u 0[1 -2(γ-1)]} (9) ×z 2(γ-1) +. . . (5) θ 1=1/(u 0)(γ-1) (10) p'=θ 1/u 0×z 2γ +. . . (6) r*'(φ)= r*(φ)/rj (11) T'=θ 1 DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 27
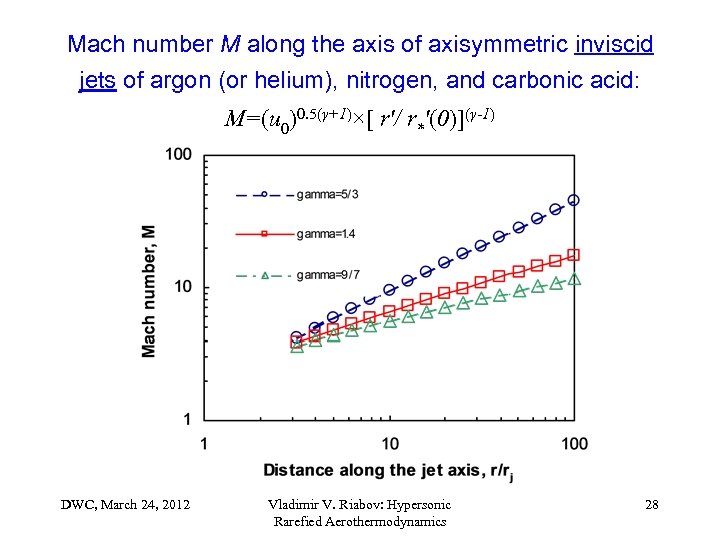
Mach number M along the axis of axisymmetric inviscid jets of argon (or helium), nitrogen, and carbonic acid: M=(u 0)0. 5(γ+1)×[ r'/ r*'(0)](γ-1) DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 28

The asymptotic solution of the Navier-Stokes equations in a hypersonic viscous gas jet region [from V. V. Riabov, Journal of Aircraft, 1995, Vol. 32, No. 3]: W=(u' - u 0)/ξλ, λ=2ω(γ-1) (13) W=-Θ/[u 0(γ-1)] - u 0Θn/(r 02 X) (18) V=v'/ξλ (14) Θ={γ(γ+1)(1 -n)ω/(r 02 X) +θ 11 -n(r 0 X)(1 -ω)/ω}1/(1 -n) (19) Θ=T'/ξλ (15) r 02(∂V/∂X-V/X)-(γu 0 X)-1∂(r 02Θ)/∂φ +nu 0Θn-1(2 X 2)-1∂Θ/∂φ = 0 (20) X=r*'(0)/(r'ξω) (16) r 0 =r*'(φ)/[r*'(0)] (21) ξ=4/[3 Rej r*'(0)], ξ → 0 (17) DWC, March 24, 2012 r' = O(Rejω), ω = 1/[2γ-1 -2(γ-1)n] Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 29
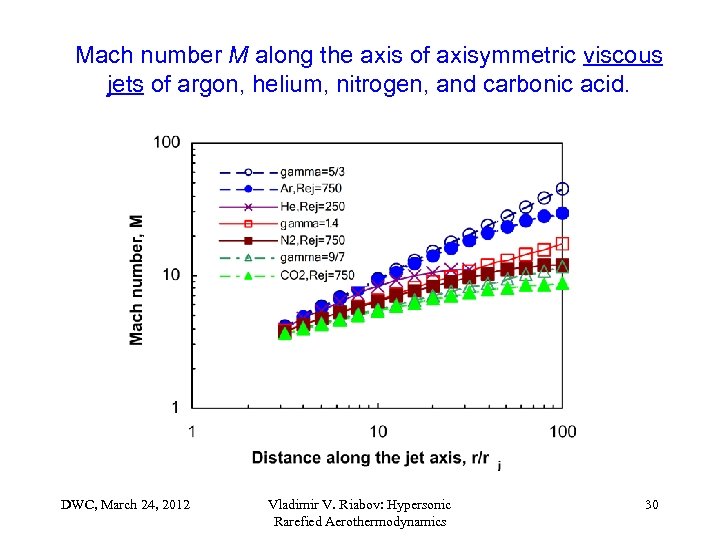
Mach number M along the axis of axisymmetric viscous jets of argon, helium, nitrogen, and carbonic acid. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 30
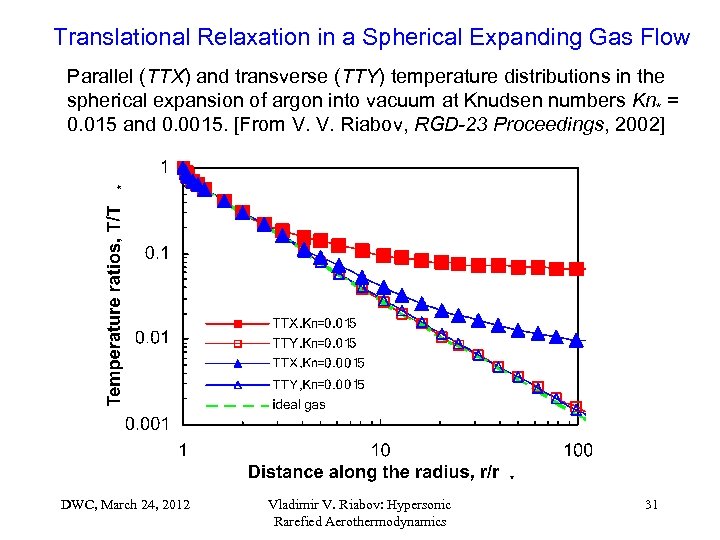
Translational Relaxation in a Spherical Expanding Gas Flow Parallel (TTX) and transverse (TTY) temperature distributions in the spherical expansion of argon into vacuum at Knudsen numbers Kn* = 0. 015 and 0. 0015. [From V. V. Riabov, RGD-23 Proceedings, 2002] DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 31
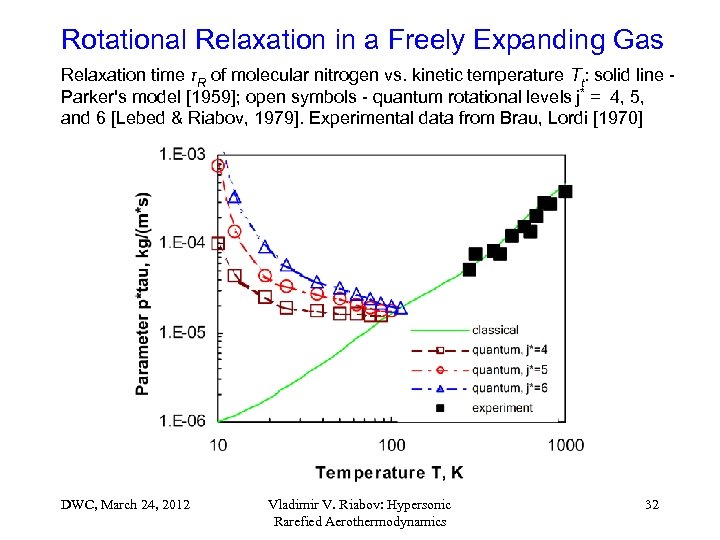
Rotational Relaxation in a Freely Expanding Gas Relaxation time τR of molecular nitrogen vs. kinetic temperature Tt: solid line - Parker's model [1959]; open symbols - quantum rotational levels j* = 4, 5, and 6 [Lebed & Riabov, 1979]. Experimental data from Brau, Lordi [1970] DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 32
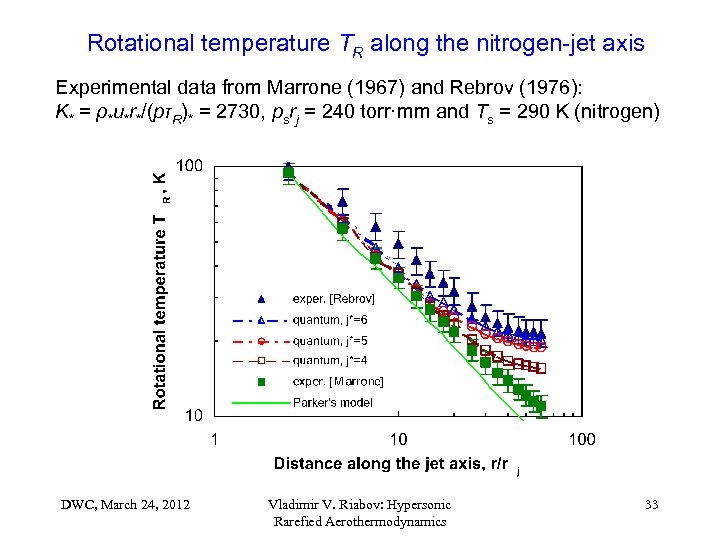
Rotational temperature TR along the nitrogen-jet axis Experimental data from Marrone (1967) and Rebrov (1976): K* = ρ*u*r*/(pτR)* = 2730, psrj = 240 torr·mm and Ts = 290 K (nitrogen) DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 33
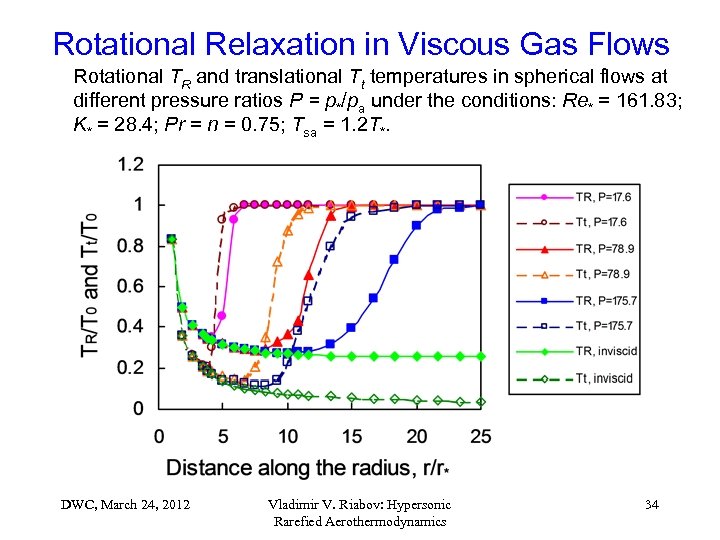
Rotational Relaxation in Viscous Gas Flows Rotational TR and translational Tt temperatures in spherical flows at different pressure ratios P = p*/pa under the conditions: Re* = 161. 83; K* = 28. 4; Pr = n = 0. 75; Tsa = 1. 2 T*. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 34

Similarity Criteria for Aerodynamic Experiments in Underexpanded Jets The interaction parameter χ for pressure approximation: χ=M∞ 2/[0. 5(γ-1)Re 0)]0. 5 The viscous-interaction parameter V for skin-friction approximation: V=1/[0. 5(γ-1)Re 0)]0. 5 The value of the Reynolds number, Re 0, can be easily changed by relocation of a model along the jet axis at different distances (x) from a nozzle exit (Re 0 ~ x--2). Other criteria: Mach number M∞, temperature factor tw; specific heat ratio γ; and parameter n in the viscosity coefficient approximation µ ~ Tn. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 35
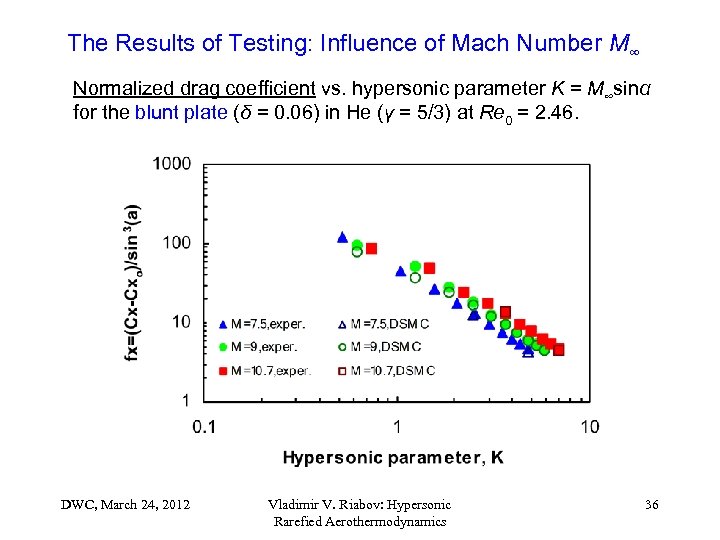
The Results of Testing: Influence of Mach Number M∞ Normalized drag coefficient vs. hypersonic parameter K = M∞sinα for the blunt plate (δ = 0. 06) in He (γ = 5/3) at Re 0 = 2. 46. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 36
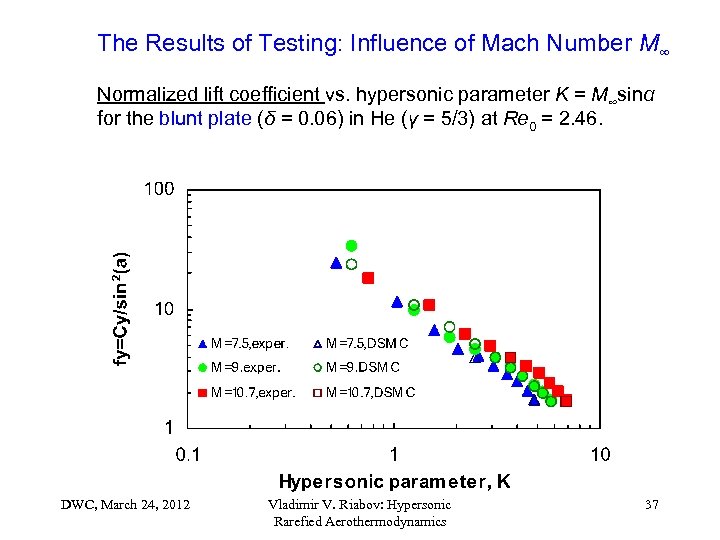
The Results of Testing: Influence of Mach Number M∞ Normalized lift coefficient vs. hypersonic parameter K = M∞sinα for the blunt plate (δ = 0. 06) in He (γ = 5/3) at Re 0 = 2. 46. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 37
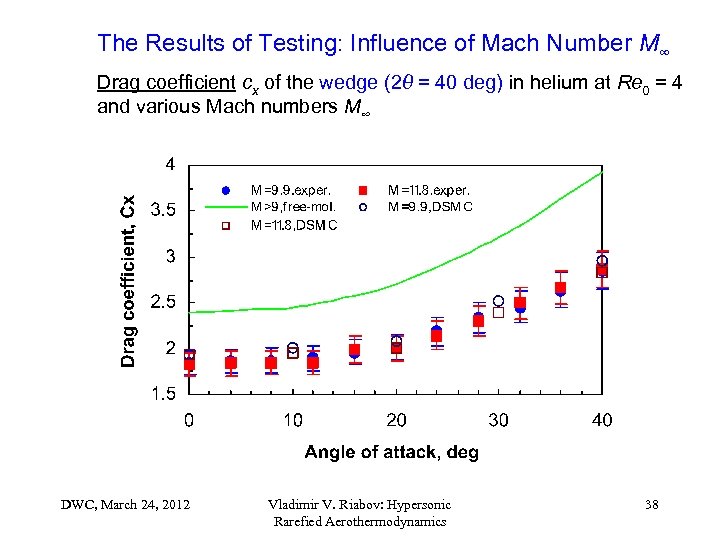
The Results of Testing: Influence of Mach Number M∞ Drag coefficient cx of the wedge (2θ = 40 deg) in helium at Re 0 = 4 and various Mach numbers M∞ DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 38
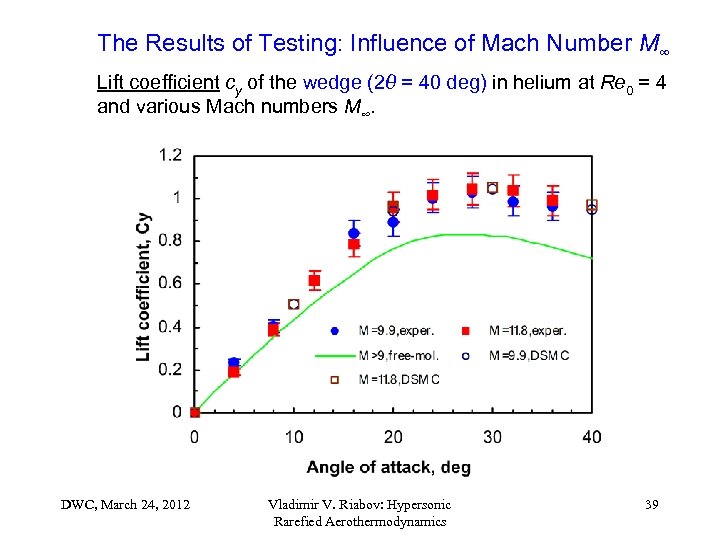
The Results of Testing: Influence of Mach Number M∞ Lift coefficient cy of the wedge (2θ = 40 deg) in helium at Re 0 = 4 and various Mach numbers M∞. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 39
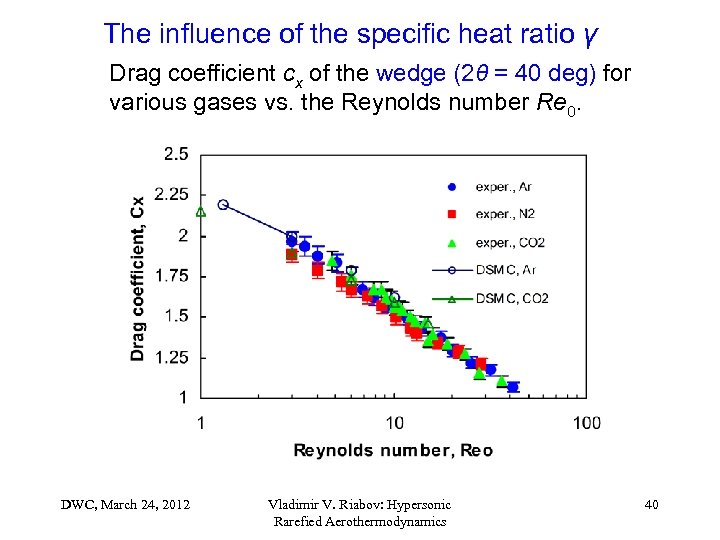
The influence of the specific heat ratio γ Drag coefficient cx of the wedge (2θ = 40 deg) for various gases vs. the Reynolds number Re 0. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 40
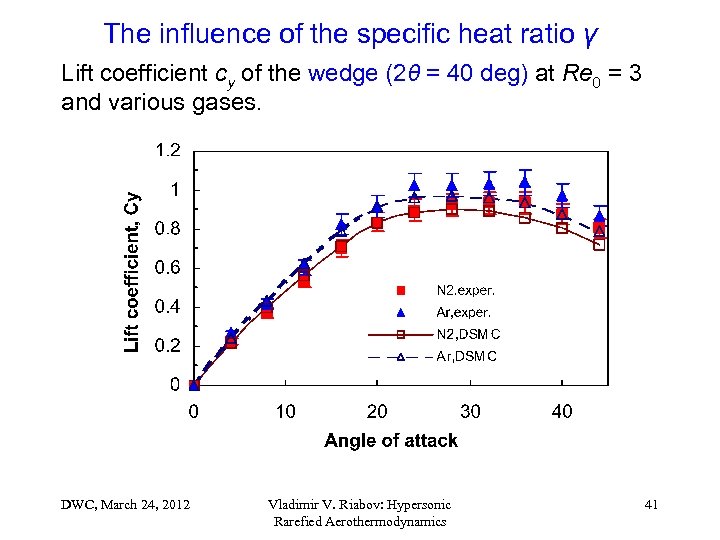
The influence of the specific heat ratio γ Lift coefficient cy of the wedge (2θ = 40 deg) at Re 0 = 3 and various gases. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 41
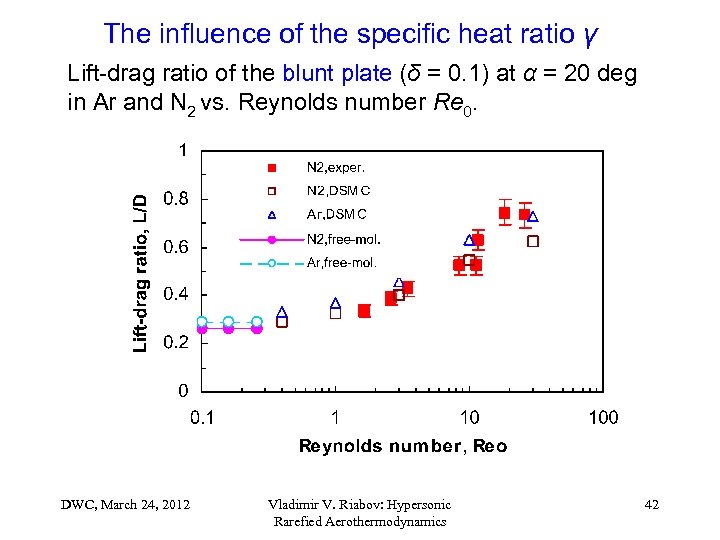
The influence of the specific heat ratio γ Lift-drag ratio of the blunt plate (δ = 0. 1) at α = 20 deg in Ar and N 2 vs. Reynolds number Re 0. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 42
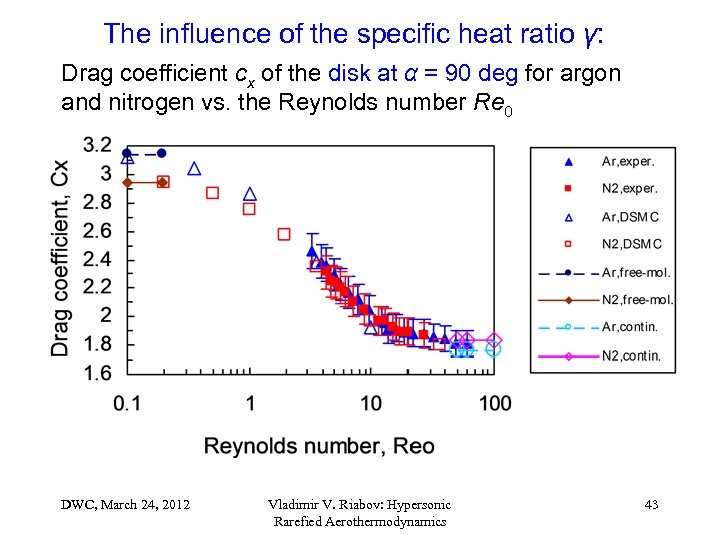
The influence of the specific heat ratio γ: Drag coefficient cx of the disk at α = 90 deg for argon and nitrogen vs. the Reynolds number Re 0 DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 43
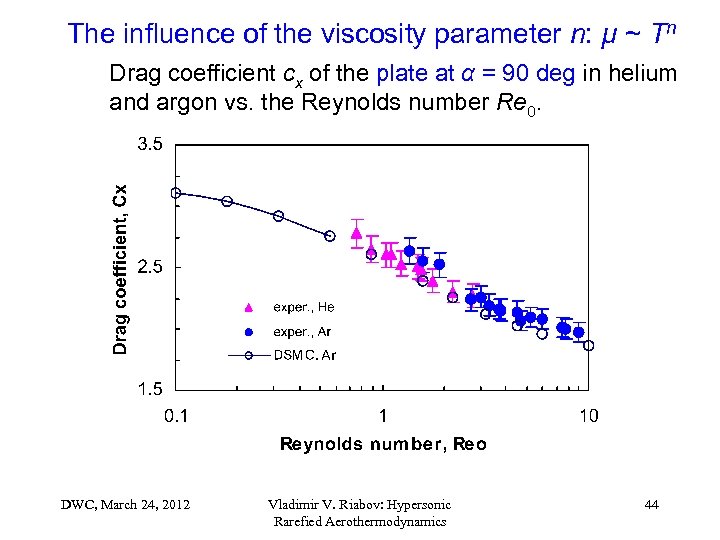
The influence of the viscosity parameter n: µ ~ Tn Drag coefficient cx of the plate at α = 90 deg in helium and argon vs. the Reynolds number Re 0. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 44
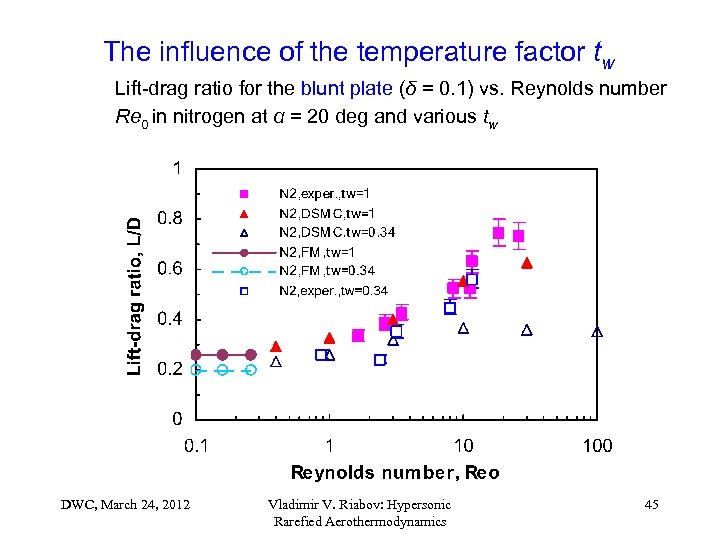
The influence of the temperature factor tw Lift-drag ratio for the blunt plate (δ = 0. 1) vs. Reynolds number Re 0 in nitrogen at α = 20 deg and various tw DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 45
![Direct Simulation Monte-Carlo (DSMC) method • The DSMC method [G. Bird, 1994] and DS Direct Simulation Monte-Carlo (DSMC) method • The DSMC method [G. Bird, 1994] and DS](https://present5.com/presentation/7568dbae6cae2c784b3ab77f12d65c8a/image-46.jpg)
Direct Simulation Monte-Carlo (DSMC) method • The DSMC method [G. Bird, 1994] and DS 2 G code (version 3. 2) [G. Bird, 1999] are used in this study; • Variable Hard Sphere (VHS) molecular collision model in air, nitrogen, carbon dioxide, helium, and argon; • Gas-surface interactions are assumed to be fully diffusive with full moment and energy accommodation; • Code validation was established [Riabov, 1998] by comparing numerical results with experimental data [Gusev et al. , 1977; Riabov, 1995] related to the simple-shape bodies; • TEST: a single plate in air flow at 0. 02 < Kn , L < 3. 2, M = 10, tw = 1; • Independence of flow profiles and aerodynamic characteristics from mesh size and number of molecules has been evaluated; • EXAMPLE: 12, 700 cells in eight zones, 139, 720 molecules; • The G. Bird’s criterion for the time step is used: 1× 10 -8 tm 1× 10 -6 s; • Ratio of the mean separation between collision partners to the local mean free path and the CTR ratio of the time step to the local mean collision time have been well under unity over flowfield; • Computing time of each variant on Intel IV PC is variable: 4 – 60 hours. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 46
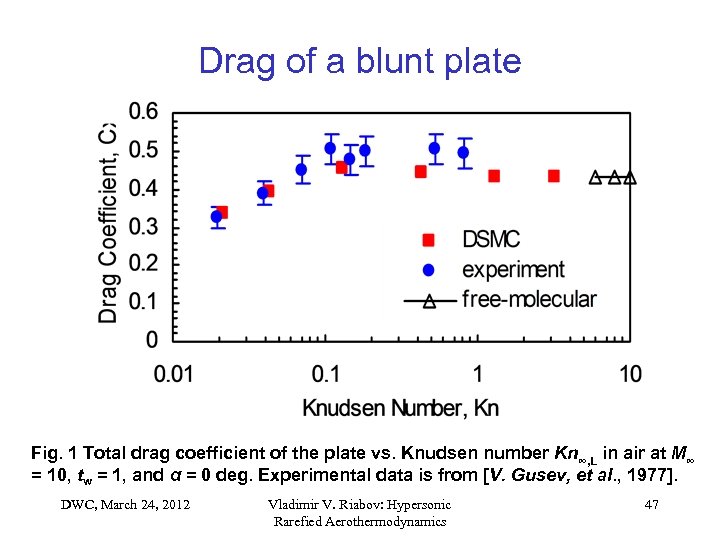
Drag of a blunt plate Fig. 1 Total drag coefficient of the plate vs. Knudsen number Kn∞, L in air at M∞ = 10, tw = 1, and α = 0 deg. Experimental data is from [V. Gusev, et al. , 1977]. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 47
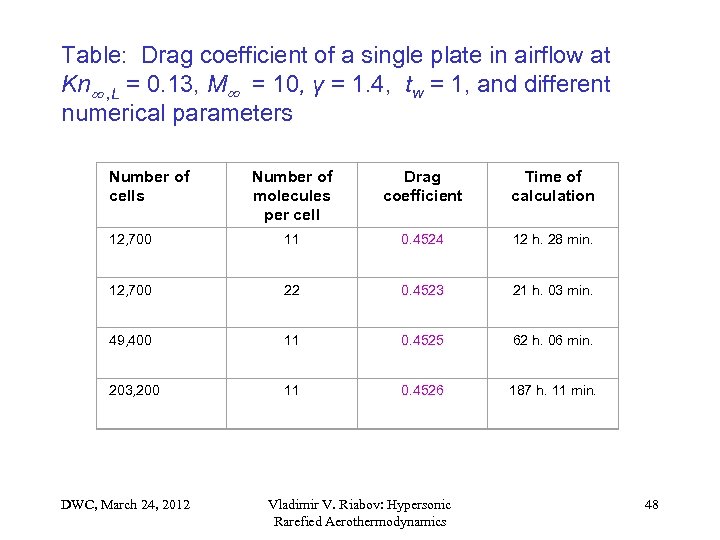
Table: Drag coefficient of a single plate in airflow at Kn , L = 0. 13, M = 10, γ = 1. 4, tw = 1, and different numerical parameters Number of cells Number of molecules per cell Drag coefficient Time of calculation 12, 700 11 0. 4524 12 h. 28 min. 12, 700 22 0. 4523 21 h. 03 min. 49, 400 11 0. 4525 62 h. 06 min. 203, 200 11 0. 4526 187 h. 11 min. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 48
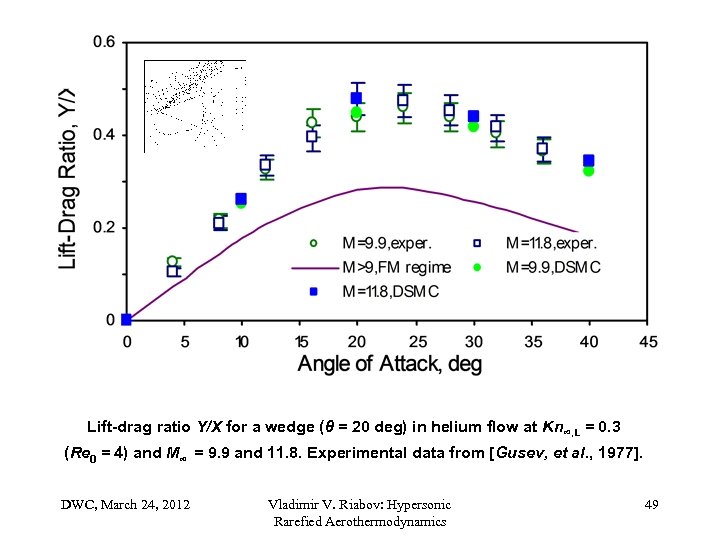
Lift-drag ratio Y/X for a wedge (θ = 20 deg) in helium flow at Kn∞, L = 0. 3 (Re 0 = 4) and M∞ = 9. 9 and 11. 8. Experimental data from [Gusev, et al. , 1977]. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 49
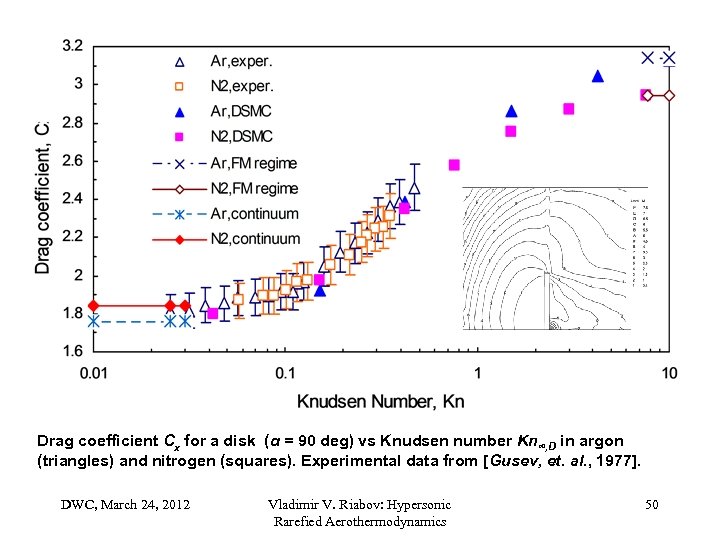
Drag coefficient Cx for a disk (α = 90 deg) vs Knudsen number Kn∞, D in argon (triangles) and nitrogen (squares). Experimental data from [Gusev, et. al. , 1977]. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 50
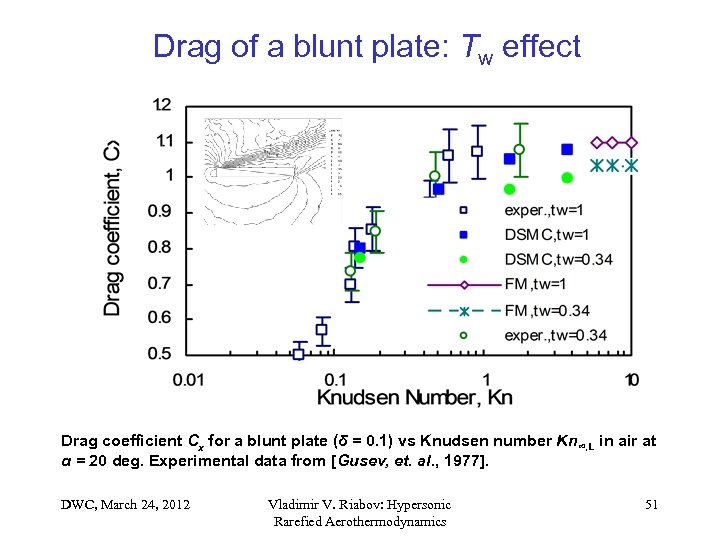
Drag of a blunt plate: Tw effect Drag coefficient Cx for a blunt plate (δ = 0. 1) vs Knudsen number Kn∞, L in air at α = 20 deg. Experimental data from [Gusev, et. al. , 1977]. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 51
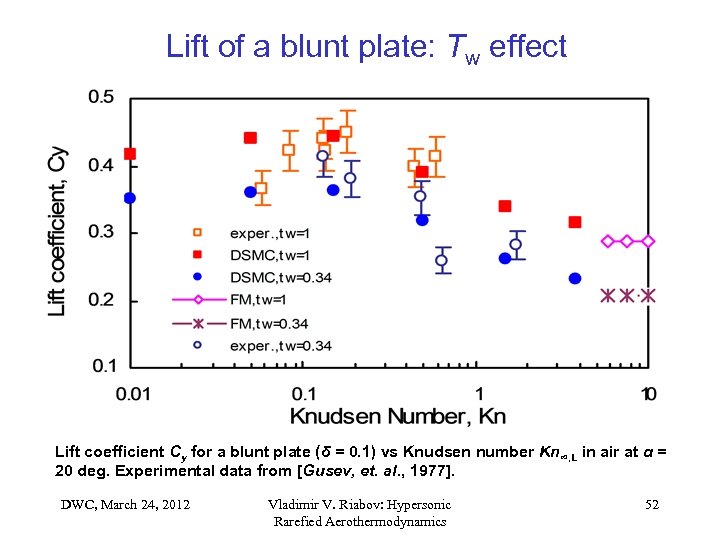
Lift of a blunt plate: Tw effect Lift coefficient Cy for a blunt plate (δ = 0. 1) vs Knudsen number Kn∞, L in air at α = 20 deg. Experimental data from [Gusev, et. al. , 1977]. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 52
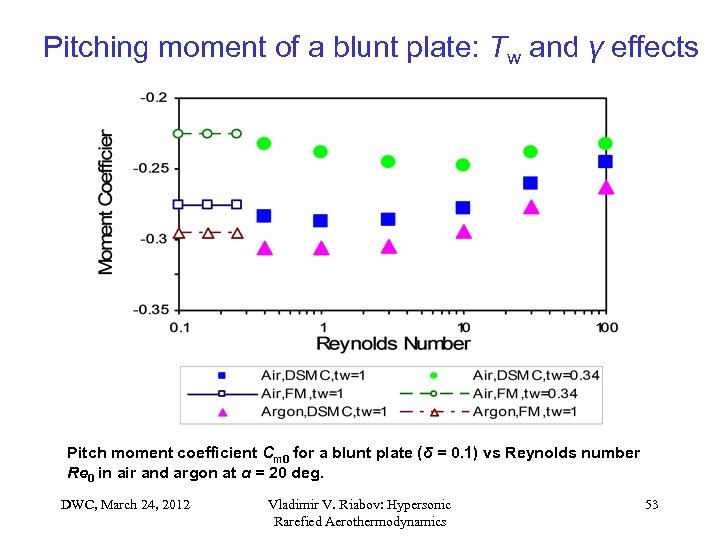
Pitching moment of a blunt plate: Tw and γ effects Pitch moment coefficient Cm 0 for a blunt plate (δ = 0. 1) vs Reynolds number Re 0 in air and argon at α = 20 deg. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 53
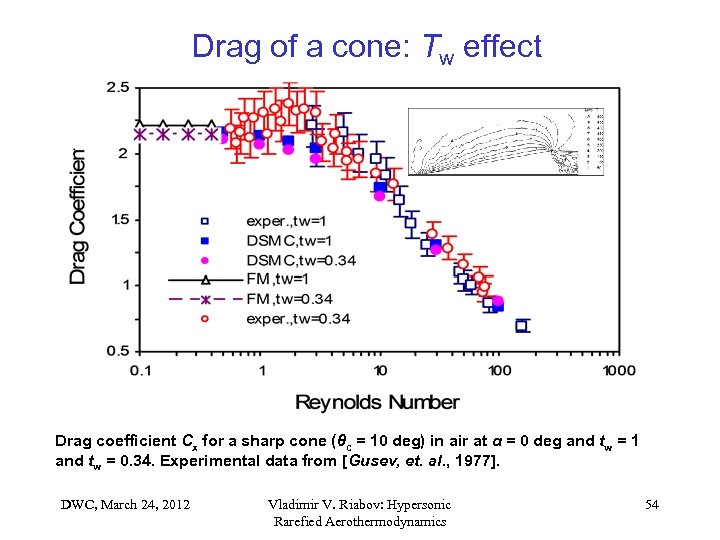
Drag of a cone: Tw effect Drag coefficient Cx for a sharp cone (θc = 10 deg) in air at α = 0 deg and tw = 1 and tw = 0. 34. Experimental data from [Gusev, et. al. , 1977]. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 54
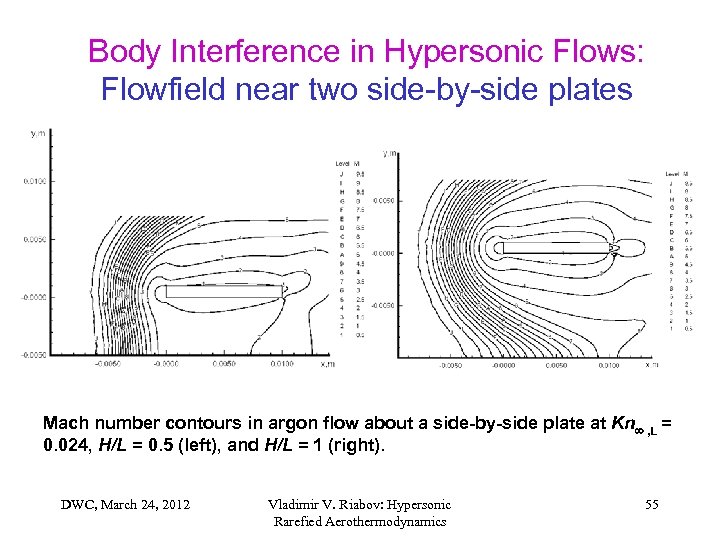
Body Interference in Hypersonic Flows: Flowfield near two side-by-side plates Mach number contours in argon flow about a side-by-side plate at Kn , L = 0. 024, H/L = 0. 5 (left), and H/L = 1 (right). DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 55
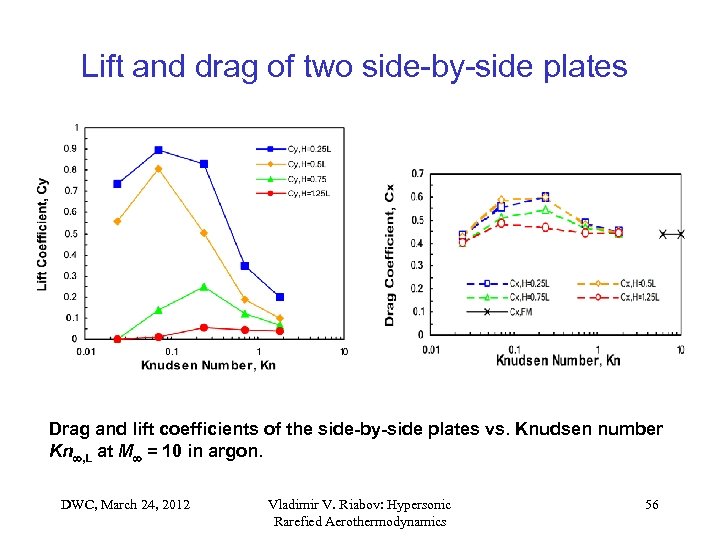
Lift and drag of two side-by-side plates Drag and lift coefficients of the side-by-side plates vs. Knudsen number Kn , L at M = 10 in argon. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 56

Aerocapture with large inflatable balloon-like decelerators (“ballutes”) Titan Explore Mission From “Ballute Missions” (http: //www 2. jpl. nasa. gov/adv_tech/ballutes/missions. htm) DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 57
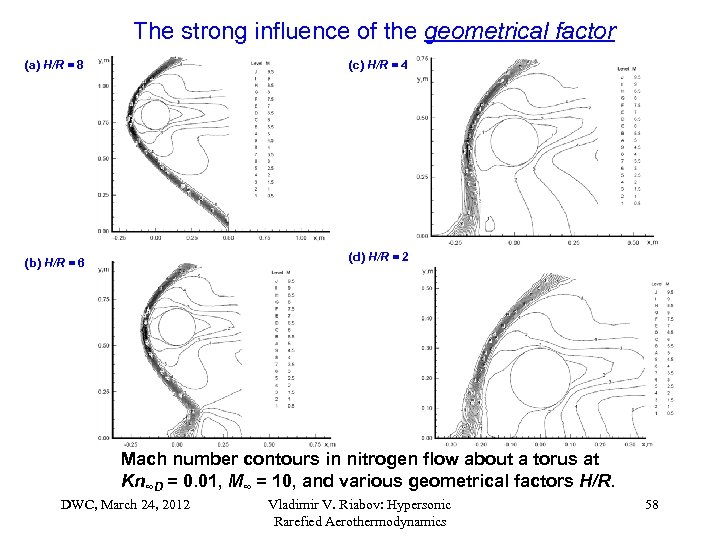
The strong influence of the geometrical factor (a) H/R = 8 (c) H/R = 4 (b) H/R = 6 (d) H/R = 2 Mach number contours in nitrogen flow about a torus at Kn∞D = 0. 01, M∞ = 10, and various geometrical factors H/R. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 58
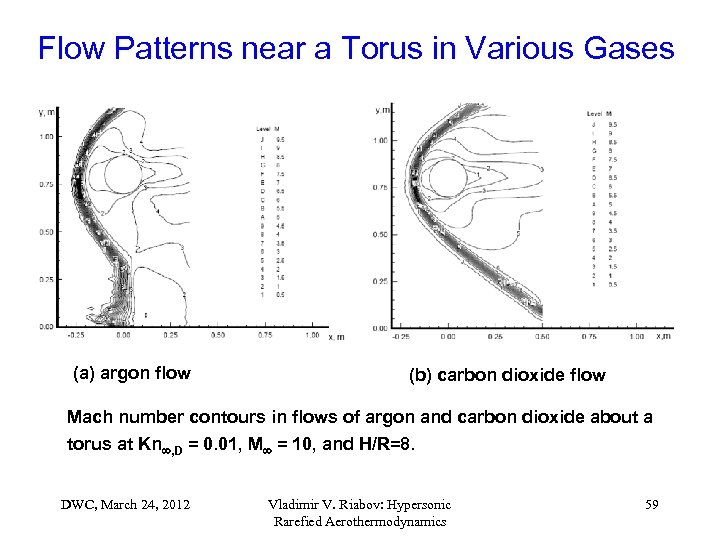
Flow Patterns near a Torus in Various Gases (a) argon flow (b) carbon dioxide flow Mach number contours in flows of argon and carbon dioxide about a torus at Kn , D = 0. 01, M = 10, and H/R=8. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 59
![Comparing Numerical Results with Experimental Data (b) experiment [Loirel, et al. , ISSW, 2001] Comparing Numerical Results with Experimental Data (b) experiment [Loirel, et al. , ISSW, 2001]](https://present5.com/presentation/7568dbae6cae2c784b3ab77f12d65c8a/image-60.jpg)
Comparing Numerical Results with Experimental Data (b) experiment [Loirel, et al. , ISSW, 2001] (a) DSMC calculation Contours of constant Mach numbers near a torus in the flow of nitrogen at Kn , D = 0. 00013 and M = 7. 11. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 60
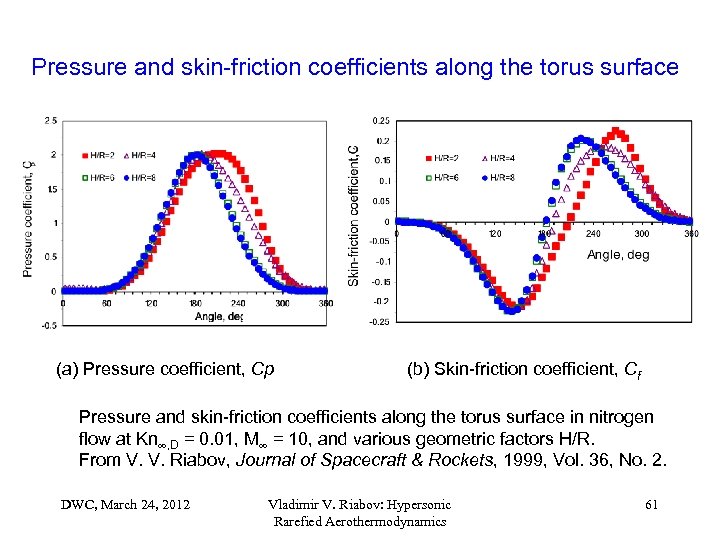
Pressure and skin-friction coefficients along the torus surface (a) Pressure coefficient, Cp (b) Skin-friction coefficient, Cf Pressure and skin-friction coefficients along the torus surface in nitrogen flow at Kn , D = 0. 01, M = 10, and various geometric factors H/R. From V. V. Riabov, Journal of Spacecraft & Rockets, 1999, Vol. 36, No. 2. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 61
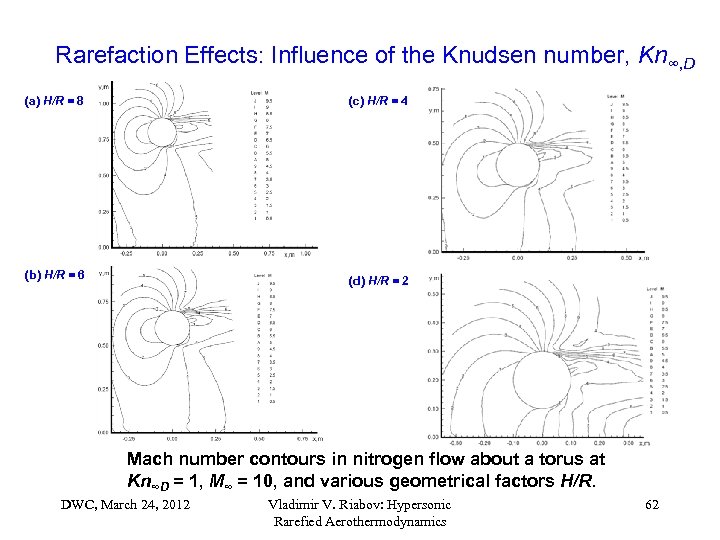
Rarefaction Effects: Influence of the Knudsen number, Kn∞, D (a) H/R = 8 (c) H/R = 4 (b) H/R = 6 (d) H/R = 2 Mach number contours in nitrogen flow about a torus at Kn∞D = 1, M∞ = 10, and various geometrical factors H/R. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 62
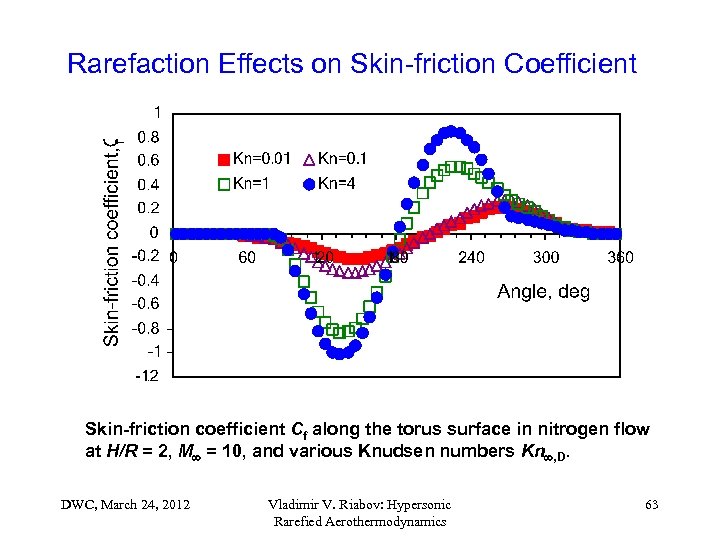
Rarefaction Effects on Skin-friction Coefficient Skin-friction coefficient Cf along the torus surface in nitrogen flow at H/R = 2, M = 10, and various Knudsen numbers Kn , D. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 63
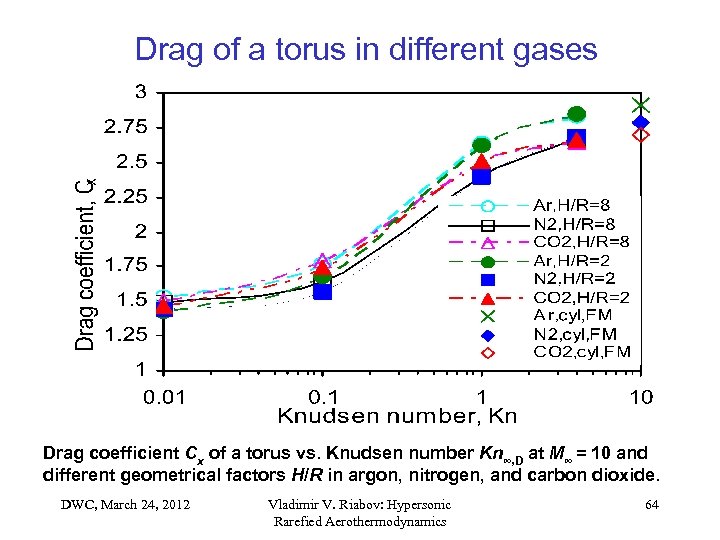
Drag of a torus in different gases Drag coefficient Cx of a torus vs. Knudsen number Kn∞, D at M∞ = 10 and different geometrical factors H/R in argon, nitrogen, and carbon dioxide. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 64

Aerodynamics of Toroidal Ballute Models The ballute model used in experiments [Loirel, et al. , AIAA Paper, No. 2894, 2002]. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 65
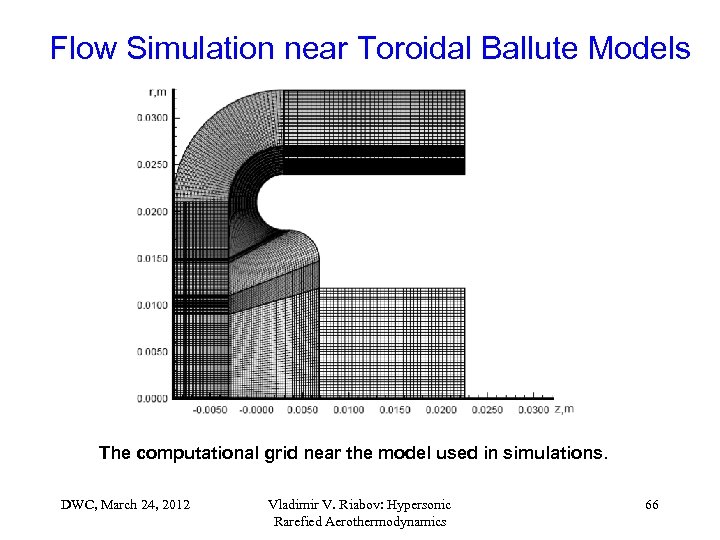
Flow Simulation near Toroidal Ballute Models The computational grid near the model used in simulations. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 66
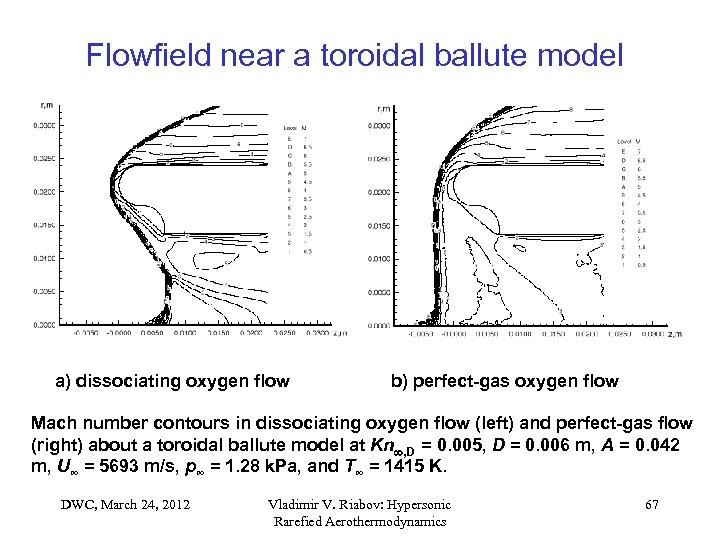
Flowfield near a toroidal ballute model a) dissociating oxygen flow b) perfect-gas oxygen flow Mach number contours in dissociating oxygen flow (left) and perfect-gas flow (right) about a toroidal ballute model at Kn , D = 0. 005, D = 0. 006 m, A = 0. 042 m, U∞ = 5693 m/s, p∞ = 1. 28 k. Pa, and T∞ = 1415 K. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 67

Aerodynamics of a spinning cylinder • At subsonic flow conditions, the speed ratio S = M∞∙(0. 5∙g )½ becomes small, and aerodynamic coefficients become very sensitive to its magnitude; • Transition flow regime has been studied numerically at M∞ = 0. 15, g = 5/3 (argon gas), and spin ratio W = 1, 3, and 6; • The incident molecules dominate when Kn. D < 0. 1, and the reflected molecules dominate when Kn. D > 0. 1; • Lift coefficient changes sign for the cylinder spinning in counterclockwise direction, and the drag coefficient becomes a function of the spin rate; • At supersonic flow conditions, the speed ratio S becomes large, and the aerodynamic coefficients become less sensitive to its magnitude. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 68
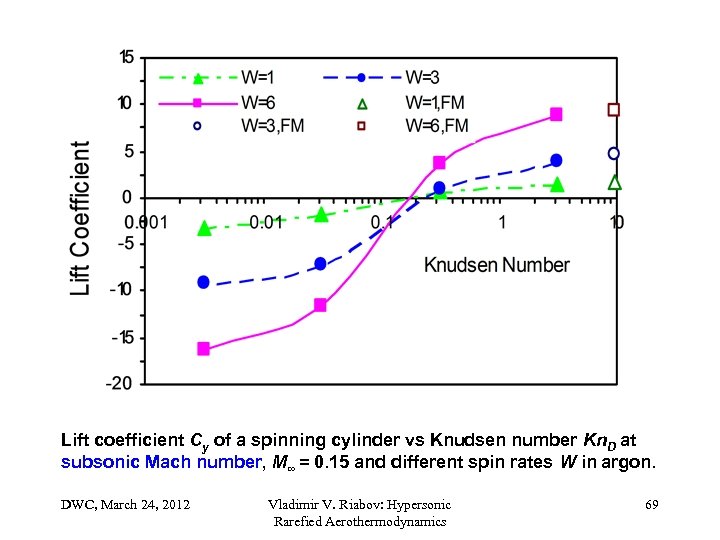
Lift coefficient Cy of a spinning cylinder vs Knudsen number Kn. D at subsonic Mach number, M∞ = 0. 15 and different spin rates W in argon. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 69
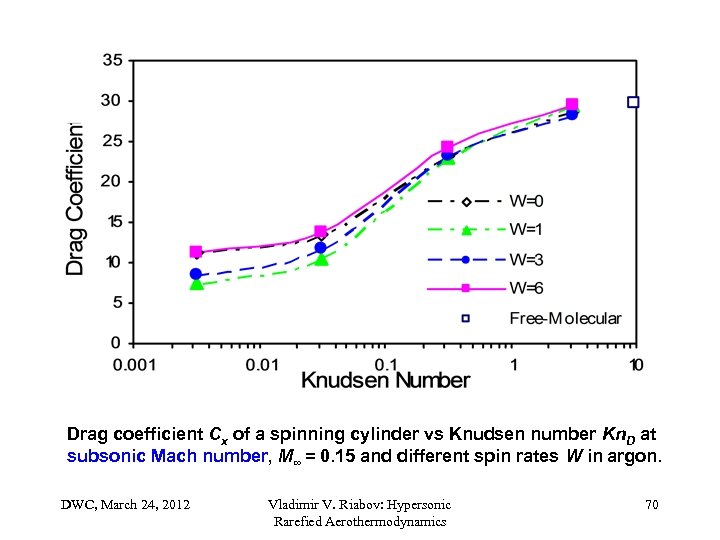
Drag coefficient Cx of a spinning cylinder vs Knudsen number Kn. D at subsonic Mach number, M∞ = 0. 15 and different spin rates W in argon. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 70
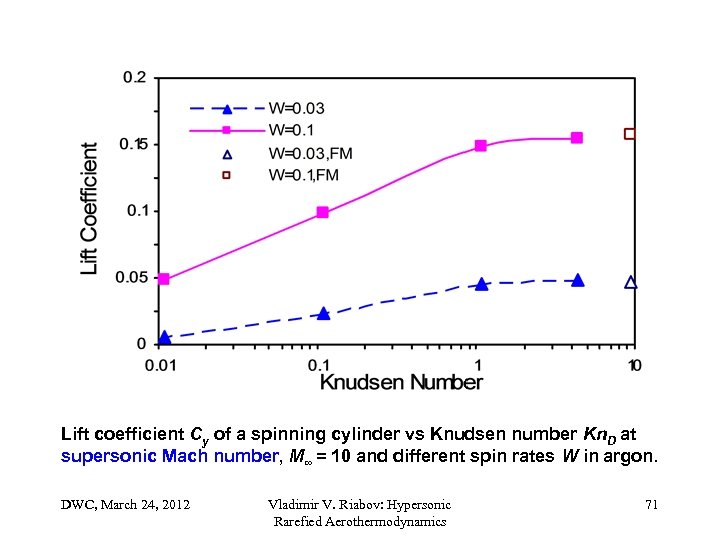
Lift coefficient Cy of a spinning cylinder vs Knudsen number Kn. D at supersonic Mach number, M∞ = 10 and different spin rates W in argon. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 71
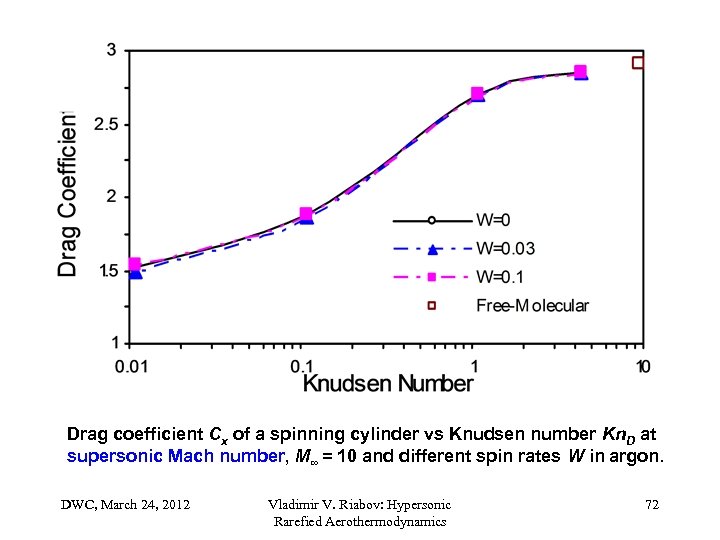
Drag coefficient Cx of a spinning cylinder vs Knudsen number Kn. D at supersonic Mach number, M∞ = 10 and different spin rates W in argon. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 72
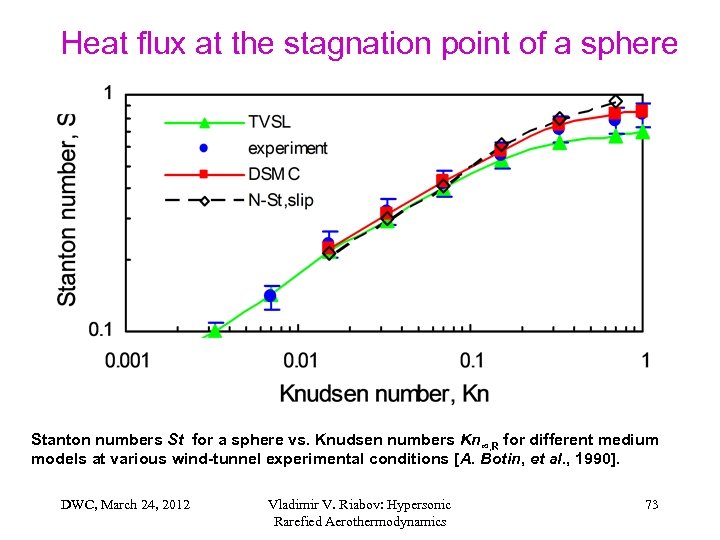
Heat flux at the stagnation point of a sphere Stanton numbers St for a sphere vs. Knudsen numbers Kn∞, R for different medium models at various wind-tunnel experimental conditions [A. Botin, et al. , 1990]. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 73
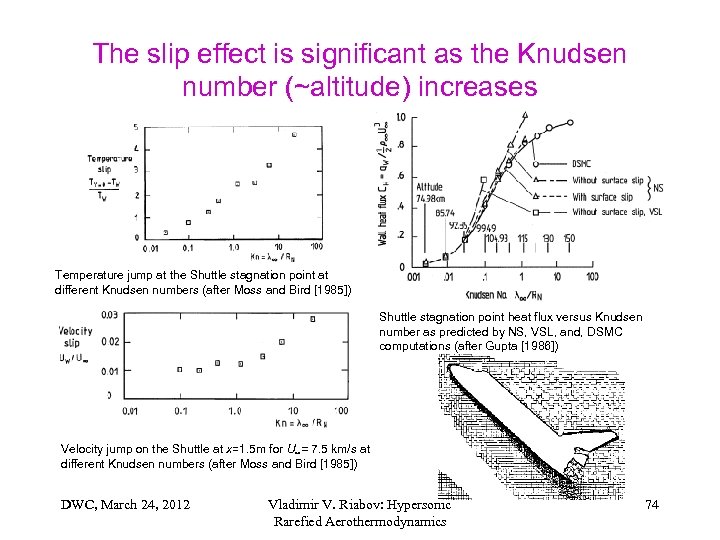
The slip effect is significant as the Knudsen number (~altitude) increases Temperature jump at the Shuttle stagnation point at different Knudsen numbers (after Moss and Bird [1985]) Shuttle stagnation point heat flux versus Knudsen number as predicted by NS, VSL, and, DSMC computations (after Gupta [1986]) Velocity jump on the Shuttle at x=1. 5 m for U∞= 7. 5 km/s at different Knudsen numbers (after Moss and Bird [1985]) DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 74
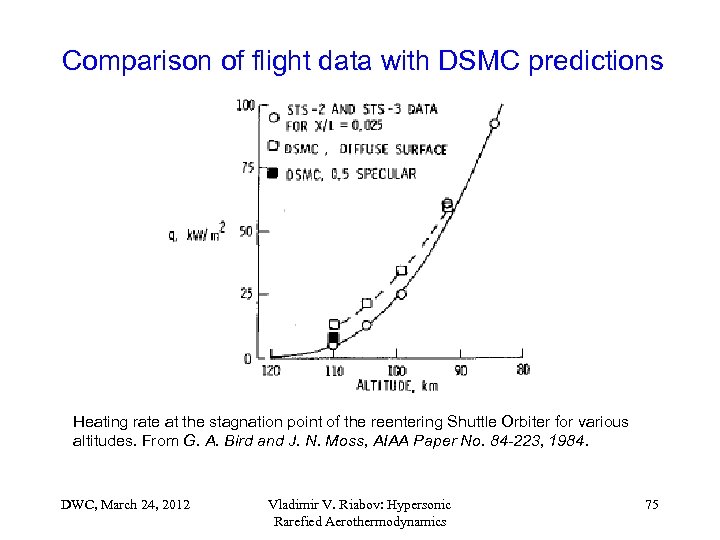
Comparison of flight data with DSMC predictions Heating rate at the stagnation point of the reentering Shuttle Orbiter for various altitudes. From G. A. Bird and J. N. Moss, AIAA Paper No. 84 -223, 1984. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 75
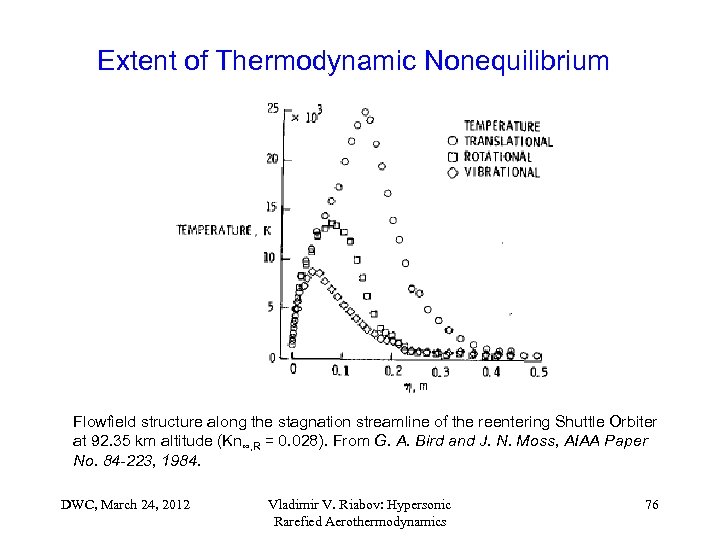
Extent of Thermodynamic Nonequilibrium Flowfield structure along the stagnation streamline of the reentering Shuttle Orbiter at 92. 35 km altitude (Kn∞, R = 0. 028). From G. A. Bird and J. N. Moss, AIAA Paper No. 84 -223, 1984. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 76
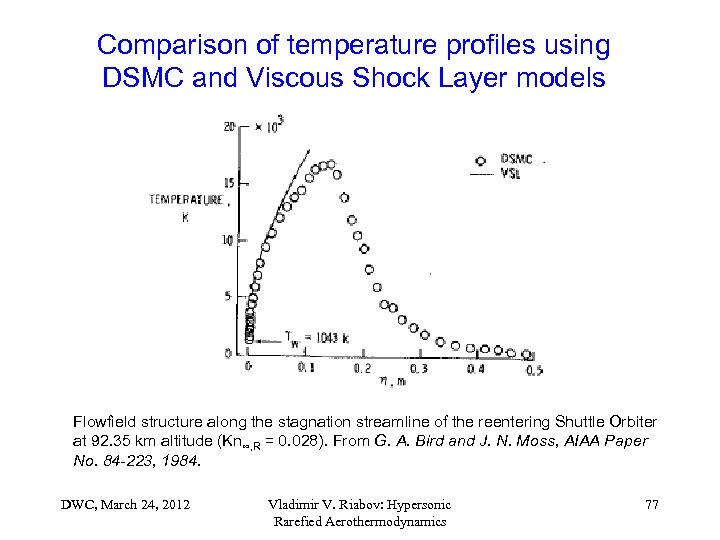
Comparison of temperature profiles using DSMC and Viscous Shock Layer models Flowfield structure along the stagnation streamline of the reentering Shuttle Orbiter at 92. 35 km altitude (Kn∞, R = 0. 028). From G. A. Bird and J. N. Moss, AIAA Paper No. 84 -223, 1984. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 77
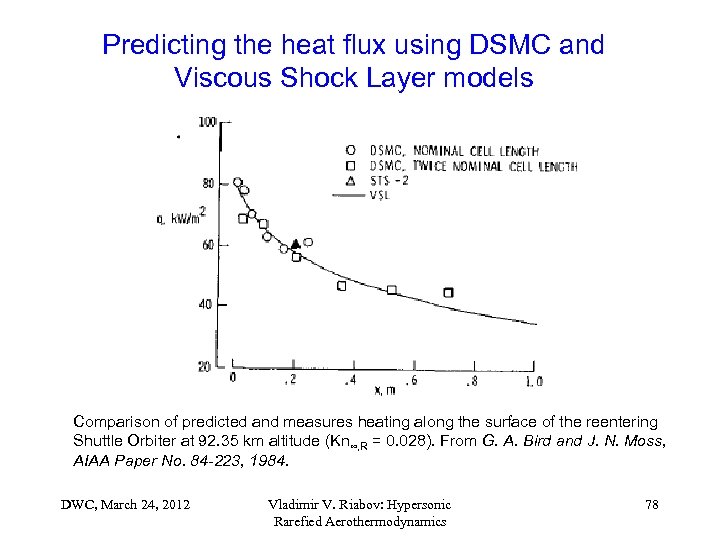
Predicting the heat flux using DSMC and Viscous Shock Layer models Comparison of predicted and measures heating along the surface of the reentering Shuttle Orbiter at 92. 35 km altitude (Kn∞, R = 0. 028). From G. A. Bird and J. N. Moss, AIAA Paper No. 84 -223, 1984. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 78
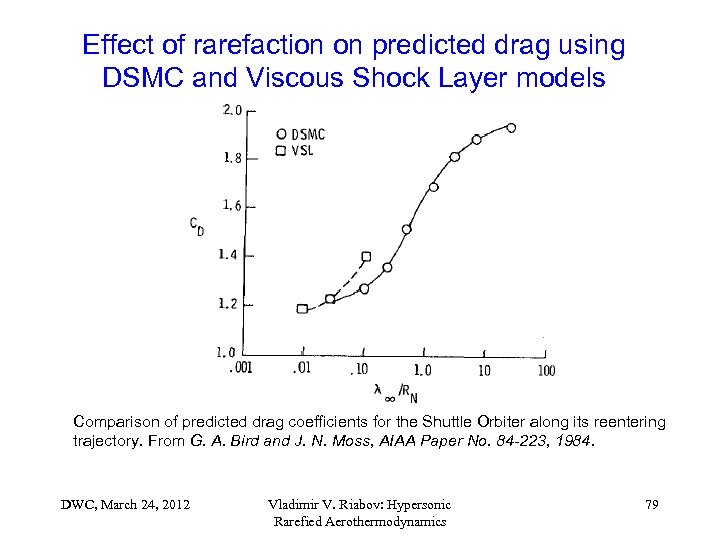
Effect of rarefaction on predicted drag using DSMC and Viscous Shock Layer models Comparison of predicted drag coefficients for the Shuttle Orbiter along its reentering trajectory. From G. A. Bird and J. N. Moss, AIAA Paper No. 84 -223, 1984. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 79

Nonequilibrium and Rarefaction Effects in the Hypersonic Multicomponent Viscous Shock Layers • The effects of rarefaction and nonequilibrium processes on hypersonic rarefied-gas flows over blunt bodies have been studied by the Direct Simulation Monte-Carlo technique (DSMC) and by solving the full Navier-Stokes equations and the equations of a thin viscous shock layer (TVSL) under the conditions of windtunnel experiments and hypersonic-vehicle flights at altitudes from 60 to 110 km. • The nonequilibrium, equilibrium and “frozen” flow regimes have been examined for various physical and chemical processes in air. • The influence of similarity parameters (Reynolds number, temperature factor, catalyticity parameters, and geometrical factors) on the flow structure near the blunt body and on its aerodynamic coefficients in hypersonic streams of dissociating air is studied. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 80

Approximation of a Thin Viscous Shock Layer (TVSL) • The TVSL equations are found from asymptotic analysis of the Navier-Stokes equations [6, 11] at ε→ 0, Reof→∞, and σ = (εReof) = const, where Reof = ρ∞U∞R/µ(Tof) is Reynolds number, ε =(γ-1)/(2γ), γ is a specific heat ratio. – Cheng H. “The blunt-body problem in hypersonic flow at low Reynolds number, ” Paper No. 63 -92, IAS, New York, 1963. – Provotorov V. and Riabov V. “Study of nonequilibrium hypersonic viscous shock layer, ” Trudy Ts. AGI, Issue 2111, pp. 142 -156, 1981 (in Russian). – Riabov, V. (2004). "Nonequilibrium and Rarefaction Effects in the Hypersonic Multicomponent Viscous Shock Layers, " Proceedings of the 24 th ICAS Congress, Paper 34, Japan. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 81

TVSL Equations of the Thin Viscous Shock Layer ∂(g 2ρu)/∂x + ∂(g 1 g 2ρv)/∂y = 0 (1) ρ(ug 1 -1∂Al/∂x + v∂Al/∂y) = -∂Jl/∂y, (6) l=1, 2, . . . , Nel-1 ρ(ug 1 -1∂u/∂x + v∂u/∂y)=-εg 1 -1 dpw/dx +σ∂(μ∂u/∂y)/∂y (2) ∂p/∂y = Kρu 2 (3) ρ(ug 1 -1∂w/∂x + v∂w/∂y) =σ∂(μ∂w/∂y)/∂y (4) ρ(ug 1 -1∂H/∂x + v∂H/∂y) = -∂q/∂y +2σ∂(μu∂u/∂y)/∂y+2σ∂(μw∂w/∂y)/∂y (5) DWC, March 24, 2012 ρ(ug 1 -1∂αi/∂x + v∂αi/∂y) = ∂ji/∂y+ωi, i= Nel, . . . , N-1 (7) Σαk = 1, 2, . . . , N (8) p= ρRg. T (9) Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 82

The generalized Rankine-Hugoniot conditions at the TVSL external boundary sinχcosφ(cosχcosφ - u) = σμ∂u/∂y (10) sinχcosφ(H∞- H) = -q +2σμ(u∂u/∂y+ w∂w/∂y) (14) ρv = - sinχcosφ (11) sinχcosφ(Al∞- Al) = - Jl (15) sinχcosφ(sinφ - w) = σμ∂w/∂y (12) sinχcosφ(αi∞- αi) = - ji (16) p=sin 2χcos 2φ (13) DWC, March 24, 2012 Here χ is a swept angle; φ is a shock incident angle. Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 83

Numerical Method • The numerical procedure of Provotorov and Riabov (1981 -1994) was used for the solution of nonlinear partially differential equations (1)-(7). • The equation terms have been approximated by using the two-point second-order Keller's scheme (1974). • The iteration process converges with the second order towards the solution. • The results have been obtained in the whole range of chemical reaction rates up to the values near equilibrium. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 84
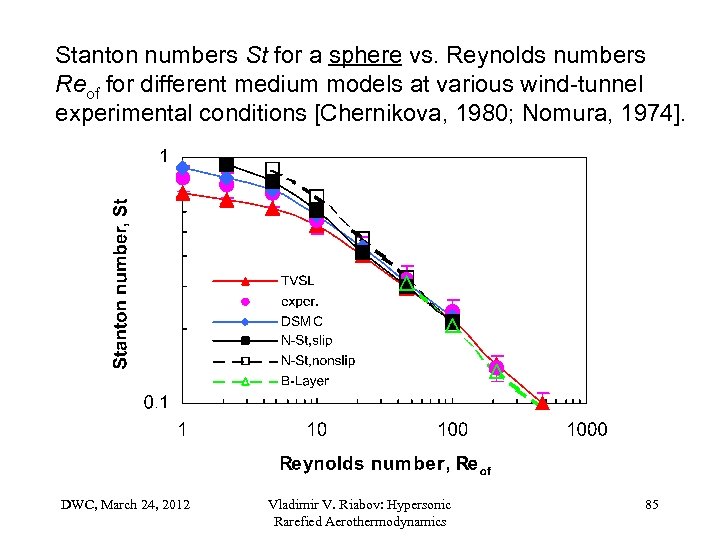
Stanton numbers St for a sphere vs. Reynolds numbers Reof for different medium models at various wind-tunnel experimental conditions [Chernikova, 1980; Nomura, 1974]. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 85
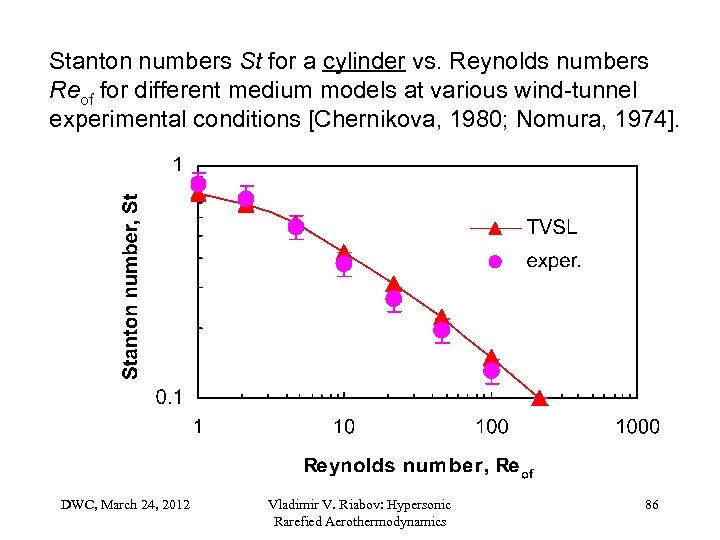
Stanton numbers St for a cylinder vs. Reynolds numbers Reof for different medium models at various wind-tunnel experimental conditions [Chernikova, 1980; Nomura, 1974]. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 86
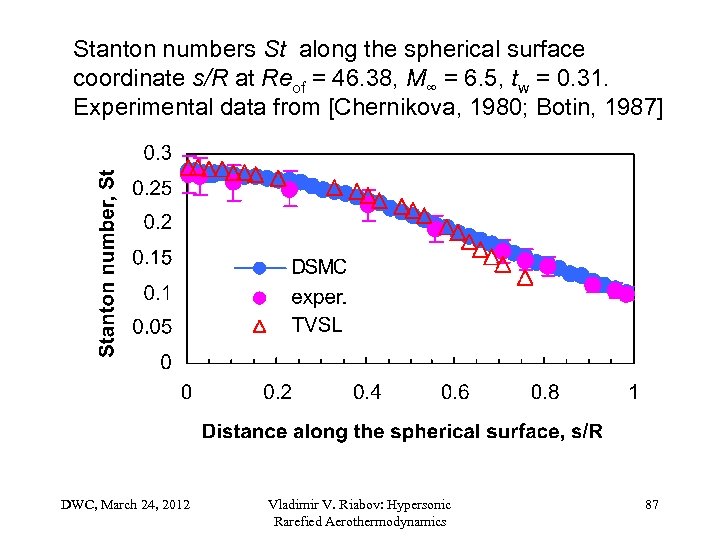
Stanton numbers St along the spherical surface coordinate s/R at Reof = 46. 38, M∞ = 6. 5, tw = 0. 31. Experimental data from [Chernikova, 1980; Botin, 1987] DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 87
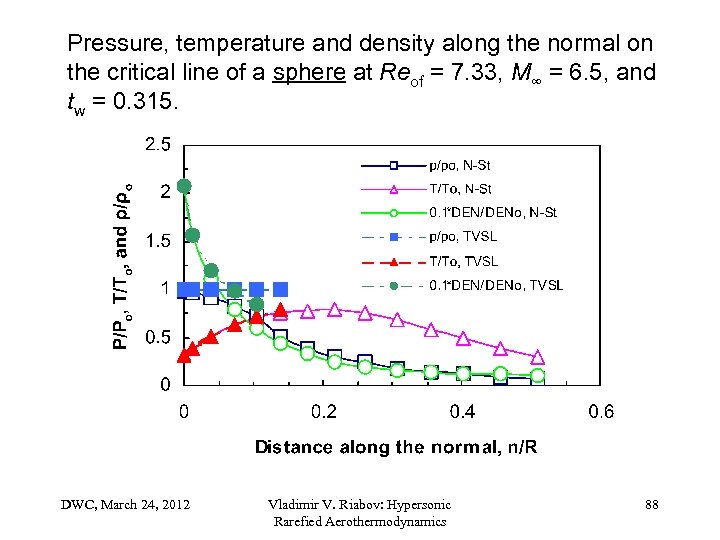
Pressure, temperature and density along the normal on the critical line of a sphere at Reof = 7. 33, M∞ = 6. 5, and tw = 0. 315. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 88
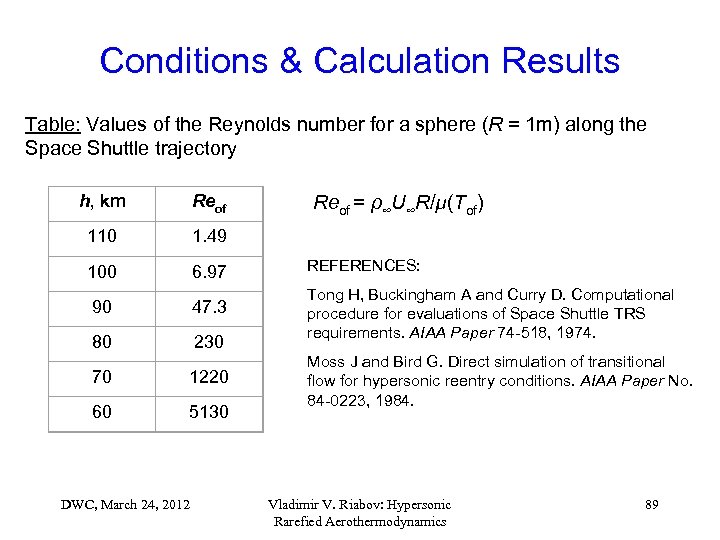
Conditions & Calculation Results Table: Values of the Reynolds number for a sphere (R = 1 m) along the Space Shuttle trajectory Reof = ρ∞U∞R/µ(Tof) h, km Reof 110 1. 49 100 6. 97 REFERENCES: 90 47. 3 80 230 Tong H, Buckingham A and Curry D. Computational procedure for evaluations of Space Shuttle TRS requirements. AIAA Paper 74 -518, 1974. 70 1220 60 5130 DWC, March 24, 2012 Moss J and Bird G. Direct simulation of transitional flow for hypersonic reentry conditions. AIAA Paper No. 84 -0223, 1984. Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 89
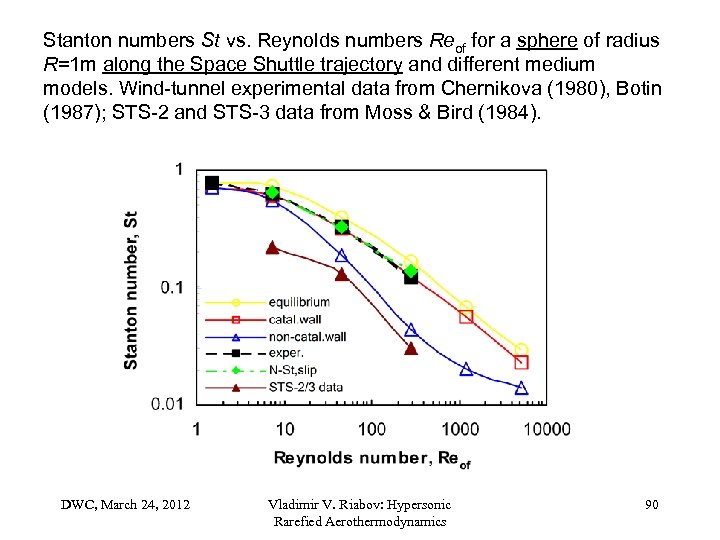
Stanton numbers St vs. Reynolds numbers Reof for a sphere of radius R=1 m along the Space Shuttle trajectory and different medium models. Wind-tunnel experimental data from Chernikova (1980), Botin (1987); STS-2 and STS-3 data from Moss & Bird (1984). DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 90
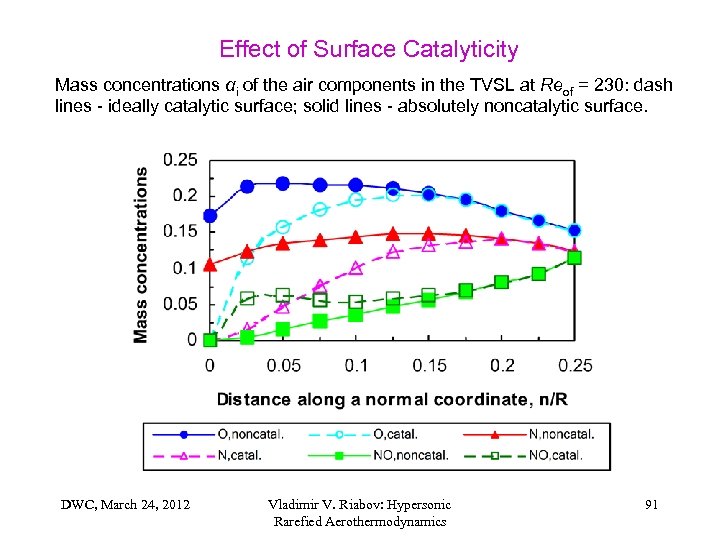
Effect of Surface Catalyticity Mass concentrations αi of the air components in the TVSL at Reof = 230: dash lines - ideally catalytic surface; solid lines - absolutely noncatalytic surface. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 91
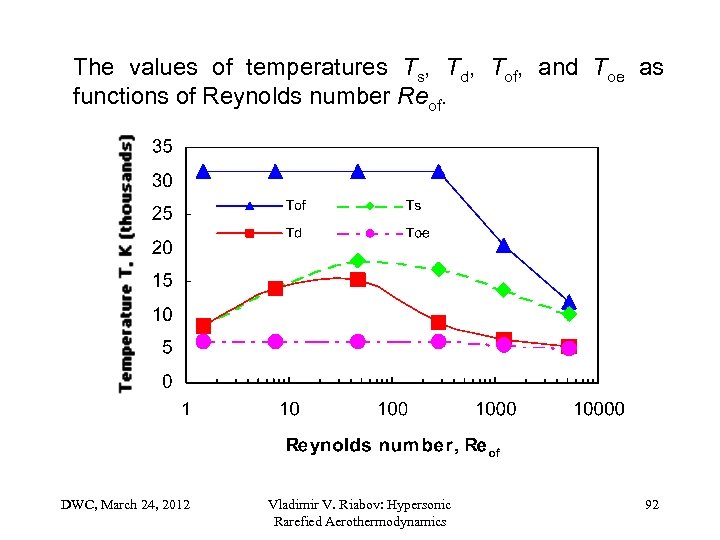
The values of temperatures Ts, Td, Tof, and Toe as functions of Reynolds number Reof. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 92
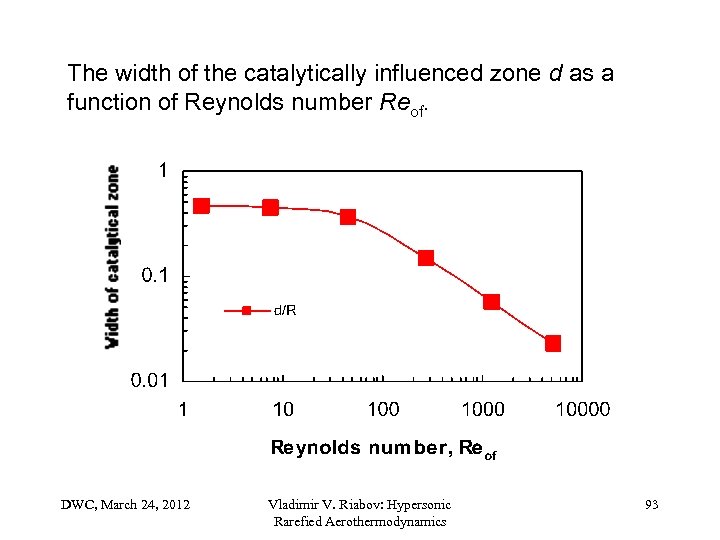
The width of the catalytically influenced zone d as a function of Reynolds number Reof. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 93
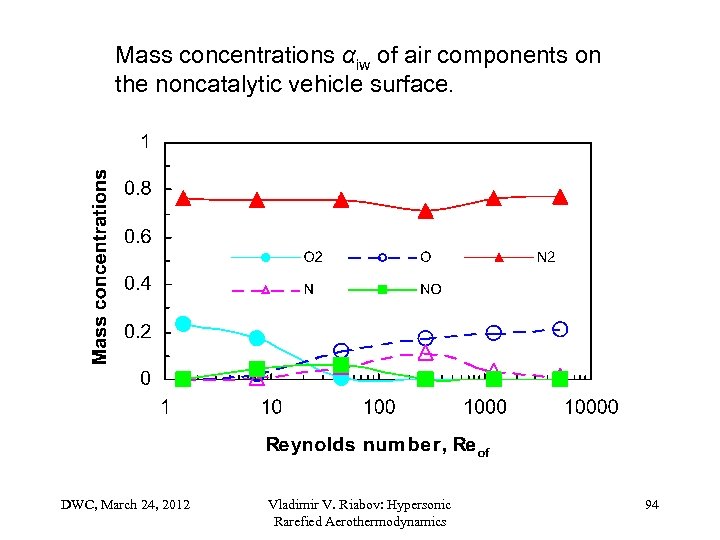
Mass concentrations αiw of air components on the noncatalytic vehicle surface. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 94
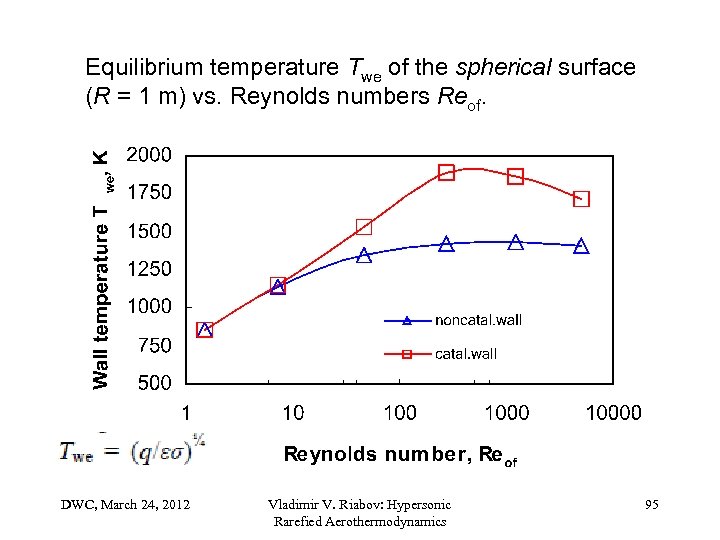
Equilibrium temperature Twe of the spherical surface (R = 1 m) vs. Reynolds numbers Reof. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 95
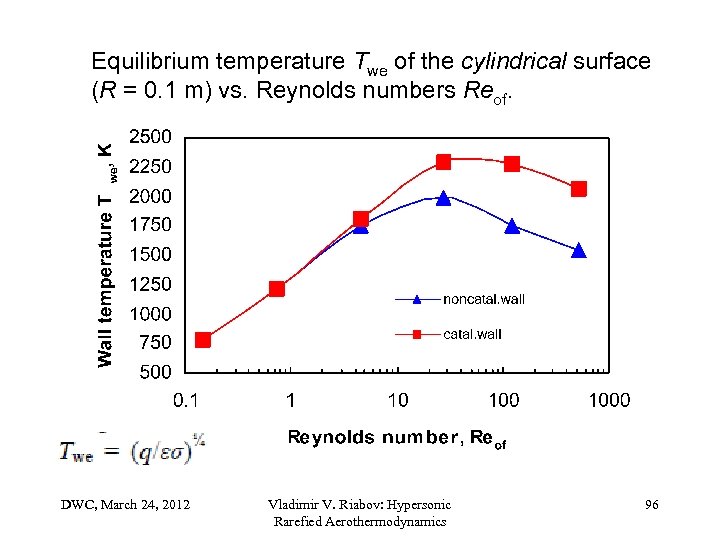
Equilibrium temperature Twe of the cylindrical surface (R = 0. 1 m) vs. Reynolds numbers Reof. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 96
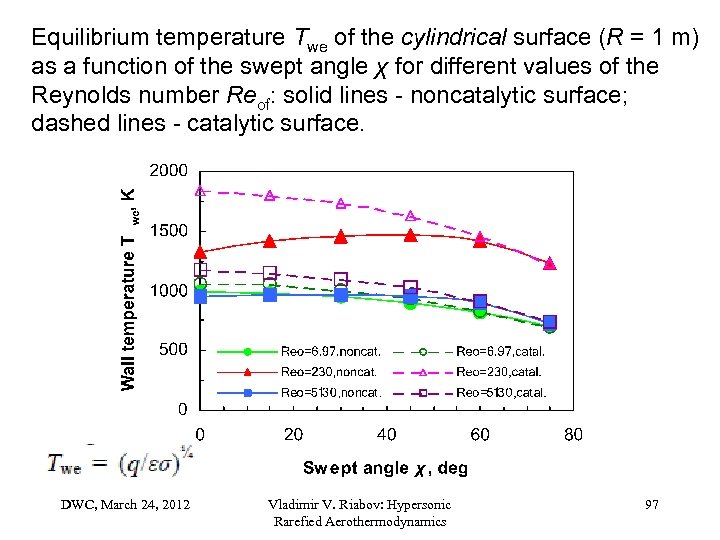
Equilibrium temperature Twe of the cylindrical surface (R = 1 m) as a function of the swept angle χ for different values of the Reynolds number Reof: solid lines - noncatalytic surface; dashed lines - catalytic surface. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 97
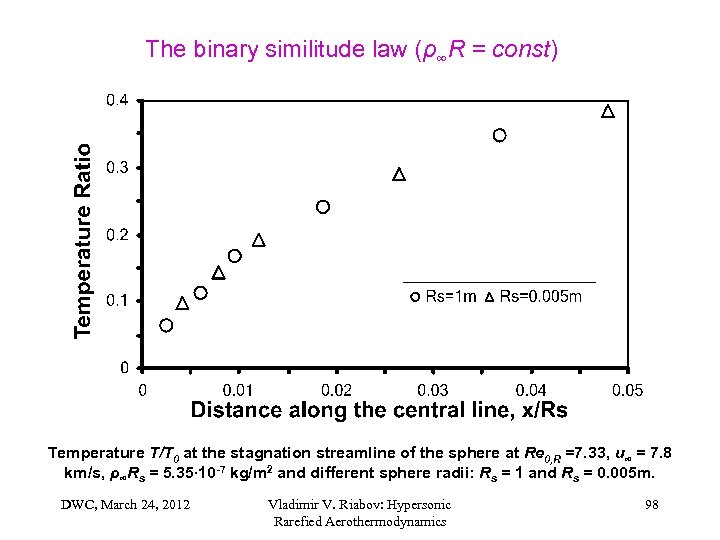
The binary similitude law (ρ∞R = const) Temperature T/T 0 at the stagnation streamline of the sphere at Re 0, R =7. 33, u∞ = 7. 8 km/s, ρ∞Rs = 5. 35∙ 10 -7 kg/m 2 and different sphere radii: Rs = 1 and Rs = 0. 005 m. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 98
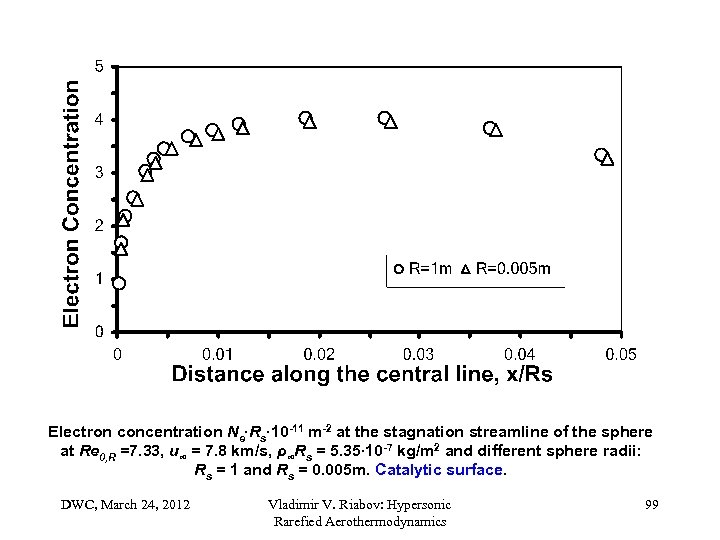
Electron concentration Ne∙Rs∙ 10 -11 m-2 at the stagnation streamline of the sphere at Re 0, R =7. 33, u∞ = 7. 8 km/s, ρ∞Rs = 5. 35∙ 10 -7 kg/m 2 and different sphere radii: Rs = 1 and Rs = 0. 005 m. Catalytic surface. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 99
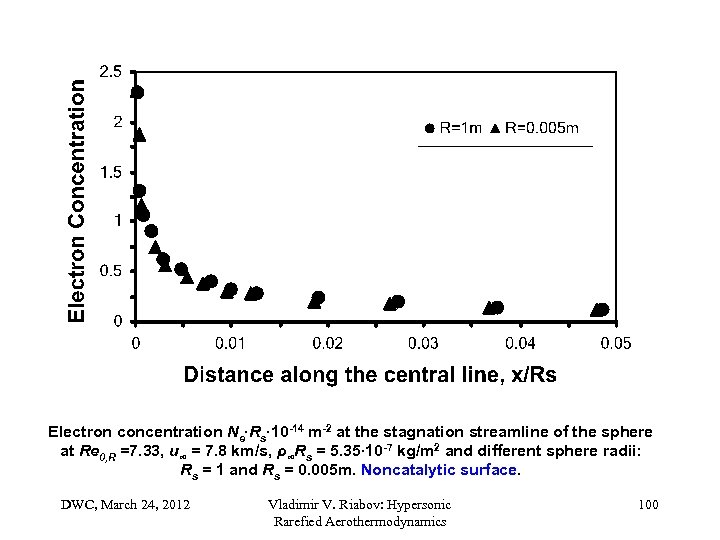
Electron concentration Ne∙Rs∙ 10 -14 m-2 at the stagnation streamline of the sphere at Re 0, R =7. 33, u∞ = 7. 8 km/s, ρ∞Rs = 5. 35∙ 10 -7 kg/m 2 and different sphere radii: Rs = 1 and Rs = 0. 005 m. Noncatalytic surface. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 100

Computation Fluid Dynamic Challenges CFD prediction of Hyper-X flow field at M∞ = 7 with engine operating. (Courtesy of NASA Dryden Flight Research Center). § The thin shock layer coming from the forebody remains very close to the vehicle surface for a large distance down the body length; § Various shock-shock and shock-boundary layer interactions occur in the vicinity of the ramp inlet; § Flow interactions with the engine exhaust and lower surface body contouring create a complex flow field under the back half of the vehicle; § All of this could take place at flight conditions where chemical reactions would be important. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 101
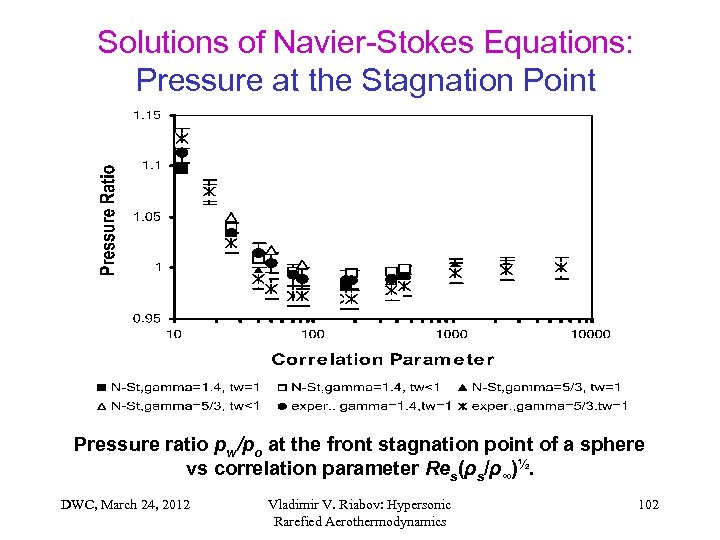
Solutions of Navier-Stokes Equations: Pressure at the Stagnation Point Pressure ratio pw/po at the front stagnation point of a sphere vs correlation parameter Res(ρs/ρ∞)½. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 102
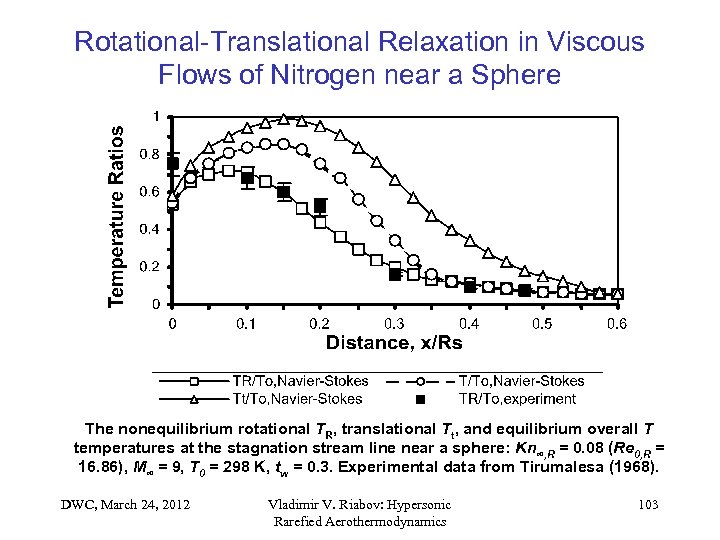
Rotational-Translational Relaxation in Viscous Flows of Nitrogen near a Sphere The nonequilibrium rotational TR, translational Tt, and equilibrium overall T temperatures at the stagnation stream line near a sphere: Kn∞, R = 0. 08 (Re 0, R = 16. 86), M∞ = 9, T 0 = 298 K, tw = 0. 3. Experimental data from Tirumalesa (1968). DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 103
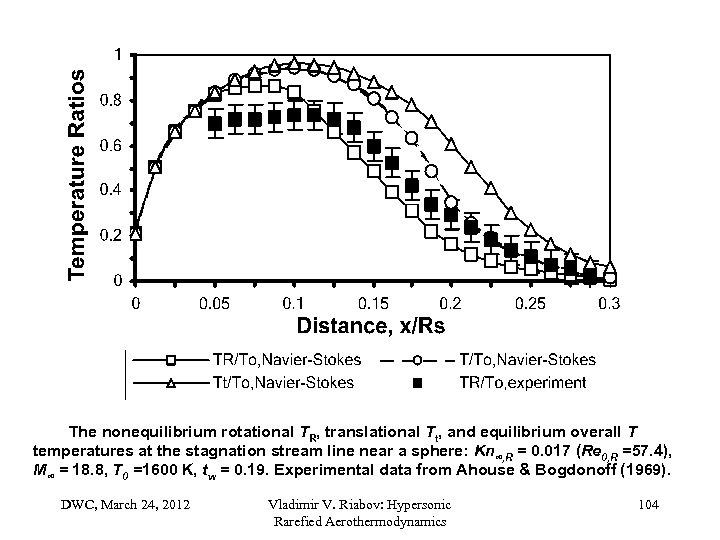
The nonequilibrium rotational TR, translational Tt, and equilibrium overall T temperatures at the stagnation stream line near a sphere: Kn∞, R = 0. 017 (Re 0, R =57. 4), M∞ = 18. 8, T 0 =1600 K, tw = 0. 19. Experimental data from Ahouse & Bogdonoff (1969). DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 104
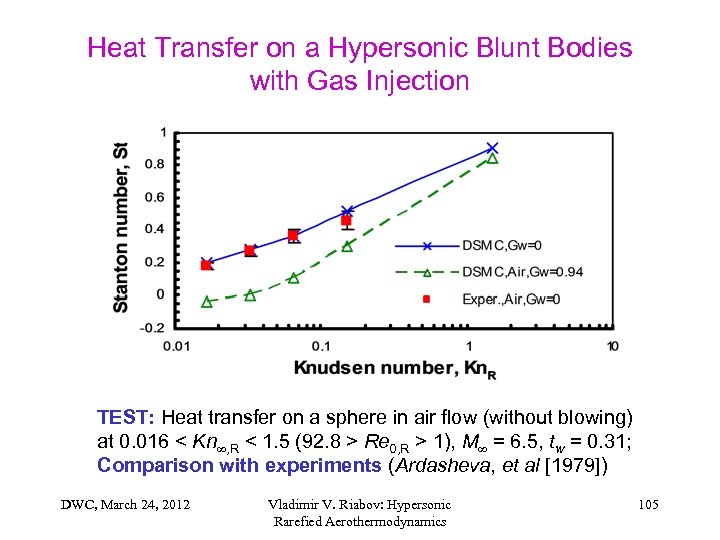
Heat Transfer on a Hypersonic Blunt Bodies with Gas Injection TEST: Heat transfer on a sphere in air flow (without blowing) at 0. 016 < Kn , R < 1. 5 (92. 8 > Re 0, R > 1), M = 6. 5, tw = 0. 31; Comparison with experiments (Ardasheva, et al [1979]) DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 105
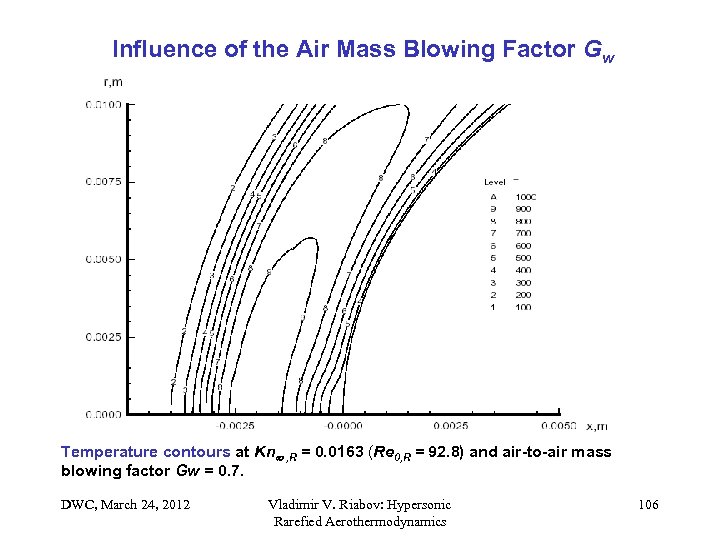
Influence of the Air Mass Blowing Factor Gw Temperature contours at Kn , R = 0. 0163 (Re 0, R = 92. 8) and air-to-air mass blowing factor Gw = 0. 7. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 106
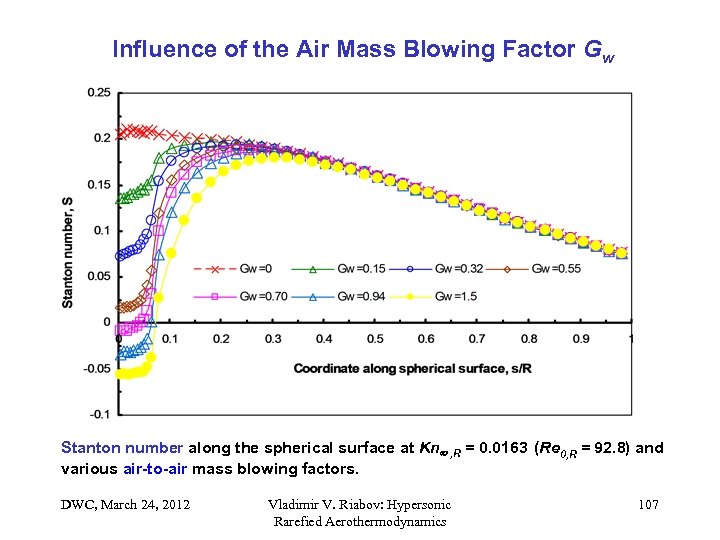
Influence of the Air Mass Blowing Factor Gw Stanton number along the spherical surface at Kn , R = 0. 0163 (Re 0, R = 92. 8) and various air-to-air mass blowing factors. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 107
![Comparison with Experimental Data (A. Botin [1987]): Air-to-Air Mass Blowing Stanton number along the Comparison with Experimental Data (A. Botin [1987]): Air-to-Air Mass Blowing Stanton number along the](https://present5.com/presentation/7568dbae6cae2c784b3ab77f12d65c8a/image-108.jpg)
Comparison with Experimental Data (A. Botin [1987]): Air-to-Air Mass Blowing Stanton number along the spherical surface at Kn , R = 0. 0326, T 0 = 1000 K and lower air-to-air mass blowing factors. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 108
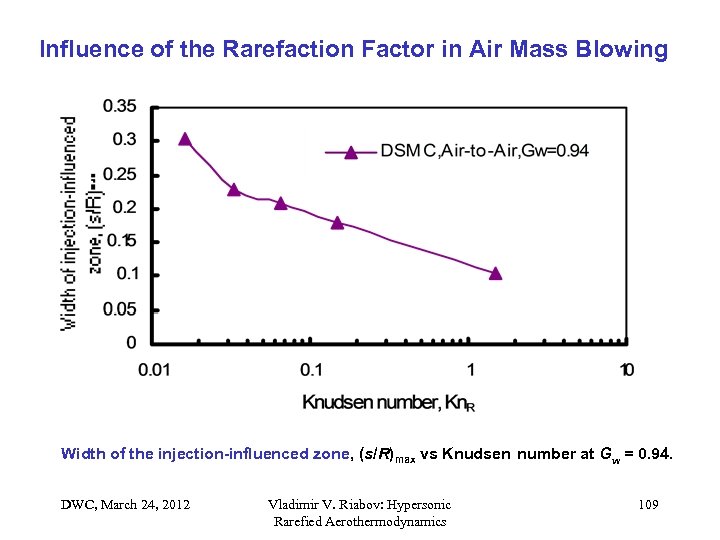
Influence of the Rarefaction Factor in Air Mass Blowing Width of the injection-influenced zone, (s/R)max vs Knudsen number at Gw = 0. 94. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 109
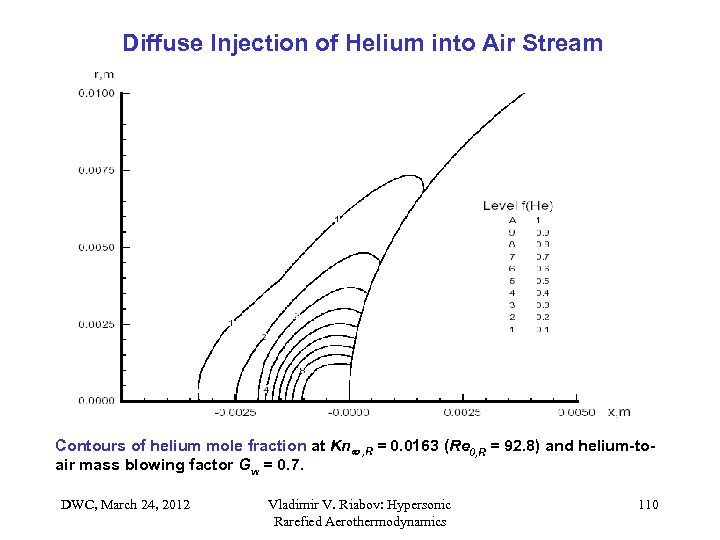
Diffuse Injection of Helium into Air Stream Contours of helium mole fraction at Kn , R = 0. 0163 (Re 0, R = 92. 8) and helium-toair mass blowing factor Gw = 0. 7. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 110
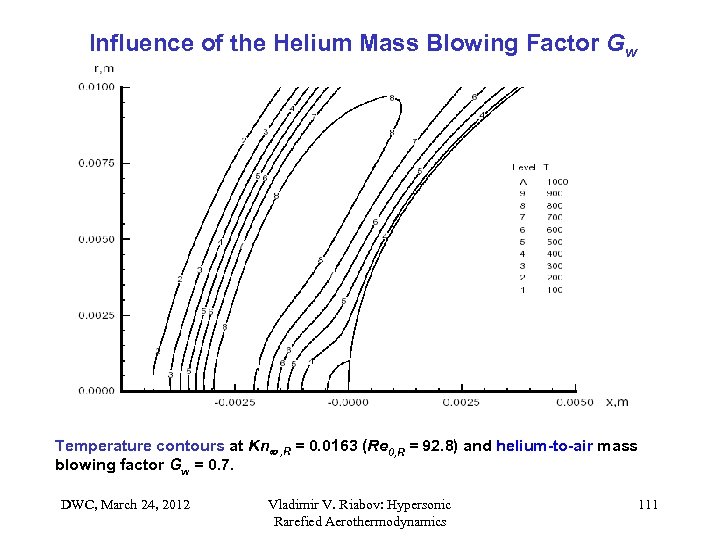
Influence of the Helium Mass Blowing Factor Gw Temperature contours at Kn , R = 0. 0163 (Re 0, R = 92. 8) and helium-to-air mass blowing factor Gw = 0. 7. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 111
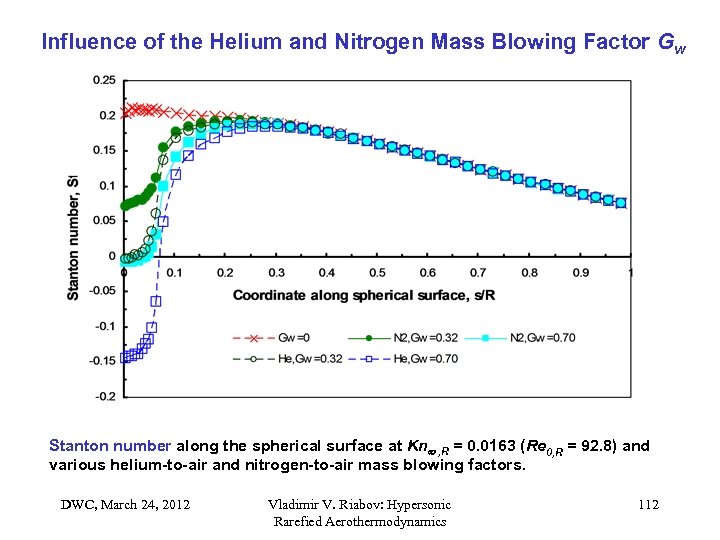
Influence of the Helium and Nitrogen Mass Blowing Factor Gw Stanton number along the spherical surface at Kn , R = 0. 0163 (Re 0, R = 92. 8) and various helium-to-air and nitrogen-to-air mass blowing factors. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 112

Hypersonic Hydrogen Combustion in Thin Viscous Shock Layer (TVSL) • Combustion of air-hydrogen mixture (11 components, 35 chemical reactions); • Two-dimensional flow in thin viscous shock layer (TVSL) near noncatalytic surface of parabolic cylinder (radius R=0. 015 m); • Flow parameters: V = 2933 m/s, T = 230 K, Tw = 600 K, Reynolds number Re 0 R = 628; • Slot or uniform (G = G 0) injection; • Modified Newton-Raphson numerical method with exponential box-schemes; • Y-Adaptive grid 101 41; • V. V. Riabov and A. V. Botin, Journal of Thermophysics and Heat Transfer, 1995; Vol. 9, No. 2, pp. 233 -239. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 113
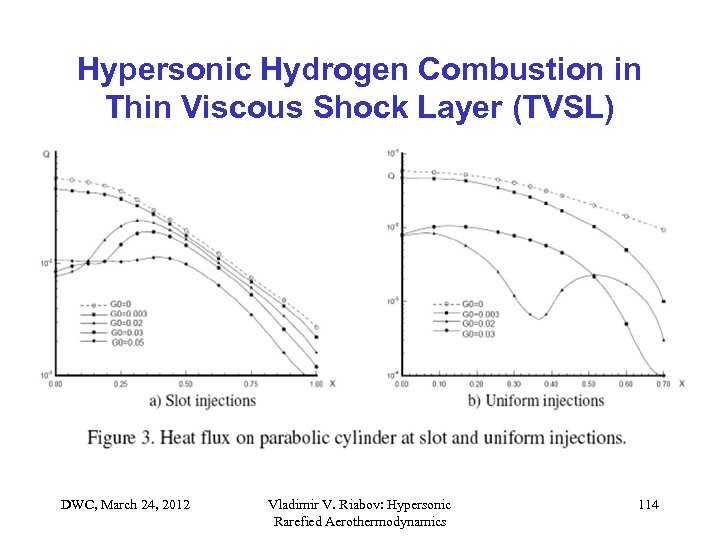
Hypersonic Hydrogen Combustion in Thin Viscous Shock Layer (TVSL) DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 114
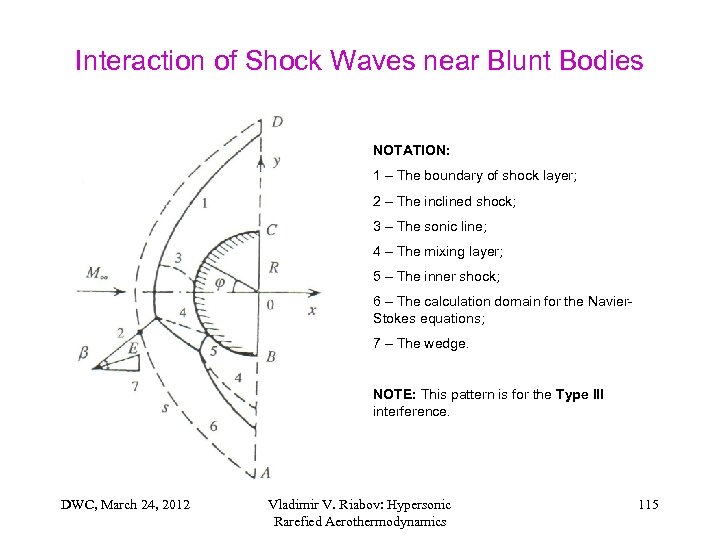
Interaction of Shock Waves near Blunt Bodies NOTATION: 1 – The boundary of shock layer; 2 – The inclined shock; 3 – The sonic line; 4 – The mixing layer; 5 – The inner shock; 6 – The calculation domain for the Navier. Stokes equations; 7 – The wedge. NOTE: This pattern is for the Type III interference. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 115

The Electron-Beam Fluorescence Technique for Flow Visualization The experiments have been carried out in a vacuum wind tunnel at low-density airflow parameters: M = 6. 5, T 0 = 1000 K, p 0 = 4000 N/m 2. The model is a plate with a cylindrical edge of radius R = 0. 01 m. The flow is characterized by the Reynolds number Re 0 = 15. 5 and the Knudsen number Kn. R = 0. 1. No interference: The plane oblique shock wave was generated by a wedge with an apex angle = 20 deg, and the angle of the shock inclination about 27 deg. A string transverse mechanism allowed moving the wedge at any position along the vertical Y-axis to simulate interactions. DWC, March 24, 2012 Type I interference is characterized by the formation of two shocks after the intersection of two oblique shocks of opposite families. The intersection point is sufficiently downstream of the sonic point on the bow shock wave. Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 116

The Electron-Beam Fluorescence Technique for Flow Visualization Type II interaction reflects the Mach phenomenon and produces two triple points separated by a normal shock after the intersection of the two oblique shock waves. DWC, March 24, 2012 In the Type III interference case, the slip line reattaches on the body surface. If the oblique shock crosses the strong bow shock, a slip line is produced separating subsonic area from a supersonic flow zone. This case would be only possible in continuum at small shockinclination angles, 20 deg. Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 117

The Electron-Beam Fluorescence Technique for Flow Visualization In the Type V interaction case, both weak oblique shock waves of the same direction would interact above the upper sonic line generating a supersonic jet after the upper multiple point. In the Type VI interference case, far from the leading critical point of the cylinder, a shock, a slip line and an expansion wave would be generated behind the triple point above the considered region. NOTE: The following cases were not found in the recent experiments: If the slip line is unable to reattach on the wall, a supersonic jet, bounded by subsonic regions develops (Type IV) [Edney, 1968]. The special case of a curved supersonic jet (Type IVa) was studied by Purpura et al. [1998]. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 118

Solving the Navier-Stokes Equations • • The full system of Navier-Stokes equations (I. Egorov, JCMMP, 31, 1991) have been solved numerically. The meridian angle is varied over the interval -90 +90 deg. The steady-state equations in the arbitrary curvilinear coordinate system = (x, y), where x and y are Cartesian coordinates, have been written in conservation form. The equations have been nondimensionalized with respect to the parameters in freestream flow. The outer boundary is divided into two parts: one part with uniform freestream conditions at the constant Mach number M , and the other with the conditions behind an inclined plane shock. The velocity slip and temperature jump effects are considered at the body surface. The numerical method has been described in detail in (A. Botin, Fluid Dyn. , 28, 1993). A set of FORTRAN standardized programs has been used to solve the problem. The grid contains 44 nodes related to the surface curvilinear coordinate and 41 nodes along the normal . The finitedifference program is a second-order accurate scheme. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 119

Mach number contours calculated by the Navier-Stokes solver at Re 0 = 15. 5 (Kn. R = 0. 1) for different types of interaction In the Type III interference case, the slip line reattaches on the body surface. If the oblique shock crosses the strong bow shock, a slip line is produced separating subsonic area from a supersonic flow zone. This case would be only possible in continuum at small shockinclination angles, 20 deg. DWC, March 24, 2012 In the Type V interaction case, both weak oblique shock waves of the same direction would interact above the upper sonic line generating a supersonic jet after the upper multiple point. Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 120
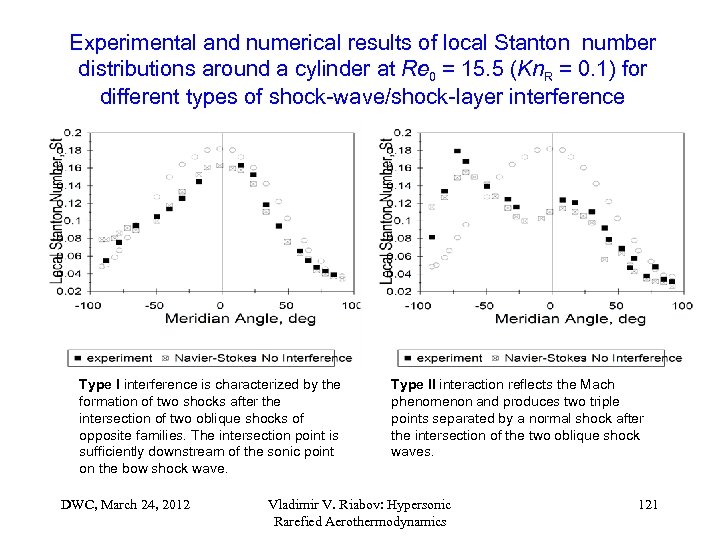
Experimental and numerical results of local Stanton number distributions around a cylinder at Re 0 = 15. 5 (Kn. R = 0. 1) for different types of shock-wave/shock-layer interference Type I interference is characterized by the formation of two shocks after the intersection of two oblique shocks of opposite families. The intersection point is sufficiently downstream of the sonic point on the bow shock wave. DWC, March 24, 2012 Type II interaction reflects the Mach phenomenon and produces two triple points separated by a normal shock after the intersection of the two oblique shock waves. Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 121
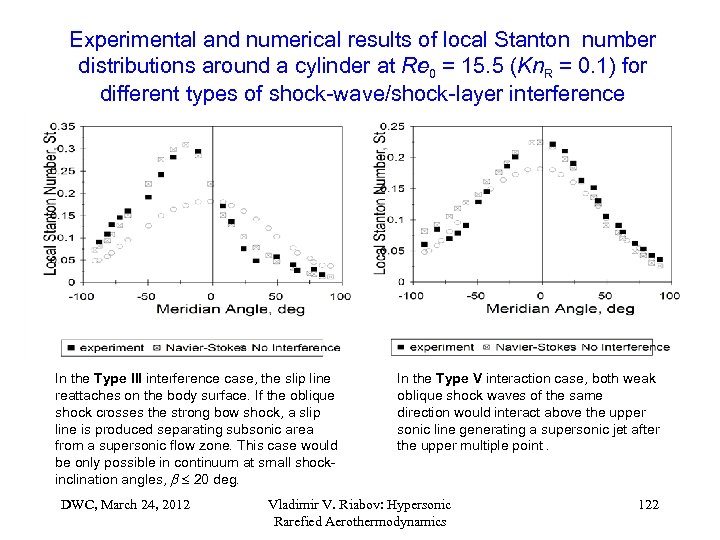
Experimental and numerical results of local Stanton number distributions around a cylinder at Re 0 = 15. 5 (Kn. R = 0. 1) for different types of shock-wave/shock-layer interference In the Type III interference case, the slip line reattaches on the body surface. If the oblique shock crosses the strong bow shock, a slip line is produced separating subsonic area from a supersonic flow zone. This case would be only possible in continuum at small shockinclination angles, 20 deg. DWC, March 24, 2012 In the Type V interaction case, both weak oblique shock waves of the same direction would interact above the upper sonic line generating a supersonic jet after the upper multiple point. Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 122
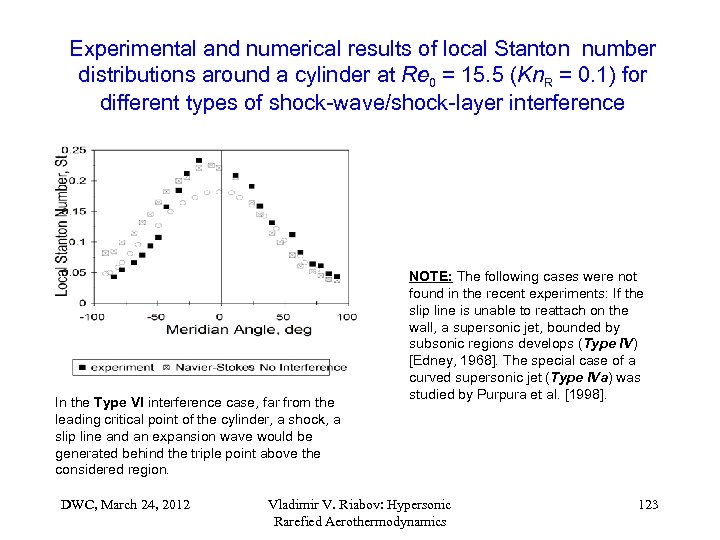
Experimental and numerical results of local Stanton number distributions around a cylinder at Re 0 = 15. 5 (Kn. R = 0. 1) for different types of shock-wave/shock-layer interference In the Type VI interference case, far from the leading critical point of the cylinder, a shock, a slip line and an expansion wave would be generated behind the triple point above the considered region. DWC, March 24, 2012 NOTE: The following cases were not found in the recent experiments: If the slip line is unable to reattach on the wall, a supersonic jet, bounded by subsonic regions develops (Type IV) [Edney, 1968]. The special case of a curved supersonic jet (Type IVa) was studied by Purpura et al. [1998]. Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 123
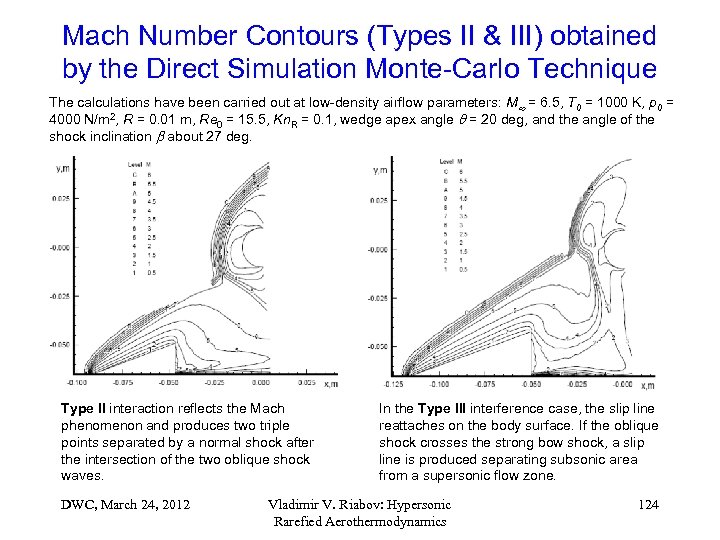
Mach Number Contours (Types II & III) obtained by the Direct Simulation Monte-Carlo Technique The calculations have been carried out at low-density airflow parameters: M = 6. 5, T 0 = 1000 K, p 0 = 4000 N/m 2, R = 0. 01 m, Re 0 = 15. 5, Kn. R = 0. 1, wedge apex angle = 20 deg, and the angle of the shock inclination about 27 deg. Type II interaction reflects the Mach phenomenon and produces two triple points separated by a normal shock after the intersection of the two oblique shock waves. DWC, March 24, 2012 In the Type III interference case, the slip line reattaches on the body surface. If the oblique shock crosses the strong bow shock, a slip line is produced separating subsonic area from a supersonic flow zone. Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 124
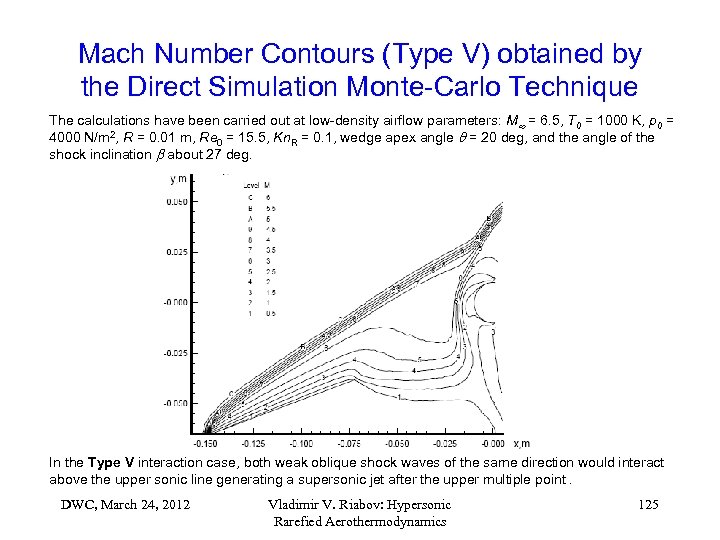
Mach Number Contours (Type V) obtained by the Direct Simulation Monte-Carlo Technique The calculations have been carried out at low-density airflow parameters: M = 6. 5, T 0 = 1000 K, p 0 = 4000 N/m 2, R = 0. 01 m, Re 0 = 15. 5, Kn. R = 0. 1, wedge apex angle = 20 deg, and the angle of the shock inclination about 27 deg. In the Type V interaction case, both weak oblique shock waves of the same direction would interact above the upper sonic line generating a supersonic jet after the upper multiple point. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 125
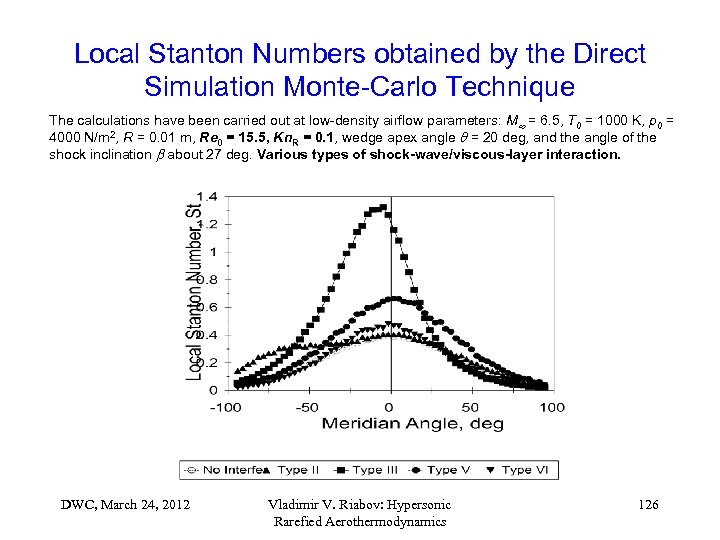
Local Stanton Numbers obtained by the Direct Simulation Monte-Carlo Technique The calculations have been carried out at low-density airflow parameters: M = 6. 5, T 0 = 1000 K, p 0 = 4000 N/m 2, R = 0. 01 m, Re 0 = 15. 5, Kn. R = 0. 1, wedge apex angle = 20 deg, and the angle of the shock inclination about 27 deg. Various types of shock-wave/viscous-layer interaction. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 126
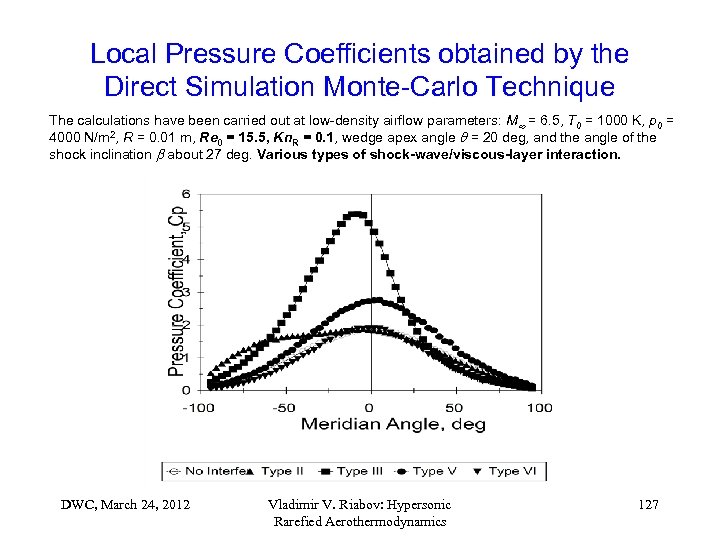
Local Pressure Coefficients obtained by the Direct Simulation Monte-Carlo Technique The calculations have been carried out at low-density airflow parameters: M = 6. 5, T 0 = 1000 K, p 0 = 4000 N/m 2, R = 0. 01 m, Re 0 = 15. 5, Kn. R = 0. 1, wedge apex angle = 20 deg, and the angle of the shock inclination about 27 deg. Various types of shock-wave/viscous-layer interaction. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 127

Conclusions • The DSMC method is effective in studies of hypersonic rarefied flows of various gases near probes in the transition regime between freemolecular and continuum regimes. • For conditions approaching the hypersonic limit, the Knudsen number (Kn∞) and temperature factor (tw) are the primary similarity parameters. • The role of the specific heat ratio (γ) is also significant in aerodynamics of a disk and a plate at various angles of attack. • Important rarefaction effects that are specific for the transition flow regime have been found: – non-monotonic lift and drag of plates, – strong repulsive force between side-by-side plates and cylinders, – dependence of drag on torus radii ratio, – at subsonic upstream conditions, the lift on a rotating cylinder has different signs in continuum and free-molecule flow regimes. The sign changes in the transition flow regime (at about Kn∞, D = 0. 1). • The acquired information could be effectively used for investigation and prediction of the aerodynamic characteristics of probes (plates, wedges, cylinders, spheres, cones, disks, and torus) in complex atmospheric conditions of the Earth, Mars, Venus, and other planets and moons. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 128

References: Experiments, DSMC Method • • Koppenwallner, G. , and Legge, H. , “Drag of Bodies in Rarefied Hypersonic Flow, ” Thermophysical Aspects of Reentry Flows, edited by J. N. Moss and C. D. Scott, Vol. 103, Progress in Astronautics and Aeronautics, AIAA, New York, 1994, pp. 44 -59. Bird, G. A. , “Rarefied Hypersonic Flow Past a Slender Sharp Cone, ” Proceedings of the 13 th International Symposium on Rarefied Gas Dynamics, edited by O. M. Belotserkovskii, M. N. Kogan, S. S. Kutateladze, and A. K. Rebrov, Vol. 1, Plenum Press, New York, 1985, pp. 349 -356. Bird, G. A. , Molecular Gas Dynamics and the Direct Simulation of Gas Flows, 1 st ed. , Oxford University Press, Oxford, England, UK, 1994. Gusev, V. N. , Erofeev, A. I. , Klimova, T. V. , Perepukhov, V. A. , Riabov, V. V. , and Tolstykh, A. I. , “Theoretical and Experimental Investigations of Flow Over Simple Shape Bodies by a Hypersonic Stream of Rarefied Gas, ” Ts. AGI Transactions, No. 1855, 1977, pp. 3 -43 (in Russian). DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 129

References (continued) • • Riabov, V. V. , “Comparative Similarity Analysis of Hypersonic Rarefied Gas Flows near Simple-Shape Bodies, ” Journal of Spacecraft and Rockets, Vol. 35, No. 4, 1998, pp. 424 -433. Gorelov, S. L. , and Erofeev, A. I. , “Qualitative Features of a Rarefied Gas Flow About Simple Shape Bodies, ” Proceedings of the 13 th International Symposium on Rarefied Gas Dynamics, edited by O. M. Belotserkovskii, M. N. Kogan, S. S. Kutateladze, and A. K. Rebrov, Vol. 1, Plenum Press, New York, 1985, pp. 515 -521. Lengrand, J. C. , Allège, J. , Chpoun, A. , and Raffin, M. , “Rarefied Hypersonic Flow Over a Sharp Flat Plate: Numerical and Experimental Results, ” Rarefied Gas Dynamics: Space Science and Engineering, edited by B. D. Shizdal and D. P. Weaver, Vol. 160, Progress in Astronautics and Aeronautics, AIAA, Washington, DC, 1994, pp. 276284. Riabov, V. V. , “Numerical Study of Hypersonic Rarefied-Gas Flows About a Torus, ” Journal of Spacecraft and Rockets, Vol. 36, No. 2, 1999, pp. 293 -296. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 130

References (continued) • Coudeville, H. , Trepaud, P. , and Brun, E. A. , “Drag Measurements in Slip and Transition Flow, ” Proceedings of the 4 th International Symposium on Rarefied Gas Dynamics, edited by J. H. de Leeuw, Vol. 1, Academic Press, New York, pp. 444 -466. • Mavriplis, C. , Ahn, J. C. , and Goulard, R. , “Heat Transfer and Flowfields in Short Microchannels Using Direct Simulation Monte Carla, ” Journal of Thermophysics and Heat Transfer, Vol. 11, No. 4, 1997, pp. 489 -496. • Oh, C. K. , Oran, E. S. , and Sinkovits, R. S. , “Computations of High. Speed, High Knudsen Number Microchannel Flows, ” Journal of Thermophysics and Heat Transfer, Vol. 11, No. 4, 1997, pp. 497505. • Bird, G. A. , The DS 2 G Program User’s Guide, Version 3. 2, G. A. B. Consulting Pty, Killara, New South Wales, Australia, 1999, pp. 1 -56. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 131

References (continued) • Bisch, C. , “Drag Reduction of a Sharp Flat Plate in a Rarefied Hypersonic Flow” in Rarefied Gas Dynamics, edited by J. L. Potter, 10 th International Symposium Proceedings, Vol. 1, AIAA, Washington, DC, 1976, pp. 361 -377. • Kogan, M. N. , Rarefied Gas Dynamics, Plenum Press, New York, 1969, pp. 345 -390. • Lourel, I. , Morgan, R. G. “The Effect of Dissociation on Chocking of Ducted Flows. ” AIAA Paper 2002 -2894. Washington, DC: AIAA; 2002. • Riabov, V. V. , “Numerical Study of Interference between Simple. Shape Bodies in Hypersonic Flows”. (Proceedings of the Fifth M. I. T. Conference on Computational Fluid and Solid Mechanics, June 17 -19, 2009, edited by K. J. Bathe). Computers and Structures, Vol. 87, 2009, pp. 651 -663. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 132

References: Ballute Missions • • • Mc. Ronald A. A light-weight inflatable hypersonic drag device for planetary entry. AIAA Paper, No. 99 -0422, 1999. Hall J and Le A. Aerocapture trajectories for spacecraft with large, towed ballutes. AAS/AIAA Space Flight Mechanics Meeting, AAS Paper 01 -235, February 2001. Rasheed A, Kujii K, Hornung H. , and Hall J. Experimental investigation of the flow over a toroidal aerocapture ballute. AIAA Paper, No. 2460, 2001. Gnoffo P. Computational aerothermodynamics in aeroassist applications. Journal of Spacecraft and Rockets, Vol. 40, No. 3, pp. 305 -312, 2003. Mc. Intyre T, Lourel I, Eichmann T, Morgan R, Jacobs P and Bishop A. Experimental expansion tube study of the flow over a toroidal ballute. Journal of Spacecraft and Rockets, Vol. 41, No. 5, pp. 716725, 2004. Moss J. Direct Simulation Monte Carlo simulations of ballute aerothermodynamics under hypersonic rarefied conditions. Journal of Spacecraft and Rockets, Vol. 44, No. 2, pp. 289 -298, 2007. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 133

Acknowledgements The author would like to express gratitude to G. A. Bird for the opportunity of using the DS 2 G computer program; to J. N. Moss for valuable discussions of the DSMC technique and results; to V. N. Gusev, M. N. Kogan, V. P. Provotorov, A. V. Botin, L. G. Chernikova, T. V. Klimova, S. G. Kryukova, A. I. Erofeev, V. A. Perepukhov, and Yu. V. Nikol’skiy for contributions at earlier stages of this research, and to I. Lourel for providing information about toroidal ballute models and their experimental conditions. DWC, March 24, 2012 Vladimir V. Riabov: Hypersonic Rarefied Aerothermodynamics 134
7568dbae6cae2c784b3ab77f12d65c8a.ppt