DAMOP 2008 focus session Atomic polarization and dispersion

DAMOP 2008 focus session: Atomic polarization and dispersion polarizabilities, atomic clocks, and magic wavelengths May 29, 2008 Marianna Safronova Bindiya arora Charles W. clark NIST, Gaithersburg

outline • Motivation • Method • Applications • Frequency-dependent polarizabilities of alkali atoms and magic frequencies • Atomic clocks: blackbody radiation shifts • Future studies

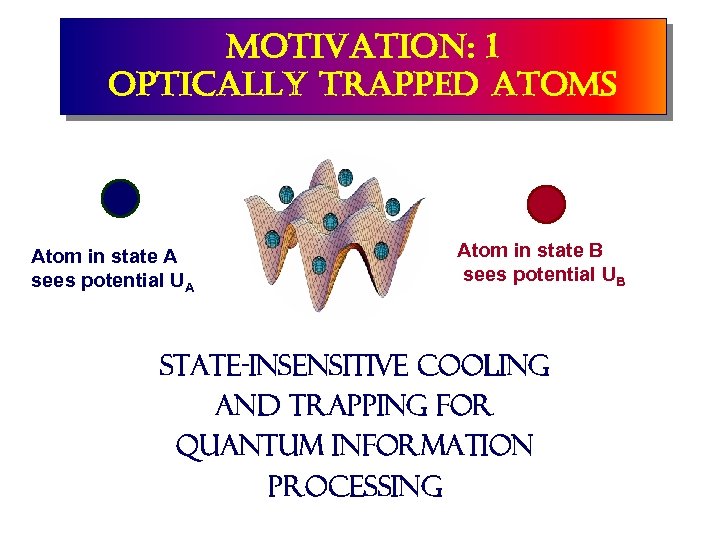motivation: 1 optically trapped atoms Atom in state A sees potential UA Atom in state B sees potential UB State-insensitive cooling and trapping for quantum information processing

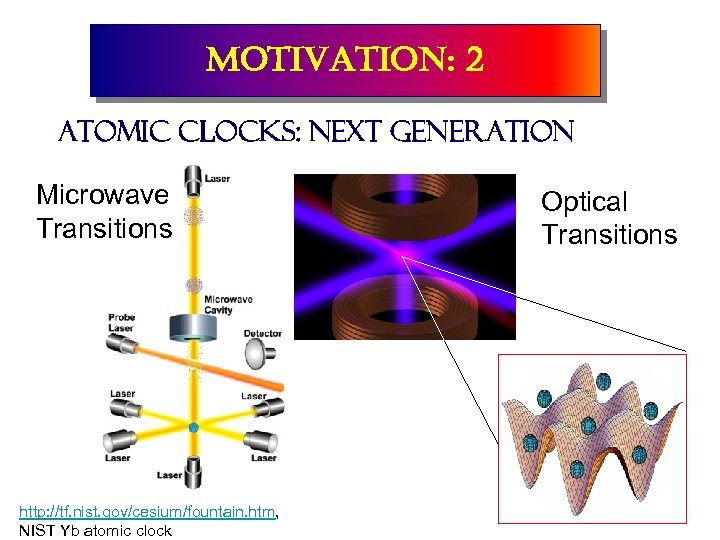motivation: 2 Atomic clocks: Next Generation Microwave Transitions http: //tf. nist. gov/cesium/fountain. htm, NIST Yb atomic clock Optical Transitions

motivation: 3 Parity violation studies with heavy atoms & search for Electron electric-dipole moment http: //CPEPweb. org, http: //public. web. cern. ch/, Cs experiment, University of Colorado

motivation • Development of the high-precision methodologies • Benchmark tests of theory and experiment • Cross-checks of various experiments • Data for astrophysics • Long-range interactions • Determination of nuclear magnetic and anapole moments • Variation of fundamental constants with time

Atomic polarizabilities

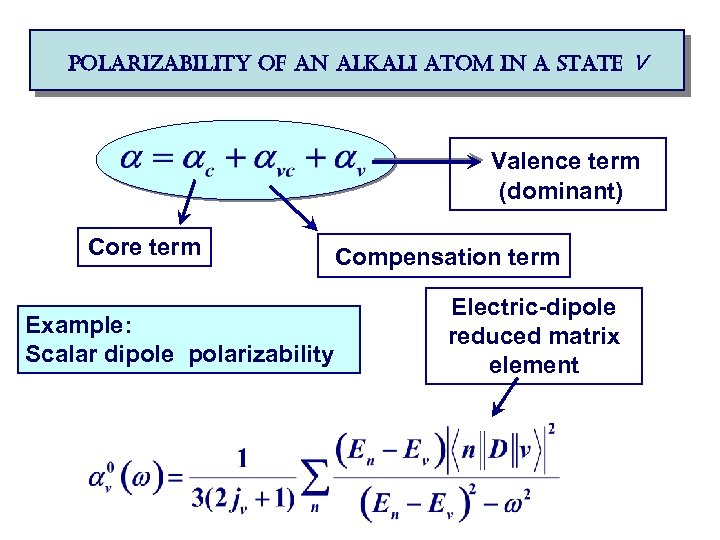polarizability of an alkali atom in a state v Valence term (dominant) Core term Example: Scalar dipole polarizability Compensation term Electric-dipole reduced matrix element

how to accurately calculate various matrix elements ? Very precise calculation of atomic properties We also need to evaluate uncertainties of theoretical values!

how to accurately calculate various matrix elements ? ! D Very precise calculation of atomic properties E T N A W We also need to evaluate uncertainties of theoretical values!

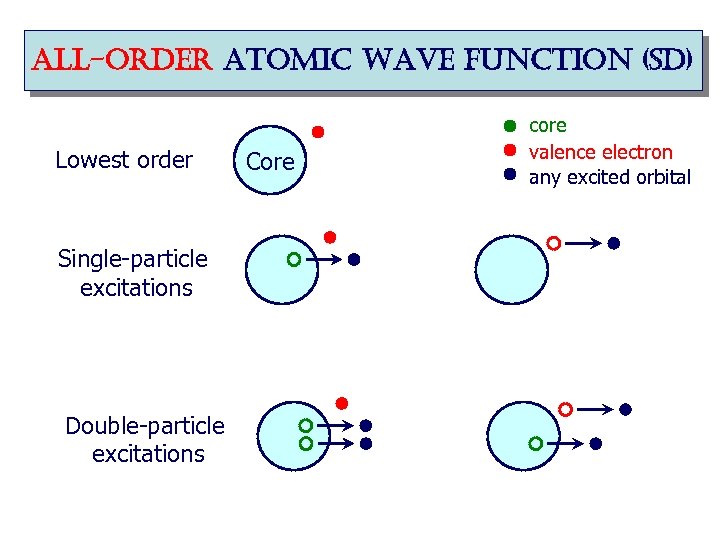all-order atomic wave function (sd) Lowest order Single-particle excitations Double-particle excitations Core core valence electron any excited orbital

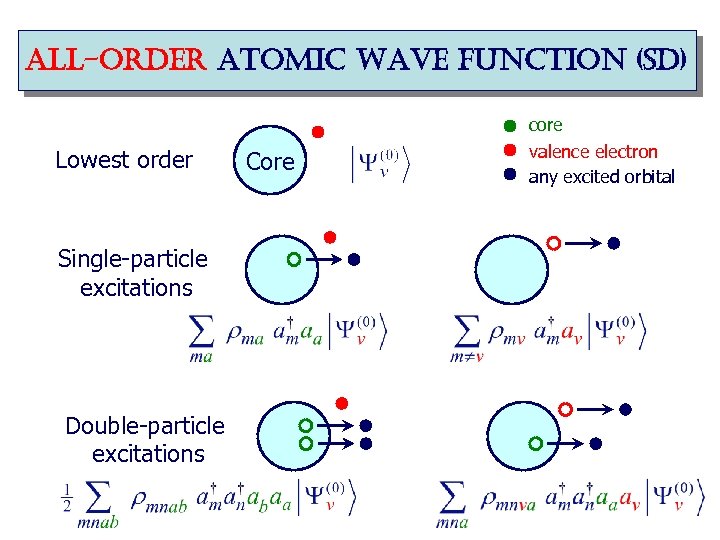all-order atomic wave function (sd) Lowest order Single-particle excitations Double-particle excitations Core core valence electron any excited orbital

Actual implementation: codes that write formulas The derivation gets really complicated if you add triples! Solution: develop analytical codes that do all the work for you! Input: ASCII input of terms of the type Output: final simplified formula in LATEX to be used in the all-order equation

Problem with all-order extensions: TOO MANY TERMS The complexity of the equations increases. Same issue with third-order MBPT for two-particle systems (hundreds of terms). What to do with large number of terms? Solution: automated code generation !

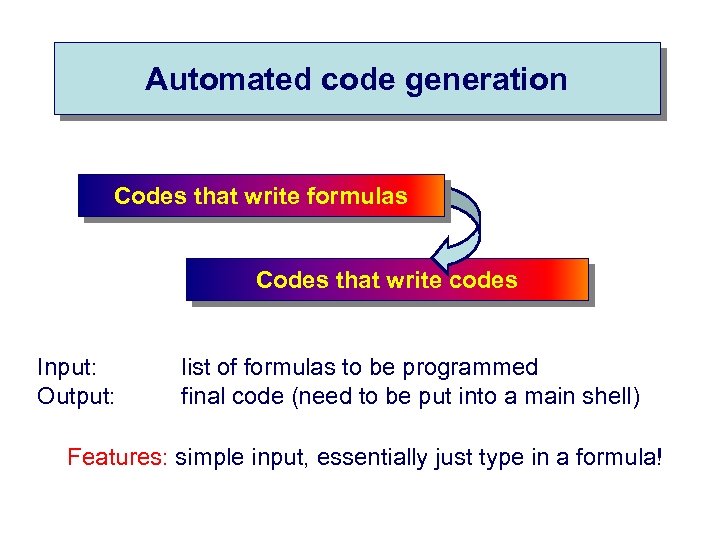Automated code generation Codes that write formulas Codes that write codes Input: Output: list of formulas to be programmed final code (need to be put into a main shell) Features: simple input, essentially just type in a formula!

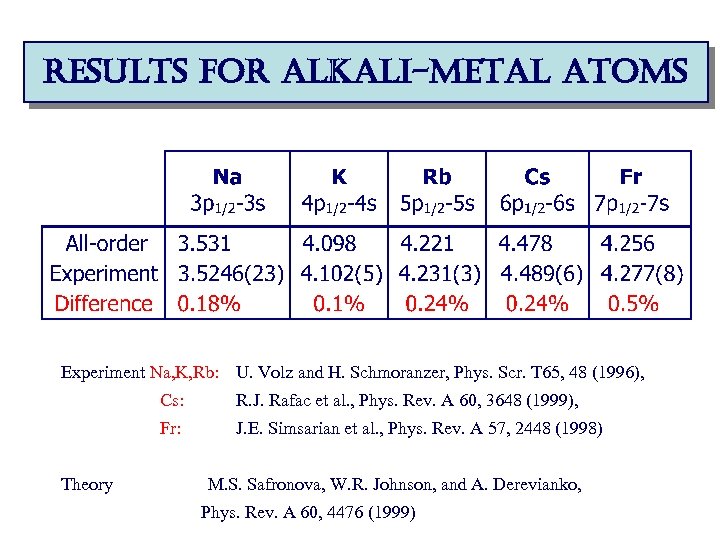results for alkali-metal atoms Experiment Na, K, Rb: U. Volz and H. Schmoranzer, Phys. Scr. T 65, 48 (1996), Cs: Fr: Theory R. J. Rafac et al. , Phys. Rev. A 60, 3648 (1999), J. E. Simsarian et al. , Phys. Rev. A 57, 2448 (1998) M. S. Safronova, W. R. Johnson, and A. Derevianko, Phys. Rev. A 60, 4476 (1999)

theory: evaluation of the uncertainty HOW TO ESTIMATE WHAT YOU DO NOT KNOW? I. Ab initio calculations in different approximations: (a) Evaluation of the size of the correlation corrections (b) Importance of the high-order contributions (c) Distribution of the correlation correction II. Semi-empirical scaling: estimate missing terms

polarizabilities: applications • Optimizing the Rydberg gate • Identification of wavelengths at which two different alkali atoms have the same oscillation frequency for simultaneous optical trapping of two different alkali species. • Detection of inconsistencies in Cs lifetime and Stark shift experiments • Benchmark determination of some K and Rb properties • Calculation of “magic frequencies” for state-insensitive cooling and trapping • Atomic clocks: problem of the BBR shift • …

polarizabilities: applications • Optimizing the Rydberg gate • Identification of wavelengths at which two different alkali atoms have the same oscillation frequency for simultaneous optical trapping of two different alkali species. • Detection of inconsistencies in Cs lifetime and Stark shift experiments • Benchmark determination of some K and Rb properties • Calculation of “magic frequencies” for state-insensitive cooling and trapping • Atomic clocks: problem of the BBR shift • …

applications frequency-dependent polarizabilities of alkali atoms from ultraviolet through infrared spectral regions Goal: First-principles calculations of the frequency-dependent polarizabilities of ground and excited states of alkali-metal atoms Determination of magic wavelengths

magic wavelengths Excited states: determination of magic frequencies in alkali-metal atoms for state-insensitive cooling and trapping, i. e. when does the ground state and excited np state has the same ac stark shift? Bindiya Arora, M. S. Safronova, and Charles W. Clark, Phys. Rev. A 76, 052509 (2007) Na, K, Rb, and Cs

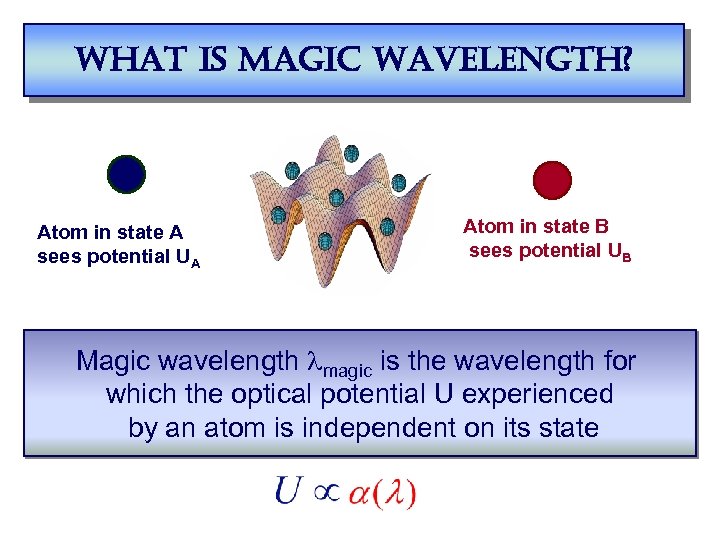what is magic wavelength? Atom in state A sees potential UA Atom in state B sees potential UB Magic wavelength lmagic is the wavelength for which the optical potential U experienced by an atom is independent on its state

locating magic wavelength α (l) S State P State wavelength

what do we need?

what do we need? lots and lots of matrix elements!

what do we need? Cs Lots and lots of matrix elements! 56 matrix elements in

what do we need? Lots and lots of matrix elements! all-order “database”: over 700 matrix elements for alkali-metal atoms and other monovalent systems

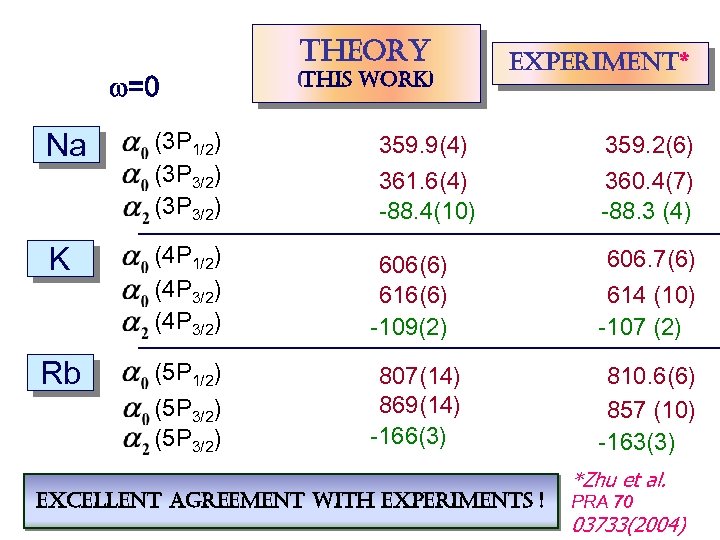theory w=0 (this work) experiment* Na (3 P 1/2) (3 P 3/2) K (4 P 1/2) (4 P 3/2) 606(6) 616(6) -109(2) 614 (10) -107 (2) (5 P 1/2) (5 P 3/2) 807(14) 869(14) -166(3) 810. 6(6) 857 (10) -163(3) Rb 359. 9(4) 361. 6(4) -88. 4(10) excellent agreement with experiments ! 359. 2(6) 360. 4(7) -88. 3 (4) 606. 7(6) *Zhu et al. PRA 70 03733(2004)

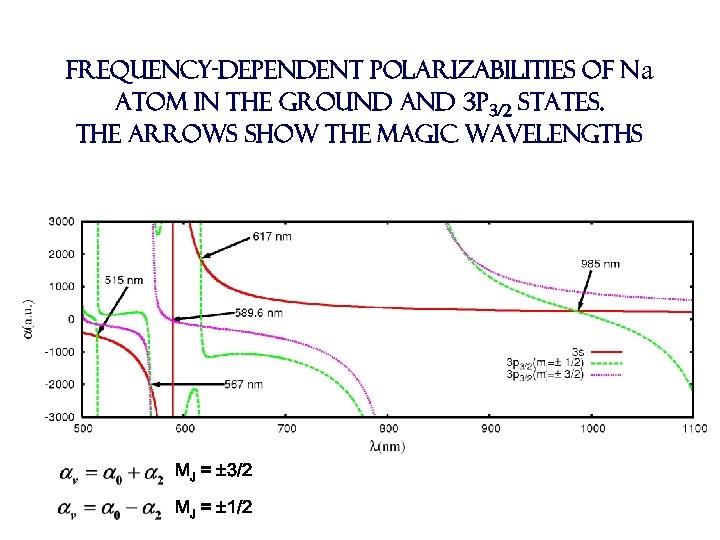Frequency-dependent polarizabilities of Na atom in the ground and 3 p 3/2 states. The arrows show the magic wavelengths MJ = ± 3/2 MJ = ± 1/2

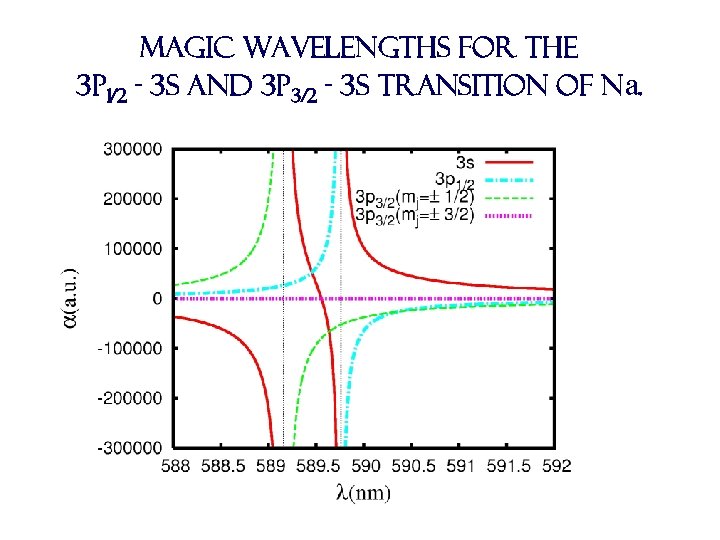Magic wavelengths for the 3 p 1/2 - 3 s and 3 p 3/2 - 3 s transition of Na.

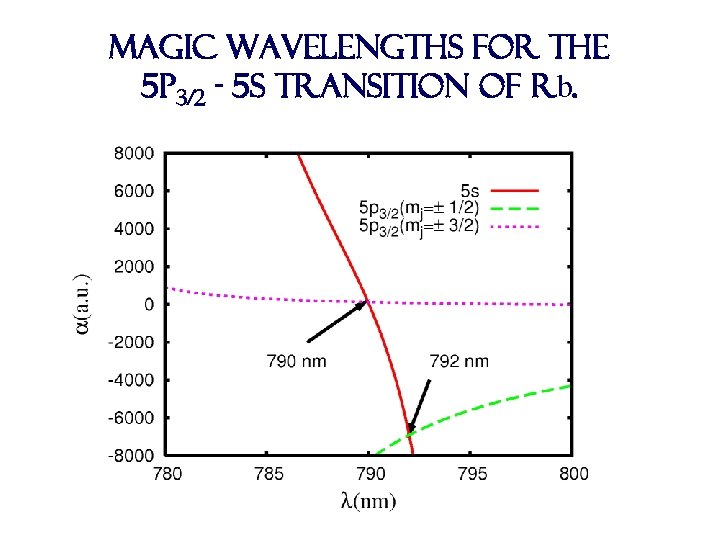Magic wavelengths for the 5 p 3/2 - 5 s transition of Rb.

ac Stark shifts for the transition from 5 p 3/2 F′=3 M′ sublevels to 5 s FM sublevels in Rb. The electric field intensity is taken to be 1 MW/cm 2.

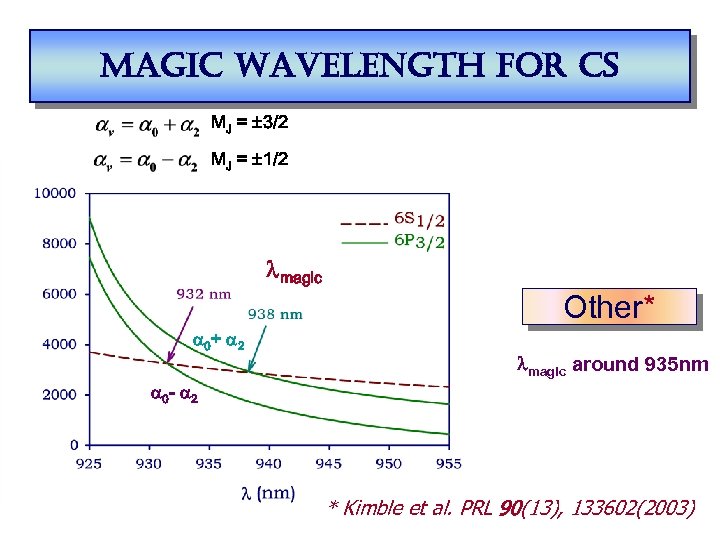magic wavelength for cs MJ = ± 3/2 MJ = ± 1/2 lmagic Other* a 0+ a 2 lmagic around 935 nm a 0 - a 2 * Kimble et al. PRL 90(13), 133602(2003)

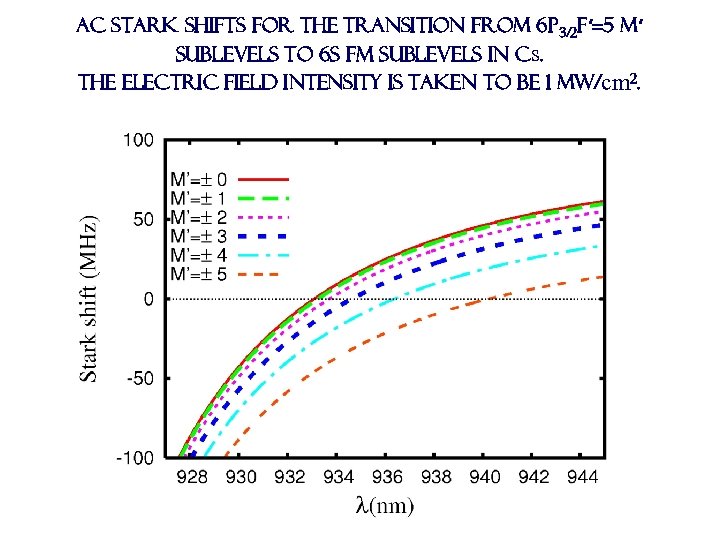ac Stark shifts for the transition from 6 p 3/2 F′=5 M′ sublevels to 6 s FM sublevels in Cs. The electric field intensity is taken to be 1 MW/cm 2.

applications: atomic clocks

atomic clocks black-body radiation ( bbr ) shift Motivation: BBR shift gives the larges uncertainties for some of the optical atomic clock schemes, such as with Ca+

blackbody radiation shift in optical frequency standard 43 ca+ ion with Bindiya Arora, M. S. Safronova, and Charles W. Clark, Phys. Rev. A 76, 064501 (2007)

motivation for ca+, the contribution from blackbody radiation gives the largest uncertainty to the frequency standard at t = 300 k DBBR = 0. 39(0. 27) Hz [1] C. Champenois et. al. Phys. Lett. A 331, 298 (2004)

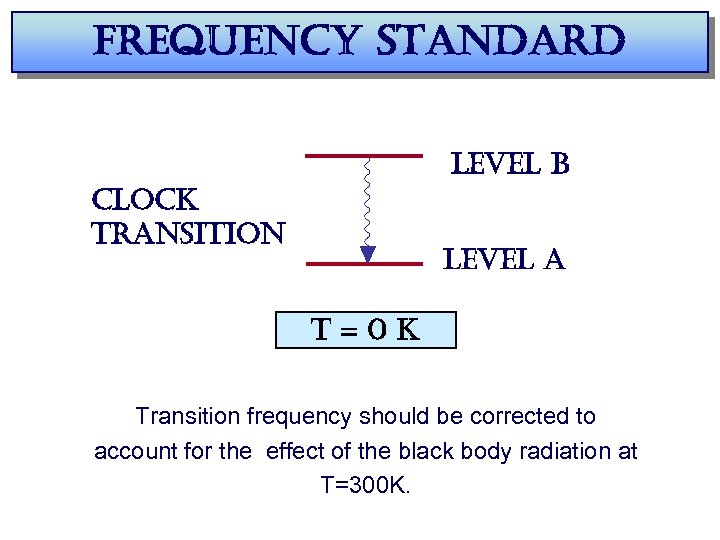frequency standard level b clock transition level a t=0 k Transition frequency should be corrected to account for the effect of the black body radiation at T=300 K.

frequency standard level b clock transition DBBR level a t = 300 k Transition frequency should be corrected to account for the effect of the black body radiation at T=300 K.

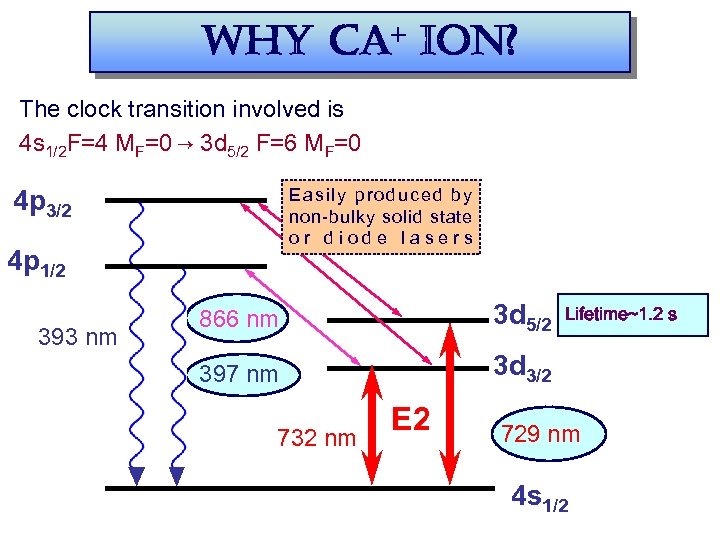why ca+ ion? The clock transition involved is 4 s 1/2 F=4 MF=0 → 3 d 5/2 F=6 MF=0 4 p 3/2 Easily produced by non-bulky solid state o r 854 d e l a s e r s d i o nm 4 p 1/2 393 nm 866 nm 3 d 5/2 397 nm 3 d 3/2 732 nm E 2 Lifetime~1. 2 s 729 nm 4 s 1/2

bbr shift of a level • The temperature-dependent electric field created by the blackbody radiation is described by (in a. u. ) : • Frequency shift caused by this electric field is: Dynamic polarizability

bbr shift and polarizability BBR shift can be expressed in terms of a scalar static polarizability: Dynamic correction ~10 -3 Hz. At the present level of accuracy the dynamic correction can be neglected. vector & tensor polarizability average out due to the isotropic nature of field.

bbr shift for a transition E ffect on the frequency of clock transition is calculated as the difference between the BBR shifts of individual states. 3 d 5/2 729 nm 4 s 1/2

need bbr shifts need ground and excited state scalar static polarizability NOTE: Tensor polarizability calculated in this work is also of experimental interest.

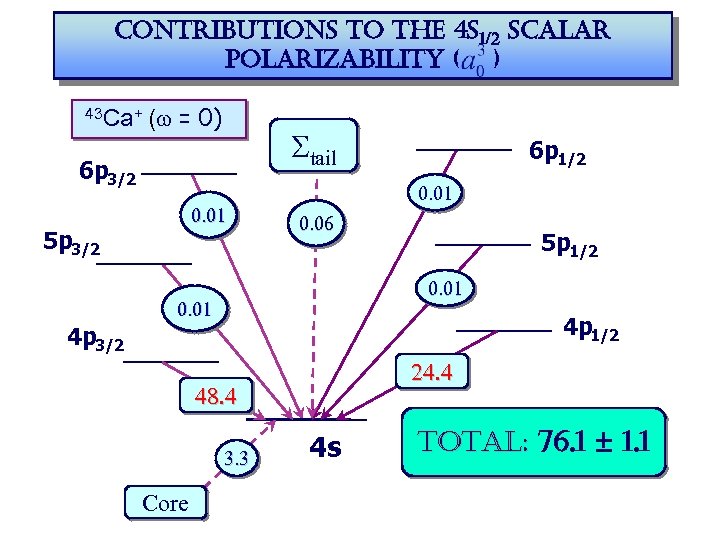contributions to the 4 s 1/2 scalar polarizability ( ) 43 Ca+ (w = 0) Stail 6 p 3/2 0. 01 5 p 3/2 6 p 1/2 0. 01 0. 06 5 p 1/2 0. 01 4 p 1/2 4 p 3/2 24. 4 48. 4 3. 3 Core 4 s total: 76. 1 ± 1. 1

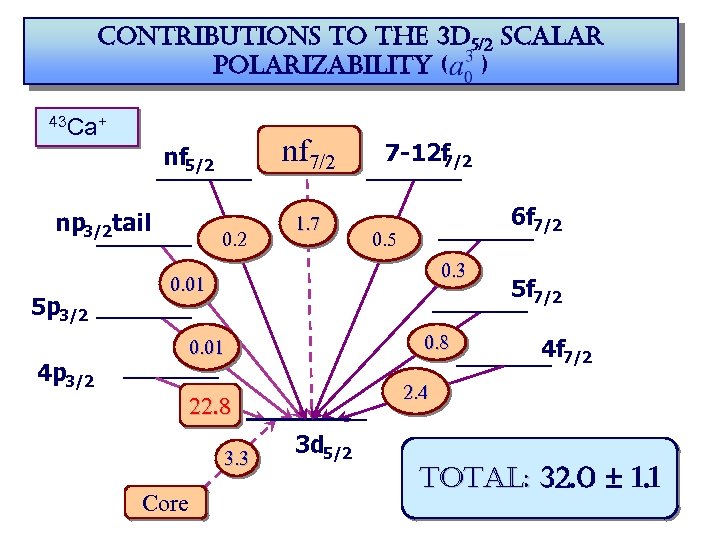contributions to the 3 d 5/2 scalar polarizability ( ) 43 Ca+ nf 7/2 nf 5/2 np 3/2 tail 5 p 3/2 4 p 3/2 0. 2 1. 7 7 -12 f 7/2 6 f 7/2 0. 5 0. 3 0. 01 0. 8 0. 01 Core 4 f 7/2 2. 4 22. 8 3. 3 5 f 7/2 3 d 5/2 total: 32. 0 ± 1. 1

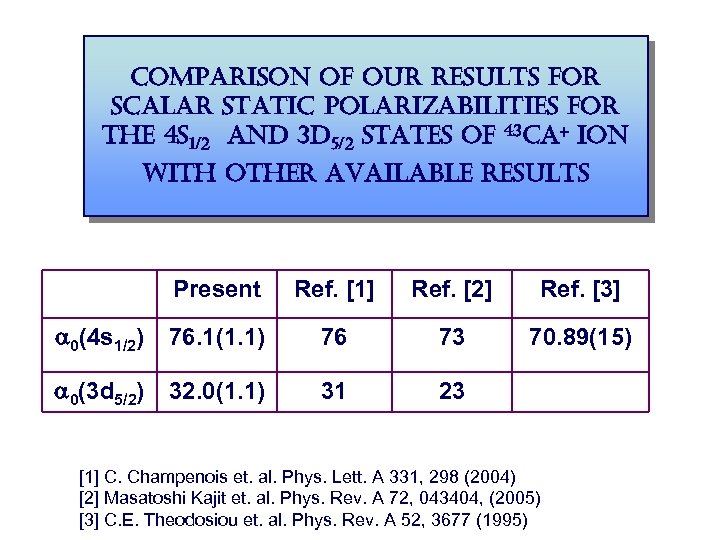comparison of our results for scalar static polarizabilities for the 4 s 1/2 and 3 d 5/2 states of 43 ca+ ion with other available results Present Ref. [1] Ref. [2] Ref. [3] a 0(4 s 1/2) 76. 1(1. 1) 76 73 70. 89(15) a 0(3 d 5/2) 32. 0(1. 1) 31 23 [1] C. Champenois et. al. Phys. Lett. A 331, 298 (2004) [2] Masatoshi Kajit et. al. Phys. Rev. A 72, 043404, (2005) [3] C. E. Theodosiou et. al. Phys. Rev. A 52, 3677 (1995)

black body radiation shift Comparison of black body radiation shift (Hz) for the 4 s 1/2 - 3 d 5/2 transition of 43 Ca+ ion at T=300 K (E=831. 9 V/m). Present D(4 s 1/2 → 3 d 5/2) Champenois[ 1] Kajita [2] 0. 38(1) 0. 39(27) 0. 4 an order of magnitude improvement is achieved with comparison to previous calculations [1] C. Champenois et. al. Phys. Lett. A 331, 298 (2004) [2] Masatoshi Kajit et. al. Phys. Rev. A 72, 043404, (2005)

black body radiation shift Comparison of black body radiation shift (Hz) for the 4 s 1/2 - 3 d 5/2 transition of 43 Ca+ ion at T=300 K (E=831. 9 V/m). Present D(4 s 1/2 → 3 d 5/2) Champenois[ 1] Kajita [2] 0. 38(1) 0. 39(27) 0. 4 sufficient accuracy to establish the uncertainty limits for the ca+ scheme [1] C. Champenois et. al. Phys. Lett. A 331, 298 (2004) [2] Masatoshi Kajit et. al. Phys. Rev. A 72, 043404, (2005)

relativistic all-order method Singly-ionized ions

future studies: more complicated system development of the ci + all-order approach* M. S. Safronova, M. Kozlov, and W. R. Johnson, in preparation

configuration interaction + all-order method CI works for systems with many valence electrons but can not accurately account for core-valence and core-core correlations. All-order method can account for core-core and core-valence correlation can not accurately describe valence-valence correlation. Therefore, two methods are combined to acquire benefits from both approaches.

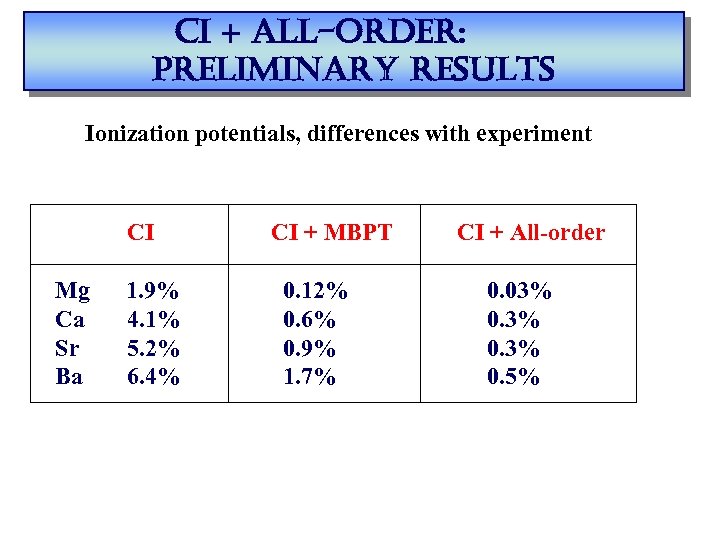ci + all-order: preliminary results Ionization potentials, differences with experiment CI Mg Ca Sr Ba 1. 9% 4. 1% 5. 2% 6. 4% CI + MBPT 0. 12% 0. 6% 0. 9% 1. 7% CI + All-order 0. 03% 0. 5%

Conclusion • Benchmark calculation of various polarizabilities and tests of theory and experiment • Determination of magic wavelengths for stateinsensitive optical cooling and trapping • Accurate calculations of the BBR shifts Future studies: Development of generally applicable CI+ all-order method for more complicated systems

conclusion Parity Violation Atomic Clocks P 1/2 Future: New Systems New Methods, New Problems D 5/2 „quantum bit“ S 1/2 Quantum information

graduate students: bindiya arora rupsi pal Jenny tchoukova dansha Jiang P 3. 8 Jenny Tchoukova and M. S. Safronova Theoretical study of the K, Rb, and Fr lifetimes Q 5. 9 Dansha Jiang, Rupsi Pal, and M. S. Safronova Third-order relativistic many-body calculation of transition probabilities for the beryllium and magnesium isoelectronic sequences U 4. 8 Binidiya Arora, M. S. Safronova, and Charles W. Clark State-insensitive two-color optical trapping