
Д/З: 24. 1 -24. 3 под б 24. 5 -24. 8 под а

Отвечай-ка: Что такое последовательность? Какие виды последовательностей вы знаете? Как задаётся числовая последовательность?

Числовые последовательности
Последовательности составляют такие элементы природы, которые можно пронумеровать Дни недели Дома на улице Классы в школе Названия месяцев Номер счёта в банке
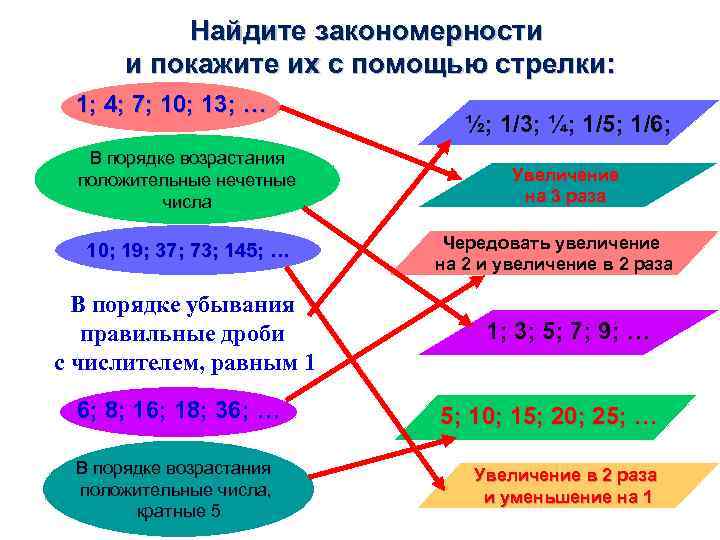
Найдите закономерности и покажите их с помощью стрелки: 1; 4; 7; 10; 13; … В порядке возрастания положительные нечетные числа 10; 19; 37; 73; 145; … В порядке убывания правильные дроби с числителем, равным 1 6; 8; 16; 18; 36; … В порядке возрастания положительные числа, кратные 5 ½; 1/3; ¼; 1/5; 1/6; Увеличение на 3 раза Чередовать увеличение на 2 и увеличение в 2 раза 1; 3; 5; 7; 9; … 5; 10; 15; 20; 25; … Увеличение в 2 раза и уменьшение на 1

Что такое последовательность? Опр-е: Числовой последовательностью называют функцию, которая задана на множестве натуральных чисел. 1, 2, 3, 4, 5, …- послед-ть натуральных чисел; 2, 4, 6, 8, 10, …- последовательность четных чисел; 1, 3, 5, 7, 9, … - последовательность нечетных чисел; 1, 4, 9, 16, 25, …- послед-ть квадратов натур-х чисел; 2, 3, 5, 7, 11, … -последовательность простых чисел;

а 1; а 2; а 3; а 4; … аn – 2 , an − 1 , аn, an + 1 , an + 2 , … члены последовательности 1, 2, 3, 4, 5, …, п - порядковый номер члена последовательности. (ап) - последовательность, в которой ап - п-ый член последовательности ап - 1 - предыдущий член последовательности ап + 1 - следующий член последовательности

Последовательности заданы формулами: an = n 4 an = 2 n - 5 an = n + 4 an= (-1)n n 2 an= - n - 2 an = 3 n - 1 Выполните следующие задания: 1. Впишите пропущенные члены последовательности: 16 1; ___; 81; 256 625; … ___; 6 7 8 5; ___; 9; … -__; 3; 11; 27 __; 3 1 - 9 16 -1; 4; ___; -25; … -3 -5 -6 ___; -4 ; ___; -7; … 26 80 242 2; 8; ___; …

an = n 4 an= (-1)n n 2 an = n + 4 an = 3 n - 1 an = 2 n - 5 an= - n - 2 2. Укажите, какими числами являются члены этих последовательностей Положительные и отрицательные Положительные Отрицательные

Опр-е: Функцию y = последовательности Способы задания f(x) , x N называют функцией натурального аргумента или числовой Словесный способ последовательностью и обозначают: y = f(n) или Правила задания последовательности описываются y 1 , y 2 , y без. . . или ( словами, 3 , . . . , yn , указанияyn )формул или когда закономерности числовая последовательность? Как задаётся между элементами последовательности нет. Пр 1: Последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, . . Пр 2: Произвольный набор чисел: 1, 4, 12, 25, 26, 33, 39, . . Аналитический способ. Любой n-й элемент последовательности можно определить с помощью формулы.

Аналитический способ. Любой n-й элемент последовательности можно определить с помощью формулы. Пр 1: Последовательность чётных чисел: y = 2 n (2, 4, 6, 8, 10, . . . , 2 n, . . ) Пр 2: Последовательность квадрата натуральных чисел: y = n 2; (1, 4, 9, 16, 25, . . . , n 2, . . ) Пр 3: Стационарная последовательность: y = C; C, C, C, . . . . Частный случай: y = 5; 5, 5, 5, . . . . Пр 4: Последовательность y = 2 n; 2, 23, 24, . . . , 2 n, . .

Рекуррентный способ Указывается правило, позволяющее вычислить n-й элемент последовательности, если известны её предыдущие элементы. х1 = 1; хn + 1 = (n + 1) xn n = 1; 2; 3; … х2 = 2 х1 х2 = 2 1 = 2 х3 = 3 х2 х3 = 3 2 = 6 х4 = 4 х3 х4 = 4 6 = 24 х5 = 5 х4 х5 = 5 24 = 120 1; 2; 6; 24; 120; 720; … Пр: Арифметическая прогрессия: a 1 = a, an + 1 = an + d, где a и d – заданные числа, d - разность арифметической прогрессии. Пусть a 1 = 5, d = 0, 7, тогда арифметическая прогрессия будет иметь вид: 5; 5, 7; 6, 4; 7, 1; 7, 8; 8, 5; . .

Пр1: Составить возможную формулу n-го элемента последовательности (yn): а) 1, 3, 5, 7, 9, 11, . . . - послед-ть нечётных чисел y= -1 y = 2 n 2 n - 1 б) 4, 8, 12, 16, 20, . . . - числовая последовательность, у которой последующий элемент больше предыдущего на 4 y = 4 n

Пр 2: Выписать первые семь элементов последовательности, заданной рекуррентно: y 1 = 1, y 2 = 2, yn = yn - 2 + yn - 1, если n = 3, 4, 5, 6, . . . y 1 = 1; y 2 = 2; y 3 = 1 + 2 = 3; y 4 = 3 + 2 = 5; y 5 = 5 + 3 = 8; y 6 = 8 + 5 = 13; y 7 = 13 + 8 = 21;

Пр 3: Последовательность (yn) задана рекуррентно: y 1 = 1, y 2 = 2, yn= 5 yn – 1 − 6 yn – 2. Задать эту последовательность аналитически. y 1 = 1; y 2 = 2; y 3 = 5 y 2 - 6 y 1 y 3 = 5 2 - 6 1 = 4; y 4 = 5 y 3 - 6 y 2 y 4 = 5 4 - 6 2 = 8; y 5 = 5 y 4 - 6 y 3 y 5 = 5 8 - 6 4 = 16; y 6 = 5 y 5 - 6 y 4 y 6 = 5 16 - 6 8 = 32; Получаем последовательность: 1; 2; 4; 8; 16; 32; . . . , которую можно представить в виде 20; 21; 22; 23; 24; 25. . . при n = 1; 2; 3; 4; 5; 6; . . Получаем следующую закономерность: y = 2 n - 1

Дана последовательность yn = 24 n + 36 - 5 n 2. а) Сколько в ней положительных членов? б) Найти наибольший элемент последовательности. в) Есть в данной последовательности наименьший элемент? Данная числовая последовательность – это функция вида y = − 5 x 2 + 24 x + 36, где x N у = − 5 x 2 + 24 x + 36 - квадратичная ф-я, гр-к – парабола, − 5 x 2 + 24 x + 36 0 ветви направленны − 5 x 2 + 24 x + 36 = 0 D = b 2 − 4 ac D = 242 − 4 (− 5) 36 = 576 + 720 = 1296 = 362

− 5 x 2 + 24 x + 36 0 -1, 2 6 − 1, 2 x 6 yn = 24 n + 36 - 5 n 2 б) Найти наибольший элемент последовательности в) Есть в данной последовательности наименьший элемент? 1, 2, 3, 4, 5 x N Значит в заданной последовательности пять положительных элементов последовательности. y 1 = 24 1 + 36 - 5 12 = 24 + 36 – 5 = 55 y = 64 – наиб-й 2 2 = 48 + 36 – 20 = 64 y 2 = 24 2 + 36 - 5 2 эл-т пос-ти y 3 = 24 3 + 36 - 5 32 = 72 + 36 – 45 = 62 y 4 = 24 4 + 36 - 5 42 = 96 + 36 – 80 = 52 наим-го эл-та 2 = 120 + 36 – 125 = 31 пос-ти НЕТ y 5 = 24 5 + 36 - 5 5

Решите номера: 24. 1 -24. 3 под в 24. 5 -24. 8 под б

1; 4; 7; 10; 13; … - последовательность чисел заданная увеличением на 3 единицы 1; 3; 5; 7; 9; … - последовательность чисел заданная в порядке возрастания положительных нечетных числ ½; 1/3; ¼; 1/5; 1/6; … - последовательность чисел заданная в порядке убывания правильных дробей с числителем, равным 1 5; 10; 15; 20; 25; …-последовательность положительных чисел кратных 5, расположенная в порядке возрастания

Д/з: конспект стр 140 - 143 24. 14(а, в), 24. 15(а, б)

Свойства числовых последовательностей

Последовательность (уn) называется ограниченной сверху, если все ее члены не больше некоторого числа. Последовательность (уn) ограничена сверху, если существует такое число М, что для любого члена выполняется неравенство уn М. Число М – верхняя граница последовательности. Ограничена сверху. М = -1 или любое число большее М (М = 0). уn = - n 2 , уn 0 уn - Ограничена сверху

Последовательность (уn) называется ограниченной снизу, если все ее члены не меньше некоторого числа. Последовательность (уn) ограничена снизу, если существует такое число m, что для любого члена выполняется неравенство уn m. Число m – нижняя граница последовательности. Ограничена снизу. m = 1 или любое число меньшее m (m = 0, 5). уn = n 2 , уn 0 уn - Ограничена снизу

Последовательность (уn) ограниченная снизу и сверху, называется ограниченной последовательностью. M = 1, m = 0

ПР: Дана числовая последовательность: Определите, является ли она ограниченной? Решение: Максимальное значение, которое может принимать эта числовая последовательность это 1, а минимальное – 0 Значит эта числовая последовательность ограниченная.

Проверьте на ограниченности заданную последовательность Рассмотрим два соседних числа an и аn+1 n+2 n+1 0

Проверьте на ограниченности заданную последовательность Проверим на ограниченность сверху 3 1

Последовательность (уn) называется возрастающей, если каждый ее член больше предыдущего: 1, 3, 5, 7, … , 2 n – 1, … - возрастающая последовательность ОПР: Последовательность аn для любого n N называется возрастающей если аn + 1 an или an + 1 – an 0 ПР: Исследуйте на монотонность Выпишем n-й и (n + 1)-й члены последовательности:

ОПР: Последовательность аn для любого n N называется возрастающей если аn + 1 an или an + 1 – an 0 Исследуйте на монотонность Выпишем n-й и (n + 1)-й члены последовательности: Найдём их разность: an + 1 – an n+2 n+3 an + 1 – an = 0 an + 1 – an 0

Последовательность (уn) называется убывающей, если каждый ее член меньше предыдущего: убывающая последовательность ОПР: Последовательность аn для любого n N называется убывающей если аn + 1 an или an + 1 – an 0 Возрастающие и убывающие последовательности являются монотонными последовательностями.

ПР: Исследовать на монотонность последовательность Выпишем n-й и (n + 1) - й члены последовательности: Найдём их разность: уn + 1 – уn 5 0

Решите номера: 24. 14(б, г), 24. 15(в, г) ОПР: Последовательность аn для любого n N называется возрастающей если аn + 1 an или an + 1 – an 0 ОПР: Последовательность аn для любого n N называется убывающей если аn + 1 an или an + 1 – an 0