D MODULE Waiting-Line Models Power Point presentation to

D MODULE Waiting-Line Models Power. Point presentation to accompany Heizer and Render Operations Management, Eleventh Edition Principles of Operations Management, Ninth Edition Power. Point slides by Jeff Heyl © 2014 Pearson Education, Inc. © 2014 Pearson Education, MD - 1

Outline ► ► ► Queuing Theory Characteristics of a Waiting-Line System Queuing Costs The Variety of Queuing Models Other Queuing Approaches © 2014 Pearson Education, Inc. MD - 2

Learning Objectives When you complete this chapter you should be able to: 1. Describe the characteristics of arrivals, waiting lines, and service systems 2. Apply the single-server queuing model equations 3. Conduct a cost analysis for a waiting line © 2014 Pearson Education, Inc. MD - 3

Learning Objectives When you complete this chapter you should be able to: 4. Apply the multiple-server queuing model formulas 5. Apply the constant-service-time model equations 6. Perform a limited-population model analysis © 2014 Pearson Education, Inc. MD - 4

Queuing Theory ▶ The study of waiting lines ▶ Waiting lines are common situations ▶ Useful in both manufacturing and service areas © 2014 Pearson Education, Inc. MD - 5

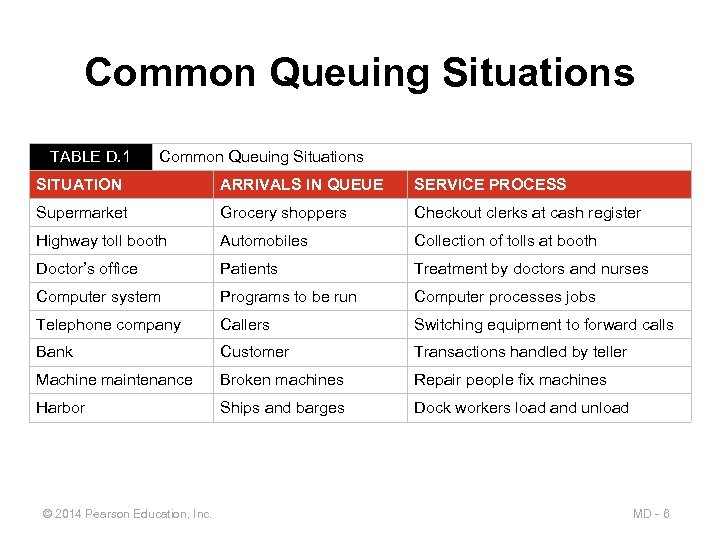Common Queuing Situations TABLE D. 1 Common Queuing Situations SITUATION ARRIVALS IN QUEUE SERVICE PROCESS Supermarket Grocery shoppers Checkout clerks at cash register Highway toll booth Automobiles Collection of tolls at booth Doctor’s office Patients Treatment by doctors and nurses Computer system Programs to be run Computer processes jobs Telephone company Callers Switching equipment to forward calls Bank Customer Transactions handled by teller Machine maintenance Broken machines Repair people fix machines Harbor Ships and barges Dock workers load and unload © 2014 Pearson Education, Inc. MD - 6

Characteristics of Waiting-Line Systems 1. Arrivals or inputs to the system ▶ Population size, behavior, statistical distribution 2. Queue discipline, or the waiting line itself ▶ Limited or unlimited in length, discipline of people or items in it 3. The service facility ▶ Design, statistical distribution of service times © 2014 Pearson Education, Inc. MD - 7

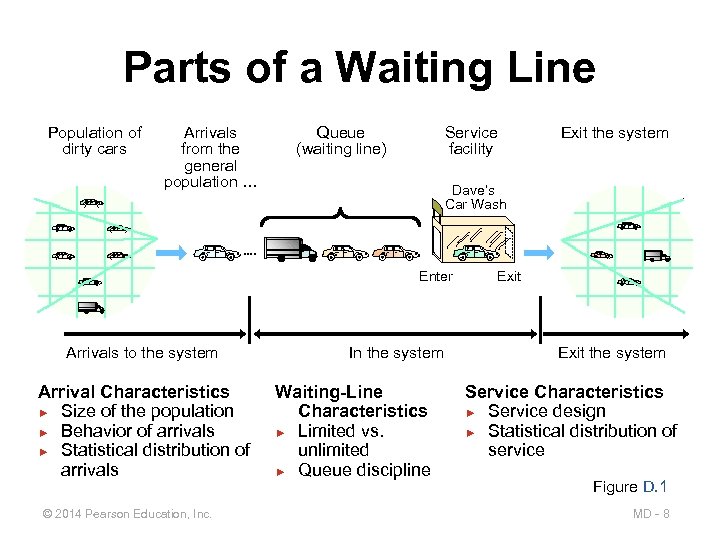Parts of a Waiting Line Population of dirty cars Arrivals from the general population … Queue (waiting line) Service facility Dave’s Car Wash Enter Arrivals to the system Arrival Characteristics ► Size of the population ► Behavior of arrivals ► Statistical distribution of arrivals © 2014 Pearson Education, Inc. Exit the system In the system Waiting-Line Characteristics ► Limited vs. unlimited ► Queue discipline Exit the system Service Characteristics ► Service design ► Statistical distribution of service Figure D. 1 MD - 8

Arrival Characteristics 1. Size of the arrival population ▶ Unlimited (infinite) or limited (finite) 2. Pattern of arrivals ▶ Scheduled or random, often a Poisson distribution 3. Behavior of arrivals ▶ Wait in the queue and do not switch lines ▶ No balking or reneging © 2014 Pearson Education, Inc. MD - 9

Poisson Distribution e- x P(x) = x! for x = 0, 1, 2, 3, 4, … where P(x) = probability of x arrivals x = number of arrivals per unit of time = average arrival rate e = 2. 7183 (which is the base of the natural logarithms) © 2014 Pearson Education, Inc. MD - 10

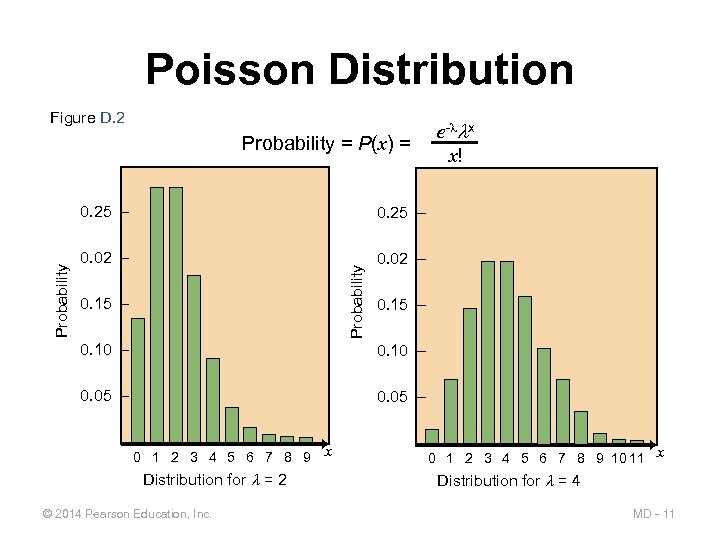Poisson Distribution Figure D. 2 e- x x! Probability = P(x) = 0. 25 – 0. 02 – Probability 0. 25 – 0. 15 – 0. 10 – 0. 05 – – 0 1 2 3 4 5 6 7 8 9 Distribution for = 2 © 2014 Pearson Education, Inc. x – 0 1 2 3 4 5 6 7 8 9 10 11 x Distribution for = 4 MD - 11

Waiting-Line Characteristics ▶ Limited or unlimited queue length ▶ Queue discipline - first-in, first-out (FIFO) is most common ▶ Other priority rules may be used in special circumstances © 2014 Pearson Education, Inc. MD - 12

Service Characteristics 1. Queuing system designs ▶ Single-server system, multiple-server system ▶ Single-phase system, multiphase system 2. Service time distribution ▶ Constant service time ▶ Random service times, usually a negative exponential distribution © 2014 Pearson Education, Inc. MD - 13

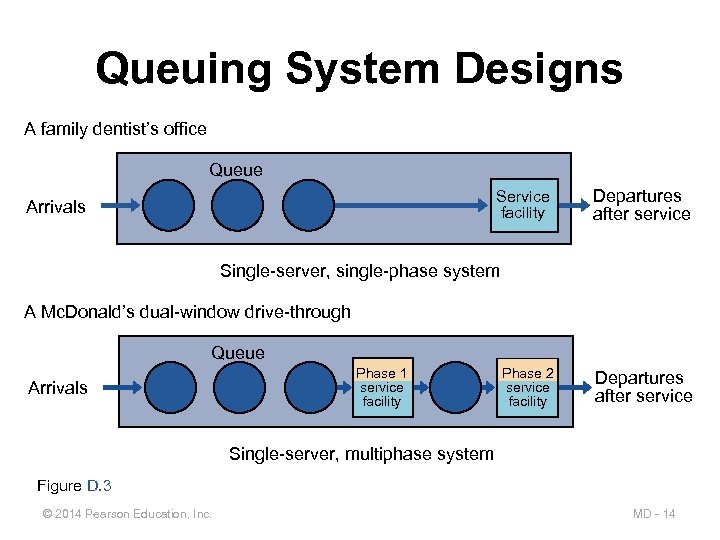Queuing System Designs A family dentist’s office Queue Service facility Arrivals Departures after service Single-server, single-phase system A Mc. Donald’s dual-window drive-through Queue Arrivals Phase 1 service facility Phase 2 service facility Departures after service Single-server, multiphase system Figure D. 3 © 2014 Pearson Education, Inc. MD - 14

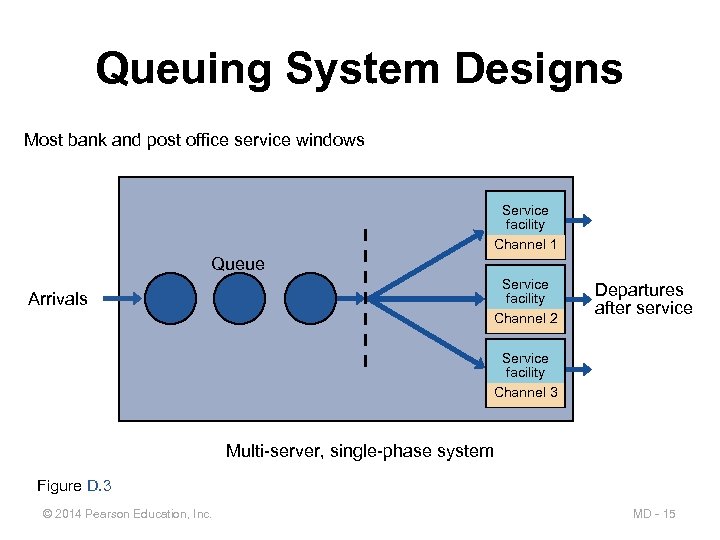Queuing System Designs Most bank and post office service windows Service facility Channel 1 Queue Arrivals Service facility Channel 2 Departures after service Service facility Channel 3 Multi-server, single-phase system Figure D. 3 © 2014 Pearson Education, Inc. MD - 15

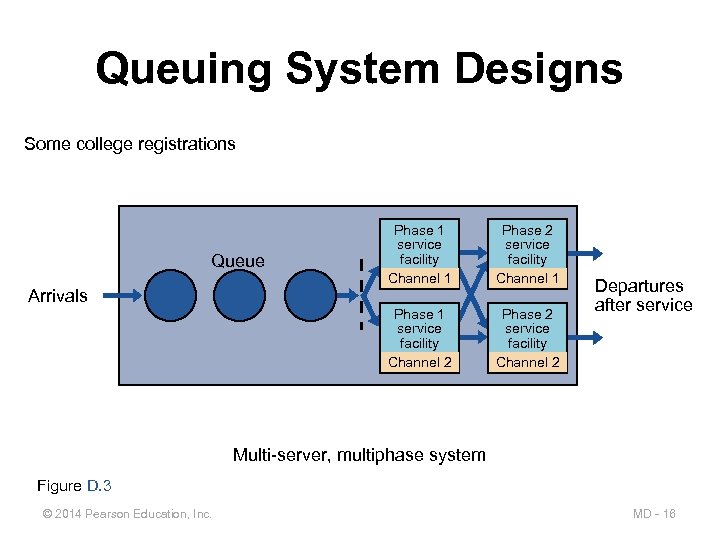Queuing System Designs Some college registrations Arrivals Phase 2 service facility Channel 1 Phase 1 service facility Channel 2 Queue Phase 1 service facility Channel 1 Phase 2 service facility Channel 2 Departures after service Multi-server, multiphase system Figure D. 3 © 2014 Pearson Education, Inc. MD - 16

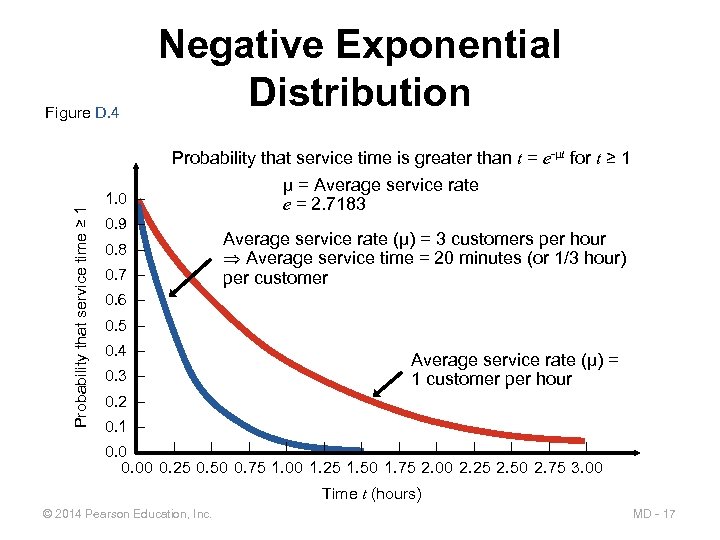Figure D. 4 Negative Exponential Distribution Probability that service time ≥ 1 Probability that service time is greater than t = e-µt for t ≥ 1 1. 0 – 0. 9 – 0. 8 – 0. 7 – µ = Average service rate e = 2. 7183 Average service rate (µ) = 3 customers per hour Average service time = 20 minutes (or 1/3 hour) per customer 0. 6 – 0. 5 – 0. 4 – 0. 3 – Average service rate (µ) = 1 customer per hour 0. 2 – 0. 1 – | | | 0. 0 |– 0. 00 0. 25 0. 50 0. 75 1. 00 1. 25 1. 50 1. 75 2. 00 2. 25 2. 50 2. 75 3. 00 Time t (hours) © 2014 Pearson Education, Inc. MD - 17

Measuring Queue Performance 1. Average time that each customer or object spends in the queue 2. Average queue length 3. Average time each customer spends in the system 4. Average number of customers in the system 5. Probability that the service facility will be idle 6. Utilization factor for the system 7. Probability of a specific number of customers in the system © 2014 Pearson Education, Inc. MD - 18

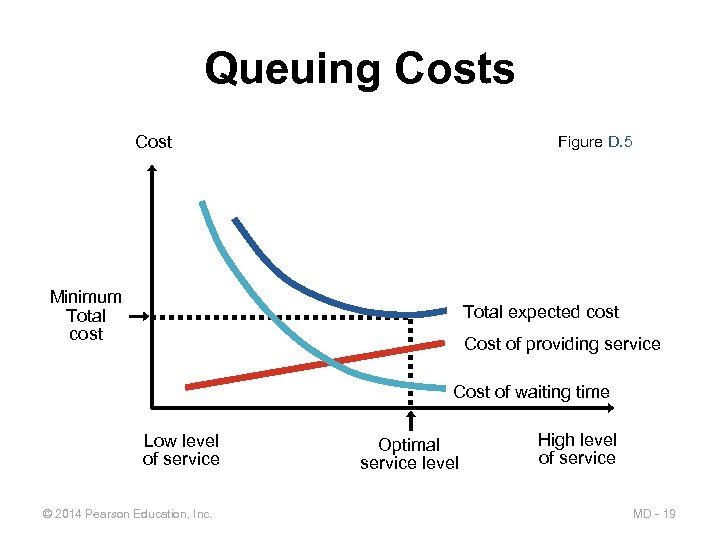Queuing Costs Cost Figure D. 5 Minimum Total cost Total expected cost Cost of providing service Cost of waiting time Low level of service © 2014 Pearson Education, Inc. Optimal service level High level of service MD - 19

Queuing Models The four queuing models here all assume: 1. Poisson distribution arrivals 2. FIFO discipline 3. A single-service phase © 2014 Pearson Education, Inc. MD - 20

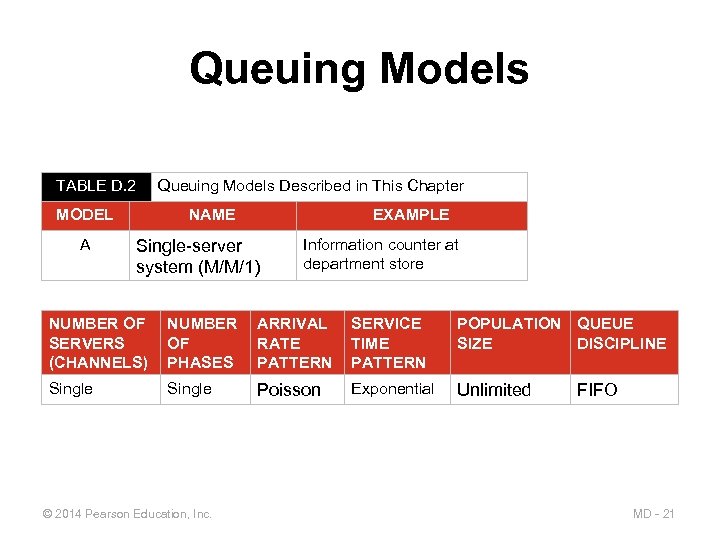Queuing Models TABLE D. 2 Queuing Models Described in This Chapter MODEL A NAME EXAMPLE Single-server system (M/M/1) Information counter at department store NUMBER OF SERVERS (CHANNELS) NUMBER OF PHASES ARRIVAL RATE PATTERN SERVICE TIME PATTERN POPULATION QUEUE SIZE DISCIPLINE Single Poisson Exponential Unlimited © 2014 Pearson Education, Inc. FIFO MD - 21

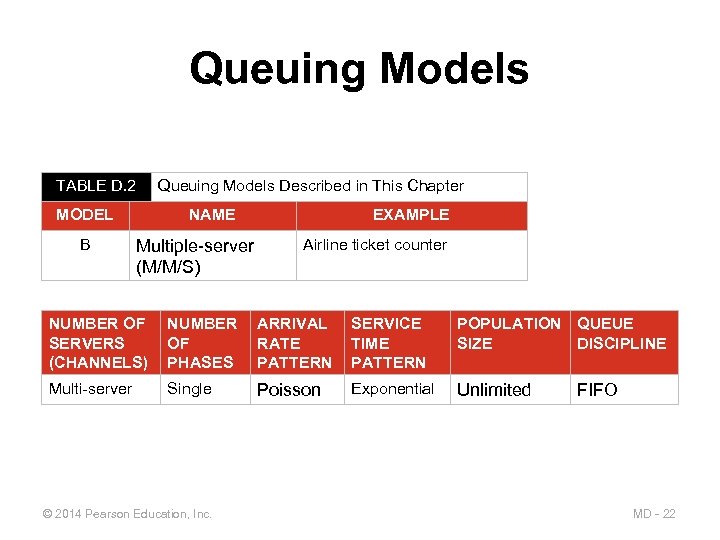Queuing Models TABLE D. 2 Queuing Models Described in This Chapter MODEL B NAME Multiple-server (M/M/S) EXAMPLE Airline ticket counter NUMBER OF SERVERS (CHANNELS) NUMBER OF PHASES ARRIVAL RATE PATTERN SERVICE TIME PATTERN POPULATION QUEUE SIZE DISCIPLINE Multi-server Single Poisson Exponential Unlimited © 2014 Pearson Education, Inc. FIFO MD - 22

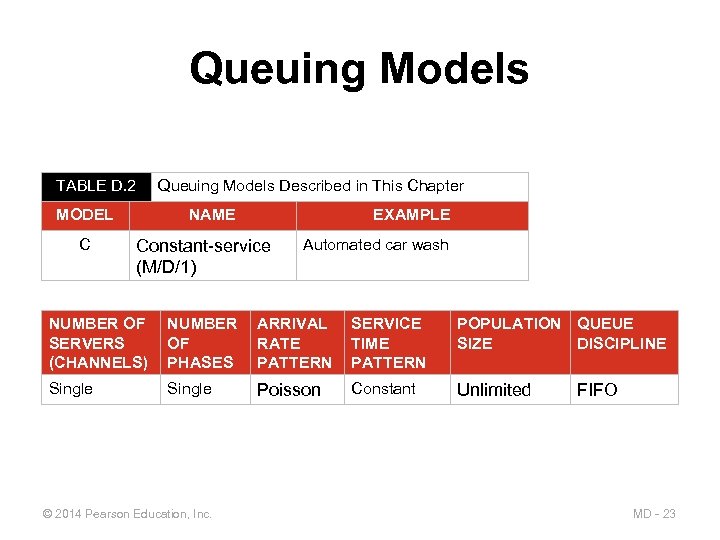Queuing Models TABLE D. 2 Queuing Models Described in This Chapter MODEL C NAME EXAMPLE Constant-service (M/D/1) Automated car wash NUMBER OF SERVERS (CHANNELS) NUMBER OF PHASES ARRIVAL RATE PATTERN SERVICE TIME PATTERN POPULATION QUEUE SIZE DISCIPLINE Single Poisson Constant Unlimited © 2014 Pearson Education, Inc. FIFO MD - 23

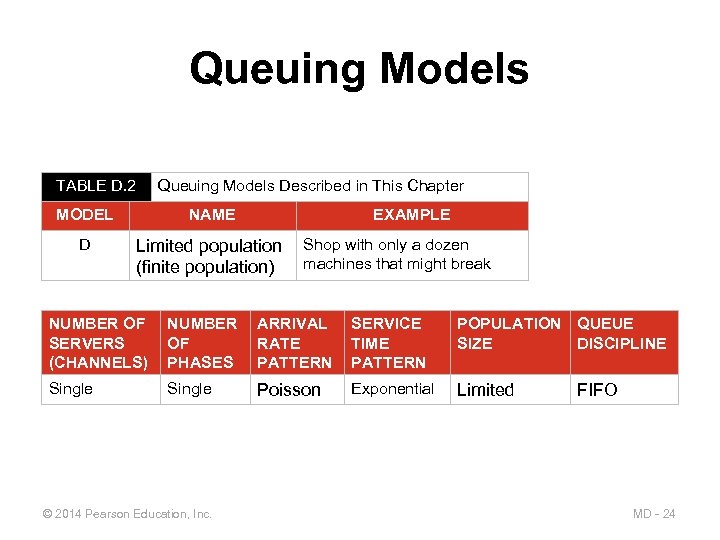Queuing Models TABLE D. 2 Queuing Models Described in This Chapter MODEL NAME EXAMPLE D Limited population (finite population) Shop with only a dozen machines that might break NUMBER OF SERVERS (CHANNELS) NUMBER OF PHASES ARRIVAL RATE PATTERN SERVICE TIME PATTERN POPULATION QUEUE SIZE DISCIPLINE Single Poisson Exponential Limited © 2014 Pearson Education, Inc. FIFO MD - 24

Model A – Single-Server 1. Arrivals are served on a FIFO basis and every arrival waits to be served regardless of the length of the queue 2. Arrivals are independent of preceding arrivals but the average number of arrivals does not change over time 3. Arrivals are described by a Poisson probability distribution and come from an infinite population © 2014 Pearson Education, Inc. MD - 25

Model A – Single-Server 4. Service times vary from one customer to the next and are independent of one another, but their average rate is known 5. Service times occur according to the negative exponential distribution 6. The service rate is faster than the arrival rate © 2014 Pearson Education, Inc. MD - 26

Model A – Single-Server TABLE D. 3 Queuing Formulas for Model A: Single-Server System, also Called M/M/1 λ = mean number of arrivals per time period μ = mean number of people or items served per time period (average service rate) Ls = average number of units (customers) in the system (waiting and being served) = λ μ–λ Ws = average time a unit spends in the system (waiting time plus service time) = 1 μ–λ © 2014 Pearson Education, Inc. MD - 27

Model A – Single-Server Queuing Formulas for Model A: Single-Server System, also Called M/M/1 TABLE D. 3 Lq = mean number of units waiting in the queue = λ 2 μ(μ – λ) Wq = average time a unit spends waiting in the queue = λ μ(μ – λ) = Lq λ ρ = utilization factor for the system = λ μ © 2014 Pearson Education, Inc. MD - 28

Model A – Single-Server Queuing Formulas for Model A: Single-Server System, also Called M/M/1 TABLE D. 3 P 0 = Probability of 0 units in the system (that is, the service unit is idle) λ =1– μ Pn>k = probability of more than k units in the system, where n is the number of units in the system = [ ] k+1 λ μ © 2014 Pearson Education, Inc. MD - 29

Single-Server Example = 2 cars arriving/hour © 2014 Pearson Education, Inc. µ = 3 cars serviced/hour MD - 30

Single-Server Example = 2 cars arriving/hour Wq = µ(µ – ) = µ = 3 cars serviced/hour 2 = 2/3 hour = 40 minute 3(3 – 2) average waiting time 2 = = = 66. 6% of time mechanic is busy µ 3 P 0 = 1 – µ © 2014 Pearson Education, Inc. =. 33 probability there are 0 cars in the system MD - 31

Single-Server Example Probability of more than k Cars in the System K Pn > k = (2/3)k + 1 0 . 667 Note that this is equal to 1 – P 0 = 1 –. 33 1 . 444 2 . 296 3 . 198 Implies that there is a 19. 8% chance that more than 3 cars are in the system 4 . 132 5 . 088 6 . 058 7 . 039 © 2014 Pearson Education, Inc. MD - 32

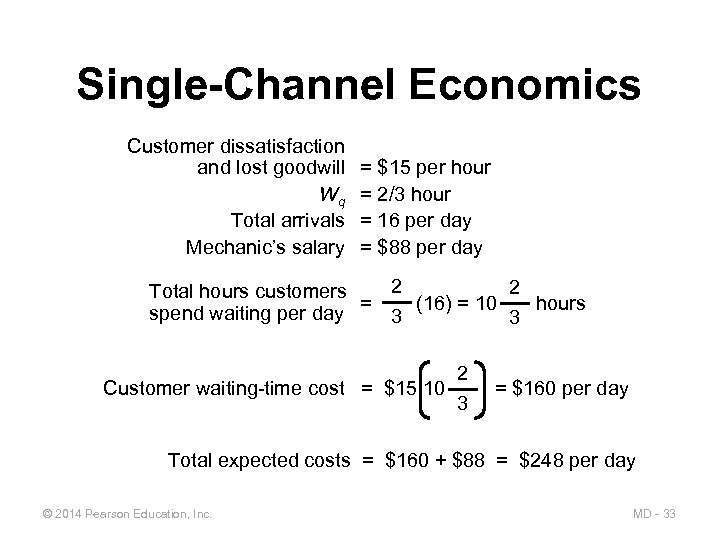Single-Channel Economics Customer dissatisfaction and lost goodwill Wq Total arrivals Mechanic’s salary = $15 per hour = 2/3 hour = 16 per day = $88 per day 2 2 Total hours customers spend waiting per day = 3 (16) = 10 3 hours Customer waiting-time cost = $15 10 2 3 = $160 per day Total expected costs = $160 + $88 = $248 per day © 2014 Pearson Education, Inc. MD - 33

Multiple-Server Model TABLE D. 4 Queuing Formulas for Model B: Multiple-Server System, also Called M/M/S M = number of servers (channels) open = average arrival rate µ = average service rate at each server (channel) The probability that there are zero people or units in the system is: © 2014 Pearson Education, Inc. MD - 34

Multiple-Server Model TABLE D. 4 Queuing Formulas for Model B: Multiple-Server System, also Called M/M/S The number of people or units in the system is: The average time a unit spends in the waiting line and being serviced (namely, in the system) is: © 2014 Pearson Education, Inc. MD - 35

Multiple-Server Model TABLE D. 4 Queuing Formulas for Model B: Multiple-Server System, also Called M/M/S The average number of people or units in line waiting for service is: The average time a person or unit spends in the queue waiting for service is: © 2014 Pearson Education, Inc. MD - 36

Multiple-Server Example = 2 © 2014 Pearson Education, Inc. µ = 3 M = 2 MD - 37

Multiple-Server Example © 2014 Pearson Education, Inc. MD - 38

Multiple-Server Example SINGLE SERVER TWO SERVERS (CHANNELS) P 0 . 33 . 5 Ls 2 cars . 75 cars Ws 60 minutes 22. 5 minutes Lq 1. 33 cars . 083 cars Wq 40 minutes 2. 5 minutes © 2014 Pearson Education, Inc. MD - 39

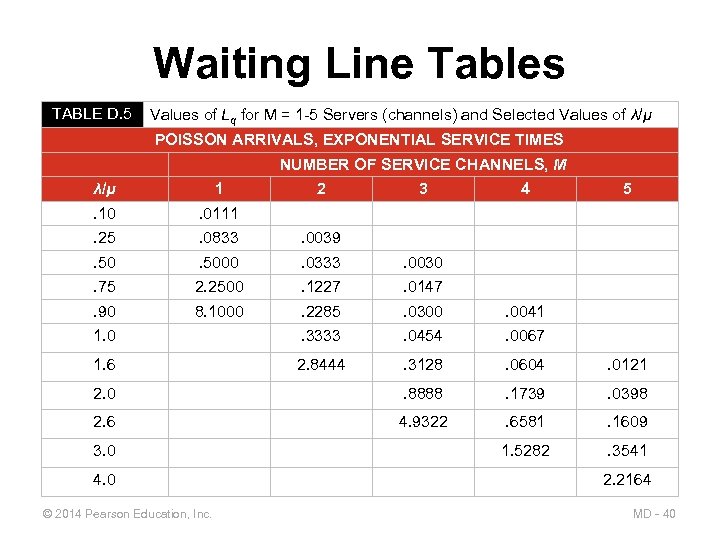Waiting Line Tables TABLE D. 5 Values of Lq for M = 1 -5 Servers (channels) and Selected Values of λ/μ POISSON ARRIVALS, EXPONENTIAL SERVICE TIMES NUMBER OF SERVICE CHANNELS, M λ/μ 1 . 10 . 0111 . 25 . 0833 . 0039 . 5000 . 0333 . 0030 . 75 2. 2500 . 1227 . 0147 . 90 8. 1000 . 2285 . 0300 . 0041 1. 0 . 3333 . 0454 . 0067 1. 6 2. 8444 . 3128 . 0604 . 0121 2. 0 . 8888 . 1739 . 0398 2. 6 4. 9322 . 6581 . 1609 1. 5282 . 3541 3. 0 4. 0 © 2014 Pearson Education, Inc. 2 3 4 5 2. 2164 MD - 40

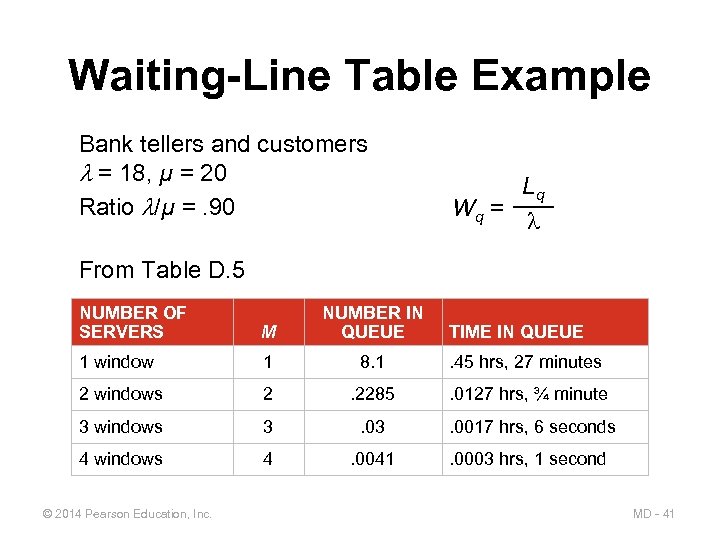Waiting-Line Table Example Bank tellers and customers = 18, µ = 20 Ratio /µ =. 90 Lq Wq = From Table D. 5 NUMBER OF SERVERS M NUMBER IN QUEUE 1 window 1 8. 1 . 45 hrs, 27 minutes 2 windows 2 . 2285 . 0127 hrs, ¾ minute 3 windows 3 . 0017 hrs, 6 seconds 4 windows 4 . 0041 . 0003 hrs, 1 second © 2014 Pearson Education, Inc. TIME IN QUEUE MD - 41

Constant-Service-Time Model TABLE D. 6 Queuing Formulas for Model C: Constant Service, also Called M/D/1 Average length of queue: Average waiting time in queue: Average number of customers in the system: Average time in the system: © 2014 Pearson Education, Inc. MD - 42

Constant-Service-Time Example Trucks currently wait 15 minutes on average Truck and driver cost $60 per hour Automated compactor service rate (µ) = 12 trucks per hour Arrival rate ( ) = 8 per hour Compactor costs $3 per truck Current waiting cost per trip = (1/4 hr)($60) = $15 /trip 1 8 Wq = = hour 12 2(12)(12 – 8) Waiting cost/trip = (1/12 hr wait)($60/hr cost) with compactor Savings with = $15 (current) – $5(new) new equipment Cost of new equipment amortized Net savings © 2014 Pearson Education, Inc. = $ 5 /trip = $10 /trip = $ 3 /trip = $ 7 /trip MD - 43

Little’s Law ► A queuing system in steady state L = W (which is the same as W = L/ Lq = Wq (which is the same as Wq = Lq/ ► ► ► Once one of these parameters is known, the other can be easily found It makes no assumptions about the probability distribution of arrival and service times Applies to all queuing models except the limited population model © 2014 Pearson Education, Inc. MD - 44

Limited-Population Model TABLE D. 7 Queuing Formulas and Notation for Model D: Limited-Population Formulas Service factor: Average number of units running: Average number waiting: Average number being serviced: Average waiting time: Number in population: Average time in the system: © 2014 Pearson Education, Inc. MD - 45

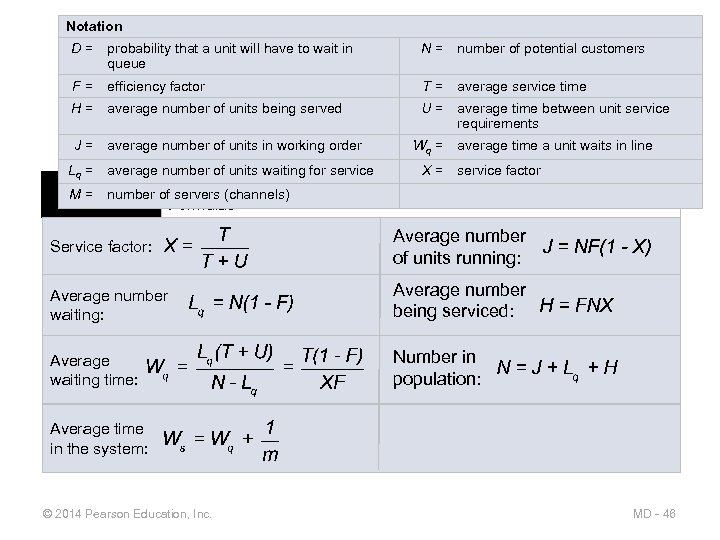Notation D= probability that a unit will have to wait in queue N= number of potential customers F= efficiency factor T= average service time H= average number of units being served U= average time between unit service requirements J= average number of units in working order Limited-Population Model Lq = average number of units waiting for service Wq = X= average time a unit waits in line service factor Queuing Formulas and Notation for Model D: Limited-Population M = number TABLE D. 7 of servers (channels) Formulas Service factor: Average number of units running: Average number waiting: Average number being serviced: Average waiting time: Number in population: Average time in the system: © 2014 Pearson Education, Inc. MD - 46

Finite Queuing Table 1. Compute X (the service factor), where X = T / (T + U) 2. Find the value of X in the table and then find the line for M (where M is the number of servers) 3. Note the corresponding values for D and F 4. Compute Lq, Wq, J, H, or whichever are needed to measure the service system’s performance © 2014 Pearson Education, Inc. MD - 47

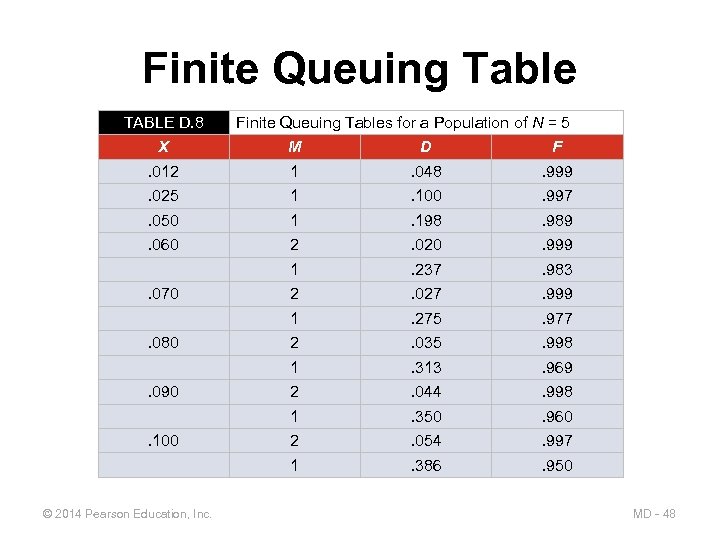Finite Queuing Table TABLE D. 8 Finite Queuing Tables for a Population of N = 5 X M D F . 012 1 . 048 . 999 . 025 1 . 100 . 997 . 050 1 . 198 . 989 . 060 2 . 020 . 999 1 . 237 . 983 2 . 027 . 999 1 . 275 . 977 2 . 035 . 998 1 . 313 . 969 2 . 044 . 998 1 . 350 . 960 2 . 054 . 997 1 . 386 . 950 . 070. 080. 090. 100 © 2014 Pearson Education, Inc. MD - 48

Limited-Population Example Each of 5 printers requires repair after 20 hours (U) of use One technician can service a printer in 2 hours (T) Printer downtime costs $120/hour Technician costs $25/hour 2 Service factor: X = =. 091 (close to. 090) 2 + 20 For M = 1, D =. 350 and F =. 960 For M = 2, D =. 044 and F =. 998 Average number of printers working: For M = 1, J = (5)(. 960)(1 -. 091) = 4. 36 For M = 2, J = (5)(. 998)(1 -. 091) = 4. 54 © 2014 Pearson Education, Inc. MD - 49

Limited-Population Example AVERAGE NUMBER COST/HR FOR Each of 5 OF TECHNICIANS NUMBER printers requires repair after 20 hours (U) PRINTERS DOWNTIME TECHNICIANS DOWN (N – J)($120/HR) ($25/HR) of TOTAL use One technician can service a printer in 2 hours (T) COST/HR 1. 64 $76. 80 $25. 00 $101. 80 Printer downtime costs $120/hour 2. 46 $55. 20 $50. 00 $105. 20 Technician costs $25/hour 2 Service factor: X = =. 091 (close to. 090) 2 + 20 For M = 1, D =. 350 and F =. 960 For M = 2, D =. 044 and F =. 998 Average number of printers working: For M = 1, J = (5)(. 960)(1 -. 091) = 4. 36 For M = 2, J = (5)(. 998)(1 -. 091) = 4. 54 © 2014 Pearson Education, Inc. MD - 50

Other Queuing Approaches ▶ The single-phase models cover many queuing situations ▶ Variations of the four single-phase systems are possible ▶ Multiphase models exist for more complex situations © 2014 Pearson Education, Inc. MD - 51

All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of the publisher. Printed in the United States of America. © 2014 Pearson Education, Inc. MD - 52