D CA B Цели урока: •

Цели урока: • Ввести понятие параллельных и скрещивающихся прямых • рассмотреть взаимное расположение 2 -х прямых в пространстве • доказать теоремы о параллельности прямых и параллельности 3 -х прямых • закрепить эти понятия на моделях куба, призмы, пирамиды

Повторение 1)Верно ли, что если концы отрезка лежат в данной плоскости, то и его середина лежит в данной плоскости? 2)Могут ли две плоскости иметь общую точку, но не иметь общей прямой? 3)Точка А не лежит в плоскости KMN. Назовите прямую пересечения плоскостей AMN и AKM. 4) Даны точки А, В, С и D. Плоскость α проходит через прямую АВ , но не проходит через точку С. Прямые AD и ВС пересекаются в точке В. Сколько данных точек лежит в плоскости α ? 1 2 3 4 5 6 7 8 Таблица ответов

Повторение 5)В пространстве даны прямая и точка. Сколько различных плоскостей можно через них провести? 6)Верно ли, что если три данные точки лежат в одной плоскости, то они не лежат на одной прямой? 7)Могут ли три прямые иметь общую точку, но не лежать в одной плоскости? 8)Три прямые пересекаются в точке А. Через данную точку необходимо провести плоскость, содержащую ровно две из трех данных прямых. Сколько таких плоскостей можно провести? Рассмотрите все возможные случаи.

Самопроверка: 1 2 3 4 5 6 7 8 Да Нет АМ три Одну или бесконеч но много Нет Да Три или не одной

1 Каково может быть взаимное расположение двух прямых на плоскости? (совпадают, пересекаются, параллельны) © Кузьмина Е. А. , Колобовская МСОШ, 20102 Дайте определение параллельных прямых на плоскости. ( )a b a , b a ∩ b. Параллельными называются прямые, лежащие в одной плоскости и не пересекающие друга.

© Кузьмина Е. А. , Колобовская МСОШ, 2010( )a b a , b a ∩ b. Параллельными прямыми в пространстве называются прямые, лежащие в одной плоскости и не пересекающие друга.

© Кузьмина Е. А. , Колобовская МСОШ, 20103 Дан куб. Являются ли параллельными прямые: D C A B D 1 C 1 A 1 B 1 1) АА 1 и DD 1 , АА 1 и СС 1 ? Ответ обоснуйте. 2) АА 1 и D С? Они пересекаются? В пространстве есть прямые, которые не пересекаются, но и не являются параллельными.

© Кузьмина Е. А. , Колобовская МСОШ, 2010 Две прямые называются скрещивающимися, если они не лежат в одной плоскости. c b

Теорема Дано: А; А ∈ а. Провести через А прямую b || а, доказать ее единственность Через любую точку пространства, не лежащую на данной прямой, можно провести прямую, параллельную данной, и только одну. Доказательство : По условию даны прямая а и не лежащая на ней точка А. По ранее доказанной теореме через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну. Проведем плоскость α. Теперь в плоскости а через току А проведем прямую b || а, а из планиметрии известно, что через точку А вне прямой а можно провести прямую, параллельную данной, и притом только одну. Теорема доказана.

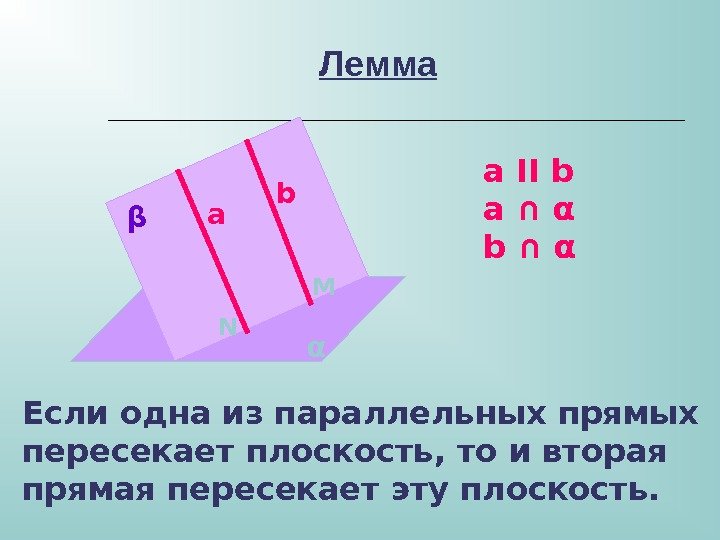
Лемма a ΙΙ b a ∩ α b ∩ αa b αβ M N Если одна из параллельных прямых пересекает плоскость, то и вторая прямая пересекает эту плоскость.

ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ Если две прямые параллельны третьей прямой, то они параллельны между собой. a ΙΙ b a ΙΙ c b ΙΙ c

© Кузьмина Е. А. , Колобовская МСОШ, 20104 По рисункам назовите: 1) пары скрещивающихся ребер; 2) пары параллельных ребер. D CA B K L NK 1 L 1 N

© Кузьмина Е. А. , Колобовская МСОШ, 20105 Всегда ли две непересекающиеся прямые в пространстве параллельны? 6 Какие две прямые в пространстве называются параллельными? 7 Сколько можно провести в пространстве прямых, проходящих через данную точку, параллельных данной прямой?