
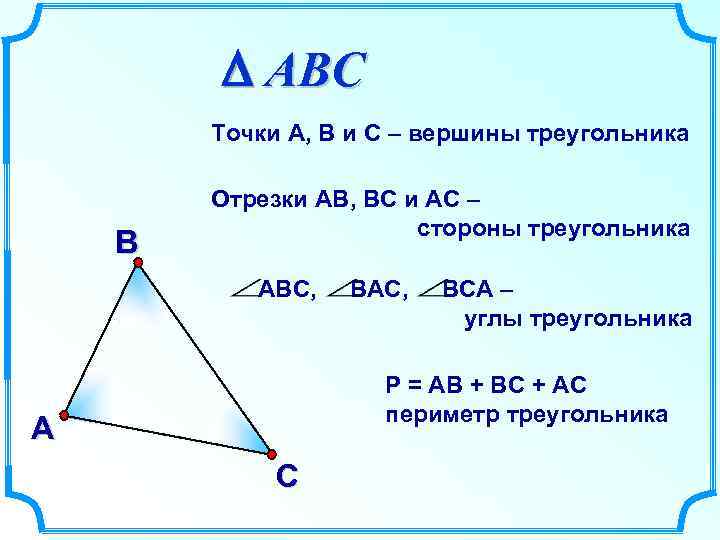
D ABC Точки А, В и С – вершины треугольника В Отрезки АВ, ВС и АС – стороны треугольника АВС, ВАС, ВСА – углы треугольника Р = АВ + ВС + АС периметр треугольника А С
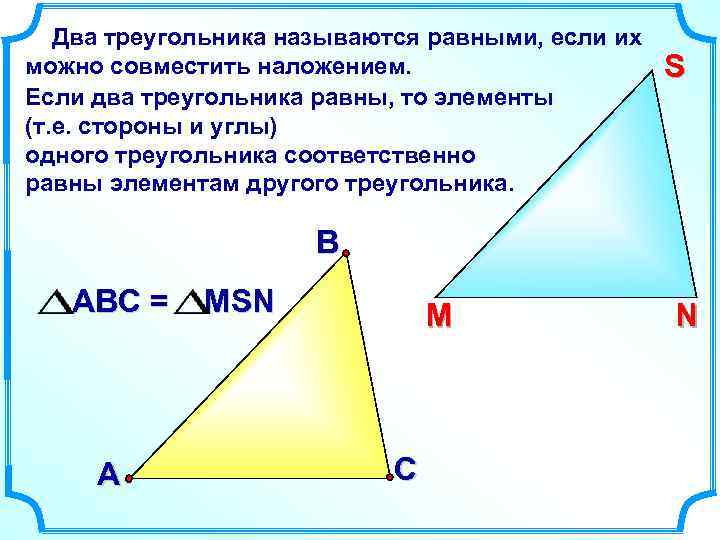
Два треугольника называются равными, если их можно совместить наложением. Если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника. S В АВС = А MSN М С N
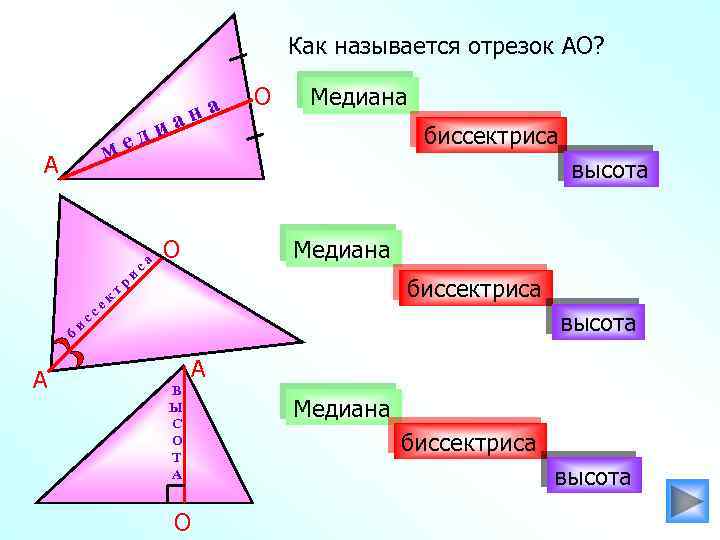
Как называется отрезок АО? м А б А и с ек с т и ед р и са а на О Медиана биссектриса высота А В Ы С О Т А О Медиана биссектриса высота
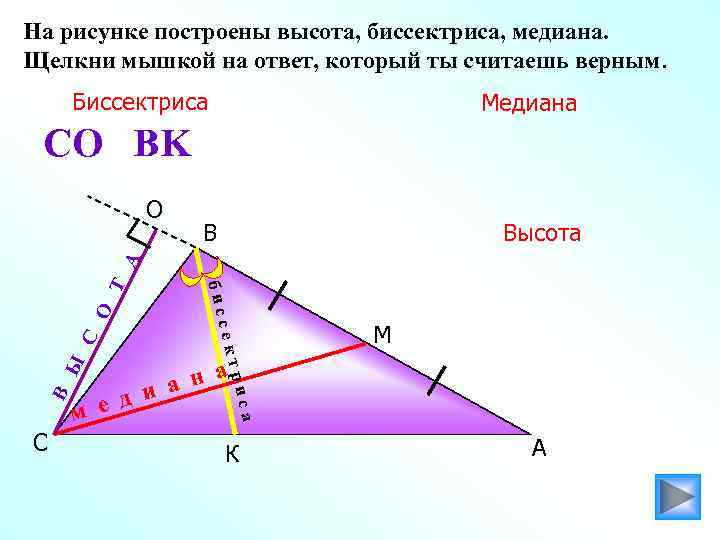
На рисунке построены высота, биссектриса, медиана. Щелкни мышкой на ответ, который ты считаешь верным. Биссектриса Медиана CO BK В Высота О С Ы н а а д и м е М три са В сек С бис Т А О К А
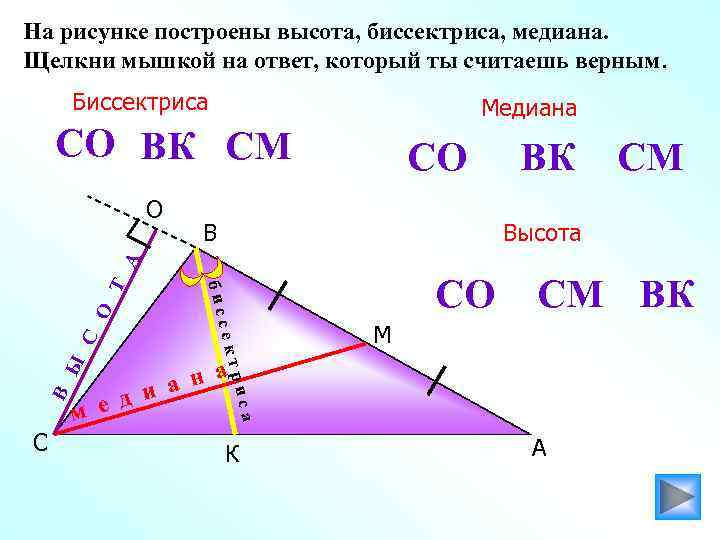
На рисунке построены высота, биссектриса, медиана. Щелкни мышкой на ответ, который ты считаешь верным. Биссектриса Медиана СО ВК СМ Высота О С Ы н а а д и м е СМ ВК М три са В сек С СО бис Т А О СО К А
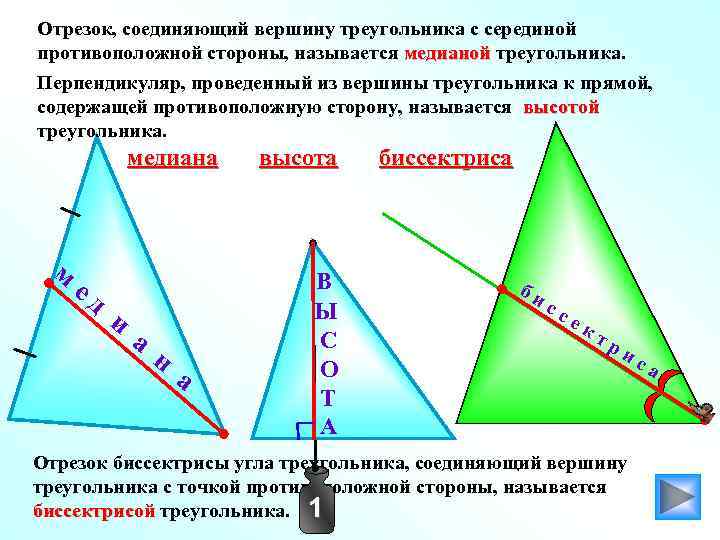
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника. Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника. медиана м ед и а н а высота В Ы С О Т А биссектриса би сс ек тр ис Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника. 1 а
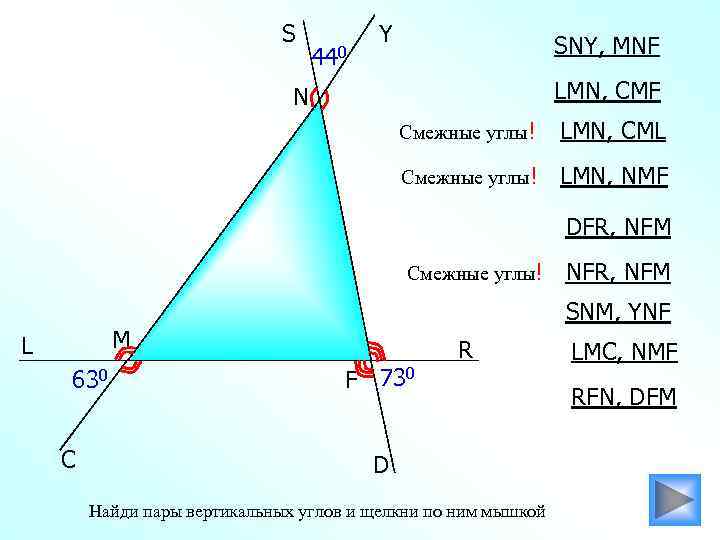
S 440 Y SNY, MNF LМN, CMF N Смежные углы! LМN, CML Смежные углы! LМN, NMF DFR, NFM Смежные углы! SNM, YNF М L 630 C NFR, NFM F 730 R D Найди пары вертикальных углов и щелкни по ним мышкой LMC, NMF RFN, DFM
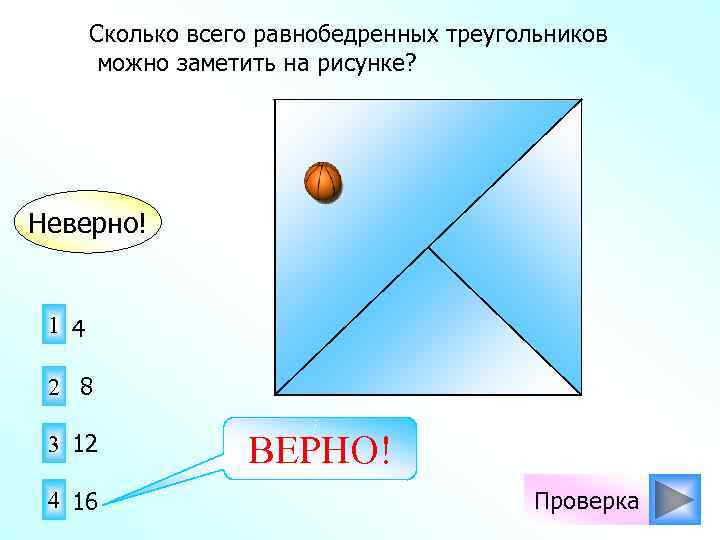
Сколько всего равнобедренных треугольников можно заметить на рисунке? Неверно! 1 4 2 8 3 12 4 16 ВЕРНО! Проверка
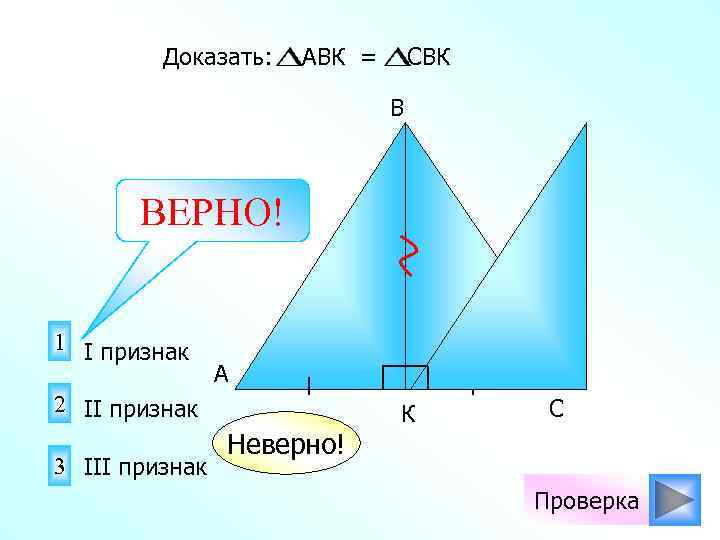
Доказать: АВК = СBК В ВЕРНО! 1 I признак A 2 II признак 3 III признак Неверно! К С Проверка
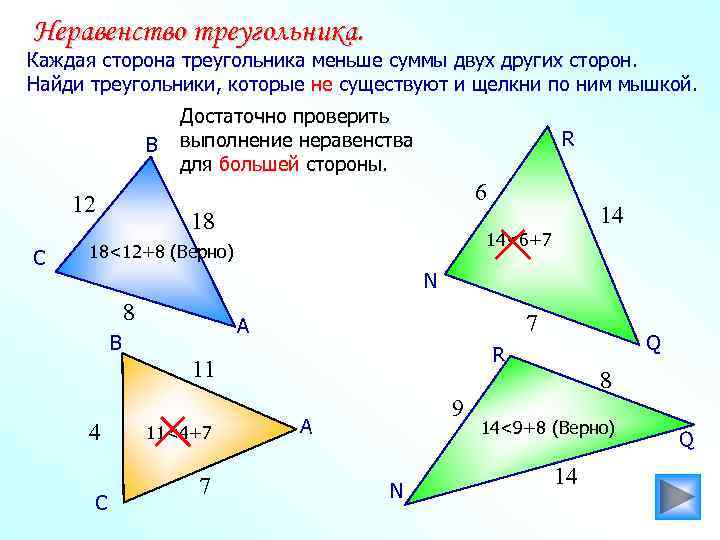
Неравенство треугольника. Каждая сторона треугольника меньше суммы двух других сторон. Найди треугольники, которые не существуют и щелкни по ним мышкой. В R 6 12 С Достаточно проверить выполнение неравенства для большей стороны. 18 14 14<6+7 18<12+8 (Верно) N 8 7 А В 11 4 С 11<4+7 7 Q R 8 9 А N 14<9+8 (Верно) 14 Q
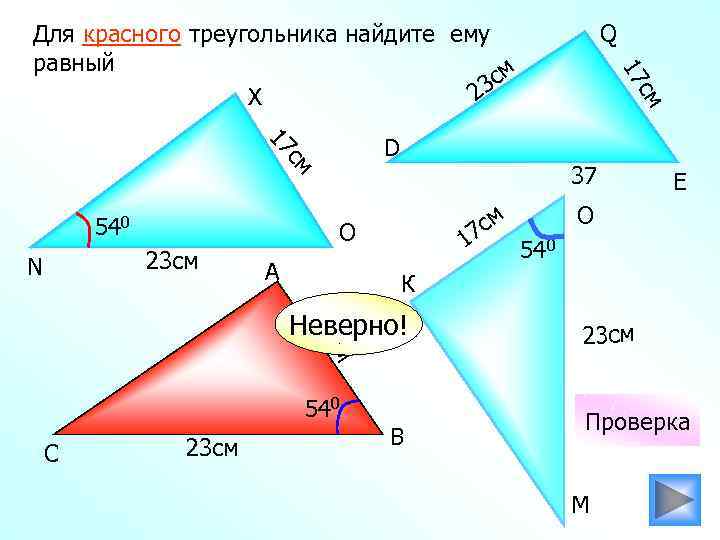
Для красного треугольника найдите ему равный см 23 X см 23 см N 37 см 7 O А 1 см 17 540 С E О 540 К Неверно! 23 см см 17 D 17 540 Q В 23 см Проверка М
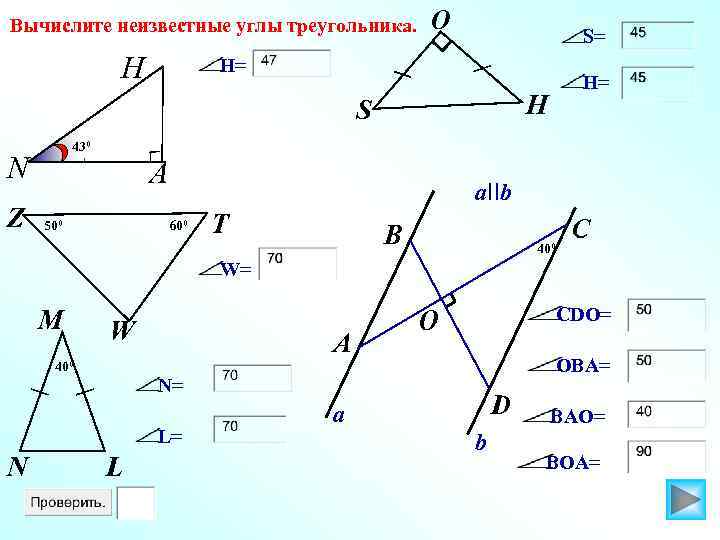
Вычислите неизвестные углы треугольника. H O S= H= H S 430 N Z H= А 500 a. IIb 600 T B 400 C W= M W A CDO= O OBA= 400 N= L= N L D a b BAO= BOA=
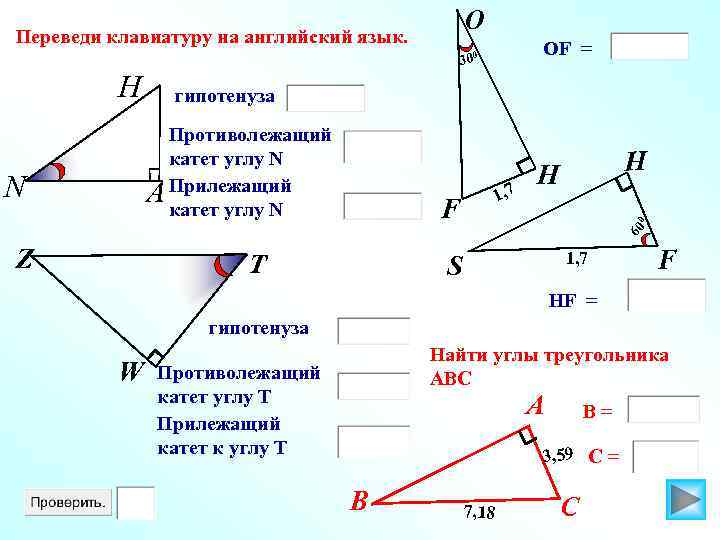
O Переведи клавиатуру на английский язык. ОF = 300 H гипотенуза Z S 1, 7 H H 60 0 А F T N Противолежащий катет углу N Прилежащий катет углу N 1, 7 F HF = гипотенуза W Найти углы треугольника АВС Противолежащий катет углу Т Прилежащий катет к углу Т A В= 3, 59 С = В 7, 18 C

Определение. Две прямые на плоскости называются параллельными, если они не пересекаются.

Найди пары накрест лежащих углов и щелкни по ним мышкой. Вертикальные углы Односторонние углы ∠ 2 и ∠ 4 c Вертикальные углы 1 4 ВЕРНО! 3 ∠ 1 и ∠ 3 ∠ 4 и ∠ 6 Вертикальные углы а 2 5 6 8 7 ∠ 4 и ∠ 5 Односторонние углы ∠ 5 и ∠ 7 b ∠ 1 и ∠ 8 ∠ 3 и ∠ 6 Соответственные углы ∠ 2 и ∠ 6 ВЕРНО! ∠ 3 и ∠ 5 Тренировочные задания. ∠ 1 и ∠ 6
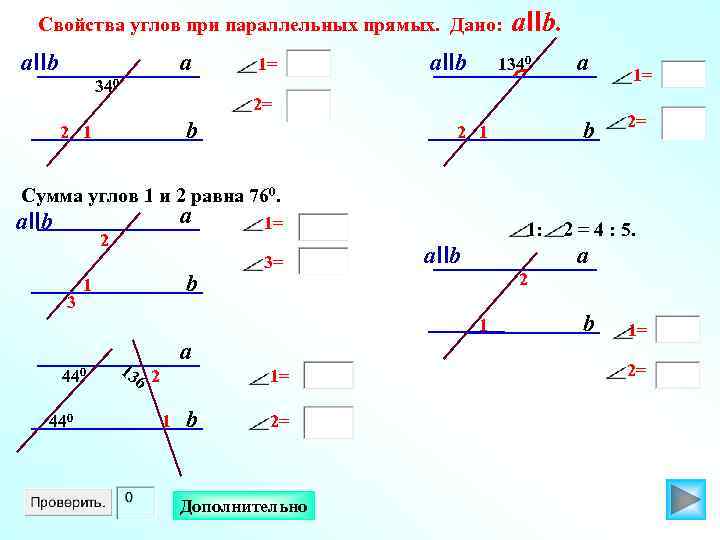
Свойства углов при параллельных прямых. Дано: a. IIb a 340 1= a. IIb. 1340 a 2= b 2 1 1= 2= Сумма углов 1 и 2 равна 760. a a. IIb 2 3 b 1 1= 3= 1: a. IIb a 2 1 440 a 13 2 6 1= 1 b 2= Дополнительно 2 = 4 : 5. b 1= 2=
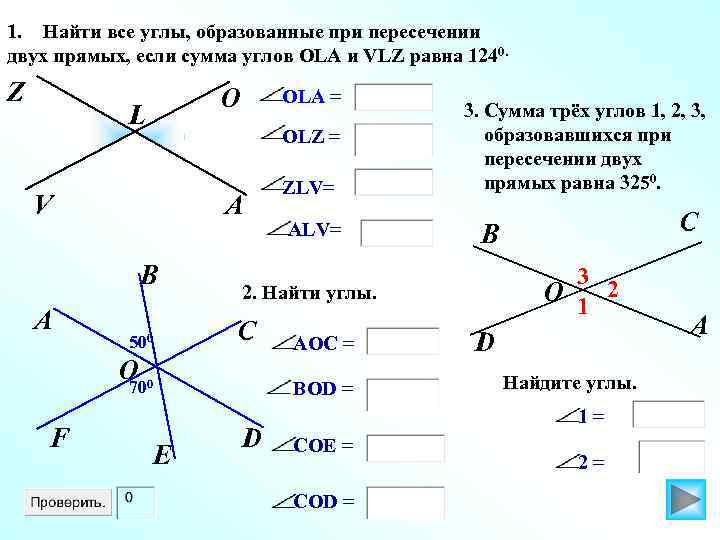
1. Найти все углы, образованные при пересечении двух прямых, если сумма углов OLA и VLZ равна 1240. Z O L OLZ = V А B A OLA = 500 C 700 E ALV= AOC = BOD = D C B 3 O 1 2 2. Найти углы. O F ZLV= 3. Сумма трёх углов 1, 2, 3, образовавшихся при пересечении двух прямых равна 3250. D Найдите углы. 1= COE = COD = 2= A
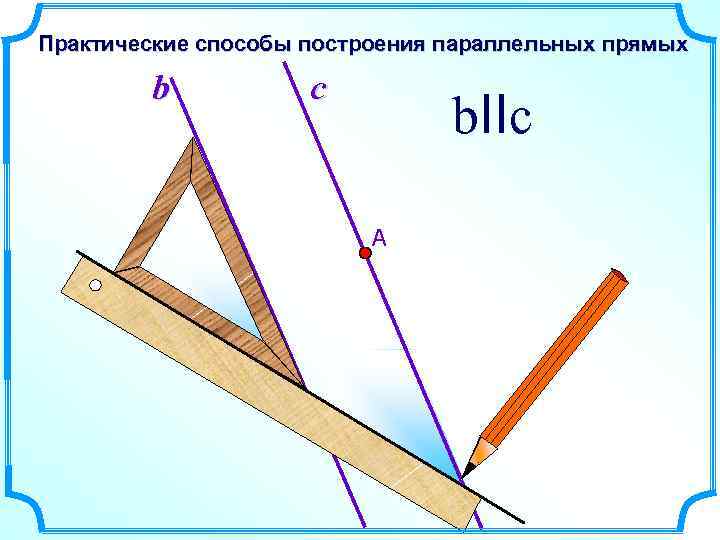
Практические способы построения параллельных прямых b c b. IIc А
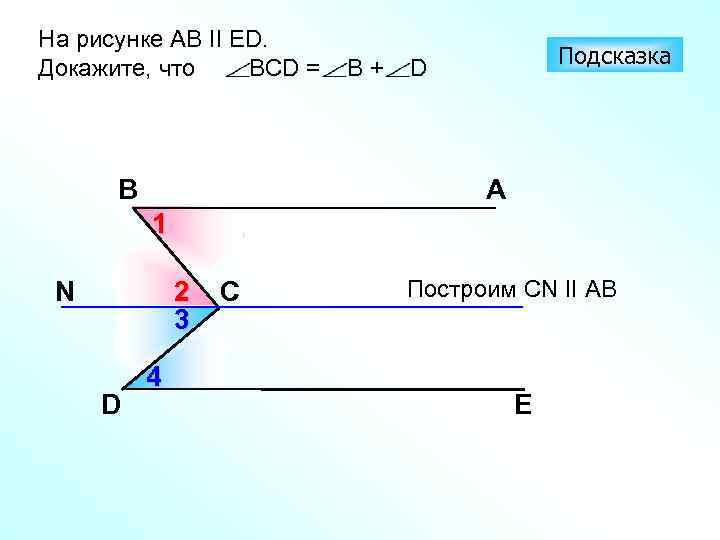
На рисунке АВ II ЕD. Докажите, что ВСD = B B+ Подсказка D A 1 N 2 3 D 4 C Построим CN II AB E
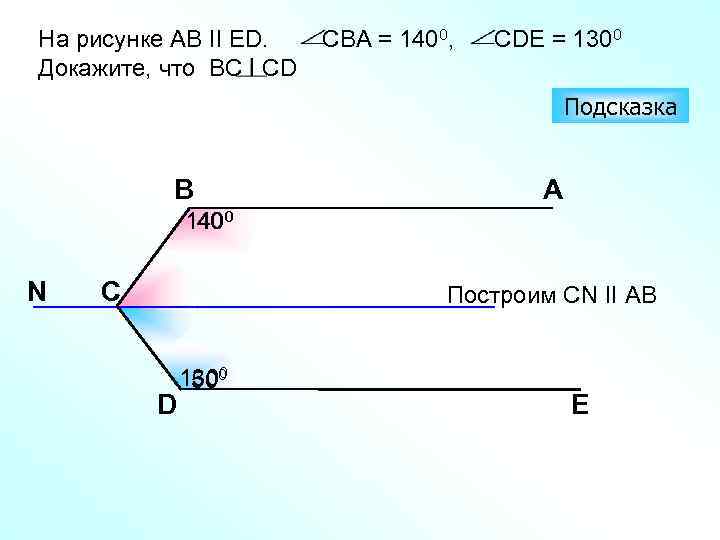
На рисунке АВ II ЕD. Докажите, что ВС СD CВА = 1400, СDE = 1300 Подсказка B A 1400 40 N C Построим CN II AB D 1300 50 E
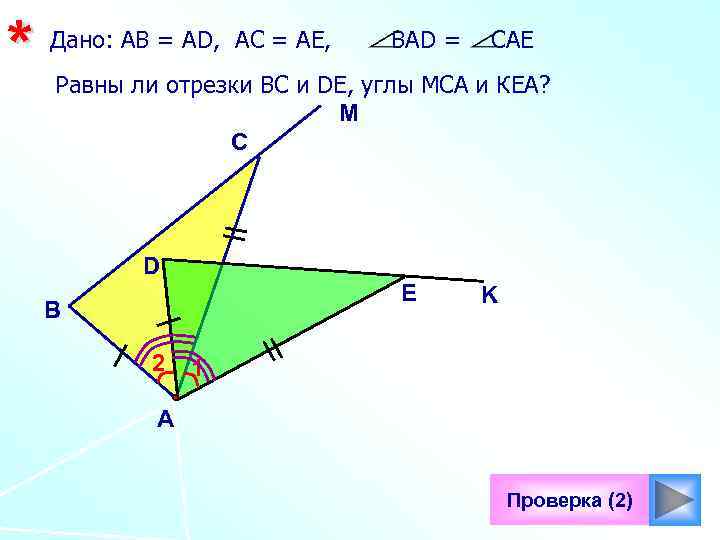
* Дано: АВ = АD, АС = АЕ, ВАD = САЕ Равны ли отрезки ВС и DE, углы МСА и КЕА? M С D E B 2 K 1 А Проверка (2)
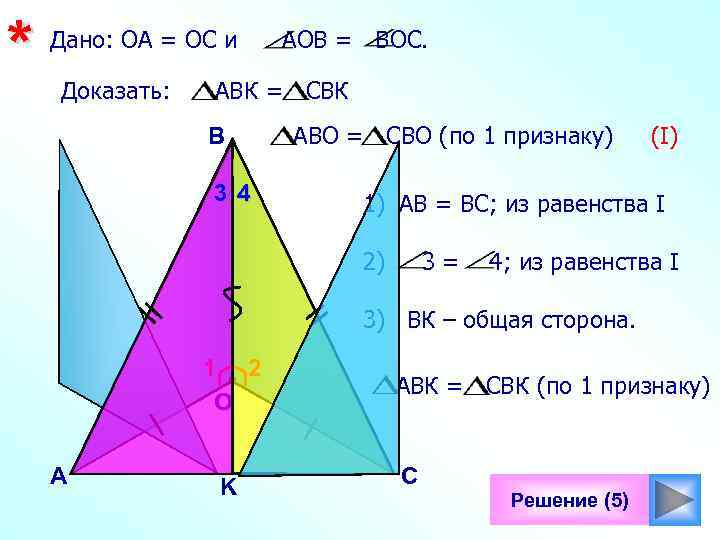
* Дано: ОА = ОС и Доказать: АОВ = ВОС. АВК = CBК B 34 АВО = CBО (по 1 признаку) (I) 1) АВ = ВС; из равенства I 2) 3= 4; из равенства I 3) ВК – общая сторона. 1 2 О А K АВК = CBК (по 1 признаку) С Решение (5)
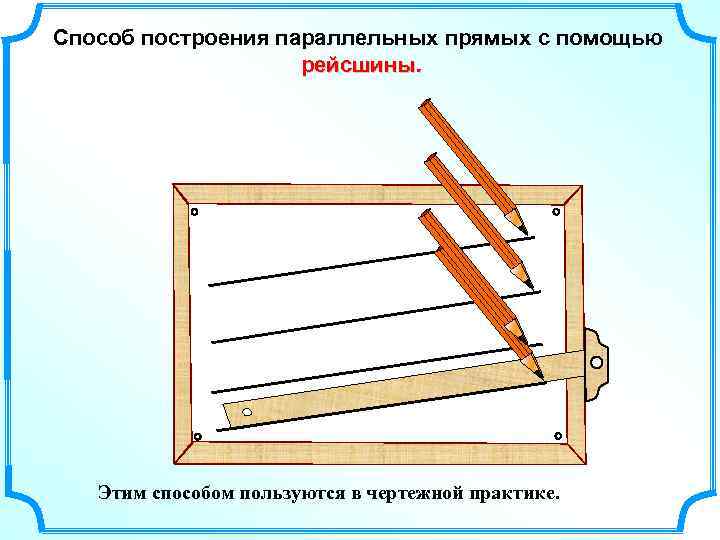
Способ построения параллельных прямых с помощью рейсшины. Этим способом пользуются в чертежной практике.