Кривые и поверхности(Лекция2).ppt
- Количество слайдов: 27
 Curves Кривые и поверхности в компьютерной графике URL: http: //www. school 30. spb. ru/cgsg/cgc/ E-mail: CGSG@yandex. ru Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Curves Кривые и поверхности в компьютерной графике URL: http: //www. school 30. spb. ru/cgsg/cgc/ E-mail: CGSG@yandex. ru Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 Представления кривых на плоскости Curves • явный способ (explicit curves) • неявный способ (implicit) • Параметрический способ (parametric curves) Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Представления кривых на плоскости Curves • явный способ (explicit curves) • неявный способ (implicit) • Параметрический способ (parametric curves) Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
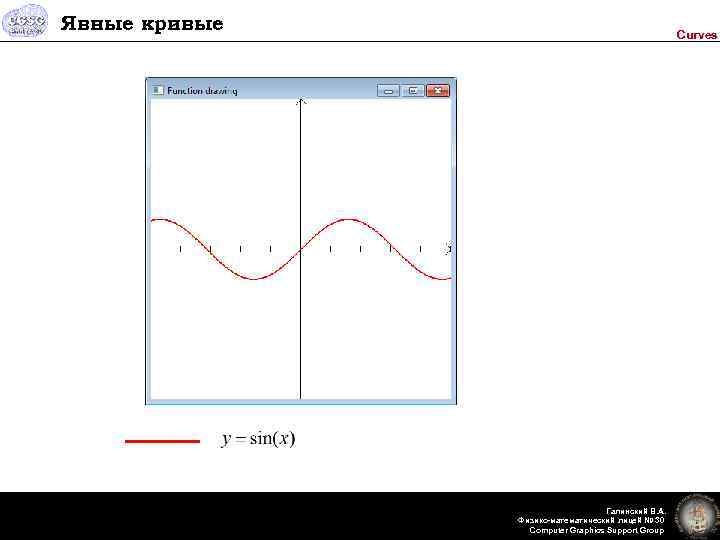 Явные кривые Curves Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Явные кривые Curves Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
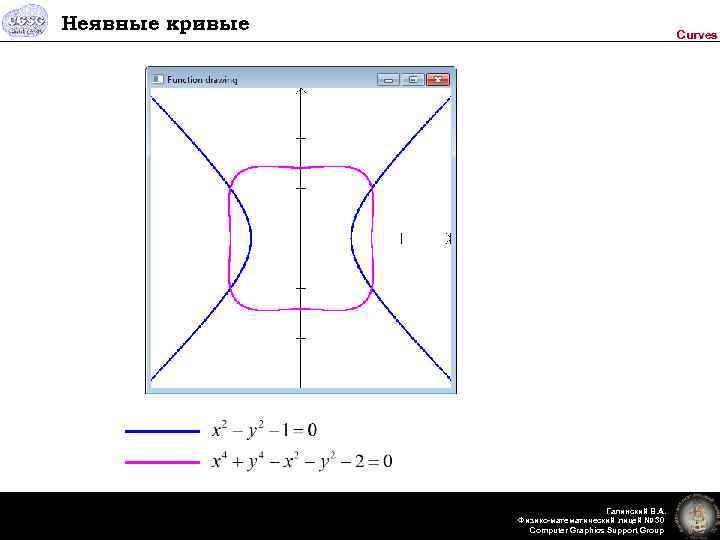 Неявные кривые Curves Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Неявные кривые Curves Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 Параметрические кртвые Curves Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Параметрические кртвые Curves Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 Кривые Безье. Pierre Bézier линейные ( ): Curves • Линейные кривые Безье • Линейная интерполяция между концевыми точками Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Кривые Безье. Pierre Bézier линейные ( ): Curves • Линейные кривые Безье • Линейная интерполяция между концевыми точками Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
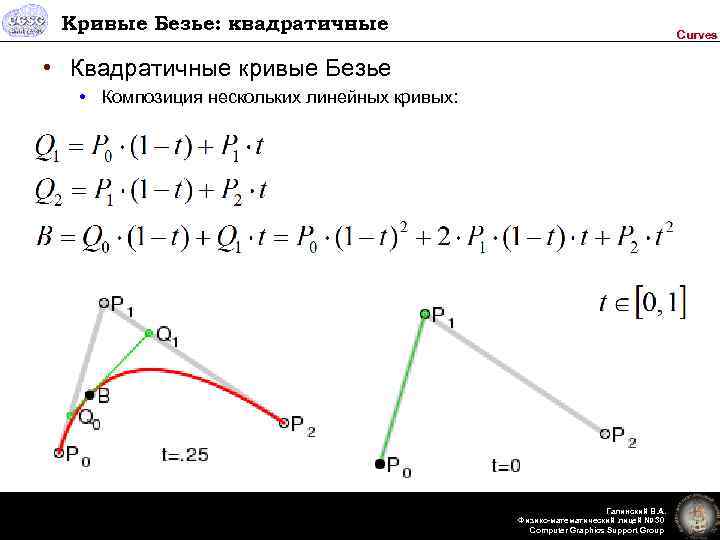 Кривые Безье: квадратичные Curves • Квадратичные кривые Безье • Композиция нескольких линейных кривых: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Кривые Безье: квадратичные Curves • Квадратичные кривые Безье • Композиция нескольких линейных кривых: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
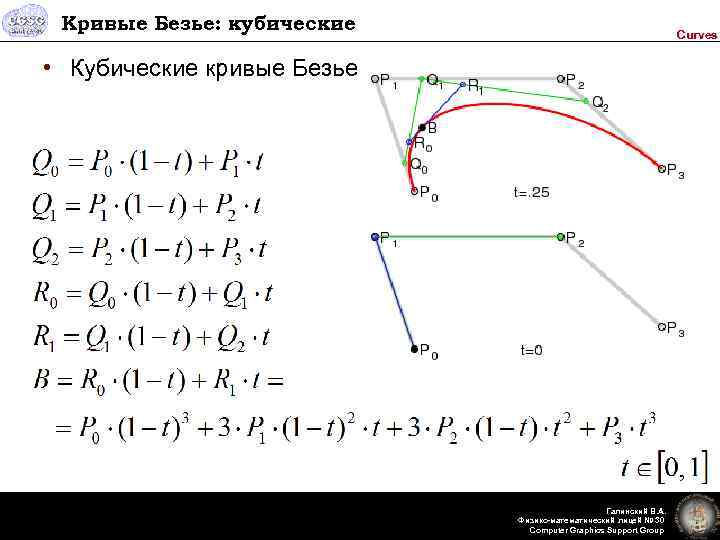 Кривые Безье: кубические Curves • Кубические кривые Безье Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Кривые Безье: кубические Curves • Кубические кривые Безье Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
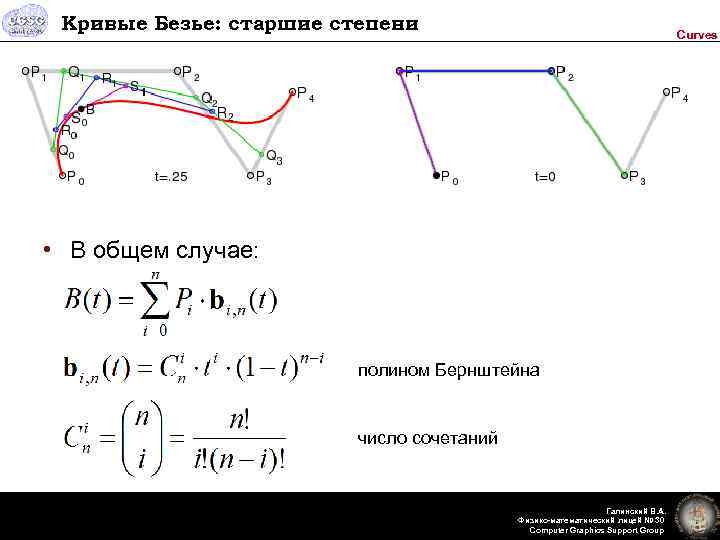 Кривые Безье: старшие степени Curves • В общем случае: полином Бернштейна число сочетаний Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Кривые Безье: старшие степени Curves • В общем случае: полином Бернштейна число сочетаний Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 Кубические кривые Безье: матричная запись Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group Curves
Кубические кривые Безье: матричная запись Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group Curves
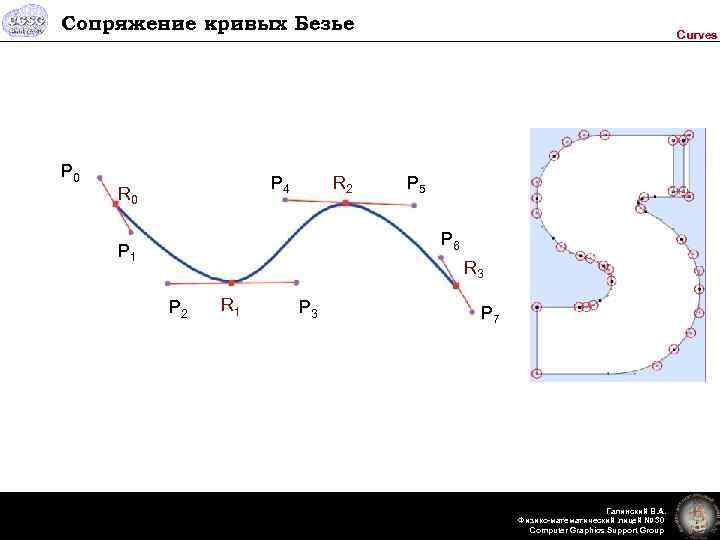 Сопряжение кривых Безье P 0 P 4 R 0 R 2 Curves P 5 P 6 P 1 R 3 P 2 R 1 P 3 P 7 Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Сопряжение кривых Безье P 0 P 4 R 0 R 2 Curves P 5 P 6 P 1 R 3 P 2 R 1 P 3 P 7 Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
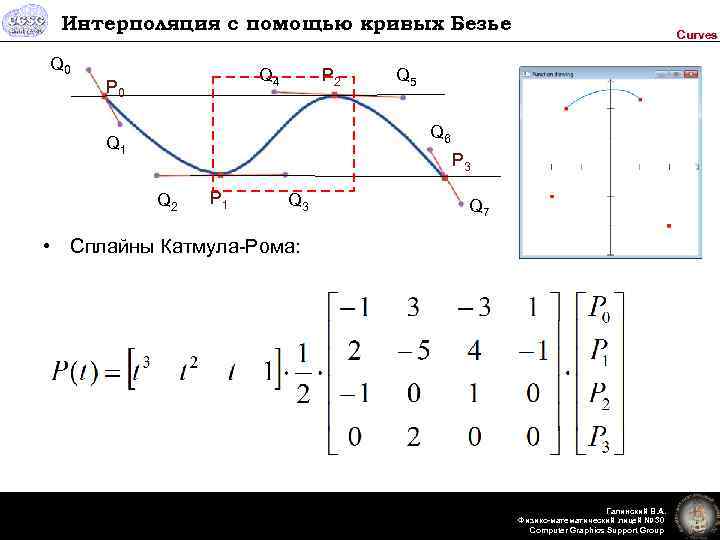 Интерполяция с помощью кривых Безье Q 0 Q 4 P 0 P 2 Curves Q 5 Q 6 Q 1 P 3 Q 2 P 1 Q 3 Q 7 • Сплайны Катмула-Рома: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Интерполяция с помощью кривых Безье Q 0 Q 4 P 0 P 2 Curves Q 5 Q 6 Q 1 P 3 Q 2 P 1 Q 3 Q 7 • Сплайны Катмула-Рома: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
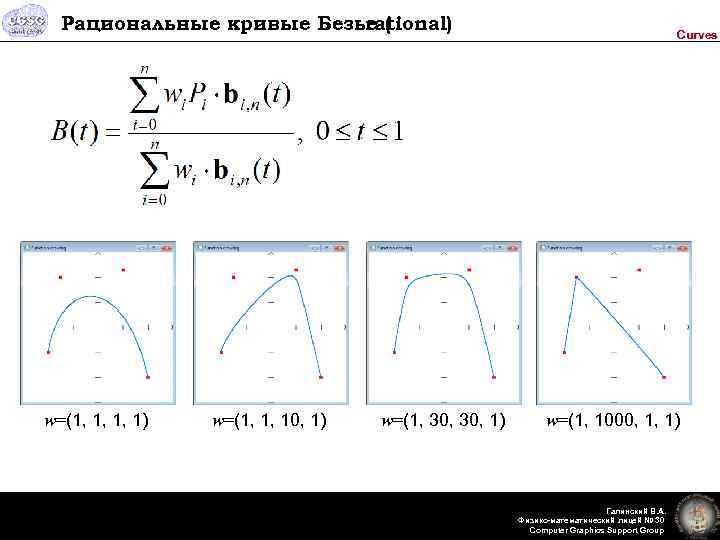 Рациональные кривые Безье ( rational) w=(1, 1, 1, 1) w=(1, 1, 10, 1) w=(1, 30, 1) Curves w=(1, 1000, 1, 1) Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Рациональные кривые Безье ( rational) w=(1, 1, 1, 1) w=(1, 1, 10, 1) w=(1, 30, 1) Curves w=(1, 1000, 1, 1) Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 B-сплайны B-splines) ( Curves • Кокс и де Бур: полагаем - узловой вектор Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
B-сплайны B-splines) ( Curves • Кокс и де Бур: полагаем - узловой вектор Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
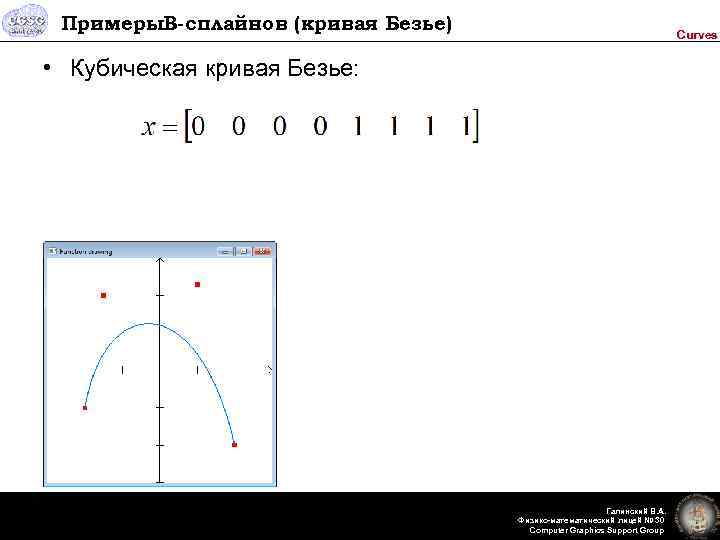 Примеры. B-сплайнов (кривая Безье) Curves • Кубическая кривая Безье: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Примеры. B-сплайнов (кривая Безье) Curves • Кубическая кривая Безье: Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 Примеры. B-сплайнов uniform) ( Curves • Униформный кубический B-spline Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Примеры. B-сплайнов uniform) ( Curves • Униформный кубический B-spline Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
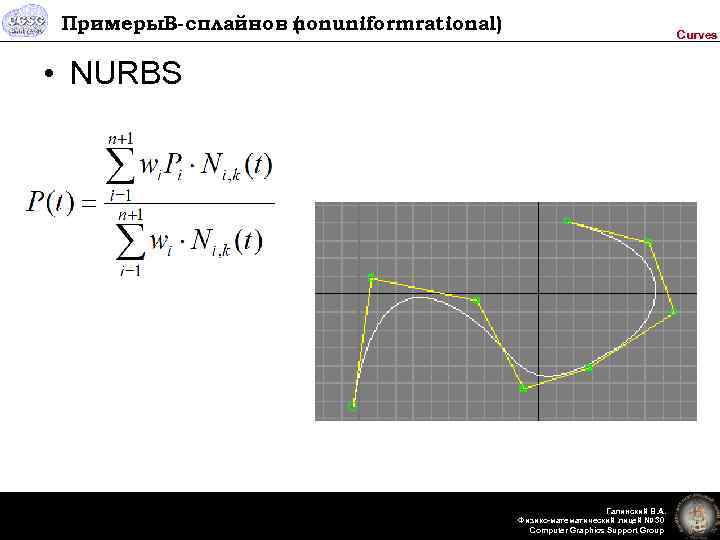 Примеры. B-сплайнов nonuniformrational) ( Curves • NURBS Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Примеры. B-сплайнов nonuniformrational) ( Curves • NURBS Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 Поверхности surfaces) ( Curves • явный способ • неявный способ • параметрический способ Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Поверхности surfaces) ( Curves • явный способ • неявный способ • параметрический способ Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
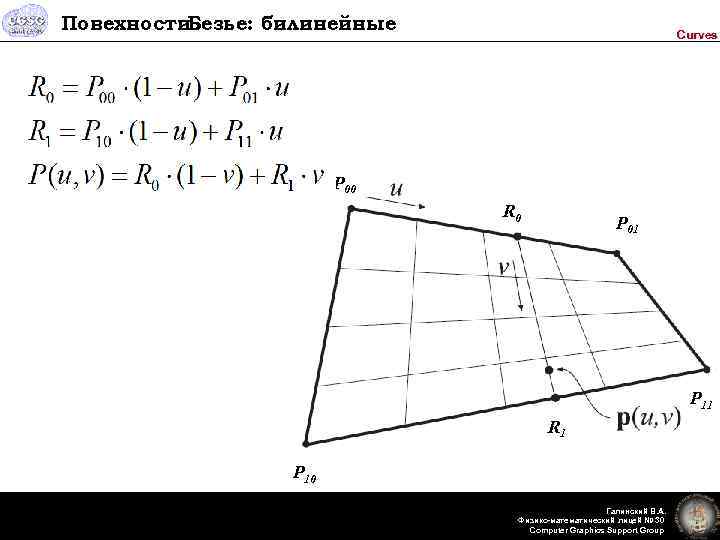 Повехности Безье: билинейные Curves P 00 R 0 P 01 P 11 R 1 P 10 Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Повехности Безье: билинейные Curves P 00 R 0 P 01 P 11 R 1 P 10 Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 Поверхность Кунса Curves • Граничные кривые: • Билинейно смешиваем (учитывая повторение угловых точек): Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Поверхность Кунса Curves • Граничные кривые: • Билинейно смешиваем (учитывая повторение угловых точек): Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 Поверхности Безье (общий случай) Curves Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Поверхности Безье (общий случай) Curves Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 Бикубическая поверхность Безье Curves Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Бикубическая поверхность Безье Curves Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
 Бикубическая поверхность Безье: сопряжение Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group Curves
Бикубическая поверхность Безье: сопряжение Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group Curves
 Бикубическая поверхность Безье: пример Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group Curves
Бикубическая поверхность Безье: пример Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group Curves
 Общий случай бикубических поверхностей uniform B-spline cubic Bezier Catmull-Rom Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group Curves
Общий случай бикубических поверхностей uniform B-spline cubic Bezier Catmull-Rom Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group Curves
 Трикубические пространства: Free Form Deformation Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group Curves
Трикубические пространства: Free Form Deformation Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group Curves
 Литература Curves • David F. Rodgers, J. van Adams. "Mathematical Elements for Computer Graphics", 2 nd ed. , Mc. Graw-Hill Publishing Company, 1990. • Alan Watt, Mark Watt. "Advanced Animation and Rendering Techniques. Theory and Practice", ACM Press, Addison-Wesley Longman Limited, 1992. • Е. Шикин, А. Плис. "Кривые и поверхности на экране компьютера". Москва: Диалог-МИФИ, 1996. • Е. В. Шикин, М. М. Франк-Каменецкий. "Кривые на плоскости и в пространстве". Москва: "ФАЗИС", 1997. Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group
Литература Curves • David F. Rodgers, J. van Adams. "Mathematical Elements for Computer Graphics", 2 nd ed. , Mc. Graw-Hill Publishing Company, 1990. • Alan Watt, Mark Watt. "Advanced Animation and Rendering Techniques. Theory and Practice", ACM Press, Addison-Wesley Longman Limited, 1992. • Е. Шикин, А. Плис. "Кривые и поверхности на экране компьютера". Москва: Диалог-МИФИ, 1996. • Е. В. Шикин, М. М. Франк-Каменецкий. "Кривые на плоскости и в пространстве". Москва: "ФАЗИС", 1997. Галинский В. А. Физико-математический лицей № 30 Computer Graphics Support Group


