2c8a41014f4fbca244053663f2c337cd.ppt
- Количество слайдов: 68

CSNB 143 Discrete Mathematical Structures Chapter 8 - Relations

Sets OBJECTIVES Student should be able to know how relation is being builds. Students should be able to apply relation and combine the knowledge with other topics in this subject.

What, which, where, when 1. Basics of relation Domain and Range (Clear / Not Clear) 2. Relation Representation Set representation Matrix representation Diagraph representation (Clear / Not Clear) 3. Concept of degree, path and cycle (Clear / Not Clear)

4. Properties of relations and how to identify it Reflexive and Irreflexive (Clear / Not Clear) Symmetric, Asymmetric and Antisymmetric (Clear / Not Clear) 5. Equivalence relation (Clear / Not Clear) 6. Relations Manipulation Complement and Inverse Intersection and union (Clear / Not Clear)

7. Transitive Closure Matrix product Warshall Algorithm (Clear / Not Clear)

Product Set An order of a pair (a, b) in which a and b will appear in dedicated order; a appear first, followed by b. If 2 set A and B are nonempty set, its product set for A x B or named Cartesian product is a set for ALL (a, b) pairs in which a A and b B. Written as A x B = {(a, b) | a A and b B}

Ex 1: Let A = {1, 2, 3} and B = {r, s} So, A x B = {(1, r), (1, s), (2, r), (2, s), (3, r), (3, s)} and B x A = {(r, 1), (r, 2), (r, 3), (s, 1), (s, 2), (s, 3)} Therefore, A x B B x A. Ex 2: A marketing research firm classifies a person according to the following two criteria: Gender: male (m); female (f) Highest level of education completed: elementary school (e); high school (h); college (c); graduate school (g)

Sol: Let S = {m, f} and L = {e, h, c, g}. The product ser S x L contains all the categories into which the population classified. There are eight categories in this classification scheme. --> {(m, e), (m, h), (m, c), (m, g), (f, e), (f, h), (f, c), (f, g)}. Thus the classification (f, g) represents a female who completed graduate school.

Relation A relation between 2 set where its value was determined by a condition. All elements in that relation must fulfill the condition. Let A and B are nonempty set. A relation from A to B is a subset for A x B. If R A x B and (a, b) R, we say that a relates to b through R and we write as a R b. Ex 3: Let A = {1, 2, 3} and B = {r, s}. Sol: R = {(1, r), (2, s), (3, r)} is a relation from A to B.

Ex 4: Let A = {1, 2, 3, 4, 5}. Define the following relation R (less than) on A. Sol: R is a relation less than on set A. a R b if and only if a < b So R = {(1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5)}
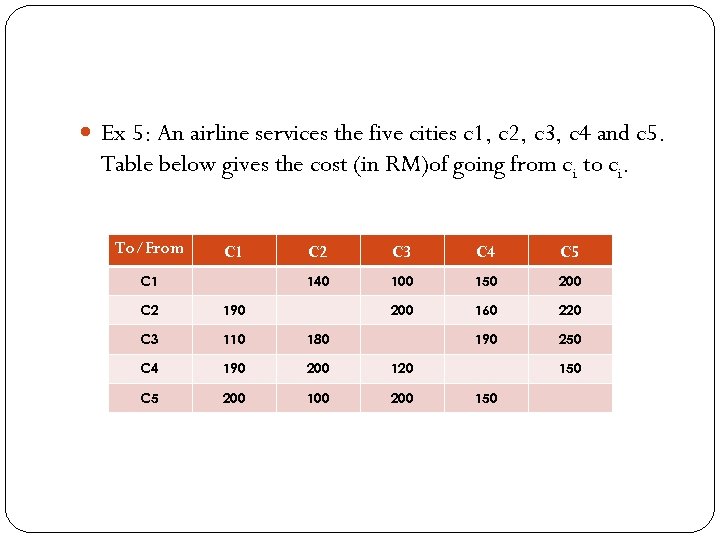
Ex 5: An airline services the five cities c 1, c 2, c 3, c 4 and c 5. Table below gives the cost (in RM)of going from ci to ci. To/From C 1 C 3 C 4 C 5 140 C 1 C 2 100 150 200 160 220 190 250 C 2 190 C 3 110 180 C 4 190 200 120 C 5 200 100 200 150

We now define the following relation r on the set of cities A = c 1, c 2, c 3, c 4, c 5 : ci R cj if and only if the cost of going from ci to ci is defined and less than or equal to RM 180. Find R. Sol: The relation R is the subset of A x A consisting of all cities (ci, ci), where the cost going from ci to ci is less than or equal to RM 180. Hence: R = {(c 1, c 2), (c 1, c 3), (c 1, c 4), (c 2, c 4), (c 3, c 1), (c 3, c 2), (c 4, c 3), (c 4, c 5), (c 5, c 2), (c 5, c 4)}

Sets arise from relations When there is a relation from A to B, we can find domain and range for the relation. Domain for R is elements in set A. That is, Dom(R) is a subset for A, is the set of all first element in the pairs that make up R Range for R is elements in set B. That is, Ran(R) is a subset for B, is the set of element in B that are second elements of pairs in R.

Ex 6: Consider Ex 4. Let A = {1, 2, 3, 4, 5}. Define the following relation R (less than) on A. So R = {(1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5)} Sol: Dom(R) is {1, 2, 3, 4}. Ran(R) is {2, 3, 4, 5}

Relation Representation A relation can be represent in three ways: 1. Set representation is in Ex 4. 2. Matrix representation is only for two finite sets. Ex 7: Let R be the relation defined in example 3. --> Let A = {1, 2, 3} and B = {r, s}. Sol: R = {(1, r), (2, s), (3, r)} is a relation from A to B. Then the matrix of R is
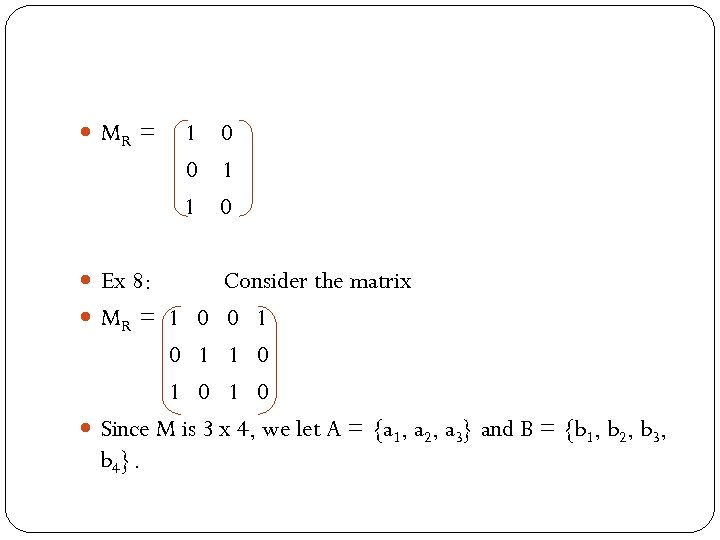
MR = Ex 8: 1 0 0 1 1 0 Consider the matrix MR = 1 0 0 1 1 0 1 0 Since M is 3 x 4, we let A = {a 1, a 2, a 3} and B = {b 1, b 2, b 3, b 4}.

Sol: Relation for set is as below: So R = {(a 1, b 1), (a 1, b 4), (a 2, b 2), (a 2, b 3). (a 3, b 1), (a 3, b 3)} 3. Diagraph (directed graph of R) Digraph representation needs both set to have the same elements. It is normally called relation on that set. Each element is called vertex and the path is called edge. Ex 9: Let A = {a, b, c, d} and R = {(a, a), (a, b), (b, a), (b, b) (b, c), (b, d), (c, d), (d, a)} Sol: The diagraph of R is shown below:
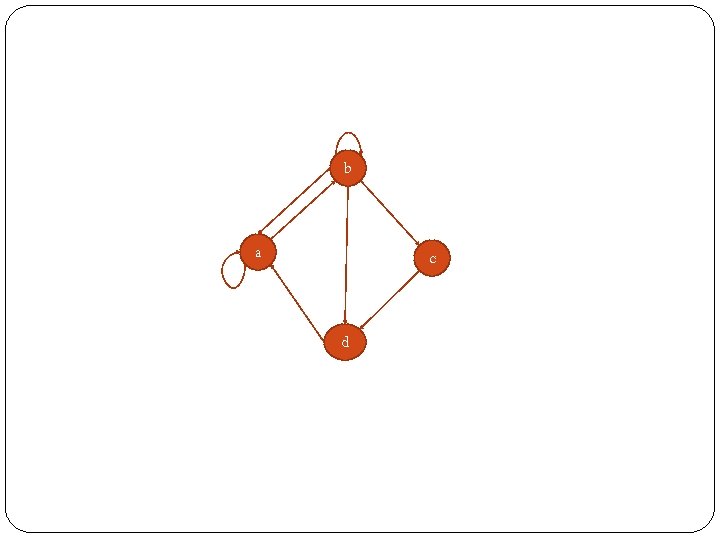
b a c d

Degree This is an important concept in relation. If R is a relation on set A and a A, then in-degree for a is the number of b A where (b, a) R. Out-degree for a is the number of b A where (a, b) R. For diagraph above, its degrees are: Vertex a b c d In-degree 3 2 1 2 Out-degree 2 4 1 1

Note: In-degree of a vertex is the number of edges terminating at the vertex Out-degree of a vertex is the number of edge leaving the vertex. To read in-degree and out-degree from matrix. Ex 10: Let A = {a, b, c, d} and R is given below: MR = 1 0 0 1 1 1 0 0 1 Note: In-degree is in the column, while out-degree is in the row.
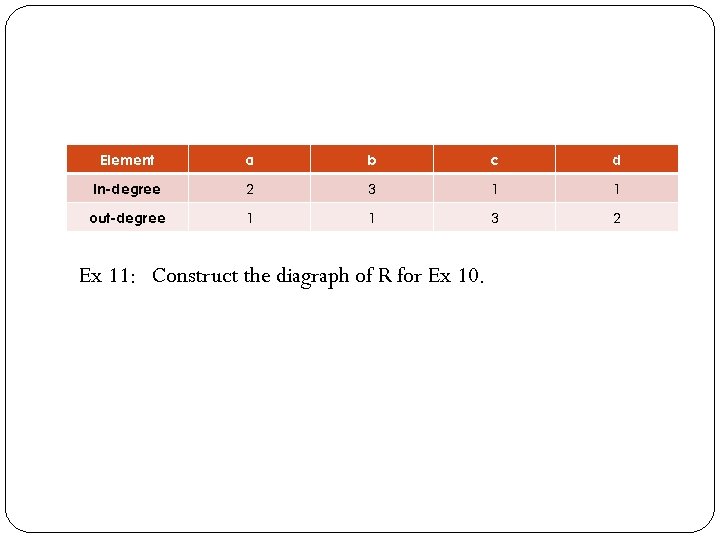
Element a b c d In-degree 2 3 1 1 out-degree 1 1 3 2 Ex 11: Construct the diagraph of R for Ex 10.
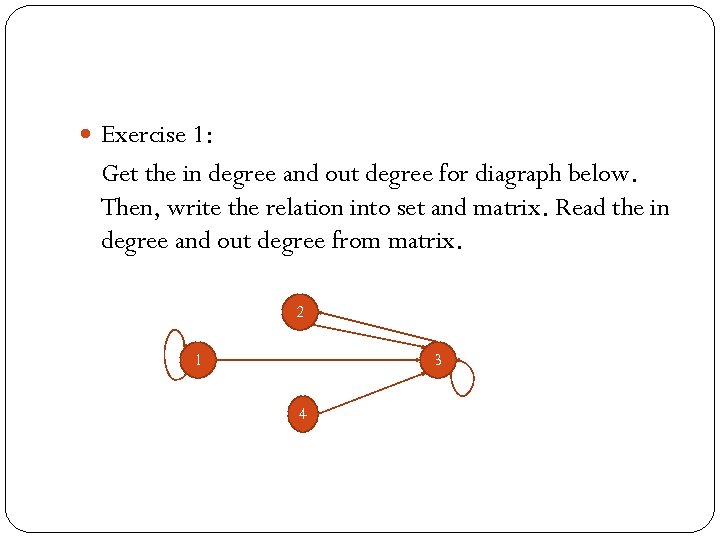
Exercise 1: Get the in degree and out degree for diagraph below. Then, write the relation into set and matrix. Read the in degree and out degree from matrix. 2 1 3 4
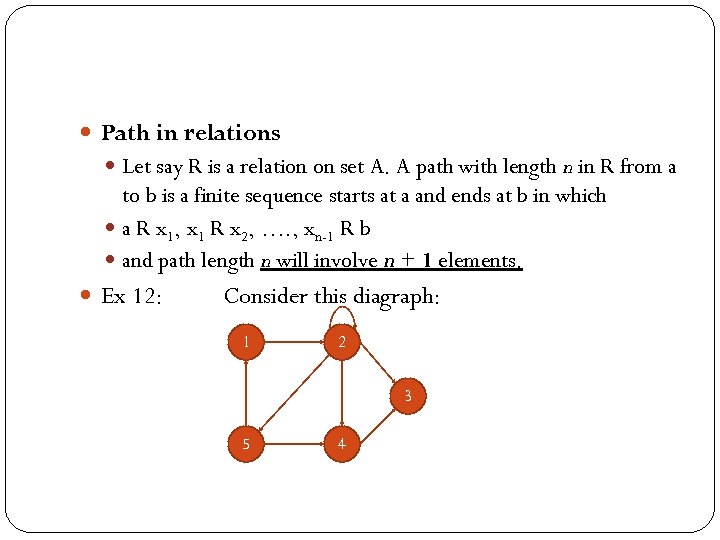
Path in relations Let say R is a relation on set A. A path with length n in R from a to b is a finite sequence starts at a and ends at b in which a R x 1, x 1 R x 2, …. , xn-1 R b and path length n will involve n + 1 elements. Ex 12: Consider this diagraph: 1 2 3 5 4

1: 1, 2, 5, 4, 3 is a path length 4 from vertex 1 to vertex 3. 2: 1, 2, 5, 1 is a path length 3 from vertex 1 to itself. 3: 2, 2 is a path length 1 from vertex 2 to itself. 4: 2, 5, 1, 2 is a path length 3 from vertex 2 to itself. A path that start and ends at the same vertex is called a cycle. 2, 3 and 4 are all cycles. 3 and 4 are cycle that starts and ends at the same vertex but different length.

In Example above 3 is cycle length 1, respectively. It is clear that paths of length 1 can be identified with the ordered pairs (x, y) that belong to R. Paths in a relation R can be used to defined new relations that are quite useful. If n is a fixed positive integer, we defined relation Rn on A as follows: x Rn y means that there is a path of length n from x to y in R. We may also defined a relation R on A by letting x R y mean that there is some path in R from x to y. The length of the path is depend on x and y.

The relation R is sometimes called the connectivity relation for R. Note that Rn(x) consists of all vertices that can be reached from x by means of a path in R of length n. The set R (x) consists of all vertices that can be reached from x by some path in R. Path length n can be found using set, matrix or diagraph representation.

Ex 13: Let A = {a, b, c, d, e} and R = {(a, a), (a, b), (b, c), (c, d), (c, e), (d, e)} Find all paths with length 2. Ans: Set: R 2 = {(a, a), (a, b), (a, c), (b, d), (b, e), (c, e)} (manual checking)
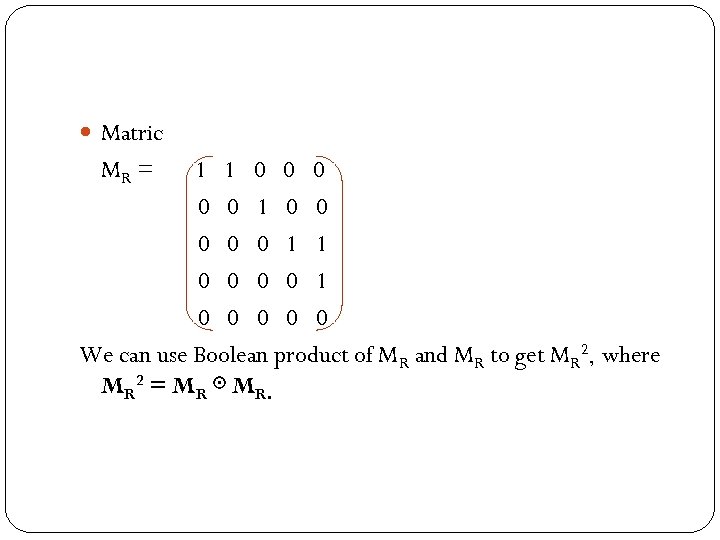
Matric MR = 1 1 0 0 0 0 0 We can use Boolean product of MR and MR to get MR 2, where MR 2 = MR ⊙ MR.

Reachability is a concept in which there is a relation between x and y in whatever length possible. Written as x R y where x and y have relations. Consider Ex 12. Identify all x R y. Answer: R = {(a, a), (a, b), ( a, c), (a, d), (a, e), (b, c), (b, d), (b, e), (c, d), (c, e), (d, e)} Exercise 2: List all path length 2 from Exercise 1 using three ways of representation. List all path length 1, 2 and 3 for Ex 10 and Ex 12.

Properties of relations Relation has few properties that have to be identified clearly, such as: a) Reflexive and Irreflexive A relation R on set A is said to be reflexive if (a, a) R for ALL element, a A, that is, a R a for ALL a A. A relation R on set A is said to be irreflexive if a R a for ALL a A. Ex 10: Let say for an equality relation on set A, that is R = {(a, a)| a A}. So, this relation is reflexive

b) Symmetric A relation R on set A is said to be symmetric if there is a R b, then b R a. Relation is said not symmetric if there a and b A with a R b, but b R a. It is like a relation ‘sibling’ between a and b. c) Asymmetric Relation R on set A is said to be asymmetric if there is a R b, then b R a. Relation is said not asymmetric if there a and b A, both a R b and b R a are exist. It is like a relation ‘mother of’ between a and b.

d) Antisymmetric A relation R on set A is said to be antisymmetric if there is a R b, and b R a, and then a = b. That is, if a b, then a R b or b R a. Relation is not antisymmetric if a b, and there is both a R b and b R a.
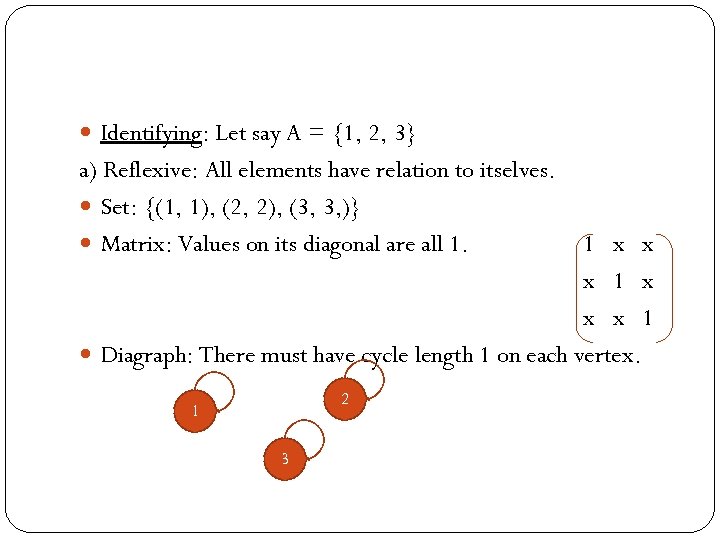
Identifying: Let say A = {1, 2, 3} a) Reflexive: All elements have relation to itselves. Set: {(1, 1), (2, 2), (3, 3, )} Matrix: Values on its diagonal are all 1. 1 x x x 1 Diagraph: There must have cycle length 1 on each vertex. 2 1 3

b) Irreflexive Set: U – R Matrix: All value on its diagonal is 0. 0 x x x 0 Diagraph: There is no cycle length 1 on each vertex,
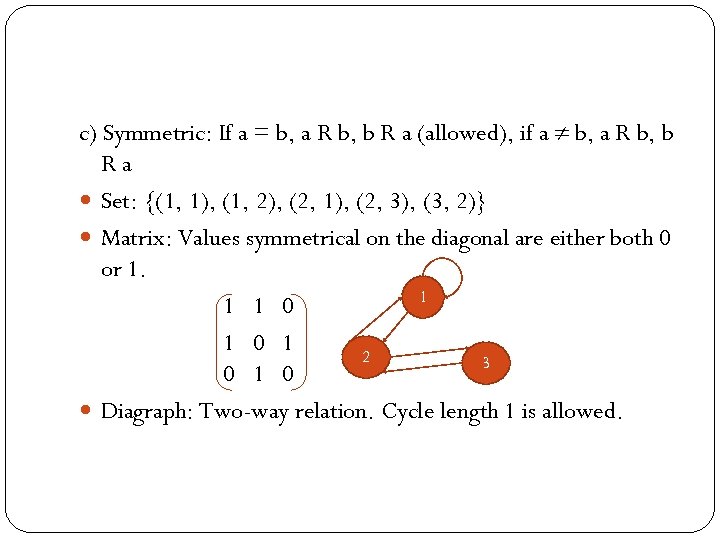
c) Symmetric: If a = b, a R b, b R a (allowed), if a b, a R b, b Ra Set: {(1, 1), (1, 2), (2, 1), (2, 3), (3, 2)} Matrix: Values symmetrical on the diagonal are either both 0 or 1. 1 1 1 0 1 2 3 0 1 0 Diagraph: Two-way relation. Cycle length 1 is allowed.
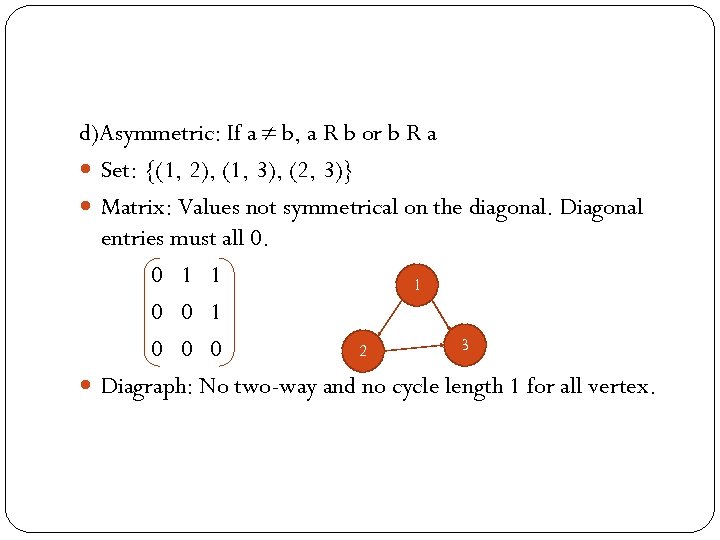
d)Asymmetric: If a b, a R b or b R a Set: {(1, 2), (1, 3), (2, 3)} Matrix: Values not symmetrical on the diagonal. Diagonal entries must all 0. 0 1 1 1 0 0 1 3 2 0 0 0 Diagraph: No two-way and no cycle length 1 for all vertex.
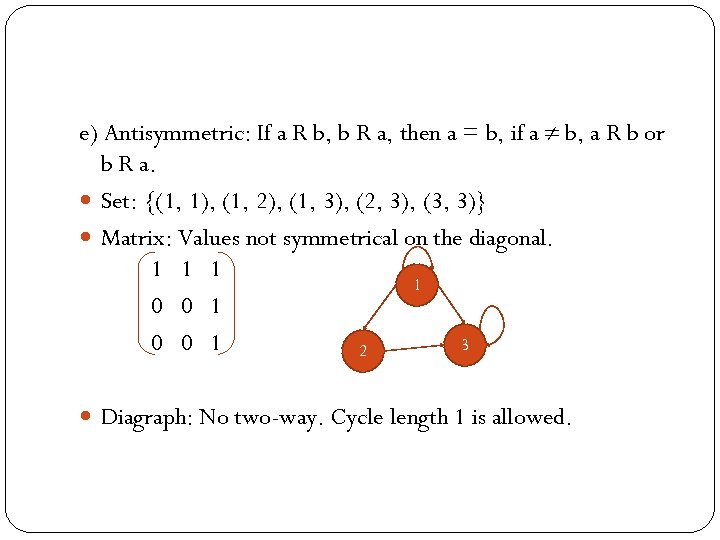
e) Antisymmetric: If a R b, b R a, then a = b, if a b, a R b or b R a. Set: {(1, 1), (1, 2), (1, 3), (2, 3), (3, 3)} Matrix: Values not symmetrical on the diagonal. 1 1 0 0 1 3 0 0 1 2 Diagraph: No two-way. Cycle length 1 is allowed.

Ex 11: Let say R is a relation defined as below: R = {(x, y) A x A | x is a cousin to y} Identify this relation either it is symmetric, asymmetric and/or antisymmetric. Ans: Symmetric: If x is a cousin to y, then y is a cousin to x. This fulfill the a R b and b R a. Asymmetric: Not asymmetric. Antisymmetric: Not antisymmetric.

Ex 12: Let say R is a relation defined as below: R = {(a, b) A x A | a < b} where this is a relation less than. Identify this relation either it is symmetric, asymmetric and/or antisymmetric. Ans: Symmetric: Not symmetric because a < b but b < a, that is a R b, but b R a Asymmetric: If a < b, then b < a, so R is asymmetric. Antisymmetric: If a b, then either a R b or b R a, so, R is antisymmetric.

Ex 13: Identify either matrix below symmetric, asymmetric and/or antisymmetric. MR 1 = 1 0 1 MR 2 = 1 1 1 MR 3 = 0 1 1 0 0 0 1 0 1 1 0 0 1 1 1 0 0 0 1 1 MR 4 = 0 0 1 1 MR 5 = 1 0 0 1 MR 6 = 0 1 1 1 0 0 0 0 1 1 0 0 0 1 0 0
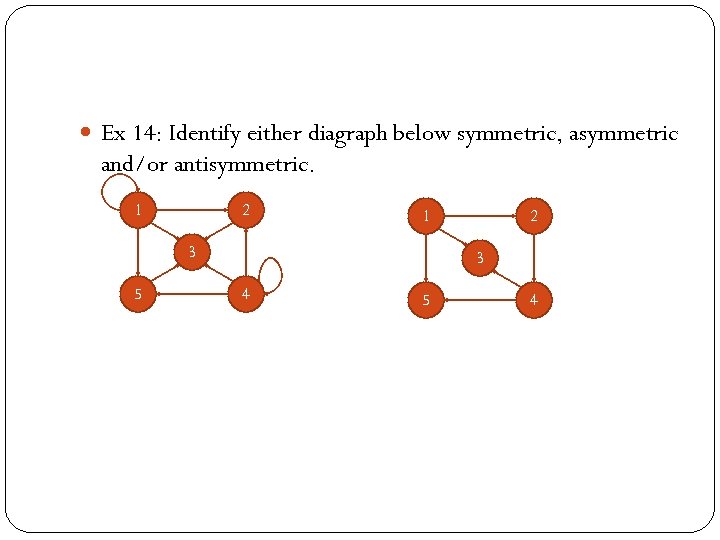
Ex 14: Identify either diagraph below symmetric, asymmetric and/or antisymmetric. 1 2 1 3 5 2 3 4 5 4
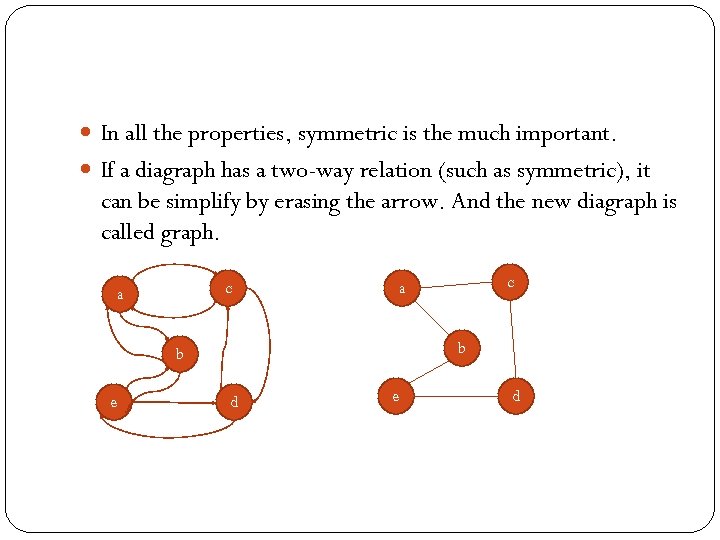
In all the properties, symmetric is the much important. If a diagraph has a two-way relation (such as symmetric), it can be simplify by erasing the arrow. And the new diagraph is called graph. c a b b e c a d e d
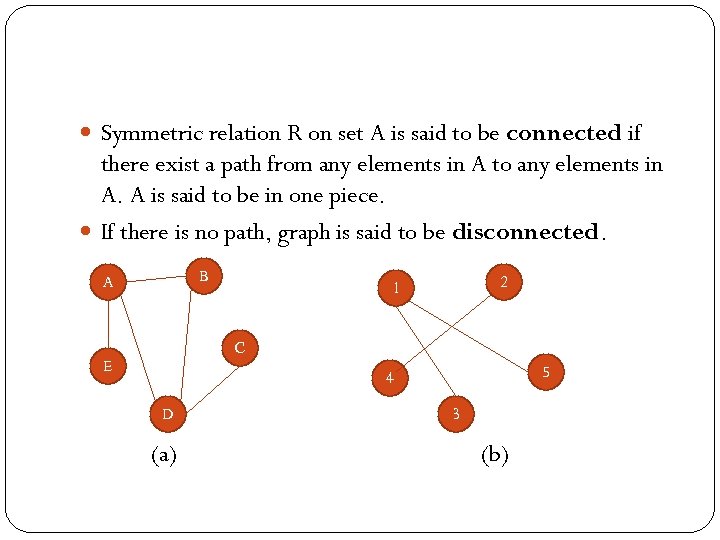
Symmetric relation R on set A is said to be connected if there exist a path from any elements in A to any elements in A. A is said to be in one piece. If there is no path, graph is said to be disconnected. B A 2 1 C E 5 4 D (a) 3 (b)

Transitive Relation We said that relation R on set A is transitive if there exist a R b and b R c, there must exist a R c. Not transitive when there exist a R b, and b R c, but a R c. If a, b and c is not exist, then R is transitive (cannot prove that it is not transitive). Ex 15: Consider Ex 12. Relation less than. Ans: This relation is transitive because if a < b, and b < c, then a < c. This meets the criteria of transitive.

Identifying: Let say A = {1, 2, 3, 4} Set: Identify manually by observation. Ex: R = {(1, 2), (1, 3), (4, 1), (4, 2)} This is transitive because we cannot prove it as not transitive. Matrix: mij = 1 and mjk = 1, then mik = 1. In short, if MR 2 = MR, then R is transitive.
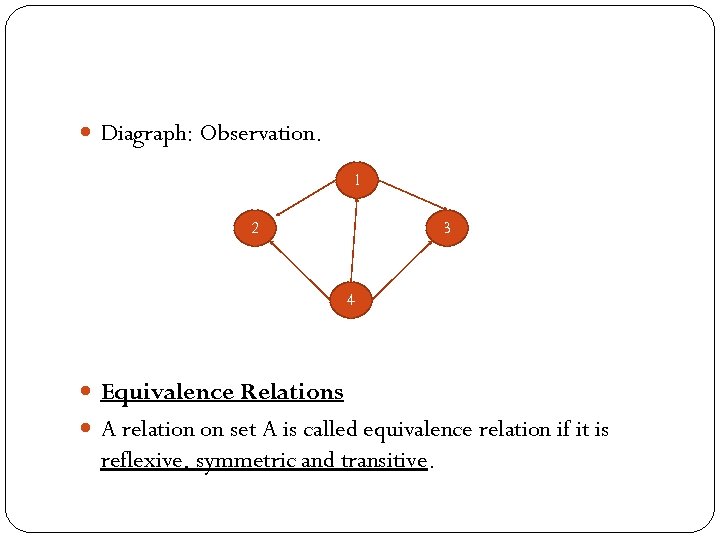
Diagraph: Observation. 1 2 3 4 Equivalence Relations A relation on set A is called equivalence relation if it is reflexive, symmetric and transitive.

Ex 16: Let say A = {1, 2, 3, 4} and let R = {(1, 1), (1, 2), (2, 1), (2, 2), (3, 4), (4, 3), (3, 3), (4, 4)} It is clear that R is an equivalence relation. Ex 17: Let set A is set integer, Z and R is defined as a R b if and only if a b. Is R an equivalence relation? Ans: We can see that a a, then R is reflexive. If a b, then it is not necessarily b a, then R is not symmetric. R is transitive because if a b, b c, then a c. But, because R is not fulfilling all the condition, therefore, R is not an equivalence relation.

Relation Manipulation We can manipulate relation with few operations to change, combine or update the previous relations. We can have new relations after manipulation. Manipulations involved either one relation such as: a) Complementary relation for R written as R(complement). This is explained by a R b if and only if a R b

b) Inverse relation is written as R-1. This is explained by b R-1 a if and only if a R b Manipulations involving two relations R and S includes: a) Intersection, Intersection relation R S is a relation in which its elements fulfill this condition: a (R S) b if and only if a R b and a S b

b) Union, Union relation R S is a relation in which its elements fulfill this condition: a (R S) b if and only if a R b or a S b Ex 18: Identify all manipulation by using all three ways of representation

Theorem involved: Theorem 1: Let say R and S are relations from A to B; a) If R S, then R-1 S-1 b) If R S, then S(complement) R(complement) Theorem 2: let R and S are relations on set A a) If R reflexive, then R-1 is also reflexive. b) If R and S reflexive, then R S and R S is also reflexive. c) R is reflexive if and only if R(complement) is irreflexive.

Theorem 3: Let say R is a relation on set A. a) R is symmetric if and only if R = R-1 b) R is antisymmetric if and only if R R-1 c) R is asymmetric if and only if R R-1 = Theorem 4: Let R and S are relations on set A. a) If R symmetric, then a R-1 and R(complement) is also symmetric b) If R and S symmetric, then R S and R S is also symmetric.

Theorem 5: Let R and S are relations on set A a) (R S)2 R 2 S 2 b) If R and S are transitive, then R S is also transitive. c) If R and S are equivalence relations, then R S is also equivalence relation.

Composition Let say there are 3 set A, B and C where R is a relation from A to B and S is a relation from B to C. A new relation, named composition can be build, written as S R. Relation S R is a relation from A to C, defined as: If (a A) and (c C), then a (S R) c if and only if (b B), and there exist a R b and b S c.

Ex 19: Let A = {1, 2, 3, 4}. R = {(1, 2), (1, 1), (1, 3), (2, 4), (3, 2)} and S = {(1, 4), (1, 3), (2, 3), (3, 1), (4, 1)}. Find S R. Ans: In R we find that (1, 2) R and (2, 3) S, then we must have (1, 3) S R. using this method, we can find that S R = {(1, 3), (1, 4), (1, 1), (2, 1), (3, 3)} # Do Ex 19 again using matrix. Theorem 6: Let R is a relation from A to B and S is a relation from B to C. Then, if A 1 is any subset for A, we can find that (S R) (A 1) = S(R(A 1))

Theorem 7: Let A, B, C and D are sets, R is a relation from A to B, S is a relation from B to C and T is a relation from C to D. Then, T (S R) = (T S) R Theorem 8: Let A, B and C are sets, R is a relation from A to B and S is a relation from B to C. Then, (S R)-1 = R-1 S-1 R S S R Ex 20: Let A = {a, b} and R and S are relations on set A. Given R = {(a, a), (b, b)} and S = {(a, b), (b, a), (b, b)}. Find S R and R S.

Closure If R is a relation on set A, R might less few elements in which R is not fulfilling the important properties such as reflexive, symmetric and transitive. We might want to and as minimum as possible, new elements in order to make R meets the criteria. The smallest relation R 1, in the relation that contains R and the new elements together so that R 1 will meets the criteria. In this case, we call R 1 as a closure of R.

Ex 21: Let A ={a, b, c} and R = {(a, a), (a, b), (b, c), (a, c)}. Then The reflexive closure for R is R 1 = {(a, a), (a, b), (b, c), (a, c), (b, b), (c, c)}. And, symmetric closure for R is R 1 = {(a, a), (a, b), (b, a), (b, c), (c, b), (a, c), (c, a)} The most important is Transitive Closure.

Transitive Closure Let R is a relation on set A and R is not transitive. So we have to make it becomes transitive. We will show that the transitivity closure of R is just the connectivity relation R. Theorem 1: Let R is a relation on set A. Then R is a transitive closure for R. There are 2 ways to find R : a) Matrix Product Matrix product require us to times MR few times until the final outcome is the same with the previous outcome.

Theorem 2: Let A is a set with |A| = n, and let R is a relation on set A. Then R = R R 2 …. . Rn. b) Warshall Algorithm Steps involved are: a) Bring down all entries value 1 from Wk-1 to Wk. b) List all location p 1, p 2, … in column k for Wk-1 in which the entries is 1, and all location q 1, q 2, … in row k for Wk-1, in which the entries is 1. c) Put all 1 in all location pi, qj for Wk (if the entries is 0).
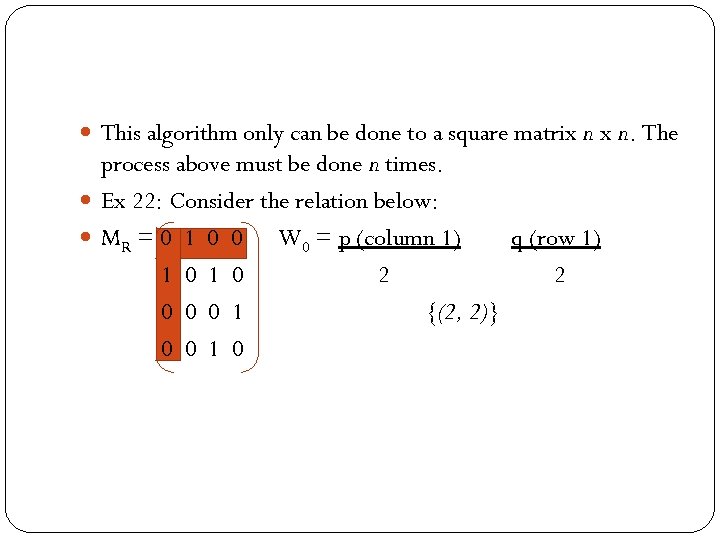
This algorithm only can be done to a square matrix n x n. The process above must be done n times. Ex 22: Consider the relation below: MR = 0 1 0 0 W 0 = p (column 1) q (row 1) 1 0 2 2 0 0 0 1 {(2, 2)} 0 0 1 0
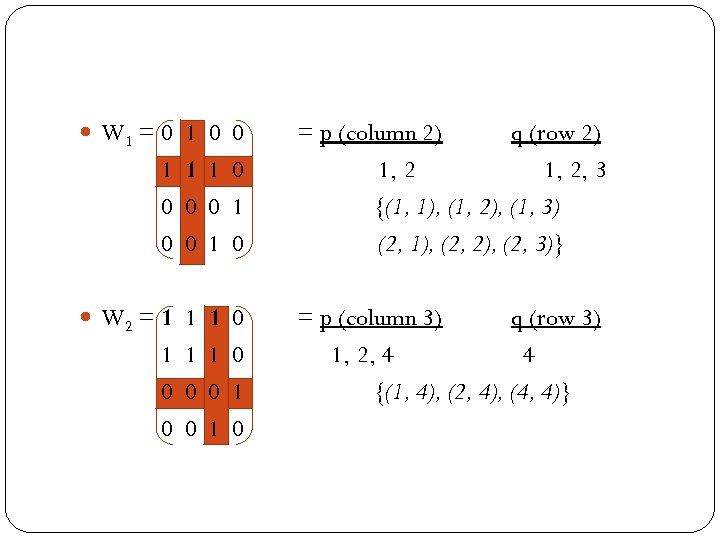
W 1 = 0 1 0 0 1 1 1 0 0 1 0 W 2 = 1 1 1 0 0 0 0 1 0 = p (column 2) q (row 2) 1, 2, 3 {(1, 1), (1, 2), (1, 3) (2, 1), (2, 2), (2, 3)} = p (column 3) q (row 3) 1, 2, 4 4 {(1, 4), (2, 4), (4, 4)}
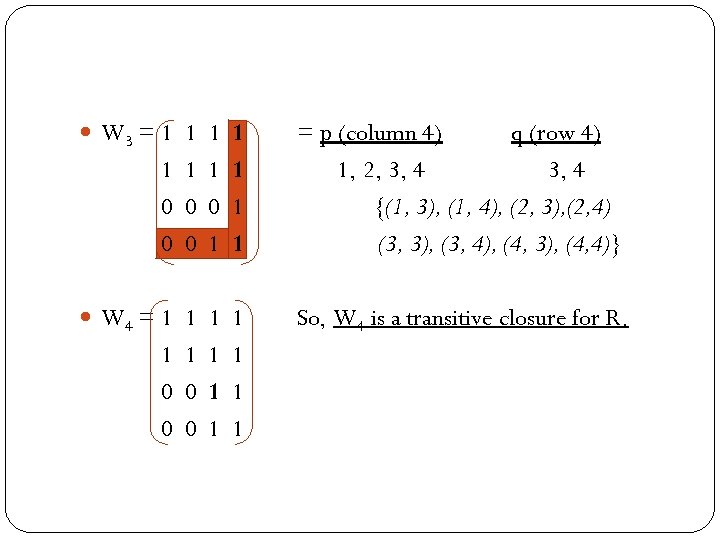
W 3 = 1 1 1 1 0 0 0 1 1 = p (column 4) q (row 4) 1, 2, 3, 4 {(1, 3), (1, 4), (2, 3), (2, 4) (3, 3), (3, 4), (4, 3), (4, 4)} W 4 = 1 1 So, W 4 is a transitive closure for R. 1 1 0 0 1 1

Exercise 3: Given A = {1, 2, 3, 4} and R and S are relation on set A. Given R = {(1, 1), (1, 3), (2, 1), (2, 4), (3, 3), (3, 2), (4, 1), (4, 4)}. Given S = {(1, 2), (1, 3), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (4, 1), (4, 3)}. Find: a) R S b) S R c) R R d) S S

Given A = {a, b, c} and R and S are relation on A. Given R = {(a, a), (b, c), (c, b)} and S = {(a, b), (a, c), (b, b), (c, a). Find: a) R S b) S R c) R R d) S S

Find the transitive closure for each MR below using Warshall Algorithm, given A = {1, 2, 3, 4}. a) MR = 1 0 0 1 1 1 0 0 0 0 1
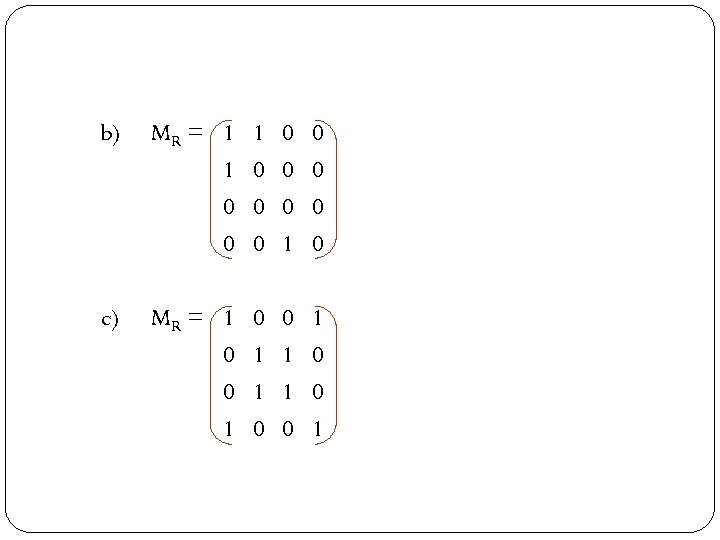
b) MR = 1 1 0 0 0 0 1 0 0 c) MR = 1 0 0 1 1 0 0 1
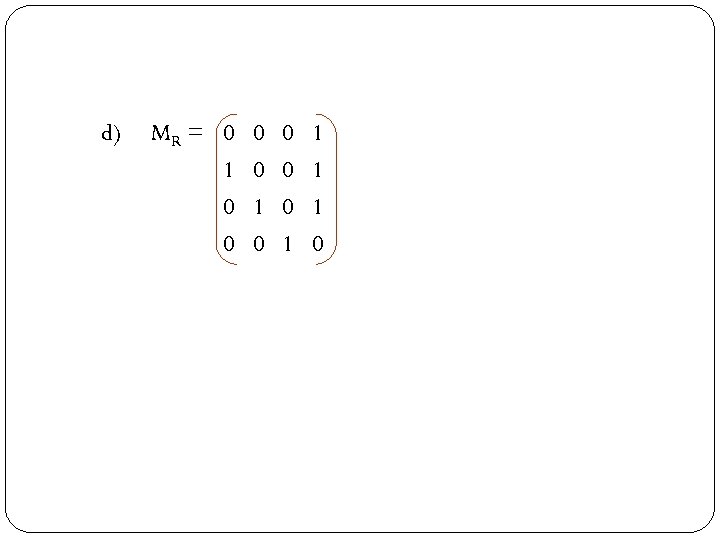
d) MR = 0 1 0 0 0 0 1 1 0
2c8a41014f4fbca244053663f2c337cd.ppt