CSCE 715 Network Systems Security Chin-Tser Huang huangct cse

CSCE 715: Network Systems Security Chin-Tser Huang huangct@cse. sc. edu University of South Carolina 9/15/2005

Key Management n n Asymmetric encryption helps address key distribution problems Two aspects n n distribution of public keys use of public-key encryption to distribute secret keys 9/15/2005 2

Distribution of Public Keys n Four alternatives of public key distribution n n Public announcement Publicly available directory Public-key authority Public-key certificates 9/15/2005 3

Public Announcement n Users distribute public keys to recipients or broadcast to community at large n n E. g. append PGP keys to email messages or post to news groups or email list Major weakness is forgery n n anyone can create a key claiming to be someone else and broadcast it can masquerade as claimed user before forgery is discovered 9/15/2005 4

Publicly Available Directory n n Achieve greater security by registering keys with a public directory Directory must be trusted with properties: n n n contains {name, public-key} entries participants register securely with directory participants can replace key at any time directory is periodically published directory can be accessed electronically Still vulnerable to tampering or forgery 9/15/2005 5

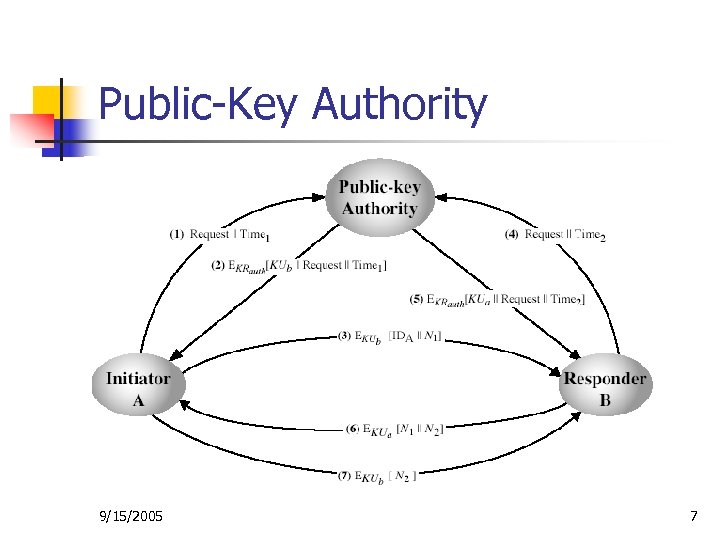
Public-Key Authority n n Improve security by tightening control over distribution of keys from directory Has properties of directory Require users to know public key for the directory Users can interact with directory to obtain any desired public key securely n require real-time access to directory when keys are needed 9/15/2005 6

Public-Key Authority 9/15/2005 7

Public-Key Certificates n n Certificates allow key exchange without realtime access to public-key authority A certificate binds identity to public key n n n usually with other info such as period of validity, authorized rights, etc With all contents signed by a trusted Public. Key or Certificate Authority (CA) Can be verified by anyone who knows the CA’s public key 9/15/2005 8

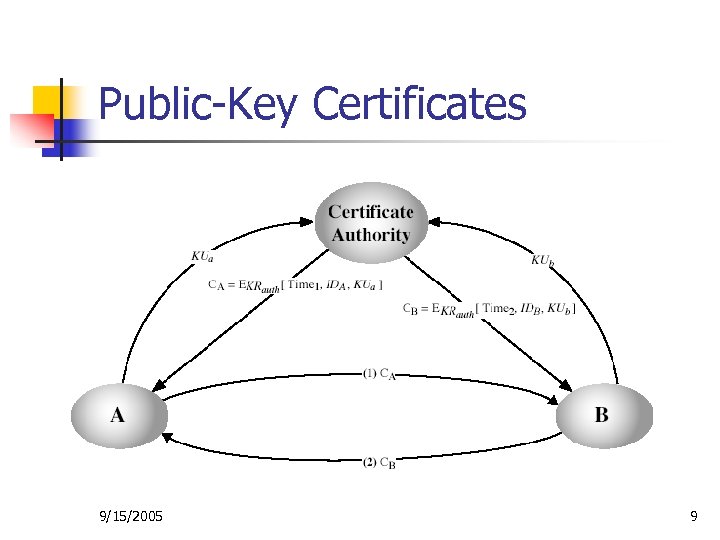
Public-Key Certificates 9/15/2005 9

Distribute Secret Keys Using Asymmetric Encryption n n Can use previous methods to obtain public key of other party Although public key can be used for confidentiality or authentication, asymmetric encryption algorithms are too slow So usually want to use symmetric encryption to protect message contents Can use asymmetric encryption to set up a session key 9/15/2005 10

Simple Secret Key Distribution n Proposed by Merkle in 1979 n n A generates a new temporary public key pair A sends B the public key and A’s identity B generates a session key Ks and sends encrypted Ks (using A’s public key) to A A decrypts message to recover Ks and both use 9/15/2005 11

Problem with Simple Secret Key Distribution n An adversary can intercept and impersonate both parties of protocol n n n A generates a new temporary public key pair {KUa, KRa} and sends KUa || IDa to B Adversary E intercepts this message and sends KUe || IDa to B B generates a session key Ks and sends encrypted Ks (using E’s public key) E intercepts message, recovers Ks and sends encrypted Ks (using A’s public key) to A A decrypts message to recover Ks and both A and B unaware of existence of E 9/15/2005 12

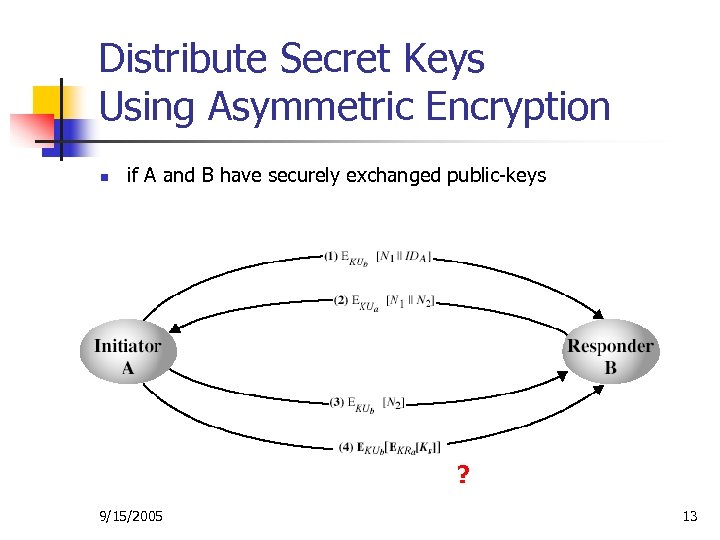Distribute Secret Keys Using Asymmetric Encryption n if A and B have securely exchanged public-keys ? 9/15/2005 13

Problem with Previous Scenario n Message (4) is not protected by N 2 n An adversary can intercept message (4) and replay an old message or insert a fabricated message 9/15/2005 14

Order of Encryption Matters n What can be wrong with the following protocol? A B: N B A: EKUa[EKRb[Ks||N]] n An adversary sitting between A and B can get a copy of secret key Ks without being caught by A and B! 9/15/2005 15

Diffie-Hellman Key Exchange n n First public-key type scheme proposed By Diffie and Hellman in 1976 along with advent of public key concepts A practical method for public exchange of secret key Used in a number of commercial products 9/15/2005 16

Diffie-Hellman Key Exchange n Use to set up a secret key that can be used for symmetric encryption n n cannot be used to exchange an arbitrary message Value of key depends on the participants (and their private and public key information) Based on exponentiation in a finite (Galois) field (modulo a prime or a polynomial) - easy Security relies on the difficulty of computing discrete logarithms (similar to factoring) – hard 9/15/2005 17

Primitive Roots n n From Euler’s theorem: aø(n) mod n=1 Consider am mod n=1, GCD(a, n)=1 n n n must exist for m= ø(n) but may be smaller once powers reach m, cycle will repeat If smallest is m= ø(n) then a is called a primitive root if p is prime and a is a primitive of p, then successive powers of a “generate” the group mod p Not every integer has primitive roots 9/15/2005 18

Primitive Root Example: Power of Integers Modulo 19 9/15/2005 19

Discrete Logarithms n n n Inverse problem to exponentiation is to find the discrete logarithm of a number modulo p Namely find x where ax = b mod p Written as x=loga b mod p or x=inda, p(b) If a is a primitive root of p then discrete logarithm always exists, otherwise may not x = 4 mod 13 has no answer n 3 x = 3 mod 13 has an answer 4 n 2 While exponentiation is relatively easy, finding discrete logarithms is generally a hard problem 9/15/2005 20

Diffie-Hellman Setup n All users agree on global parameters n n n Each user (e. g. A) generates its key n n n large prime integer or polynomial q α which is a primitive root mod q choose a private key (number): x. A < q x. A compute its public key: y. A = α mod q Each user publishes its public key 9/15/2005 21

Diffie-Hellman Key Exchange n n n Shared session key for users A and B is KAB: x x KAB = α A. B mod q x. B = y. A mod q (which B can compute) x. A = y. B mod q (which A can compute) KAB is used as session key in symmetric encryption scheme between A and B Attacker needs x. A or x. B, which requires solving discrete log 9/15/2005 22

Diffie-Hellman Example n n n Given Alice and Bob who wish to swap keys Agree on prime q=353 and α=3 Select random secret keys: n n Compute public keys: 97 n n n A chooses x. A=97, B chooses x. B=233 y. A=3 mod 353 = 40 (Alice) 233 y. B=3 mod 353 = 248 (Bob) Compute shared session key as: x 97 KAB= y. B A mod 353 = 248 = 160 x. B 233 KAB= y. A mod 353 = 40 = 160 9/15/2005 (Alice) (Bob) 23

Elliptic Curve Cryptography n n Majority of public-key crypto (RSA, D-H) use either integer or polynomial arithmetic with very large numbers/polynomials Imposes a significant load in storing and processing keys and messages An alternative is to use elliptic curves Offers same security with smaller bit sizes 9/15/2005 24

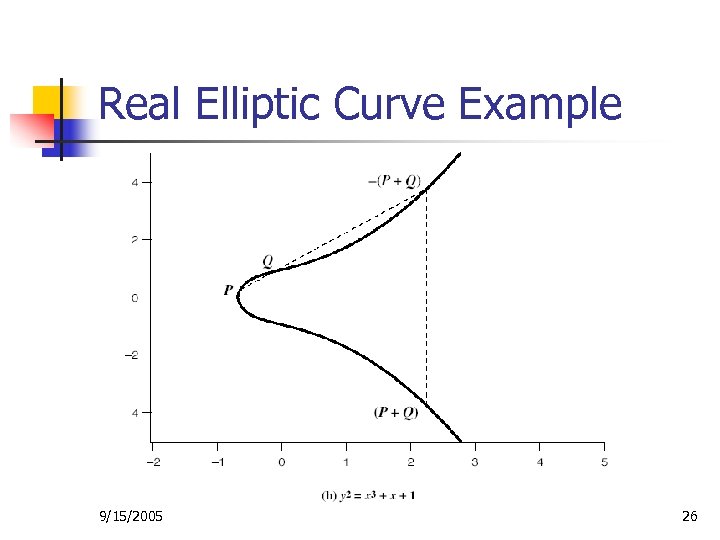
Real Elliptic Curves n n An elliptic curve is defined by an equation in two variables x and y, with coefficients Consider a cubic elliptic curve of form n n y 2 = x 3 + ax + b where x, y, a, b are all real numbers also define zero point O Have addition operation for elliptic curve n geometrically sum of P+Q is reflection of intersection R 9/15/2005 25

Real Elliptic Curve Example 9/15/2005 26

Finite Elliptic Curves n n Elliptic curve cryptography uses curves whose variables and coefficients are finite Two families are commonly used n prime curves Ep(a, b) defined over Zp n n n use integers modulo a prime best in software binary curves E 2 m(a, b) defined over GF(2 m) n n 9/15/2005 use polynomials with binary coefficients best in hardware 27

Elliptic Curve Cryptography n n n ECC addition is analog of modulo multiply ECC repeated addition is analog of modulo exponentiation Need a “hard” problem equivalent to discrete logarithm n n n Q=k. P, where Q, P belong to a prime curve is “easy” to compute Q given k, P but “hard” to find k given Q, P known as the elliptic curve logarithm problem Certicom example: E 23(9, 17) 9/15/2005 28

ECC Diffie-Hellman n n n Can do key exchange analogous to D-H Users select a suitable curve Ep(a, b) Select base point G=(x 1, y 1) with large order n s. t. n. G=O A and B select private keys n. A

ECC Encryption/Decryption n n Must first encode any message M as a point on the elliptic curve Pm Select suitable curve and point G as in D-H Each user chooses private key n. A

ECC Security n n n Relies on elliptic curve logarithm problem Fastest method is “Pollard rho method” Compared to factoring, can use much smaller key sizes than with RSA etc For equivalent key lengths computations are roughly equivalent Hence for similar security ECC offers significant computational advantages 9/15/2005 31

Next Class n n n Hashing functions Message digests Read Chapters 11 and 12 9/15/2005 32