eac491abbf4e5cb3bcc425d77e39222b.ppt
- Количество слайдов: 64

CSCE 552 Spring 2010 Animation By Jijun Tang

Announcements n Homework #3 due Mar 19 th ¡ ¡ n Group based A model to be used in your own game Second demo ¡ ¡ Very Early April A demo is needed

Animation Overview n n n n n Fundamental Concepts Animation Storage Playing Animations Blending Animations Motion Extraction Mesh Deformation Inverse Kinematics Attachments & Collision Detection Conclusions

Different types of animation n n Particle effects (fire, smoke, etc) Procedural / Physics “Hard” object animation (door, robot) “Soft” object animation (tree swaying in the wind, flag flapping the wind) Character animation
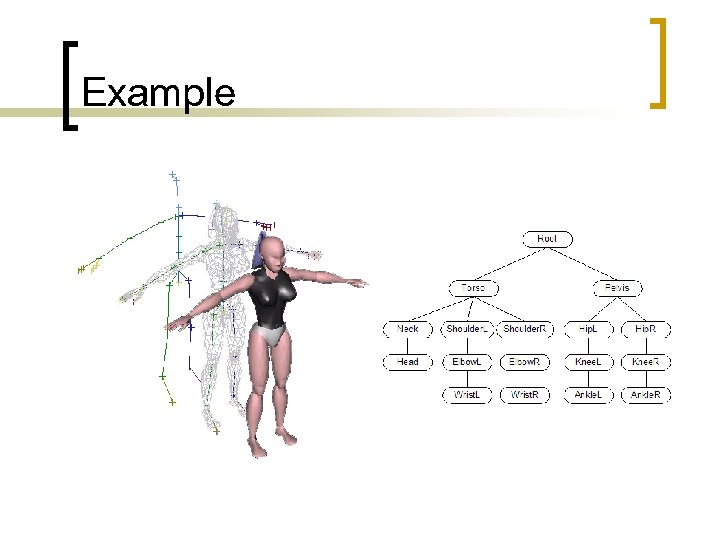
Example

Quaternions n n Quaternions are an interesting mathematical concept with a deep relationship with the foundations of algebra and number theory Invented by W. R. Hamilton in 1843 In practice, they are most useful to use as a means of representing orientations A quaternion has 4 components

Keyframes n n n Motion is usually smooth Only store every nth frame (key frames) Interpolate between keyframes ¡ ¡ n Linear Interpolate Inbetweening or “tweening” Different anims require different rates ¡ ¡ Sleeping = low, running = high Choose rate carefully
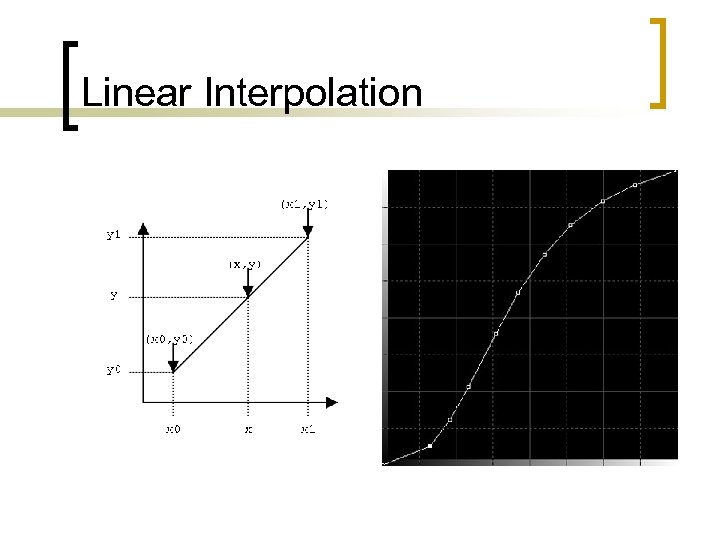
Linear Interpolation
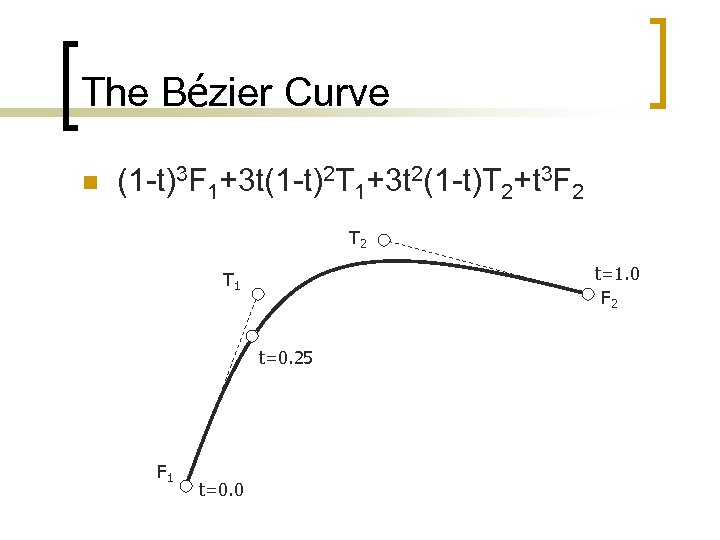
The Bézier Curve n (1 -t)3 F 1+3 t(1 -t)2 T 1+3 t 2(1 -t)T 2+t 3 F 2 T 2 t=1. 0 F 2 T 1 t=0. 25 F 1 t=0. 0

Animation Blending n n The animation blending system allows a model to play more than one animation sequence at a time, while seamlessly blending the sequences Used to create sophisticated, life-like behavior ¡ ¡ Walking and smiling Running and shooting

Blending Animations n n n The Lerp Quaternion Blending Methods Multi-way Blending Bone Masks The Masked Lerp Hierarchical Blending

The Lerp n n n Foundation of all blending “Lerp”=Linear interpolation Blends A, B together by a scalar weight ¡ ¡ n Translation, scale, shear lerp are obvious ¡ n lerp (A, B, i) = i. A + (1 -i)B i is blend weight and usually goes from 0 to 1 Componentwise lerp Rotations are trickier – normalized quaternions is usually the best method.

Quaternion Blending n Normalizing lerp (nlerp) ¡ ¡ ¡ n Lerp each component Normalize (can often be approximated) Follows shortest path Not constant velocity Multi-way-lerp is easy to do Very simple and fast Many others: ¡ ¡ Spherical lerp (slerp) Log-quaternion lerp (exp map)

Spherical lerp (slerp) n n n Usual textbook method Follows shortest path Constant velocity Multi-way-lerp is not obvious Moderate cost 14

Log-quaternion lerp (exp map) n n n Rather obscure method Does not follow shortest path Constant velocity Multi-way-lerp is easy to do Expensive 15

Which is the Best n n n No perfect solution! Each missing one of the features All look identical for small interpolations ¡ ¡ n n This is the 99% case Blending very different animations looks bad whichever method you use Multi-way lerping is important So use cheapest - nlerp

Multi-way Blending n Can use nested lerps ¡ ¡ ¡ n Weighted sum associates nicely ¡ ¡ n lerp (A, B, i), C, j) But n-1 weights - counterintuitive Order-dependent (i. A + j. B + k. C + …) / (i + j + k + … ) But no i value can result in 100% A More complex methods ¡ ¡ Less predictable and intuitive Can be expensive

Bone Masks n Some animations only affect some bones ¡ ¡ Wave animation only affects arm Walk affects legs strongly, arms weakly n n Bone mask stores weight for each bone ¡ ¡ ¡ n Arms swing unless waving or holding something Multiplied by animation’s overall weight Each bone has a different effective weight Each bone must be blended separately Bone weights are usually static ¡ Overall weight changes as character changes animations

The Masked Lerp n Two-way lerp using weights from a mask ¡ n n n Mask value of 1 means bone is 100% A Mask value of 0 means bone is 100% B Solves weighted-sum problem ¡ n Each bone can be lerped differently (no weight can give 100% A) No simple multi-way equivalent ¡ Just a single bone mask, but two animations

Hierarchical Blending n n Combines all styles of blending A tree or directed graph of nodes Each leaf is an animation Each node is a style of blend ¡ n Blends results of child nodes Construct programmatically at load time ¡ ¡ ¡ Evaluate with identical code each frame Avoids object-specific blending code Nodes with weights of zero not evaluated

Triangles n Fundamental primitive of pipelines ¡ ¡ n n Three points define a plane Triangle plane is mapped with data ¡ ¡ n Everything else constructed from them (except lines and point sprites) Textures Colors “Rasterized” to find pixels to draw

Mesh

Vertices n n A vertex is a point in space Plus other attribute data ¡ ¡ n Colors Surface normal Texture coordinates Whatever data shader programs need Triangles use three vertices ¡ Vertices shared between adjacent triangles

Textures n Array of texels ¡ ¡ n 1 D, 2 D, 3 D and “cube map” arrays ¡ ¡ ¡ n Same as pixel, but for a texture Nominally R, G, B, A but can mean anything 2 D is by far the most common Basically just a 2 D image bitmap Often square and power-of-2 in size Cube map - six 2 D arrays makes hollow cube ¡ ¡ Approximates a hollow sphere of texels For environmental
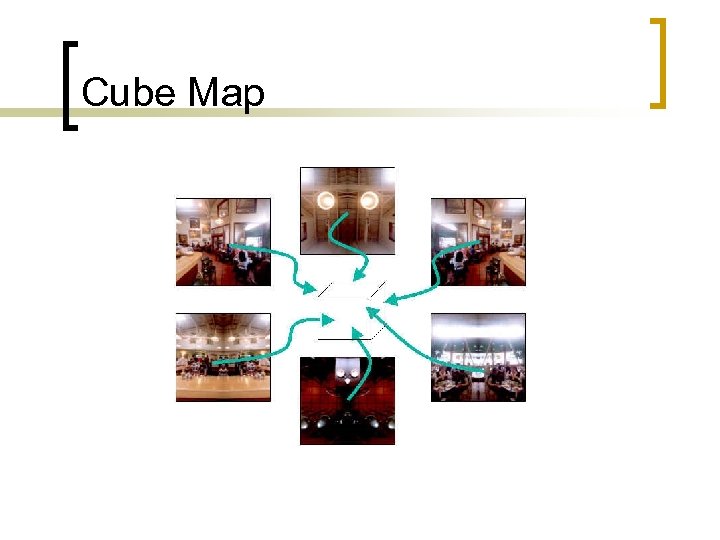
Cube Map

Texture Example

High-Level Organization n n n Gameplay and Rendering Render Objects Render Instances Meshes Skeletons Volume Partitioning

Gameplay and Rendering n Rendering speed varies according to scene ¡ ¡ n Gameplay is constant speed ¡ ¡ ¡ n Some scenes more complex than others Typically 15 -60 frames per second Camera view should not change game In multiplayer, each person has a different view, but there is only one shared game 1 update per second (RTS) to thousands (FPS) Keep the two as separate as possible!

Render Objects n n n Description of renderable object type Mesh data (triangles, vertices) Material data (shaders, textures, etc) Skeleton (+rig) for animation Shared by multiple instances

Render Instances n n A single entity in a world References a render object ¡ n n n Decides what the object looks like Position and orientation Lighting state Animation state

Meshes n n Triangles Vertices Single material “Atomic unit of rendering” ¡ n Not quite atomic, depending on hardware Single object may have multiple meshes ¡ ¡ Each with different shaders, textures, etc Level-Of-Distance (LOD)

LOD n n n Objects have different mesh for different distance from the player The mesh should be simpler if object is faraway Many games have LOD, for example, Microsoft Train Simulator

Volume Partitioning n Cannot draw entire world every frame ¡ n n n Lots of objects – far too slow Need to decide quickly what is visible Partition world into areas Decide which areas are visible Draw things in each visible area Many ways of partitioning the world

Volume Partitioning - Portals n Nodes joined by portals ¡ n n n See if any portal of node is visible If so, draw geometry in node See if portals to other nodes are visible ¡ ¡ n Usually a polygon, but can be any shape Check only against visible portal shape Common to use screen bounding boxes Recurse to other nodes
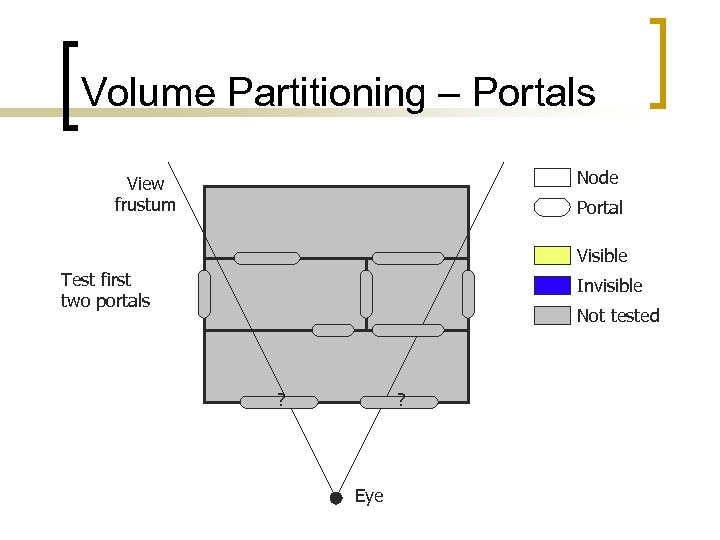
Volume Partitioning – Portals Node View frustum Portal Visible Test first two portals Invisible Not tested ? ? Eye
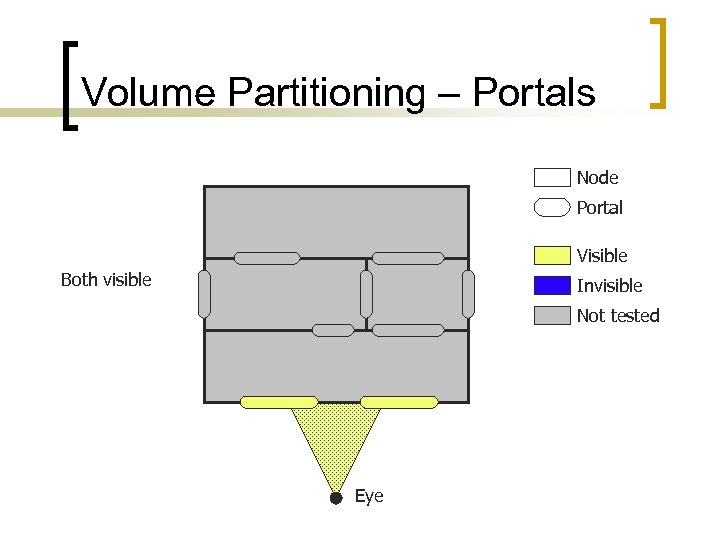
Volume Partitioning – Portals Node Portal Visible Both visible Invisible Not tested Eye
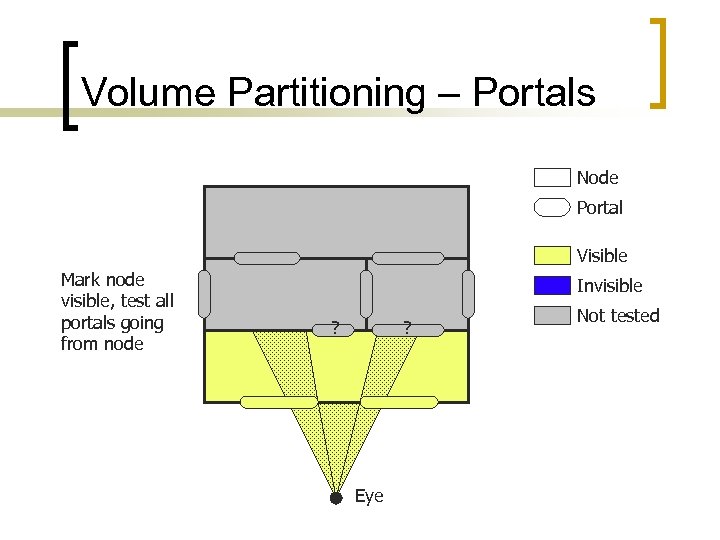
Volume Partitioning – Portals Node Portal Visible Mark node visible, test all portals going from node Invisible ? ? Eye Not tested
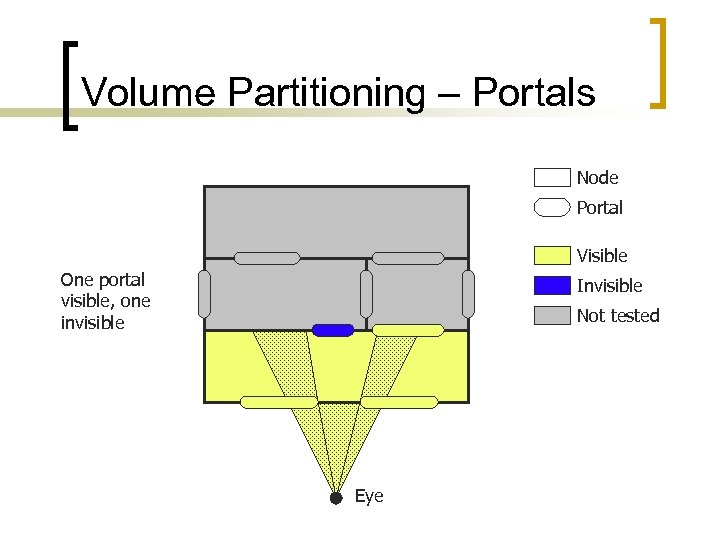
Volume Partitioning – Portals Node Portal Visible One portal visible, one invisible Invisible Not tested Eye
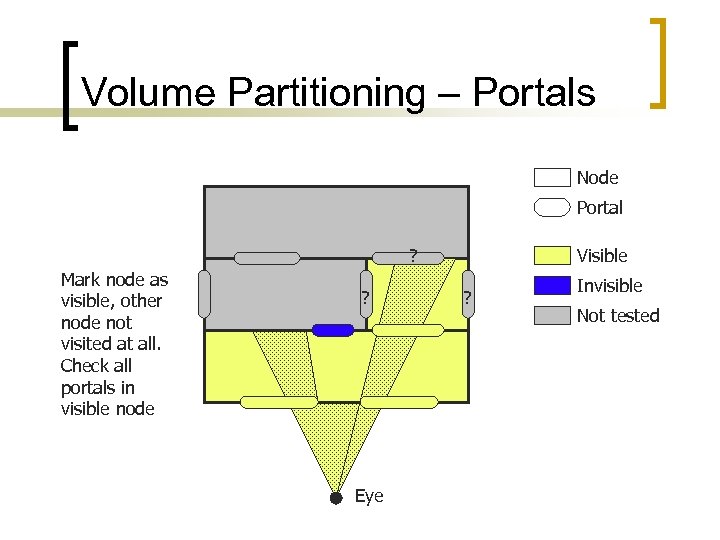
Volume Partitioning – Portals Node Portal ? Mark node as visible, other node not visited at all. Check all portals in visible node ? Eye Visible ? Invisible Not tested
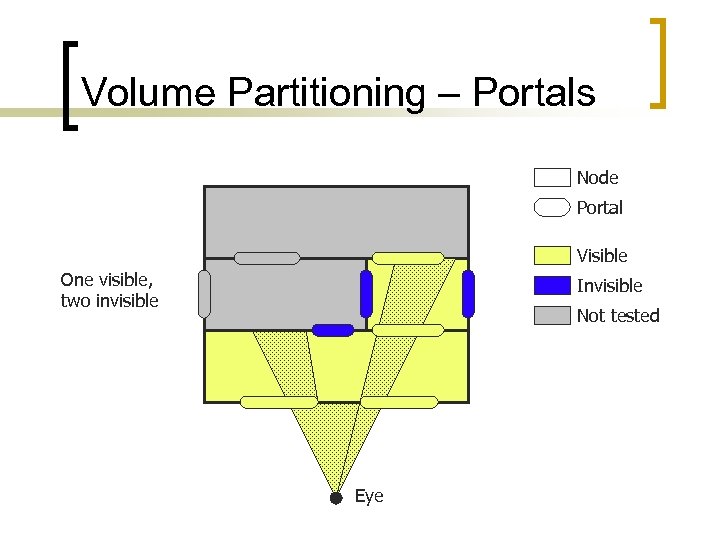
Volume Partitioning – Portals Node Portal Visible One visible, two invisible Invisible Not tested Eye
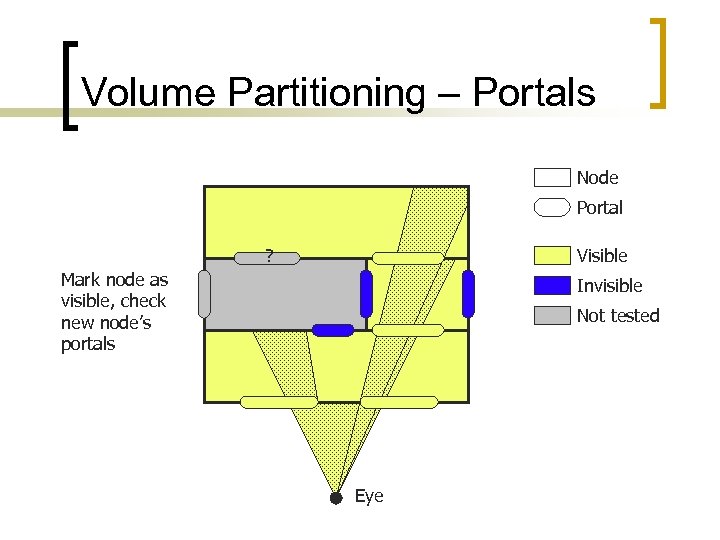
Volume Partitioning – Portals Node Portal ? Visible Mark node as visible, check new node’s portals Invisible Not tested Eye
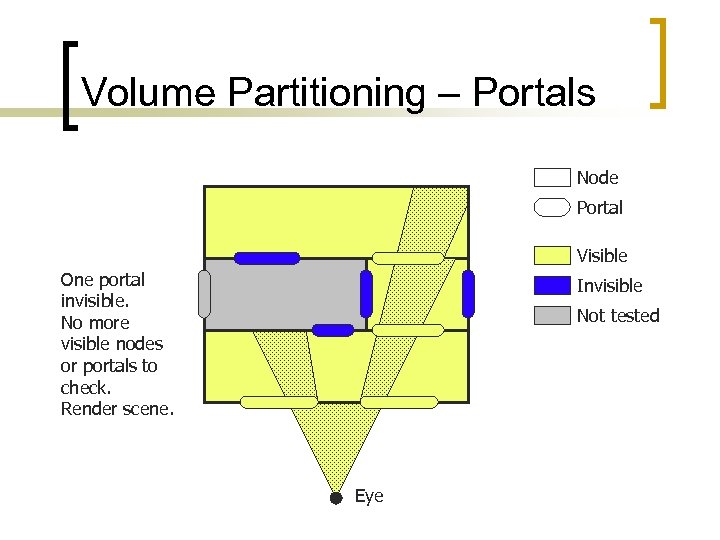
Volume Partitioning – Portals Node Portal Visible One portal invisible. No more visible nodes or portals to check. Render scene. Invisible Not tested Eye

Real Example

Volume Partitioning – Portals n n n Portals are simple and fast Low memory footprint Automatic generation is difficult, and generally need to be placed by hand Hard to find which node a point is in, and must constantly track movement of objects through portals Best at indoor scenes, outside generates too many portals to be efficient

Volume Partitioning – BSP n n n Binary space partition tree Tree of nodes Each node has plane that splits it in two child nodes, one on each side of plane Some leaves marked as “solid” Others filled with renderable geometry
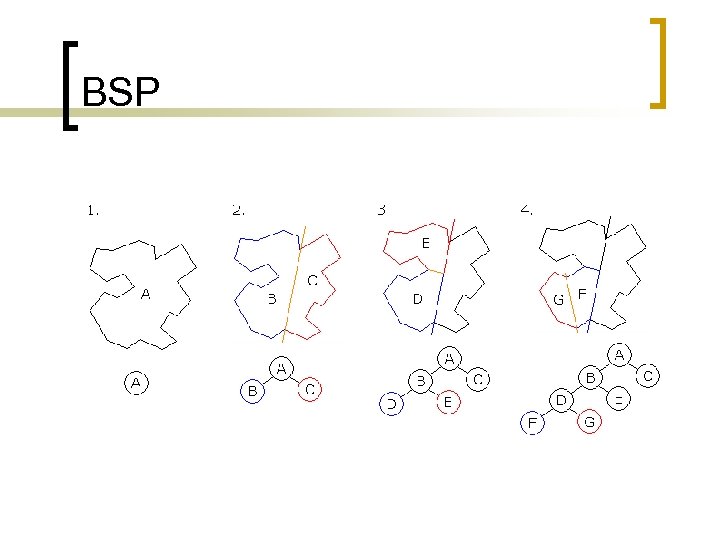
BSP

Volume Partitioning – BSP n Finding which node a point is in is fast ¡ ¡ n Visibility determination is similar to portals ¡ n n Start at top node Test which side of the plane the point is on Move to that child node Stop when leaf node hit Portals implied from BSP planes Automated BSP generation is common Generates far more nodes than portals ¡ Higher memory requirements

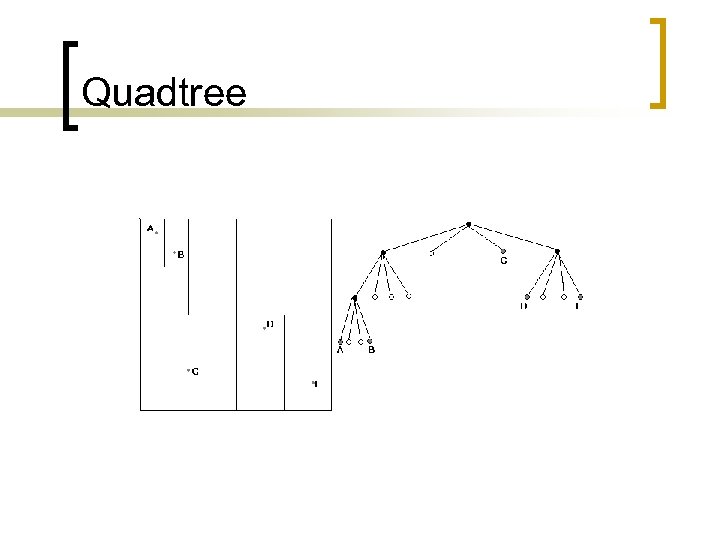
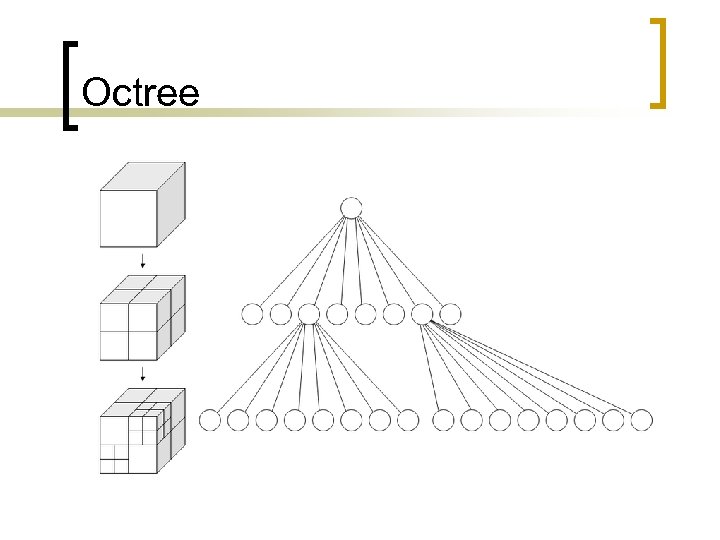
Volume Partitioning: Quadtree n Quadtree (2 D) and octree (3 D) ¡ ¡ n Each node is square ¡ n n Quadtrees described here Extension to 3 D octree is obvious Usually power-of-two in size Has four child nodes or leaves Each is a quarter of size of parent
Quadtree
Octree

Volume Partitioning: Quadtree n n n Fast to find which node a point is in Mostly used for simple frustum culling Not very good at indoor visibility ¡ n n Quadtree edges usually not aligned with real geometry Very low memory requirements Good at dynamic moving objects ¡ Insertion and removal is very fast

Volume Partitioning - PVS n n Potentially visible set Based on any existing node system For each node, stores list of which nodes are potentially visible Use list for node that camera is currently in ¡ n Ignore any nodes not on that list – not visible Static lists ¡ ¡ ¡ Precalculated at level authoring time Ignores current frustum Cannot deal with moving occluders
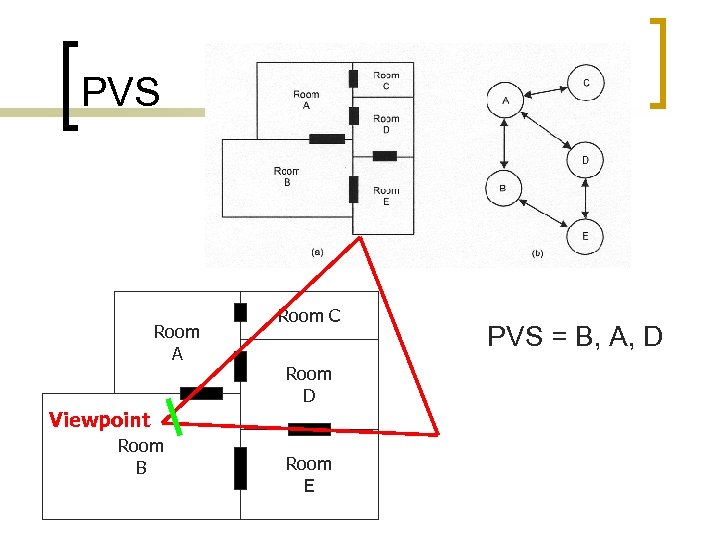
PVS Room A Room C Room D Viewpoint Room B Room E PVS = B, A, D

Volume Partitioning - PVS n Very fast ¡ n n Still need frustum culling Difficult to calculate ¡ ¡ n No recursion, no calculations Intersection of volumes and portals Lots of tests – very slow Most useful when combined with other partitioning schemes

Volume Partitioning n n Different methods for different things Quadtree/octree for outdoor views ¡ ¡ n n Does frustum culling well Hard to cull much more for outdoor views Portals or BSP for indoor scenes BSP or quadtree for collision detection ¡ Portals not suitable

Rendering Primitives n n Strips, Lists, Fans Indexed Primitives The Vertex Cache Quads and Point Sprites
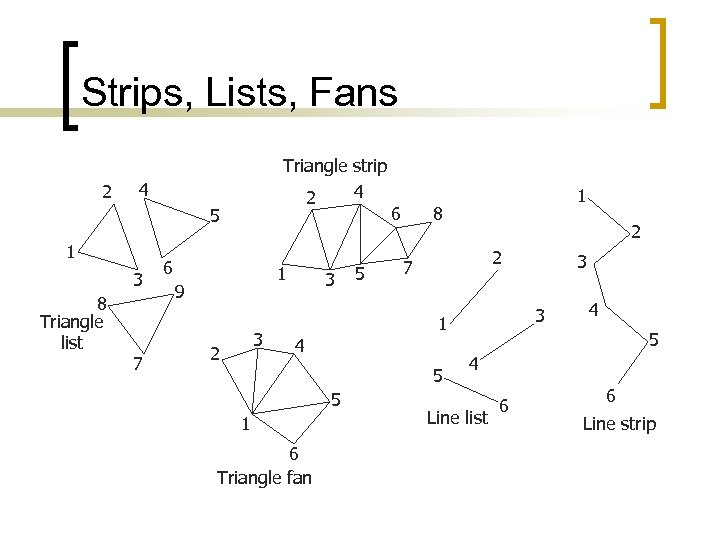
Strips, Lists, Fans 2 Triangle strip 4 2 4 5 1 3 8 Triangle list 7 6 1 9 3 2 3 5 6 8 2 7 5 5 6 Triangle fan 2 3 3 1 4 1 1 4 5 4 Line list 6 6 Line strip

Vertex Sharing n List has no sharing ¡ n Vertex count = triangle count * 3 Strips and fans share adjacent vertices ¡ ¡ Vertex count = triangle count + 2 Lower memory Topology restrictions Have to break into multiple rendering calls

Vertex Counts n Using lists duplicates vertices a lot! ¡ ¡ n Total of 6 x number of rendering vertices Most meshes: tri count = 2 x vert count Strips or fans still duplicate vertices ¡ ¡ Each strip/fan needs its own set of vertices More than doubles vertex count n ¡ ¡ Typically 2. 5 x with good strips Hard to find optimal strips and fans Have to submit each as separate rendering call
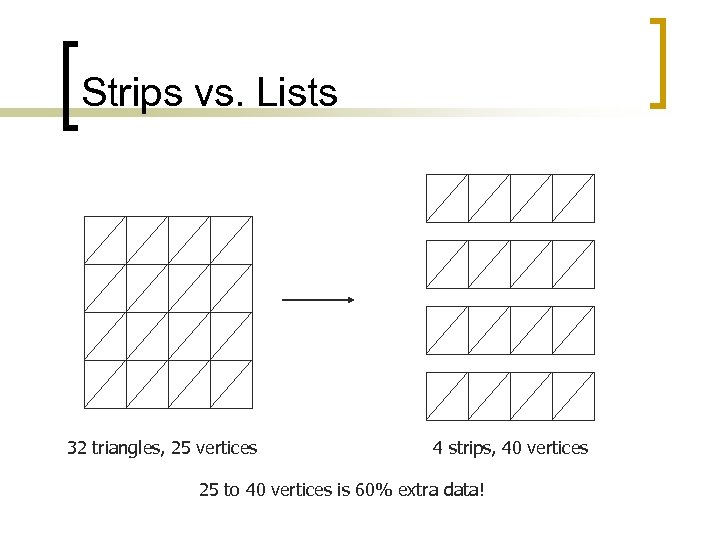
Strips vs. Lists 32 triangles, 25 vertices 4 strips, 40 vertices 25 to 40 vertices is 60% extra data!

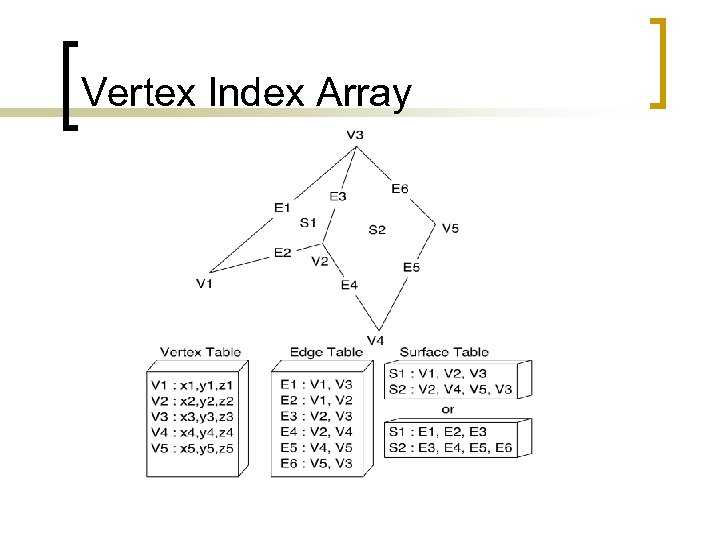
Indexed Primitives n Vertices stored in separate array ¡ ¡ ¡ n n No duplication of vertices Called a “vertex buffer” or “vertex array” 3 numbers (int/float/double) per vertex Triangles hold indices, not vertices Index is just an integer ¡ ¡ ¡ Typically 16 bits (65, 536) Duplicating indices is cheap Indexes into vertex array
Vertex Index Array

The Vertex Cache n n n Vertices processed by vertex shader Results used by multiple triangles Avoid re-running shader for each triangle Storing results in video memory is slow So store results in small cache ¡ ¡ Requires indexed primitives Cache typically 16 -32 vertices in size, resulted in around 95% efficiency

Cache Performance n Size and type of cache usually unknown ¡ ¡ ¡ n LRU (least recently used) or FIFO (first in first out) replacement policy Also odd variants of FIFO policy Variable cache size according to vertex type Reorder triangles to be cache-friendly ¡ ¡ Not the same as finding optimal strips! Render nearby triangles together “Fairly good” is easy to achieve Ideal ordering still a subject for research
eac491abbf4e5cb3bcc425d77e39222b.ppt