CSC 3323 Notes Introduction Algorithm Analysis

CSC 3323 Notes – Introduction Algorithm Analysis

Algorithm Analysis • The goal of this class: learning to analyze algorithms for specific problems. – Given a specific problem • Consider the processing to be done • Consider the range of algorithmic solutions to the problem – existing solutions, or new ones • Select the best algorithm for the specific contest • Encode it correctly in a program

Sample problem: Street Numbers A computer programmer lives in a street with houses numbered consecutively (from 1) down one side of the street. Every evening she walks her dog by leaving her house and randomly turning left or right and walking to the end of the street and back. One night she adds up the street numbers of the houses she passes (excluding her own). The next time she walks the other way she repeats this and finds, to her astonishment, that the two sums are the same. Although this is determined in part by her house number and in part by the number of houses in the street, she nevertheless feels that this is a desirable property for her house to have and decides that all her subsequent houses should exhibit it.

Sample problem: Street Numbers Write a program to find pairs of numbers that satisfy this condition. To start your list the first two pairs are: (house number, last number): 6 8 35 49 Input and Output There is no input for this program. Output will consist of 10 lines each containing a pair of numbers, each printed right-justified in a field of width 10 (as shown above).

Algorithm Analysis • Basic properties of algorithms include: – Correctness – including effectiveness and termination – Efficiency – of both time and space – Complexity – Optimality – comparing best case, worst case and expected case • In the “real world”, we normally focus on “bottlenecks”.

Algorithm Analysis • Examples: – find an element in a list • Look at each element – time N • Look until finding the value – avg time N/2 • If sorted, use binary search – max time log(N) – Find maximum of a list • Compare each to each – time N 2 • Compare each to max – time N • If sorted, pick the last – time 1 • Think about an efficient algorithm to find BOTH the minimum and the maximum of a list.

Algorithm Analysis • An optimal min/max algorithm: max = min = L[0] for i = 1 to max by 2 do if L[i] > L[i+1] then if L[i] > max then max = L[i] if L[i+1] < min then min = L[i+1] else if L[i+1] > max then max = L[i+1] if L[i] < min then min = L[i] This takes time 3 N/2.

Algorithm Analysis • What if you vary the assumptions? • Can you write a recursive max algorithm? • What about a recursive max/min? • Danger! Likely errors in implementation of a good algorithm

Algorithm Analysis • Example: raise a number to a power. • Obvious algorithm: int power( int x, int n) int i, result = 1; for i = 1 to N do result *= x return result

Algorithm analysis Less obvious algorithm: int power ( int x, int n) 1) if ( n == 0 ) return 1 2) if ( n == 1 ) return x 3) if ( is_even(n) ) return power (x*x, n/2) 4) else return power (x*x, n/2 ) * x) Line 2 is actually unnecessary Line 3 has several incorrect alternatives!

Algorithm Analysis 1) 2) 3) 4) int power ( int x, int n) if ( n == 0 ) return 1 if ( n == 1 ) return x if ( is_even(n) ) return power (x*x, n/2) return power (power(x, 2) , n/2) return power (power(x, n/2), 2) return power (x, n/2) * power (x, n/2)) else return power (x*x, n/2 ) * x)

Formal Analysis Statement: sum = 0; for (i = 0; i < N; i++) sum += i*i return sum Time: 1 2*N+1 3*N 1 Total time = 5 N + 3 O(5 N + 3) = O(5 N) = O(N)

Formal Analysis for i = 0 to N do A[i] = 0; Time is O(N) for i = 0 to N do for j = 0 to N do A[i] += A[j] + i + j Time is O(N 2) Time for both loops together is still O(N 2)

Formal analysis • T(n) ε O(f(n)) iff there exist c & n 0 > 0 such that T(n) ≤ cf(n) when n > n 0 (upper bound) • T(n) ε Ω(f(n)) iff there exist c & n 0 > 0 such that T(n) ≥ cf(n) when n > n 0 (lower bound) • T(n) ε Θ(f(n)) iff T(n) ε O(f(n)) and T(n) ε Ω(f(n)) (upper and lower bound) • T(n) ε o(f(n)) iff T(n) ε O(f(n)) and T(n) not in Ω(f(n)) (upper but not lower bound) • Alternative: L’Hopital’s rule, p. 47, Lemma 1. 5, p. 45.

Formal analysis • if T 1(n) ε O(f(n)) and T 2(n) ε O(g(n)) then – T 1(n) + T 2(n) ε max( O(f(n)), O(g(n))) – T 1(n) * T 2(n) ε O(f(n) * g(n)) • if T(x) is a polynomial of degree n, then – T(x) ε O(xn) • logk(n) ε O(n) for any k – logarithms grow slowly • nc ε O(kn) for any c and k > 1 – exponentials grow very quickly

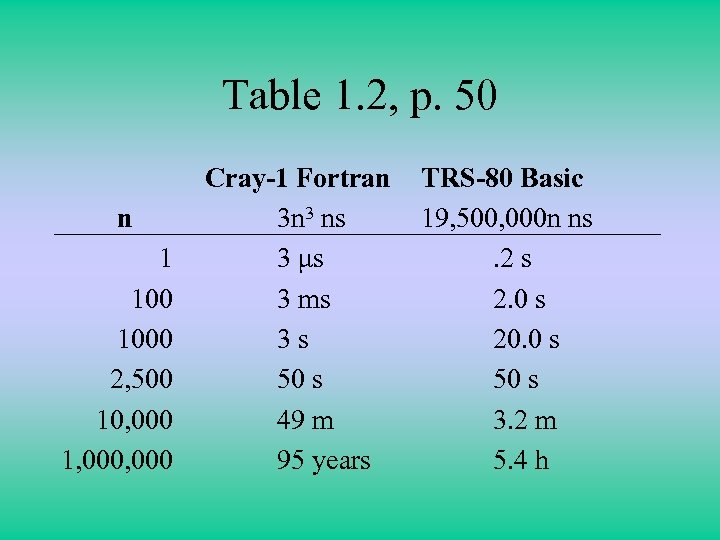Table 1. 2, p. 50 n 1 1000 2, 500 10, 000 1, 000 Cray-1 Fortran 3 n 3 ns 3 μs 3 ms 3 s 50 s 49 m 95 years TRS-80 Basic 19, 500, 000 n ns. 2 s 2. 0 s 20. 0 s 50 s 3. 2 m 5. 4 h

Sample problems • • • pp. 61 ff 1. 23 1. 24 1. 27 1. 30** 1. 31 a 1. 45 1. 47** 1. 50

Algorithm comparison example Multiplication example input: bit arrays X and Y of size n output: bit array Z of size 2 n Simple multiplication (SM): S=0 for j = 0 to 2 n-1 do (bits of the answer) for i = 0 to n-1 do (bits of the multiplier) if 0 ≤ j-i ≤ n-1 then S = S + X[i] * Y[j-i] Z[j] = S mod 2 (calculate digit) S = S div 2 (calculate carry bit) return Z TSM(n) ε Θ(n 2) 1011 (11) 1101 (13) -----1011 0000 1011 ------10001111 (143)

Algorithm comparison example Use some algebra to restate the formulas: X = XL * 2 m + XR ( m = n / 2) ( XL + XR ) * (YL + YR) = XLYL+ XLYR+ XRYL + XRYR ( XL + XR ) * (YL + YR) - XLYL - XRYR = XLYR+ XRYL (X * Y) = (XL * 2 m + XR) * (YL * 2 m + YR) = XLYL * 22 m + ( XLYR+ XRYL ) * 2 m + XRYR = XLYL*22 m + ((XL+XR )*(YL+YR)-XLYL-XRYR)*2 m+XRYR

Algorithm comparison example Block multiplication (BM): if n ≤ 3 then return SM(x, y) m = n div 2 (rounded up) P 1 = BM( X[0. . m-1], Y[0. . m-1]) X LY L P 2 = BM( X[m. . n-1], Y[m. . n-1]) X R YR P 3 = BM( Add( X[0. . m-1], X[m. . n-1]), (XL+XR )*(YL+YR) Add( Y[0. . m-1], Y[m. . n-1])) D = Sub( P 3, P 1), P 2) Z[0. . 2 m-1] = P 1 Z[2 m. . 2 n-1] = P 2 Z[m. . 2 n-1] = Add( D[0. . 2 m+1], Z[m. . 2 n-1]) return Z TBM(n) ε O(n 1. 59) ε o(TSM(n))