CSC 3315 Programming Paradigms Scheme Language Hamid Harroud

CSC 3315 Programming Paradigms Scheme Language Hamid Harroud School of Science and Engineering, Akhawayn University http: //www. aui. ma/~H. Harroud/csc 3315/ CSC 3315 (Spring 2009) 1

Functional Programming & Lisp n n n Designed by John Mc. Carthy at MIT (1956 – 1959) for AI applications Derived from -calculus theory (allows functions to be values in an expression) Various dialects: Lisp 1. 5 (1960), Scheme (1975), Common Lisp (1985)…[LISP = LISt Processor] Rich Language: functional, symbolic. Uniform Syntax and Semantics

Functional Programming & Scheme n In Scheme: Symbolic calculus. n n Basic objets : atoms (words), Atoms groups: lists (sentences). Atoms + Lists = Symbolic Expressions (S-expr) Scheme manipulates S-exprs: A scheme program is a S-expr Programs and Data have the same representation.

Functional Programming & Scheme n Domains: non numerical applications, especially: n n AI (expert systems, natural languages, . . . ) Automatic reasoning (proof of theorems, proof of programs, . . . ) Formal calculus Games

Functional Programming & Scheme n Functional Programming: n n basic entity = function control structure = recursion A function is a first class that can be created, assigned to variables, passed as a parameter or returned as a value. Scheme is implemented as an interactif loop (read-eval-print loop).

Basic Expressions n n Numbers: integers / floats. A variable is a name associated to a data, for example: (define pi 3. 14159) ; pi is a global variable A variable has an implicit type, depending on its value. It can have a value of another type: (set! pi 3. 141592) (set! pi 'alpha) (set! pi (cons pi '(rho))) A variable can be local to a block: (let ((var 1 E 1)(var 2 E 2). . . ) )

Composed Expressions n The general format of a list is: (E 1 E 2. . . En) where Ei is a S-expression. n A list can be processed as a data: '((William Shakespeare) (The Tempest)) or as a function call with variables passed by value: (append x y)

Defining a Function n Two ways: >(define (carre x) (* x x)) or: >(define carre (lambda (x) (* x x))) >(carre 2) 4 n Functions may not have names! >((lambda (x) (* x x)) 3) 9

Defining a Function > (define (f x) (* (+ x 1)(- x 1))) > (define (fact n) ( if (> n 0) ( * n (fact (- n 1))) 1 ) ) >(fact 40) 81591528324789773434561126959611589427200000

Quote n quote avoids the evaluation of an argument (expression or atom): (quote pi) or 'pi n If pi est defined as: (define pi 3. 141592) n (write 'pi) displays pi symbol n (write pi) displays 3. 141592 n (* 2. 0 pi) returns 6. 283184 n (* 2. 0 'pi) invalid parameter

Primitive Functions n cons, car, cdr are primitives (functions) that allow the construction and access to lists. n n lists are defined recusively: empty list: (), non-empty list: (cons a x) where x is a list. The head and the tail of a list: (car (cons a x)) returns a (cdr (cons a x)) returns x (car '()) and (cdr '()): invalid parameter

Primitive Functions n Predicates: functions that return #t or #f. n (symbol? x) #t if x is a symbol, n (number? x) #t if x is a number, n (eq? x y) #t if x and y are equal symbols.

More Functions n Can be defined using primitive functions: (equal? x y) if x and y are identical objects (not necesary atoms) (null? x) if x is () – empty list. (append x y) concatenate x and y. (if (f. . . ) (g. . . ) "hello")

More Functions: Example > ( define ( Number. Lists? x ) ( if ( not ( list? x ) ) #f ( if ( null? x ) #t ( if ( not ( number? ( car x ) ) ) #f ( Number. Lists? ( cdr x ) ) ) ) > ( Number. Lists? '( 1 2 3 4 )) #t

More Functions: Example > ( define ( number. List? x ) ( cond ( ( not ( list? x ) ) #f ) ( ( null? x ) #t ) ( ( not ( number? ( car x ) ) ) #f ) ( else ( number. List? ( cdr x ) ) ) > ( number. List? ' ( 1 2 3 4 ) ) #t > ( number. List? ' ( 1 2 3 bad 4 ) ) #f

More Functions n Elements Access in a list: (caar x) (car x)) (cdadr x) (cdr (car (cdr x)))) n For example, the following evaluation is made in 4 steps: (caadar '((p ((q r) s) u) (v))) (caadr '(p ((q r) s) u)) (caar '(((q r) s) u)) (car '((q r) s)) '(q r) n The second element of a list (if it exists): (cadr x) n The third element : (caddr x), (cadddr x), . . .

Example 2 (define (same_neighbours? l) (cond ((null? l) #f) ((null? (cdr l)) #f) ((equal? (car l)(cadr l)) #t) (else (same_neighbours? (cdr l))) ) )

Example 3 > ( define ( eq. Expr? x y ) ( cond ( ( symbol? x ) ( eq? x y ) ) ( ( number? x ) ( eq? x y ) ) ; x is a list: ( ( null? x ) ( null? y ) ) ; x is non-empty list: ( ( null? y ) #f ) ( ( eq. Expr? ( car x ) ( car y ) ) ( eq. Expr? ( cdr x ) ( cdr y ) ) ) ( else #f ) ) )

Example 4 >(define (repeated. Elems L) (if (list? L) (do. Repeated. Elems L) ‘list-error) ) (define (do. Repeated. Elems L) (cond ((null? L) '()) ((member (car L) (cdr L)) (do. Repeated. Elems (cdr L))) (else (cons (car L) (do. Repeated. Elems (cdr L)))) ) )

More Examples >(define reverse (lambda (x) (if (null? x) ’() (append (reverse (cdr x)) (list (car x)) ) > (reverse '(a b c)) (c b a)

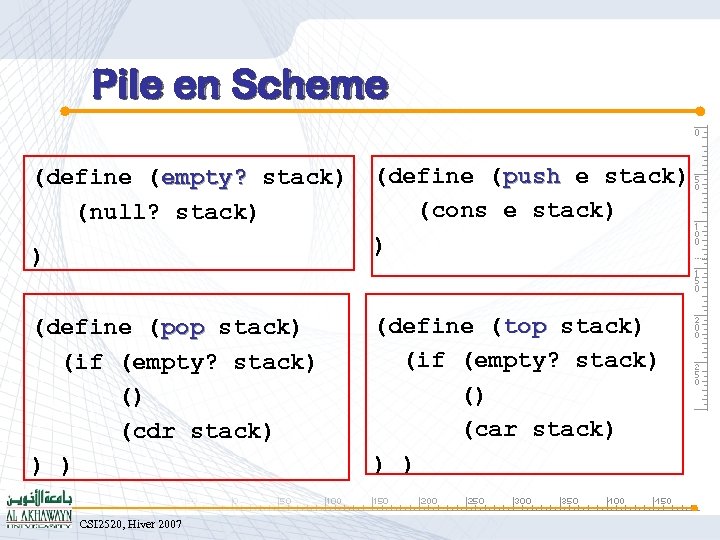Pile en Scheme (define (empty? stack) empty? (null? stack) ) (define (pop stack) pop (if (empty? stack) (cdr stack) ) ) CSI 2520, Hiver 2007 (define (push e stack) push (cons e stack) ) (define (top stack) top (if (empty? stack) (car stack) ) )

Minimum of a List (define (min x) (cond ((not (numberlist? x)) (list 'not-number-list x)) ((null? x) x) (else (min-aux (car x) (cdr x))) ) ) (define (min-aux elt x) (cond ((null? x) elt) ((> elt (car x) (min-aux (car x)(cdr x))) (else (min-aux elt (cdr x))) ) )

Minimum of a List: local variables (define (min. L-aux Elt Lst) (if (null? Lst) Elt (let ((v 1 (car Lst)) (v 2 (cdr Lst))) (if (> Elt v 1) (minl-aux v 1 v 2) (minl-aux Elt v 2) ) )

Concatenation of two lists (define append (lambda (x y) (cond ((null? x) y) (else (cons (car x) (append (cdr x) y))) ) > (append '(a b c) '(d e)) (a b c d e) > (string-append “abc” “ 123”) “abc 123”

Member Function (define member? (lambda (x y) (cond ((null? y) #f) ((equal? x (car y)) #t) (else (member? x (cdr y))) ) > (member? 'aa '(bb ccc aa eeee rr ttttt)) #t > (member? 'aa '(bb ccc (aa) eeee rr ttttt)) #f > (member 'aa '(bb ccc aa eeee rr ttttt)) (aa eeee rr ttttt)

High-level functions: Functions as Parameters Some functions can have other functions as parameters. > (define (combine f 1 f 2 x) (f 1 (f 2 x)) ) > (combine (lambda (x) (+ 1 x)) (lambda (x) (* 2 x)) 6) 13 > (combine (lambda (x) (* 2 x)) (lambda (x) (+ 1 x)) 6) 14 Équivalent to: > ((lambda (x) (+ 1 x)) ((lambda (x) (* 2 x)) 6)) > ((lambda (x) (* 2 x)) ((lambda (x) (+ 1 x)) 6))

High-level functions: Functions as Parameters (define f (lambda (x) (lambda (y) (lambda (z) (+ x y z) ) ) > (((f 1) 2) 3) 6 (define g ((f 1) 2)) >(g 3) 6

High-level Functions: map: applies a function to each element of a list: (E 1 E 2. . . En) ((f E 1) (f E 2) . . . (f En)) (define (map F Lst) (if (null? Lst) Lst (cons (F (car Lst)) (map F (cdr Lst))) ) ) For example(map (lambda(x) (+ x 1)) '(1 2 3)) returns: (2 3 4)

High-level Functions: map ( map car '((a b) (c d) (e f)) ) ( map cadr '((a b) (c d) (e f)) ) ( map (lambda (x) (cons 3 (list x))) '(a b c d) )

High-level functions: Reducers Consider a function F with two parameters, and F 0 a constant. We want to have the following transformation (F E 1 (F E 2 (F. . . (F En F 0) ). . . ) Which can be represented using an infix notation: (E 1 E 2. . . En) E 1 F E 2 F. . . F En F F 0

High-level functions: Reducers Example: (E 1 E 2. . . En) E 1 + E 2 +. . . + En + 0 (E 1 E 2. . . En) E 1 * E 2 *. . . * En * 1 (define (reduce F F 0 L) (if (null? L) F 0 (F (car L) (reduce F F 0 (cdr L))) ))

High-level functions: Reducers > (reduce + 0 '(1 2 3 4)) > (reduce * 1 '(1 2 3 4)) > (reduce (lambda (x y) (+ x y 1)) 8 '(1 2 3)) > (reduce cons '() '(1 2 3 4)) > (reduce append '() '((1) (2) (3)))

Pre-defined Functions Lists Manipulation car cdr cons append list length caar, cadr, cdar, cddr, caaaar, cddddr, . . . To define Functions define lambda

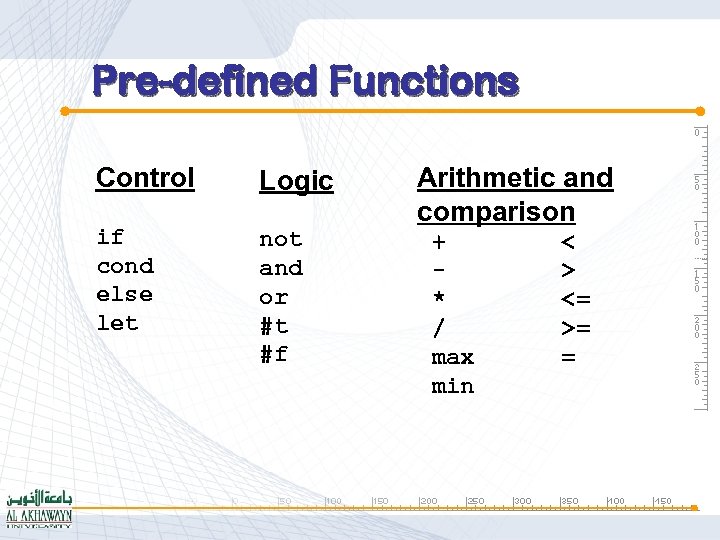Pre-defined Functions Control Logic Arithmetic and comparison if cond else let not + < and - > or * <= #t / >= #f max = min

Pre-defined Functions Predicates I/O symbol? Functions number? read integer? write list? display null? print eq? equal? procedure? member?

Pre-defined Functions Other functions quote ---> ‘a, ‘(1 2) set! ---> (define a 1) (set! a (+ a 1)) load ---> (load “scm 1. txt”) map eval ---> (eval ‘(+ 1 2)) apply ---> (apply + ‘(1 2)) CSI 2520, Hiver 2007