CSC 3130 Formal Languages and Automata Theory Tutorial

CSC 3130 Formal Languages and Automata Theory Tutorial 9 Undecidable Problem KN Hung SHB 1026 1

Agenda • Recap – Decidibility, Undecidibility, Turing. Recognizable … • Reduction • Undecidable Problem 2

Recap 3

Recap: Recognize • Given a language L and a machine M “M recognizes L” iff “For any w ∈ L, M halts and goes to an accepting state” • “M is a recognizer for L” • However, for w ∉ L, M may – Reject – Loop forever 4

Recap: Decide • Given a language L and a machine M “M decides L” iff “For any w ∈ L, M halts and accepts AND Otherwise, M rejects” • “M is a decider for L” • Meaning: M can determine whether a given string is in L or not 5

Recognize VS Decide • • Recognize = Halts for accepting input Decide = Halts for all inputs Decide => Recognize Make sure that you can distinguish these two concepts! 6

Recap: ~able / ~ability • L is Turing-recognizable iff there is a TM that recognizes L • L is decidable iff there is a TM that decides L • L is undecidable iff there is no TM that decides L 7

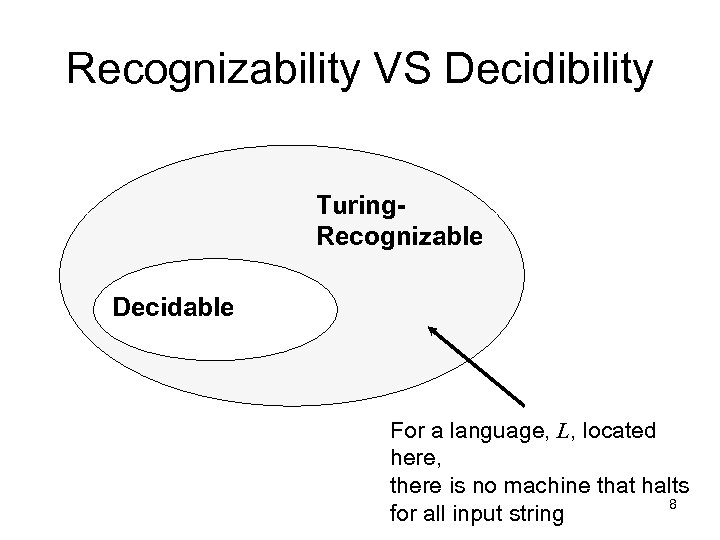Recognizability VS Decidibility Turing. Recognizable Decidable For a language, L, located here, there is no machine that halts 8 for all input string

Some Decidable Problems • The following problems are decidable – ADFA = { | A is a DFA that accepts w} – ANFA = { | A is a NFA that accepts w} – EDFA = { | A is a DFA and L(A) = Ø} – EQDFA = { | A, B are DFAs, L(A) = L(B)} – ACFG = { | G is a CFG that generates w} 9

Some Undecidable Problems • The following problems are undecidable – ATM = { | M is a TM that accepts w} • To prove undecidability of a problem using reduction, ATM is used very frequently (nearly in all situations) • Used in Example 1 and 2 (Later slides) 10

Reduction 11

Reduction • • Occurs in daily life… Problem A: Travel to Japan Problem B: Buying a air ticket to Japan Problem A reduces to Problem B – Meaning: Settling B automatically solves A – Put in logical statement: B is solvable A is solvable 12

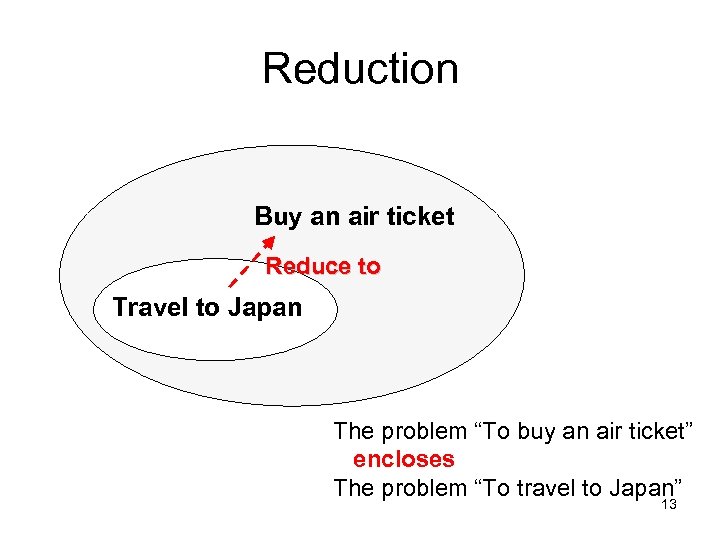Reduction Buy an air ticket Reduce to Travel to Japan The problem “To buy an air ticket” encloses The problem “To travel to Japan” 13

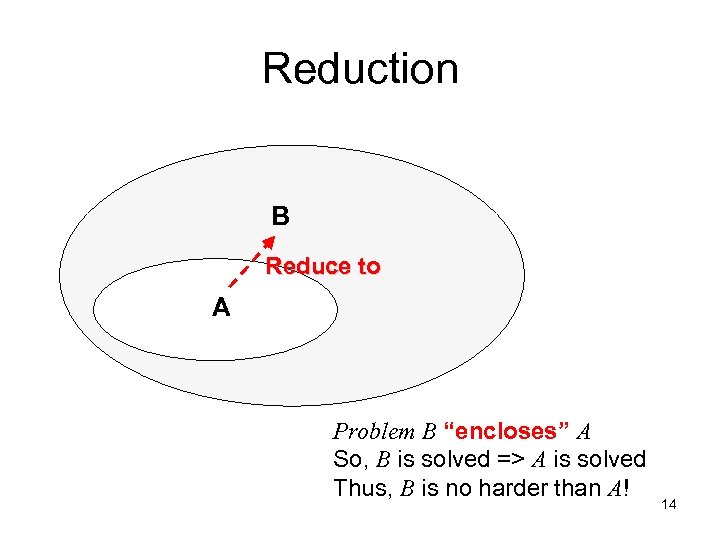Reduction B Reduce to A Problem B “encloses” A So, B is solved => A is solved Thus, B is no harder than A! 14

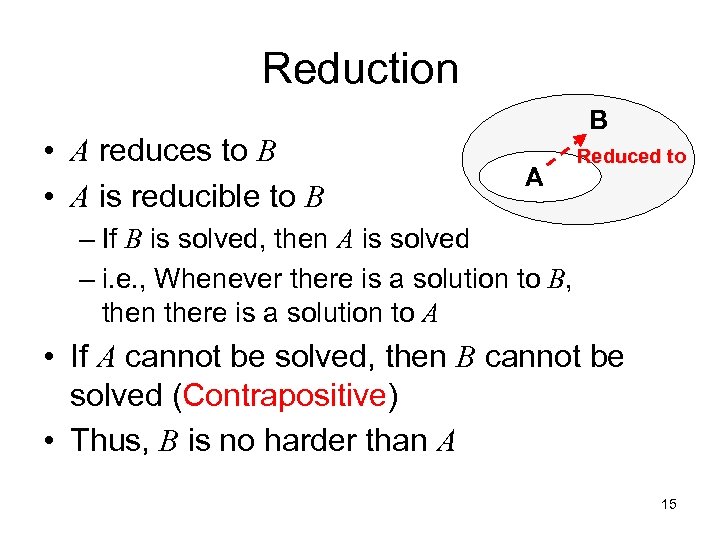Reduction • A reduces to B • A is reducible to B B A Reduced to – If B is solved, then A is solved – i. e. , Whenever there is a solution to B, then there is a solution to A • If A cannot be solved, then B cannot be solved (Contrapositive) • Thus, B is no harder than A 15

Undecidable Problems 16

Example 1 • Show that REGULARTM is undecidable • REGULARTM = { | M is a TM and L(M) is a regular language} 17

REGULARTM is undecidable? • Idea (By Contradiction): – Assume there is a TM R that decides REGULARTM – Construct a TM S that decides ATM – Contradiction! 18

Construction of S • On input – where M is a TM and w is a string: • Construct M’ by M and w • Run R on • Output the answer 19

Idea of M’ • Strategy: Convert M into another TM M’: M’ recognizes a regular language iff M accepts w • If M accepts w, let M’ recognizes {0, 1}* • Otherwise, let M’ recognizes {0 n 1 n} • With the above properties – When we run R on , the output is “accept” iff M accepts w – Why…? [See next few slides…] 20

Construction of M’ • M’ = “On input x: 1. If x has the form 0 n 1 n, accept 2. If x does not have this form, run M on input w and output answer” • {0 n 1 n} is recognized by M’ anyway • How about the other strings? 21

Construction of M’ • For strings of form 0 n 1 n, M’ accepts • For all the other strings, listing all cases… – If M accepts w • they are all accepted by M’ – If M rejects w • they are all rejected by M’ – If M loops on w M’ = “On input x: • they all loop on M’ 1. If x has the form 0 n 1 n, accept 2. If x does not have this form, run M on input w and output answer” 22

L(M’) in relation to S • If M accepts w – M’ recognizes {0 n 1 n}∪{0, 1}* – {0, 1}* is regular – R will accept M’ • If M does not accept w – M’ recognizes {0 n 1 n}∪Ø – {0 n 1 n} is not regular – R will reject M’ 23

REGULARTM is undecidable • • Assume “R that decides REGULARTM” exists We construct S to decide ATM “On input , where M is a TM and w is a string: 1. Construct the following TM M’ M’ = “On input x: 1. If x has the form 0 n 1 n, accept 2. If x does not have this form, run M on input w and accept if M accepts w” 2. Run R on input 3. Output the output of R” • Now, S decides ATM… Contradiction! 24

Example 2 • L = { | M accepts all strings shorter than w} • Show that L is undecidable 25

L is undecidable? • L = { | M accepts all strings shorter than w} • Again, we try to use the undecidability of ATM to achieve a contradiction • Idea (By Contradiction): – Assume there is a TM R that decides L – Construct a TM (by R), S that decides ATM – Contradiction! 26

Construction of S • On input – where M is a TM and w is a string: • Construct M’ by M and w • Run R on – This time, we have a TM that takes 2 arguments – a TM, and a string – as inputs – Think what string to put as the 2 nd input • Output the answer 27

Idea of M’ • Strategy: Convert M into another TM M’: M’ accepts all strings shorter than z iff M accepts w • We want to achieve the following: – When we run R on , the output is “accept” iff M accepts w 28

Idea of M’ • Strategy: Convert M into another TM M’: M’ accepts all strings shorter than “ 1” iff M accepts w • We want to achieve the following: – When we run R on , the output is “accept” iff M accepts w 29

Construction of M’ • M’ = “On input x: 1. If x =ε Run M on w Output the answer 2. If x ≠ε Reject 30

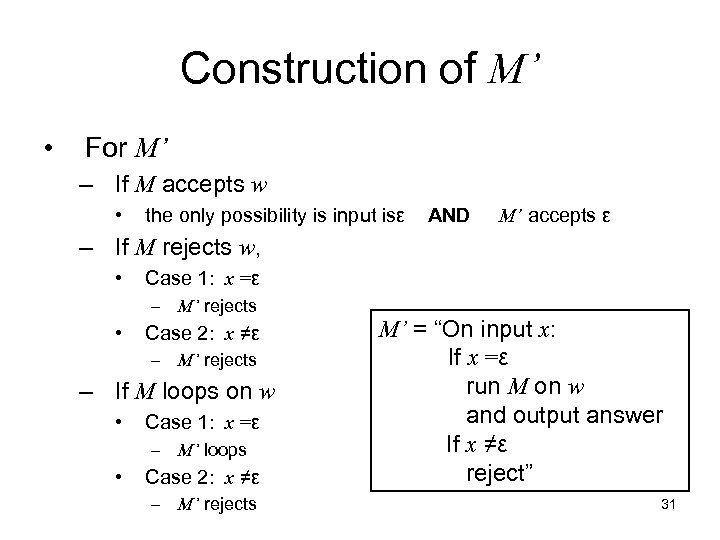Construction of M’ • For M’ – If M accepts w • the only possibility is input isε AND M’ accepts ε – If M rejects w, • Case 1: x =ε – M’ rejects • Case 2: x ≠ε – M’ rejects – If M loops on w • Case 1: x =ε – M’ loops • Case 2: x ≠ε – M’ rejects M’ = “On input x: If x =ε run M on w and output answer If x ≠ε reject” 31

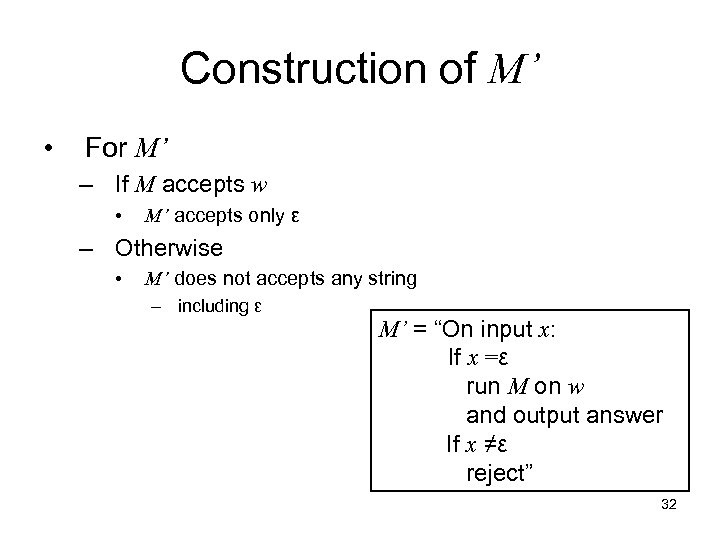Construction of M’ • For M’ – If M accepts w • M’ accepts only ε – Otherwise • M’ does not accepts any string – including ε M’ = “On input x: If x =ε run M on w and output answer If x ≠ε reject” 32

L(M’) in relation to S • If M accepts w – L(M’) = {ε} – {ε} is exactly the language that contains all string shorter than “ 1” – S accepts • Otherwise (i. e. , M loops on or rejects w) – L(M’) = Ø – S rejects 33

L is undecidable • Assume “R that decides REGULARTM” exists • We construct S to decide ATM “On input , where M is a TM and w is a string: 1. Construct the following TM M’ M’ = “On input x: 1. If x =ε Run M on x Output the answer 2. If x ≠ε Reject 2. Run R on input 3. Output the output of R” • Now, S decides ATM… Contradiction! 34

Conclusion 35

Pf: Undecidability by Reduction • Given an undecidable language, L • Assume such a decider TM R, exists R 36

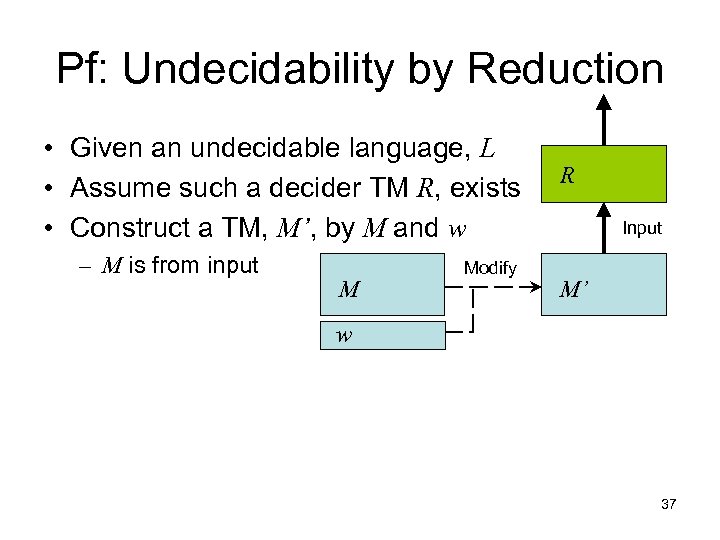Pf: Undecidability by Reduction • Given an undecidable language, L • Assume such a decider TM R, exists • Construct a TM, M’, by M and w – M is from input M Modify R Input M’ w 37

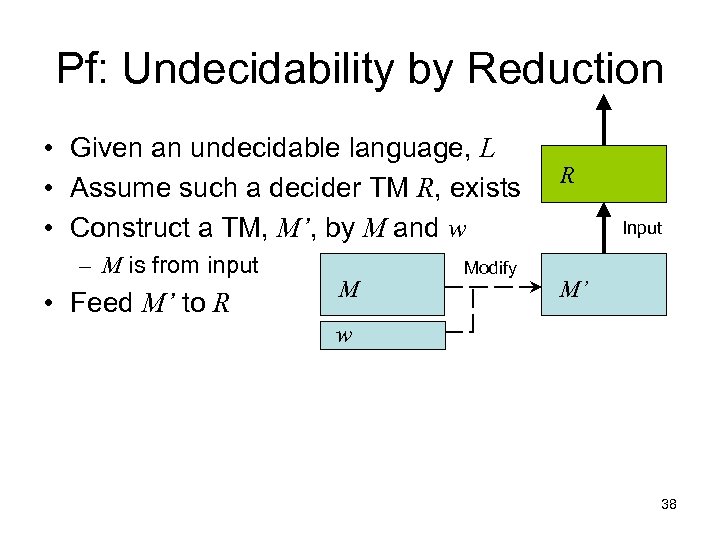Pf: Undecidability by Reduction • Given an undecidable language, L • Assume such a decider TM R, exists • Construct a TM, M’, by M and w – M is from input • Feed M’ to R M Modify R Input M’ w 38

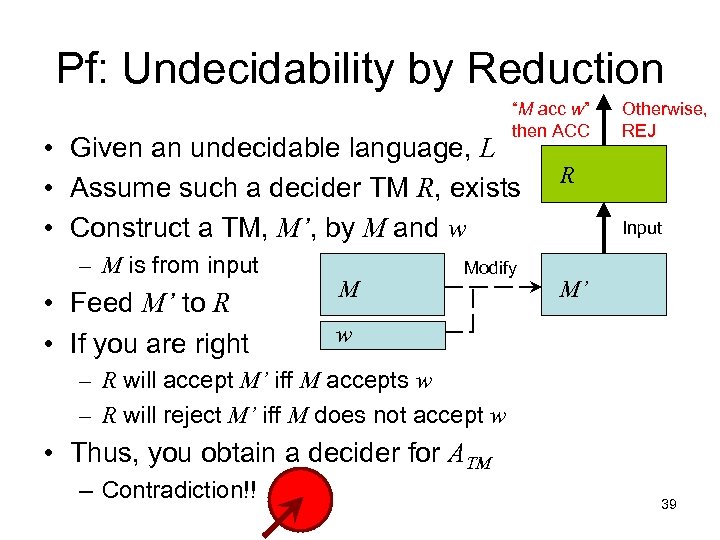Pf: Undecidability by Reduction “M acc w” then ACC • Given an undecidable language, L • Assume such a decider TM R, exists • Construct a TM, M’, by M and w – M is from input • Feed M’ to R • If you are right M Modify Otherwise, REJ R Input M’ w – R will accept M’ iff M accepts w – R will reject M’ iff M does not accept w • Thus, you obtain a decider for ATM – Contradiction!! 39

Q&A • Thanks for coming! • I understand that this topic is confusing… • Should have some questions? 40