2717ae4f0468311f128d65504eee02fe.ppt
- Количество слайдов: 107

CS 5263 & 4593 Bioinformatics Introduction to Microarray Data Analysis

Outline • What is microarray – Basic categories of microarray – How can microarray be used • Computational and statistical methods involved in microarray – – – Probe design Image processing Pre-processing Differentially expressed gene identification Clustering and classification Network / pathway modeling
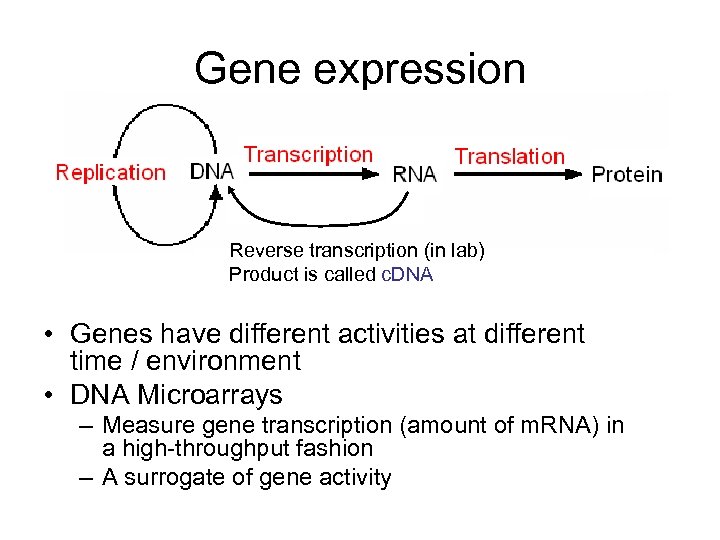
Gene expression Reverse transcription (in lab) Product is called c. DNA • Genes have different activities at different time / environment • DNA Microarrays – Measure gene transcription (amount of m. RNA) in a high-throughput fashion – A surrogate of gene activity
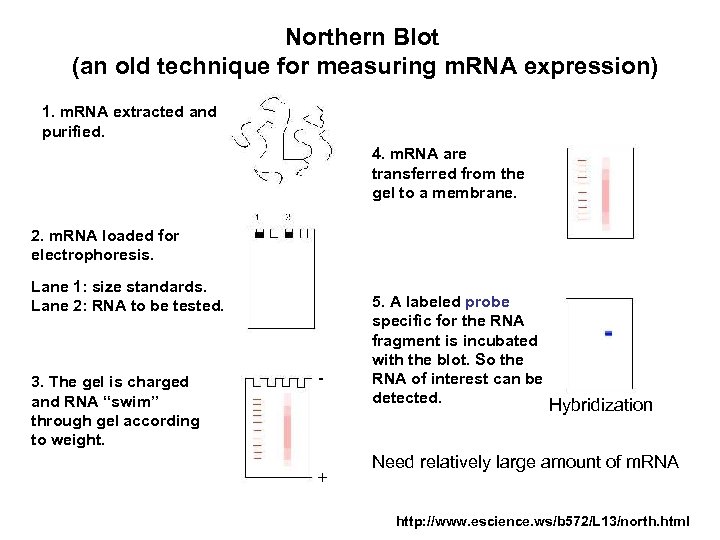
Northern Blot (an old technique for measuring m. RNA expression) 1. m. RNA extracted and purified. 4. m. RNA are transferred from the gel to a membrane. 2. m. RNA loaded for electrophoresis. Lane 1: size standards. Lane 2: RNA to be tested. 3. The gel is charged and RNA “swim” through gel according to weight. - + 5. A labeled probe specific for the RNA fragment is incubated with the blot. So the RNA of interest can be detected. Hybridization Need relatively large amount of m. RNA http: //www. escience. ws/b 572/L 13/north. html

RT-PCR (reverse transcription-polymerase chain reaction) 1. RNA is reverse transcribed to DNA. 2. PCR procedures can be used amplify DNA at exponential rate. 3. Gel quantification for the amplified product. ---- an semi-quantitative method. Smaller amount of sample needed. See animation of RT-PCR: http: //www. bio. davidson. edu/courses/Immunology/Flash/RT_PCR. html real-time RT-PCR 1. The PCR amplification can be monitored by fluorescence in “real time”. 2. The fluorescence values recorded in each cycle represent the amount of amplified product. Often used to validate microarray ---- a quantitative method. The current most advanced and accurate analysis for m. RNA abundance. Usually used to validate microarray result. http: //www. ambion. com/techlib/basics/rtpcr/

Limitation of the old techniques 1. Labor intensive 2. Can only detect up to dozens of genes. (gene-by-gene analysis)

What is a microarray • A 2 D array of DNA sequences from thousands of genes • Each spot has many copies of same gene (probe) • Allow m. RNAs from a sample to hybridize – Form RNA-DNA double-strand • Measure number of hybridizations per spot

What is a Microarray (2) Gene 9 Conceptually similar to (reverse) Northern blot (Many) probes, rather than m. RNAs, are fixed on some surface, in an ordered way

Microarray categories • c. DNAs microarray – Each probe is the c. DNA of a gene (length: hundreds to thousands nucleotides) – Stanford, Brown Lab • Oligonucleotide microarray – Each probe is a synthesized short DNA (uniquely corresponding to a substring of a gene) – Affymetrix: ~ 25 mers – Agilent: ~ 60 mers • Others

Spotted c. DNA microarray

Array Manufacturing Each tube contains c. DNAs corresponding to a unique gene. Pre-amplified, and spotted onto a glass slide
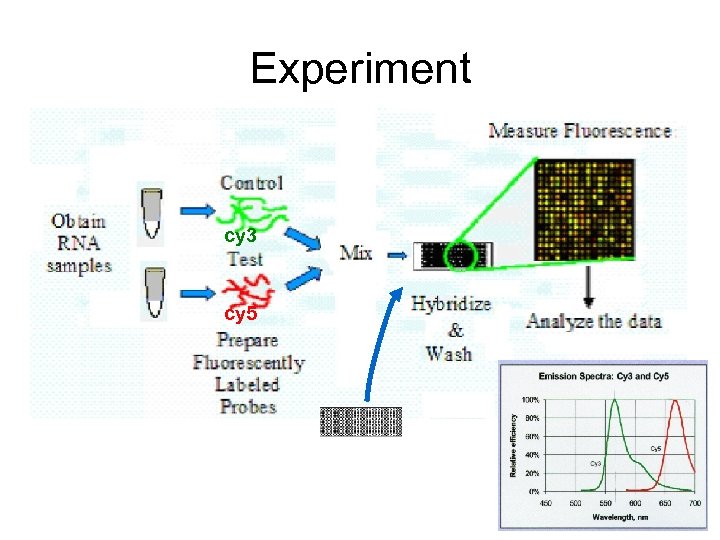
Experiment cy 3 cy 5

Data acquisition Computer programs are used to process the image into digital signals. • Segmentation: determine the boundary between signal and background • Results: gene expression ratios between two samples

c. DNA Microarray Methodology Animation

Affymetrix Gene. Chip®
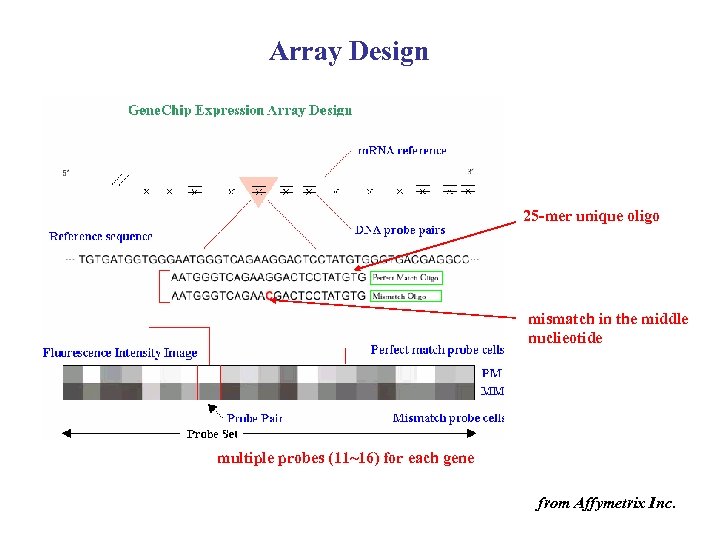
Array Design 25 -mer unique oligo mismatch in the middle nuclieotide multiple probes (11~16) for each gene from Affymetrix Inc.
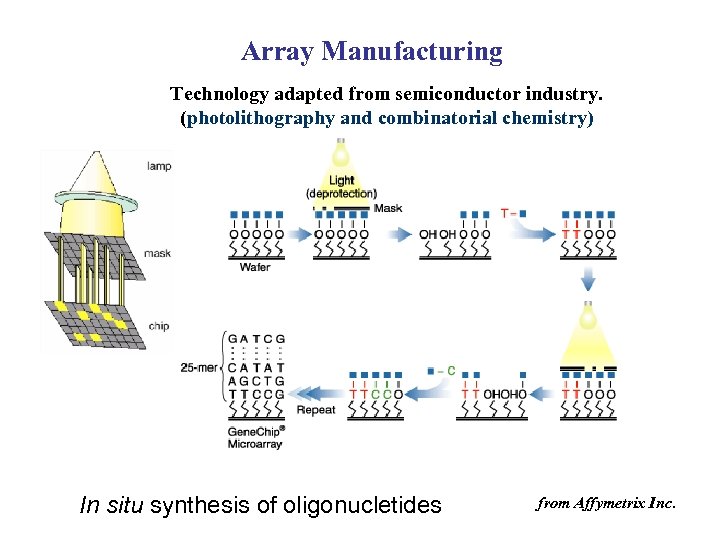
Array Manufacturing Technology adapted from semiconductor industry. (photolithography and combinatorial chemistry) In situ synthesis of oligonucletides from Affymetrix Inc.
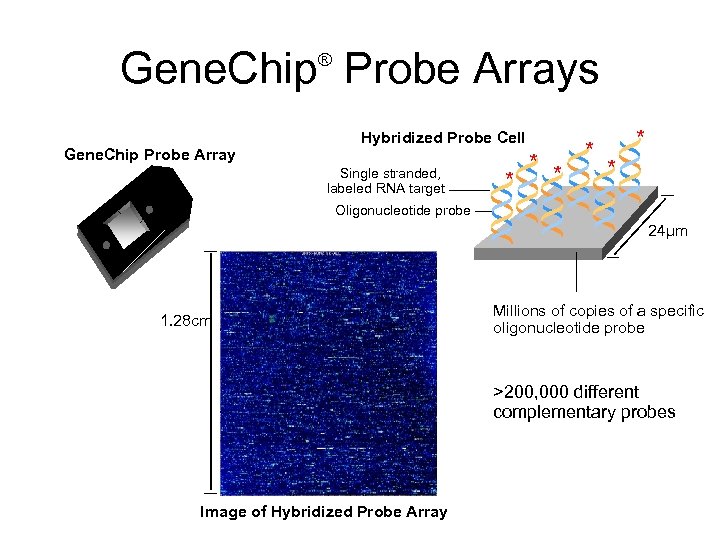
Gene. Chip Probe Arrays ® Gene. Chip Probe Array Hybridized Probe Cell Single stranded, labeled RNA target * * * Oligonucleotide probe 24µm 1. 28 cm Millions of copies of a specific oligonucleotide probe >200, 000 different complementary probes Image of Hybridized Probe Array
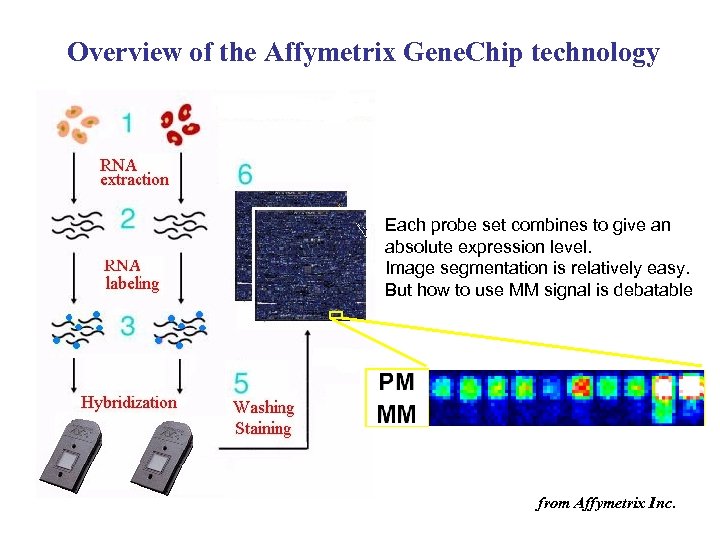
Overview of the Affymetrix Gene. Chip technology Each probe set combines to give an absolute expression level. Image segmentation is relatively easy. But how to use MM signal is debatable from Affymetrix Inc.
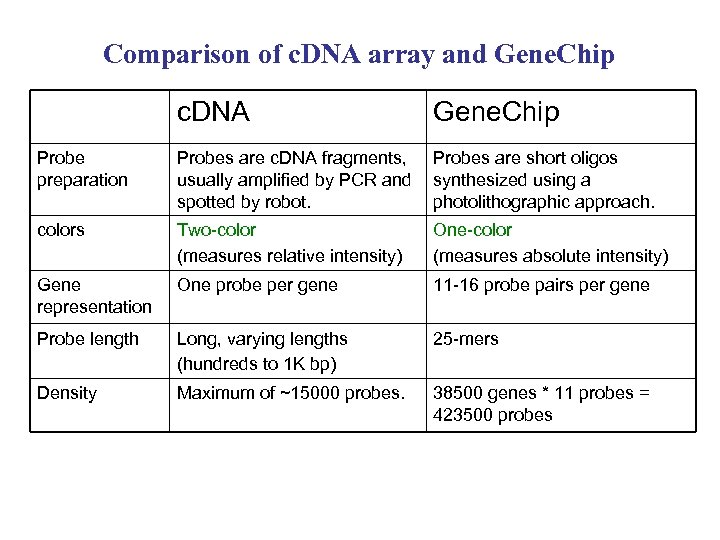
Comparison of c. DNA array and Gene. Chip c. DNA Gene. Chip Probe preparation Probes are c. DNA fragments, usually amplified by PCR and spotted by robot. Probes are short oligos synthesized using a photolithographic approach. colors Two-color (measures relative intensity) One-color (measures absolute intensity) Gene representation One probe per gene 11 -16 probe pairs per gene Probe length Long, varying lengths (hundreds to 1 K bp) 25 -mers Density Maximum of ~15000 probes. 38500 genes * 11 probes = 423500 probes
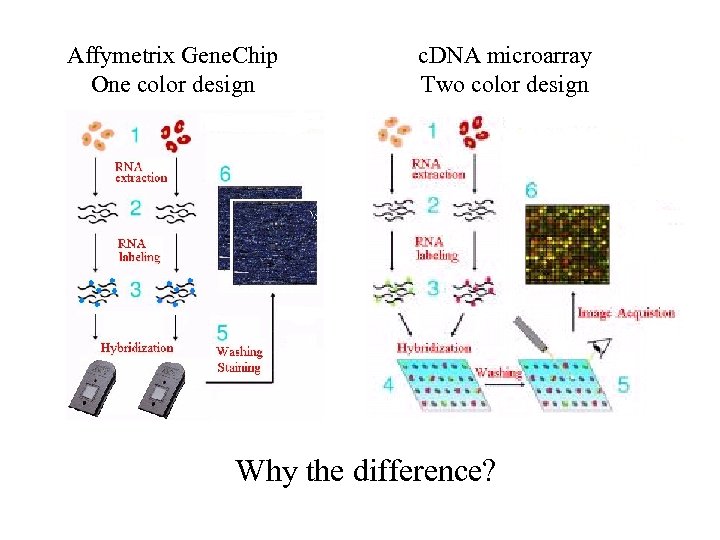
Affymetrix Gene. Chip One color design c. DNA microarray Two color design Why the difference?
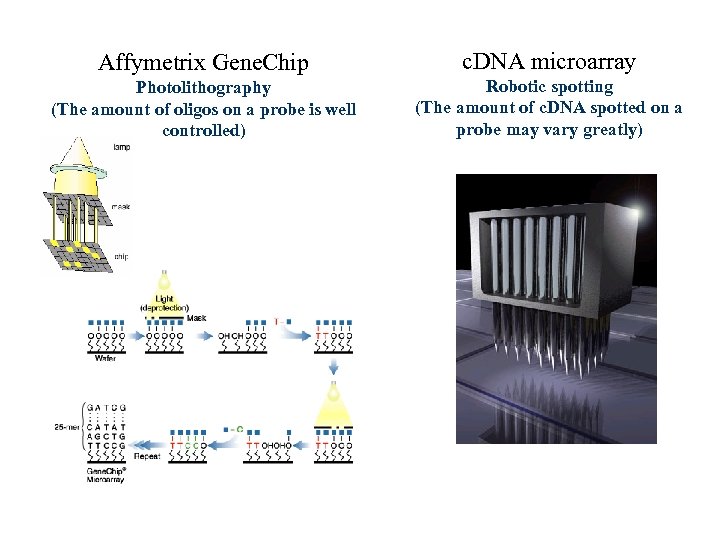
Affymetrix Gene. Chip c. DNA microarray Photolithography (The amount of oligos on a probe is well controlled) Robotic spotting (The amount of c. DNA spotted on a probe may vary greatly)

Advantage and disadvantage of c. DNA array and Gene. Chip c. DNA microarray Affymetrix Gene. Chip The data can be noisy and with variable quality Specific and sensitive. Result very reproducible. Cross(non-specific) hybridization can often happen. Hybridization more specific. May need a RNA amplification procedure. Can use small amount of RNA. More difficulty in image analysis. Image analysis and intensity extraction is easier. Need to search the database for gene annotation. More widely used. Better quality of gene annotation. Cheap. (both initial cost and per slide cost) Expensive (~$400 per array+labeling and hybridization) Can be custom made for special species. Only several popular species are available Do not need to know the exact DNA sequence. Need the DNA sequence for probe selection.
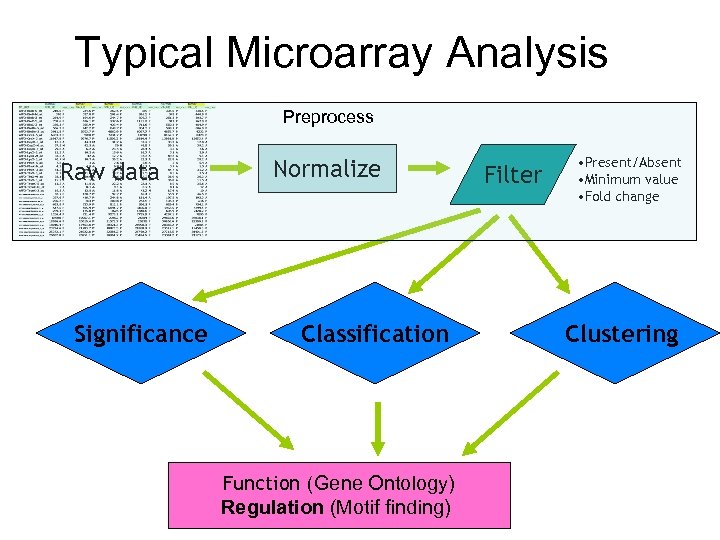
Typical Microarray Analysis Preprocess Raw data Significance Normalize Classification Function (Gene Ontology) Regulation (Motif finding) Filter • Present/Absent • Minimum value • Fold change Clustering

Preprocessing • Background subtraction – Account for non-specific hybridization • Transformation (e. g. to log scale) – Convenience – Convert data into a certain distribution (e. g. normal) assumed by many statistical procedures • Normalization – Remove systematic biases – Make data from different samples comparable • Filtering, averaging, etc. – Remove random noises Garbage in => Garbage out Order may be different. May be combined.
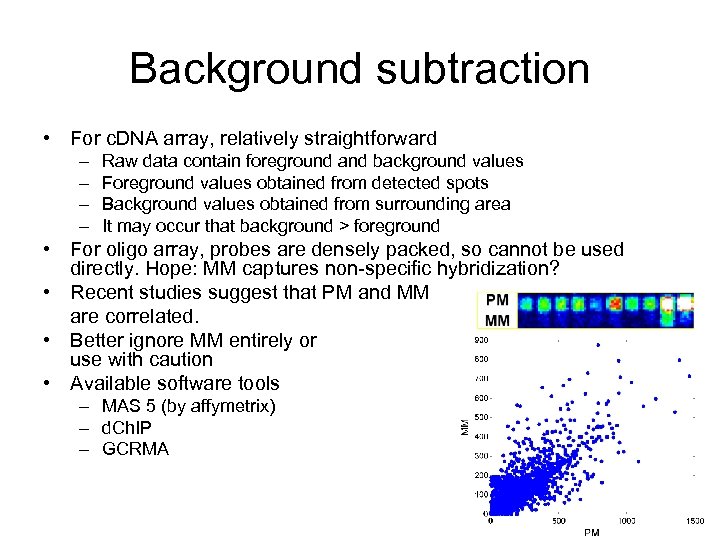
Background subtraction • For c. DNA array, relatively straightforward – – Raw data contain foreground and background values Foreground values obtained from detected spots Background values obtained from surrounding area It may occur that background > foreground • For oligo array, probes are densely packed, so cannot be used directly. Hope: MM captures non-specific hybridization? • Recent studies suggest that PM and MM are correlated. • Better ignore MM entirely or use with caution • Available software tools – MAS 5 (by affymetrix) – d. Ch. IP – GCRMA

Normalization • Where errors could come from? • Random noises – Repeat the same experiment twice, get diff results – Using multiple replicates reduces the problem • Systematic errors – Arrays manufactured at different time – On the same array, probes printed with different printer tips may have different biases – Dye effect: difference between Cy 5 and Cy 3 labeling – Experimental factors • Array A being applied more m. RNAs than array B • Sample preparation procedure • Experiments carried out at different time, by different users, etc.

c. DNA microarray data preprocessing

Typical experiments Wide-type cells vs mutated cells Diseased cells with normal cells Cells under normal growth condition vs cells treated with chemicals Typically repeated for several times Ratios Probes (genes) • •
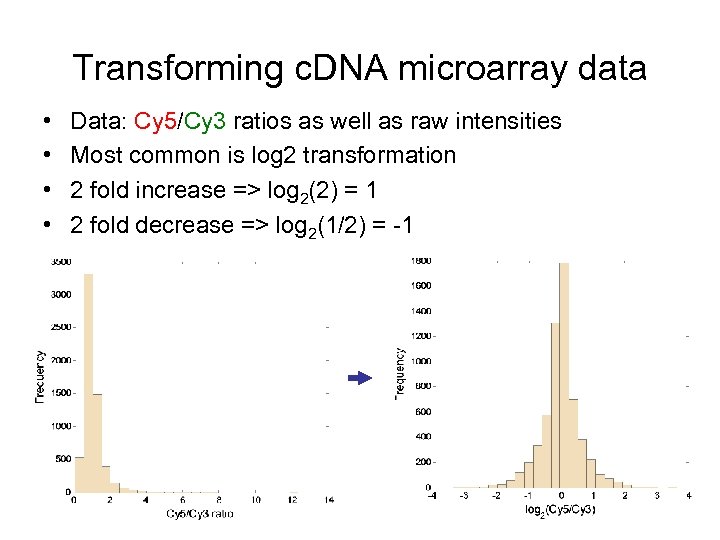
Transforming c. DNA microarray data • • Data: Cy 5/Cy 3 ratios as well as raw intensities Most common is log 2 transformation 2 fold increase => log 2(2) = 1 2 fold decrease => log 2(1/2) = -1

Dye effect c. DNA microarray experiments using two identical samples. Observation: Cy 5 consistently lower than Cy 3. (mean log (cy 5/cy 3) < 0) Solution: dye swapping.

Dye swapping • • • Chip 1: label test by cy 5 and control by cy 3 Chip 2: label test by cy 3 and control by cy 5 Ideally cy 5/cy 3 = cy 3/cy 5 Not so due to dye effect Compute average ratio: ½ log 2 (cy 5/cy 3 on chip 1) + ½ log 2 (cy 3/cy 5 on chip 2)
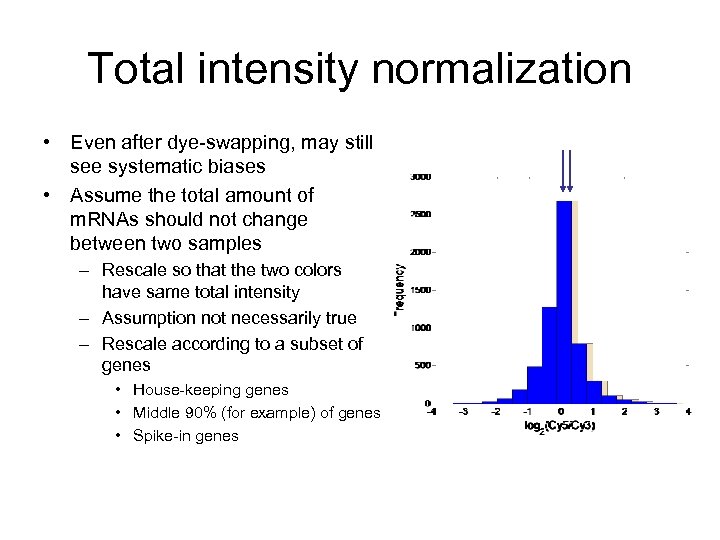
Total intensity normalization • Even after dye-swapping, may still see systematic biases • Assume the total amount of m. RNAs should not change between two samples – Rescale so that the two colors have same total intensity – Assumption not necessarily true – Rescale according to a subset of genes • House-keeping genes • Middle 90% (for example) of genes • Spike-in genes
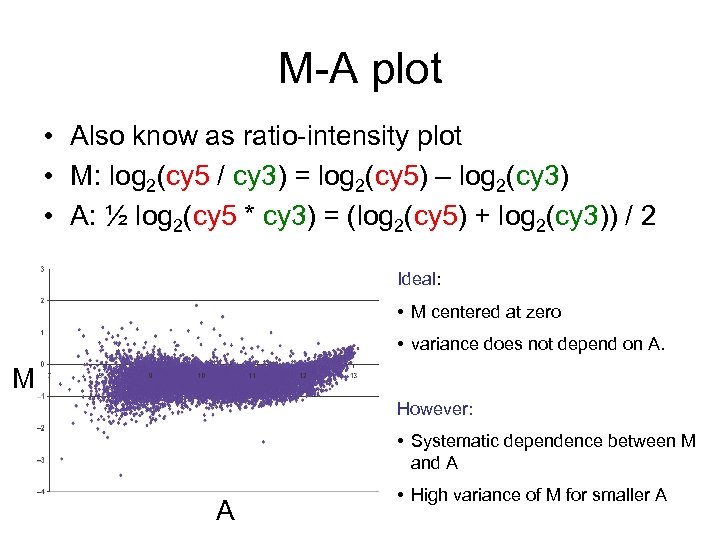
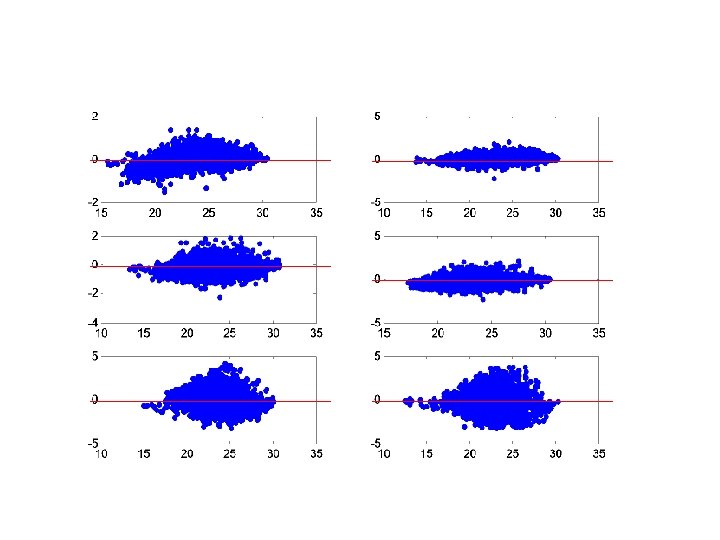
M-A plot • Also know as ratio-intensity plot • M: log 2(cy 5 / cy 3) = log 2(cy 5) – log 2(cy 3) • A: ½ log 2(cy 5 * cy 3) = (log 2(cy 5) + log 2(cy 3)) / 2 Ideal: • M centered at zero • variance does not depend on A. M However: • Systematic dependence between M and A A • High variance of M for smaller A
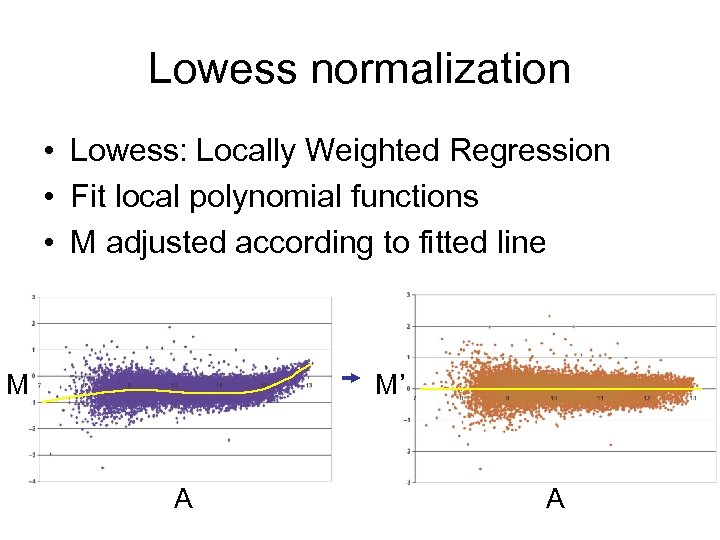
Lowess normalization • Lowess: Locally Weighted Regression • Fit local polynomial functions • M adjusted according to fitted line M M’ A A
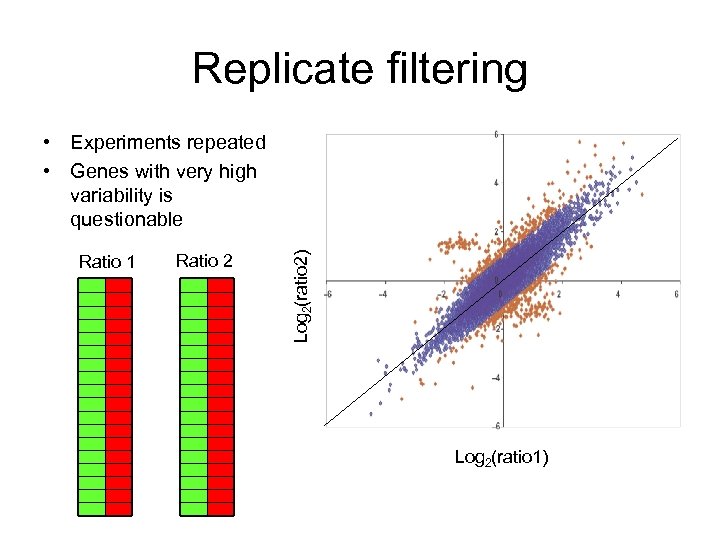
Replicate filtering Ratio 1 Ratio 2 Log 2(ratio 2) • Experiments repeated • Genes with very high variability is questionable Log 2(ratio 1)

oligo microarray data preprocessing (Affymetrix chip)

Typical experiments • Multiple microarrays – n samples (from different time, location, condition, treatment, etc. ) – k replicates for each samples • For example – Samples collected from 100 healthy people and 100 cancer patients – Cells treated with some drugs, take samples every 10 minutes • Repeat on 3 – 5 microarrays for each sample – Improve reliability of the results – Often averaged after some preprocessing

Main characteristics • For each gene, there are multiple PM and MM probes (11 -16 pairs) – how to obtain overall intensities from these probe-level intensities? • Array outputs are absolute values rather than ratios – Cross-array normalization is important for them to be comparable
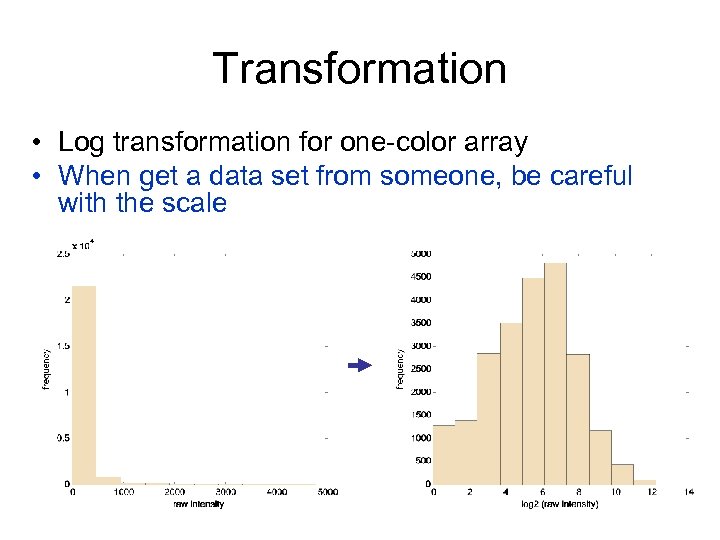
Transformation • Log transformation for one-color array • When get a data set from someone, be careful with the scale

Normalization • Ideas similar to c. DNA microarrays – For c. DNA microarrays, normalize on log ratios. • May have one or more arrays. – Here, normalize absolute expression values. • Usually multiple array. • Total intensity normalization – Each array has the same mean intensity – Can be based on all genes or a selected subset of genes • House-keeping genes • Middle 90% (for example) of genes • Spike-in genes • Lowess: using a common reference, or cyclic • Many useful tools implemented in R (Bioconductor)
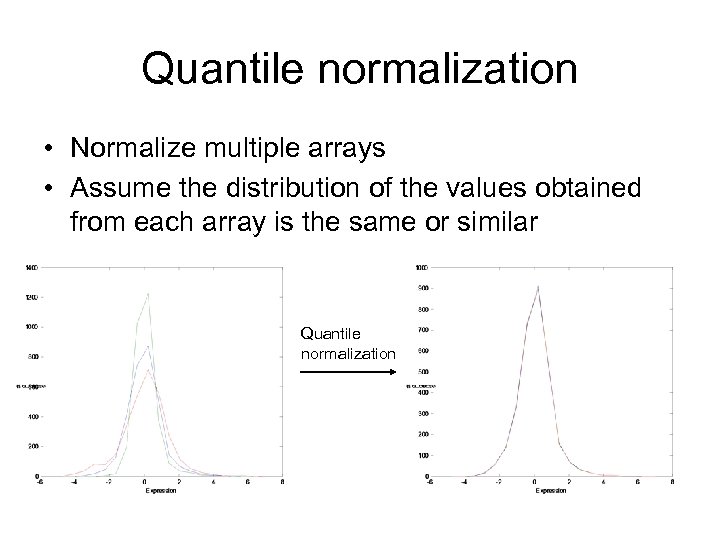
Quantile normalization • Normalize multiple arrays • Assume the distribution of the values obtained from each array is the same or similar Quantile normalization
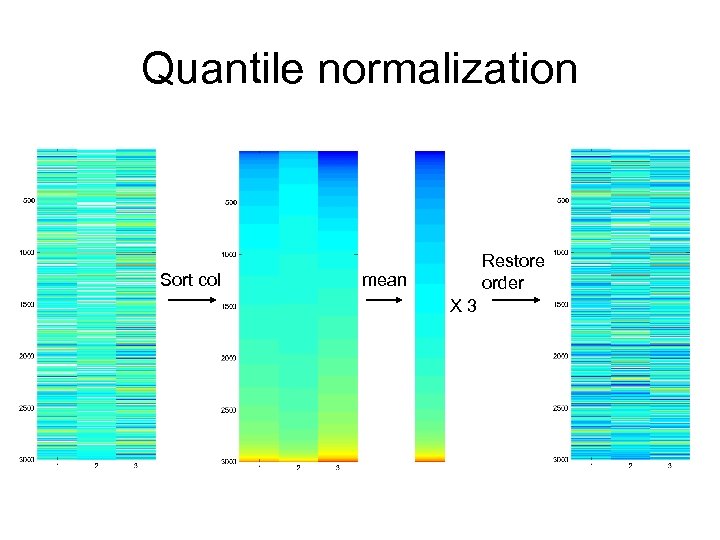
Quantile normalization Sort col Restore order mean X 3

An example data set • J De. Risi, V Iyer, and P Brown, “Exploring the Metabolic and Genetic Control of Gene Expression on a Genomic Scale”, Science, 278: 680 – 686, 1997 – Yeast cells grow in glucose medium – When glucose was depleted, cells change their metabolic pathways • c. DNA microarray – – – Test: 2, 4, 6, 8, 10, 12, 14 hours after growth Control: 0 hour Total data points: ~6000 x 7 No replicates! No normalization! Use fold-change to get differentially expressed genes!
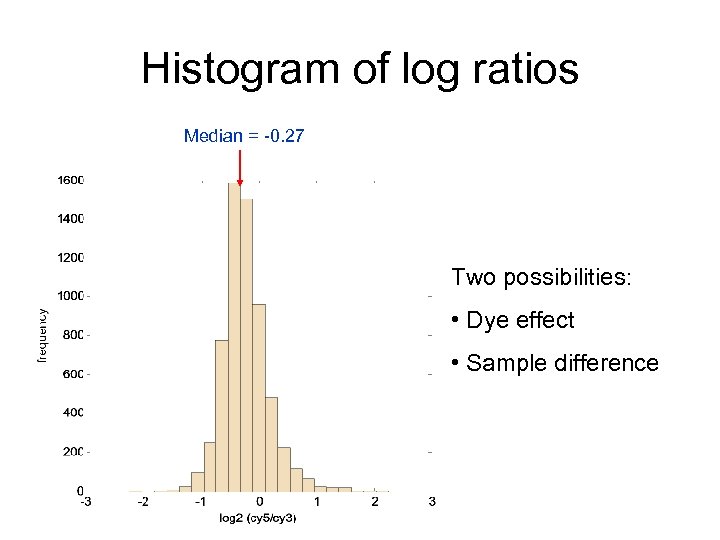
Histogram of log ratios Median = -0. 27 Two possibilities: • Dye effect • Sample difference
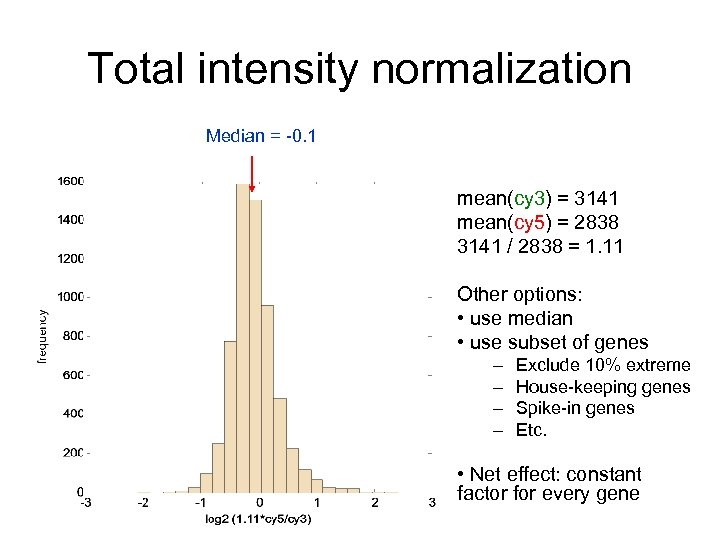
Total intensity normalization Median = -0. 1 mean(cy 3) = 3141 mean(cy 5) = 2838 3141 / 2838 = 1. 11 Other options: • use median • use subset of genes – – Exclude 10% extreme House-keeping genes Spike-in genes Etc. • Net effect: constant factor for every gene
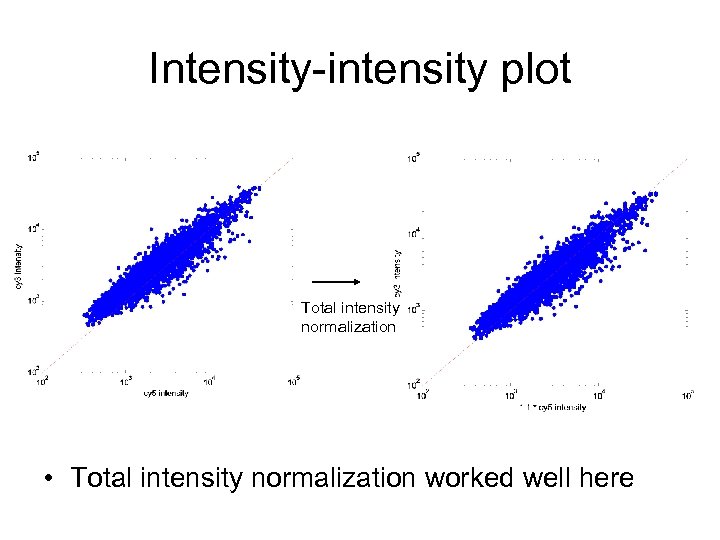
Intensity-intensity plot Total intensity normalization • Total intensity normalization worked well here
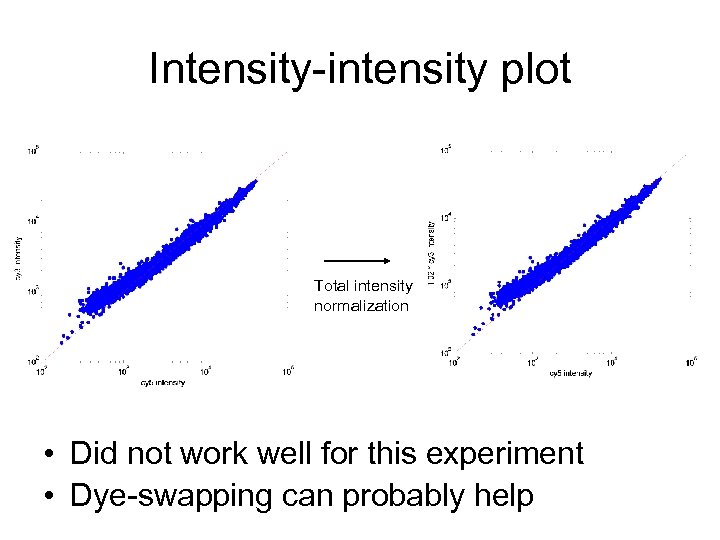
Intensity-intensity plot Total intensity normalization • Did not work well for this experiment • Dye-swapping can probably help

M-A plot A: log 2(cy 5 * cy 3) = log 2(cy 5)+log 2(cy 3) M: log 2(cy 5 / cy 3) = = log 2(cy 5)-log 2(cy 3)

M-A plot Dependency of M on A
Box plot

Conclusions • Microarray provides a way to measure thousands of genes simultaneously and make the global monitoring of cellular activities possible. • The method produces noisy data and normalization is crucial. • Real Time RT-PCR for validation of small number of genes.

Limitation • Measures m. RNA instead of proteins. Actual protein abundance and post-translation modification can not be detected. • Suitable for global monitoring and should be used to generate further hypothesis or should combine with other carefully designed experiments.

Mechanisms in microarray Important mechanisms that make microarray work: 1. Reverse transcription: m. RNA => c. DNA. This is usually also the step to label dyes. (Protein can not be reverse translated to m. RNA or to another form. So difficult to label dyes. ) 2. Double strand binding of complimentary DNA sequences. (Protein does not enjoy such a good property; there are 20 amino acids without complementary binding)
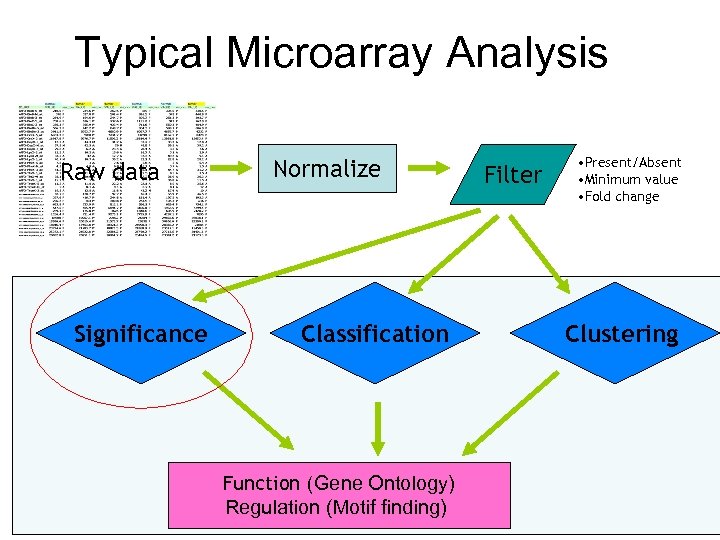
Typical Microarray Analysis Raw data Significance Normalize Classification Function (Gene Ontology) Regulation (Motif finding) Filter • Present/Absent • Minimum value • Fold change Clustering

Identify differentially expressed genes • Two samples: one normal, one cancer – Which set of genes have significantly different expression levels between the two samples? • Naïve approach: fold change threshold (e. g. two fold) – Log 2 (cy 5 / cy 3) > 1: up-regulated / induced – Log 2(cy 5 / cy 3) < -1: down-regulated / repressed • Still widely used – very simple • Main problem: genes with low expression levels may have a large fold change by chance – From 10 to 100: ten fold – From 1000 to 3000: three fold – However: low-intensity => relatively high variance
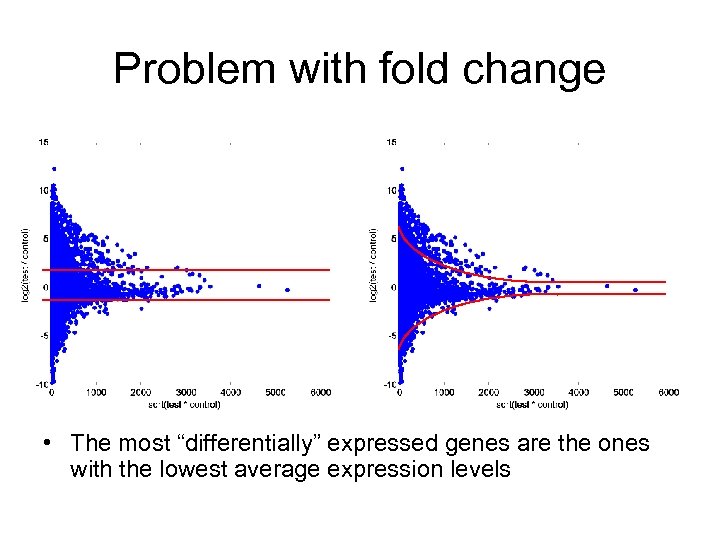
Problem with fold change • The most “differentially” expressed genes are the ones with the lowest average expression levels
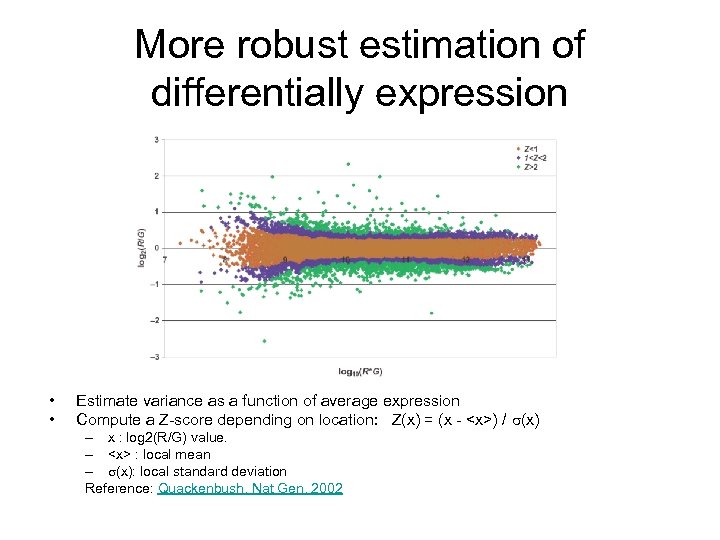
More robust estimation of differentially expression • • Estimate variance as a function of average expression Compute a Z-score depending on location: Z(x) = (x - <x>) / (x) – x : log 2(R/G) value. – <x> : local mean – (x): local standard deviation Reference: Quackenbush, Nat Gen, 2002

SAM (Significance Analysis of Microarrays) • • Tusher et. al. PNAS 2001, 98: 5116 -5121 Excel add-in (free download, technical details) Most cited method of microarray data analysis Example: Test - 3 reps; Control - 3 reps T 1 T 2 T 3 C 1 C 2 C 3 Ratio Gene 1 1000 2000 1500 200 300 250 6 Gene 2 1000 2000 3000 1500 2 Gene 3 1000 100 20 80 50 8 Gene 4 1800 1700 1900 1000 800 900 2 Which one is more significantly differentially expressed?
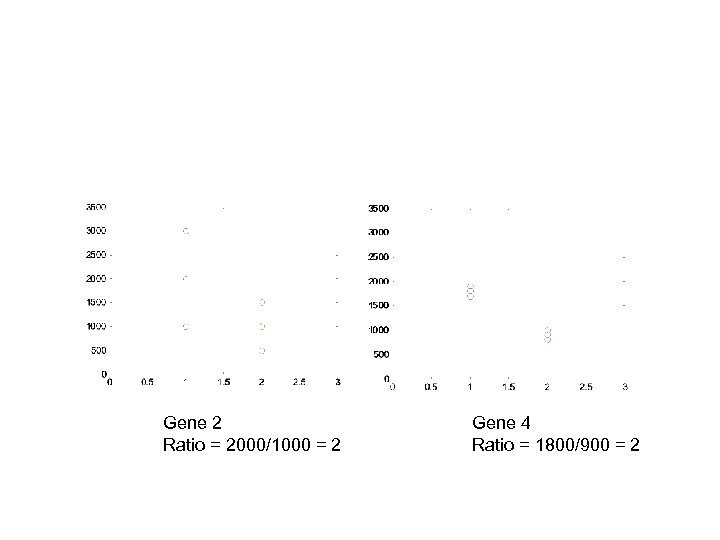
Gene 2 Ratio = 2000/1000 = 2 Gene 4 Ratio = 1800/900 = 2

SAM (Significance Analysis of Microarrays) • Basic idea: compute a statistic (e. g. Student’s t-test) + S 0 To avoid small sample problem • Larger t => higher significance • P-value can be directly computed for t-test or estimated from permutation test T 1 T 2 T 3 C 1 C 2 C 3 Ratio t Gene 1 1000 2000 1500 200 300 250 6 4. 3 Gene 2 1000 2000 3000 1500 2 1. 5 Gene 3 1000 100 20 80 50 8 1. 2 Gene 4 1800 1700 1900 1000 800 900 2 11. 0
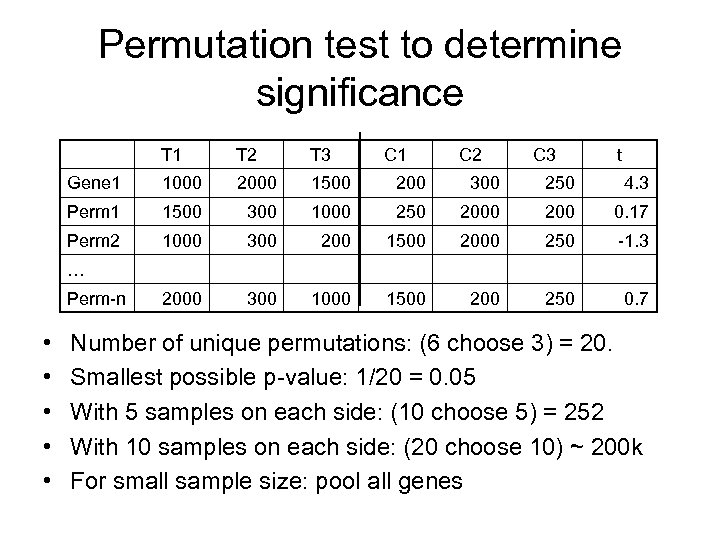
Permutation test to determine significance T 1 T 2 T 3 C 1 C 2 C 3 t Gene 1 1000 2000 1500 200 300 250 4. 3 Perm 1 1500 300 1000 250 200 0. 17 Perm 2 1000 300 200 1500 2000 250 -1. 3 2000 300 1000 1500 250 0. 7 … Perm-n • • • Number of unique permutations: (6 choose 3) = 20. Smallest possible p-value: 1/20 = 0. 05 With 5 samples on each side: (10 choose 5) = 252 With 10 samples on each side: (20 choose 10) ~ 200 k For small sample size: pool all genes

Permutation test Sorted Real t t 1 t 2 … tn tavg Treal - tavg -
SAM

False Discovery Rate (FDR) • Multiple testing problem – – P-value cutoff = 0. 05 We tested 10000 genes Would expect 500 genes by chance at this significance level Found 600 genes with p < 0. 05. Many might be due to noise. • Bonferroni correction – Use p-value cutoff 0. 05 / 10000 – Among all genes selected, P(at least one false positive) <= 0. 05 – Too conservative. Very few genes can be selected. • False Discovery Rate (FDR) – FDR = 0. 1, meaning among all genes selected, (say 100), we would expect 10 to be false positive – FDR as high as 0. 5 may be acceptable to biologists – Several different approaches to estimate (Most popular: Benjamini & Hochberg)
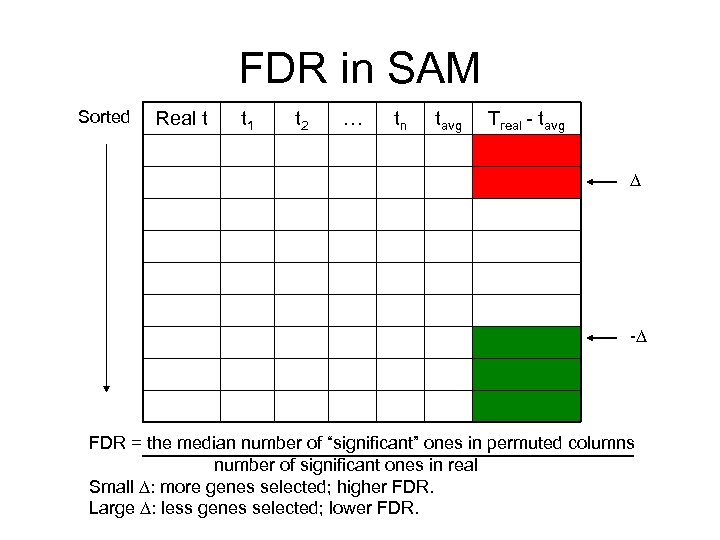
FDR in SAM Sorted Real t t 1 t 2 … tn tavg Treal - tavg - FDR = the median number of “significant” ones in permuted columns number of significant ones in real Small : more genes selected; higher FDR. Large : less genes selected; lower FDR.
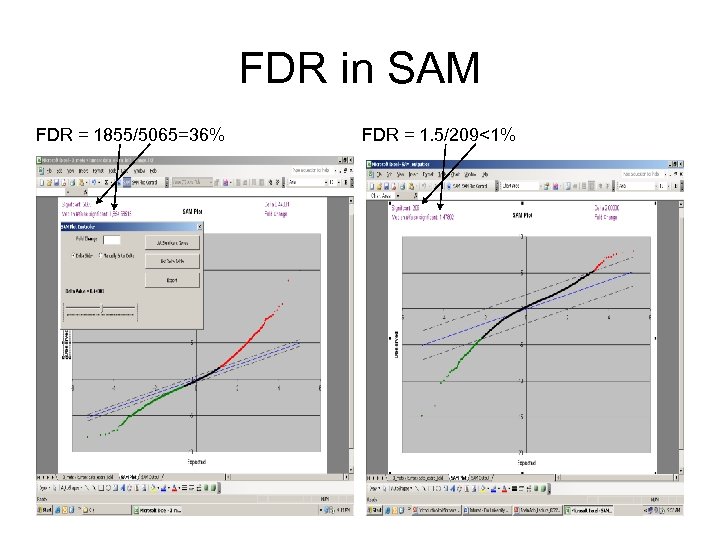
FDR in SAM FDR = 1855/5065=36% FDR = 1. 5/209<1%
Typical Microarray Analysis Raw data Significance Normalize Classification Function (Gene Ontology) Regulation (Motif finding) Filter • Present/Absent • Minimum value • Fold change Clustering
Source: “Practical Microarray Analysis”, Presentation by Benedikt Brors, German Cancer Research Center

Classification (Supervised learning) • (Clustering: unsupervised learning) • Classification: separate items into groups based on features of the items and based on a training set of previously labeled items • Many classification algorithms: – Decision tree, SVM, naïve bayes, nearest neighbors, neural networks, etc. – Some tell you how the classification is made, which might help biologists to understand the molecular mechanisms – Some are black boxes – In most cases, performance by different algs is similar. Having the right features (predictor variables) is the key.
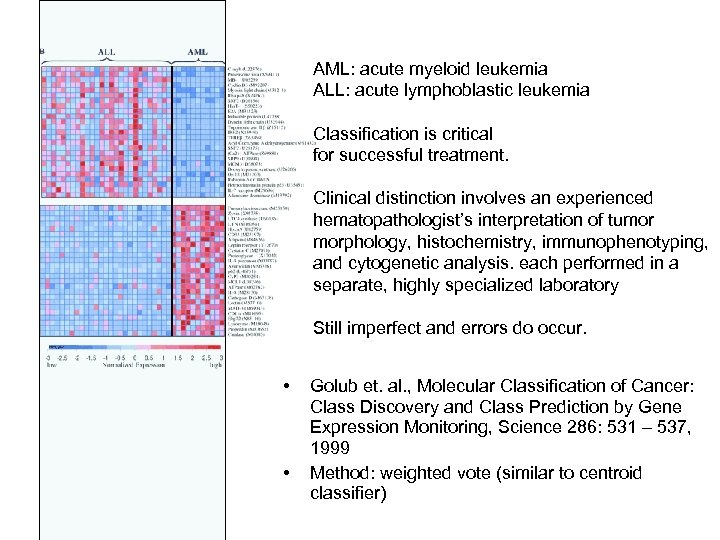
AML: acute myeloid leukemia ALL: acute lymphoblastic leukemia Classification is critical for successful treatment. Clinical distinction involves an experienced hematopathologist’s interpretation of tumor morphology, histochemistry, immunophenotyping, and cytogenetic analysis. each performed in a separate, highly specialized laboratory Still imperfect and errors do occur. • • Golub et. al. , Molecular Classification of Cancer: Class Discovery and Class Prediction by Gene Expression Monitoring, Science 286: 531 – 537, 1999 Method: weighted vote (similar to centroid classifier)

Centroid-based classifier • Model Training: Based on the training data calculate the centroid for each class. G 1 x? d 1 * * c 1 * * d 2 * * oo o c 2 o o o • Classification: 1. Given a data point, calculate the distance between the point and each of the class centroids. 2. Assign the point to the closest class ALL ? centroid AML centroid G 2

K-Nearest-Neighbour classifier • Model Training: none • Classification: – Given a data point, locate K nearest points. – Returns the most common class label among the k points nearest to x • We usually set K > 1 to avoid outliers • Variations: – Can also use a radius threshold rather than K. – We can also set a weight for each neighbour that takes into account how far it is from the query point _ _ _ ++ + _ . _ + + x _ _ + +

Cancer classification • Tons of papers have been published. Many claimed high accuracy. – Be careful when evaluating those papers. – Very easy to overfit: much more number of genes than number of samples • Simple methods often outperform fancy ones – SVM and KNN among best • Simple methods usually also mean robustness and easy to interpret • In most cases, performance by different algs is similar. Having the right features (predictor variables) is the key.

Clustering microarray data • Unsupervised learning • Group genes into co-expressed sets – Genes with similar expression patterns across multiple experiments may be co-regulated • Group experiments into clusters – Experiments within the same group may have similar “gene expression” signature – For example, disease sub-types that can be classified from gene expression data

Clustering microarray data • How to tell if two expression vectors are similar? – Define the (dis)-similarity measure between two vectors • How to group multiple profiles into meaningful subsets ? – Describe the clustering procedure • Are the results meaningful ? – Evaluate biological meaning of a clustering

(Dis)-similarity measures • Two genes, X=(x 1, …, xm) and Y=(y 1…, ym). • Euclidean distance • Pearson correlation coefficient • Cosine similarity • Mutual information • Etc.

Clustering algorithms • • Hierarchical clustering K-means clustering Self Organizing Maps (SOMs) Spectral clustering Model-based Graph-based Etc. • Jiang and Zhang, Cluster Analysis for Gene Expression Data: A Survey, IEEE Transactions on Knowledge and Data Engineering, Vol. 16, No. 11. (2004), pp. 1370 -1386

Hierarchical clustering • Agglomerative or divisive (less popular) • Agglomerative basic idea: – Given n genes – Initially every gene in a single cluster – for each iteration • find two most similar genes (or gene groups), combine into one cluster • Terminate when only one cluster is left • (how to define similarity between two groups? )
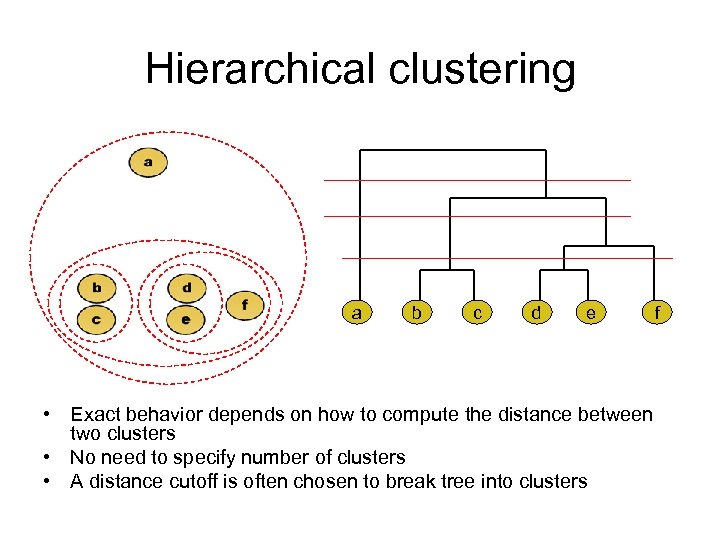
Hierarchical clustering a b c d e • Exact behavior depends on how to compute the distance between two clusters • No need to specify number of clusters • A distance cutoff is often chosen to break tree into clusters f
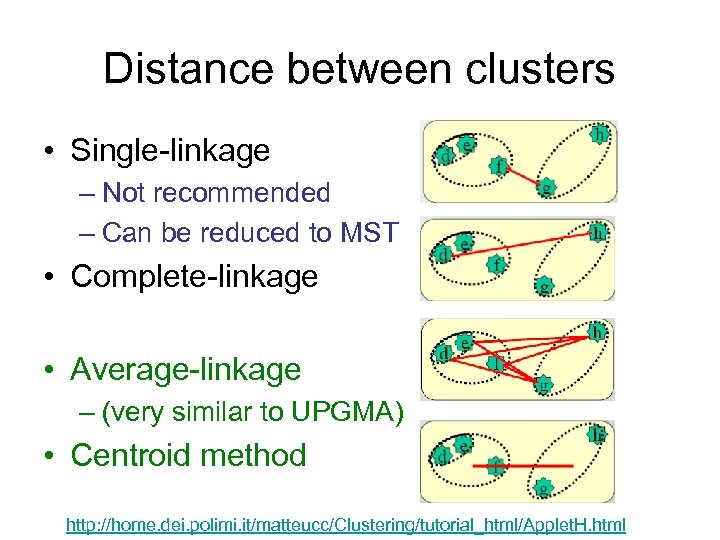
Distance between clusters • Single-linkage – Not recommended – Can be reduced to MST • Complete-linkage • Average-linkage – (very similar to UPGMA) • Centroid method http: //home. dei. polimi. it/matteucc/Clustering/tutorial_html/Applet. H. html
An example Genes Experiments
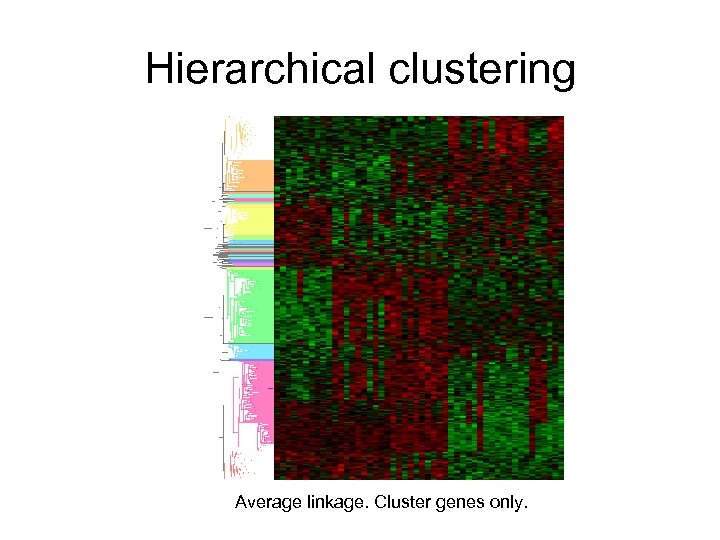
Hierarchical clustering Average linkage. Cluster genes only.
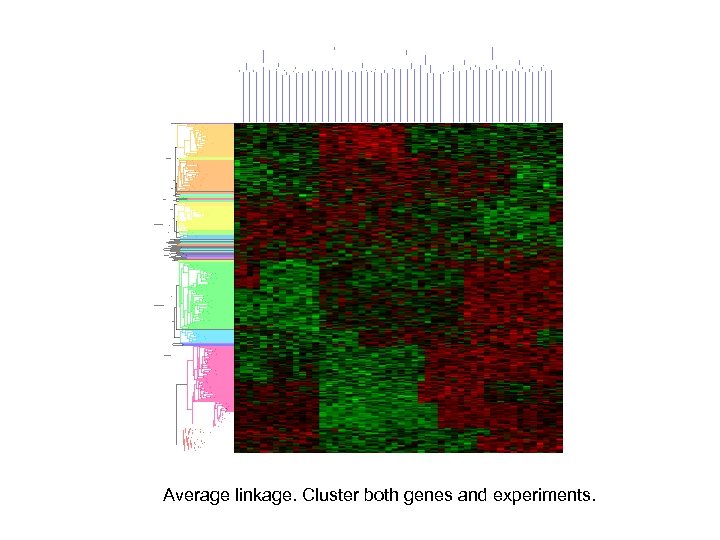
Average linkage. Cluster both genes and experiments.
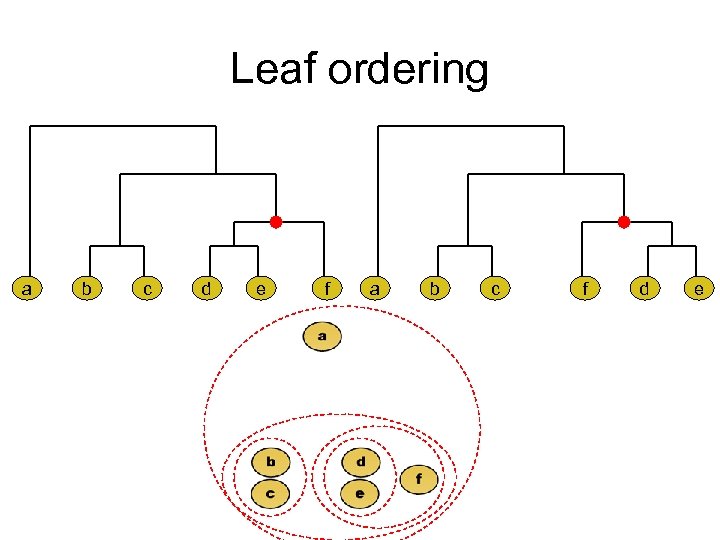
Leaf ordering a b c d e f a b c f d e
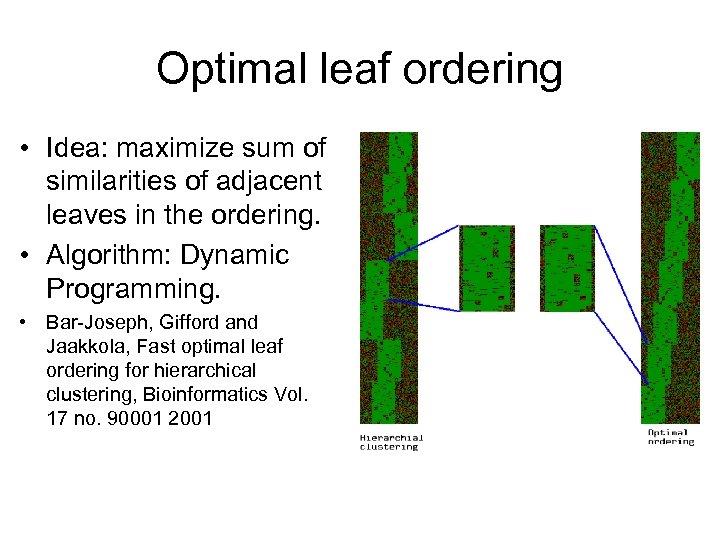
Optimal leaf ordering • Idea: maximize sum of similarities of adjacent leaves in the ordering. • Algorithm: Dynamic Programming. • Bar-Joseph, Gifford and Jaakkola, Fast optimal leaf ordering for hierarchical clustering, Bioinformatics Vol. 17 no. 90001 2001
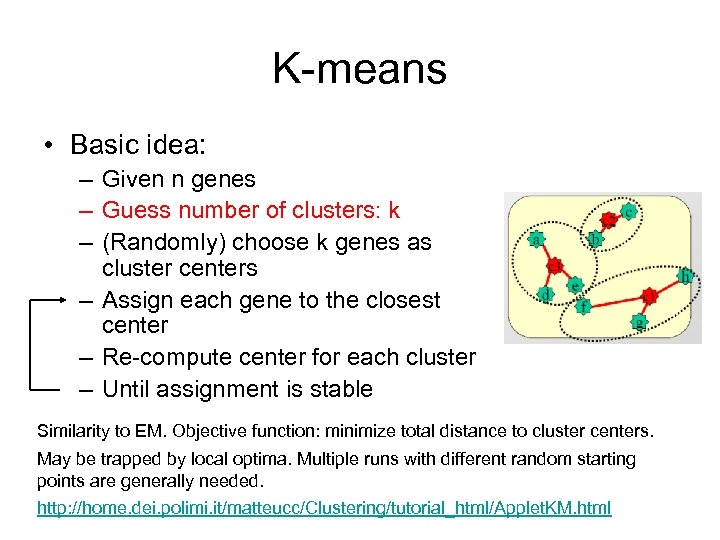
K-means • Basic idea: – Given n genes – Guess number of clusters: k – (Randomly) choose k genes as cluster centers – Assign each gene to the closest center – Re-compute center for each cluster – Until assignment is stable Similarity to EM. Objective function: minimize total distance to cluster centers. May be trapped by local optima. Multiple runs with different random starting points are generally needed. http: //home. dei. polimi. it/matteucc/Clustering/tutorial_html/Applet. KM. html
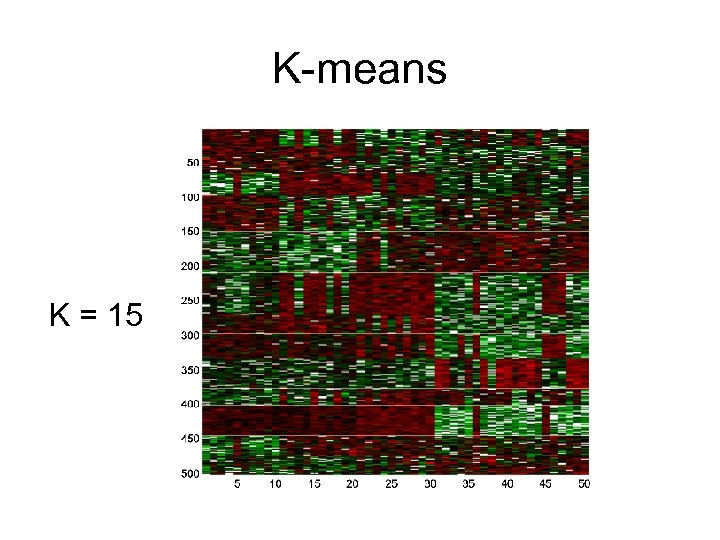
K-means K = 15
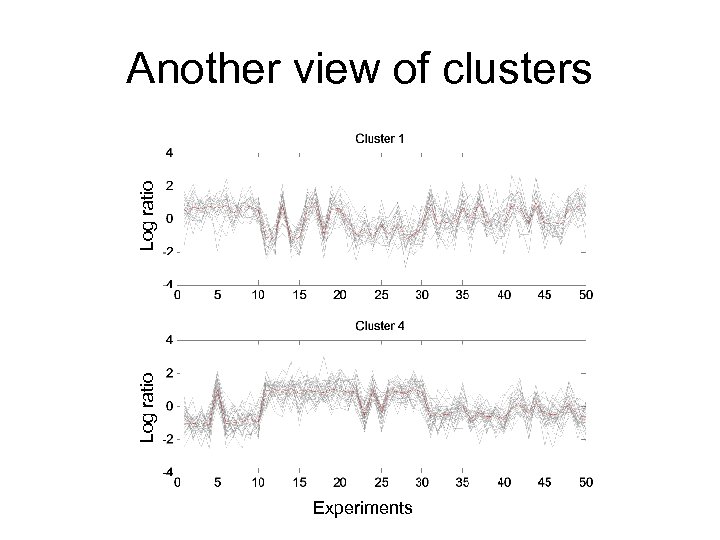
Log ratio Another view of clusters Experiments

How to determine number of clusters? • An open problem • Larger K: – More homogeneity within clusters – Less separation between clusters • Small K: – The opposite • Many heuristic methods have been proposed, none is uniformly good
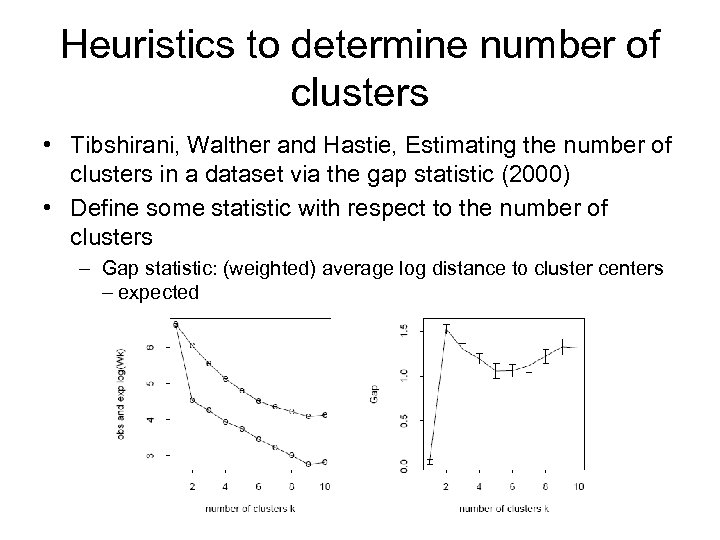
Heuristics to determine number of clusters • Tibshirani, Walther and Hastie, Estimating the number of clusters in a dataset via the gap statistic (2000) • Define some statistic with respect to the number of clusters – Gap statistic: (weighted) average log distance to cluster centers expected
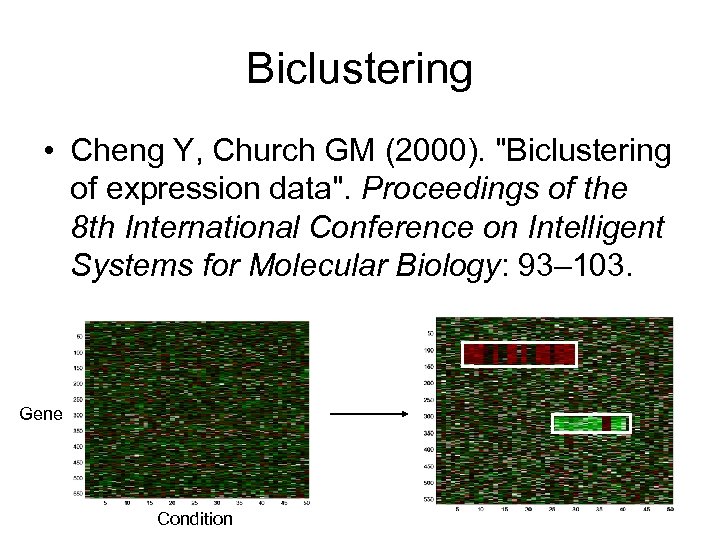
Biclustering • Cheng Y, Church GM (2000). "Biclustering of expression data". Proceedings of the 8 th International Conference on Intelligent Systems for Molecular Biology: 93– 103. Gene Condition

Evaluating clustering • Do genes in the same cluster share similar functions? – Functional enrichment analysis • Do genes in the same cluster share similar cis-regulatory motifs? – Motif finding

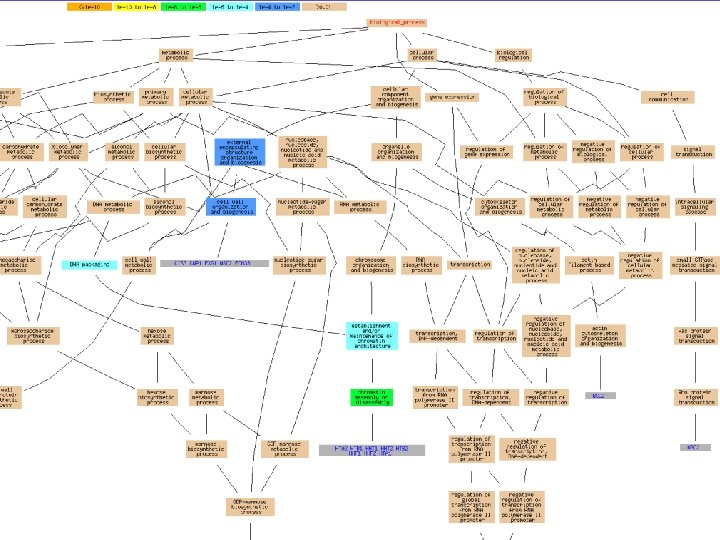
Gene Ontology (GO) • Gene functions were often defined using free text • Hard to extract, transfer, revise, predict, annotate, comprehend, manage … • The list of vocabularies should be predefined and commonly agreed • Gene Ontology provides a controlled vocabulary to describe gene and gene product attribute

Gene ontology • Two parts – Ontology: list of vocabularies (terms) to use – Annotations: characterizing genes using ontology terms • Three ontology categories – Biological process – Molecular function – Cellular components
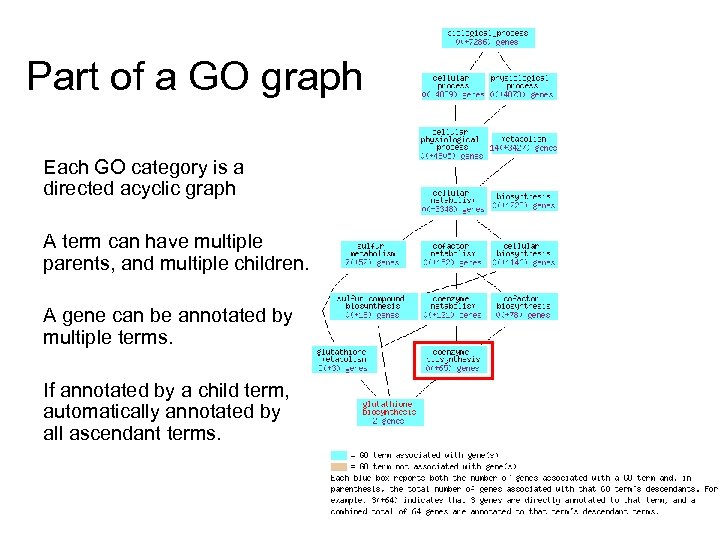
Part of a GO graph Each GO category is a directed acyclic graph A term can have multiple parents, and multiple children. A gene can be annotated by multiple terms. If annotated by a child term, automatically annotated by all ascendant terms.
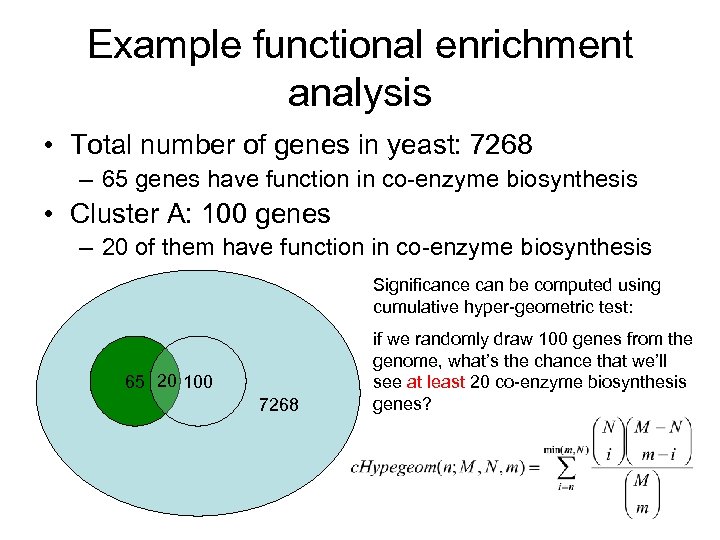
Example functional enrichment analysis • Total number of genes in yeast: 7268 – 65 genes have function in co-enzyme biosynthesis • Cluster A: 100 genes – 20 of them have function in co-enzyme biosynthesis Significance can be computed using cumulative hyper-geometric test: 65 20 100 7268 if we randomly draw 100 genes from the genome, what’s the chance that we’ll see at least 20 co-enzyme biosynthesis genes?
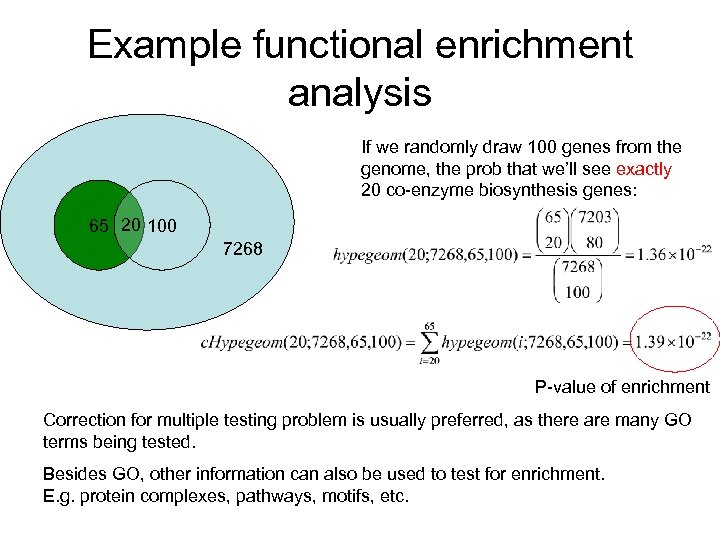
Example functional enrichment analysis If we randomly draw 100 genes from the genome, the prob that we’ll see exactly 20 co-enzyme biosynthesis genes: 65 20 100 7268 P-value of enrichment Correction for multiple testing problem is usually preferred, as there are many GO terms being tested. Besides GO, other information can also be used to test for enrichment. E. g. protein complexes, pathways, motifs, etc.

Gene Ontology Tools • geneontology. org – Download ontology files, species-specific annotation files – Links to many useful analysis tools • Tools for enrichment analysis – GO: Term. Finder. Downloadable. (Web interface available at SGD for yeast only) – Func. Associate: Web tool. ~a dozen model organisms (human, mouse, fruit fly, c. elegan, yeast, Arabidopsis, etc). – DAVID Bioinformatics Resources: Web tool. (Downloadable). Mammalian genes.

An example application • • • Tavazoie et al, Systematic determination of genetic network architecture, Nature Genetics, 22, 1999 3000 yeast genes, 15 time points during “cell cycle” Use k-means clustering, k=30 – Clusters correlate well with known function • Align. ACE motif finding – From 600 -bp upstream regions – Found many known motifs
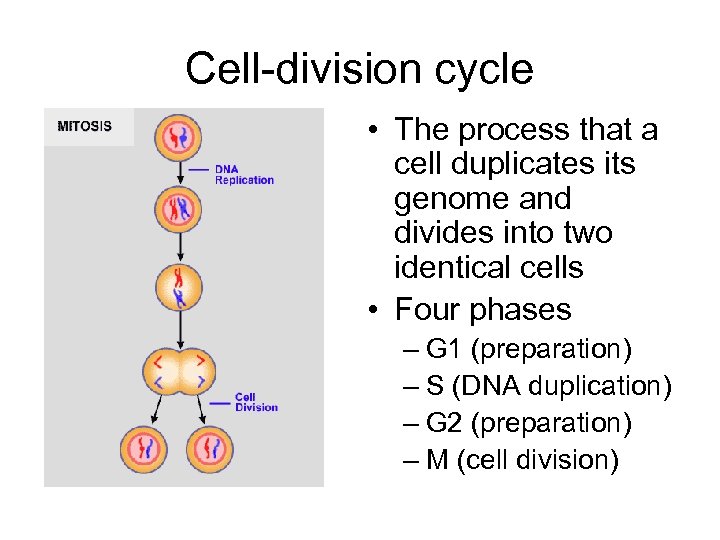
Cell-division cycle • The process that a cell duplicates its genome and divides into two identical cells • Four phases – G 1 (preparation) – S (DNA duplication) – G 2 (preparation) – M (cell division)
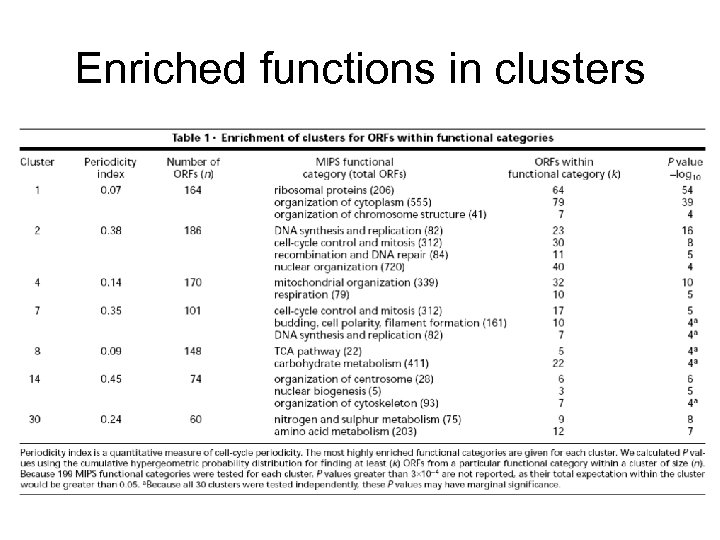
Enriched functions in clusters
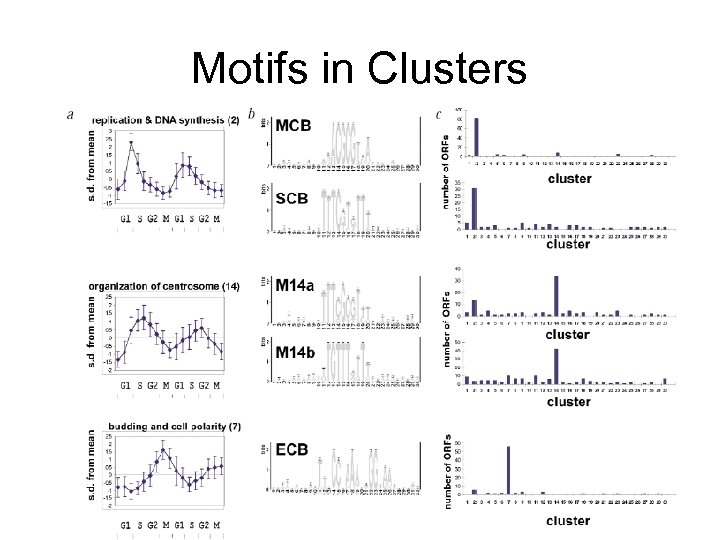
Motifs in Clusters

Comparing clustering results • When true clustering is known – Confusion matrix – Jaccard Index, Wallace Index, Rand Index, etc. • M. Meila, Comparing clusterings--an information based distance, Journal of Multivariate Analysis, 2007, 98: 873 - 895 • When true clustering is unknown – Use Gene Ontology, e. g. • Total number of enriched GO terms (affected by # of clusters) • Product of enrichment p-values (affected by # of clusters) • Above measurement compared to random (e. g. Z-score) – Gibbons and Roth, Judging the Quality of Gene Expression. Based Clustering Methods Using Gene Annotation, Genome Res, 2002, 12: 1574 -81
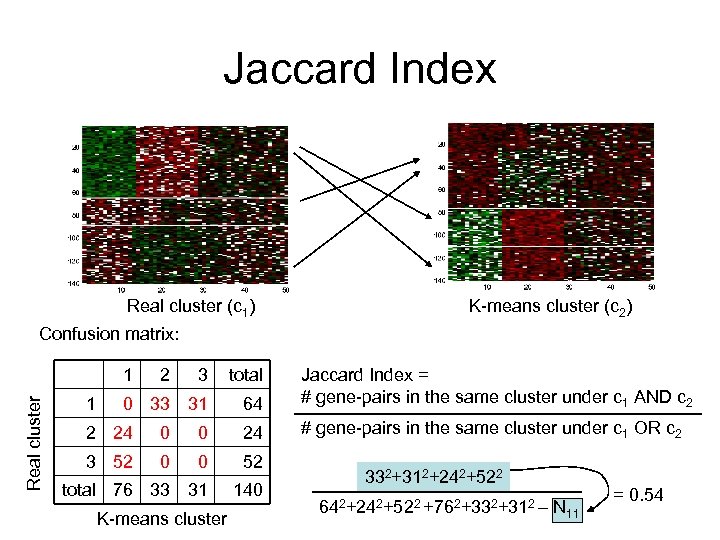
Jaccard Index Real cluster (c 1) K-means cluster (c 2) Confusion matrix: Real cluster 1 1 2 3 total 0 33 31 64 Jaccard Index = # gene-pairs in the same cluster under c 1 AND c 2 # gene-pairs in the same cluster under c 1 OR c 2 2 24 0 0 24 3 52 0 0 52 total 76 33 31 140 K-means cluster 332+312+242+522 642+242+522 +762+332+312 – N 11 = 0. 54
2717ae4f0468311f128d65504eee02fe.ppt