743e00e0a17f416f23acd4656b807ff0.ppt
- Количество слайдов: 34

CS 525 – In Byzantium The Byzantine Generals Problem Leslie Lamport, Robert Shostak, and Marshall Pease ACM TOPLAS 1982 Presented by Keun Soo Yim March 19, 2009 Dr. Lamport - Byzantine - Clock Sync. - Dist. Snapshot
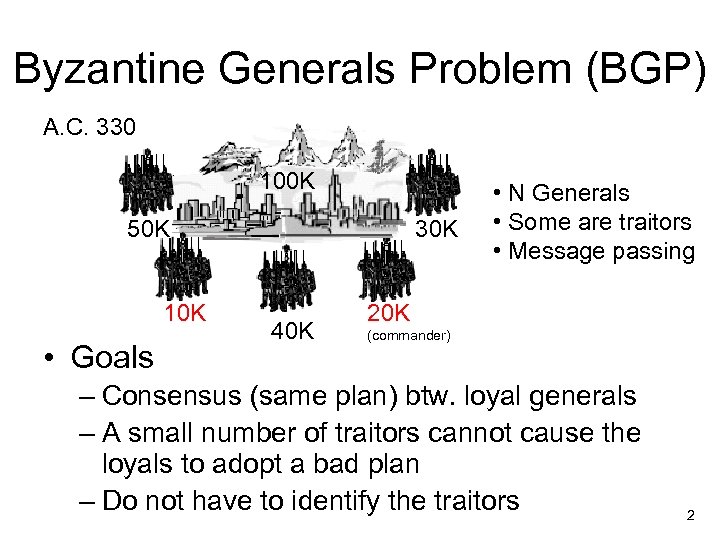
Byzantine Generals Problem (BGP) A. C. 330 100 K 50 K 10 K • Goals 30 K 40 K • N Generals • Some are traitors • Message passing 20 K (commander) – Consensus (same plan) btw. loyal generals – A small number of traitors cannot cause the loyals to adopt a bad plan – Do not have to identify the traitors 2

BGP in Distributed Systems A thousand years later… • N Computers • Some misbehave • HW Fault, SW bug, Security attack, misconfiguration • Message passing • Goals – All correct nodes share the same global info. – Ensure that N corrupted nodes can not change the shared global info. , and maximize N – Identification of corrupted nodes would be needed • What’s difference btw. BGP and consensus algo. ? – Fail-stop vs. fail-silent violation. Design goal. 3
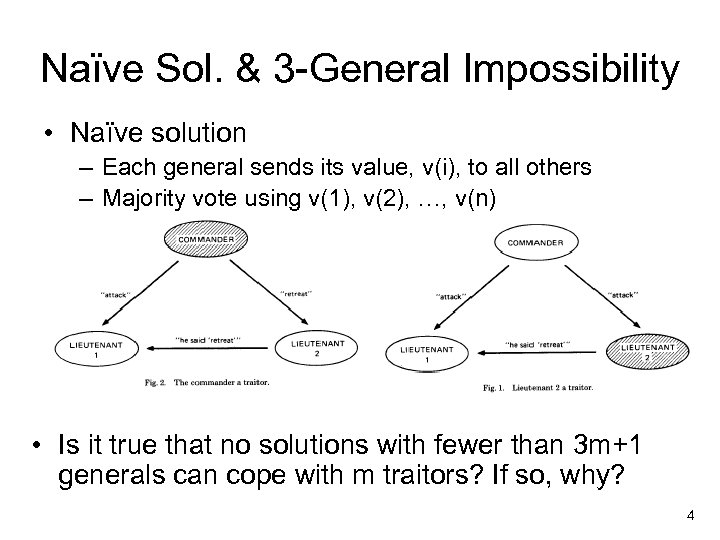
Naïve Sol. & 3 -General Impossibility • Naïve solution – Each general sends its value, v(i), to all others – Majority vote using v(1), v(2), …, v(n) • Is it true that no solutions with fewer than 3 m+1 generals can cope with m traitors? If so, why? 4
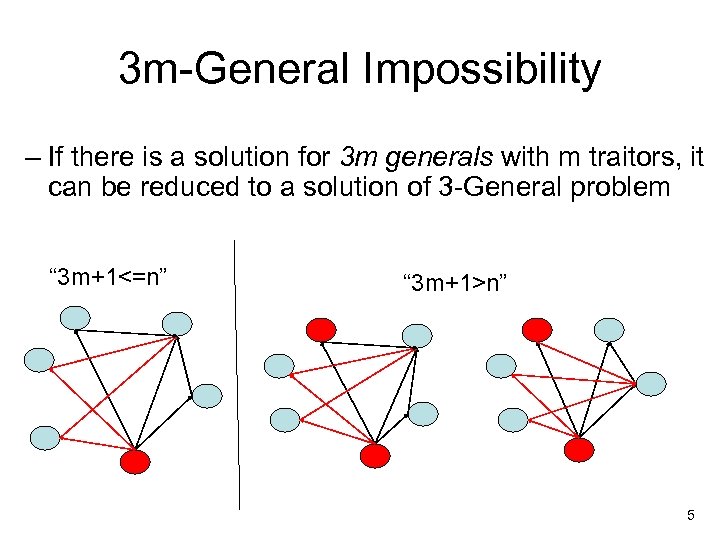
3 m-General Impossibility – If there is a solution for 3 m generals with m traitors, it can be reduced to a solution of 3 -General problem “ 3 m+1<=n” “ 3 m+1>n” 5
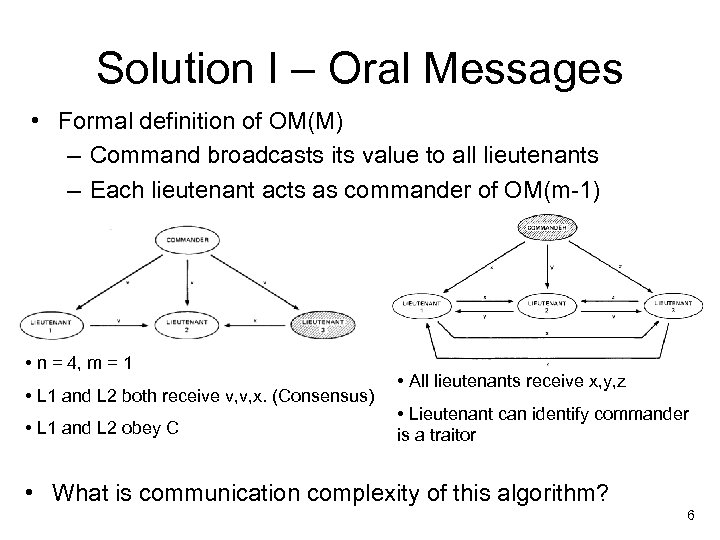
Solution I – Oral Messages • Formal definition of OM(M) – Command broadcasts its value to all lieutenants – Each lieutenant acts as commander of OM(m-1) • n = 4, m = 1 • L 1 and L 2 both receive v, v, x. (Consensus) • L 1 and L 2 obey C • All lieutenants receive x, y, z • Lieutenant can identify commander is a traitor • What is communication complexity of this algorithm? 6

Communication Complexity • O(nm) OM(m) triggers n-1 OM(m-1) triggers n-2 OM(m-2) … OM(m-k) will be called by (n-1)…(n-k) times … OM(0) 7

Solution II – Signed Messages • Can we cope with any number of traitors? If so, how? • • Prevent traitors lie about the commander’s order Message are signed by commander The sign can be verified by all loyal lieutenants When lieutenant receives no new messages, and select majority as the desired action • All loyals receive the same set of cmds eventually • If the commander is loyal, it works • What if the commander is not loyal? 8

Discussion Point • Are the assumptions realistic? • Reliable communication channel – Absence of a message can be detected. (e. g. , Timeouts or synchronized clocks ) • Failure of communication line cannot be distinguished from failure of nodes. – This is acceptable since we tolerate failures of m nodes. • Can we determine the origin of message? Anyone can verify authenticity of signature? – Unforgeable signatures using asymmetric cryptograph. 9

Peer. Review: Practical accountability for distributed systems Andreas Haeberlen, Petr Kuznetsov, and Peter Druschel SOSP 2007 (Acknowledgement: Some of this presentation slide are borrowed from the original author’s one)
Practical Use Case of BGP • Distributed file systems – Many small, latency-sensitive requests (tampering with files, lost updates) • Overlay multicast – Transfers large volume of data (tampering with content, freeloading) • P 2 P email – Complex, large, decentralized (Denial of service by misrouting) Not only consensus but also identifying faulty nodes is important!

Peer. Review § § Providing accountability for distributed systems § Stores all I/O events as a log § Selected nodes are responsible for auditing the log Assumptions: § System is modeled as deterministic state machines § State machines have reference implementations § Eventual communication § Signe d message 12
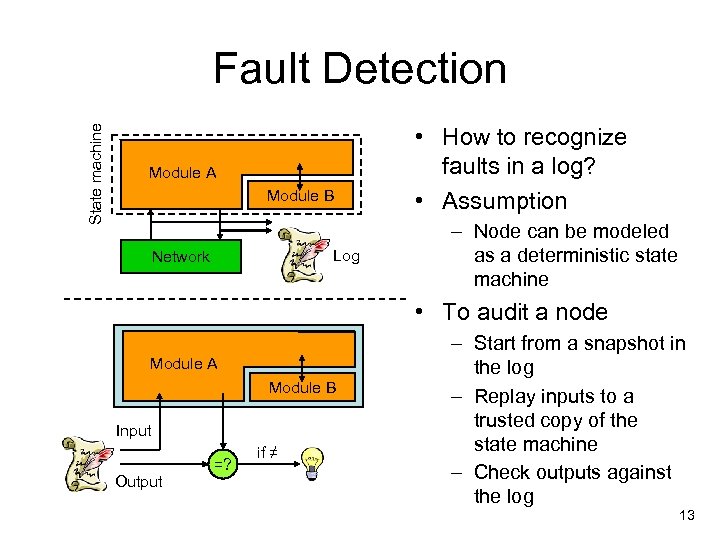
State machine Fault Detection Module A Module B Log Network • How to recognize faults in a log? • Assumption – Node can be modeled as a deterministic state machine • To audit a node Module A Module B Input Output =? if ≠ – Start from a snapshot in the log – Replay inputs to a trusted copy of the state machine – Check outputs against the log 13

Communication Algorithrm A's witnesses – Including all messages C D E A A's log • All nodes keep a log of their inputs & outputs M • Each node has a set of witnesses, who audit its log periodically • If the witnesses detect misbehavior, they – generate evidence – make the evidence available to other nodes M B B's log • Other nodes check evidence, report fault 14

Tamper-Proofing Message Hash(log) B A ACK Hash(log) What if a node modifies its log entries ? Log entries form a hash chain Inspired by secure histories [Maniatis 02] B's log ain H 4 Recv(M) Ha s h ch H 3 H 1 H 0 Send(Z) H 2 Recv(Y) Send(X) Signed hash is included with every message mi = (si, ti, ci) hi = H(hi-1||si||ti||H(ci)) Commitement protocol Sender and recevier commit to its current state 15

Provable Guarantees 1) Completeness: Faults will be detected If node commits a fault and has a correct witness, then witness obtains a proof of misbehavior (Po. M), or a challenge that the faulty node cannot answer 2) Accuracy: Good nodes cannot be accused If node is correct there can never be a Po. M, and it can answer any challenge 16
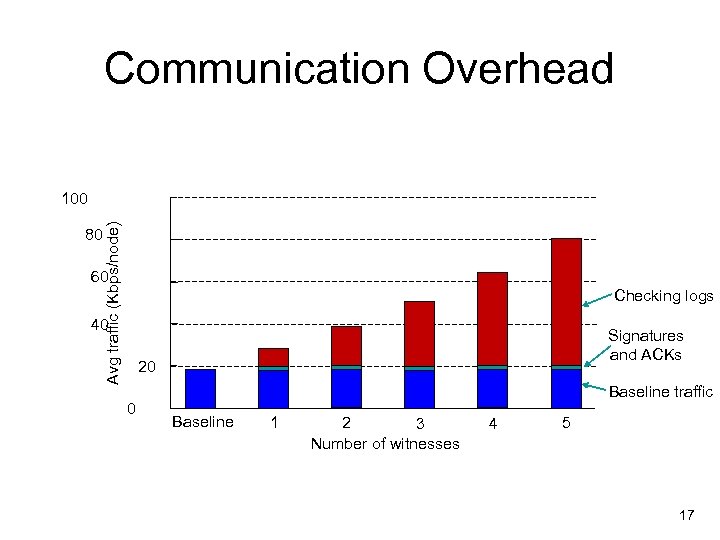
Communication Overhead 80 Avg traffic (Kbps/node) 100 60 Checking logs 40 Signatures and ACKs 20 0 Baseline traffic Baseline 1 2 3 Number of witnesses 4 5 17

Discussion Point • How would you determine the number of witnesses in a practical system? How to select them? • Peer. Review is the first, practically applicable, faulty node detection technique. Then how can we make a consensus between correct nodes in a scalable manner? 18

Zyzzyva: Speculative Byzantine Fault Tolerance Ramakrishna Kotla, Lorenzo Alvisi, Mike Dahlin, Allen Clement and Edmund Wong University of Texas at Austin SOSP 2007 Presented by Hui Xue, UIUC

Motivation Byzantine Fault Tolerance • Why we need BFT systems? – Software systems : Valuable + Not reliable enough • Amazon S 3 crashed for hours in 2008 Reason: One corrupted bit • Akami central nodes – Hardware : Cheaper now • Idea – Use more hardware Make software systems more reliable
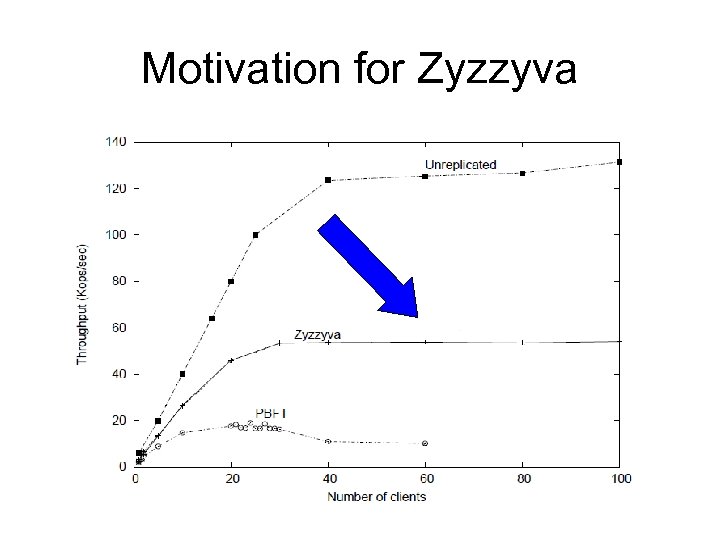
Motivation for Zyzzyva

Assumptions (System Model) • (Almost) asynchronous system • Multicast; unordered • Independent failures – Replica: at most f any kind of faults – Network: unreliable – can delay, duplicate, corrupt or drop messages • Sufficiently strong cryptographic techniques • All public keys known by everyone • Need bounded msg delay in rare cases (liveness)

Background: Practical Byzantine Fault Tolerance PBFT: establish order before execution Pre-Prepare Client Prepare Commit Req, # n? Reply OK, Req, # n! Primary Replica Faulty Replica Before execution What is the 4 network delays problem? Many messages
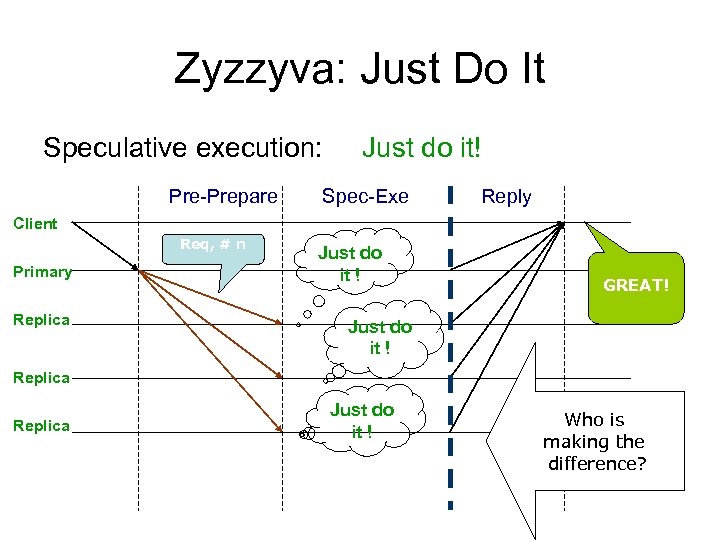
Zyzzyva: Just Do It Speculative execution: Pre-Prepare Just do it! Spec-Exe Reply Client Req, # n Primary Replica Just do it ! GREAT! Just do it ! Replica Just do it ! Who is making the difference?
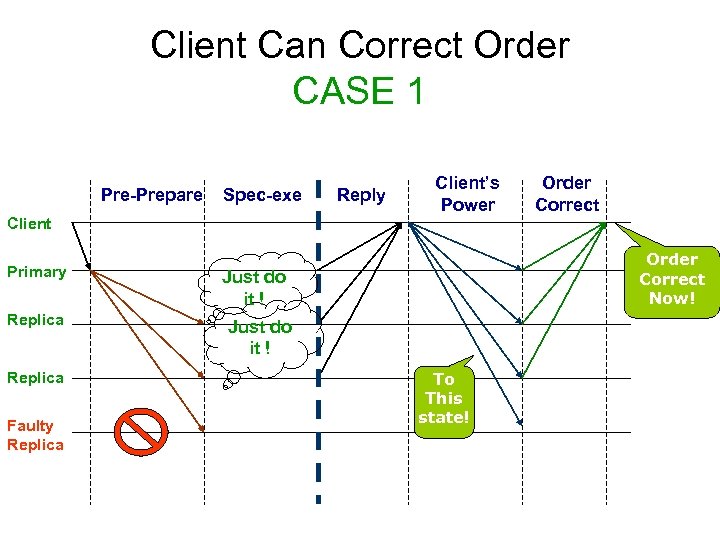
Client Can Correct Order CASE 1 Pre-Prepare Spec-exe Reply Client’s Power Order Correct Client Primary Replica Faulty Replica Order Correct Now! Just do it ! To This state!
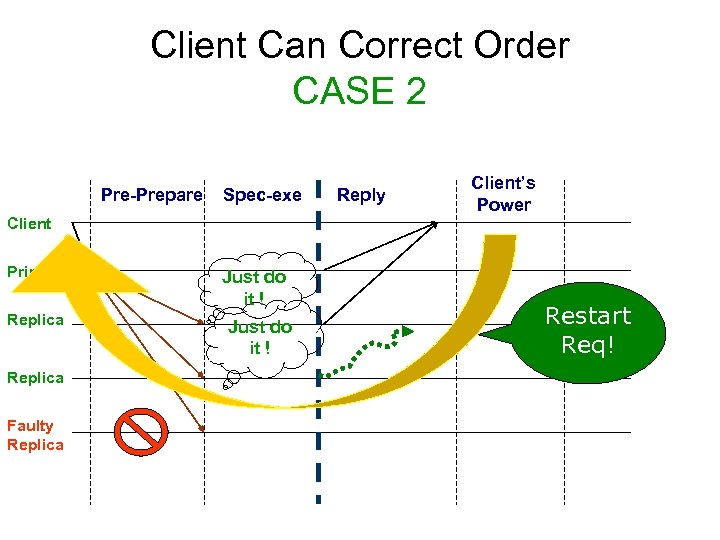
Client Can Correct Order CASE 2 Pre-Prepare Spec-exe Reply Client’s Power Client Primary Replica Faulty Replica Just do it ! Restart Req!
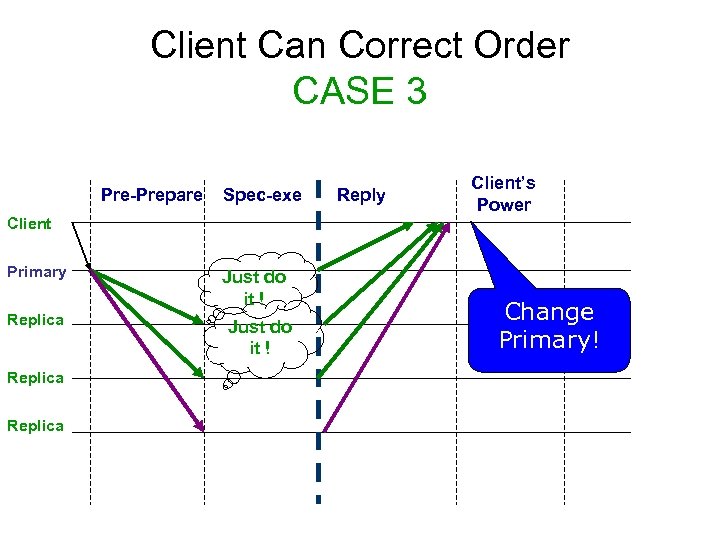
Client Can Correct Order CASE 3 Pre-Prepare Spec-exe Reply Client’s Power Client Primary Replica Just do it ! Change Primary!

Design of Protocol • Other Sub protocols: – Fill hole Sequence # received: N+4 Sequence # expected: N+1 < N+4 (hole in between) Send <FILL-HOLE> to 1. Primary 2. Slow primary, then all replicas

Optimizations – Separating agreement from execution – Batching requests – Caching out of order requests – Read only operations: 2 f+1 consistent is enough – Single full response
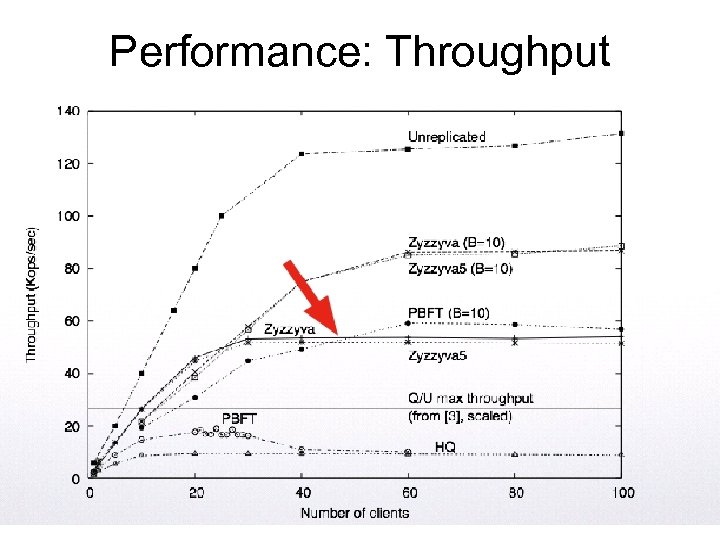
Performance: Throughput
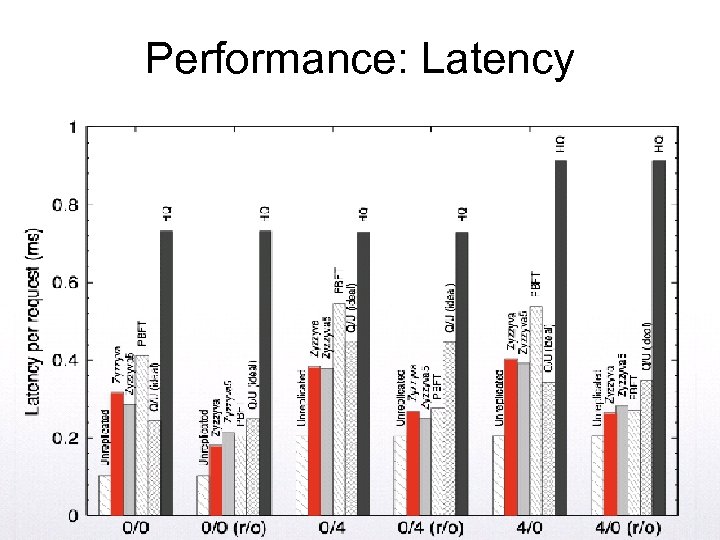
Performance: Latency

Conclusion • Clever Observation: – We can execute before the order is established, hoping we are right. • Pros – Practical, High throughput + low latency • Cons – BFT suffer from deterministic bugs – Malicious behaviors may affect performance

Questions • Why Zyzzyva is fast? • What is the main difference between Zyzzyva and previous BFT papers? • What does “zyzzyva” mean? • Do you buy the idea of BFT at all? • Name some examples of BFT in real applications.

Thank you! • This is the end of Zyzzyva – Questions?
743e00e0a17f416f23acd4656b807ff0.ppt