CS 430 Computer Graphics Programming with Affine Transformations

CS 430 Computer Graphics Programming with Affine Transformations Chi-Cheng Lin, Winona State University

Topics Affine Transformations in Open. GL l Saving Current Transformation l Drawing 3 D Scenes with Open. GL l Open. GL Functions for Modeling and Viewing l 2

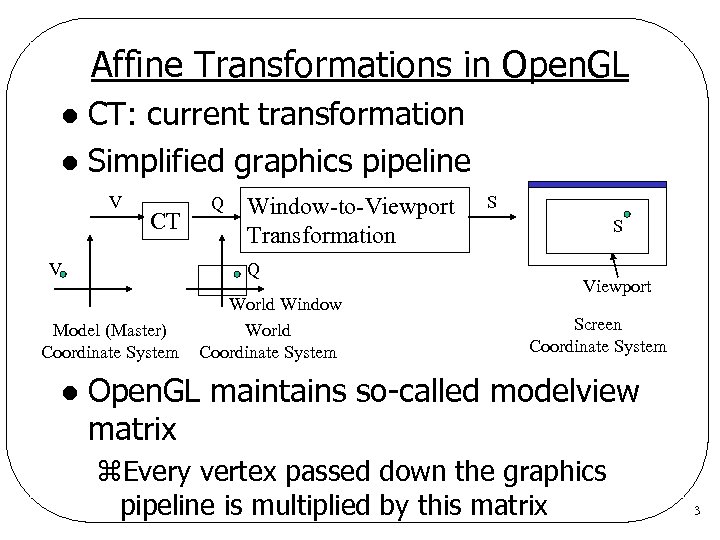Affine Transformations in Open. GL CT: current transformation l Simplified graphics pipeline l V CT V Window-to-Viewport Transformation Q Model (Master) Coordinate System l Q World Window World Coordinate System S S Viewport Screen Coordinate System Open. GL maintains so-called modelview matrix z. Every vertex passed down the graphics pipeline is multiplied by this matrix 3

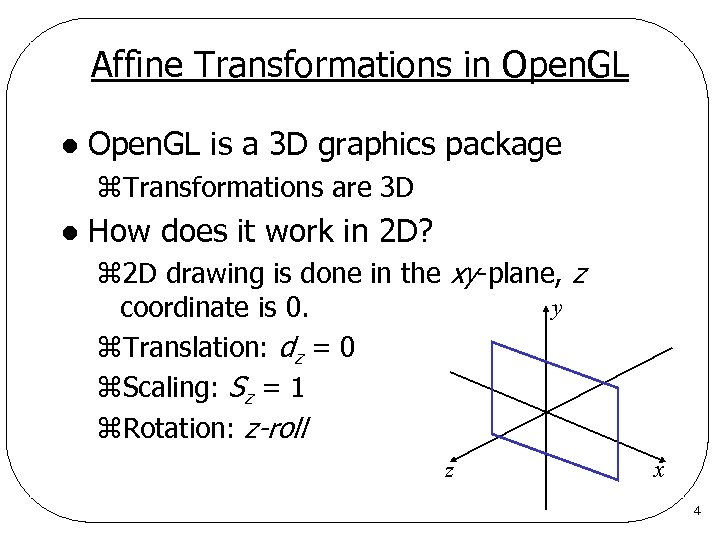Affine Transformations in Open. GL l Open. GL is a 3 D graphics package z. Transformations are 3 D l How does it work in 2 D? z 2 D drawing is done in the xy-plane, z y coordinate is 0. z. Translation: dz = 0 z. Scaling: Sz = 1 z. Rotation: z-roll z x 4

Affine Transformations in Open. GL l Fundamental Transformations z. Translation: gl. Translated(dx, dy, dz) for 2 D: gl. Translated(dx, dy, 0) z. Scaling: gl. Scaled(sx, sy, sz) for 2 D: gl. Scaled(sx, sy, 1. 0) z. Rotation: gl. Rotated(angle, ux, uy, uz) for 2 D: gl. Rotated(angle, 0, 0, 1) l Transformations does not set CT directly, a matrix is postmultiplied to CT z. CT = CT M 5

Affine Transformations in Open. GL l Canvas functions zvoid Canvas: : init. CT(void) { gl. Matrix. Mode(GL_MODELVIEW); gl. Load. Identity(); } zvoid Canvas: : scale 2 D(double sx, double sy) { gl. Matrix. Mode(GL_MODELVIEW); gl. Scaled(dx, dy, 1. 0); } 6

Affine Transformations in Open. GL l Canvas functions zvoid Canvas: : translate 2 D(double dx, double dy) { gl. Matrix. Mode(GL_MODELVIEW); gl. Translated(dx, dy, 0); } zvoid Canvas: : rotate 2 D(double angle) { gl. Matrix. Mode(GL_MODELVIEW); gl. Rotated(angle, 0. 0, 1. 0); } 7

Transformations Example l Draw a house. Draw another house by rotating it through -30° and then translating it through (32, 25) zcvs. init. CT(); house(); cvs. translate 2 D(32, 25); cvs. rotate 2 D(-30. 0); house(); 8

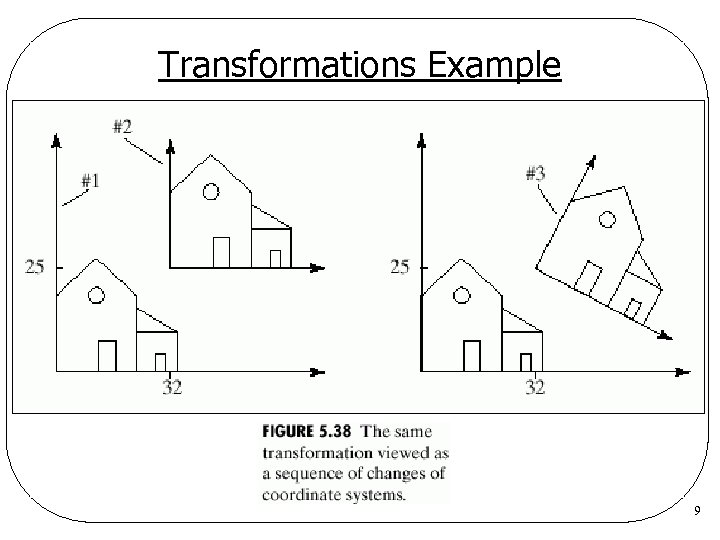Transformations Example 9

Transformations Example l Think of it in two different ways z. Q =T(32, 25)R(-30)P CT = CT T(32, 25) R(-30) z. Translate the coordinate system through (32, 25) and then rotate it through – 30° The code generated by these two ways is identical. l More examples l z. Examples 5. 5. 1, 5. 5. 2, 5. 5. 3, and 5. 5. 4 10

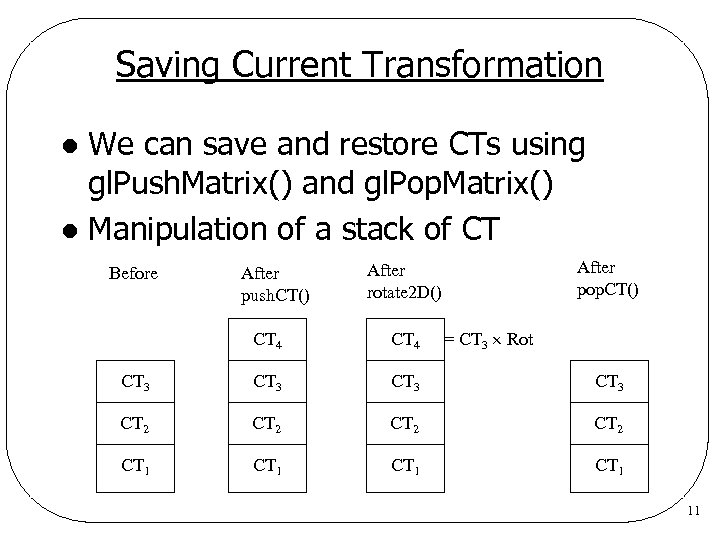Saving Current Transformation We can save and restore CTs using gl. Push. Matrix() and gl. Pop. Matrix() l Manipulation of a stack of CT l Before After push. CT() After pop. CT() After rotate 2 D() = CT 3 Rot CT 4 CT 3 CT 2 CT 1 11

Saving Current Transformation l Canvas functions zvoid Canvas: : push. CT(void) { gl. Matrix. Mode(GL_MODELVIEW); gl. Push. Matrix(); } zvoid Canvas: : pop. CT(void) { gl. Matrix. Mode(GL_MODELVIEW); gl. Pop. Matrix(); } 12

Saving CT Examples Example 5. 5. 5 l Example 5. 5. 6 l z. Master coordinate system: where an object is defined z. Modeling transformation: transforms an object from its master coordinate system to world coordinate system to produce an instance z. Instance: a picture of an object in the scene 13

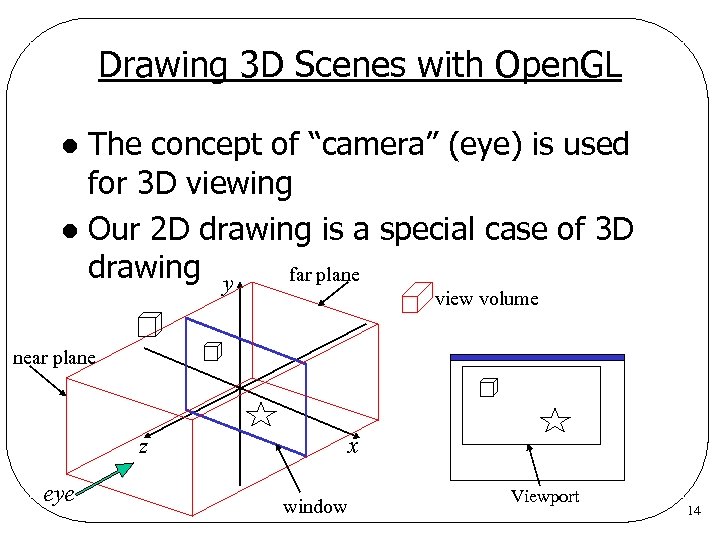Drawing 3 D Scenes with Open. GL The concept of “camera” (eye) is used for 3 D viewing l Our 2 D drawing is a special case of 3 D drawing y far plane l view volume near plane z eye x window Viewport 14

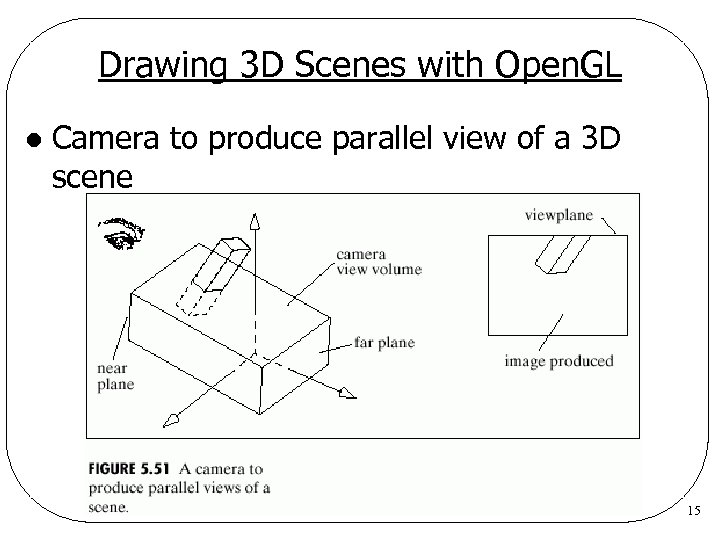Drawing 3 D Scenes with Open. GL l Camera to produce parallel view of a 3 D scene 15

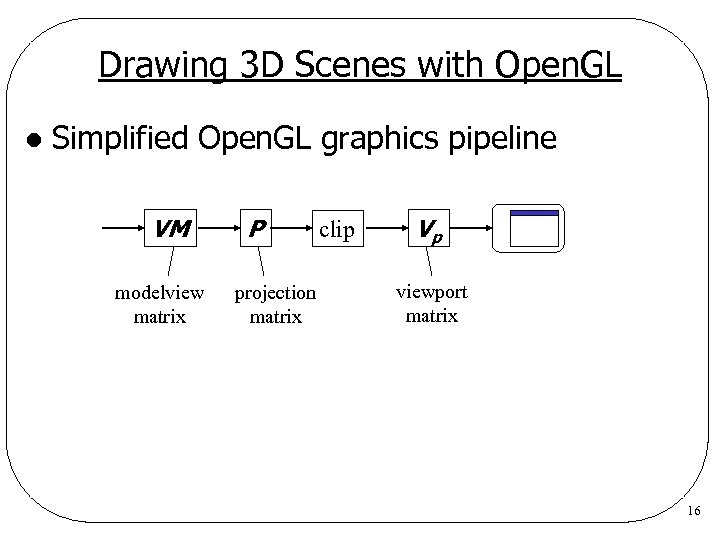Drawing 3 D Scenes with Open. GL l Simplified Open. GL graphics pipeline VM modelview matrix P projection matrix clip Vp viewport matrix 16

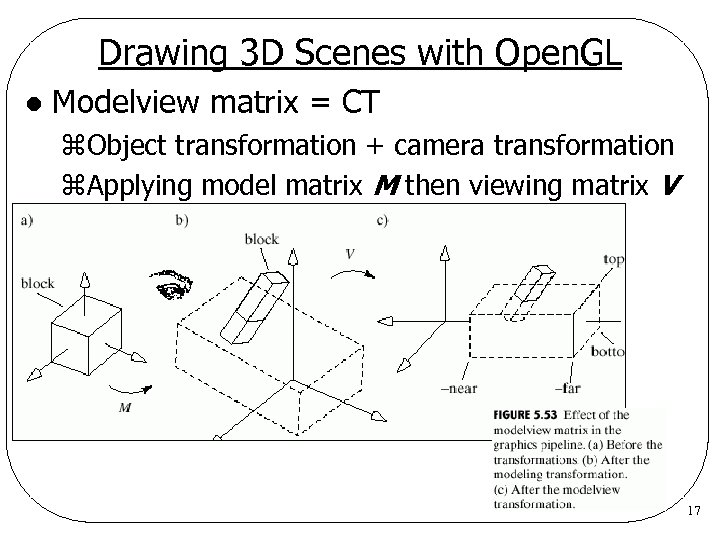Drawing 3 D Scenes with Open. GL l Modelview matrix = CT z. Object transformation + camera transformation z. Applying model matrix M then viewing matrix V 17

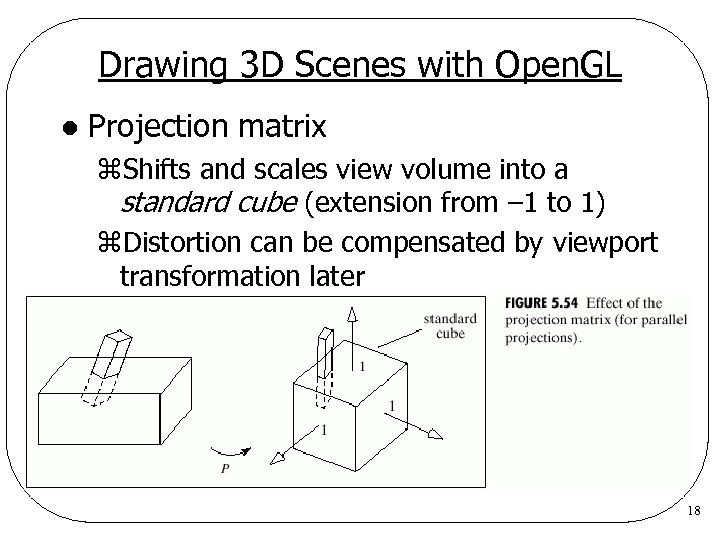Drawing 3 D Scenes with Open. GL l Projection matrix z. Shifts and scales view volume into a standard cube (extension from – 1 to 1) z. Distortion can be compensated by viewport transformation later 18

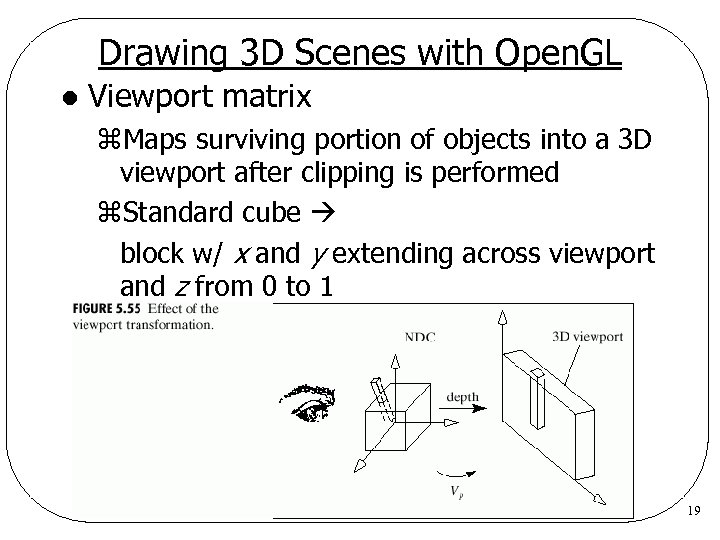Drawing 3 D Scenes with Open. GL l Viewport matrix z. Maps surviving portion of objects into a 3 D viewport after clipping is performed z. Standard cube block w/ x and y extending across viewport and z from 0 to 1 19

Open. GL Modeling and Viewing Functions l Modeling transformation z. Translation: gl. Translated(dx, dy, dz) z. Scaling: gl. Scaled(sx, sy, sz) z. Rotation: gl. Rotated(angle, ux, uy, uz) l Camera for parallel projection zgl. Matrix. Mode(GL_PROJECTION); gl. Load. Identity(); gl. Ortho(left, right, bottom, top, near, far) z. Example ynear=2: near plane is 2 units in front of eye far=20: far plane is 20 units in front of eye 20

Open. GL Modeling and Viewing Functions l Positioning and aiming camera zgl. Matrix. Mode(GL_MODELVIEW); gl. Load. Identity(); glut. Look. At(eye. x, eye. y, eye. z, // eye position look. x, look. y, look. z, // look at point up. x, up. y, up. z) // up vector z. Up vector is often set to (0, 1, 0) l glut. Look. At() builds a matrix that converts world coordinates into eye coordinates. 21

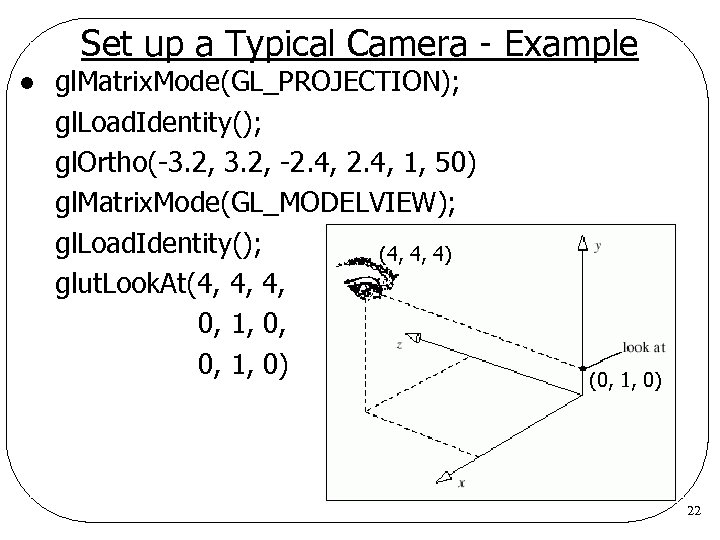Set up a Typical Camera - Example l gl. Matrix. Mode(GL_PROJECTION); gl. Load. Identity(); gl. Ortho(-3. 2, -2. 4, 1, 50) gl. Matrix. Mode(GL_MODELVIEW); gl. Load. Identity(); (4, 4, 4) glut. Look. At(4, 4, 4, 0, 1, 0) (0, 1, 0) 22

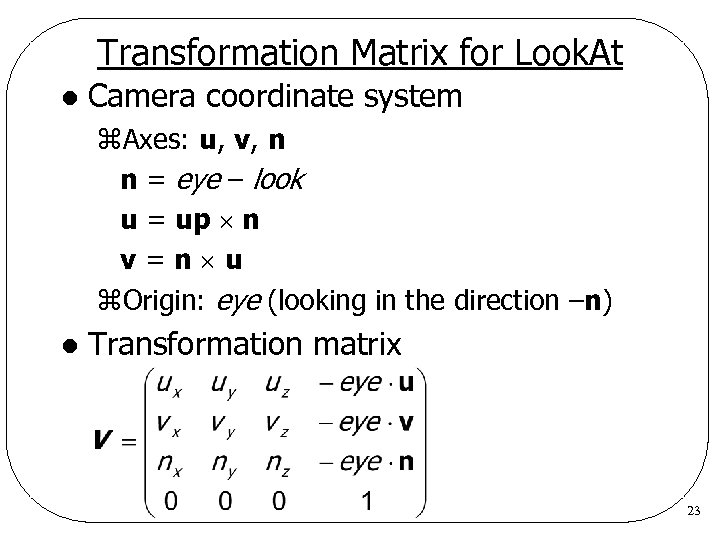Transformation Matrix for Look. At l Camera coordinate system z. Axes: u, v, n n = eye – look u = up n v=n u z. Origin: eye (looking in the direction –n) l Transformation matrix 23

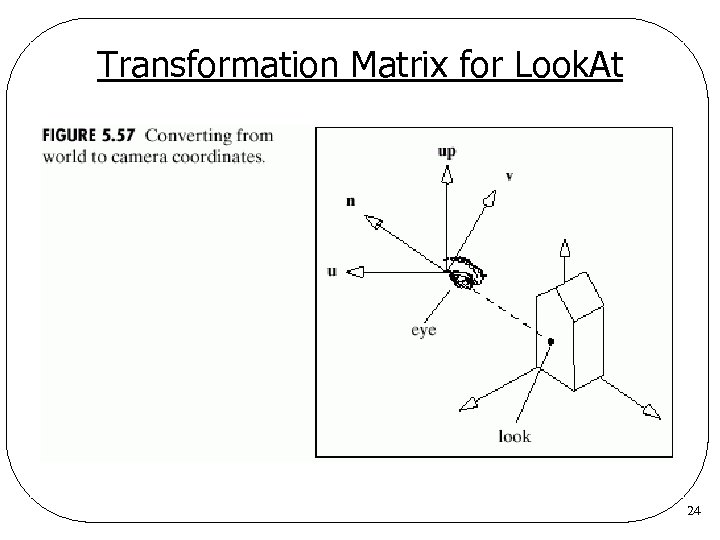Transformation Matrix for Look. At 24

Elementary 3 D Shapes Provided by Open. GL l Cube zglut. Wire. Cube(GLdouble size) zsize = length of a side l Sphere zglut. Wire. Sphere(GLdouble radius, GLint n. Slices, GLint n. Stacks) z. Approximated by polygonal faces zn. Slices = #polygons around z-axis zn. Stacks = #bands along z-axis 25

Elementary 3 D Shapes Provided by Open. GL l Torus zglut. Wire. Torus(GLdouble in. Rad, GLdouble out. Rad, GLint n. Slices, GLint n. Stacks) z. Approximated by polygonal faces l Teapots zglut. Wire. Teapot(GLdouble size) l There are solid counterparts of the wire objects 26

Plantonic Solids Provided by Open. GL l Tetrahedron zglut. Wire. Tetrahedron() l Octahedron zglut. Wire. Octahedron() l Dodecahedron zglut. Wire. Dodecahedron() l Icosahedron zglut. Wire. Icosahedron() l All of them are centered at the origin 27

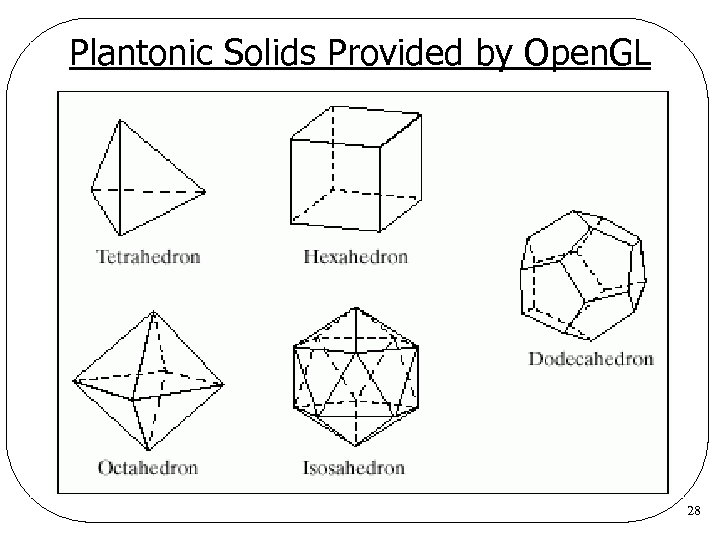Plantonic Solids Provided by Open. GL 28

Cone Provided by Open. GL l Cone zglut. Wire. Cone(GLdouble base. Rad, GLdouble height, GLint n. Slices, GLint n. Stacks) Axis coincides with the z-axis l Base rests on xy-plane and extends to z = height l base. Rad: radius at z = 0 l 29

Tapered Cylinder Provided by Open. GL l Tapered cylinder zglu. Cylinder(GLUquadric. Obj *qobj, GLdouble base. Rad, GLdouble top. Rad, GLdouble height, GLint n. Slices, GLint n. Stacks) Axis coincides with the z-axis l Base rests on xy-plane and extends to z = height l base. Rad: radius at z = 0 l top. Rad: radius at z = height l 30

Tapered Cylinder Provided by Open. GL A family of shapes distinguished by the value of top. Rad l To draw, we have to l z. Deifne a new quadric object z. Set drawing style y. GLU_LINE: wire frame y. GLU_FILL: solid rendering z. Draw the object 31

Tapered Cylinder Provided by Open. GL l Example – wire frame cylinder z. GLUquadric. Obj *qobj; qobj = glu. New. Quadric(); glu. Quadric. Draw. Style(qobj, GLU_LINE); glu. Cylinder(qobj, base. Rad, top. Rad, height, n. Slices, n. Stacks); l Study Example 5. 6. 2 32

33

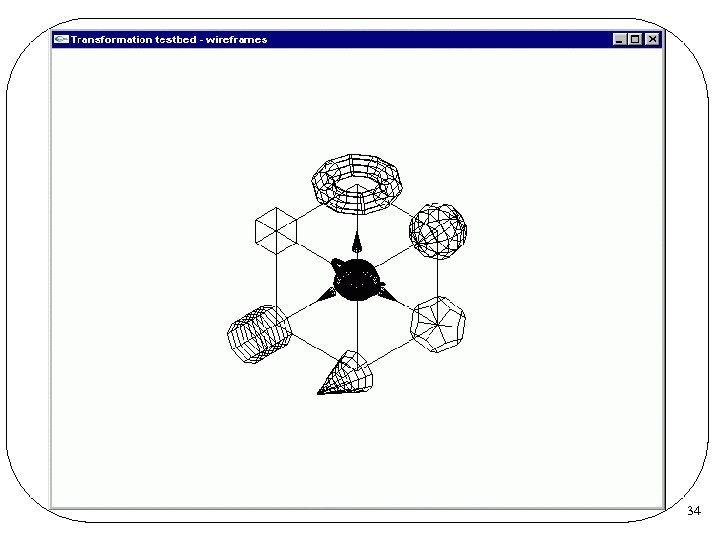34

#include //<<<<<<<<<< axis >>>>>>> void axis(double length) { // draw a z-axis, with cone at end gl. Push. Matrix(); gl. Begin(GL_LINES); gl. Vertex 3 d(0, 0, 0); gl. Vertex 3 d(0, 0, length); // along the z -axis gl. End(); gl. Translated(0, 0, length -0. 2); glut. Wire. Cone(0. 04, 0. 2, 12, 9); gl. Pop. Matrix(); } 35

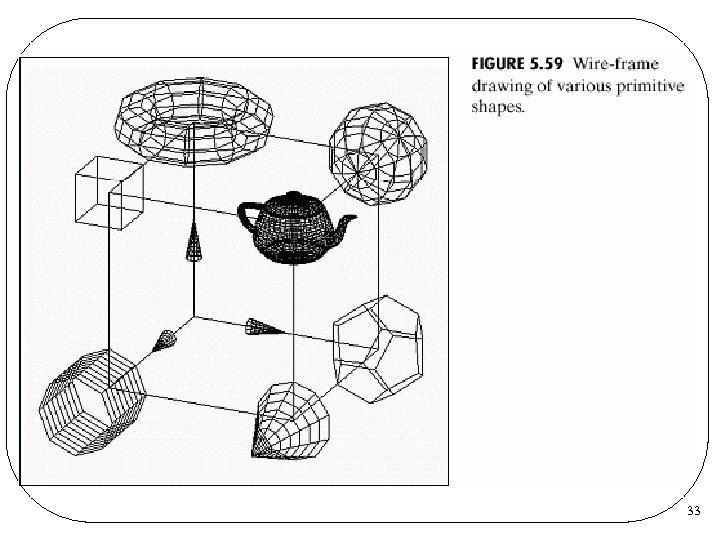
//<<<<<<< display. Wire >>>>>>> void display. Wire(void) { gl. Matrix. Mode(GL_PROJECTION); // set the view volume shape gl. Load. Identity(); gl. Ortho(-2. 0*64/48. 0, -2. 0, 0. 1, 100); gl. Matrix. Mode(GL_MODELVIEW); // position and aim the camera gl. Load. Identity(); glu. Look. At(2. 0, 0. 0, 1. 0, 0. 0); // to obtain the picture shown in Figure 5. 59 we have to // change the eye location as follows // glu. Look. At(1. 0, 2. 0, 0. 0, 1. 0, 0. 0); 36

gl. Clear(GL_COLOR_BUFFER_BIT); // clear the screen gl. Color 3 d(0, 0, 0); // draw black lines axis(0. 5); // z-axis gl. Push. Matrix(); gl. Rotated(90, 0, 1, 0); axis(0. 5); // x-axis gl. Rotated(-90, 1, 0, 0); axis(0. 5); // y-axis gl. Pop. Matrix(); gl. Push. Matrix(); gl. Translated(0. 5, 0. 5); // big cube at (0. 5, 0. 5) glut. Wire. Cube(1. 0); gl. Pop. Matrix(); 37

gl. Push. Matrix(); gl. Translated(1. 0, 0); // sphere at (1, 1, 0) glut. Wire. Sphere(0. 25, 10, 8); gl. Pop. Matrix(); gl. Push. Matrix(); gl. Translated(1. 0, 0, 1. 0); // cone at (1, 0, 1) glut. Wire. Cone(0. 2, 0. 5, 10, 8); gl. Pop. Matrix(); gl. Push. Matrix(); gl. Translated(1, 1, 1); glut. Wire. Teapot(0. 2); // teapot at (1, 1, 1) gl. Pop. Matrix(); 38

gl. Push. Matrix(); gl. Translated(0, 1. 0 , 0); // torus at (0, 1, 0) gl. Rotated(90. 0, 1, 0, 0); glut. Wire. Torus(0. 1, 0. 3, 10); gl. Pop. Matrix(); gl. Push. Matrix(); gl. Translated(1. 0, 0 , 0); // dodecahedron at (1, 0, 0) gl. Scaled(0. 15, 0. 15); glut. Wire. Dodecahedron(); gl. Pop. Matrix(); 39

gl. Push. Matrix(); gl. Translated(0, 1. 0); // small cube at (0, 1, 1) glut. Wire. Cube(0. 25); gl. Pop. Matrix(); gl. Push. Matrix(); gl. Translated(0, 0 , 1. 0); // cylinder at (0, 0, 1) GLUquadric. Obj * qobj; qobj = glu. New. Quadric(); glu. Quadric. Draw. Style(qobj, GLU_LINE); glu. Cylinder(qobj, 0. 2, 0. 4, 8, 8); gl. Pop. Matrix(); gl. Flush(); } 40

//<<<<<<<< main >>>>>>>> void main(int argc, char **argv) { glut. Init(&argc, argv); glut. Init. Display. Mode(GLUT_SINGLE | GLUT_RGB ); glut. Init. Window. Size(640, 480); glut. Init. Window. Position(100, 100); glut. Create. Window("Transformation testbed - wireframes"); glut. Display. Func(display. Wire); gl. Clear. Color(1. 0 f, 0. 0 f); // background is white gl. Viewport(0, 0, 640, 480); glut. Main. Loop(); } 41