CS 395 T Formal Model for Secure Key

CS 395 T Formal Model for Secure Key Exchange

Main Idea: Compositionality u. Protocols don’t run in a vacuum • Security protocols are typically used as building blocks in a larger secure system • For example, a key exchange protocol such as IKE can be used to implement secure sessions u. A protocol can be “correct” when used in standalone mode, but completely broken when used as a building block in a larger system u. Objective: modular, composable definitions of protocol security

“Compositional” Definition of Security Read and understand this paper! [Shoup ’ 99] u. Definition should describe guarantees provided by a key exchange protocol to higher-level protocols • Security properties must hold in any environment in which the key exchange protocol is used u. Different types of attack • Static corruptions: adversary may operate under aliases, but honest users remain honest • Adaptive corruptions: adversary corrupts honest users – Learns either the long-term secret, or all of user’s internal data u. Support anonymous (password-only) users

Station-to-Station Protocol gx mod p k=gxy A gy mod p, enck(sig. B(gx, gy)) [Diffie et al. ’ 92] k=gxy B enck(sig. A(gx, gy)) Interleaving attack: Adversary replays B’s own encryption back to B. Result: B thinks he is talking to himself, A thinks he is talking to B. This encryption is critical. Without it, adversary can send sig. C(gx, gy). Result: B thinks he is talking to C, while sharing a key with A, who thinks he is talking to B.

Protocol Interference Attack u. What if, in addition to STS, A executes some protocol where this interaction takes place: A Random challenge m enck(m) Adversary picks sig. C(gx, gy) as m, and learns enck(sig. C(gx, gy)) , which he passes to B in the STS protocol, convincing B that B is talking to C. u. Problem: challenge-response protocols may be used as encryption oracles by the adversary u. Problem: “hijacking” of honest user’s public key • Fool CA into binding A’s public key to a different identity

Simulatability u. Security is indistinguishability between the ideal world and the real world u. In the ideal world, the protocol is secure by design • Key are distributed “magically” (no communication) u. The real protocol is secure if it can be simulated in the ideal world • Intuitively, this means that the real protocol leaks no more information than a protocol with “magic” channels • Transcripts (records of everything that happened) should be indistinguishable between the real world and a simulation in the ideal world

Ideal World u. Adversary creates and connects user instances • Users magically obtain secret keys that are hidden from the adversary • If users are “connected, ” then they magically share a common key which is hidden from the adversary • Adversary does not learn any information about the keys except what is leaked through their use u. No cryptography, no certificates, no messages u. Pure abstraction of the service that key exchange protocol provides to higher-level protocols

Adversary and Ring Master u. Define a game between the adversary and the “ring master” • Ring master generates random values and executes operations issued by the adversary • Interaction between the ring master and the adversary models permissible information leakage from protocol u. Operations allow the adversary to set up a secure session in the ideal world • Create users and user instances • Create and abort sessions between user instances • Apply a function

Ideal World: User Instances u. Initialize. User(i, IDi) • Assign unique identity (bit string) IDi to the ith user • User in the ideal world is simply a placeholder; he does not actually do anything – Recall that session keys will be created magically u. Initialize. User. Instance(i, j, roleij, PIDij) • Same user may participate in multiple instances of the same protocol • Iij is the identity of the new instance, which is communicating with some counterparty PIDij Adversary creates an instance • roleij is either 0, or 1 of user i who will be talking to an instance of user j.

Ideal World: Session Key Generation u. Start. Session(i, j, , [adversary. Key]) Only permitted if PID ij hasn’t been assigned (static corruptions only) • Create: ring master generates Kij as random bit string • Connect(i’, j’): ring master sets Kij equal to Ki’j’ • Compromise: ring master sets Kij equal to adversary. Key – “Create” models creation of a brand-new session key to be used between the ith and jth user – “Connect” models establishment of this session (the key magically becomes known to both user instances) – “Compromise” models adversary’s corruption of a user • Add Start. Session(i, j) to the transcript u. Abort. Session(i, j) • This models failed attempt to establish a session

Ideal World: Information Leakage u. Application(f) • Ring master gives to the adversary f(R, {Kij}) where R is some known random bit string and {Kij} is the set of all session keys. This is recorded in transcript. – f is a function or a program, may have side effects • Intuitively, function f defines what adversary may be able to learn after shared key has been established – For example, he may able to learn ciphertexts computed by user using some randomized symmetric cipher and the new key. We encode this cipher as function f. u. Implementation(comment) • Adversary puts arbitrary bit string into transcript

Real World: Registering Identities u. Initialize. User(i, IDi) • Assign unique identity (bit string) IDi to the ith user • User registers his identity with trusted third party T via protocol-specific, probabilistic registration routine – This models issuance of a public-key certificate u. Register(ID, registration. Request) Not in the ideal world! • Adversary runs registration protocol directly with T, using protocol-specific registration. Request bitstring – This models PKI attacks: adversary obtains a certificate for an identity of his choice • The sets of identities in Initialize. User and Register must be disjoint

Real World: User Instances u. Initialize. User. Instance(i, j, roleij, PIDij) • Iij is the identity of the new instance, which is communicating with some counterparty PIDij • roleij is either 0, or 1 • User instance is a probabilistic state machine. Upon delivery of a message, it updates its state, generates a response message and reports status: – Continue: prepared to receive another message – Accept: finished & has generated session key Kij – Reject: finished & refuses to generate session key In the ideal world, user instances are placeholders

Real World: Messages u. Deliver. Message(i, j, in. Msg) • Adversary delivers message in. Msg to user instance Iij • User instance updates its state, generates response message out. Msg and reports its status – This models active interaction between the adversary controlling the network and the user in actual protocol • The following is recorded in the transcript: – Implementation(Deliver. Message, i, j, in. Msg, out. Msg, status) – Start. Session(i, j) if status=accept This is used to simulate real– Abort. Session(i, j) if status=reject world messages in ideal world u. Deliver. Message. To. TTP(in. Msg) (no messages in ideal world!) • Adversary delivers in. Msg to T and receives out. Msg

Real World: Higher-Level Protocols u. Application(f) • Same in the real world as in the ideal world, except that f(R, {Kij}) is computed as a function of actual session keys {Kij} and random input R – R is independent of any randomness used in initialization of user instances and protocol execution • As in the ideal world, add Application(f, f(R, {Kij})) to the transcript

Definition of Security u. Termination • Any real-world user instances terminates after a receiving a polynomially-bounded number of messages u. Liveness • If adversary faithfully delivers msgs between two realworld user instances, they accept & share same key u. Simulatability • For any efficient real-world adversary A, there exists an efficient ideal-world adversary A’ such that transcripts Real. World(A) and Ideal. World(A’) are computationally indistinguishable

Discussion u. Compositionality is much more than key secrecy • Application operation allows keys to be used in an arbitrary way by higher-level protocols – Can encode any higher-level key-based functionality as some function f, and then add Application(f) to the transcript • The real protocol is indistinguishable from the ideal functionality regardless of how keys are used later on – Can use key exchange protocol as it were perfectly secure u. Adversary’s freedom to set up connections in the ideal world is illusory • To simulate a secure real-world protocol, connections will have to be set up in a very specific way

Simple Exercise u. Prove that protocol cannot satisfy simulatability if real-world adversary A can output session key after it has been established, but not yet used • Using constant f in Application, A records his guess of the key in the transcript. Using identity as f in Application, he has ring master record the actual key. • In real world, they are always equal – By assumption, A knows the key in the real world • In ideal world, they are equal with negligible probability – Key is generated randomly by ring master • This immediately gives a statistical test to distinguish the real and the ideal world

Crypto Review: DDH Assumption u. Let’s review some crypto G is a group of large prime order q For g 1, g 2, u 1, u 2 G define DHP(g 1, g 2, u 1, u 2) = 1 if x Zq s. t. u 1=g 1 x, u 2=g 2 x 0 otherwise u. Decisional Diffie-Hellman (DDH) Assumption says that there exists no efficient algorithm for computing DHP correctly with negligible error probability on all inputs

More DDH u. The following is implied by the DDH Assumption: Distributions g, {gxi}, {gyj}, {gxiyj} and g, {gxi}, {gyj}, {gzij} where 1 i n, 1 j m, g, xi, yj, zij random are computationally indistinguishable u. DDH and Leftover Hash Lemma imply that the following are computationally indistinguishable: g, gx, gy, k, Hk(gxy) and g, gx, gy, k, K where K is random bit string

Security of Digital Signatures It is infeasible for adversary to win following game: 1. Signing key is generated and given to the signing oracle. The corresponding public key is given to the adversary. 2. Adversary requests signatures on any messages of his choice. Messages may depend on received signatures. 3. Adversary wins the game if he outputs a message other than those on which he previously requested signatures along with a valid signature on that message. This is known as security against existential forgery

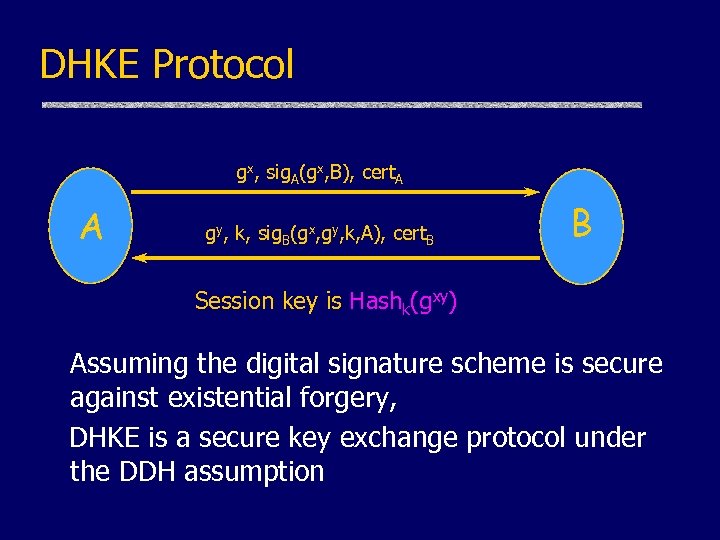DHKE Protocol gx, sig. A(gx, B), cert. A A gy, k, sig. B(gx, gy, k, A), cert. B B Session key is Hashk(gxy) Assuming the digital signature scheme is secure against existential forgery, DHKE is a secure key exchange protocol under the DDH assumption

Proof of Simulatability u. Given real-world adversary A, construct ideal-world adversary A’ who simulates protocol execution to A • A should not be able to tell whether he is in the real or ideal (perfectly secure) world – Prove that no probab. poly-time test can distinguish transcript of real-world protocol execution from a simulation created by A’ u. Basic idea: A’ runs A as a subroutine • When a session is established in the real world, A’ “connects” corresponding user instances in ideal world • Ring master in the ideal world substitutes real-world session keys with randomly generated ideal keys u. Must prove that key substitutions are undetectable

DHKE: Security for Responder (1) u. Suppose user instance B received 1 st message and accepted u. If PIDB is not assigned to user, then “compromise” B in the ideal world • PIDB is initiator’s identity (in responder’s view) – PIDB not assigned means that the protocol is being executed with the adversary (or adversary-controlled user) as initiator • Extract session key from the responder in the real world, and use it as argument to the “compromise” operation in the ideal world

DHKE: Security for Responder (2) u. If PIDB has been assigned to user, then “create” B in the ideal world • This means that the protocol is being executed with an honest user as the initiator • “Create” models key creation in ideal world. Ring master creates a random session key for B. In the real world, the key is not random. It is computed as Hashk(gxy). u. DDH Assumption and Leftover Hash Lemma imply that Hashk(gxy) is computationally indistinguishable from a random key even if gx, gy, and k are known

DHKE: Security for Responder (3) u. The indistinguishability argument only works if A has not been, nor ever will be compromised u. Fortunately, “compromised” connections are not allowed if PIDA has been assigned • PIDA is responder’s identity (in initiator’s view). Because initiator sent 1 st message to B, this means that PIDA=B and “compromise” is not allowed. • Intuition: corruptions are static. Once honest A starts talking to B, he cannot be compromised.

DHKE: Security for Initiator (1) u. Suppose user instance A received 2 nd message and accepted u. If PIDA is not assigned to any user, then “compromise” A in the ideal world • PIDA is responder’s identity (in initiator’s view) – PIDA not assigned means that the protocol is being executed with the adversary (or adversary-controlled user) as responder • Extract session key from the responder in the real world, and use it as argument to the “compromise” operation in the ideal world

DHKE: Security for Initiator (2) u. If PIDA has been assigned to user B, then “connect” A and B in the ideal world • Protocol is being executed with honest responder B • “Connect” magically gives B’s random session key to A u. Security of digital signature scheme guarantees that A’s and B’s values of gx, gy, and k match • Therefore, A’s and B’s keys are equal in the real world u. There is no detectable difference between worlds • A’s and B’s keys are equal in both worlds • In ideal world, keys are random. In real world, they are DH values, but this is not computationally detectable

Crypto Review: Non-Malleability Same as CCA-2 indistinguishability, i. e. , adversary’s probability of winning following game is close to ½: 1. Adversary requests encryption of any plaintext and/or decryption of any ciphertext 2. Adversary picks two plaintexts m 0 and m 1, and receives an encryption of mb (b is a randomly chosen bit) 3. Adversary requests encryption of any plaintext and/or decryption of any ciphertext except that returned in step 2 4. Adversary wins if he outputs b’=b Non-malleability says adversary can neither learn plaintext, nor modify it

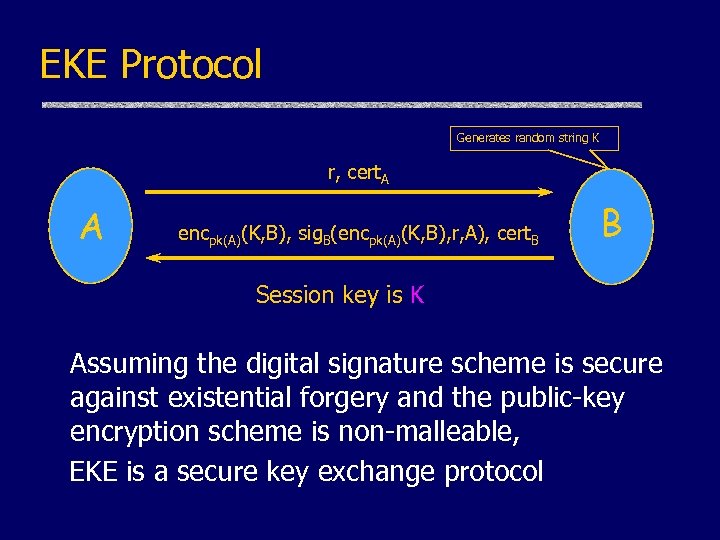EKE Protocol Generates random string K r, cert. A A encpk(A)(K, B), sig. B(encpk(A)(K, B), r, A), cert. B B Session key is K Assuming the digital signature scheme is secure against existential forgery and the public-key encryption scheme is non-malleable, EKE is a secure key exchange protocol

EKE: Security for Responder (1) u. Suppose user instance B received 1 st message and accepted u. If PIDB is not assigned to user, then “compromise” B in the ideal world • PIDB is initiator’s identity (in responder’s view) – PIDB not assigned means that the protocol is being executed with the adversary (or adversary-controlled user) as initiator • Extract session key from the responder in the real world, and use it as argument to the “compromise” operation in the ideal world

EKE: Security for Responder (2) u. If PIDB has been assigned to user, then “create” B in the ideal world • This means that the protocol is being executed with an honest user as the initiator • In the ideal world, ring master creates a random session key for B. This key is not equal to the key that B sent to A under encryption in the real world. u. Real-world adversary cannot tell the difference between a random key generated by ring master and the key that B sent under encryption • Holds only if ciphertext sent by B is never decrypted • Proving this will rely on non-malleability

EKE: Security for Initiator (1) u. Suppose user A received 2 nd message, but PIDA has not been assigned to a user u. If encpk(A)(K, B’) was generated by B’, A rejects • Some honest user B’ thinks he is responding to A, but his identity doesn’t match identity PIDA expected by A • Rejection does not require decrypting encpk(A)(K, B’) – This is important! Otherwise, ideal-world adversary would not know when to tell the ideal-world instance of A to reject. u. If encpk(A)(K, B’) not from another user, let A run. If A accepts, “compromise” A and extract key. • Requires decrypting encpk(A)(K, B’). This is Ok, since it was not created by an honest user.

EKE: Security for Initiator (2) u. If PIDA has been assigned to user B, then “connect” A and B in the ideal world • If signature verifies correctly, then encpk(A)(K, B) must have been created by B who thinks he is talking to A – Recall that A’s identity is signed by B • No need to decrypt the ciphertext • Connection is valid because random values r are unique u. There is no detectable difference between worlds • A’s and B’s keys are equal in both worlds

Anonymous Users u. Add user with special “anonymous” identity • Treat all anonymous users as a single user u. Start. Session(i, j, Compromise, adversary. Key) is legal if PIDij=“anonymous” • An anonymous user may be the adversary himself, so permit adversary to compromise anonymous users u. Simulatability-based definition of security naturally supports password protocols • Use secure key exchange to establish a secure channel, then authenticate with password on this channel • Like any other functionality based on secure sessions

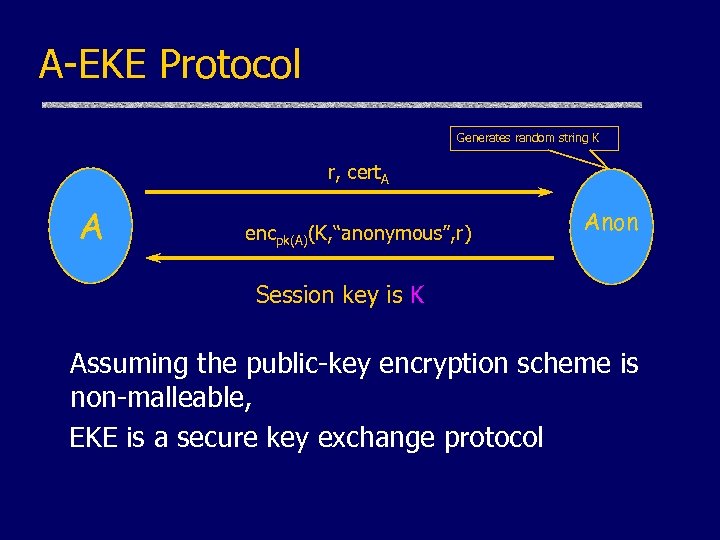A-EKE Protocol Generates random string K r, cert. A A encpk(A)(K, “anonymous”, r) Anon Session key is K Assuming the public-key encryption scheme is non-malleable, EKE is a secure key exchange protocol

A-EKE: Security for Initiator u. Suppose PIDA=“anonymous” • Initiator thinks he is talking to the anonymous user u. If encpk(A)(K, “anonymous”, r) was not generated by “anonymous”, let A run. If A accepts, compromise A and extract key. • Requires decrypting encpk(A)(…). This is Ok, since it was not created by an honest user with identity. u. If encpk(A)(K, “anonymous”, r) was generated by “anonymous” and r received by “anonymous” matches r sent by A, connect. u. If r does not match, reject.

Adaptive Corruptions u. Users may be corrupted during protocol execution • Adversary learns user’s long-term secret (private key) • Strong adaptive corruptions: learns user’s entire state u. Corrupt. User(i) operation in the ideal world • Gives no information to ideal-world adversary u. Start. Session(i, j, Compromise, …) is legal if PIDij is assigned to corrupt user or user Ui is corrupt • Compromise is now allowed if either party in the protocol session is corrupt u. Neither DHKE, nor EKE is secure against adaptive corruptions

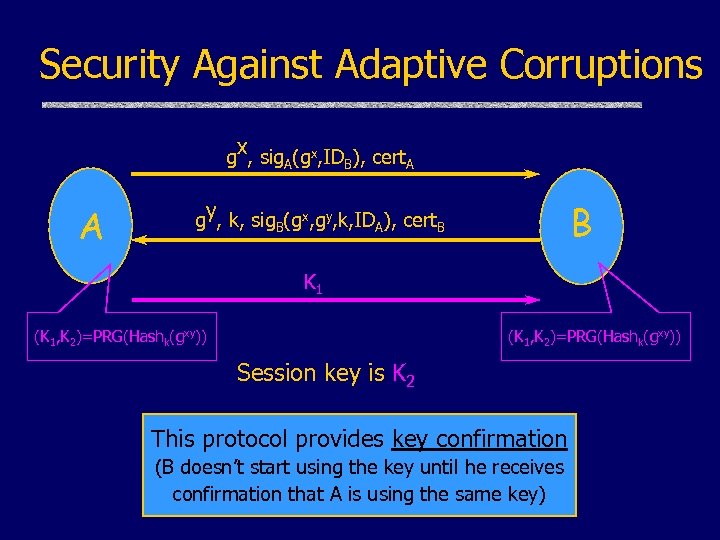Security Against Adaptive Corruptions gx, sig. A(gx, IDB), cert. A A B gy, k, sig. B(gx, gy, k, IDA), cert. B K 1 (K 1, K 2)=PRG(Hashk(gxy)) Session key is K 2 This protocol provides key confirmation (B doesn’t start using the key until he receives confirmation that A is using the same key)