CS 395 495 -25 Spring 2005 IBMR Wrapping the

CS 395/495 -25: Spring 2005 IBMR: Wrapping the world around your Camera: Warps, Morphs, Panoramas, and Mirror Spheres Jack Tumblin jet@cs. northwestern. edu

A Tour of Some Image Changes WARP DEMO: http: //www. axlrosen. net/ MORPH DEMO: http: //www. dt. org/html/morph. html PANORAMIC DEMO: http: //www. panoguide. com/publish/software/go 360. html

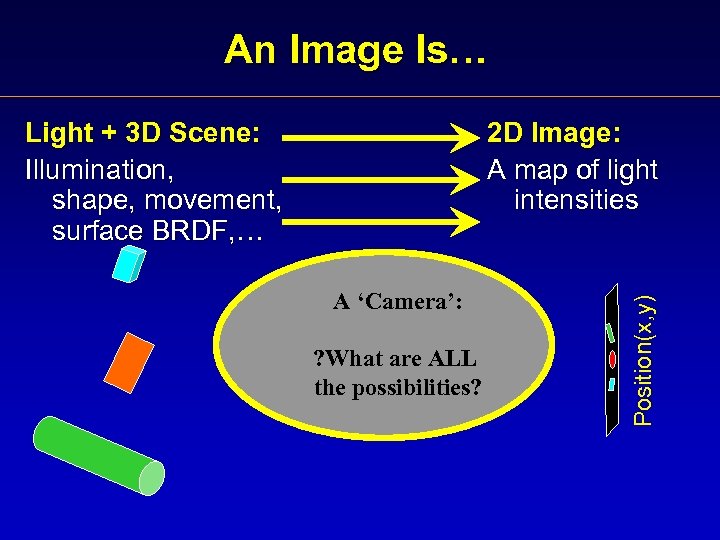
An Image Is… 2 D Image: A map of light intensities A ‘Camera’: ? What are ALL the possibilities? Position(x, y) Light + 3 D Scene: Illumination, shape, movement, surface BRDF, …

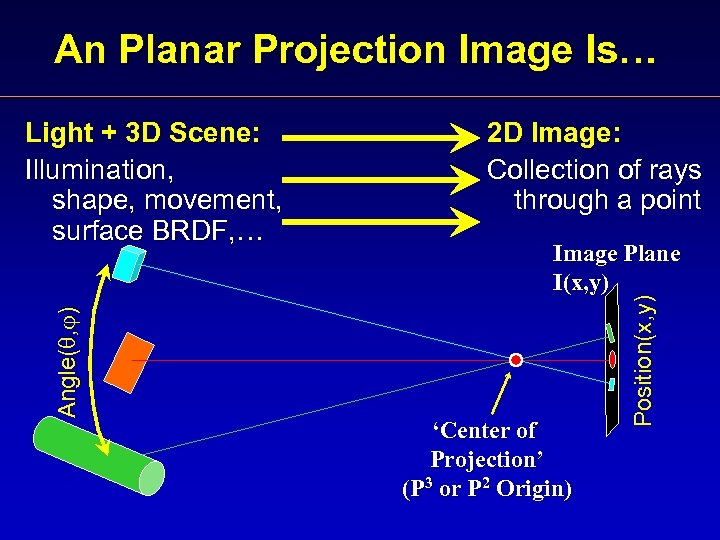
An Planar Projection Image Is… 2 D Image: Collection of rays through a point Image Plane I(x, y) ‘Center of Projection’ (P 3 or P 2 Origin) Position(x, y) Angle( , ) Light + 3 D Scene: Illumination, shape, movement, surface BRDF, …

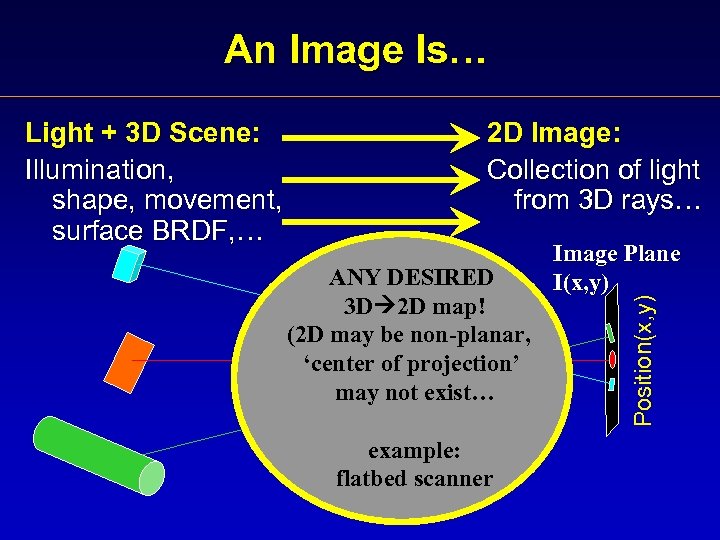
An Image Is… 2 D Image: Collection of light from 3 D rays… ANY DESIRED 3 D 2 D map! (2 D may be non-planar, ‘center of projection’ may not exist… example: flatbed scanner Image Plane I(x, y) Position(x, y) Light + 3 D Scene: Illumination, shape, movement, surface BRDF, …

‘Projective Image’ : Angle Position Map • So far: – planar perspective projection – P 2 projective transformations (P 3 soon) – how to find these transformations from images. • But Planar Perspective Projection is just ONE KIND of mapping, and • P 2 and P 3 linear projective transformation H is just ONE KIND of image warping H = HSHAHP

‘Image’ : Angle Position Map • Many kinds of camera projections: ‘Fun-House Mirrors’ – Non-planar perspective projections: • Spherical, Conical, cylindrical, hyperbolic; even ‘centerless’ projections (Rademacher, SIGG 1998) – How can we convert between them? • All Cameras have imperfect geometry. How can we dectect/correct the errors? • Warp, morph the 1 st forms of IBMR? (1980 s: I built warp/morph-based flight sim…)

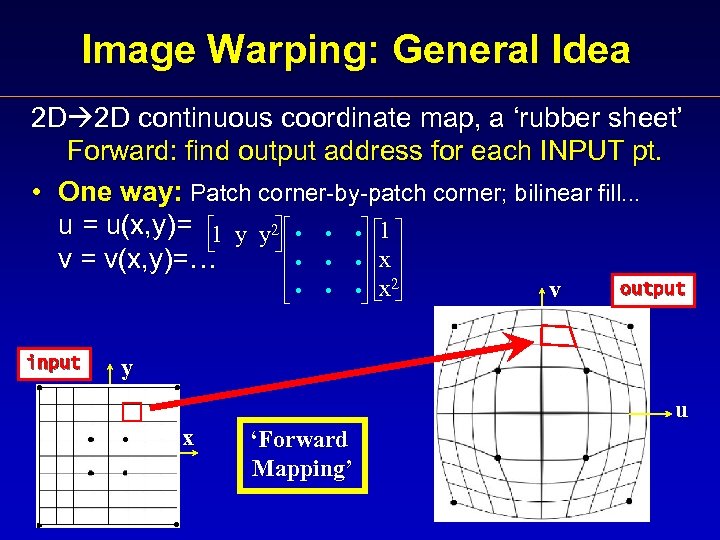
Image Warping: General Idea 2 D 2 D continuous coordinate map, a ‘rubber sheet’ Forward: find output address for each INPUT pt. • One way: Patch corner-by-patch corner; bilinear fill. . . u = u(x, y)= 1 y y 2 1 x v = v(x, y)=… input x 2 v output y u x ‘Forward Mapping’

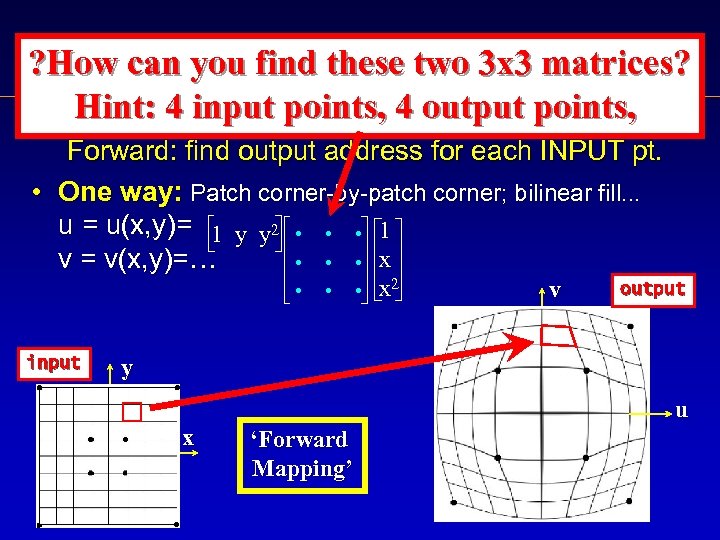
Image Warping: General Idea ? How can you find these two 3 x 3 matrices? Hint: 4 input points, 4 output points, 2 D 2 D continuous coordinate map, a ‘rubber sheet’ Forward: find output address for each INPUT pt. • One way: Patch corner-by-patch corner; bilinear fill. . . u = u(x, y)= 1 y y 2 1 x v = v(x, y)=… input x 2 v output y u x ‘Forward Mapping’

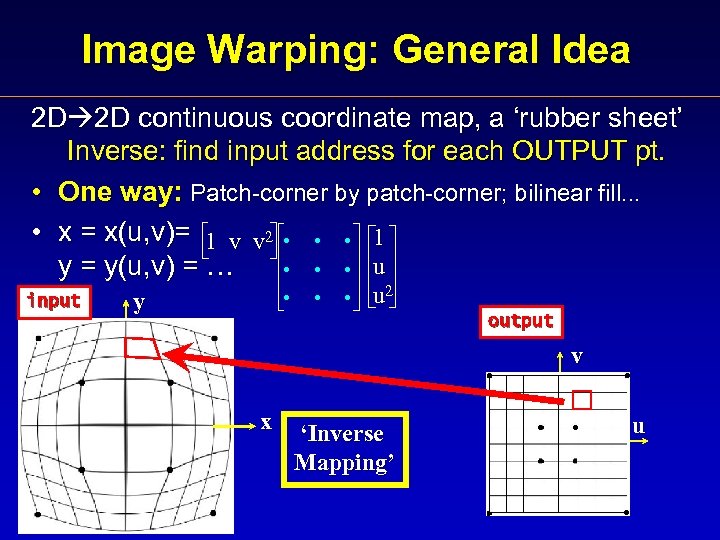
Image Warping: General Idea 2 D 2 D continuous coordinate map, a ‘rubber sheet’ Inverse: find input address for each OUTPUT pt. • One way: Patch-corner by patch-corner; bilinear fill. . . • x = x(u, v)= 1 v v 2 1 u y = y(u, v) = … input y u 2 output v x ‘Inverse Mapping’ u

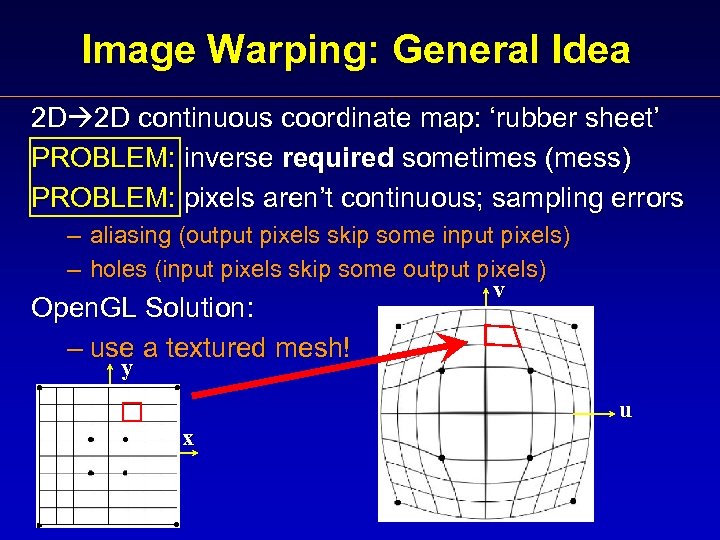
Image Warping: General Idea 2 D 2 D continuous coordinate map: ‘rubber sheet’ PROBLEM: inverse required sometimes (mess) PROBLEM: pixels aren’t continuous; sampling errors – aliasing (output pixels skip some input pixels) – holes (input pixels skip some output pixels) v Open. GL Solution : – use a textured mesh! y u x

Image Warping: IBMR Form 2 D 2 D continuous coordinate map: ‘rubber sheet’ PROBLEM: inverse required sometimes (mess) IBMR Answer: H matrix is (usually) invertible PROBLEM: pixels aren’t continuous; sampling errors IBMR Answer: Use vertices, not pixels: let Open. GL texture mapping keep the image “continuous” x 2 x 3 x 1

Further Reading on Warps: • Many Misc. SIGGRAPH tutorials, many on-line • T. Beier and S. Neely. Feature Based Image Metamorphosis. Computer Graphics (Siggraph'92 Proceedings), Vol. 26 : pages 35 --42, July 1992 • George Wolberg Digital Image Warping (book)© 1990, Wiley & Sons • Jonas Gomes, Lucia Darsa, Bruno Costa, Luiz Velho, Warping and Morphing of Graphical Objects © 1999 Morgan Kaufmann Publishers

Image Warping: IBMR Form • Projective transformation H in P 2 is a planar ‘warp’ • But many other kinds of warps possible! • P 2 change object/camera position for viewing a plane • P 3 changes object/camera postion for viewing a 3 D shape • But shape changes are limited. . .

Panoramas: Planar ‘Bow-Tie’ – – For limited-size mosaics only (angle limits) Find all H from correspondence in overlapped regions Choose a (central) reference image (Zisserman pg. 196) Reproject, cross-dissolve in reference image plane

Planar Panoramas in P 2 (or P 3) • Choose a ‘reference’ image plane, extend it • Add images: for each one, – find H from overlap correspondences (in P 2) – transform new image to reference plane – re-sample, ‘blend’ x 2 (weighted sum) to one image H 1 x 3 H 2 H 3… x 1 x 3 x 1

Panorama Making Planar: • Start with overlapped planar proj. images • Do 4 -point corresp. (or better) for alignment • Merge images by cross-dissolve: (R, G, B)out = (R, G, B)1· + (R, G, B)2·(1 - ) where: 1 = opacity of image 1 use barycentric coords linear interp within overlap: 2

Why use P 3 at all? Make Projective Images from Non-planar objects Separate camera & imaged object coordinates Separate projective x 4 from the R 3 ‘z’ coord; P 2 seems to bridge 2 D & 3 D, but doesn’t: – -z, +z axis in R 3 ‘folds back on itself’ – -x 3, +x 3 in P 2 MUST be symmetric! “P 2 is a symmetric half-space” (Zisserman) – The only +/-z is “camera’s direction of gaze” P 3 includes full, complete 3 D space; – -z, +z can be asymmetric – no ‘camera direction’ BUT ALSO: Non-Planar Panoramas. . .

Non-Planar P 2 Panoramas Can’t use planar method beyond 180° FOV; • Make spherical image: ‘wrap around’ origin • How? Spherical coords – write 3 D sphere eqn in P 2 coords: x 1 = cos( ) x 3 = -sin( )cos( ) x 2 = cos( ) =longitude, = latitude – ‘Inverse Map’ warp: • • • Output pixel m, n: = 2 n/nmax, = n/nmax - /2 Find x’ = H-1·[x 1, x 2, x 3] for each image x 1 Blend color(s) found at x’ for each image x 2 -x 3

Example: Quick. Time VR (Chen, Williams ’ 93) 1) Four Planar Images 1 Cylindrical Panorama: IN: OUT:

Example: Quick. Time VR (Chen, Williams ’ 93) 2) Windowing, Horizontal-only Reprojection: IN: OUT:

Spherical Panoramas: • Note wildly non-uniform sampling in , : Richard Szeliski et al, Microsoft Research, 1998

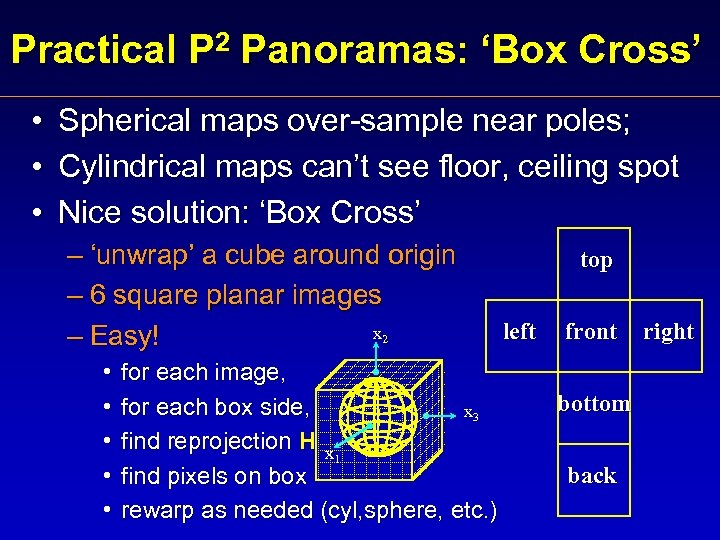
Practical P 2 Panoramas: ‘Box Cross’ • • • Spherical maps over-sample near poles; Cylindrical maps can’t see floor, ceiling spot Nice solution: ‘Box Cross’ – ‘unwrap’ a cube around origin – 6 square planar images x 2 – Easy! • • • for each image, for each box side, x 3 find reprojection H x 1 find pixels on box rewarp as needed (cyl, sphere, etc. ) top left front bottom back right

Example: Spherical Panorama a CAREFUL! EASY TO MISS SOMETHING! Paul Debevec, from SIGGRAPH 2001 short course ‘Image-Based Lighting”

Commonplace Camera Distortions Correct many camera/lens errors in P 2 • Place raw camera input at (x, y, 1) plane • Write equations for 3 D ‘projection surface’ Example: scaleable, offset sphere for spherical distortion x 1 = a+ b*sin( )cos( ); x 3 = c+ d*sin( )cos( ); x 2 = e+f*cos( ) • Scan projection surface to find output pixels x 2 Example: take equal-sized steps in ( , ); sample input image x 3 x 1

Panoramic Cameras Panoramics without ‘stitching’: • ‘Fisheye’ Lenses, conics, … • Slit-scan: (Wide. Lux, Noblex, Pano. Scan…) – cyl. or spherical image – slow! no action shots • Multiple Planar Cams – Fast, flexible, expensive – can do panor. movies • History: 1843…http: //www. panoramicphoto. com/timeline. htm

Light Probes • Example images (see Debevec’s site) Paul Debevec, SIGGRAPH 2001 course “Image Based Lighting”

Try it yourself…. Paul Debevec, SIGGRAPH 2001 short course “Image Based Lighting”

Try it yourself…. Paul Debevec, SIGGRAPH 2001 short course “Image Based Lighting” Better! We ordered 4 Chrome Spheres for IBMR students to borrow. . .

Mirror Ball Panorama Conversion Makes an offset ‘virtual’ sphere camera located at mirror ball center: • ? How can we write this in P 2 and/or P 3? Mirror Ball Camera yc xc zc ym zm xm

Mirror Ball Panorama Conversion Not Documented? !? Then figure it out… – Parameterize ball as ‘rings’ of constant – (Ignore invisible backside of sphere) – Warp 1: get ring colors from camera image Mirror Ball Camera yc ym xc zc zm xm

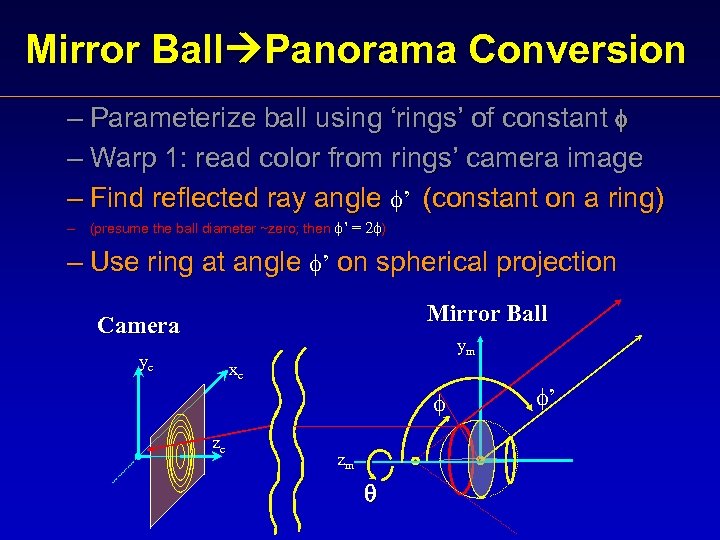
Mirror Ball Panorama Conversion – Parameterize ball using ‘rings’ of constant – Warp 1: read color from rings’ camera image – Find reflected ray angle ’ (constant on a ring) – (presume the ball diameter ~zero; then ’ = 2 ) – Use ring at angle ’ on spherical projection Mirror Ball Camera ym yc xc zc zm ’

Light Probes • ‘One-shot’ panoramic camera! • Clever, fast, simple, cheap, flexible • Probe position != Camera position; telephotos… – allows small probes in tight, risky spaces – Little/no image alignment / mosaicing • Drawbacks: – Highly non-uniform sampling – Camera ALWAYS in the image • Daydreams: a better probe? – – Huge: mirrored weather balloon? Tiny, stochastic: bubbles in a liquid? Dynamic shapes: whirling mirror on arm? Other shapes: Nayyar, Carlbom, Shum(MSRChina) etc.

END