CS 376 Introduction to Computer Graphics 03

CS 376 Introduction to Computer Graphics 03 / 02 / 2007 Instructor: Michael Eckmann

• Questions? Today’s Topics • finish with Arbitrary view examples • Review for exam • 3 D view volume clipping

Arbitrary 3 d View examples • Let's take a look at a couple of examples in the handout. • 1 st let's look at the world coordinates of the object (house) • 2 nd look at figure 6. 29 and then its results in 6. 28 • 3 rd look at figure 6. 30 which gives the same result with different parameters (change VRP, causes a required change in PRP and the Window Coordinates too to give the same result. ) • Because VRP changes, the origin of the u-v-n VRC system changes. Therefore, since PRP and CW and the umin, umax, vmin and vmax are all within VRC, they are affected.

Arbitrary 3 d View examples • Let's look at the two point perspective view given in 6. 22 • We need to orient the view plane so that it cuts both the x and z coordinate axes. See figure 6. 32 and that VPN is (1, 0, 1) which is a vector from the origin on the x-z plane at 45 degrees between the positive x and positive z axes. (I'll draw on board. ) • So, that VPN makes the view plane oriented such that it cuts both x and z axes at the same angle. What can you say about the view plane in relation to y? • The parameters as stated in the handout have the VRP at the bottom right corner of object, so that makes the view plane oriented via the VPN and positioned so that VRP is on it.

Arbitrary 3 d View examples • Also, VRP being where it is has an effect on where you place PRP and the window parameters because these are in the VRC system of which VRP (in WCS) is at the origin (in VRC).

Arbitrary 3 d View examples • In the handout description of the viewing parameters for figure 6. 34 it says all parameters are the same except view up vector is 10 degrees away from y axis. • Notice the house is tilted slightly to the right (compared to the figure 6. 22) so the up direction is tilted towards the left. • I believe that VPN would need to be in a direction 10 degrees from where it was to tilt the view plane. Changing only the direction of VUP won't do it. So, I think there's an error there. • But if we wanted to try it --- we could compute the VUP that is 10 degrees away from (0, 1, 0) --- we can keep the same x and y and solve for z of the new vector.

Arbitrary 3 d View examples • So, the dot product of v 1=(0, 1, 0) with v 2=(0, 1, z) is 1. • Then use other equation for dot product: |v 1||v 2|cos. A = 1 • |v 1| = 1 • |v 2| = sqrt(1+z*z) • So, sqrt(1+z*z) cos A = 1 • A=10 degrees. so, cos. A is about. 985 • So, sqrt(1+z*z) = 1/. 985, then square both sides to get • 1+z*z = 1. 0307, z*z = 0. 0307, then sqrt of both to get • z = 0. 175 • The handout then says Vup vector of (0, 1, 0. 175) would have that effect on the view.

Review for exam • Given v 1 = (2, 1, 0) and v 2 = (0, 5, 1) • draw them in 3 d coordinates • what is the magnitude of each? • what is their dot product? • what is the angle between them? • what is their cross product? • Given v 1 = (1, 2, 0) and v 2 = (0, 0, 17) • what is the angle between them? • Given these three points: (1, 2, 2), (1, 2, 0), (0, 2, 5) what plane do they define?

Review for exam • Given these three points: (1, 2, 2), (1, 2, 0), (0, 2, 5) what plane do they define? • recall that the cross product of [p 1 -p 2] and [p 3 -p 2] gives us a normal vector • and recall that the general equation of a plane is • Ax+By+Cz+D=0 • The (A, B, C) is a normal vector, so we can use what we calculated earlier as A, B, C • Then, to get D, – we just need to take the dot product of the normal vector with a point on the plane (any of the 3 given points). This is Ax + By + Cz. So, that number + D equals 0.

Review for exam • Produce a matrix that transforms from a 2 d window in world coordinates to a 2 d viewport. • Let's say the window in the world is from (10, 10) to (30, 50) and the viewport in screen coordinates is from (. 1, . 1) to (. 9, . 9).

Review for exam • Suppose you want to display a circle with center (4, 7) and you have the coordinates of the pixels for the 2 nd octant. How would you plot the pixels for the other 7 octants? • Is the radius necessary?

Review for exam • Suppose you want to display a circle with center (4, 7) and you have the (x, y) coordinates of the pixels for the 2 nd octant. What are the coordinates of the pixels for the other 7 octants? • we know that if the center is at the origin, then an (x, y) in octant 2 will correspond to the following pixels in the other 7 octants: – (y, x), (x, -y), (y, -x), (-x, y), (-y, x) (-x, -y), (-y, -x) • but for us, the center is at (4, 7) so we need to translate the (x, y) by (-4, -7) and then compute the 7 pixels and add (4, 7) to each before plotting • so for each pixel in the 2 nd octant, (x, y), : – (x-4, y-7) leads to the 7 pixels (with center 0) of – (y-7, x-4), (y-7, 4 -x), (x-4, 7 -y), (4 -x, y-7), – (4 -x, 7 -y), (7 -y, x-4), (7 -y, 4 -x) • then add (4, 7) to each to get the actual answer: – (y-3, x+3), (y-3, 11 -x), (x, 14 -y), (8 -x, y), – (8 -x, 14 -y), (11 -y, x+3), (11 -y, 11 -x)

Review for exam • Let's glance at the midterm topics list I sent out.

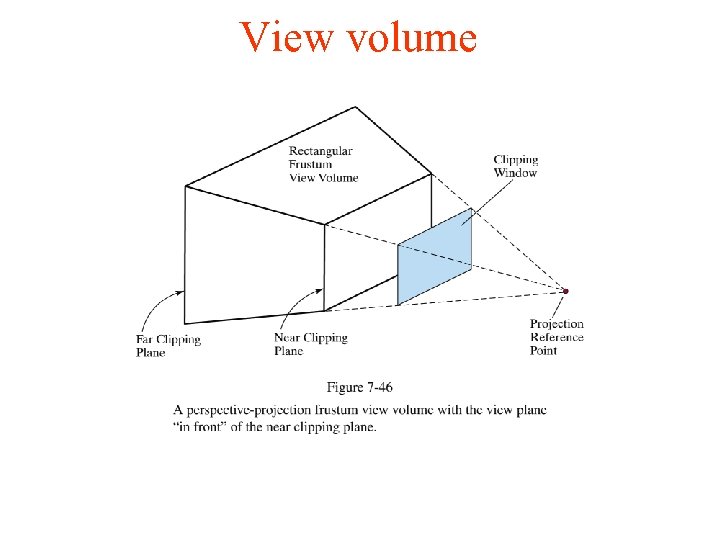View volume

3 d Clipping • The view volume on the last slide has 6 faces • For a canonical view volume the faces are the on the following planes: • x = z, x = -z, y = -z, z = -zmin, z = -1 • the 2 vertical faces (the front and back clipping planes) are on z = -zmin, z = -1 • the two side faces are on x = z, x = -z • the top and bottom faces are on y = z, y = -z • the view volume lives totally in -z, so which plane is the top face on? y = z or y = -z

3 d Clipping • Cohen Sutherland's extension into 3 d from 2 d. • A six bit (as opposed to 4 in 2 d) outcode is used here. • 1 = true, 0 = false – Bit 1 – Bit 2 – Bit 3 – Bit 4 – Bit 5 – Bit 6 = above view volume = below view volume = right of view volume = left of view volume = behind view volume = in front of view volume (y > -z) (y < z) (x > -z) (x < z) (z < -1) (z > zmin) This leads to 27 different outcode volumes See drawing on board.

3 d Clipping • Trivially accept if both endpoints have outcodes of 000000. • Trivially reject if logical AND of the outcodes of the endpoints is NOT 000000. • When would the logical AND of the outcodes NOT be 000000? • Calculate intersection with borders in order if can't trivially accept or reject. • Is it possible to have a line that cannot be trivially rejected (i. e. the AND of the outcodes is 000000) yet still be completely outside of the view volume?

3 d Clipping • the parametric equation of a line is: • x = x 0 + t (x 1 – x 0) • y = y 0 + t (y 1 – y 0) • z = z 0 + t (z 1 – z 0), 0 <= t <= 1 • To calculate the intersections of lines with the unit slope planes of the cvv, is easy. • For y = z, y 0 + t (y 1 – y 0) = z 0 + t (z 1 – z 0) and we can solve for t. Then use t to find the x and y coordinate and z = y so we already know z.

3 d Clipping • Then, once we have the x y and z coordinates of the intersection we can determine if • the intersection is actually on a face of the view volume • or the intersection is not on a face of the view volume – if the intersection is not on a face, then we exclude the portion of the line outside that plane (away from the view volume) and recalculate the region code of the intersection – if the intersection is on a face, we keep that intersection as a final endpoint and exclude the portion of the line outside that plane, recalculate region code too. • Another nice feature of this algorithm is that when given two endpoints of the line segment and their region codes, even if we can't trivially accept or reject them, we can tell which planes they intersect (when corresponding bits are different. ) Therefore, we only have to clip that line against those planes.

3 d Clipping • Calculating the intersections at unit slopes is easier than at arbitrary slopes, hence the decision to normalize to a canonical view volume. • x = x 0 + t (x 1 – x 0) • y = y 0 + t (y 1 – y 0) • z = z 0 + t (z 1 – z 0), 0 <= t <= 1 • Recall an arbitrary plane is Ax + By + Cz + D = 0 (the equation of a plane. ) • Now, it should be obvious that more calculations are involved in finding the intersection of a line with an arbitrary plane than with simple planes like y = z, z = -1, etc.