CS 347: Parallel and Distributed Data Management Notes 02: Distributed DB Design Hector Garcia-Molina CS 347 Notes 02 1
Distributed DB Design Chapter 5 Ozsu & Valduriez Top-down approach: - have DB… - how to split and allocate the sites Multi-DBs (or bottom-up): no design issues! CS 347 Notes 02 2
Two issues in DDB design: • Fragmentation • Allocation Note: issues not independent, but will cover separately CS 347 Notes 02 3
Example Employee relation E (#, name, loc, sal, …) 40% of queries: Qa: select * Qb: select * from E where loc=Sa where loc=Sb and… and. . . CS 347 Notes 02 4
Example Employee relation E (#, name, loc, sal, …) 40% of queries: Qa: select * Qb: select * from E where loc=Sa where loc=Sb and… and. . . Motivation: Two sites: Sa, Sb Qa Sa Sb Qb CS 347 Notes 02 5
• It does not take a rocket scientist to figure out fragmentation. . . CS 347 Notes 02 6
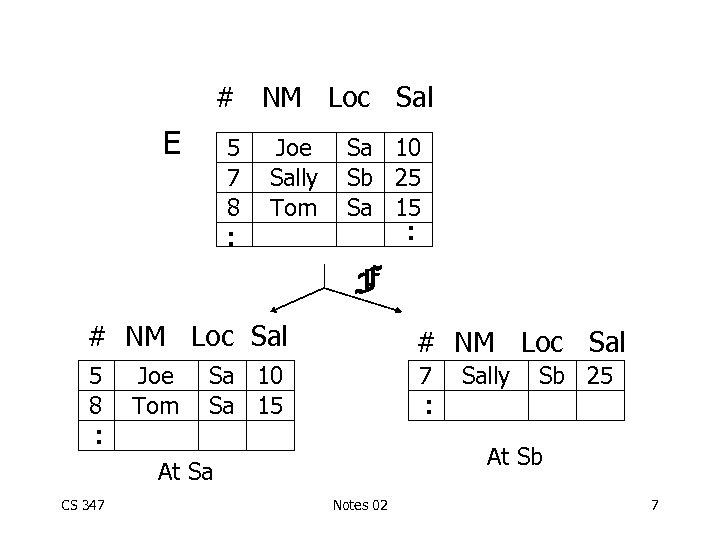
# NM Loc Sal Joe Sally Tom . . 5 7 8 Sa 10 Sb 25 Sa 15 . . E F # NM Loc Sal 5 8 7 Sb 25 At Sb At Sa CS 347 Sally . . Sa 10 Sa 15 . . Joe Tom Notes 02 7
F = { F 1, F 2 } F 1 = CS 347 loc=Sa E F 2 = Notes 02 loc=Sb E 8
F = { F 1, F 2 } F 1 = loc=Sa E F 2 = loc=Sb E called primary horizontal fragmentation CS 347 Notes 02 9
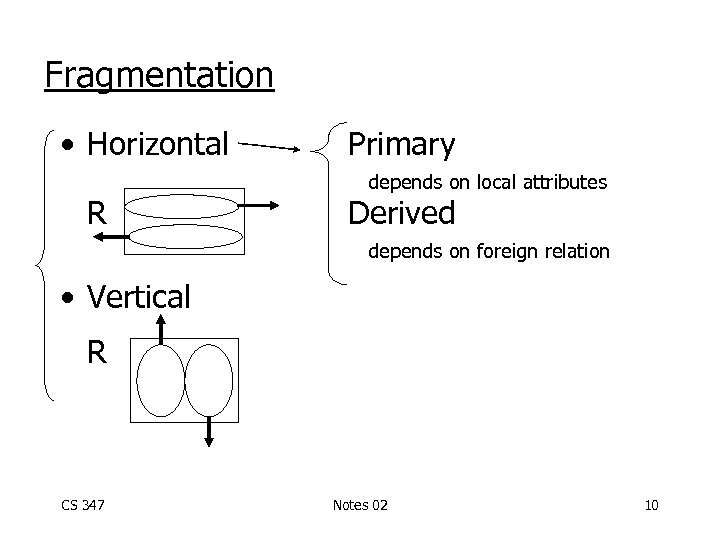
Fragmentation • Horizontal R Primary depends on local attributes Derived depends on foreign relation • Vertical R CS 347 Notes 02 10
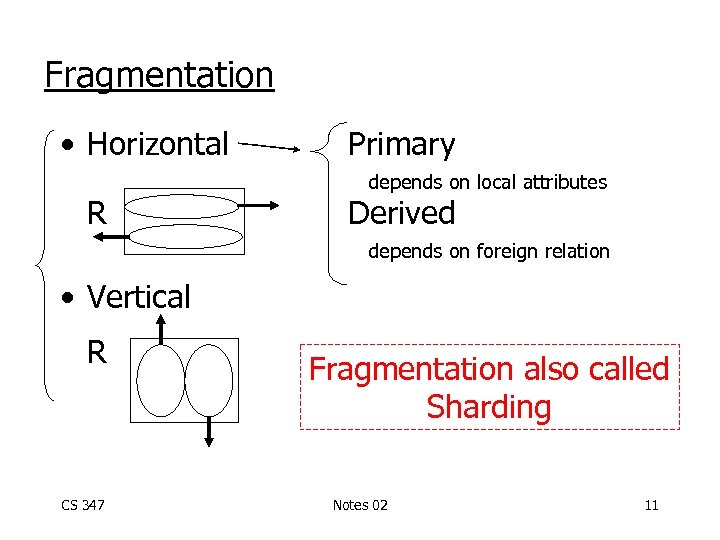
Fragmentation • Horizontal R Primary depends on local attributes Derived depends on foreign relation • Vertical R CS 347 Fragmentation also called Sharding Notes 02 11
Three common horizontal partitioning techniques • Round robin • Hash partitioning • Range partitioning CS 347 Notes 02 12
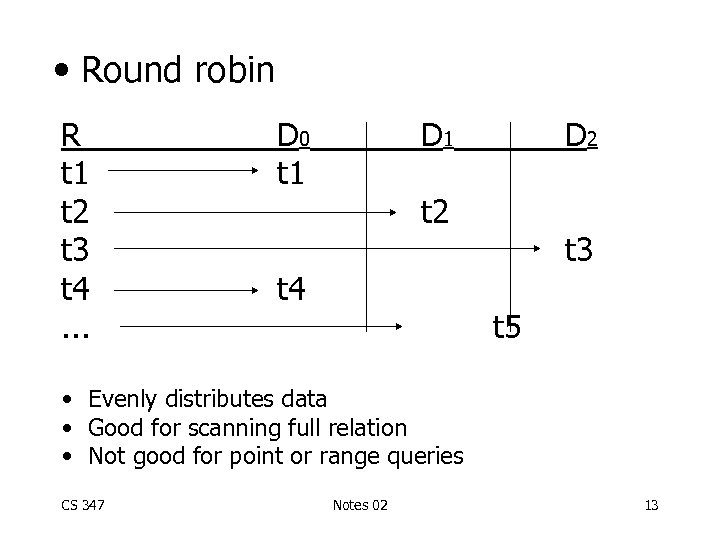
• Round robin R t 1 t 2 t 3 t 4. . . D 0 t 1 D 2 t 4 t 3 t 5 • Evenly distributes data • Good for scanning full relation • Not good for point or range queries CS 347 Notes 02 13
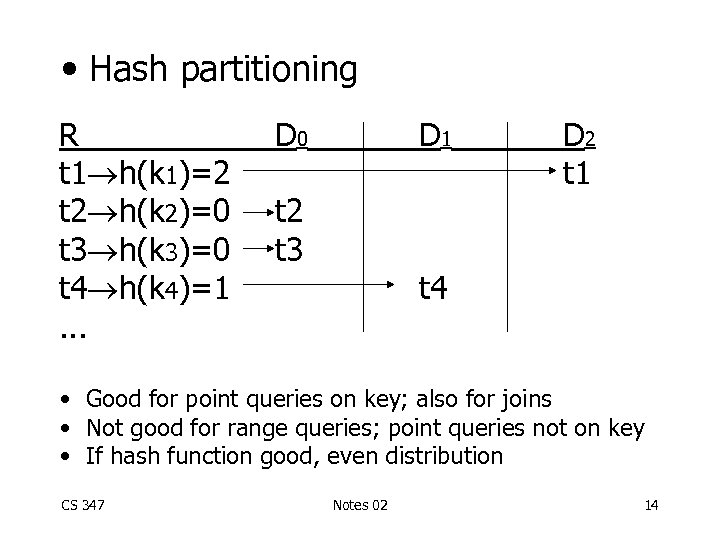
• Hash partitioning R t 1 h(k 1)=2 t 2 h(k 2)=0 t 3 h(k 3)=0 t 4 h(k 4)=1. . . D 0 D 1 t 2 t 3 D 2 t 1 t 4 • Good for point queries on key; also for joins • Not good for range queries; point queries not on key • If hash function good, even distribution CS 347 Notes 02 14
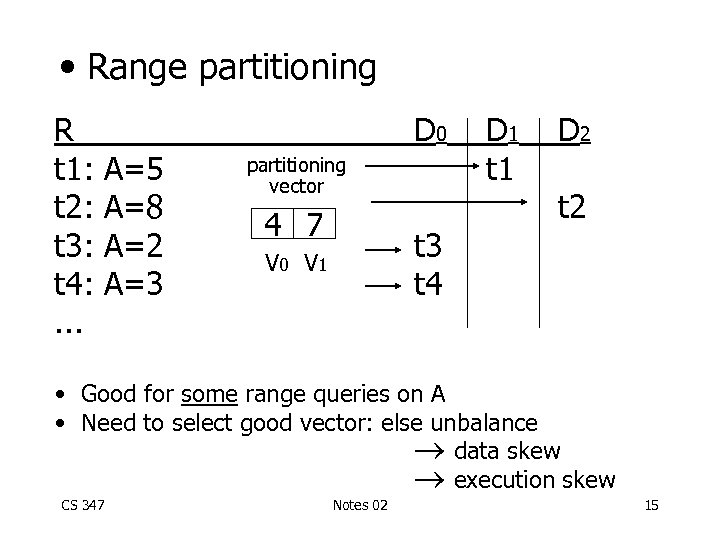
• Range partitioning R t 1: t 2: t 3: t 4: . . . A=5 A=8 A=2 A=3 D 0 partitioning vector 4 7 t 3 t 4 V 0 V 1 D 1 t 1 D 2 t 2 • Good for some range queries on A • Need to select good vector: else unbalance data skew execution skew CS 347 Notes 02 15
Which are good fragmentations? Example: F= F 1 = CS 347 { F 1, F 2 } sal<10 E F 2 = Notes 02 sal>20 E 16
Which are good fragmentations? Example: F= F 1 = { F 1, F 2 } sal<10 CS 347 E F 2 = sal>20 E Problem: Some tuples lost! Notes 02 17
Which are good fragmentations? Second example: F= F 3 = CS 347 { F 3, F 4 } sal<10 E F 4 = Notes 02 sal>5 E 18
Which are good fragmentations? Second example: F= F 3 = { F 3, F 4 } sal<10 E F 4 = sal>5 E Tuples with 5 < sal < 10 are duplicated. . . CS 347 Notes 02 19
Prefer to deal with replication explicitly Example: F = F 5 = 7 F = { F 5, F 6, F 7 } E sal 5 sal F 6 = E 10 E 5< sal <10 Then replicate F 6 if convenient (part of allocation problem) CS 347 Notes 02 20
Desired properties for horizontal fragmentation R F ={ F 1, F 2, … } (1) Completeness t R, Fi F such that t Fi CS 347 Notes 02 21
(2) Disjointness t Fi, Fj such that t Fj, i j, Fi, Fj F (3) Reconstruction - ignore CS 347 Notes 02 22
How do we get completeness and disjointness? (1) Check it “manually”! e. g. , F 1 = CS 347 sal<10 E ; F 2 = Notes 02 sal 10 E 23
How do we get completeness and disjointness? (2) “Automatically” generate fragments with these properties Desired simple predicates Fragments CS 347 Notes 02 24
Example of generation • Say queries use predicates: A<10, A>5, Loc = SA, Loc = SB • Next: CS 347 - generate “minterm” predicates - eliminate useless ones Notes 02 25
Minterm predicates (part I) (1) (2) (3) (4) (5) (6) (7) (8) A<10 A<10 CS 347 A>5 Loc=SA Loc=SB A>5 Loc=SA ¬(Loc=SB) A>5 ¬(Loc=SA) Loc=SB A>5 ¬(Loc=SA) ¬(Loc=SB) ¬(A>5) Loc=SA Loc=SB ¬(A>5) Loc=SA ¬(Loc=SB) ¬(A>5) ¬(Loc=SA) Loc=SB ¬(A>5) ¬(Loc=SA) ¬(Loc=SB) Notes 02 26
Minterm predicates (part I) (1) (2) (3) (4) (5) (6) (7) (8) A<10 A<10 CS 347 A>5 Loc=SA Loc=SB A>5 Loc=SA ¬(Loc=SB) A>5 ¬(Loc=SA) Loc=SB A>5 ¬(Loc=SA) ¬(Loc=SB) ¬(A>5) Loc=SA Loc=SB ¬(A>5) Loc=SA ¬(Loc=SB) ¬(A>5) ¬(Loc=SA) Loc=SB ¬(A>5) ¬(Loc=SA) ¬(Loc=SB) Notes 02 27
5 < A < 10 Minterm predicates (part I) (1) (2) (3) (4) (5) (6) (7) (8) A<10 A<10 A>5 Loc=SA Loc=SB A>5 Loc=SA ¬(Loc=SB) A>5 ¬(Loc=SA) Loc=SB A>5 ¬(Loc=SA) ¬(Loc=SB) ¬(A>5) Loc=SA Loc=SB ¬(A>5) Loc=SA ¬(Loc=SB) ¬(A>5) ¬(Loc=SA) Loc=SB ¬(A>5) ¬(Loc=SA) ¬(Loc=SB) A 5 CS 347 Notes 02 28
Minterm predicates (part II) (9) (10) (11) (12) (13) (14) (15) (16) ¬(A<10) A>5 Loc=SA Loc=SB ¬(A<10) A>5 Loc=SA ¬(Loc=SB) ¬(A<10) A>5 ¬(Loc=SA) Loc=SB ¬(A<10) A>5 ¬(Loc=SA) ¬(Loc=SB) ¬(A<10) ¬(A>5) Loc=SA Loc=SB ¬(A<10) ¬(A>5) Loc=SA ¬(Loc=SB) ¬(A<10) ¬(A>5) ¬(Loc=SA) Loc=SB ¬(A<10) ¬(A>5) ¬(Loc=SA) ¬(Loc=SB) CS 347 Notes 02 29
Minterm predicates (part II) (9) (10) (11) (12) (13) (14) (15) (16) ¬(A<10) A>5 Loc=SA Loc=SB ¬(A<10) A>5 Loc=SA ¬(Loc=SB) ¬(A<10) A>5 ¬(Loc=SA) Loc=SB ¬(A<10) A>5 ¬(Loc=SA) ¬(Loc=SB) ¬(A<10) ¬(A>5) Loc=SA Loc=SB ¬(A<10) ¬(A>5) Loc=SA ¬(Loc=SB) ¬(A<10) ¬(A>5) ¬(Loc=SA) Loc=SB ¬(A<10) ¬(A>5) ¬(Loc=SA) ¬(Loc=SB) A 10 CS 347 Notes 02 30
Final fragments: F 2: F 3: F 6: F 7: F 10: F 11: CS 347 5 < A < 10 A 5 A 10 Notes 02 Loc=SA Loc=SB 31
Note: elimination of useless fragments depends on application semantics: e. g. : if LOC could be SA, SB, we need to add fragments F 4: 5 <A <10 Loc SA Loc SB F 8: A 5 Loc SA Loc SB F 12: A 10 Loc SA Loc SB CS 347 Notes 02 32
Why does this work? Predicates: p 1 p 2 p 3 p 4 p 1 p 2 p 3 ¬ p 4. . . ¬ p 1 ¬ p 2 ¬ p 3 ¬ p 4 CS 347 Notes 02 33
(1) Completeness: Take t R pi(t) must be T or F! Say p 1(t) =T p 2(t) = T p 3(t) =F p 4(t) =F Then t is in fragment with predicate p 1 p 2 ¬ p 3 ¬ p 4 CS 347 Notes 02 34
(2) Disjointness Say t Fragment p 1 p 2 ¬ p 3 ¬ p 4 Then: p 1(t) = T, p 2(t) = T, p 3(t) = F, p 4(t)= F t cannot be in any other fragment! CS 347 Notes 02 35
Summary • Given simple predicates Pr= { p 1, p 2, . . pm } minterm predicates are M={m | m = p *, p P k k r 1 k m } where pk* is pk or is ¬ pk • Fragments m R for all m M are complete and disjoint CS 347 Notes 02 36
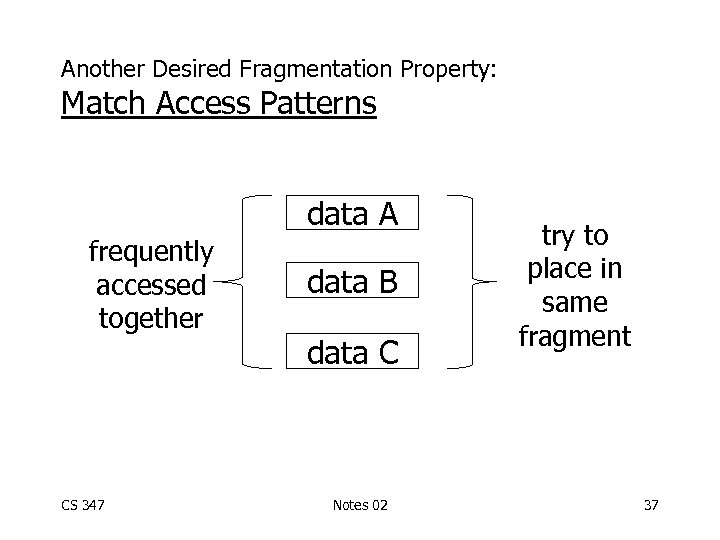
Another Desired Fragmentation Property: Match Access Patterns data A frequently accessed together CS 347 data B data C Notes 02 try to place in same fragment 37
Return to example: E(#, NM, LOC, SAL, …) Common queries: Qa: select * from E where LOC=Sa and … CS 347 Notes 02 Qb: select * from E where LOC=Sb and. . . 38
Three choices: (1) Pr = { } F 1 ={ E } (2) Pr = {LOC=Sa, LOC=Sb} F 2={ E, loc=Sb E } (3) Pr = {LOC=Sa, LOC=Sb, Sal<10} loc=Sa F 3={ loc=Sa sal<10 E, loc=Sa sal 10 E, loc=Sb sal<10 E, loc=Sb sal 10 E } CS 347 Notes 02 39
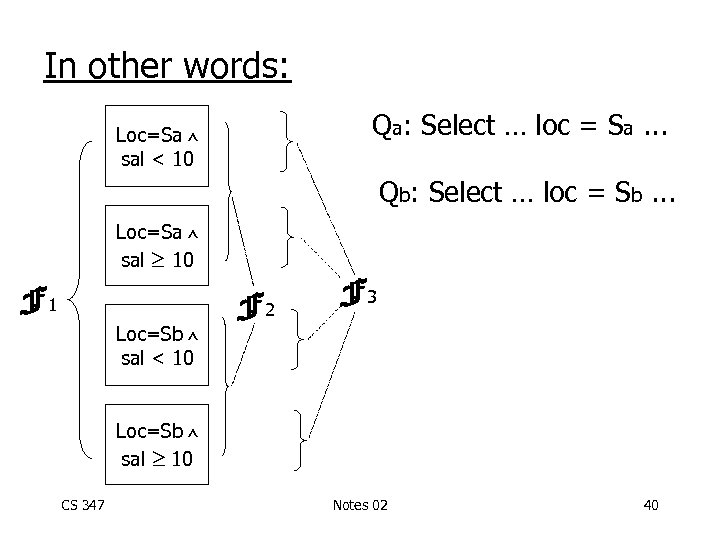
In other words: Qa: Select … loc = Sa. . . Loc=Sa sal < 10 Qb: Select … loc = Sb. . . Loc=Sa sal 10 F 1 Loc=Sb sal < 10 F 2 F 3 Loc=Sb sal 10 CS 347 Notes 02 40
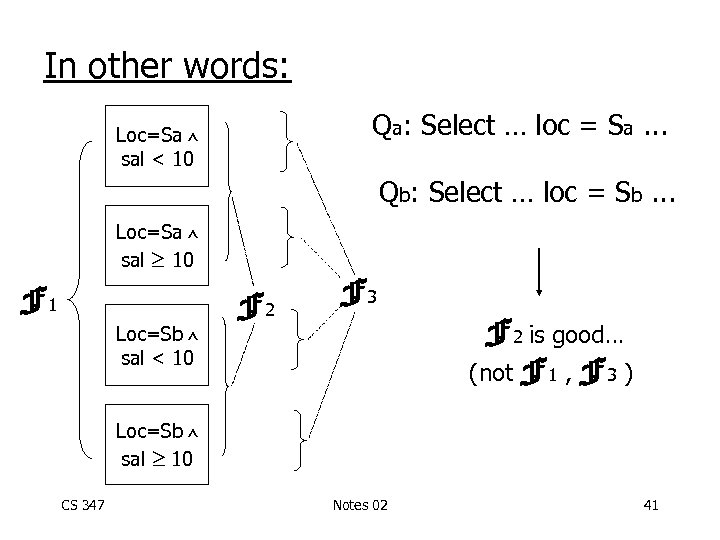
In other words: Qa: Select … loc = Sa. . . Loc=Sa sal < 10 Qb: Select … loc = Sb. . . Loc=Sa sal 10 F 1 Loc=Sb sal < 10 F 2 F 3 F 2 is good… (not F 1 , F 3 ) Loc=Sb sal 10 CS 347 Notes 02 41
Derived horizontal fragmentation Example: E(#, NM, SAL, LOC) F={ E 1, E 2} by LOC J(#, DES, …) Common query for project: [Given employee name, list projects (s)he works in] CS 347 Notes 02 42
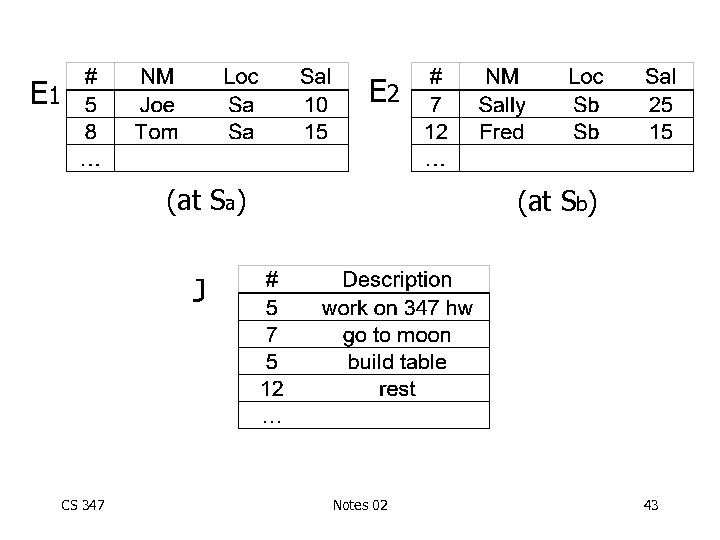
E 2 E 1 (at Sa) (at Sb) J CS 347 Notes 02 43
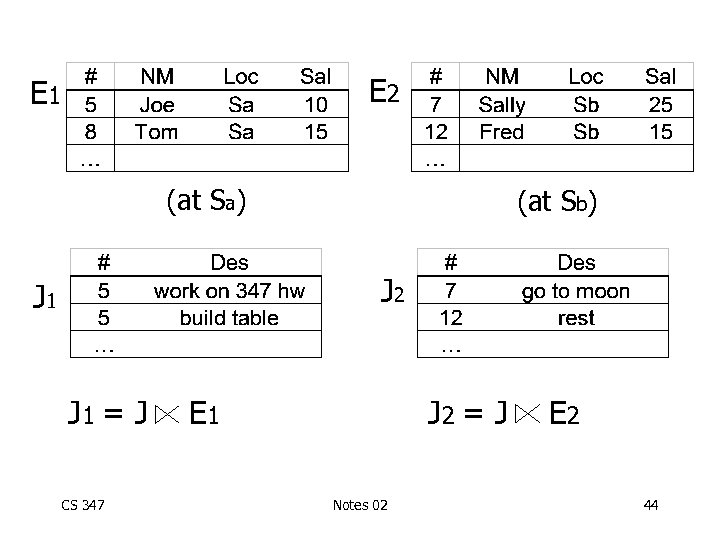
E 2 E 1 (at Sa) (at Sb) J 2 J 1 = J CS 347 E 1 J 2 = J Notes 02 E 2 44
Derived horizontal fragmentation R, F could be primary or derived F = { F 1, F 2, . . . Fn} S, D = {D 1, D 2, …Dn} where Di =S Fi Convention: R is owner S is member CS 347 Notes 02 45
• Checking completeness and disjointness of derived fragmentation Example: Say J is: But no #= 33 in E 1 nor in E 2! This J tuple will not be in J 1 nor J 2 Fragmentation not complete CS 347 Notes 02 46
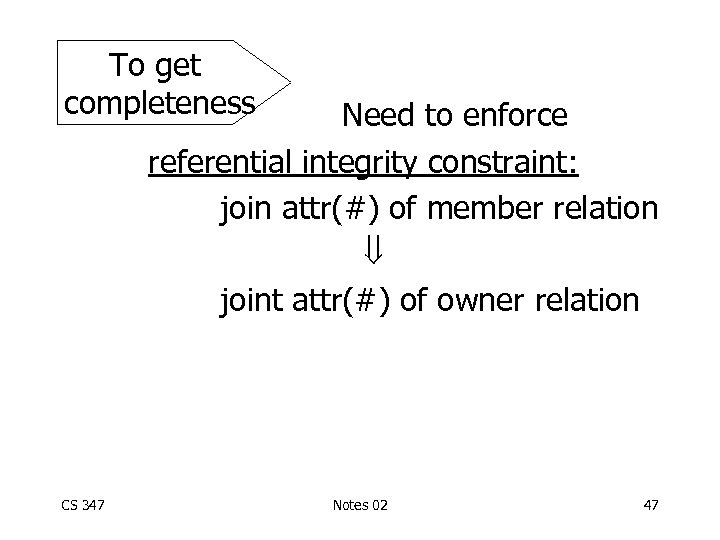
To get completeness Need to enforce referential integrity constraint: join attr(#) of member relation joint attr(#) of owner relation CS 347 Notes 02 47
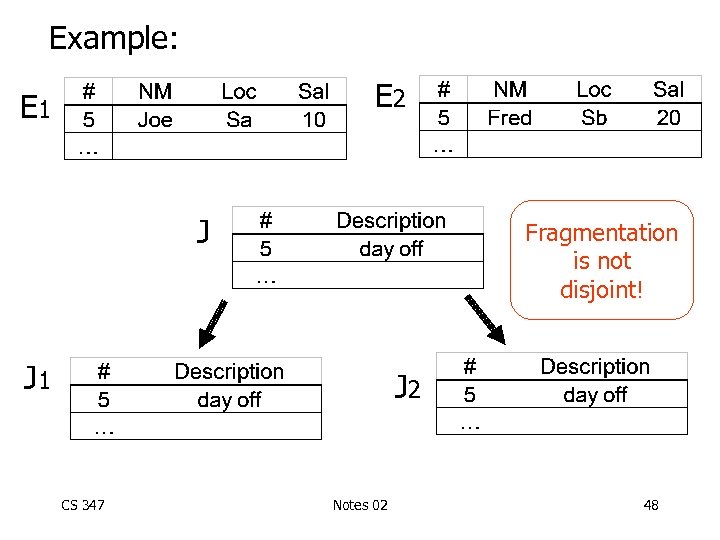
Example: E 2 E 1 J Fragmentation is not disjoint! J 1 J 2 CS 347 Notes 02 48
To get disjointness CS 347 Join attribute(#) should be key of owner relation Notes 02 49
Summary: horizontal fragmentation • Type: primary, derived • Properties: completeness, disjointness CS 347 Notes 02 50
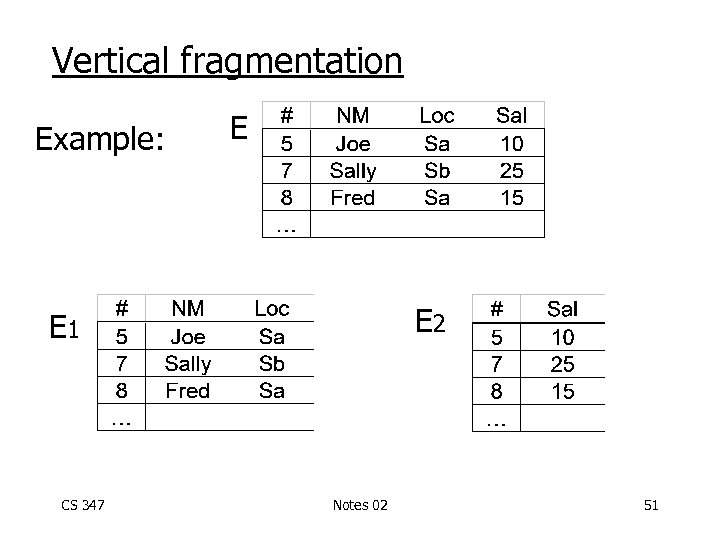
Vertical fragmentation Example: E E 2 E 1 CS 347 Notes 02 51
![R 1[T 1] Ti T . . . R[T] Rn[Tn] Just like normalization of](https://present5.com/presentation/e86fb87f7cacd8d11369e4eb75b0466a/image-52.jpg "R 1[T 1] Ti T . . . R[T] Rn[Tn] Just like normalization of")
R 1[T 1] Ti T . . . R[T] Rn[Tn] Just like normalization of relations CS 347 Notes 02 52
![Properties: R[T] Ri[Ti] (1) Completeness U Ti = T all i CS 347 Notes](https://present5.com/presentation/e86fb87f7cacd8d11369e4eb75b0466a/image-53.jpg "Properties: R[T] Ri[Ti] (1) Completeness U Ti = T all i CS 347 Notes")
Properties: R[T] Ri[Ti] (1) Completeness U Ti = T all i CS 347 Notes 02 53
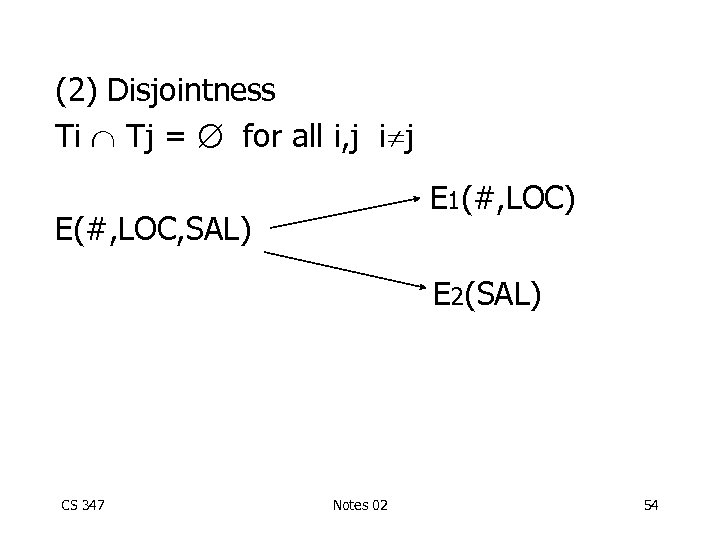
(2) Disjointness Ti Tj = for all i, j i j E 1(#, LOC) E(#, LOC, SAL) E 2(SAL) CS 347 Notes 02 54
(2) Disjointness Ti Tj = for all i, j i j E 1(#, LOC) E(#, LOC, SAL) E 2(SAL) Not a desirable property!! (could not reconstruct R!) CS 347 Notes 02 55
(3) Lossless join all i Ri = R One way to achieve lossless join: Repeat key in all fragments, i. e. , Key Ti for all i CS 347 Notes 02 56
How do we decide what attributes are grouped with which? E 1(#, NM, LOC) E 2(#, SAL) Example: E(#, NM, LOC, SAL) E 1(#, NM) E 2(#, LOC) E 3(#, SAL) ? CS 347 Notes 02 57
Attribute affinity matrix A 1 A 2 A 3 A 4 A 5 CS 347 A 2 A 3 A 4 A 5 - - - 50 - - 45 48 - - - 1 2 0 - - 0 0 4 75 - Notes 02 58
Attribute affinity matrix A 1 A 2 A 3 A 4 A 5 A 2 A 3 A 5 - - - 50 - - 45 48 - - - 1 2 0 - - 0 0 4 75 - R 1[K, A 1, A 2, A 3] CS 347 A 4 R 2[K, A 4, A 5] Notes 02 59
• Textbook (Ozsu & Valduriez) discusses – How to build affinity matrix – How to identify attribute clusters – How to partition relation • You are not responsible for – Clustering and partitioning algorithms (i. e. , Skip pages 135 -145) CS 347 Notes 02 60
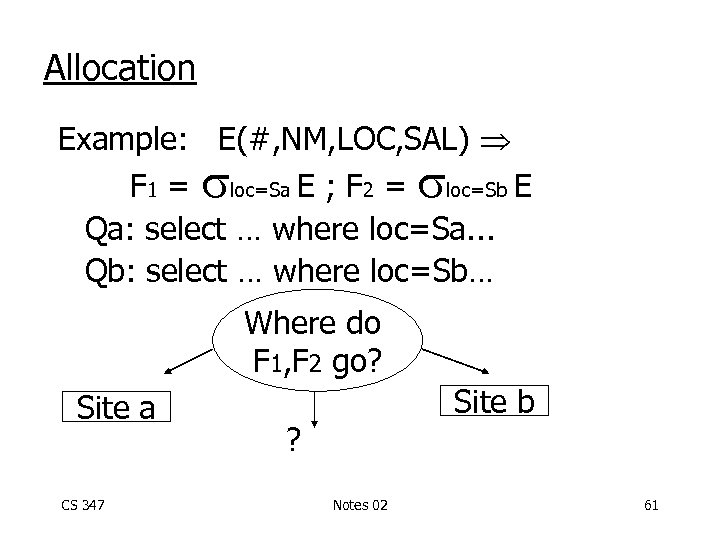
Allocation Example: E(#, NM, LOC, SAL) F 1 = loc=Sa E ; F 2 = loc=Sb E Qa: select … where loc=Sa. . . Qb: select … where loc=Sb… Where do F 1, F 2 go? Site a CS 347 Site b ? Notes 02 61
Issues • Where do queries originate • What is communication cost? and size of answers, relations, … • What is storage capacity, cost at sites? and size of fragments? • What is processing power at sites? CS 347 Notes 02 62
More Issues • What is query processing strategy? – How are joins done? – Where answers collected? CS 347 Notes 02 63
Do we replicate fragments? • Cost of updating copies? • Writes and concurrency control? • . . . CS 347 Notes 02 64
Optimization problem: • What is best placement of fragments and/or best number of copies to: – minimize query response time – maximize throughput – minimize “some cost” –. . . • Subject to constraints? – Available storage – Available bandwidth, power, … – Keep 90% of response time below X –. . . CS 347 Notes 02 65
Optimization problem: • What is best placement of fragments and/or best number of copies to: – minimize query response time – maximize throughput This is an incredibly – minimize “some cost” hard problem –. . . • Subject to constraints? – Available storage – Available bandwidth, power, … – Keep 90% of response time below X –. . . CS 347 Notes 02 66
![Example: Single fragment F m Read cost: [ti MIN Cij] i=1 j i: Originating](https://present5.com/presentation/e86fb87f7cacd8d11369e4eb75b0466a/image-67.jpg "Example: Single fragment F m Read cost: [ti MIN Cij] i=1 j i: Originating")
Example: Single fragment F m Read cost: [ti MIN Cij] i=1 j i: Originating site of request ti: Read traffic at Si Cij: Retrieval cost Accessing fragment F at Sj from Si CS 347 Notes 02 67
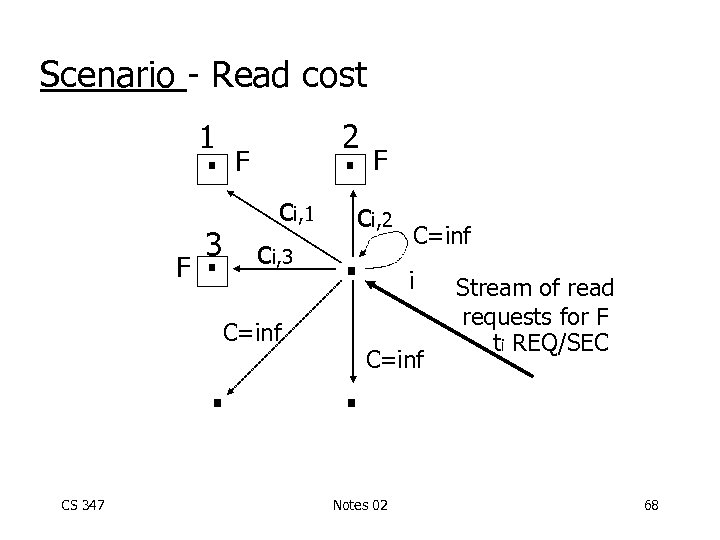
Scenario - Read cost 1 . F 2 . F ci, 1 3. ci, 3 ci, 2 . C=inf . CS 347 F . C=inf i C=inf Notes 02 Stream of read requests for F ti REQ/SEC 68
Write cost m m Xj ui C’ij i=1 j=1 i: Originating site of request j: Site being updated Xj: 0 if F not stored at Sj 1 if F stored at Sj ui: Write traffic at Si C’ij: Write cost Updating F at Sj from Si CS 347 Notes 02 69
Scenario - write cost F . CS 347 . . . F . i Notes 02 Updates ui updates/sec 70
Storage cost: m i=1 X i: d i: CS 347 Xi d i 0 if F not stored at Si 1 if F stored at Si storage cost at Si Notes 02 71
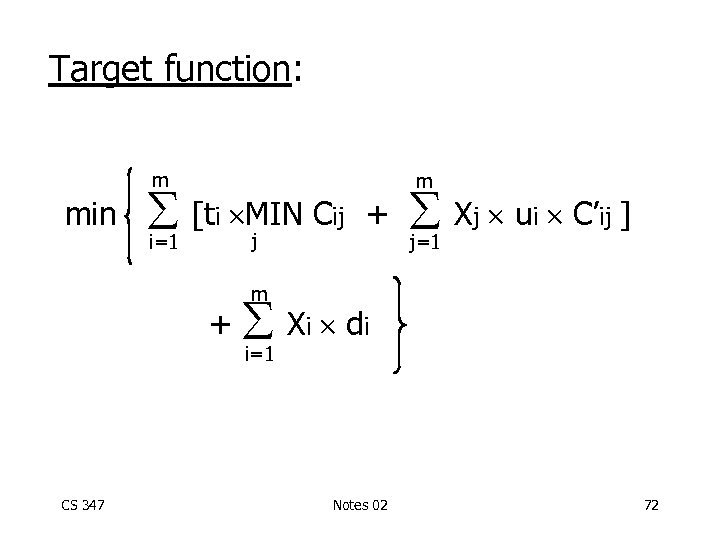
Target function: m min i=1 m [ti MIN Cij + CS 347 m i=1 j=1 Xj ui C’ij ] Xi d i Notes 02 72
Can add more complications: Examples: - Multiple fragments - Fragment sizes - Concurrency control cost CS 347 Notes 02 73
Case Study: PNUTS • Where in the World is My Data? Sudarshan Kadambi, Jianjun Chen, Brian F. Cooper, David Lomax, Raghu Ramakrishnan, Adam Silberstein, Erwin Tam, Hector Garcia -Molina; VLDB 2011 • Distributed object/tuple store for Yahoo! CS 347 Notes 02 74
Case Study: PNUTS • Issue: Where to locate data • Issue: What and where to replicate CS 347 Notes 02 75
PNUTS Discussion • Dynamic vs Static fragment placement • Caching vs Replication CS 347 Notes 02 76
Policy Constraints • MIN_COPIES: The minimum number of full replicas of the record that must exist. • INCL_LIST: An inclusion list -- the locations where a full replica of the record must exist. • EXCL_LIST: An exclusion list -- the locations where a full replica of the record cannot exist. CS 347 Notes 02 77
Example Rule • Rule 1: • IF TABLE_NAME = "Users“ THEN SET 'MIN_COPIES' = 2 CONSTRAINT_PRI = 0 CS 347 Notes 02 78
Another Example Rule • Rule 2: • IF TABLE_NAME = "Users" AND FIELD STR('home location') = 'France‘ THEN SET 'MIN_COPIES' = 3 AND SET 'EXCL LIST' = 'USWest, USEast‘ CONSTRAINT PRI = 1 CS 347 Notes 02 79
Summary • • Description of fragmentation Good fragmentations Design of fragmentation Allocation CS 347 Notes 02 80
Скачать презентацию CS 347 Parallel and Distributed Data Management Notes
e86fb87f7cacd8d11369e4eb75b0466a.ppt