CS 259 Key Exchange Protocols J Mitchell

CS 259 Key Exchange Protocols J. Mitchell

Next few lectures u. Today 1/17 u. Thursday 1/19 u. Next Tues 1/24 u. Next Thurs 1/26 u. Project presentation #1 2/2 • Brief cryptography background • Key exchange protocols and properties • Wireless security: 802. 11 i • Choose your project partner • Password authentication protocols • Contract-signing protocols Talk about protocols for a while before looking at more tools

Basic Concepts in Cryptography u Encryption scheme: • functions to encrypt, decrypt data • key generation algorithm u Secret key vs. public key • Public key: publishing key does not reveal key-1 • Secret key: more efficient, generally key = key-1 u Hash function, MAC • Map input to short hash; ideally, no collisions • MAC (keyed hash) used for message integrity u Signature scheme • Functions to sign data, verify signature

Cryptosystem u. A cryptosystem consists of five parts • • A set P of plaintexts A set C of ciphertexts A set K of keys A pair of functions encrypt: K P C decrypt: K C P such that for every key k K and plaintext p P decrypt(k, encrypt(k, p)) = p

What is a “secure” cryptosystem? u. One idea • If enemy intercepts ciphertext, cannot recover plaintext u. Issues in making this precise • What else might your enemy know? – The kind of encryption function you are using – Some plaintext-ciphertext pairs from last year – Some information about how you choose keys • What do we mean by “cannot recover plaintext” ? – Ciphertext contains no information about plaintext – No efficient computation could make a reasonable guess – Cannot use ciphertext for any nontrivial purpose

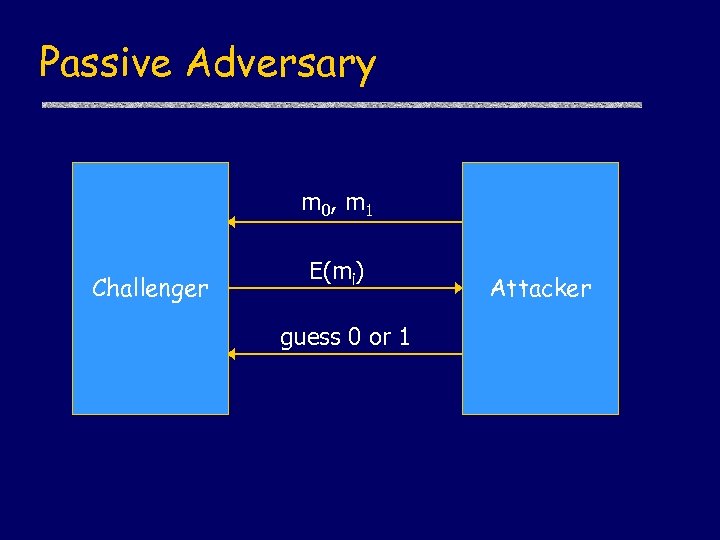Passive Adversary m 0, m 1 Challenger E(mi) guess 0 or 1 Attacker

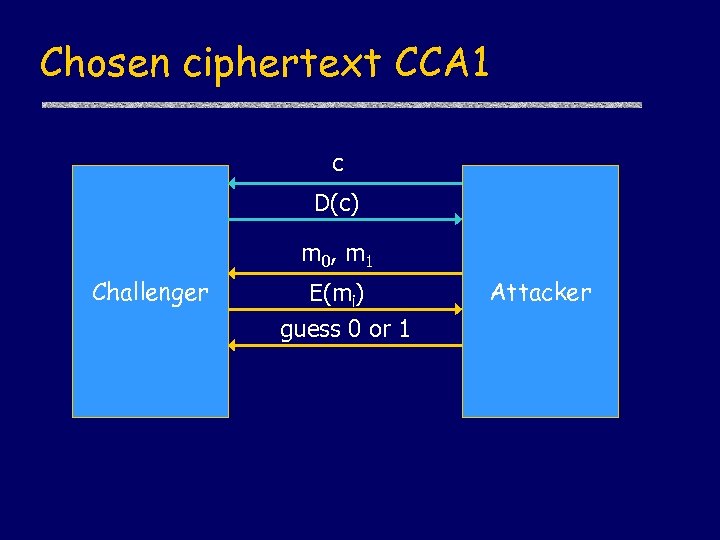Chosen ciphertext CCA 1 c D(c) m 0, m 1 Challenger E(mi) guess 0 or 1 Attacker

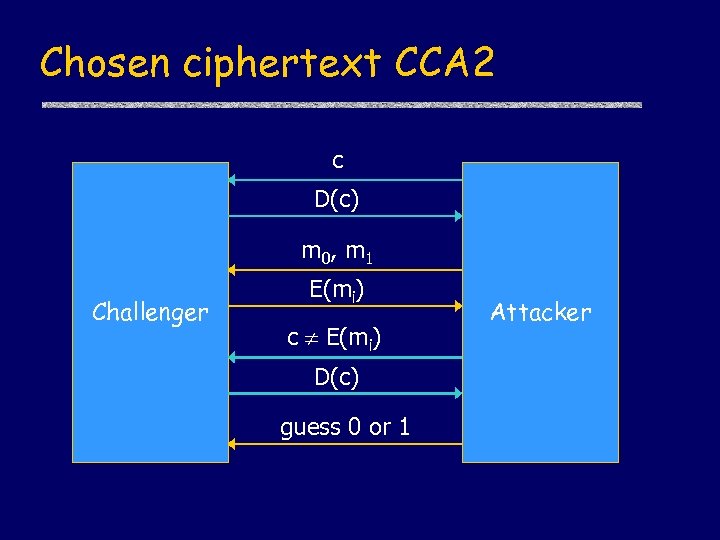Chosen ciphertext CCA 2 c D(c) m 0, m 1 Challenger E(mi) c E(mi) D(c) guess 0 or 1 Attacker

Public-key Cryptosystem u. Different keys to encrypt and decrypt • encrypt(key, message) key pair • decrypt(key -1, encrypt(key, message)) = message u. Encryption key does not help decrypt • Cannot compute m from encrypt(key, m) and key, unless you have key-1

Example: RSA u. Arithmetic modulo pq n • Generate secret primes p, q • Generate secret numbers a, b with xab x mod pq u. Public encryption key n, a • Encrypt( n, a , x) = xa mod n u. Private decryption key n, b • Decrypt( n, b , y) = yb mod n u. Main properties • This works • Cannot compute b from n, a – Apparently, need to factor n = pq

Cryptographic hash functions u. Length-reducing function h • Map arbitrary strings to strings of fixed length u. One way (“preimage resistance”) • Given y, hard to find x with h(x)=y u. Collision resistant • Hard to find any distinct m, m’ with h(m)=h(m’) u. Also useful: 2 nd preimage resistance • Given x and y=h(x) hard to find x’ x with h(x’)=h(x) • Collision resistance 2 nd preimage resistance

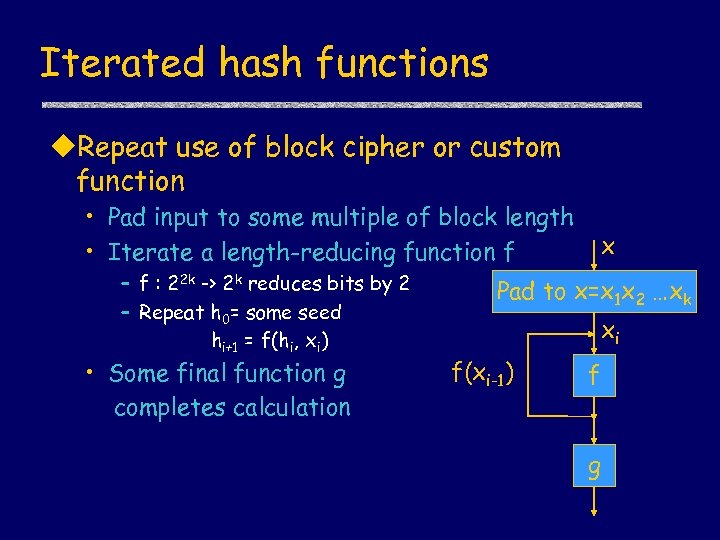Iterated hash functions u. Repeat use of block cipher or custom function • Pad input to some multiple of block length • Iterate a length-reducing function f – f : 22 k -> 2 k reduces bits by 2 – Repeat h 0= some seed hi+1 = f(hi, xi) • Some final function g completes calculation x Pad to x=x 1 x 2 …xk xi f(xi-1) f g

Applications of one-way hash u. Password files u. Digital signatures (one way) (collision resistant) • Sign hash of message instead of entire message u. Data integrity • Compute and store hash of some data • Check later by recomputing hash and comparing u. Keyed hash for message authentication • MAC – Message Authentication Code

Digital Signatures u. Public-key encryption • Alice publishes encryption key • Anyone can send encrypted message • Only Alice can decrypt messages with this key u. Digital signature scheme • Alice publishes key for verifying signatures • Anyone can check a message signed by Alice • Only Alice can send signed messages

Properties of signatures u. Functions to sign and verify • Sign(Key-1, message) • Verify(Key, x, m) = u. Resists forgery true if x = Sign(Key-1, m) false otherwise • Cannot compute Sign(Key-1, m) from m and Key • Resists existential forgery: given Key, cannot produce Sign(Key-1, m) for any random or otherwise arbitrary m

Basic Concepts in Cryptography u Encryption scheme: • functions to encrypt, decrypt data • key generation algorithm u Secret key vs. public key • Public key: publishing key does not reveal key-1 • Secret key: more efficient, generally key = key-1 u Hash function, MAC • Map input to short hash; ideally, no collisions • MAC (keyed hash) used for message integrity u Signature scheme • Functions to sign data, verify signature

Key Management u. Out of band • Can set up some keys this way (Kerberos) u. Public-key infrastructure (PKI) • Leverage small # of public signing keys u. Protocols for session keys • • Generate short-lived session key Avoid extended use of important secret Don’t use same key for encryption and signing Forward secrecy Cryptography reduces many problems to key management

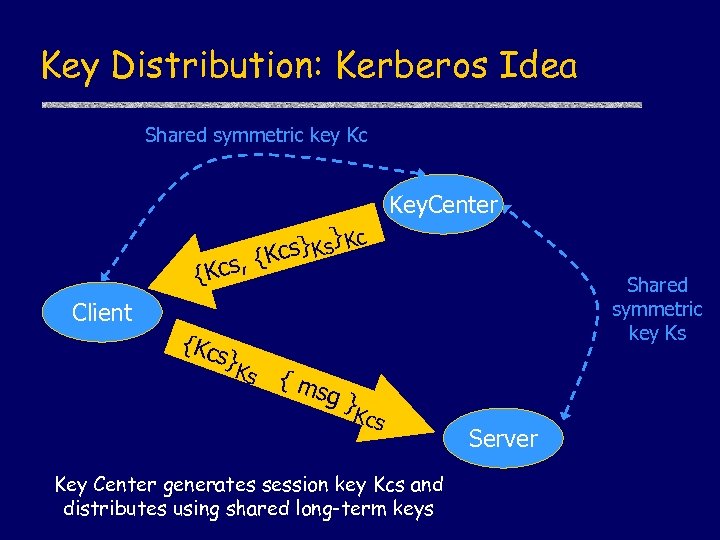Key Distribution: Kerberos Idea Shared symmetric key Kc Key. Center {Kcs Client {Kc } c cs} Ks K , {K s} K s Shared symmetric key Ks {m sg } Kcs Key Center generates session key Kcs and distributes using shared long-term keys Server

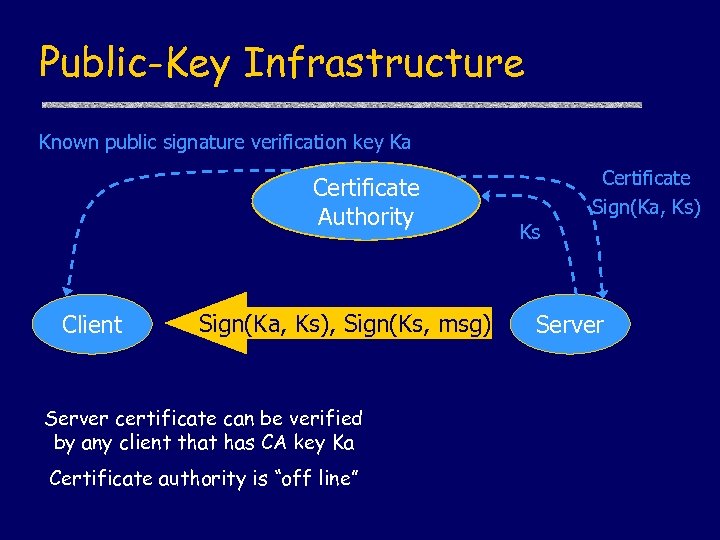Public-Key Infrastructure Known public signature verification key Ka Certificate Authority Client Sign(Ka, Ks), Sign(Ks, msg) Server certificate can be verified by any client that has CA key Ka Certificate authority is “off line” Certificate Sign(Ka, Ks) Ks Server

Key Exchange u. Parties may have initial information u. Generate and agree on session key • • Authentication – know ID of other party Secrecy – key not known to any others Avoid replay attack Forward secrecy Avoid denial of service Identity protection – disclosure to others Other properties you can think of? ? ?

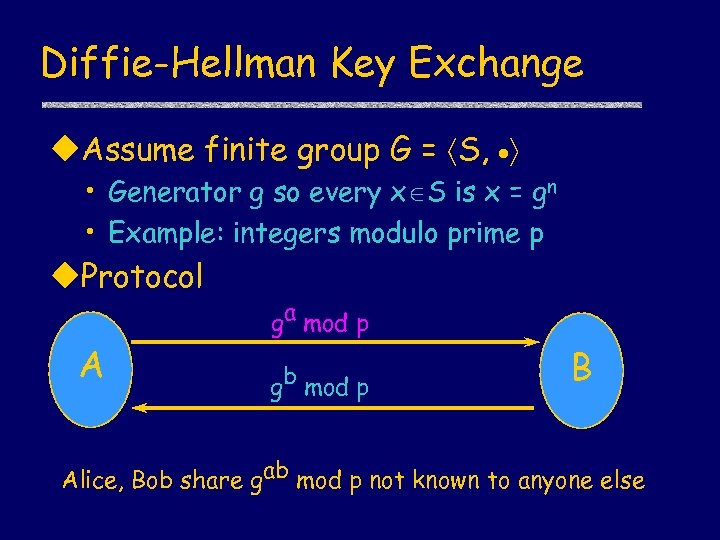Diffie-Hellman Key Exchange u. Assume finite group G = S, • Generator g so every x S is x = gn • Example: integers modulo prime p u. Protocol A ga mod p gb mod p B Alice, Bob share gab mod p not known to anyone else

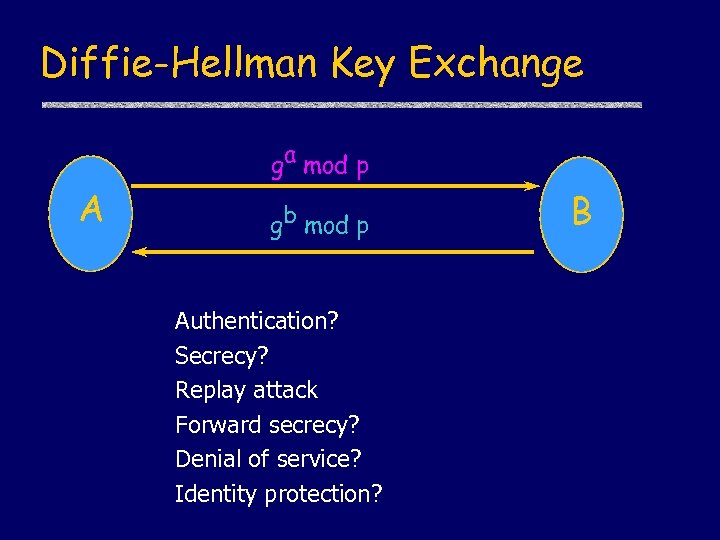Diffie-Hellman Key Exchange ga mod p A gb mod p Authentication? Secrecy? Replay attack Forward secrecy? Denial of service? Identity protection? B

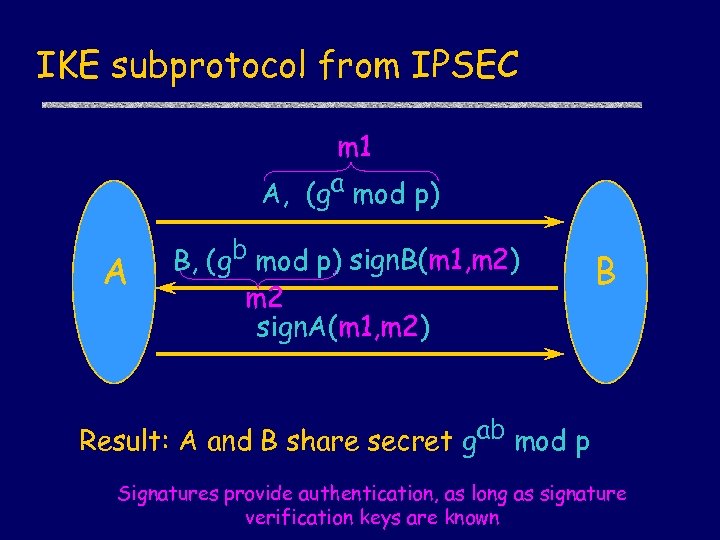IKE subprotocol from IPSEC m 1 A, (ga mod p) A , B, (gb mod p) sign. B(m 1, m 2) m 2 sign. A(m 1, m 2) B Result: A and B share secret gab mod p Signatures provide authentication, as long as signature verification keys are known

IPSec: Network Layer Security u Authentication Header (AH) • Access control and authenticate data origins • replay protection • No confidentiality u Encapsulated Secure Payload (ESP) • Encryption and/or authentication u Internet Key management (IKE) • Determine and distribute secret keys • Oakley + ISAKMP • Algorithm independent u Security policy database (SPD) • discarded, or bypass

IKE: Many modes u. Main mode • • Authentication by pre-shared keys Auth with digital signatures Auth with public-key encryption Auth with revised public-key encryption u. Quick mode • Compress number of messages • Also four authentication options

Aug 2001 Position Statement u In the several years since the standardization of the IPSEC protocols (ESP, AH, and ISAKMP/IKE), … several security problems…, most notably IKE. u Formal and semi-formal analyses by Meadows, Schneier et al, and Simpson, have shown … security problems in IKE stem directly from its complexity. u It seems … only a matter of time before serious *implementation* problems become apparent, again due to the complex nature of the protocol, and the complex implementation that must surely follow. u The Security Area Directors have asked the IPSEC working group to come up with a replacement for IKE.

How to study complex protocol

General Problem in Security u. Divide-and-conquer is fundamental • Decompose system requirements into parts • Develop independent software modules • Combine modules to produce required system u. Common belief: • Security properties do not compose Difficult system development problem

Example protocol P 1 A B : {message}KB A B : KA-1 u. This satisfies basic requirements • Message is transmitted under encryption • Revealing secret key KA-1 does not reveal message

Similar protocol P 2 B A : {message’}KA B A : KB-1 u. Transmits msg securely from B to A • Message is transmitted under encryption • Revealing secret key KB-1 does not reveal message

Composition P 1; P 2 u. Sequential composition of two protocols A B : {message}KB A B : KA-1 B A : {message’}KA B B : KB-1 u. Definitely not secure • Eavesdropper learns both keys, decrypts messages

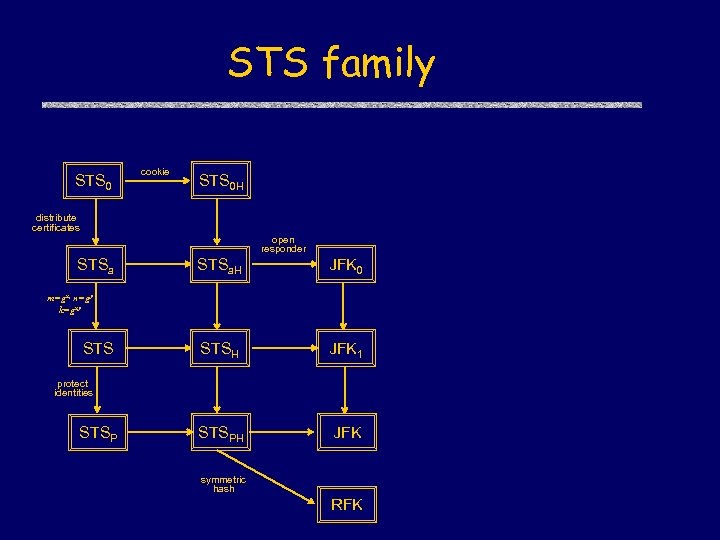STS family STS 0 cookie STS 0 H distribute certificates open responder STSa. H JFK 0 STSH JFK 1 STSPH JFK m=gx, n=gy k=gxy STS protect identities STSP symmetric hash RFK

Example u. Construct protocol with properties: • • Shared secret Authenticated Identity Protection Do. S Protection u. Design requirements for IKE, JFK, IKEv 2 (IPSec key exchange protocol)

Component 1 u. Diffie-Hellman A B: ga B A: gb • Shared secret (with someone) – A deduces: Knows(Y, gab) (Y = A) ۷ Knows(Y, b) • Authenticated • Identity Protection • Do. S Protection

Component 2 u. Challenge Response: A B: m, A B A: n, sig. B {m, n, A} A B: sig. A {m, n, B} • Shared secret (with someone) • Authenticated – A deduces: Received (B, msg 1) Λ Sent (B, msg 2) • Identity Protection • Do. S Protection

Composition u. ISO 9798 -3 protocol: A B: ga, A B A: gb, sig. B {ga, gb, A} A B: sig. A {ga, gb, B} • • Shared secret: gab Authenticated Identity Protection Do. S Protection m : = ga n : = gb

Refinement u. Encrypt signatures: A B: ga, A B A: gb, EK {sig. B {ga, gb, A}} A B: EK {sig. A {ga, gb, B}} • • Shared secret: gab Authenticated Identity Protection Do. S Protection

Transformation u. Use cookie: JFK core protocol A B: ga, A B A: gb, hash. KB {gb, ga} A B: ga, gb, hash. KB {gb, ga} EK {sig. A {ga, gb, B}} B A: gb, EK {sig. B {ga, gb, A}} • • Shared secret: gab Authenticated Identity Protection Do. S Protection (Here B must store b in step 2, but we’ll fix this later…)

Cookie transformation u. Typical protocol • Client sends request to server • Server sets up connection, responds • Client may complete session or not (DOS) u. Cookie version • Client sends request to server • Server sends hashed data back – Send message #2 later after client confirms • Client confirms by returning hashed data • Need extra step to send postponed message

Cookie in JFK u. Protocol susceptible to DOS eh 1 A B: ga, A B A: gb, EK {sig. B {ga, gb, A}} A B: EK {sig. A {ga, gb, B}} eh 2 u. Use cookie: JFK core protocol A B: B A: g a, A gb, hash. KB {gb, ga} ga, gb, hash. KB {gb, ga}, eh 2 gb, eh 1

Efficiency: Reuse D-H key u. Costly to compute ga, gb, gab u. Solution • Keep medium-term ga, gb (change ~10 min) • Replace ga by pair ga, nonce u. JFKi, JFKr protocols (except cert or grpinfo, …) A B: Na, ga, A B A: Nb, gb, hash. KB {Nb, Na, gb, ga} A B: Na, Nb, ga, gb, hash. KB {Nb, Na, gb, ga}, EK {sig. A {Na, Nb, ga, gb, B}} B A: gb, EK {sig. B {Na, Nb, ga, gb, A}} Note: B does not need to store any short-term data in step 2

Conclusion u. Many protocol properties • Authentication Secrecy • Prevent replay Forward secrecy • Denial of service Identity protection u. Systematic understanding is possible • But be careful; easy to make mistakes • State of the art: need to analyze complete protocol

Block cipher modes (for DES, AES, …) u ECB – Electronic Code Book mode • Divide plaintext into blocks • Encrypt each block independently, with same key u CBC – Cipher Block Chaining • XOR each block with encryption of previous block • Use initialization vector IV for first block u OFB – Output Feedback Mode • Iterate encryption of IV to produce stream cipher u CFB – Cipher Feedback Mode • Output block yi = input xi + encyrpt. K(yi-1)

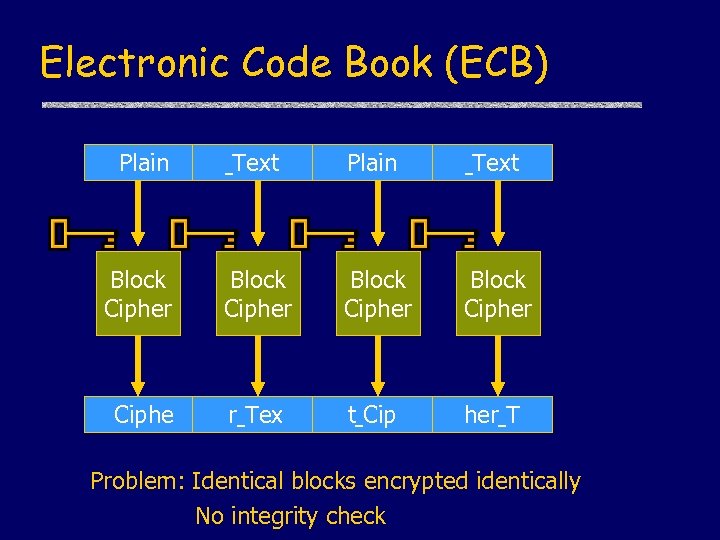Electronic Code Book (ECB) Plain Text Block Cipher Ciphe r Tex t Cip her T Problem: Identical blocks encrypted identically No integrity check

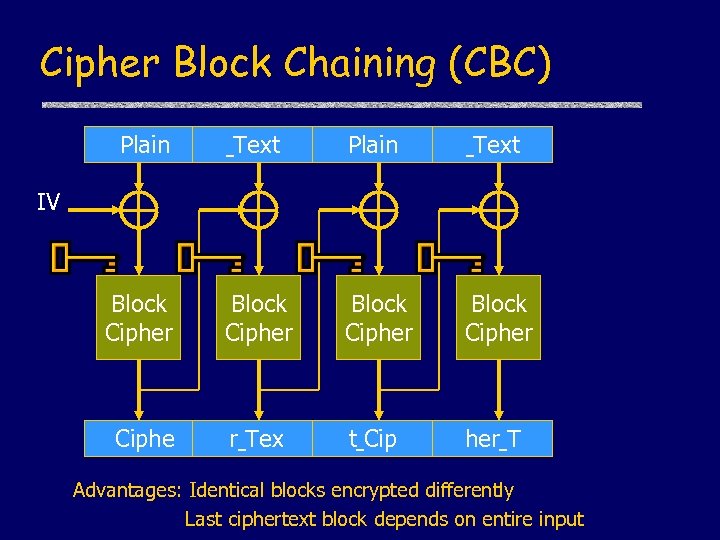Cipher Block Chaining (CBC) Plain Text Block Cipher Ciphe r Tex t Cip her T IV Advantages: Identical blocks encrypted differently Last ciphertext block depends on entire input

Comparison (for AES, by Bart Preneel) Similar plaintext blocks produce similar ciphertext (see outline of head) No apparent pattern