CS 245: Database System Principles Notes 6: Query Processing Hector Garcia-Molina CS 245 Notes 6 1
Query Processing Q Query Plan CS 245 Notes 6 2
Query Processing Q Query Plan Focus: Relational System • Others? CS 245 Notes 6 3
Example Select B, D From R, S Where R. A = “c” S. E = 2 R. C=S. C CS 245 Notes 6 4
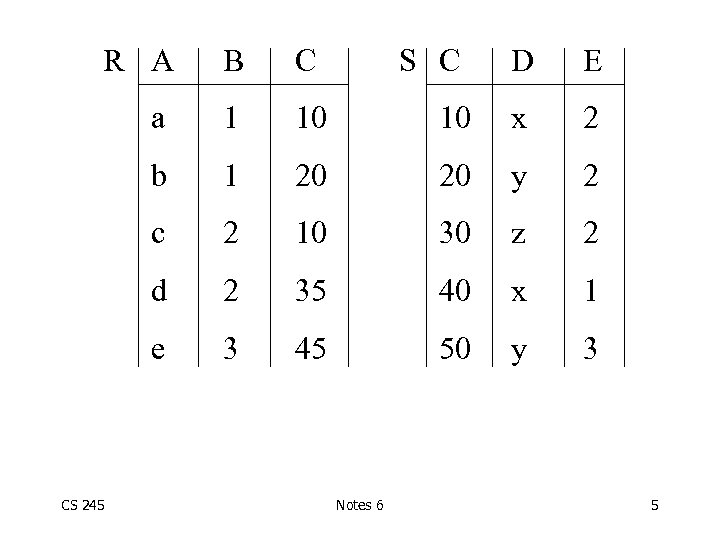
R A B C a 1 10 b 1 c D E 10 x 2 20 20 y 2 2 10 30 z 2 d 2 35 40 x 1 e CS 245 S C 3 45 50 y 3 Notes 6 5
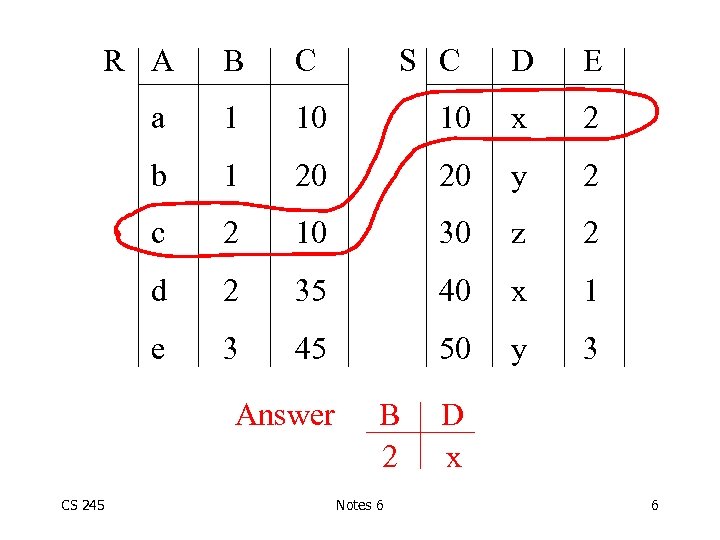
R A B C a 1 10 b 1 c D E 10 x 2 20 20 y 2 2 10 30 z 2 d 2 35 40 x 1 e 3 45 50 y 3 Answer CS 245 S C B 2 Notes 6 D x 6
• How do we execute query? One idea CS 245 - Do Cartesian product - Select tuples - Do projection Notes 6 7
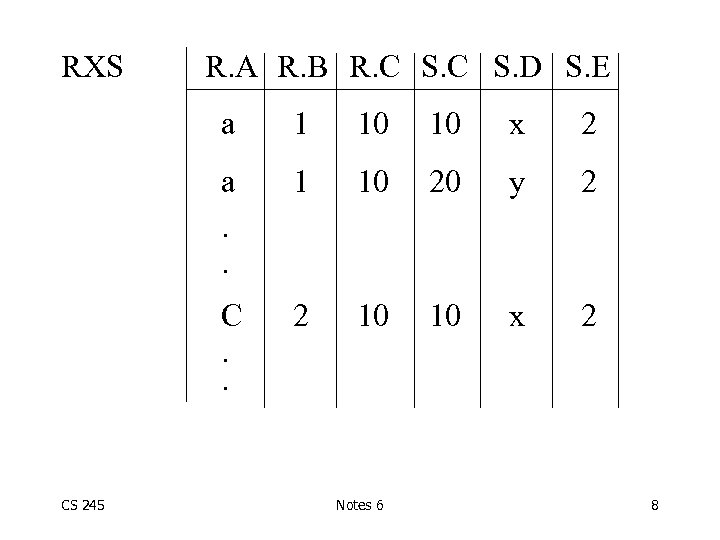
RXS R. A R. B R. C S. D S. E a 10 10 x 2 a. . 1 10 20 y 2 C. . CS 245 1 2 10 10 x 2 Notes 6 8
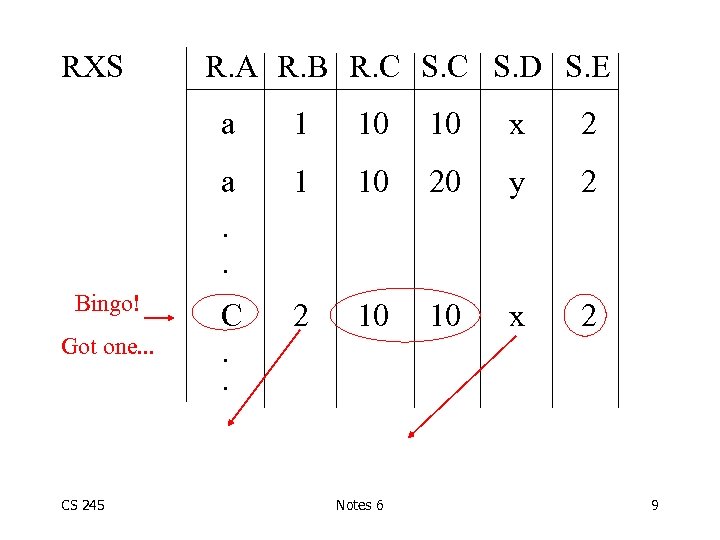
RXS R. A R. B R. C S. D S. E a Got one. . . CS 245 10 10 x 2 a. . Bingo! 1 1 10 20 y 2 C. . 2 10 10 x 2 Notes 6 9
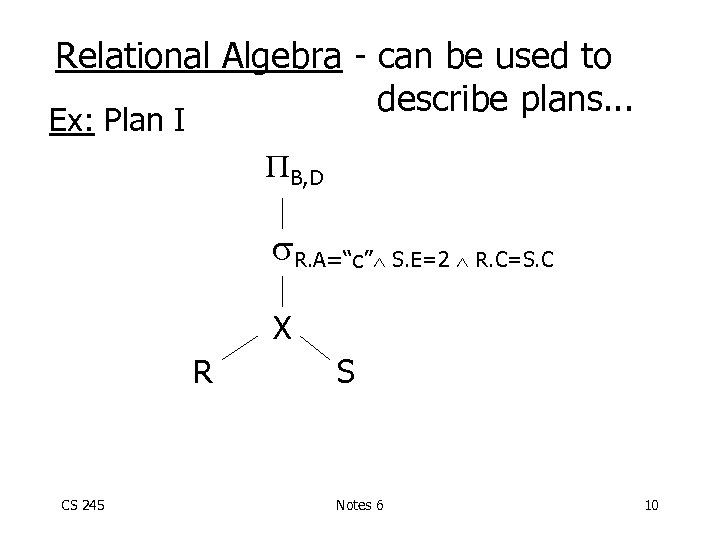
Relational Algebra - can be used to describe plans. . . Ex: Plan I B, D R. A=“c” S. E=2 R. C=S. C X R CS 245 S Notes 6 10
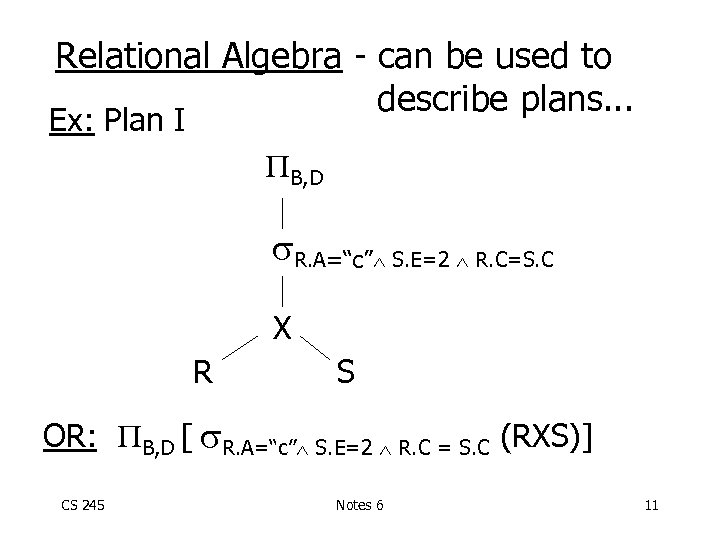
Relational Algebra - can be used to describe plans. . . Ex: Plan I B, D R. A=“c” S. E=2 R. C=S. C X R S OR: B, D [ R. A=“c” S. E=2 R. C = S. C (RXS)] CS 245 Notes 6 11
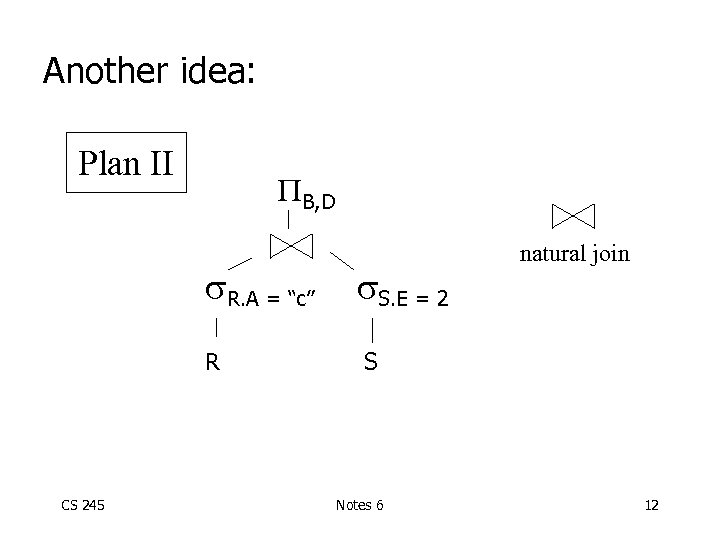
Another idea: Plan II B, D R. A = “c” R CS 245 S. E = 2 natural join S Notes 6 12
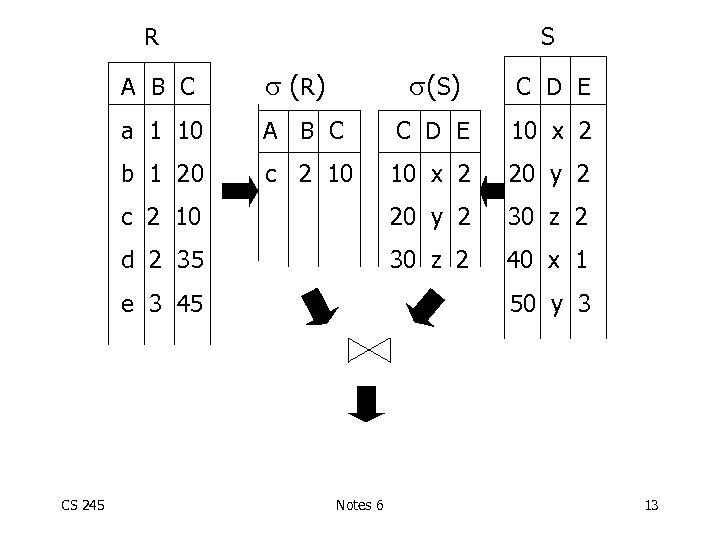
R S A B C ( R) (S) C D E a 1 10 A B C C D E 10 x 2 b 1 20 c 2 10 10 x 2 20 y 2 c 2 10 20 y 2 30 z 2 d 2 35 30 z 2 40 x 1 e 3 45 CS 245 50 y 3 Notes 6 13
Plan III Use R. A and S. C Indexes (1) Use R. A index to select R tuples with R. A = “c” (2) For each R. C value found, use S. C index to find matching tuples CS 245 Notes 6 14
Plan III Use R. A and S. C Indexes (1) Use R. A index to select R tuples with R. A = “c” (2) For each R. C value found, use S. C index to find matching tuples (3) Eliminate S tuples S. E 2 (4) Join matching R, S tuples, project B, D attributes and place in result CS 245 Notes 6 15
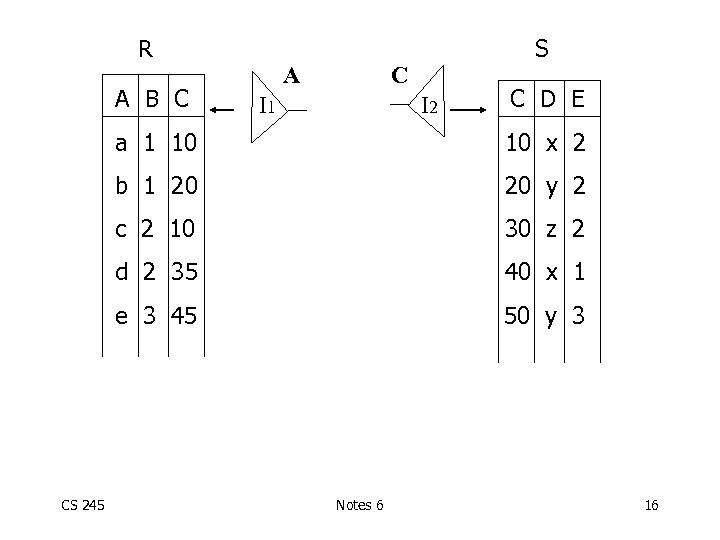
R A B C A S C I 1 I 2 C D E a 1 10 b 1 20 20 y 2 c 2 10 30 z 2 d 2 35 40 x 1 e 3 45 CS 245 10 x 2 50 y 3 Notes 6 16
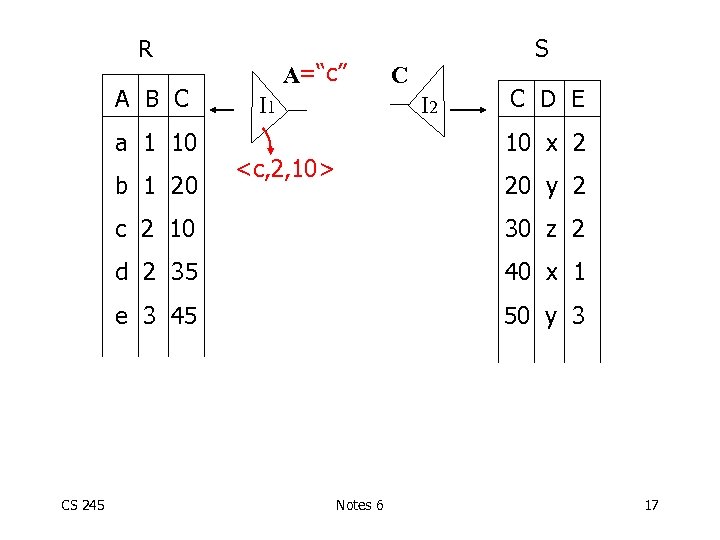
R A B C a 1 10 b 1 20 A=“c” I 1 S C I 2 C D E 10 x 2 <c, 2, 10> 20 y 2 c 2 10 d 2 35 40 x 1 e 3 45 CS 245 30 z 2 50 y 3 Notes 6 17
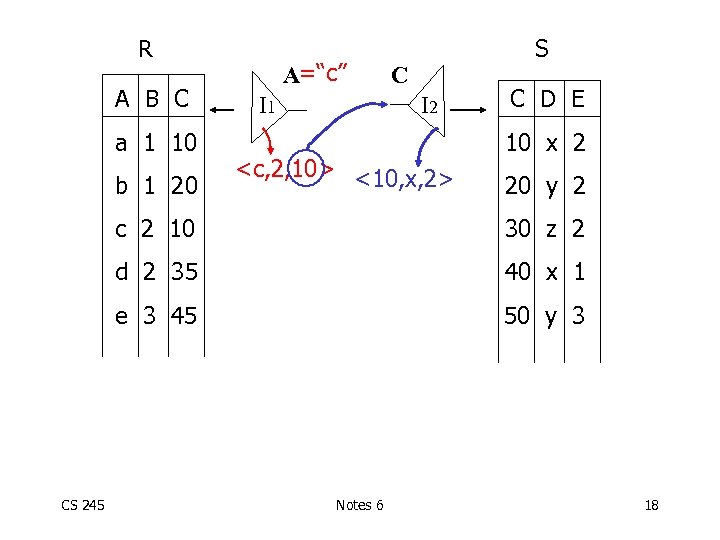
R A B C a 1 10 b 1 20 A=“c” I 1 S C I 2 <c, 2, 10> <10, x, 2> C D E 10 x 2 20 y 2 c 2 10 d 2 35 40 x 1 e 3 45 CS 245 30 z 2 50 y 3 Notes 6 18
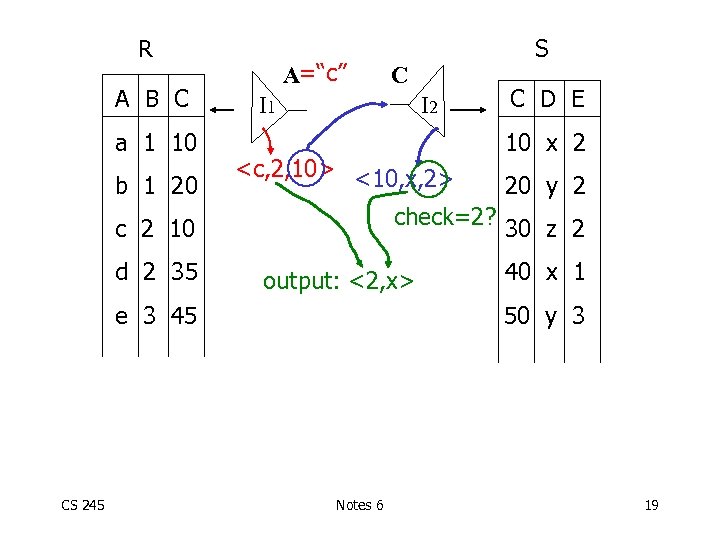
R A B C a 1 10 b 1 20 A=“c” I 2 <c, 2, 10> <10, x, 2> check=2? output: <2, x> e 3 45 CS 245 C I 1 c 2 10 d 2 35 S C D E 10 x 2 20 y 2 30 z 2 40 x 1 50 y 3 Notes 6 19
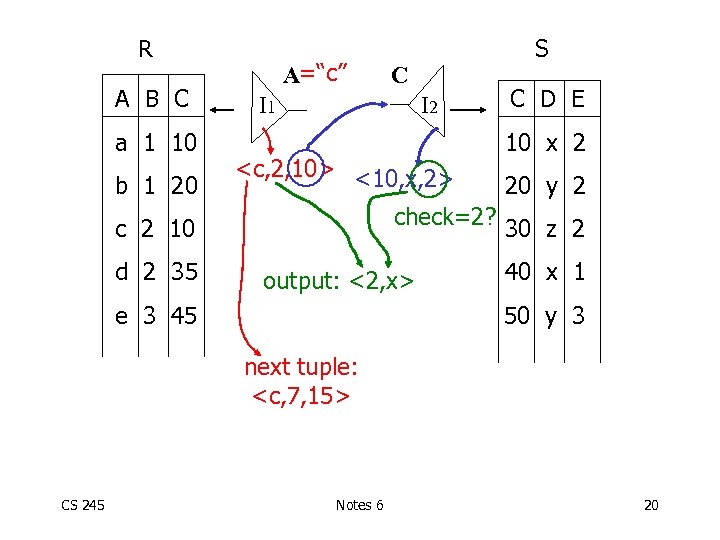
R A B C a 1 10 b 1 20 A=“c” C I 1 I 2 <c, 2, 10> <10, x, 2> check=2? c 2 10 d 2 35 S output: <2, x> e 3 45 C D E 10 x 2 20 y 2 30 z 2 40 x 1 50 y 3 next tuple: <c, 7, 15> CS 245 Notes 6 20
Overview of Query Optimization CS 245 Notes 6 21
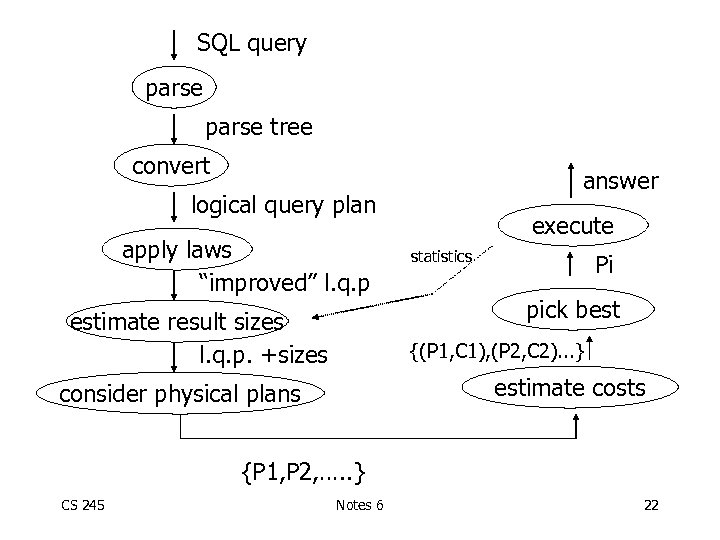
SQL query parse tree convert answer logical query plan apply laws “improved” l. q. p estimate result sizes l. q. p. +sizes execute statistics Pi pick best {(P 1, C 1), (P 2, C 2). . . } estimate costs consider physical plans {P 1, P 2, …. . } CS 245 Notes 6 22
Example: SQL query SELECT title FROM Stars. In WHERE star. Name IN ( SELECT name FROM Movie. Star WHERE birthdate LIKE ‘%1960’ ); (Find the movies with stars born in 1960) CS 245 Notes 6 23
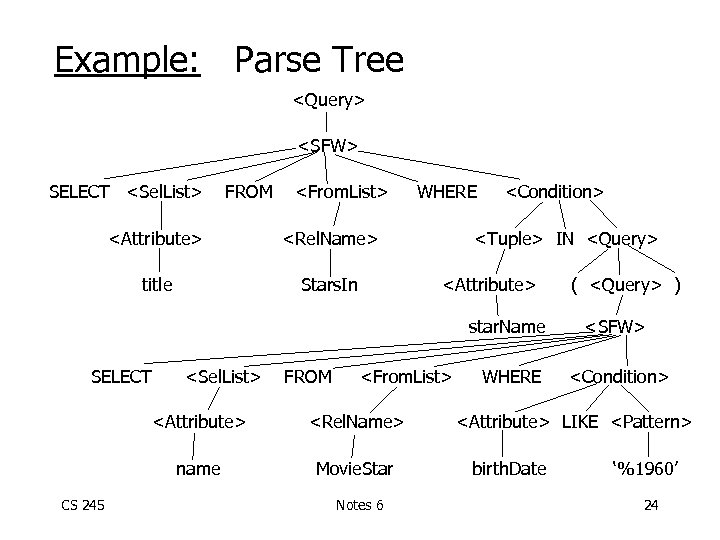
Example: Parse Tree <Query> <SFW> SELECT <Sel. List> FROM <From. List> <Attribute> <Rel. Name> title Stars. In WHERE <Condition> <Tuple> IN <Query> <Attribute> ( <Query> ) star. Name SELECT <Sel. List> FROM <From. List> <Attribute> name CS 245 <Rel. Name> Movie. Star Notes 6 <SFW> WHERE <Condition> <Attribute> LIKE <Pattern> birth. Date ‘%1960’ 24
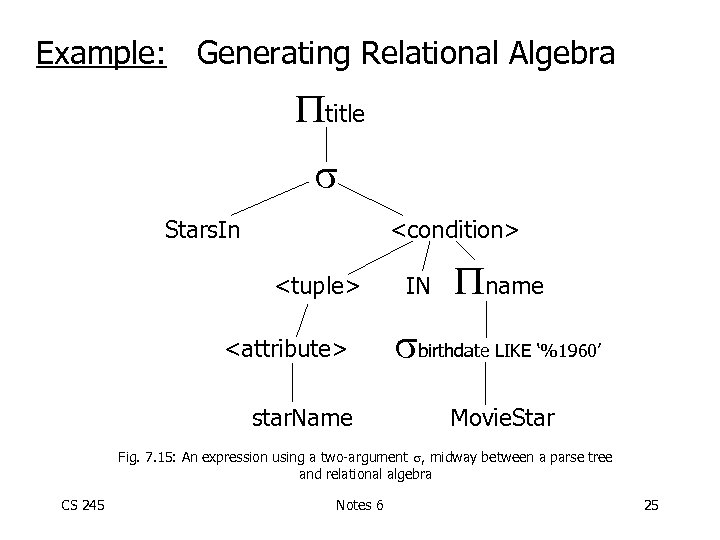
Example: Generating Relational Algebra title Stars. In <condition> <tuple> <attribute> star. Name IN name birthdate LIKE ‘%1960’ Movie. Star Fig. 7. 15: An expression using a two-argument , midway between a parse tree and relational algebra CS 245 Notes 6 25
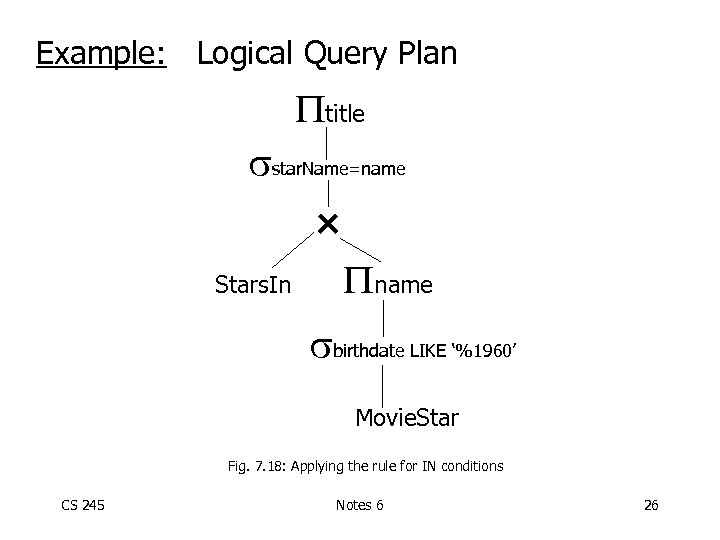
Example: Logical Query Plan title star. Name=name Stars. In name birthdate LIKE ‘%1960’ Movie. Star Fig. 7. 18: Applying the rule for IN conditions CS 245 Notes 6 26
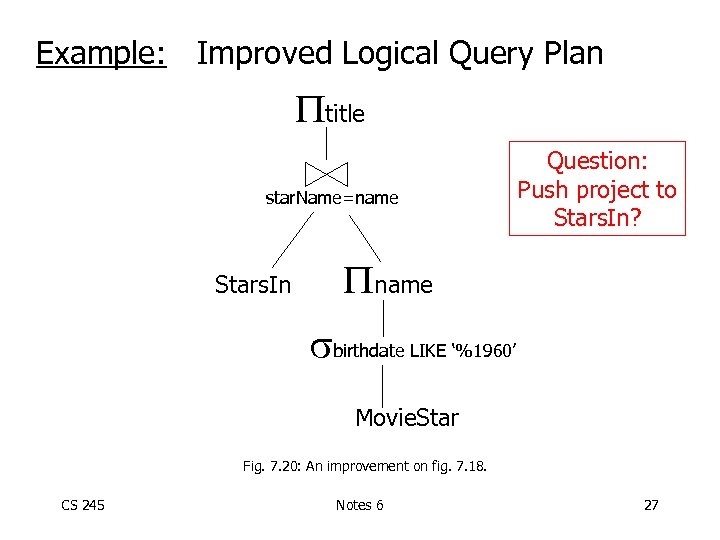
Example: Improved Logical Query Plan title star. Name=name Stars. In Question: Push project to Stars. In? name birthdate LIKE ‘%1960’ Movie. Star Fig. 7. 20: An improvement on fig. 7. 18. CS 245 Notes 6 27
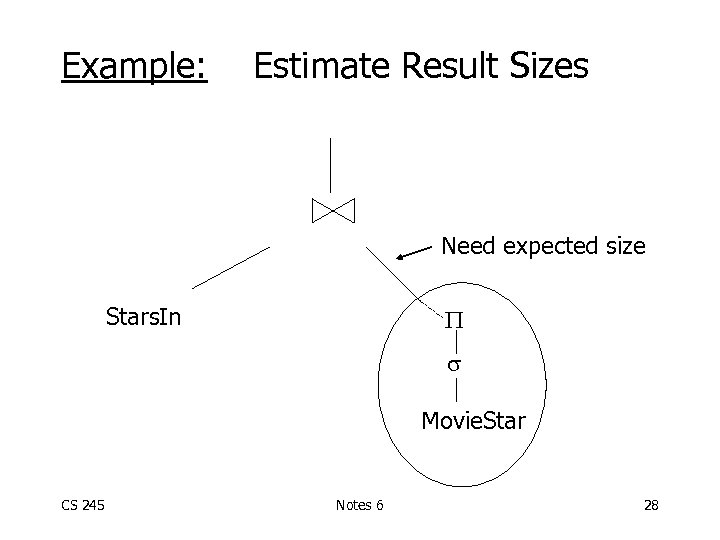
Example: Estimate Result Sizes Need expected size Stars. In Movie. Star CS 245 Notes 6 28
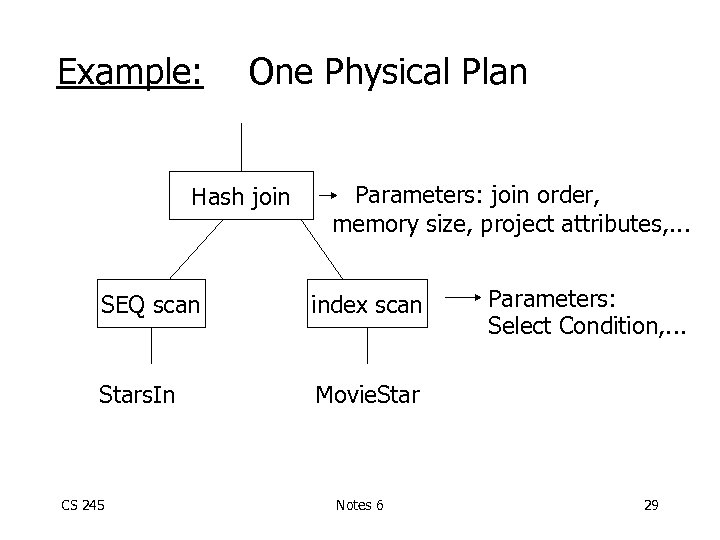
Example: One Physical Plan Hash join Parameters: join order, memory size, project attributes, . . . SEQ scan index scan Stars. In Parameters: Select Condition, . . . Movie. Star CS 245 Notes 6 29
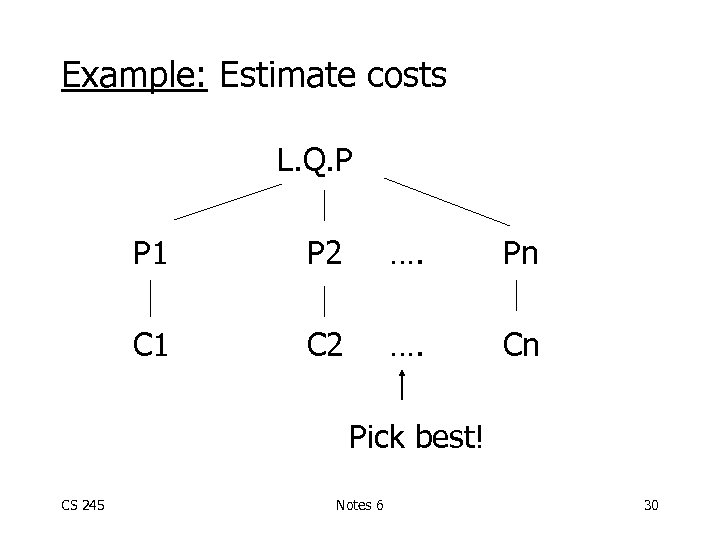
Example: Estimate costs L. Q. P P 1 P 2 …. Pn C 1 C 2 …. Cn Pick best! CS 245 Notes 6 30
![Textbook outline Chapter 15 5 Algebra for queries [Ch 5] [bags vs sets] -](https://present5.com/presentation/d719f6e359313f283e5049833ed14be8/image-31.jpg "Textbook outline Chapter 15 5 Algebra for queries [Ch 5] [bags vs sets] -")
Textbook outline Chapter 15 5 Algebra for queries [Ch 5] [bags vs sets] - Select, project, join, …. [project list a, a+b->x, …] - Duplicate elimination, grouping, sorting 15. 1 Physical operators [15. 1] - Scan, sort, … 15. 2 - 15. 6 Implementing operators + [15. 2 -15. 6] estimating their cost CS 245 Notes 6 31
![Chapter 16 16. 1[16. 1] 16. 2[16. 2] 16. 3[16. 3] Parsing Algebraic laws](https://present5.com/presentation/d719f6e359313f283e5049833ed14be8/image-32.jpg "Chapter 16 16. 1[16. 1] 16. 2[16. 2] 16. 3[16. 3] Parsing Algebraic laws")
Chapter 16 16. 1[16. 1] 16. 2[16. 2] 16. 3[16. 3] Parsing Algebraic laws Parse tree -> logical query plan 16. 4[16. 4] Estimating result sizes 16. 5 -7[16. 5 -7] Cost based optimization CS 245 Notes 6 32
Reading textbook - Chapters 15, 16 Optional: – Sections 15. 7, 15. 8, 15. 9 [15. 7, 15. 8] – Sections 16. 6, 16. 7 [16. 6, 16. 7] Optional: Duplicate elimination operator grouping, aggregation operators CS 245 Notes 6 33
Query Optimization - In class order • Relational algebra level (A) • Detailed query plan level – Estimate Costs (B) • without indexes • with indexes – Generate and compare plans (C) CS 245 Notes 6 34
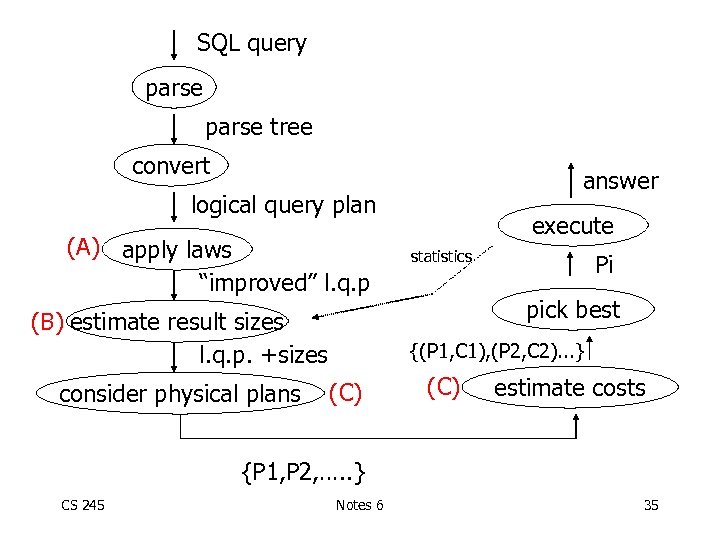
SQL query parse tree convert answer logical query plan (A) apply laws “improved” l. q. p (B) estimate result sizes l. q. p. +sizes consider physical plans execute statistics Pi pick best {(P 1, C 1), (P 2, C 2). . . } (C) estimate costs {P 1, P 2, …. . } CS 245 Notes 6 35
Relational algebra optimization • Transformation rules (preserve equivalence) • What are good transformations? CS 245 Notes 6 36
Rules: R (R CS 245 Natural joins & cross products & union S = S) T S R =R (S Notes 6 T) 37
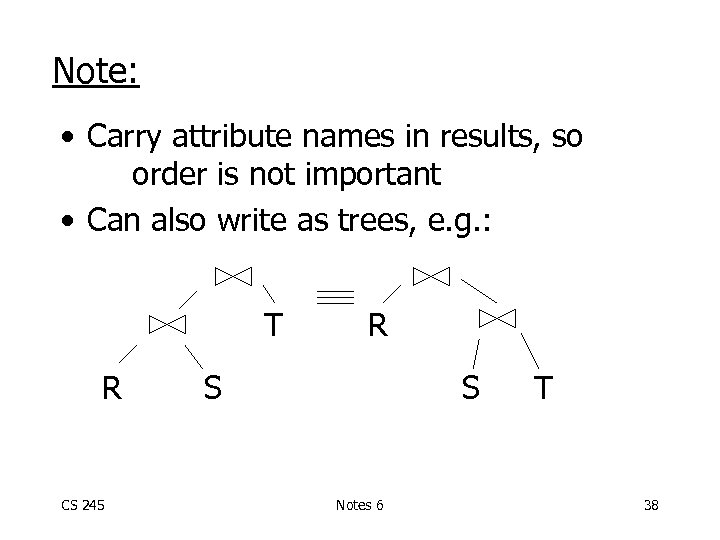
Note: • Carry attribute names in results, so order is not important • Can also write as trees, e. g. : T R CS 245 R S S Notes 6 T 38
Rules: R (R Natural joins & cross products & union S = S) T S R =R (S T) Rx. S=Sx. R (R x S) x T = R x (S x T) RUS=SUR R U (S U T) = (R U S) U T CS 245 Notes 6 39
Rules: Selects p 1 p 2(R) = p 1 vp 2(R) = CS 245 Notes 6 40
Rules: Selects p 1 p 2(R) = p 1 vp 2(R) = CS 245 p 1 [ p 2 (R)] [ p 1 (R)] U [ p 2 (R)] Notes 6 41
Bags vs. Sets R = {a, a, b, b, b, c} S = {b, b, c, c, d} RUS = ? CS 245 Notes 6 42
Bags vs. Sets R = {a, a, b, b, b, c} S = {b, b, c, c, d} RUS = ? • Option 1 SUM RUS = {a, a, b, b, b, c, c, c, d} • Option 2 MAX RUS = {a, a, b, b, b, c, c, d} CS 245 Notes 6 43
Option 2 (MAX) makes this rule work: p 1 vp 2 (R) = p 1(R) U p 2(R) Example: R={a, a, b, b, b, c} P 1 satisfied by a, b; P 2 satisfied by b, c CS 245 Notes 6 44
Option 2 (MAX) makes this rule work: p 1 vp 2 (R) = p 1(R) U p 2(R) Example: R={a, a, b, b, b, c} P 1 satisfied by a, b; P 2 satisfied by b, c p 1 vp 2 (R) = {a, a, b, b, b, c} p 1(R) = {a, a, b, b, b} p 2(R) = {b, b, b, c} p 1(R) U p 2 (R) = {a, a, b, b, b, c} CS 245 Notes 6 45
“Sum” option makes more sense: Senators (……) T 1 = T 1 Rep (……) pyr, state Senators; Yr 14 16 15 State CA CA AZ T 2 = T 2 pyr, state Reps Yr 16 16 15 State CA CA CA Union? CS 245 Notes 6 46
Executive Decision -> Use “SUM” option for bag unions -> Some rules cannot be used for bags CS 245 Notes 6 47
Rules: Project Let: X = set of attributes Y = set of attributes XY = X U Y pxy (R) = CS 245 Notes 6 48
Rules: Project Let: X = set of attributes Y = set of attributes XY = X U Y pxy (R) = px [py (R)] CS 245 Notes 6 49
Rules: Project Let: X = set of attributes Y = set of attributes XY = X U Y pxy (R) = px [py (R)] CS 245 Notes 6 50
Rules: + combined Let p = predicate with only R attribs q = predicate with only S attribs m = predicate with only R, S attribs p (R S) = q (R S) = CS 245 Notes 6 51
Rules: + combined Let p = predicate with only R attribs q = predicate with only S attribs m = predicate with only R, S attribs p (R S) = q (R S) = CS 245 [ p (R)] R [ Notes 6 S q (S)] 52
Rules: + combined (continued) Some Rules can be Derived: p q (R p q m (R pvq (R CS 245 S) = Notes 6 53
![Do one, others for homework: p q (R S) = [ p (R)] [](https://present5.com/presentation/d719f6e359313f283e5049833ed14be8/image-54.jpg "Do one, others for homework: p q (R S) = [ p (R)] [")
Do one, others for homework: p q (R S) = [ p (R)] [ q (S)] p q m (R S) = m [( p R) ( q S)] pvq (R S) = [( p R) S] U [R ( q S)] CS 245 Notes 6 54
--> Derivation for first one: p q (R CS 245 S) = Notes 6 55
--> Derivation for first one: p q (R S) = p [ q (R S) ] = p [ R q (S) ] = [ p (R)] [ q (S)] CS 245 Notes 6 56
Rules: p, combined Let x = subset of R attributes z = attributes in predicate P (subset of R attributes) p x [ p ( R ) ] = CS 245 Notes 6 57
Rules: p, combined Let x = subset of R attributes z = attributes in predicate P (subset of R attributes) p x [ p ( R ) ] = CS 245 { p [ px Notes 6 ( R) ]} 58
Rules: p, combined Let x = subset of R attributes z = attributes in predicate P (subset of R attributes) pxz px[ p (R) ] = px { p [ px CS 245 Notes 6 ( R) ]} 59
Rules: p, combined Let x = subset of R attributes y = subset of S attributes z = intersection of R, S attributes pxy (R CS 245 S) = Notes 6 60
Rules: p, combined Let x = subset of R attributes y = subset of S attributes z = intersection of R, S attributes pxy (R S) = pxy{[pxz (R) ] CS 245 Notes 6 [pyz (S) ]} 61
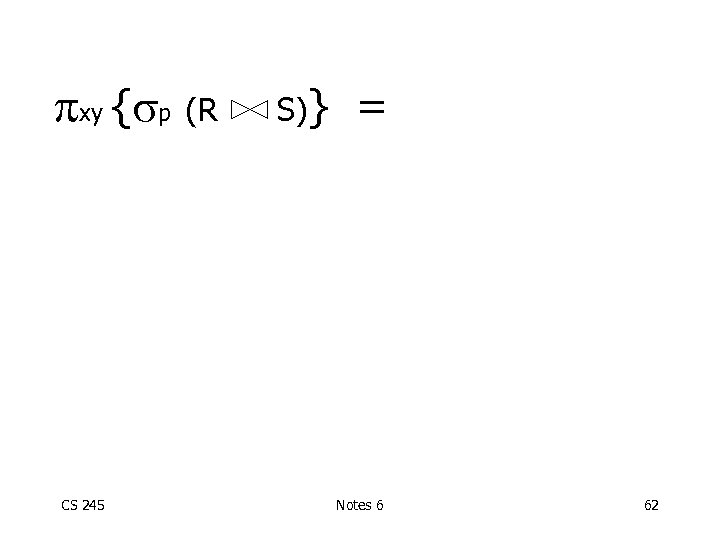
pxy { p (R CS 245 S)} = Notes 6 62
![pxy { p (R S)} = pxy { p [pxz’ (R) pyz’ (S)]} z’](https://present5.com/presentation/d719f6e359313f283e5049833ed14be8/image-63.jpg "pxy { p (R S)} = pxy { p [pxz’ (R) pyz’ (S)]} z’")
pxy { p (R S)} = pxy { p [pxz’ (R) pyz’ (S)]} z’ = z U {attributes used in P CS 245 Notes 6 } 63
Rules for , p combined with X similar. . . e. g. , CS 245 p (R X S) = ? Notes 6 64
Rules , U combined: p(R U S) = p(R) U p(S) p(R - S) = p(R) - S = p(R) - p(S) CS 245 Notes 6 65
Which are “good” transformations? p 1 p 2 (R) p 1 [ p 2 (R)] p (R S) [ p (R)] S R S S R px [ p (R)] px { p [pxz (R)]} CS 245 Notes 6 66
Conventional wisdom: do projects early Example: R(A, B, C, D, E) x={E} P: (A=3) (B=“cat”) px { p (R)} CS 245 vs. p. E { p{p. ABE(R)}} Notes 6 67
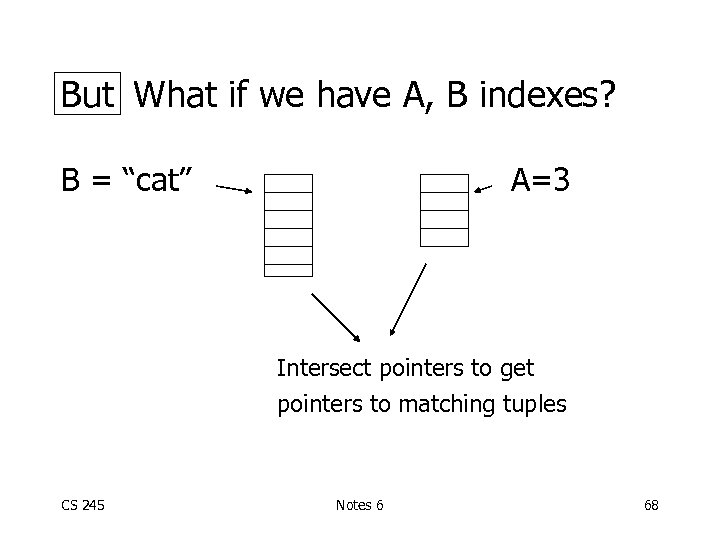
But What if we have A, B indexes? B = “cat” A=3 Intersect pointers to get pointers to matching tuples CS 245 Notes 6 68
Bottom line: • No transformation is always good • Usually good: early selections CS 245 Notes 6 69
In textbook: more transformations • Eliminate common sub-expressions • Other operations: duplicate elimination CS 245 Notes 6 70
Outline - Query Processing • Relational algebra level – transformations – good transformations • Detailed query plan level – estimate costs – generate and compare plans CS 245 Notes 6 71
• Estimating cost of query plan (1) Estimating size of results (2) Estimating # of IOs CS 245 Notes 6 72
Estimating result size • Keep statistics for relation R – T(R) : # tuples in R – S(R) : # of bytes in each R tuple – B(R): # of blocks to hold all R tuples – V(R, A) : # distinct values in R for attribute A CS 245 Notes 6 73
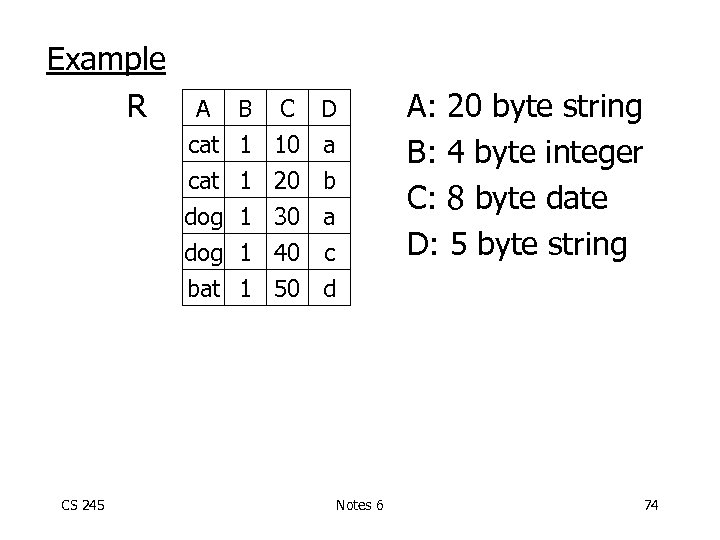
Example R B C D cat dog bat CS 245 A 1 1 10 20 30 40 50 a b a c d Notes 6 A: 20 byte string B: 4 byte integer C: 8 byte date D: 5 byte string 74
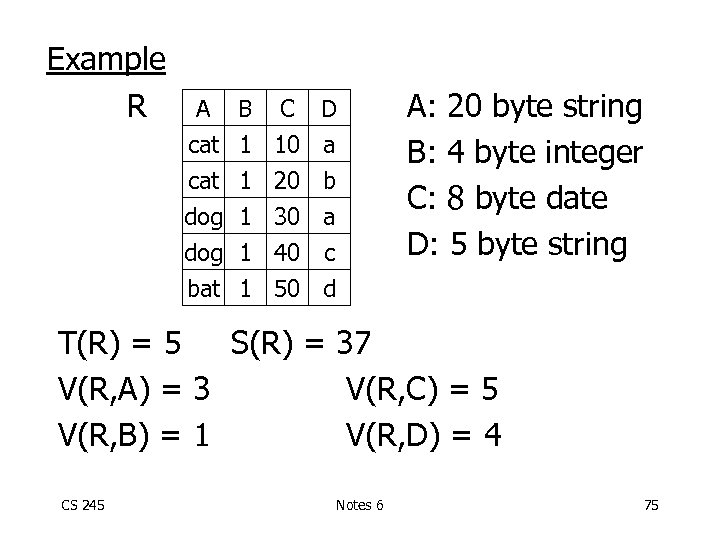
Example R A B C D cat dog bat 1 1 10 20 30 40 50 a b a c d A: 20 byte string B: 4 byte integer C: 8 byte date D: 5 byte string T(R) = 5 S(R) = 37 V(R, A) = 3 V(R, C) = 5 V(R, B) = 1 V(R, D) = 4 CS 245 Notes 6 75
Size estimates for W = R 1 x R 2 T(W) = S(W) = CS 245 Notes 6 76
Size estimates for W = R 1 x R 2 T(W) = T(R 1) T(R 2) S(W) = S(R 1) + S(R 2) CS 245 Notes 6 77
Size estimate for W = A=a (R) S(W) = S(R) T(W) = ? CS 245 Notes 6 78
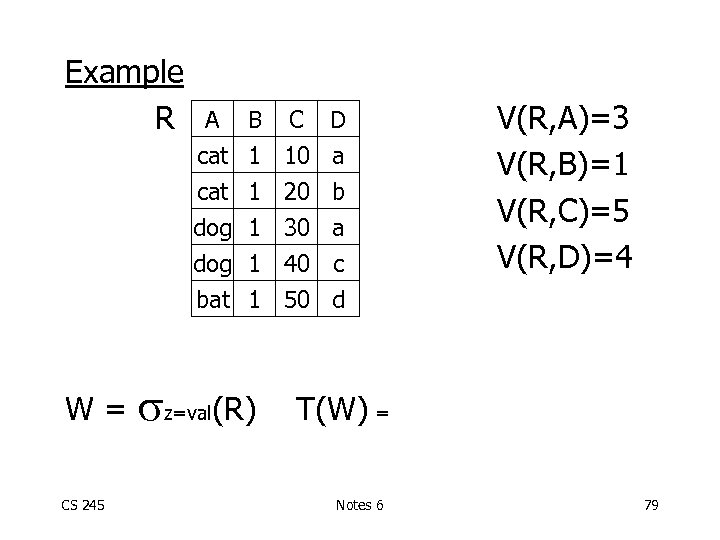
Example R CS 245 B C D cat dog bat W= A 1 1 10 20 30 40 50 a b a c d z=val(R) V(R, A)=3 V(R, B)=1 V(R, C)=5 V(R, D)=4 T(W) = Notes 6 79
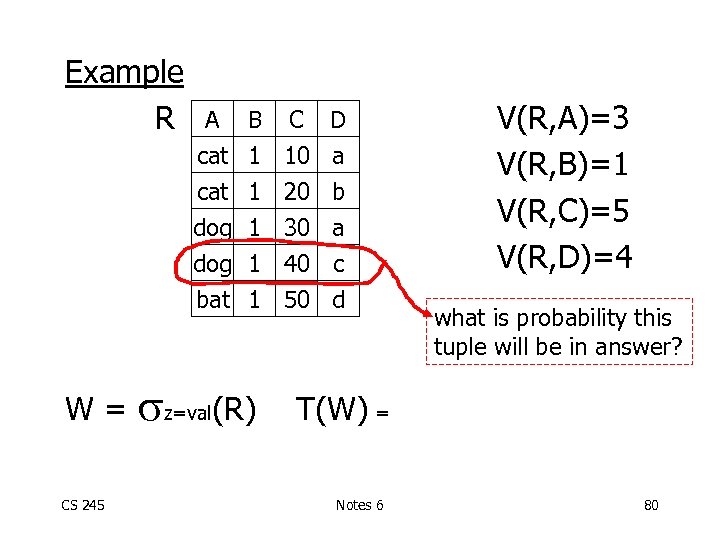
Example R CS 245 B C D cat dog bat W= A 1 1 10 20 30 40 50 a b a c d z=val(R) V(R, A)=3 V(R, B)=1 V(R, C)=5 V(R, D)=4 what is probability this tuple will be in answer? T(W) = Notes 6 80
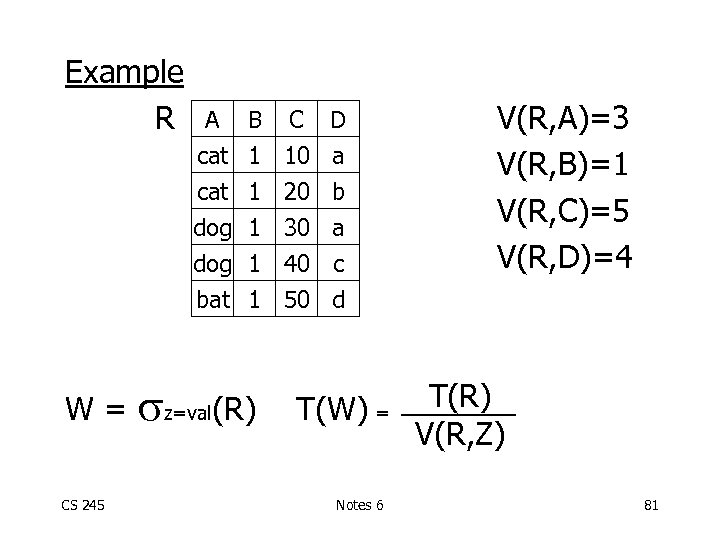
Example R CS 245 B C D cat dog bat W= A 1 1 10 20 30 40 50 a b a c d z=val(R) T(W) = Notes 6 V(R, A)=3 V(R, B)=1 V(R, C)=5 V(R, D)=4 T(R) V(R, Z) 81
Assumption: Values in select expression Z = val are uniformly distributed over possible V(R, Z) values. CS 245 Notes 6 82
Alternate Assumption: Values in select expression Z = val are uniformly distributed over domain with DOM(R, Z) values. CS 245 Notes 6 83
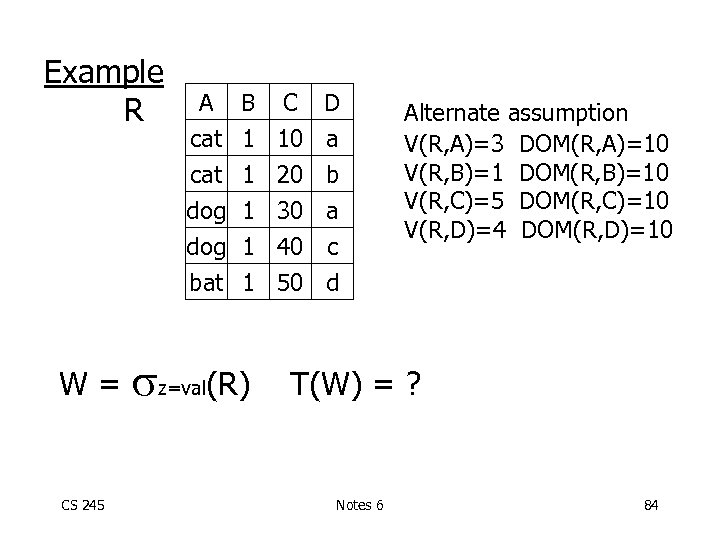
Example R A B C D cat 1 10 a cat dog bat W= CS 245 1 1 z=val(R) 20 30 40 50 b a c d Alternate assumption V(R, A)=3 DOM(R, A)=10 V(R, B)=1 DOM(R, B)=10 V(R, C)=5 DOM(R, C)=10 V(R, D)=4 DOM(R, D)=10 T(W) = ? Notes 6 84
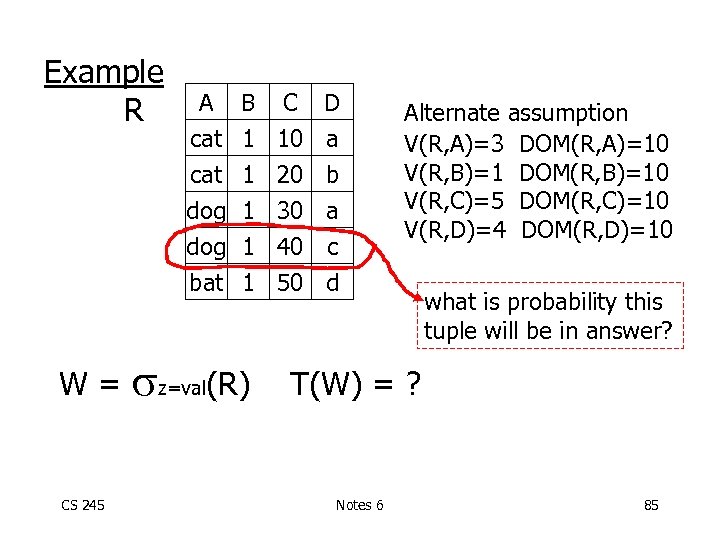
Example R A B C D cat 1 10 a cat dog bat W= CS 245 1 1 z=val(R) 20 30 40 50 b a c d Alternate assumption V(R, A)=3 DOM(R, A)=10 V(R, B)=1 DOM(R, B)=10 V(R, C)=5 DOM(R, C)=10 V(R, D)=4 DOM(R, D)=10 what is probability this tuple will be in answer? T(W) = ? Notes 6 85
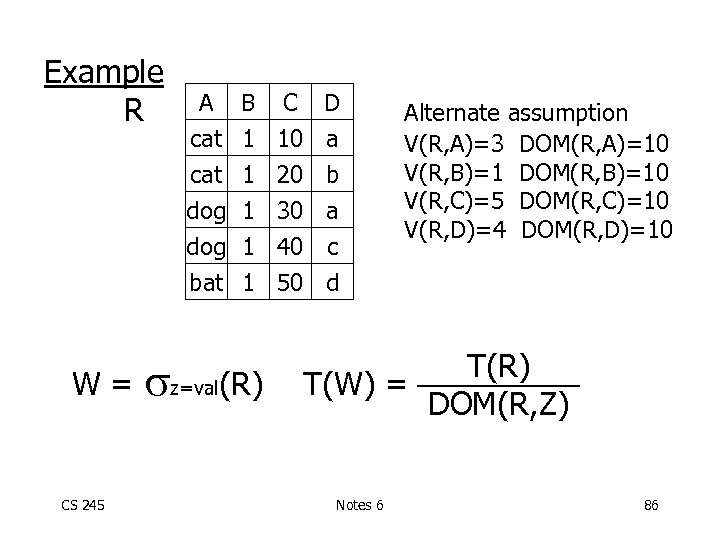
Example R A B C D cat 1 10 a cat dog bat W= CS 245 1 1 z=val(R) 20 30 40 50 b a c d Alternate assumption V(R, A)=3 DOM(R, A)=10 V(R, B)=1 DOM(R, B)=10 V(R, C)=5 DOM(R, C)=10 V(R, D)=4 DOM(R, D)=10 T(R) T(W) = DOM(R, Z) Notes 6 86
Selection cardinality SC(R, A) = average # records that satisfy equality condition on R. A T(R) V(R, A) SC(R, A) = T(R) DOM(R, A) CS 245 Notes 6 87
What about W = z val (R) ? T(W) = ? CS 245 Notes 6 88
z val (R) What about W = ? T(W) = ? • Solution # 1: T(W) = T(R)/2 CS 245 Notes 6 89
z val (R) What about W = ? T(W) = ? • Solution # 1: T(W) = T(R)/2 • Solution # 2: T(W) = T(R)/3 CS 245 Notes 6 90
• Solution # 3: Estimate values in range Example R Z Min=1 V(R, Z)=10 W= z 15 (R) Max=20 CS 245 Notes 6 91
• Solution # 3: Estimate values in range Example R Z Min=1 V(R, Z)=10 W= z 15 (R) Max=20 f = 20 -15+1 = 6 20 -1+1 20 (fraction of range) T(W) = f T(R) CS 245 Notes 6 92
![Equivalently: f V(R, Z) = fraction of distinct values T(W) = [f V(Z, R)]](https://present5.com/presentation/d719f6e359313f283e5049833ed14be8/image-93.jpg "Equivalently: f V(R, Z) = fraction of distinct values T(W) = [f V(Z, R)]")
Equivalently: f V(R, Z) = fraction of distinct values T(W) = [f V(Z, R)] T(R) = f T(R) V(Z, R) CS 245 Notes 6 93
Size estimate for W = R 1 R 2 Let x = attributes of R 1 y = attributes of R 2 CS 245 Notes 6 94
Size estimate for W = R 1 R 2 Let x = attributes of R 1 y = attributes of R 2 Case 1 X Y= Same as R 1 x R 2 CS 245 Notes 6 95
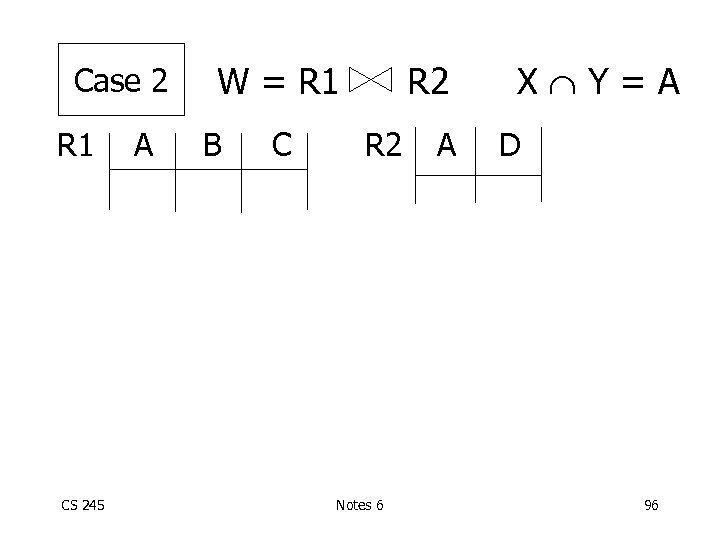
Case 2 R 1 CS 245 A W = R 1 B C R 2 Notes 6 A X Y=A D 96
W = R 1 Case 2 R 1 A B C R 2 A X Y=A D Assumption: V(R 1, A) V(R 2, A) Every A value in R 1 is in R 2 V(R 2, A) V(R 1, A) Every A value in R 2 is in R 1 “containment of value sets” Sec. 7. 4. 4 CS 245 Notes 6 97
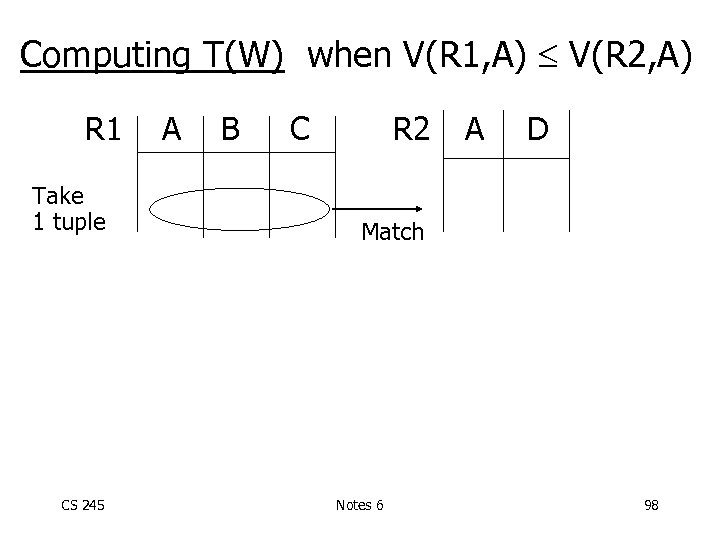
Computing T(W) when V(R 1, A) V(R 2, A) R 1 Take 1 tuple CS 245 A B C R 2 A D Match Notes 6 98
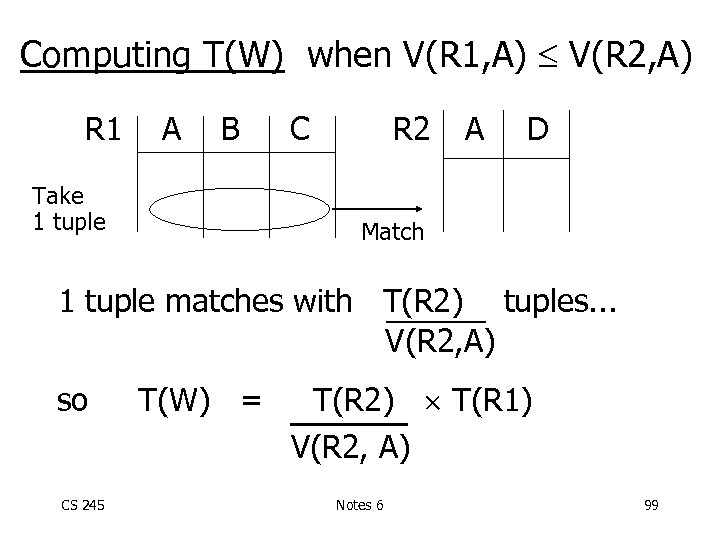
Computing T(W) when V(R 1, A) V(R 2, A) R 1 A B Take 1 tuple C R 2 A D Match 1 tuple matches with T(R 2) tuples. . . V(R 2, A) so CS 245 T(W) = T(R 2) T(R 1) V(R 2, A) Notes 6 99
• V(R 1, A) V(R 2, A) T(W) = T(R 2) T(R 1) V(R 2, A) • V(R 2, A) V(R 1, A) T(W) = T(R 2) T(R 1) V(R 1, A) [A is common attribute] CS 245 Notes 6 100
In general T(W) = CS 245 W = R 1 R 2 T(R 2) T(R 1) max{ V(R 1, A), V(R 2, A) } Notes 6 101
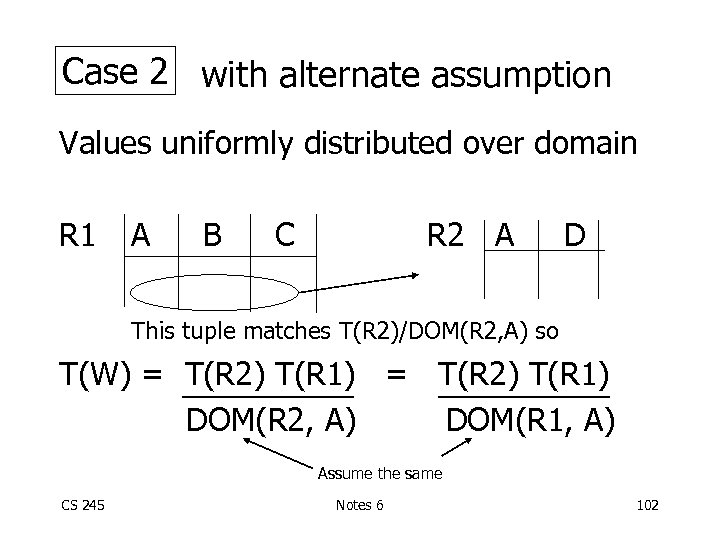
Case 2 with alternate assumption Values uniformly distributed over domain R 1 A B C R 2 A D This tuple matches T(R 2)/DOM(R 2, A) so T(W) = T(R 2) T(R 1) DOM(R 2, A) DOM(R 1, A) Assume the same CS 245 Notes 6 102
In all cases: S(W) = S(R 1) + S(R 2) - S(A) size of attribute A CS 245 Notes 6 103
Using similar ideas, we can estimate sizes of: AB (R) …. . Sec. 16. 4. 2 (same for either edition) A=a B=b (R) …. Sec. 16. 4. 3 R S with common attribs. A, B, C Sec. 16. 4. 5 Union, intersection, diff, …. Sec. 16. 4. 7 CS 245 Notes 6 104
Note: for complex expressions, need intermediate T, S, V results. E. g. W = [ A=a (R 1) ] R 2 Treat as relation U T(U) = T(R 1)/V(R 1, A) S(U) = S(R 1) Also need V (U, *) !! CS 245 Notes 6 105
To estimate Vs E. g. , U = A=a (R 1) Say R 1 has attribs A, B, C, D V(U, A) = V(U, B) = V(U, C) = V(U, D) = CS 245 Notes 6 106
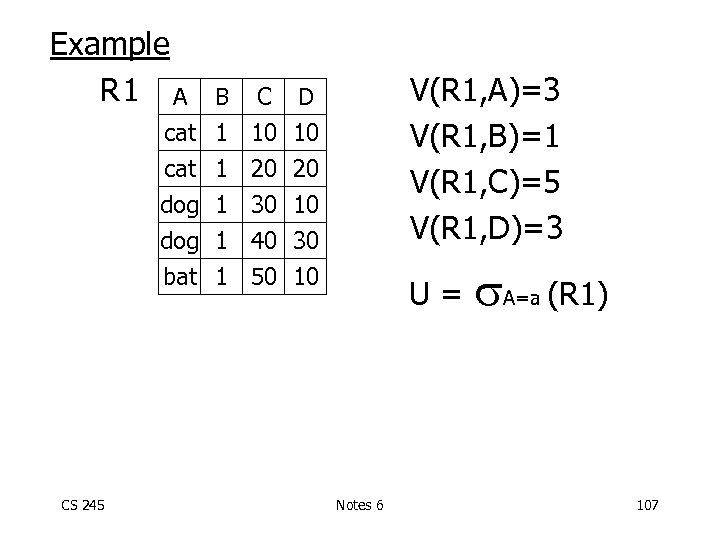
Example R 1 A V(R 1, A)=3 V(R 1, B)=1 V(R 1, C)=5 V(R 1, D)=3 B C D cat 1 10 10 cat 1 20 20 dog 1 30 10 dog 1 40 30 bat 1 50 10 CS 245 U= Notes 6 A=a (R 1) 107
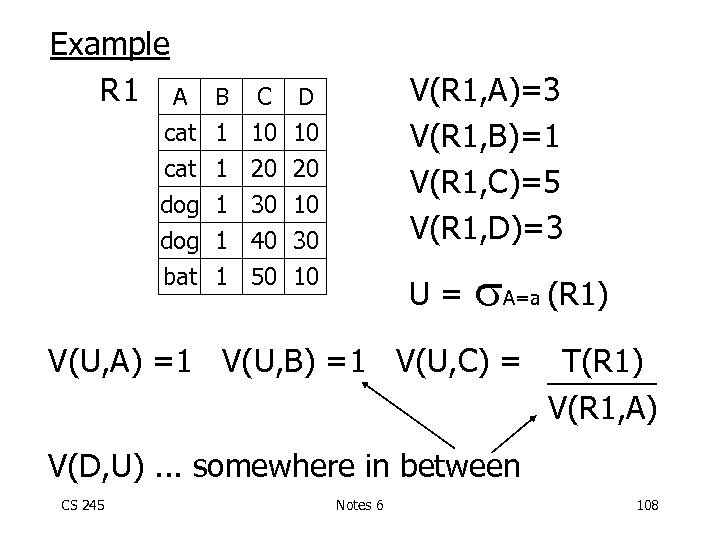
Example R 1 A V(R 1, A)=3 V(R 1, B)=1 V(R 1, C)=5 V(R 1, D)=3 B C D cat 1 10 10 cat 1 20 20 dog 1 30 10 dog 1 40 30 bat 1 50 10 U= A=a (R 1) V(U, A) =1 V(U, B) =1 V(U, C) = T(R 1) V(R 1, A) V(D, U). . . somewhere in between CS 245 Notes 6 108
Possible Guess V(U, A) V(U, B) CS 245 U= A=a (R) =1 = V(R, B) Notes 6 109
For Joins U = R 1(A, B) R 2(A, C) V(U, A) = min { V(R 1, A), V(R 2, A) } V(U, B) = V(R 1, B) V(U, C) = V(R 2, C) [called “preservation of value sets” in section 7. 4. 4] CS 245 Notes 6 110
Example: Z = R 1(A, B) R 1 R 2 R 3 CS 245 R 2(B, C) R 3(C, D) T(R 1) = 1000 V(R 1, A)=50 V(R 1, B)=100 T(R 2) = 2000 V(R 2, B)=200 V(R 2, C)=300 T(R 3) = 3000 V(R 3, C)=90 V(R 3, D)=500 Notes 6 111
Partial Result: U = R 1 T(U) = 1000 200 CS 245 R 2 V(U, A) = 50 V(U, B) = 100 V(U, C) = 300 Notes 6 112
Z=U R 3 T(Z) = 1000 2000 3000 V(Z, A) = 50 200 300 V(Z, B) = 100 V(Z, C) = 90 V(Z, D) = 500 CS 245 Notes 6 113
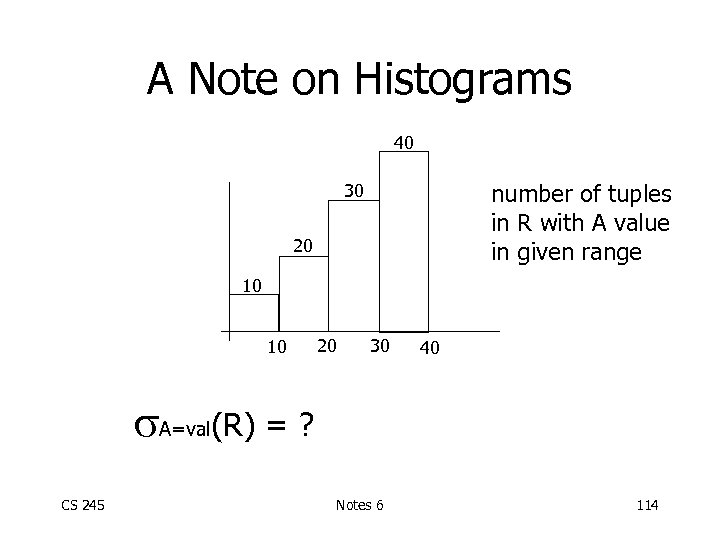
A Note on Histograms 40 number of tuples in R with A value in given range 30 20 10 10 20 30 40 A=val(R) = ? CS 245 Notes 6 114
Summary • Estimating size of results is an “art” • Don’t forget: Statistics must be kept up to date… (cost? ) CS 245 Notes 6 115
Outline • Estimating cost of query plan – Estimating size of results – Estimating # of IOs done! next… • Generate and compare plans CS 245 Notes 6 116
Скачать презентацию CS 245 Database System Principles Notes 6 Query
d719f6e359313f283e5049833ed14be8.ppt