CS 201 Data Structures and Discrete Mathematics I

CS 201: Data Structures and Discrete Mathematics I Linked Lists, Stacks and Queues

Data Structure • A construct that can be defined within a programming language to store a collection of data – one may store some data in an array of integers, an array of objects, or an array of arrays 3/18/2018 CS 201

Abstract Data Type (ADT) • Definition: a collection of data together with a set of operations on that data – specifications indicate what ADT operations do, but not how to implement them – data structures are part of an ADT’s implementation • Programmer can use an ADT without knowing its implementation. 3/18/2018 CS 201

Typical Operations on Data • Add data to a data collection • Remove data from a data collection • Ask questions about the data in a data collection. E. g. , what is the value at a particular location, and is x in the collection? 3/18/2018 CS 201

Why ADT • • • Hide the unnecessary details Help manage software complexity Easier software maintenance Functionalities are less likely to change Localised rather than global changes 3/18/2018 CS 201

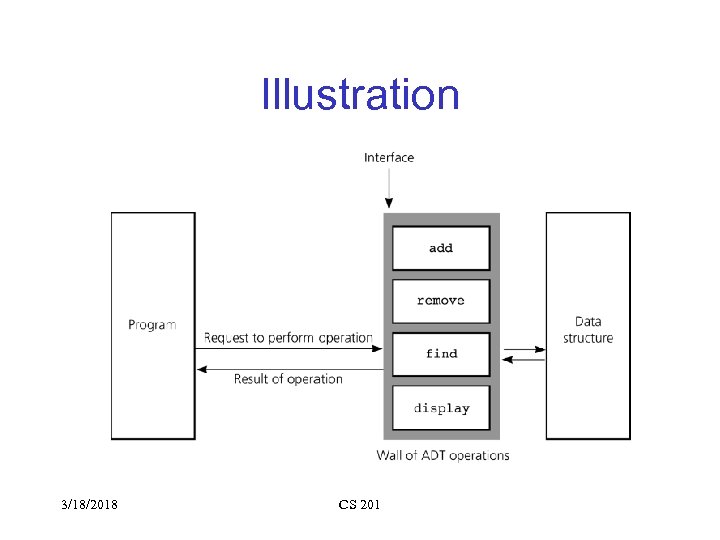Illustration 3/18/2018 CS 201

Linked Lists

Lists • List: a finite sequence of data items a 1, a 2, a 3, …, an • Lists are pervasive in computing – e. g. class list, list of chars, list of events • Typical operations: – – – – 3/18/2018 Creation Insert / remove an element Test for emptiness Find an item/element Current element / next / previous Find k-th element Print the entire list CS 201

Array-Based List Implementation • One simplementation is to use arrays – A sequence of n-elements • Maximum size is anticipated a priori. • Internal variables: – – Maximum size max. Size (m) Current size cur. Size (n) Current index cur Array of elements list. Array cur. Size n an 0 3/18/2018 a 1 a 2 a 3 n-1 1 2 CS 201 unused m

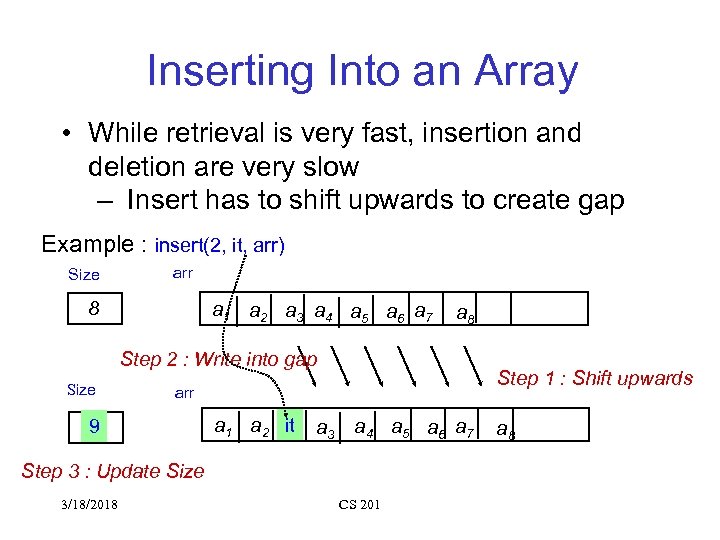Inserting Into an Array • While retrieval is very fast, insertion and deletion are very slow – Insert has to shift upwards to create gap Example : insert(2, it, arr) Size arr 8 a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 Step 2 : Write into gap Size Step 1 : Shift upwards arr 9 8 a 1 a 2 it a 3 a 4 a 5 a 6 a 7 Step 3 : Update Size 3/18/2018 CS 201 a 8

Coding typedef int int } LIST struct { arr[MAX]; max; size; void insert(int j, int it, LIST *pl) { // pre : 1<=j<=size+1 int i; for (i=pl->size; i>=j; i=i-1) // Step 1: Create gap { pl->arr[i+1]= pl->arr[i]; }; pl->arr[j]= it; } 3/18/2018 // Step 2: Write to gap pl->size = pl->size + 1; // Step 3: Update size CS 201

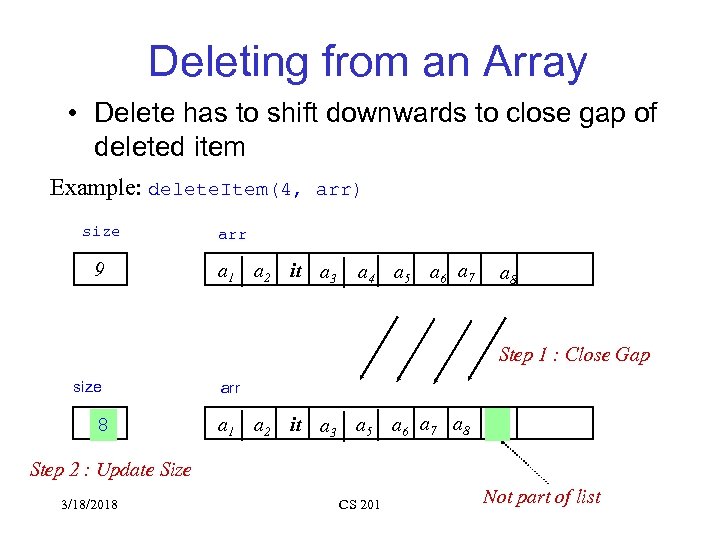Deleting from an Array • Delete has to shift downwards to close gap of deleted item Example: delete. Item(4, arr) size 9 arr a 1 a 2 it a 3 a 4 a 5 a 6 a 7 a 8 Step 1 : Close Gap size 9 8 arr a 1 a 2 it a 3 a 5 a 6 a 7 a 8 Step 2 : Update Size 3/18/2018 CS 201 Not part of list

Coding void delete(int j, LIST *pl) { // pre : 1<=j<=size for (i=j+1; i<=pl->size; i=i+1) // Step 1: Close gap { pl->arr[i-i]=pl->arr[i]; }; // Step 2: Update size pl->size = pl->size - 1; } 3/18/2018 CS 201

Linked List Approach • Main problem of array is the slow deletion/insertion since it has to shift items in its contiguous memory • Solution: linked list where items need not be contiguous item next with nodes of the form ai • Sequence (list) of four items < a 1, a 2 , a 3 , a 4 > can be represented by: head represents null a 1 3/18/2018 a 2 a 3 CS 201 a 4

Pointer-Based Linked Lists • A node in a linked list is usually a struct Node A node { int item Node *next; }; //end struct • A node is dynamically allocated Node *p; p = malloc(sizeof(Node)); 3/18/2018 CS 201

Pointer-Based Linked Lists • The head pointer points to the first node in a linked list • If head is NULL, the linked list is empty – head=NULL • head=malloc(sizeof(Node)) 3/18/2018 CS 201

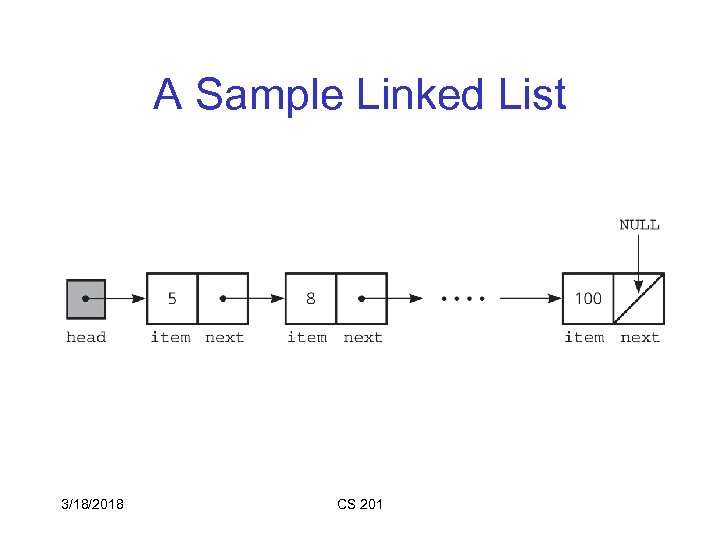A Sample Linked List 3/18/2018 CS 201

Traverse a Linked List • Reference a node member with the -> operator p->item; • A traverse operation visits each node in the linked list – A pointer variable cur keeps track of the current node for (Node *cur = head; cur != NULL; cur = cur->next) x = cur->item; 3/18/2018 CS 201

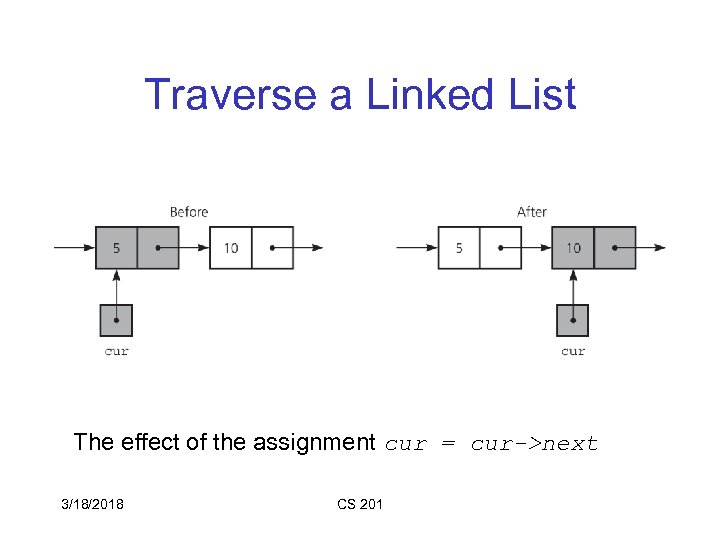Traverse a Linked List The effect of the assignment cur = cur->next 3/18/2018 CS 201

Delete a Node from a Linked List • Deleting an interior/last node prev->next=cur->next; • Deleting the first node head=head->next; • Return deleted node to system cur->next = NULL; free(cur); cur=NULL; 3/18/2018 CS 201

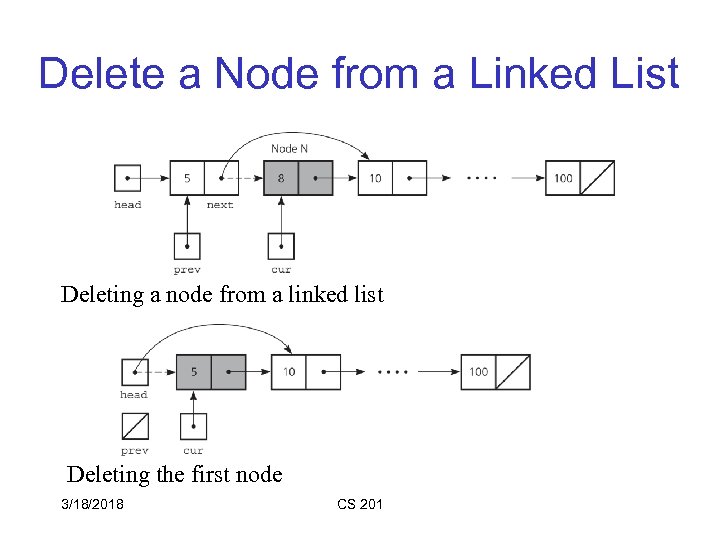Delete a Node from a Linked List Deleting a node from a linked list Deleting the first node 3/18/2018 CS 201

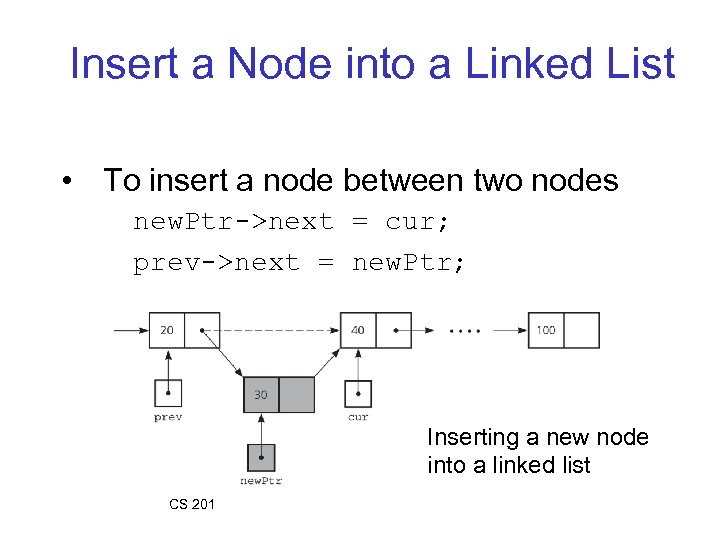Insert a Node into a Linked List • To insert a node between two nodes new. Ptr->next = cur; prev->next = new. Ptr; Inserting a new node into a linked list CS 201

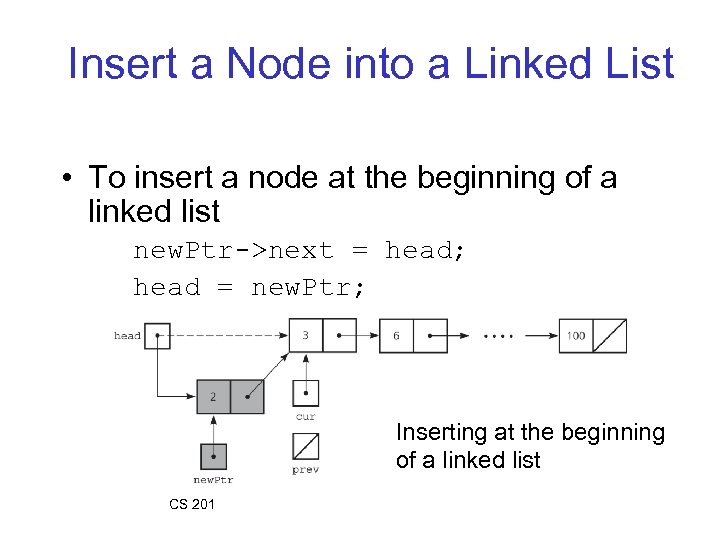Insert a Node into a Linked List • To insert a node at the beginning of a linked list new. Ptr->next = head; head = new. Ptr; Inserting at the beginning of a linked list CS 201

Insert a Node into a Linked List • Inserting at the end of a linked list is not a special case if cur is NULL new. Ptr->next = cur; prev->next = new. Ptr; Inserting at the end of a linked list CS 201

Look up BOOLEAN lookup (int x, Node *L) { if (L == NULL) return FALSE else if (x == L->item) return TRUE else return lookup(x, L-next); } 3/18/2018 CS 201

An ADT Interface for List • Functions – is. Empty – get. Length – insert – delete – Lookup –… 3/18/2018 • Data Members – head – Size • Local variables to member functions – cur – prev CS 201

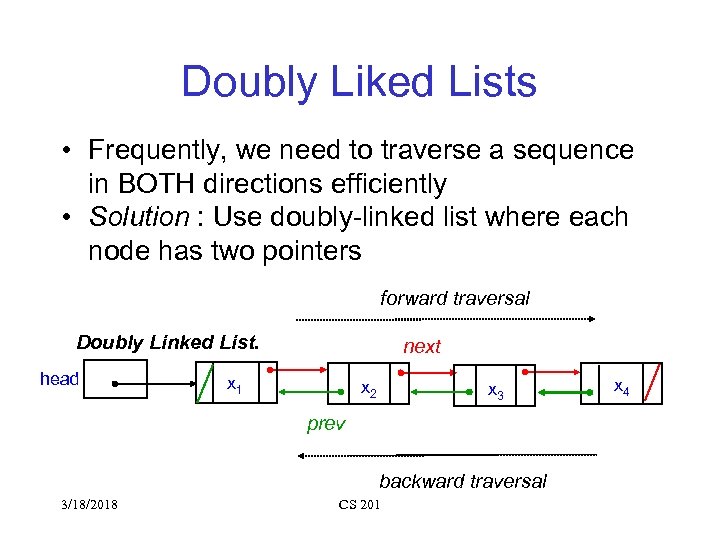Doubly Liked Lists • Frequently, we need to traverse a sequence in BOTH directions efficiently • Solution : Use doubly-linked list where each node has two pointers forward traversal Doubly Linked List. head next x 1 x 2 x 3 prev backward traversal 3/18/2018 CS 201 x 4

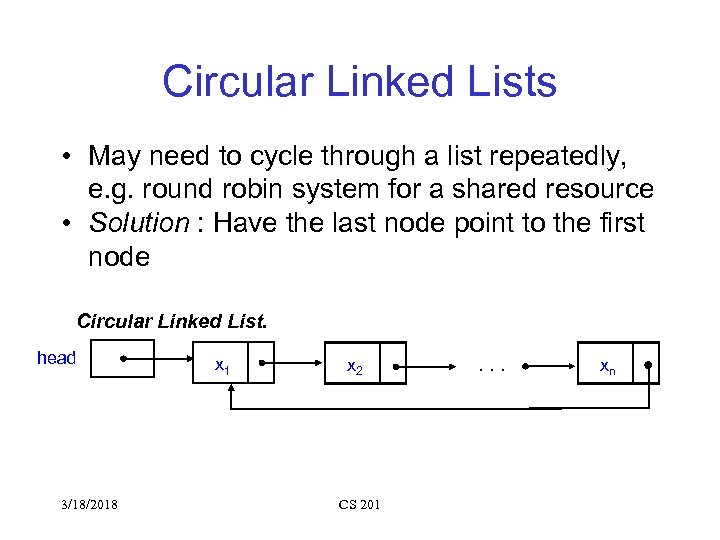Circular Linked Lists • May need to cycle through a list repeatedly, e. g. round robin system for a shared resource • Solution : Have the last node point to the first node Circular Linked List. head 3/18/2018 x 1 x 2 CS 201 . . . xn

Stacks

What is a Stack? • A stack is a list with the restriction that insertions and deletions can be performed in only one position, namely, the end of the list, called the top. • The operations: push (insert) and pop (delete) push(o) pop Top 3/18/2018 3 2 7 6 CS 201

Stack ADT Interface • The main functions in the Stack ADT are (S is the stack) boolean is. Empty(); // return true if empty boolean is. Full(S); // return true if full void push(S, item); // insert item into stack void pop(S); // remove most recent item void clear(S); // remove all items from stack Item top(S); // retrieve most recent item Item top. And. Pop(S); // return & remove most recent item 3/18/2018 CS 201

Sample Operation Stack S = malloc(sizeof(stack)); push(S, “a”); s push(S, “b”); d top push(S, “c”); c e d=top(S); b pop(S); a push(S, “e”); pop(S); 3/18/2018 CS 201

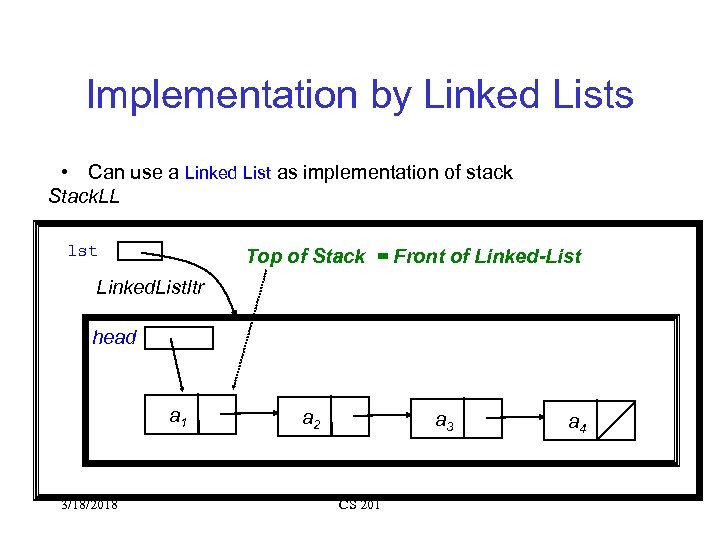Implementation by Linked Lists • Can use a Linked List as implementation of stack Stack. LL lst Top of Stack = Front of Linked-List Linked. List. Itr head a 1 3/18/2018 a 2 a 3 CS 201 a 4

Code struct Node { int element; Node * next; }; typedef struct Node * STACK; 3/18/2018 CS 201

More code 3/18/2018 CS 201

More Code 3/18/2018 CS 201

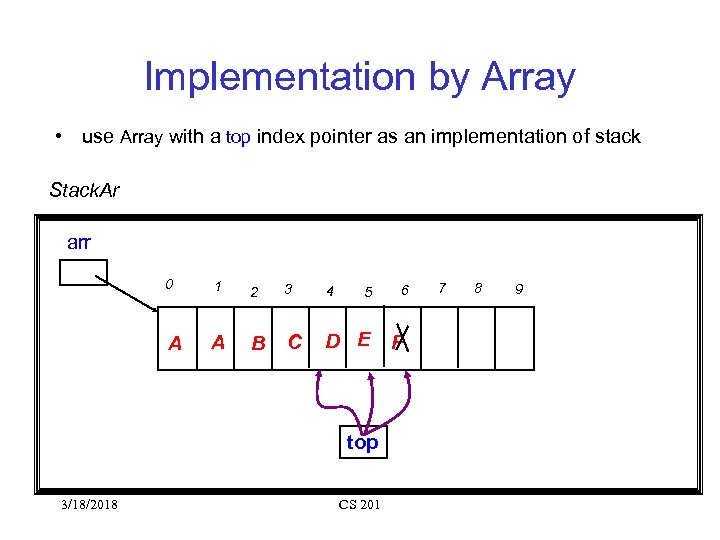Implementation by Array • use Array with a top index pointer as an implementation of stack Stack. Ar arr 0 1 2 3 4 A A B C D E 5 top 3/18/2018 CS 201 6 F 7 8 9

Code 3/18/2018 CS 201

More code 3/18/2018 CS 201

More code 3/18/2018 CS 201

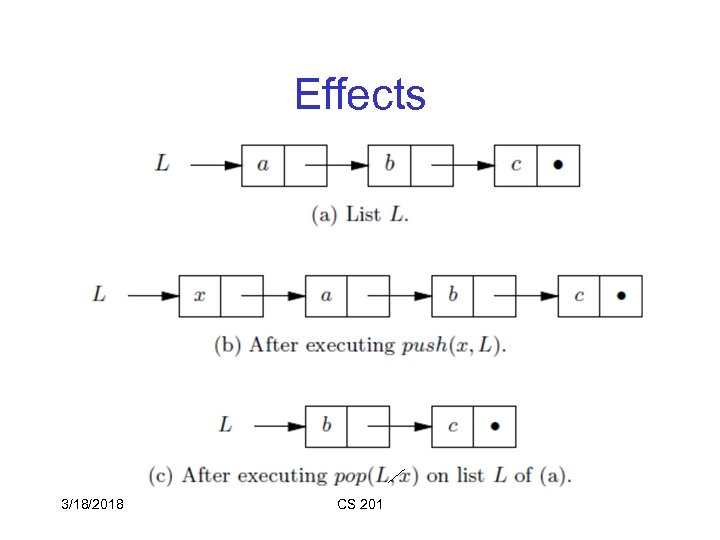Effects 3/18/2018 CS 201

Applications • Many application areas use stacks: – line editing – bracket matching – postfix calculation – function call stack 3/18/2018 CS 201

Line Editing • A line editor would place characters read into a buffer but may use a backspace symbol (denoted by ) to do error correction • Refined Task – read in a line – correct the errors via backspace – print the corrected line in reverse Input Corrected Input abc_defgh 2 klpqr wxyz : : abc_defg 2 klpwxyz Reversed Output : zyxwplk 2 gfed_cba 3/18/2018 CS 201

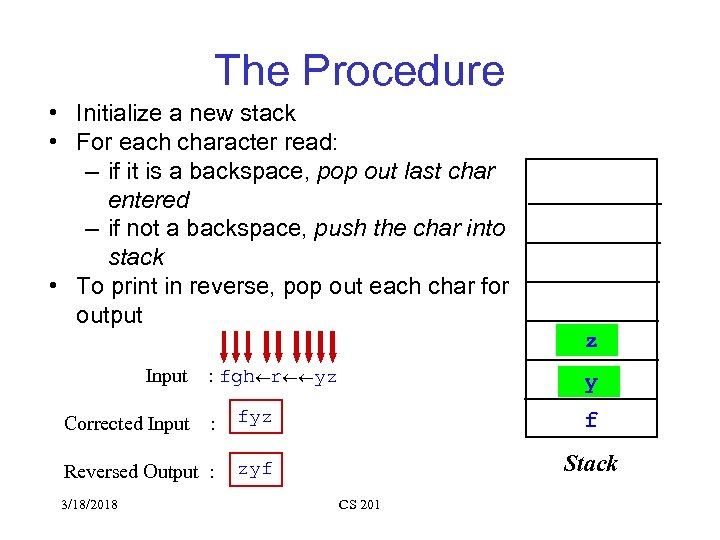The Procedure • Initialize a new stack • For each character read: – if it is a backspace, pop out last char entered – if not a backspace, push the char into stack • To print in reverse, pop out each char for output Input : fgh r yz r z h y g : fyz f Reversed Output : zyf Stack Corrected Input 3/18/2018 CS 201

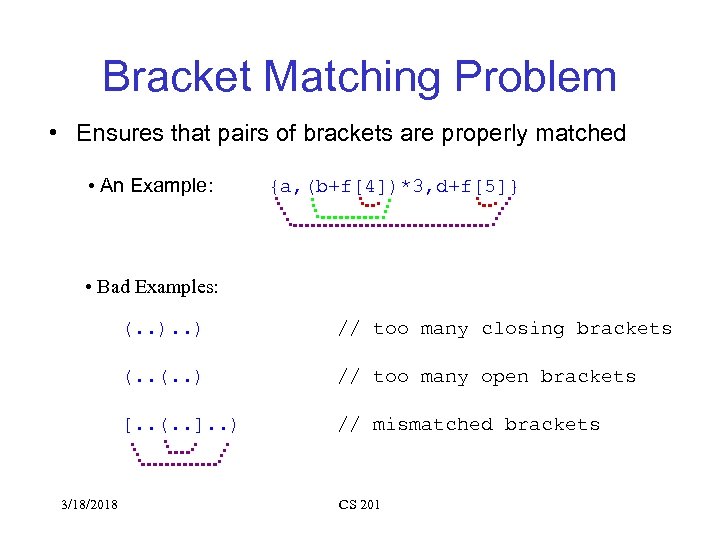Bracket Matching Problem • Ensures that pairs of brackets are properly matched • An Example: {a, (b+f[4])*3, d+f[5]} • Bad Examples: (. . ) // too many open brackets [. . (. . ]. . ) 3/18/2018 // too many closing brackets // mismatched brackets CS 201

Informal Procedure Initialize the stack to empty For every char read if open bracket then push onto stack if close bracket, then return & remove most recent item from the stack if doesn’t match then flag error if non-bracket, skip the char read [ Example {a, (b+f[4])*3, d+f[5]} ] [ ) ( ] { } Stack 3/18/2018 CS 201

Postfix Calculator • Computation of arithmetic expressions can be efficiently carried out in Postfix notation with the help of a stack. Infix Prefix Postfix - arg 1 op arg 2 - op arg 1 arg 2 - arg 1 arg 2 op postfix infix 2 3 * 4 + (2*3)+4 2*3+4 2 3 4 + * 2*(3+4) 3/18/2018 CS 201

Informal Procedure Initialise stack S For each item read. If it is an operand, push on the stack If it is an operator, pop arguments from stack; perform operation; push result onto the stack Expr 2 3 4 + * 3/18/2018 push(S, 2) push(S, 3) push(S, 4) arg 2=top. And. Pop(S) arg 1=top. And. Pop(S) push(S, arg 1+arg 2) arg 2=top. And. Pop(S) arg 1=top. And. Pop(S) push(S, arg 1*arg 2) CS 201 4 3+4=7 3 2*7=14 2 Stack

Summary • The ADT stack operations have a lastin, first-out (LIFO) behavior • Stack has many applications – algorithms that operate on algebraic expressions – a strong relationship between recursion and stacks exists • Stack can be implemented using arrays or linked lists 3/18/2018 CS 201

Queues

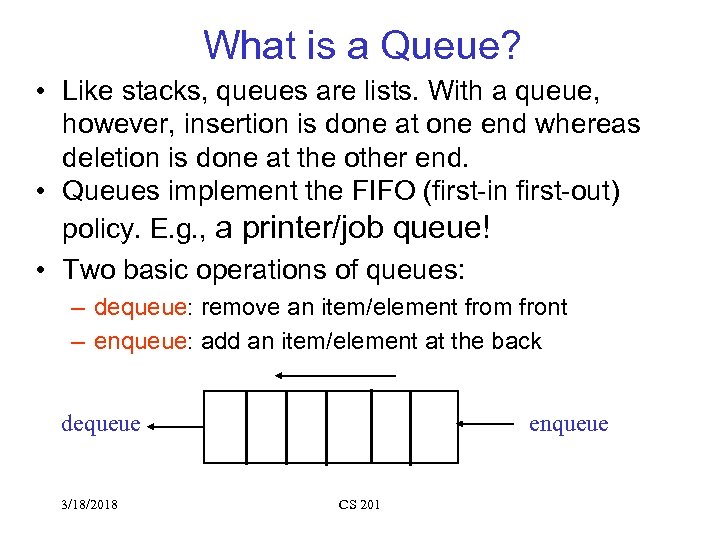What is a Queue? • Like stacks, queues are lists. With a queue, however, insertion is done at one end whereas deletion is done at the other end. • Queues implement the FIFO (first-in first-out) policy. E. g. , a printer/job queue! • Two basic operations of queues: – dequeue: remove an item/element from front – enqueue: add an item/element at the back dequeue 3/18/2018 enqueue CS 201

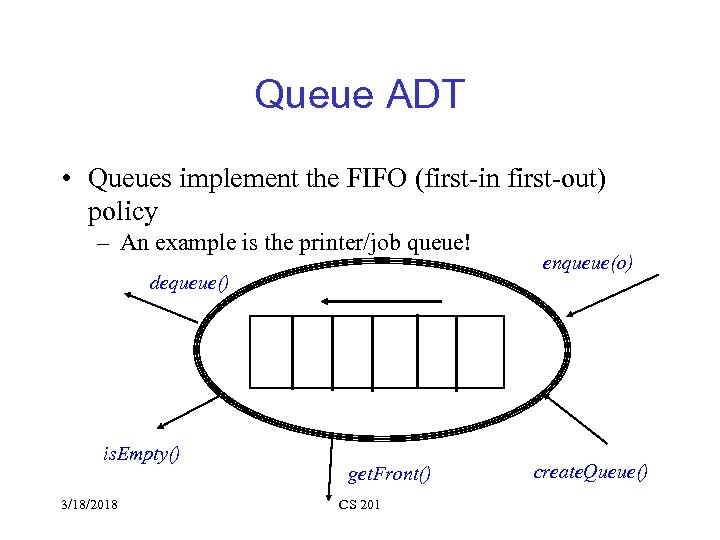Queue ADT • Queues implement the FIFO (first-in first-out) policy – An example is the printer/job queue! dequeue() is. Empty() 3/18/2018 get. Front() CS 201 enqueue(o) create. Queue()

Sample Operation Queue *Q; enqueue(Q, “a”); q enqueue(Q, “b”); enqueue(Q, “c”); d=get. Front(Q); d dequeue(Q); a b c e enqueue(Q, “e”); dequeue(Q); 3/18/2018 back front CS 201

Queue ADT interface • The main functions in the Queue ADT are (Q is the queue) void enqueue(o, Q) // insert o to back of Q void dequeue(Q); // remove oldest item Item get. Front(Q); // retrieve oldest item boolean is. Empty(Q); // checks if Q is empty boolean is. Full(Q); // checks if Q is full void clear(Q); // make Q empty } 3/18/2018 CS 201

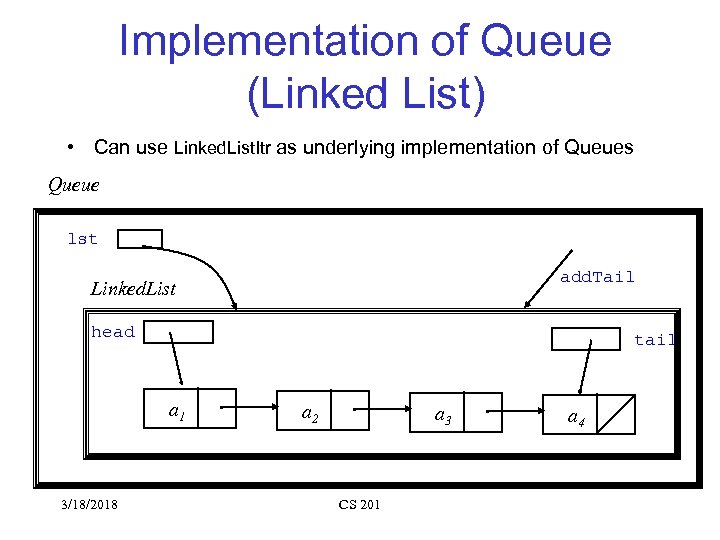Implementation of Queue (Linked List) • Can use Linked. List. Itr as underlying implementation of Queues Queue lst add. Tail Linked. List head tail a 1 3/18/2018 a 2 a 3 CS 201 a 4

Code struct Node { int element; Node * next; }; struct QUEUE { Node * front; Node * rear; }; 3/18/2018 CS 201

More code 3/18/2018 CS 201

More code CELL is a list node 3/18/2018 CS 201

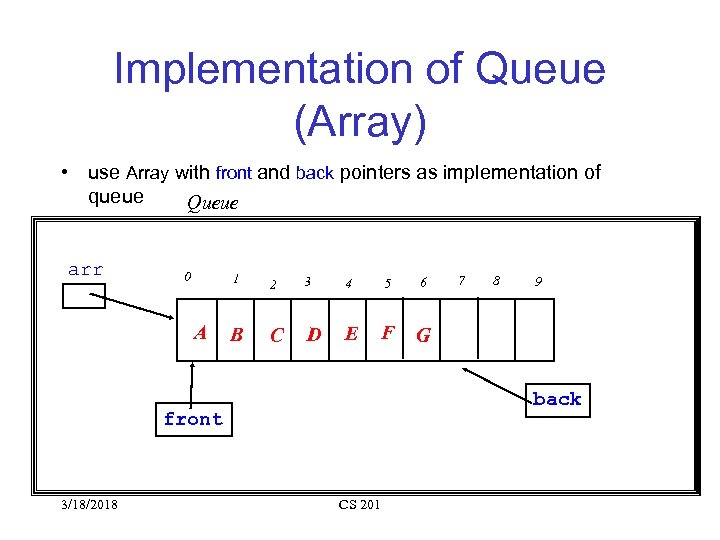Implementation of Queue (Array) • use Array with front and back pointers as implementation of queue Queue arr 0 1 A 2 3 4 5 6 B C D E F G 8 9 back front 3/18/2018 7 CS 201

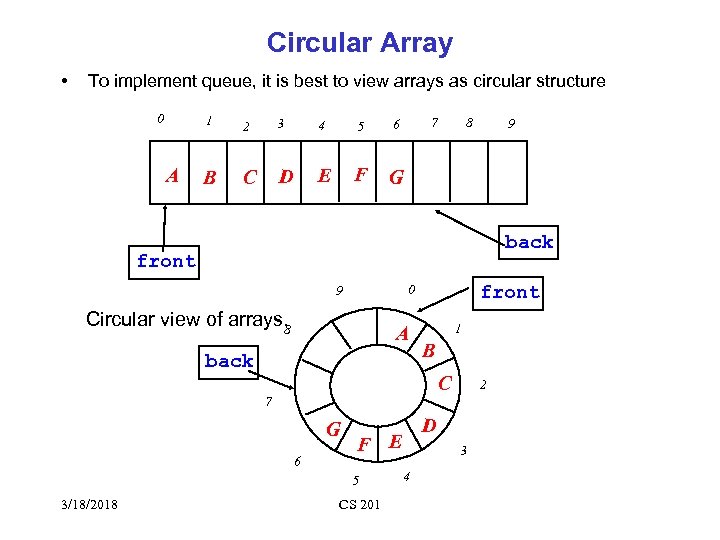Circular Array • To implement queue, it is best to view arrays as circular structure 0 1 A 2 3 4 5 6 B C D E F G 7 8 9 back front 0 9 Circular view of arrays. 8 A back 1 B C 7 G 6 3/18/2018 D F E 5 CS 201 2 3 4

How to Advance • Both front & back pointers should make advancement until they reach end of the array. Then, they should re-point to beginning of the array front = adv(front); back = adv(back); int adv(int p) { int r = p+1; if (r

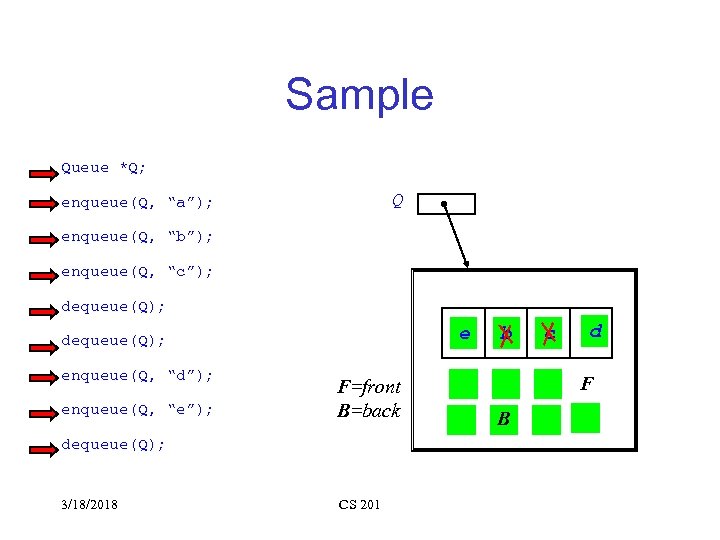Sample Queue *Q; Q enqueue(Q, “a”); enqueue(Q, “b”); enqueue(Q, “c”); dequeue(Q); enqueue(Q, “d”); enqueue(Q, “e”); F=front B=back dequeue(Q); 3/18/2018 d e a dequeue(Q); CS 201 b c F F B B

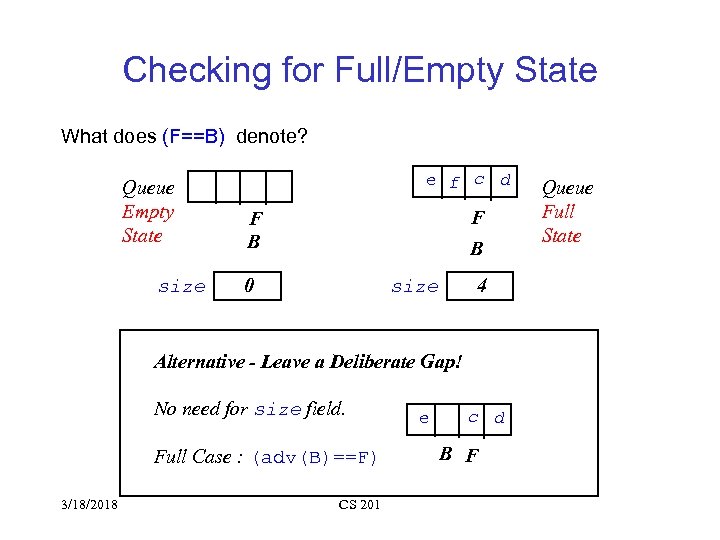Checking for Full/Empty State What does (F==B) denote? Queue Empty State size e f c d F F B B 0 4 size Alternative - Leave a Deliberate Gap! No need for size field. Full Case : (adv(B)==F) 3/18/2018 CS 201 e c d B F Queue Full State

Summary • The definition of the queue operations gives the ADT queue first-in, first-out (FIFO) behavior • The queue can be implemented by linked lists or by arrays • There are many applications – Printer queues, – Telecommunication queues, – Simulations, – Etc. 3/18/2018 CS 201