CS 1104 Computer Organization http www comp

CS 1104 – Computer Organization http: //www. comp. nus. edu. sg/~cs 1104 Aaron Tan Tuck Choy School of Computing National University of Singapore

Lecture 13: Sequential Logic Counters and Registers Counters § § § Introduction: Counters Asynchronous (Ripple) Counters Asynchronous Counters with MOD number < 2 n Asynchronous Down Counters Cascading Asynchronous Counters CS 1104 -13 Lecture 13: Sequential Logic: Counters and Registers 2

Lecture 13: Sequential Logic Counters and Registers § § § Synchronous (Parallel) Counters Up/Down Synchronous Counters Designing Synchronous Counters Decoding A Counters with Parallel Load CS 1104 -13 Lecture 13: Sequential Logic: Counters and Registers 3

Lecture 13: Sequential Logic Counters and Registers § Introduction: Registers v Simple Registers v Registers with Parallel Load § Using Registers to implement Sequential Circuits § Shift Registers v Serial In/Serial Out Shift Registers v Serial In/Parallel Out Shift Registers v Parallel In/Serial Out Shift Registers v Parallel In/Parallel Out Shift Registers CS 1104 -13 Lecture 13: Sequential Logic: Counters and Registers 4

Lecture 13: Sequential Logic Counters and Registers § Bidirectional Shift Registers § An Application – Serial Addition § Shift Register Counters v Ring Counters v Johnson Counters § Random-Access Memory (RAM) CS 1104 -13 Lecture 13: Sequential Logic: Counters and Registers 5

Introduction: Counters § Counters are circuits that cycle through a specified number of states. § Two types of counters: v synchronous (parallel) counters v asynchronous (ripple) counters § Ripple counters allow some flip-flop outputs to be used as a source of clock for other flip-flops. § Synchronous counters apply the same clock to all flipflops. CS 1104 -13 Introduction: Counters 6

Asynchronous (Ripple) Counters § Asynchronous counters: the flip-flops do not change states at exactly the same time as they do not have a common clock pulse. § Also known as ripple counters, as the input clock pulse “ripples” through the counter – cumulative delay is a drawback. § n flip-flops a MOD (modulus) 2 n counter. (Note: A MOD-x counter cycles through x states. ) § Output of the last flip-flop (MSB) divides the input clock frequency by the MOD number of the counter, hence a counter is also a frequency divider. CS 1104 -13 Asynchronous (Ripple) Counters 7

Asynchronous (Ripple) Counters § Example: 2 -bit ripple binary counter. § Output of one flip-flop is connected to the clock input of the next more-significant flip-flop. HIGH Q 0 J C K CLK FF 0 CLK 1 2 3 Q 0 Q 1 J C K FF 1 4 Q 0 Timing diagram Q 0 0 1 0 Q 1 0 0 1 1 00 01 10 11 00. . . 0 CS 1104 -13 Asynchronous (Ripple) Counters 8

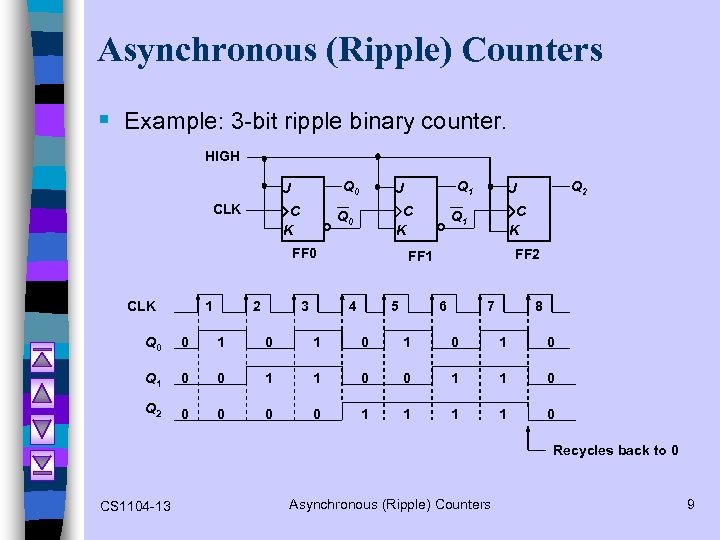Asynchronous (Ripple) Counters § Example: 3 -bit ripple binary counter. HIGH Q 0 J CLK C K Q 0 FF 0 CLK 1 2 3 Q 1 J C K Q 1 FF 2 FF 1 4 5 Q 2 J 6 7 8 Q 0 0 1 0 1 0 Q 1 0 0 1 1 0 Q 2 0 0 1 1 0 Recycles back to 0 CS 1104 -13 Asynchronous (Ripple) Counters 9

Asynchronous (Ripple) Counters § Propagation delays in an asynchronous (rippleclocked) binary counter. § If the accumulated delay is greater than the clock pulse, some counter states may be misrepresented! CLK 1 2 3 4 Q 0 Q 1 Q 2 t. PLH (CLK to Q 0) CS 1104 -13 t. PHL (CLK to Q 0) t. PLH (Q 0 to Q 1) Asynchronous (Ripple) Counters t. PHL (CLK to Q 0) t. PHL (Q 0 to Q 1) t. PLH (Q 1 to Q 2) 10

Asynchronous (Ripple) Counters § Example: 4 -bit ripple binary counter (negative-edge triggered). HIGH Q 0 J CLK Q 1 J C K FF 0 C K FF 1 FF 2 Q 2 J Q 3 C K FF 3 CLK 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Q 0 Q 1 Q 2 Q 3 CS 1104 -13 Asynchronous (Ripple) Counters 11

Asyn. Counters with MOD no. < 2 n § States may be skipped resulting in a truncated sequence. § Technique: force counter to recycle before going through all of the states in the binary sequence. § Example: Given the following circuit, determine the counting sequence (and hence the modulus no. ) C All J, K inputs are 1 (HIGH). CS 1104 -13 Q J B CLK K Q CLR Q J CLK K Q CLR A Q J CLK K Q CLR B C Asynchronous Counters with MOD number < 2^n 12

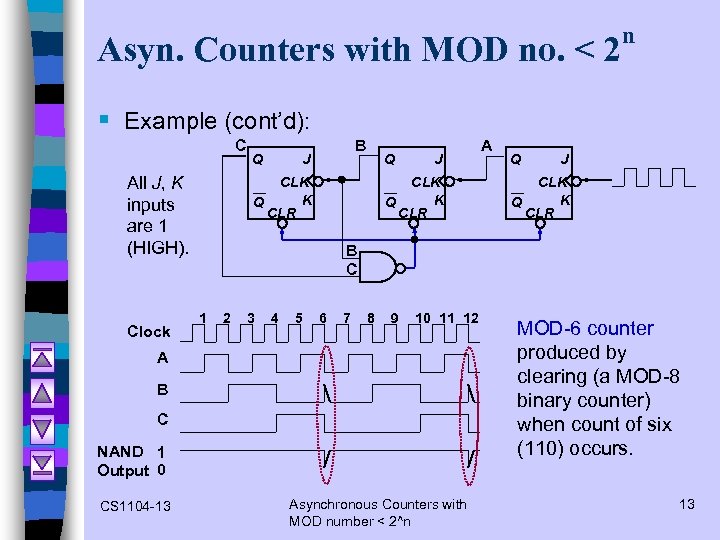Asyn. Counters with MOD no. < 2 n § Example (cont’d): C All J, K inputs are 1 (HIGH). Clock Q B J Q CLK K Q CLR J CLK K Q CLR Q J CLK K Q CLR B C 1 2 3 4 5 6 7 8 9 10 11 12 A B C NAND 1 Output 0 CS 1104 -13 A Asynchronous Counters with MOD number < 2^n MOD-6 counter produced by clearing (a MOD-8 binary counter) when count of six (110) occurs. 13

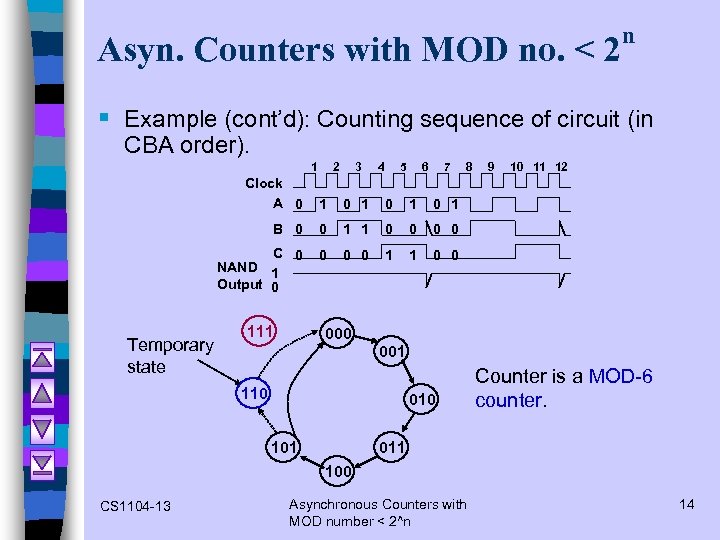Asyn. Counters with MOD no. < 2 n § Example (cont’d): Counting sequence of circuit (in CBA order). 1 2 3 4 5 6 7 Clock A 0 0 1 0 1 1 0 0 0 1 1 10 11 12 0 0 C 0 NAND 1 Output 0 9 0 1 B 0 Temporary state 1 8 0 0 111 000 001 110 010 101 Counter is a MOD-6 counter. 011 100 CS 1104 -13 Asynchronous Counters with MOD number < 2^n 14

Asyn. Counters with MOD no. < 2 n § Exercise: How to construct an asynchronous MOD-5 counter? MOD-7 counter? MOD-12 counter? § Question: The following is a MOD-? counter? F Q J Q K CLR E Q J Q K CLR D Q J Q K CLR C Q J Q B K CLR C D E F CS 1104 -13 Q J Q K CLR All J = K = 1. Asynchronous Counters with MOD number < 2^n 15

Asyn. Counters with MOD no. < 2 n § Decade counters (or BCD counters) are counters with 10 states (modulus-10) in their sequence. They are commonly used in daily life (e. g. : utility meters, odometers, etc. ). § Design an asynchronous decade counter. (A. C)' HIGH J Q D J Q C J Q B J Q CS 1104 -13 C C K CLR CLK K CLR Asynchronous Counters with MOD number < 2^n 16

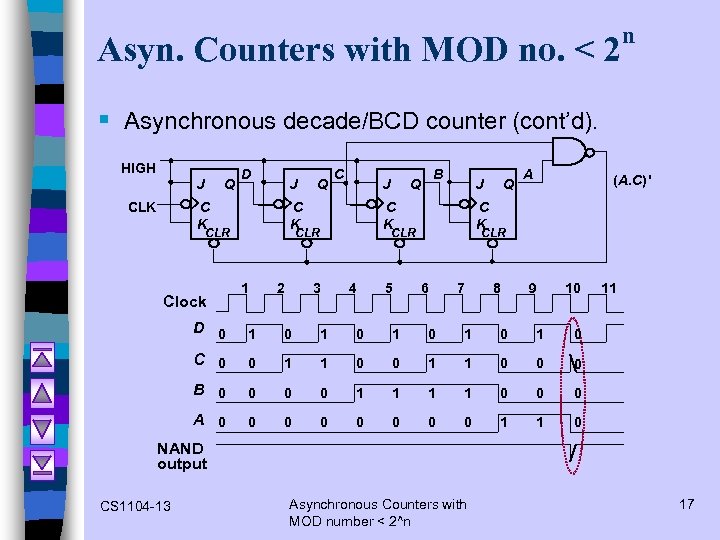Asyn. Counters with MOD no. < 2 n § Asynchronous decade/BCD counter (cont’d). HIGH J Q D J C K CLK C J C K CLR Clock Q 2 J C K CLR 1 B Q 4 5 A (A. C)' C K CLR 3 Q CLR 6 7 8 9 10 D 0 1 0 1 0 1 0 C 0 0 1 1 0 0 0 B 0 0 1 1 0 0 0 A 0 0 0 0 1 1 11 0 NAND output CS 1104 -13 Asynchronous Counters with MOD number < 2^n 17

Asynchronous Down Counters § So far we are dealing with up counters. Down counters, on the other hand, count downward from a maximum value to zero, and repeat. § Example: A 3 -bit binary (MOD-23) down counter. 1 J CLK Q Q 0 J Q Q 1 C K Q' C Q' K J Q Q 2 C K Q' 3 -bit binary up counter 1 J CLK CS 1104 -13 Q C Q' K Q 0 J Q C K Q' Q 1 J Q Q 2 C K Q' Asynchronous Down Counters 3 -bit binary down counter 18

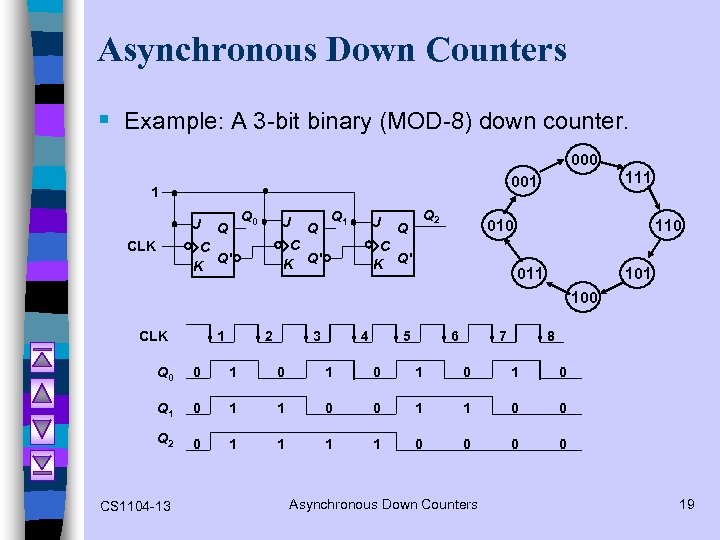Asynchronous Down Counters § Example: A 3 -bit binary (MOD-8) down counter. 000 1 J CLK 111 001 Q 0 Q J Q Q 1 J C K Q' C Q' K Q Q 2 010 C K Q' 110 011 100 CLK 1 2 3 4 5 6 7 8 Q 0 0 1 0 1 0 Q 1 0 1 1 0 0 Q 2 0 1 1 0 0 CS 1104 -13 Asynchronous Down Counters 19

Cascading Asynchronous Counters § Larger asynchronous (ripple) counter can be constructed by cascading smaller ripple counters. § Connect last-stage output of one counter to the clock input of next counter so as to achieve highermodulus operation. § Example: A modulus-32 ripple counter constructed from a modulus-4 counter and a modulus-8 counter. Q 0 J CLK Q C Q' K Q 1 J Q C K Q' Modulus-4 counter CS 1104 -13 Q 2 J Q 3 J Q C Q' K Q C K Q' Q 4 J Q C K Q' Modulus-8 counter Cascading Asynchronous Counters 20

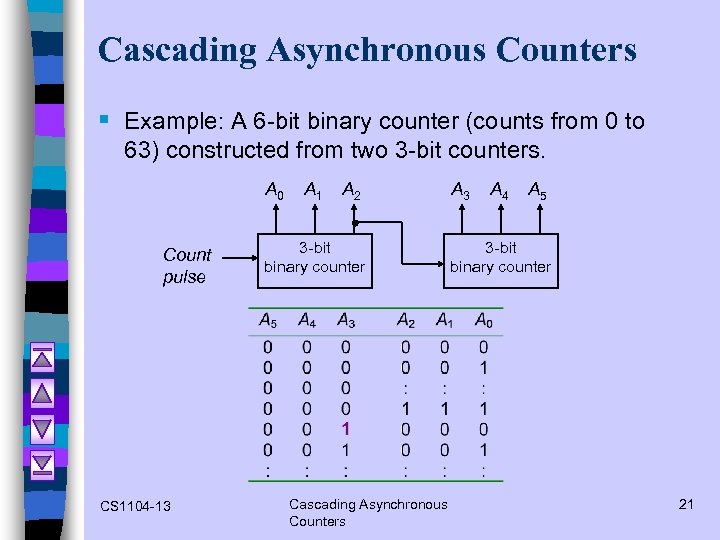Cascading Asynchronous Counters § Example: A 6 -bit binary counter (counts from 0 to 63) constructed from two 3 -bit counters. A 0 Count pulse CS 1104 -13 A 1 A 2 3 -bit binary counter Cascading Asynchronous Counters A 3 A 4 A 5 3 -bit binary counter 21

Cascading Asynchronous Counters § If counter is a not a binary counter, requires additional output. § Example: A modulus-100 counter using two decade counters. 1 CTEN Decade counter TC C Q 3 Q 2 Q 1 Q 0 CLK freq/10 CTEN Decade freq/100 counter TC C Q 3 Q 2 Q 1 Q 0 freq TC = 1 when counter recycles to 0000 CS 1104 -13 Cascading Asynchronous Counters 22

Synchronous (Parallel) Counters § Synchronous (parallel) counters: the flip-flops are clocked at the same time by a common clock pulse. § We can design these counters using the sequential logic design process (covered in Lecture #12). § Example: 2 -bit synchronous binary counter (using T flip-flops, or JK flip-flops with identical J, K inputs). 00 11 CS 1104 -13 01 10 Synchronous (Parallel) Counters 23

Synchronous (Parallel) Counters § Example: 2 -bit synchronous binary counter (using T flip-flops, or JK flip-flops with identical J, K inputs). TA 1 = A 0 TA 0 = 1 1 J Q C Q' K A 0 J Q A 1 C K Q' CLK CS 1104 -13 Synchronous (Parallel) Counters 24

Synchronous (Parallel) Counters § Example: 3 -bit synchronous binary counter (using T flip-flops, or JK flip-flops with identical J, K inputs). A 1 1 A 2 1 A 0 TA 2 = A 1. A 0 CS 1104 -13 1 A 2 1 1 1 1 A 0 TA 1 = A 0 TA 0 = 1 Synchronous (Parallel) Counters 25

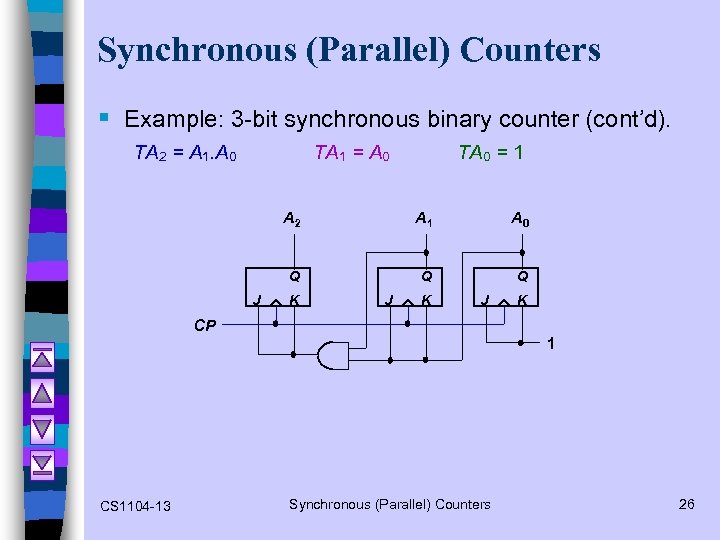Synchronous (Parallel) Counters § Example: 3 -bit synchronous binary counter (cont’d). TA 2 = A 1. A 0 TA 1 = A 0 TA 0 = 1 A 2 A 0 Q J A 1 Q Q K J K CP 1 CS 1104 -13 Synchronous (Parallel) Counters 26

Synchronous (Parallel) Counters § Note that in a binary counter, the nth bit (shown underlined) is always complemented whenever 011… 11 100… 00 or 111… 11 000… 00 § Hence, Xn is complemented whenever Xn-1 Xn-2. . . X 1 X 0 = 11… 11. § As a result, if T flip-flops are used, then TXn = Xn-1. Xn-2. . . X 1. X 0 CS 1104 -13 Synchronous (Parallel) Counters 27

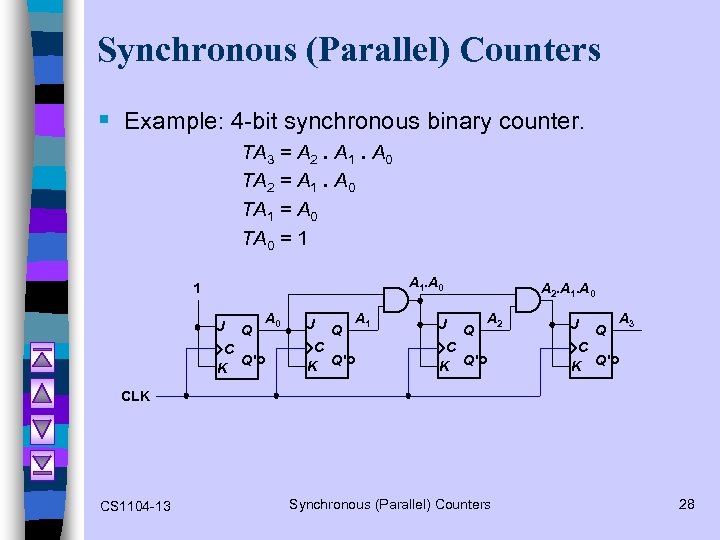Synchronous (Parallel) Counters § Example: 4 -bit synchronous binary counter. TA 3 = A 2. A 1. A 0 TA 2 = A 1. A 0 TA 1 = A 0 TA 0 = 1 A 1. A 0 1 J Q C Q' K A 0 J Q C K Q' A 1 J A 2. A 1. A 0 Q A 2 C K Q' J Q A 3 C K Q' CLK CS 1104 -13 Synchronous (Parallel) Counters 28

Synchronous (Parallel) Counters § Example: Synchronous decade/BCD counter. T 0 = 1 T 1 = Q 3'. Q 0 T 2 = Q 1. Q 0 T 3 = Q 2. Q 1. Q 0 + Q 3. Q 0 CS 1104 -13 Synchronous (Parallel) Counters 29

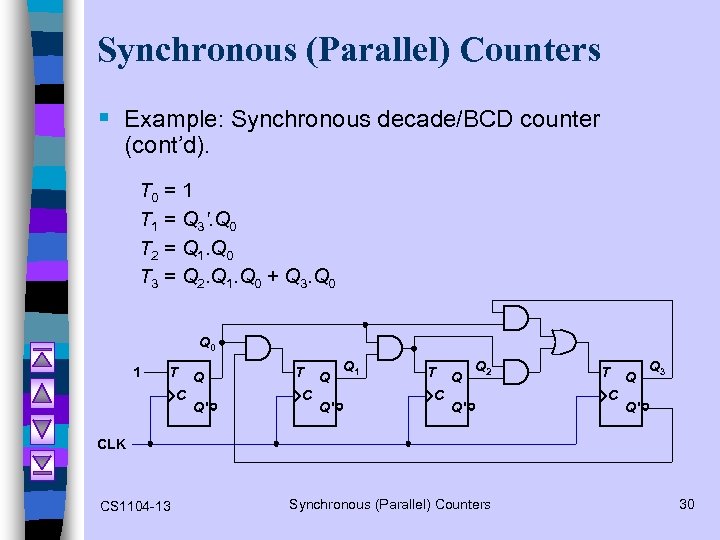Synchronous (Parallel) Counters § Example: Synchronous decade/BCD counter (cont’d). T 0 = 1 T 1 = Q 3'. Q 0 T 2 = Q 1. Q 0 T 3 = Q 2. Q 1. Q 0 + Q 3. Q 0 1 T C Q Q' Q 1 T C Q Q 2 Q' T C Q Q 3 Q' CLK CS 1104 -13 Synchronous (Parallel) Counters 30

Up/Down Synchronous Counters § Up/down synchronous counter: a bidirectional counter that is capable of counting either up or down. § An input (control) line Up/Down (or simply Up) specifies the direction of counting. v Up/Down = 1 Count upward v Up/Down = 0 Count downward CS 1104 -13 Up/Down Synchronous Counters 31

Up/Down Synchronous Counters § Example: A 3 -bit up/down synchronous binary counter. TQ 0 = 1 TQ 1 = (Q 0. Up) + (Q 0'. Up' ) TQ 2 = ( Q 0. Q 1. Up ) + (Q 0'. Q 1'. Up' ) CS 1104 -13 Up counter TQ 0 = 1 TQ 1 = Q 0 TQ 2 = Q 0. Q 1 Up/Down Synchronous Counters Down counter TQ 0 = 1 TQ 1 = Q 0’ TQ 2 = Q 0’. Q 1’ 32

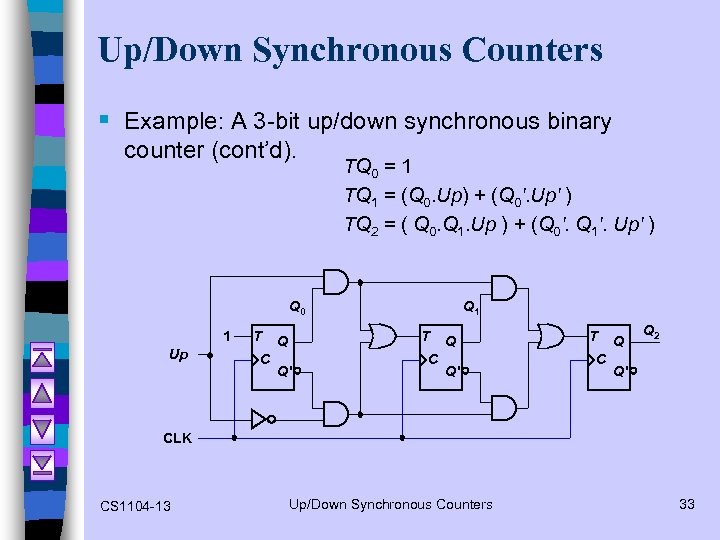Up/Down Synchronous Counters § Example: A 3 -bit up/down synchronous binary counter (cont’d). TQ 0 = 1 TQ 1 = (Q 0. Up) + (Q 0'. Up' ) TQ 2 = ( Q 0. Q 1. Up ) + (Q 0'. Q 1'. Up' ) Q 0 1 Up T C Q 1 T Q Q' C Q Q' T C Q Q 2 Q' CLK CS 1104 -13 Up/Down Synchronous Counters 33

Designing Synchronous Counters § Covered in Lecture #12. § Example: A 3 -bit Gray code counter (using JK flip-flops). 000 100 001 101 011 111 010 110 CS 1104 -13 Designing Synchronous Counters 34

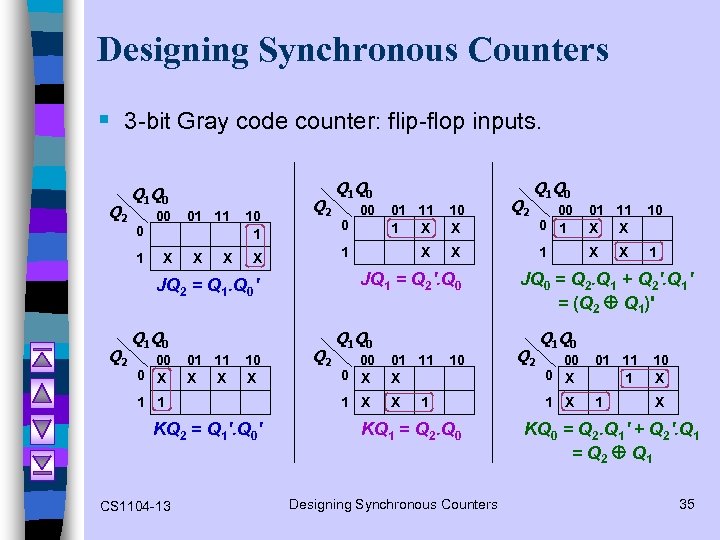Designing Synchronous Counters § 3 -bit Gray code counter: flip-flop inputs. Q 2 Q 1 Q 0 0 1 00 X 01 11 X X 10 1 Q 2 00 0 X 01 11 X X 10 X 1 1 KQ 2 = Q 1'. Q 0' CS 1104 -13 01 11 1 X 10 X X Q 2 Q 1 Q 0 X JQ 1 = Q 2'. Q 0 JQ 2 = Q 1. Q 0' Q 2 0 00 1 X Q 1 Q 0 00 0 X 01 11 X X 10 1 KQ 1 = Q 2. Q 0 Designing Synchronous Counters 00 0 1 01 11 X X 10 1 X JQ 0 = Q 2. Q 1 + Q 2'. Q 1' = (Q 2 Q 1)' Q 2 Q 1 Q 0 00 0 X 01 11 1 10 X 1 X KQ 0 = Q 2. Q 1' + Q 2'. Q 1 = Q 2 Q 1 35

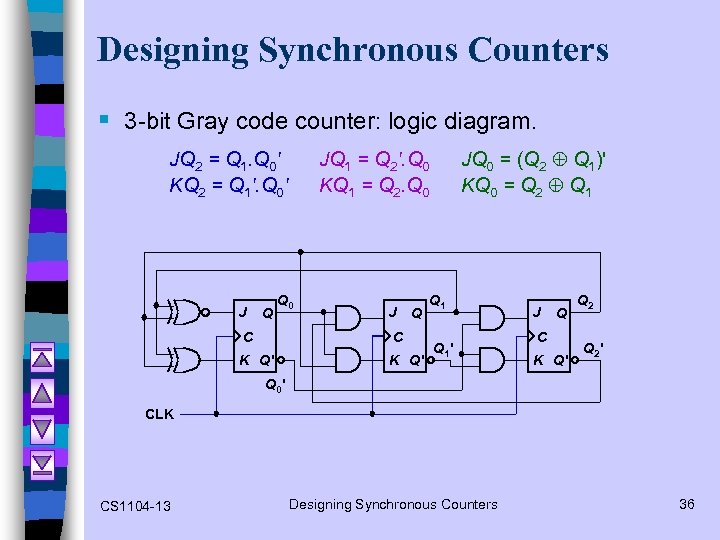Designing Synchronous Counters § 3 -bit Gray code counter: logic diagram. JQ 2 = Q 1. Q 0' KQ 2 = Q 1'. Q 0' J Q JQ 0 = (Q 2 Q 1)' KQ 0 = Q 2 Q 1 JQ 1 = Q 2'. Q 0 KQ 1 = Q 2. Q 0 J Q C C K Q' Q 1' J Q C K Q' Q 2' Q 0' CLK CS 1104 -13 Designing Synchronous Counters 36

Decoding A Counter § Decoding a counter involves determining which state in the sequence the counter is in. § Differentiate between active-HIGH and active-LOW decoding. § Active-HIGH decoding: output HIGH if the counter is in the state concerned. § Active-LOW decoding: output LOW if the counter is in the state concerned. CS 1104 -13 Decoding A Counter 37

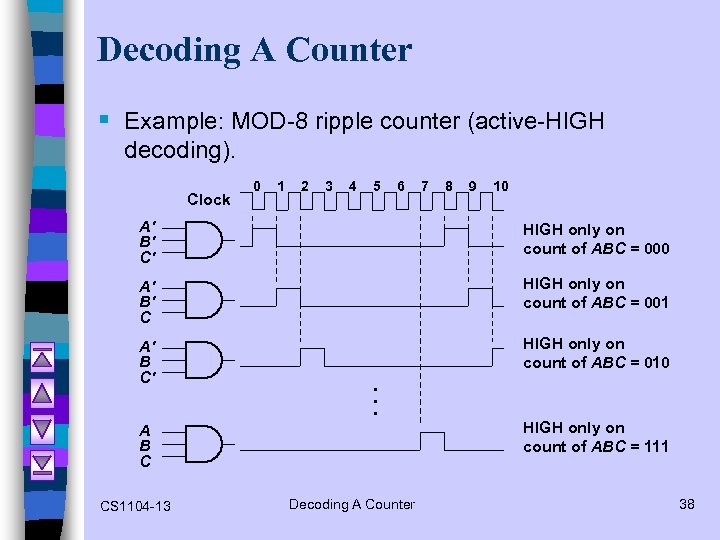Decoding A Counter § Example: MOD-8 ripple counter (active-HIGH decoding). Clock 0 1 2 3 4 5 6 7 8 9 10 A' B' C' HIGH only on count of ABC = 000 A' B' C HIGH only on count of ABC = 001 A' B C' HIGH only on count of ABC = 010 . . . A B C CS 1104 -13 Decoding A Counter HIGH only on count of ABC = 111 38

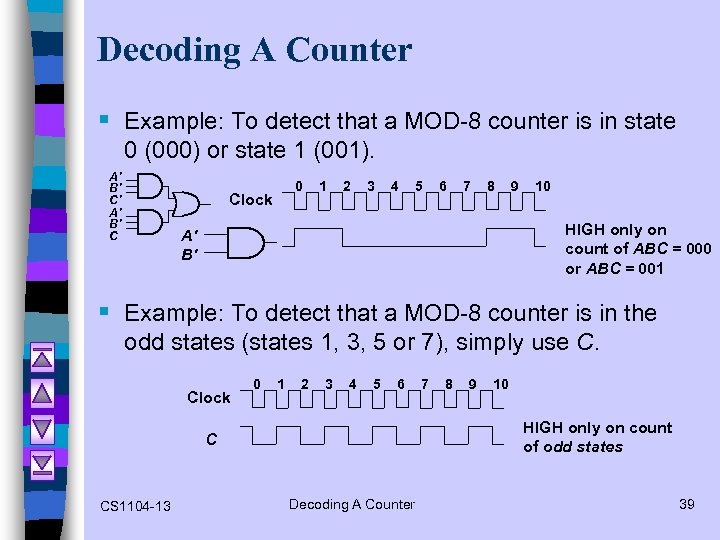Decoding A Counter § Example: To detect that a MOD-8 counter is in state 0 (000) or state 1 (001). A' B' C' A' B' C 0 Clock 1 2 3 4 5 6 7 8 9 10 HIGH only on count of ABC = 000 or ABC = 001 A' B' § Example: To detect that a MOD-8 counter is in the odd states (states 1, 3, 5 or 7), simply use C. Clock 0 1 2 3 4 5 6 8 9 10 HIGH only on count of odd states C CS 1104 -13 7 Decoding A Counter 39

Counters with Parallel Load § Counters could be augmented with parallel load capability for the following purposes: v To start at a different state v To count a different sequence v As more sophisticated register with increment/decrement functionality. CS 1104 -13 Counters with Parallel Load 40

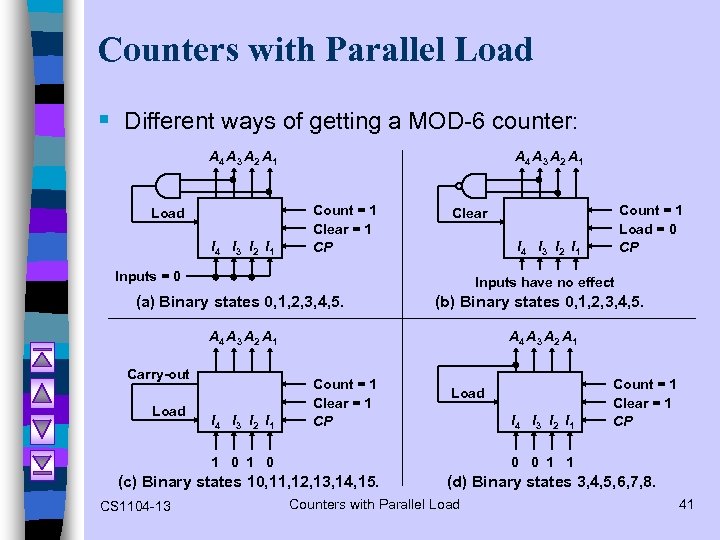Counters with Parallel Load § Different ways of getting a MOD-6 counter: A 4 A 3 A 2 A 1 Load I 4 I 3 I 2 I 1 A 4 A 3 A 2 A 1 Count = 1 Clear = 1 CP Count = 1 Load = 0 CP Clear I 4 I 3 I 2 I 1 Inputs = 0 Inputs have no effect (a) Binary states 0, 1, 2, 3, 4, 5. (b) Binary states 0, 1, 2, 3, 4, 5. A 4 A 3 A 2 A 1 Carry-out Load I 4 I 3 I 2 I 1 Count = 1 Clear = 1 CP Load I 4 I 3 I 2 I 1 1 0 0 0 1 1 (c) Binary states 10, 11, 12, 13, 14, 15. CS 1104 -13 Count = 1 Clear = 1 CP (d) Binary states 3, 4, 5, 6, 7, 8. Counters with Parallel Load 41

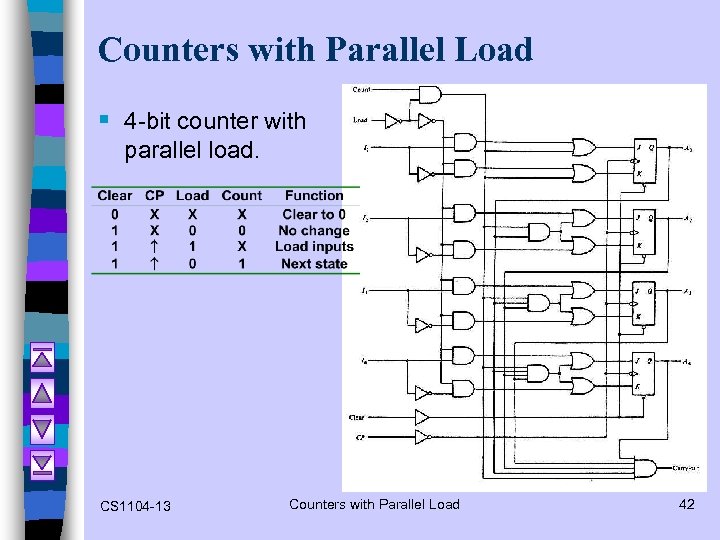Counters with Parallel Load § 4 -bit counter with parallel load. CS 1104 -13 Counters with Parallel Load 42

Introduction: Registers § An n-bit register has a group of n flip-flops and some logic gates and is capable of storing n bits of information. § The flip-flops store the information while the gates control when and how new information is transferred into the register. § Some functions of register: v retrieve data from register v store/load new data into register (serial or parallel) v shift the data within register (left or right) CS 1104 -13 Introduction: Registers 43

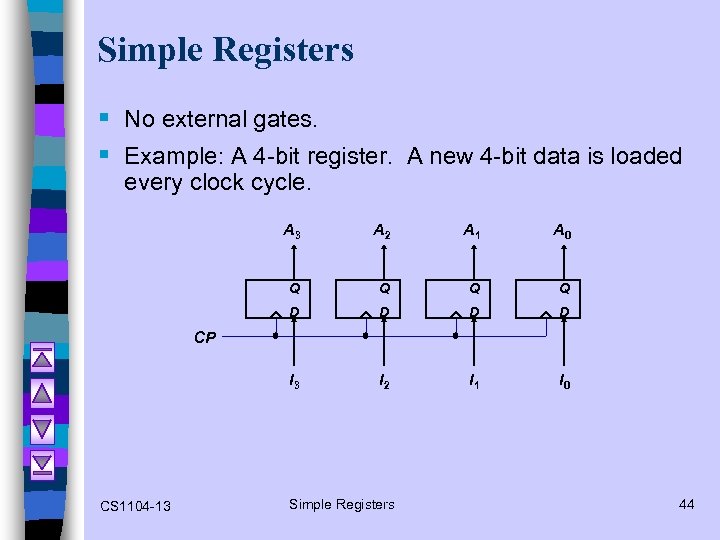Simple Registers § No external gates. § Example: A 4 -bit register. A new 4 -bit data is loaded every clock cycle. A 3 A 2 A 1 A 0 Q Q D D I 3 I 2 I 1 I 0 CP CS 1104 -13 Simple Registers 44

Registers With Parallel Load § Instead of loading the register at every clock pulse, we may want to control when to load. § Loading a register: transfer new information into the register. Requires a load control input. § Parallel loading: all bits are loaded simultaneously. CS 1104 -13 Registers With Parallel Load 45

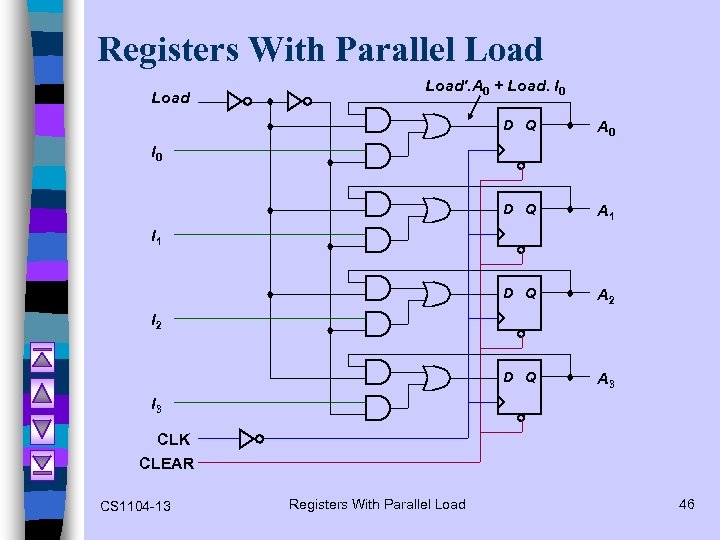Registers With Parallel Load'. A 0 + Load. I 0 D Q A 1 D Q A 2 D Q A 3 I 0 I 1 I 2 I 3 CLK CLEAR CS 1104 -13 Registers With Parallel Load 46

Using Registers to implement Sequential Circuits § A sequential circuit may consist of a register (memory) and a combinational circuit. Next-state value Register Clock Inputs Combinational circuit Outputs § The external inputs and present states of the register determine the next states of the register and the external outputs, through the combinational circuit. § The combinational circuit may be implemented by any of the methods covered in MSI components and Programmable Logic Devices. CS 1104 -13 Using Registers to implement Sequential Circuits 47

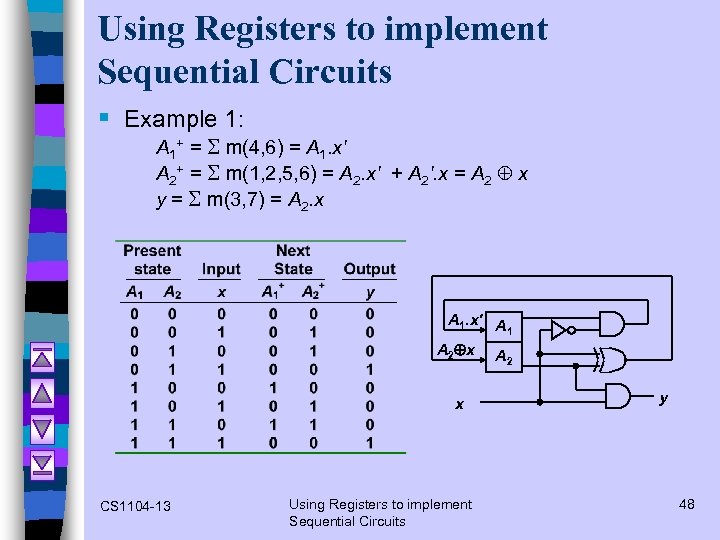Using Registers to implement Sequential Circuits § Example 1: A 1+ = S m(4, 6) = A 1. x' A 2+ = S m(1, 2, 5, 6) = A 2. x' + A 2'. x = A 2 x y = S m(3, 7) = A 2. x A 1. x' A 1 A 2 x CS 1104 -13 Using Registers to implement Sequential Circuits y 48

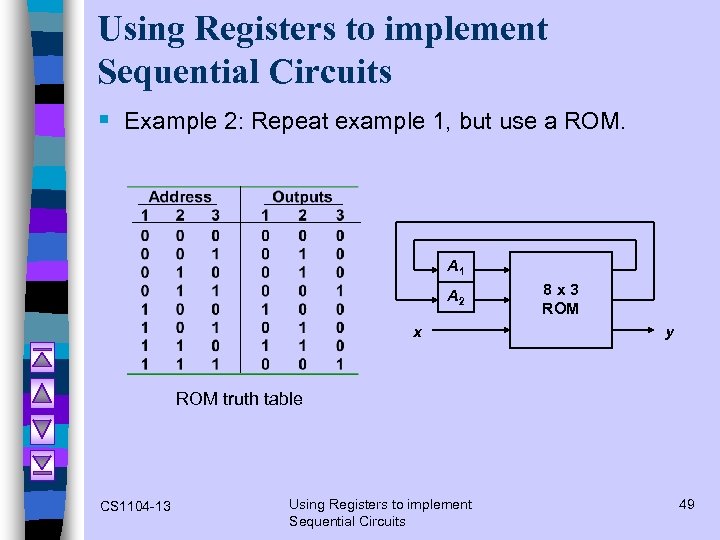Using Registers to implement Sequential Circuits § Example 2: Repeat example 1, but use a ROM. A 1 A 2 x 8 x 3 ROM y ROM truth table CS 1104 -13 Using Registers to implement Sequential Circuits 49

Shift Registers § Another function of a register, besides storage, is to provide for data movements. § Each stage (flip-flop) in a shift register represents one bit of storage, and the shifting capability of a register permits the movement of data from stage to stage within the register, or into or out of the register upon application of clock pulses. CS 1104 -13 Shift Registers 50

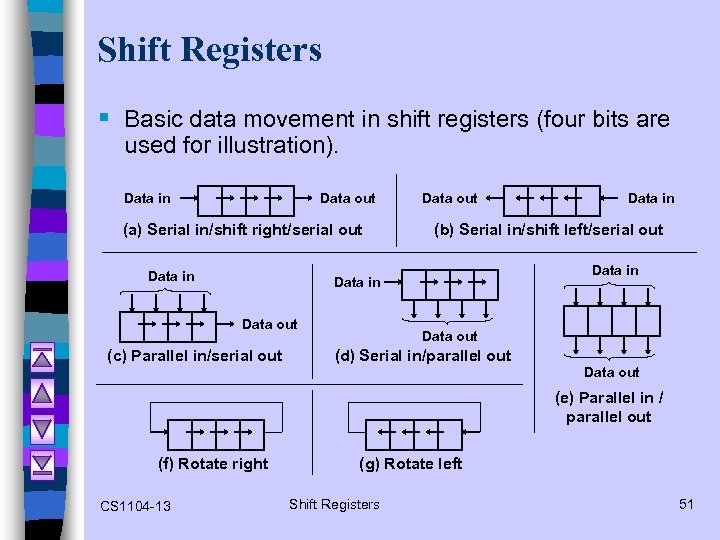Shift Registers § Basic data movement in shift registers (four bits are used for illustration). Data in Data out (a) Serial in/shift right/serial out Data in Data out (b) Serial in/shift left/serial out Data in Data out (c) Parallel in/serial out Data in Data out (d) Serial in/parallel out Data out (e) Parallel in / parallel out (f) Rotate right CS 1104 -13 (g) Rotate left Shift Registers 51

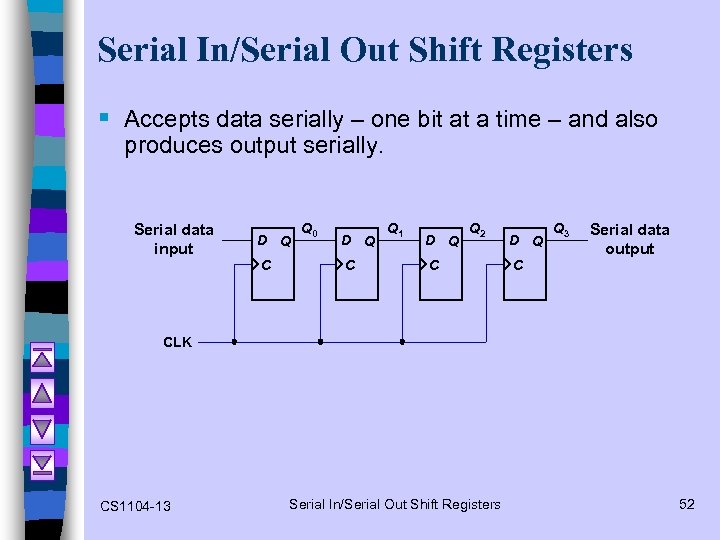Serial In/Serial Out Shift Registers § Accepts data serially – one bit at a time – and also produces output serially. Serial data input D Q C Q 0 D Q C Q 1 D Q Q 2 C D Q C Q 3 Serial data output CLK CS 1104 -13 Serial In/Serial Out Shift Registers 52

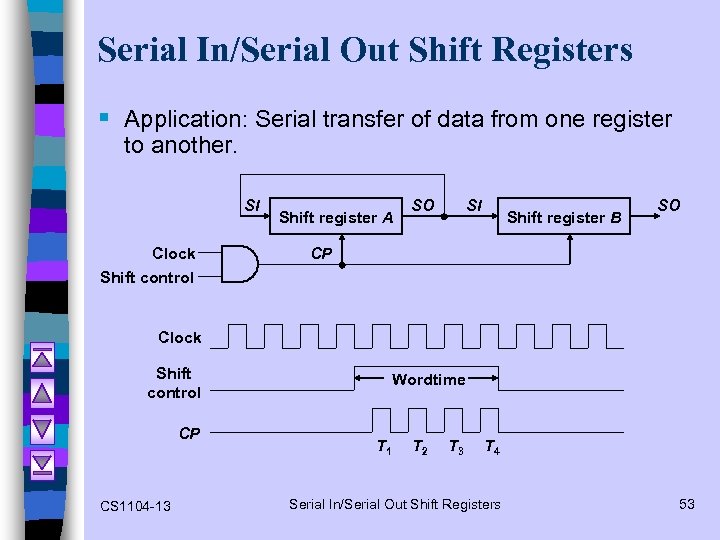Serial In/Serial Out Shift Registers § Application: Serial transfer of data from one register to another. SI Clock Shift register A SO SI Shift register B SO CP Shift control Clock Shift control CP CS 1104 -13 Wordtime T 1 T 2 T 3 T 4 Serial In/Serial Out Shift Registers 53

Serial In/Serial Out Shift Registers § Serial-transfer example. CS 1104 -13 Serial In/Serial Out Shift Registers 54

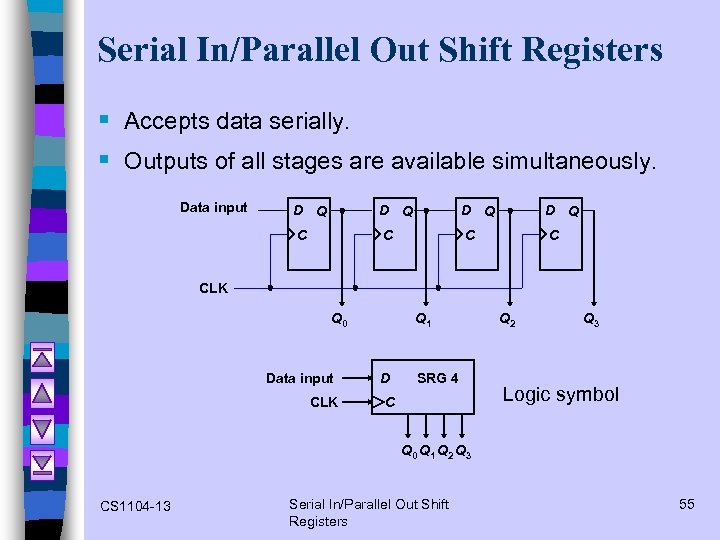Serial In/Parallel Out Shift Registers § Accepts data serially. § Outputs of all stages are available simultaneously. Data input D Q D Q C C CLK Q 0 Data input CLK Q 1 D SRG 4 C Q 2 Q 3 Logic symbol Q 0 Q 1 Q 2 Q 3 CS 1104 -13 Serial In/Parallel Out Shift Registers 55

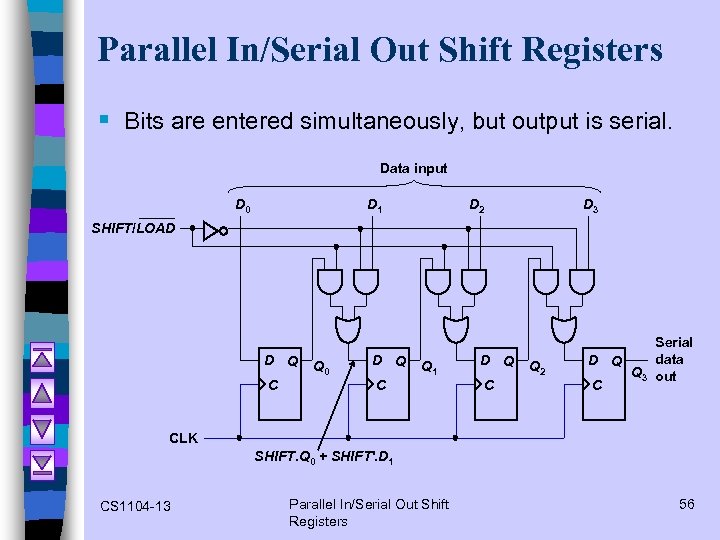Parallel In/Serial Out Shift Registers § Bits are entered simultaneously, but output is serial. Data input D 0 D 1 D 2 D 3 SHIFT/LOAD D Q C Q 0 D Q Q 1 C D Q C Q 2 Serial data D Q Q 3 out C CLK SHIFT. Q 0 + SHIFT'. D 1 CS 1104 -13 Parallel In/Serial Out Shift Registers 56

Parallel In/Serial Out Shift Registers § Bits are entered simultaneously, but output is serial. Data in D 0 D 1 D 2 D 3 SHIFT/LOAD CLK SRG 4 C Serial data out Logic symbol CS 1104 -13 Parallel In/Serial Out Shift Registers 57

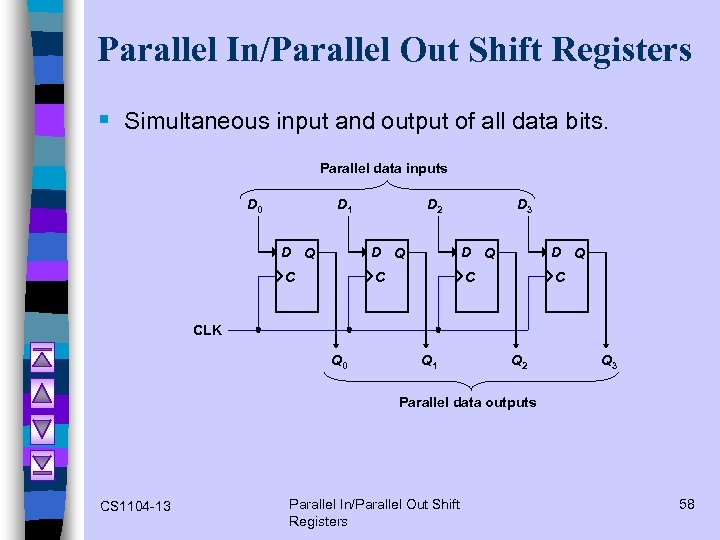Parallel In/Parallel Out Shift Registers § Simultaneous input and output of all data bits. Parallel data inputs D 0 D 1 D 2 D 3 D Q D Q C C CLK Q 0 Q 1 Q 2 Q 3 Parallel data outputs CS 1104 -13 Parallel In/Parallel Out Shift Registers 58

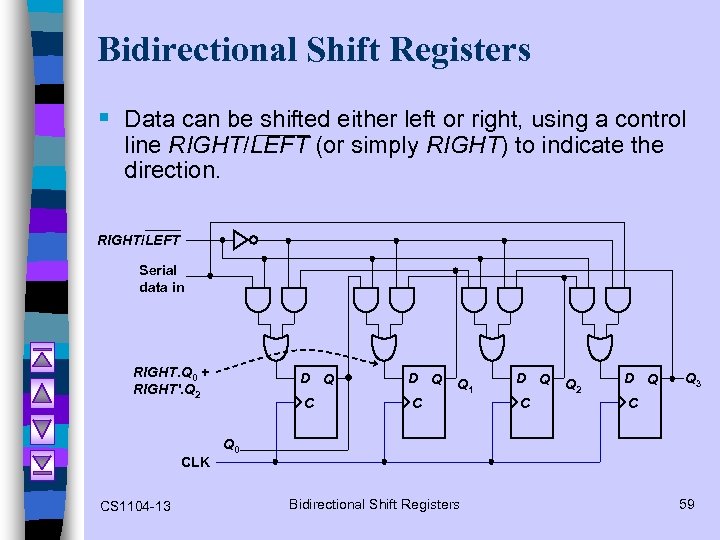Bidirectional Shift Registers § Data can be shifted either left or right, using a control line RIGHT/LEFT (or simply RIGHT) to indicate the direction. RIGHT/LEFT Serial data in RIGHT. Q 0 + RIGHT'. Q 2 CLK CS 1104 -13 D Q C C Q 1 D Q C Q 2 D Q Q 3 C Q 0 Bidirectional Shift Registers 59

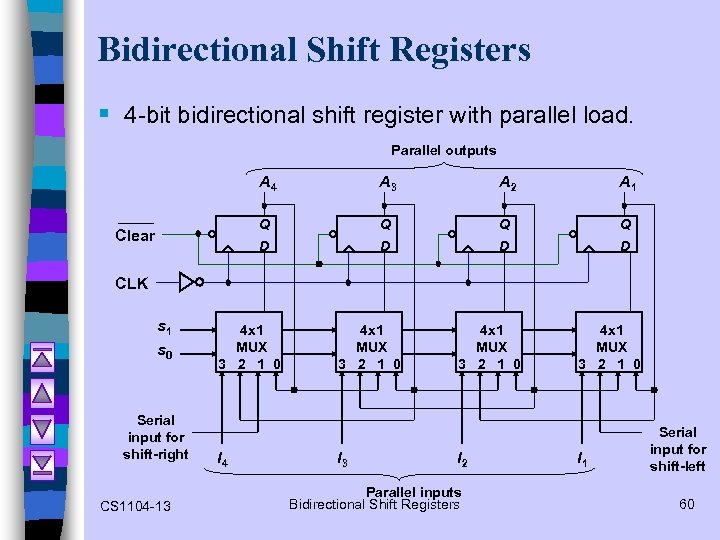Bidirectional Shift Registers § 4 -bit bidirectional shift register with parallel load. Parallel outputs A 4 A 2 A 1 Q Q D Clear A 3 D D D CLK s 1 s 0 Serial input for shift-right CS 1104 -13 4 x 1 MUX 3 2 1 0 I 4 4 x 1 MUX 3 2 1 0 I 3 4 x 1 MUX 3 2 1 0 I 2 Parallel inputs Bidirectional Shift Registers 4 x 1 MUX 3 2 1 0 I 1 Serial input for shift-left 60

Bidirectional Shift Registers § 4 -bit bidirectional shift register with parallel load. CS 1104 -13 Bidirectional Shift Registers 61

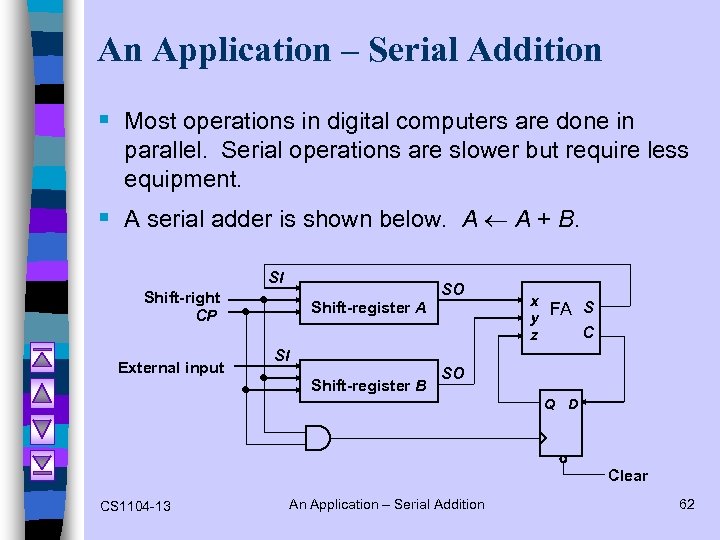An Application – Serial Addition § Most operations in digital computers are done in parallel. Serial operations are slower but require less equipment. § A serial adder is shown below. A A + B. SI SO Shift-right CP External input Shift-register A x S y FA C z SI Shift-register B SO Q D Clear CS 1104 -13 An Application – Serial Addition 62

An Application – Serial Addition § A = 0100; B = 0111. A + B = 1011 is stored in A after 4 clock pulses. Initial: Q: 0 Step 1: 0 + 1 + 0 S = 1, C = 0 A: 1 0 B: x 0 1 1 Q: 0 Step 2: 0 + 1 + 0 S = 1, C = 0 A: 1 1 0 1 B: x x 0 1 Q: 0 Step 3: 1 + 0 S = 0, C = 1 A: 0 1 1 0 B: x x x 0 Q: 1 Step 4: 0 + 1 S = 1, C = 0 CS 1104 -13 A: 0 1 0 0 B: 0 1 1 1 A: 1 0 1 1 B: x x Q: 0 An Application – Serial Addition 63

Shift Register Counters § Shift register counter: a shift register with the serial output connected back to the serial input. § They are classified as counters because they give a specified sequence of states. § Two common types: the Johnson counter and the Ring counter. CS 1104 -13 Shift Register Counters 64

Ring Counters § One flip-flop (stage) for each state in the sequence. § The output of the last stage is connected to the D input of the first stage. § An n-bit ring counter cycles through n states. § No decoding gates are required, as there is an output that corresponds to every state the counter is in. CS 1104 -13 Ring Counters 65

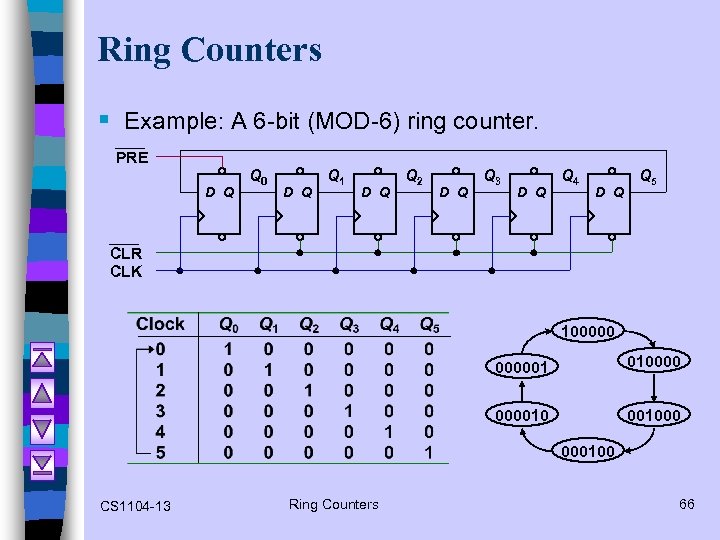Ring Counters § Example: A 6 -bit (MOD-6) ring counter. PRE D Q Q 0 D Q Q 1 D Q Q 2 D Q Q 3 D Q Q 4 D Q Q 5 CLR CLK 1000001 01000010 001000 000100 CS 1104 -13 Ring Counters 66

Johnson Counters § The complement of the output of the last stage is connected back to the D input of the first stage. § Also called the twisted-ring counter. § Require fewer flip-flops than ring counters but more flip-flops than binary counters. § An n-bit Johnson counter cycles through 2 n states. § Require more decoding circuitry than ring counter but less than binary counters. CS 1104 -13 Johnson Counters 67

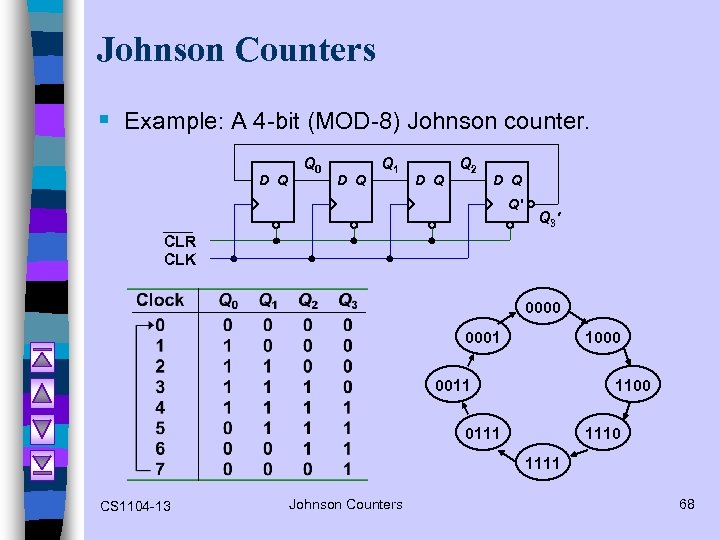Johnson Counters § Example: A 4 -bit (MOD-8) Johnson counter. D Q Q 0 D Q Q 1 D Q Q 2 D Q Q' Q 3' CLR CLK 0000 0001 1000 0011 1100 0111 1110 1111 CS 1104 -13 Johnson Counters 68

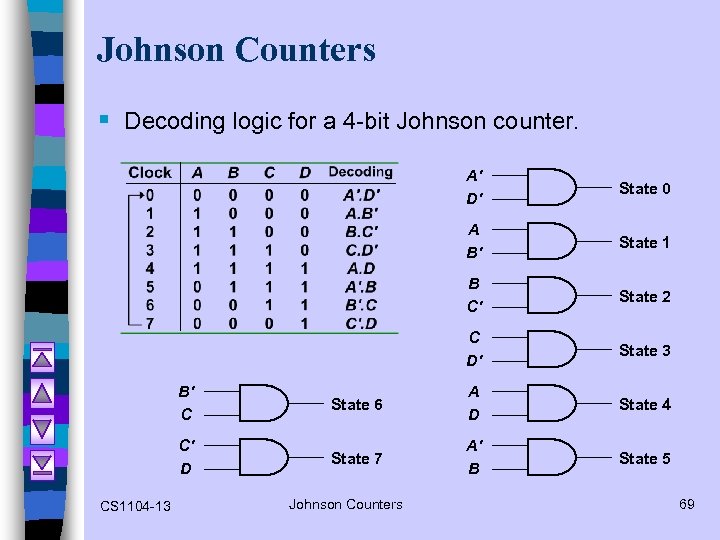Johnson Counters § Decoding logic for a 4 -bit Johnson counter. A' D' State 0 A B' State 1 B C' State 2 C D' State 3 B' C A D State 4 C' D CS 1104 -13 State 6 State 7 A' B State 5 Johnson Counters 69

Random Access Memory (RAM) § A memory unit stores binary information in groups of § § § bits called words. The data consists of n lines (for n-bit words). Data input lines provide the information to be stored (written) into the memory, while data output lines carry the information out (read) from the memory. The address consists of k lines which specify which word (among the 2 k words available) to be selected for reading or writing. The control lines Read and Write (usually combined into a single control line Read/Write) specifies the direction of transfer of the data. CS 1104 -13 Random Access Memory (RAM) 70

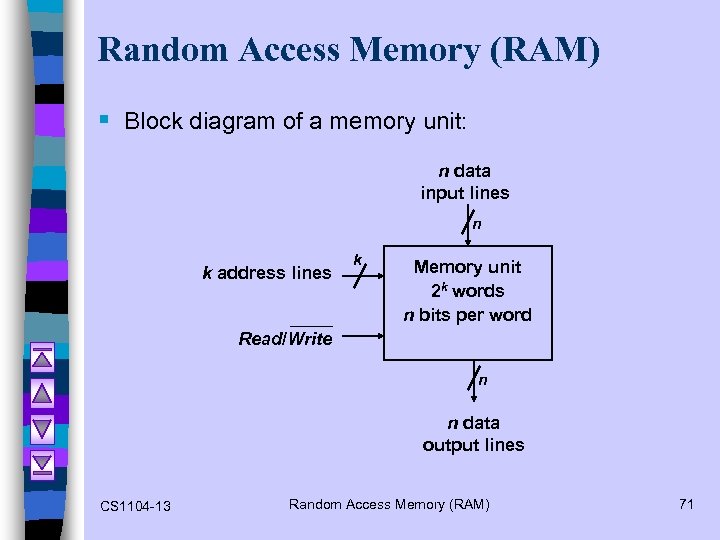Random Access Memory (RAM) § Block diagram of a memory unit: n data input lines n k address lines k Memory unit 2 k words n bits per word Read/Write n n data output lines CS 1104 -13 Random Access Memory (RAM) 71

Random Access Memory (RAM) § Content of a 1024 x 16 -bit memory: Memory address binary Memory content 000001 000010 : : 111101 111110 11111 CS 1104 -13 decimal 0 1 2 : : 1021 1022 1023 101101011101 1010000110 001001110001 : : 111001010010 0011111010101110 10110010101 Random Access Memory (RAM) 72

Random Access Memory (RAM) § The Write operation: v Transfers the address of the desired word to the address lines v Transfers the data bits (the word) to be stored in memory to the data input lines v Activates the Write control line (set Read/Write to 0) § The Read operation: v Transfers the address of the desired word to the address lines v Activates the Read control line (set Read/Write to 1) CS 1104 -13 Random Access Memory (RAM) 73

Random Access Memory (RAM) § The Read/Write operation: § Two types of RAM: Static and dynamic. v Static RAMs use flip-flops as the memory cells. v Dynamic RAMs use capacitor charges to represent data. Though simpler in circuitry, they have to be constantly refreshed. CS 1104 -13 Random Access Memory (RAM) 74

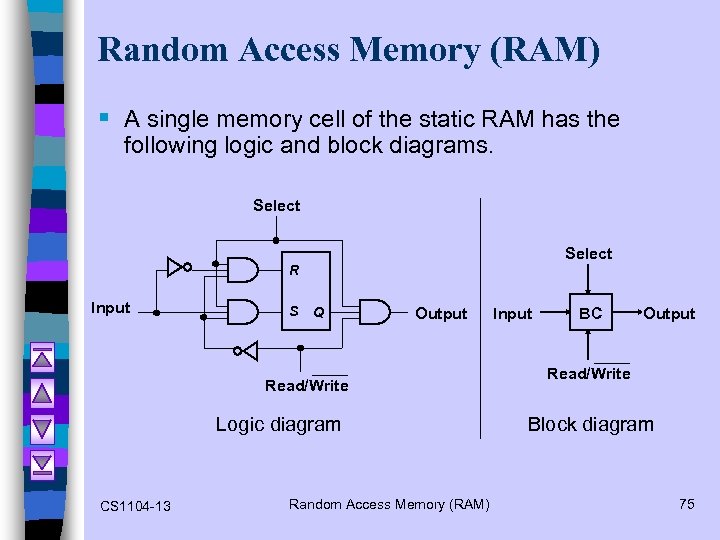Random Access Memory (RAM) § A single memory cell of the static RAM has the following logic and block diagrams. Select R Input S Q Output Read/Write Logic diagram CS 1104 -13 Random Access Memory (RAM) Input BC Output Read/Write Block diagram 75

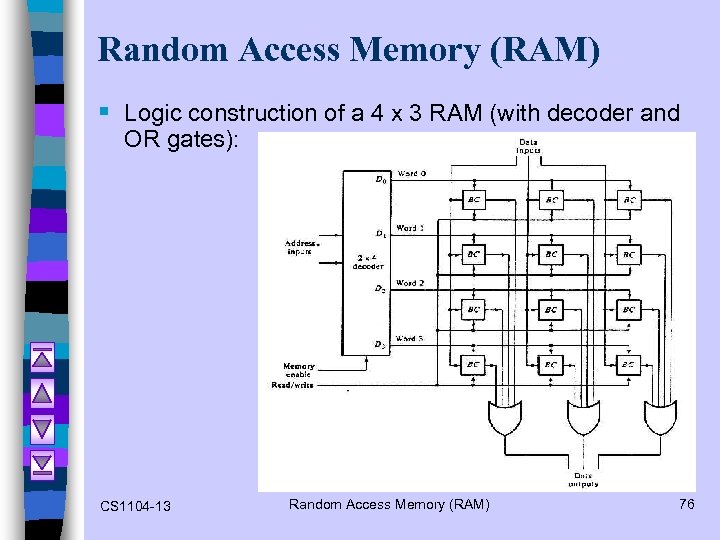Random Access Memory (RAM) § Logic construction of a 4 x 3 RAM (with decoder and OR gates): CS 1104 -13 Random Access Memory (RAM) 76

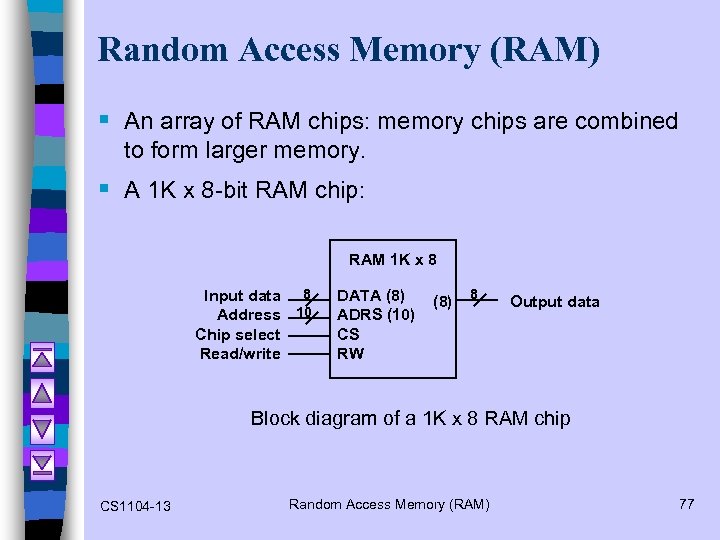Random Access Memory (RAM) § An array of RAM chips: memory chips are combined to form larger memory. § A 1 K x 8 -bit RAM chip: RAM 1 K x 8 Input data 8 Address 10 Chip select Read/write DATA (8) ADRS (10) CS RW (8) 8 Output data Block diagram of a 1 K x 8 RAM chip CS 1104 -13 Random Access Memory (RAM) 77

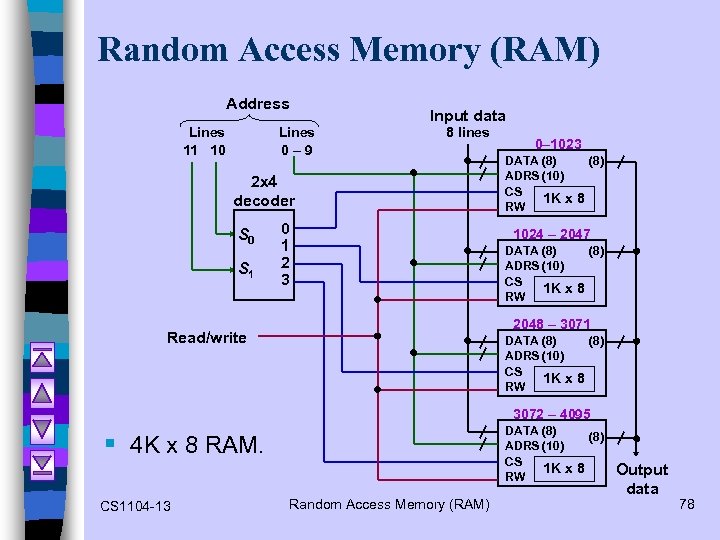Random Access Memory (RAM) Address Lines 11 10 Lines 0– 9 Input data 8 lines 2 x 4 decoder S 0 S 1 0 1 2 3 0– 1023 DATA (8) ADRS (10) CS 1 K x 8 RW 1024 – 2047 DATA (8) ADRS (10) CS 1 K x 8 RW 2048 – 3071 Read/write DATA (8) ADRS (10) CS 1 K x 8 RW 3072 – 4095 DATA (8) ADRS (10) CS 1 K x 8 RW § 4 K x 8 RAM. CS 1104 -13 Random Access Memory (RAM) Output data 78

End of segment