CS 1001 Programing Fundamental Lecture 5 Top-Down Design

CS 1001 Programing Fundamental Lecture 5 Top-Down Design with Functions (Chapter 3) Lecturer: Narong Wesnarat Lecture 5 -1

Building Programs from Existing Information and programs n Programs are often developed from existing solution(s) to other problems or other programs n write a new program by editing source code of an existing program can safe time in typing necessary parts of the program, for examples n n Preprocessor directives and macros Constant and variable declarations #include #define PI 3. 14159 int main(void) { double x, y, z; int i, j, k; /* printf, scanf definitions */ /* The constant PI */ these statements are common to all programs Lecture 5 -2

Building Programs from Existing Information and programs n System documentation during software development phase are useful and may be reused n n n description of a problem’s data requirement solution algorithms Initial algorithm and its refinements can be used as program comments int main(void) { double miles; double kms; /* input - distance in miles. /* output - distance in kilometers /* Get the distance in miles. ………………. insert C statement(s) here /* Convert the distance to kilometers. /* Distance in kilometers is 1. 609 * distance in miles. ………………. insert C statement(s) here /* Display the distance in kilometers. ………………. insert C statement(s) here return (0); */ */ */ Lecture 5 -3

Case Study: Finding the Area and Circumference Problem n n Get the radius of a circle. Compute and display the circled’s area and circumference. ANALYSIS n n n Clearly, the input is the circle’s radius Two outputs are required n n n the circle’s area the circumference These variable should be type double because input/outputs may contain fraction parts Data Requirements n n Problem Constant n n radius /* radius of a circle */ area circum /*area of a circle */ /* circumference of a circle */ Problem Outputs n n n 3. 14159 Problem Input n n PI Relevant Formulas n n area of a circle = ¶ x radius 2 circumference of a circle = 2 ¶ x radius Lecture 5 -4

Finding the Area and Circumference of a Circle Design Case Study: n n Initial Algorithm 1. 2. 3. 4. n get the circle radius calculate the area calculate the circumference display the area and the circumference Algorithm Refinements n Step 2 Refinement n n 2. 1 Assign PI * radius to area Step 3 Refinement n 3. 1 Assign 2* PI * radius to circum. Lecture 5 -5

Finding the Area and Circumference of a Circle Case Study: n IMPLEMENTATION Figure 3. 2 Outline of Program Circle /* * Calculates and displays the area and circumference of a circle */ #include #define PI 3. 14159 int { main(void) double radius; double area; double circum; /* input - radius of a circle /* output - area of a circle /* output - circumference */ */ */ /* Get the circle radius */ /* Calculate the area */ /* Assign PI * radius to area. */ /* Calculate the circumference */ /* Assign 2 * PI * radius to circum. */ /* Display the area and circumference */ return (0); Lecture 5 -6

Case Study: Finding the Area and Circumference Figure 3. 3 Calculating the Area and the Circumference of a Circle /* * Calculates and displays the area and circumference of a circle */ #include #define PI 3. 14159 int main(void) (continued) Figure 3. 3 (continued) { double radius; /* input - radius of a circle */ double area; /* output - area of a circle */ double circum; /* output - circumference */ /* Get the circle radius */ printf("Enter radius> "); scanf("%lf", &radius); /* Calculate the area */ area = PI * radius; Sample Run: Enter radius> 5. 0 The area is 78. 5397 The circumference is 31. 4159 /* Calculate the circumference */ circum = 2 * PI * radius; /* Display the area and circumference */ printf("The area is %. 4 fn", area); printf("The circumference is %. 4 fn", circum); return (0); } Lecture 5 -7

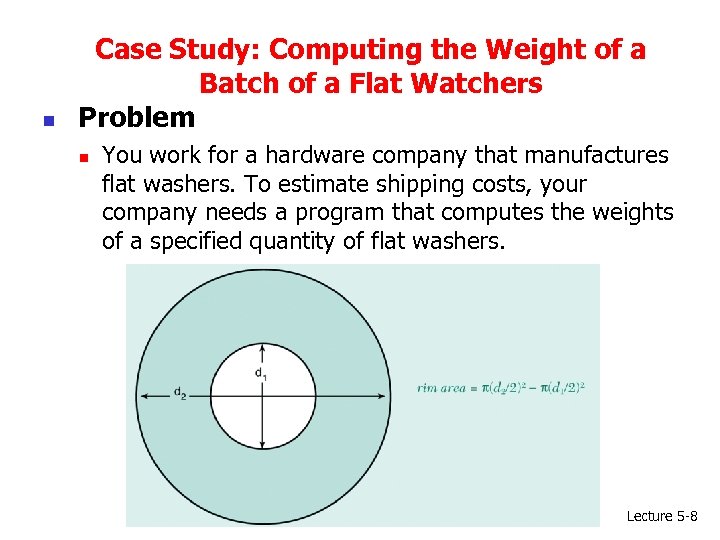n Case Study: Computing the Weight of a Batch of a Flat Watchers Problem n You work for a hardware company that manufactures flat washers. To estimate shipping costs, your company needs a program that computes the weights of a specified quantity of flat washers. Lecture 5 -8

Case Study: Computing the Weight of a Batch of a Flat Watchers n ANALYSIS n To compute the weight of a single flat washers you need to know n n its rim area its thickness the density of material Data Requirements n Problem Constant n n PI 3. 14159 Problem Inputs double hole_diameter; double edge_diameter; double thickness; double density; double quantity; /* input - diameter of hole /* input - diameter of outer edge /* input - thickness of washer /* input - density of material used /* input - number of washers made */ */ */ Lecture 5 -9

Case Study: Computing the Weight of a Batch of a Flat Watchers n Problem Outputs double weight; n /* output - weight of washer batch */ Program Variables double hole_radius; /* radius of hole double edge_radius; /* radius of outer edge double rim_area; /* area of rim double unit_weight; /* weight of 1 washer n */ */ Relevant Formulas n n area of a circle = ¶ x radius 2 radius of a circle = diameter/2 rim area = area of outer circle – area of hole unit weight = rim area x thickness x density Lecture 5 -10

Case Study: Computing the Weight of a Batch of a Flat Watchers n Design n Initial Algorithm 1. 2. 3. 4. 5. 6. n Step 3 Refinement n n n Get the washer’s inner diameter, outer diameter, thickness Get the material density and quantity of washers manufactured Compute the rim area Compute the weight of one flat washer Computer the weight of the batch of washers Display the weight of the batch of washers 3. 1 Compute hole_radius and edge_radius 3. 2 rim_area is PI * edge_radius – PI * hole_radius Step 4 Refinement n 4. 1 unit_weight is rim_area * thichness * density Lecture 5 -11

Case Study: Computing the Weight of a Batch of a Flat Watchers Figure 3. 5 Flat Washer Program /* Computes the weight of a batch of flat washers. #include #define PI 3. 14159 int { */ Implementation main(void) double double double hole_diameter; edge_diameter; thickness; density; quantity; weight; hole_radius; edge_radius; rim_area; unit_weight; /* /* /* input - diameter of hole input - diameter of outer edge input - thickness of washer input - density of material used input - number of washers made output - weight of washer batch radius of hole radius of outer edge area of rim weight of 1 washer */ */ */ /* Get the inner diameter, outer diameter, and thickness. */ printf("Inner diameter in centimeters> "); scanf("%lf", &hole_diameter); printf("Outer diameter in centimeters> "); scanf("%lf", &edge_diameter); printf("Thickness in centimeters> "); scanf("%lf", &thickness); Lecture 5 -12

Case Study: Computing the Weight of a Batch of a Flat Watchers /* Get the material density and quantity manufactured. */ printf("Material density in grams per cubic centimeter> "); scanf("%lf", &density); printf("Quantity in batch> "); scanf("%lf", &quantity); Implementation (cont. ) /* Compute the rim area. */ hole_radius = hole_diameter / 2. 0; edge_radius = edge_diameter / 2. 0; rim_area = PI * edge_radius PI * hole_radius; /* Compute the weight of a flat washer. */ unit_weight = rim_area * thickness * density; /* Compute the weight of the batch of washers. */ weight = unit_weight * quantity; /* Display the weight of the batch of washers. */ printf("n. The expected weight of the batch is %. 2 f", weight); printf(" grams. n"); return (0); } Inner diameter in centimeters> 1. 2 Outer diameter in centimeters> 2. 4 Thickness in centimeters> 0. 1 Material density in grams per cubic centimeter> 7. 87 Quantity in batch> 1000 The expected weight of the batch is 2670. 23 grams. Lecture 5 -13

3. 2 Library Functions n Predefined Functions and Code Reuse n A Goal of Software Engineering n n n write error-free code Code Reuse, reusing program fragments that have already been written and tested whenever possible. Promotion of Code Reuse in C n n predefined functions C’s standard math library n Example: a function sqrt( ) performs the square root computation function call y = sqrt(x); function name argument Lecture 5 -14

Fig. 3. 7 Square Root Program Enter the first number> 9. 0 /* * Performs three square root computations The square root of the first number is 3. 00 */ Enter the second number> 16. 0 #include /* definitions of printf, scanf */ The square root of the second number is 4. 00 #include /* definition of sqrt */ The square root of the sum of the two numbers is 5. 00 int main(void) { double first, second, /* input - two data values */ first_sqrt, /* output - square root of first */ second_sqrt, /* output - square root of second */ sum_sqrt; /* output - square root of sum */ /* Get first number and display its square root. */ printf("Enter the first number> "); scanf("%lf", &first); first_sqrt = sqrt(first); printf("The square root of the first number is %. 2 fn", first_sqrt); /* Get second number and display its square root. */ printf("Enter the second number> "); scanf("%lf", &second); second_sqrt = sqrt(second); printf("The square root of the second number is %. 2 fn", second_sqrt); /* Display the square root of the sum of the two numbers. */ sum_sqrt = sqrt(first + second); printf("The square root of the sum of the two numbers is %. 2 fn", sum_sqrt); return (0); } Lecture 5 -15

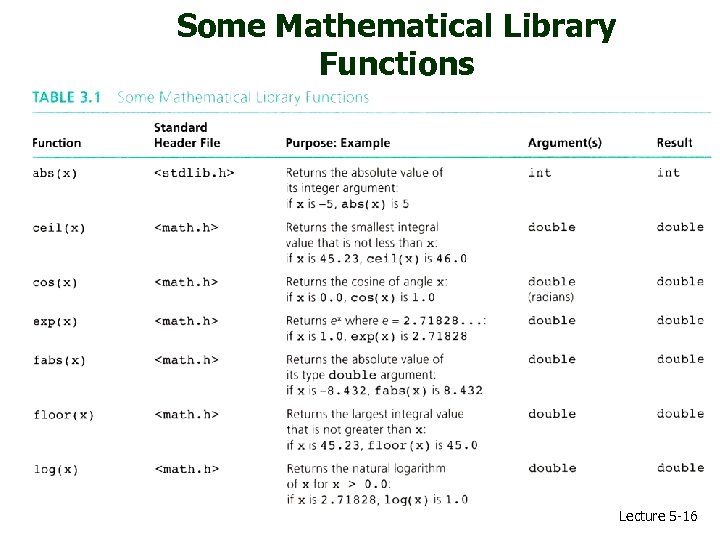Some Mathematical Library Functions Lecture 5 -16

Some Mathematical Library Functions (cont. ) Lecture 5 -17

Using C Library Functions Example 3. 2 Lecture 5 -18

Using C Library Functions n Example 3. 3 Triangle with an Unknown Side If we know the lengths of two sides (b and c 0 of a triangle and the angle between them in degree ( α), the length of the third side (a) can be computed a 2 = b 2 + c 2 – 2 bc cos α n In C language: a = sqrt(pow(b, 2) + pow(c, 2) - 2*b*c*cos(alpha *PI/180. 0)); n Lecture 5 -19

3. 3 Top-Down Design and Structure Charts n n Some algorithms are more complex Programmers must break up the problem into sub-problems to develop the program solution Attempting to solve a problem at one level, new sub-problems at lower levels may be needed This process is called “Top-Down Design” approach n n proceeds from the original problem at the top level to the sub-problems at each lower level Structure Chart is a documentation tool for Top -Down Design Lecture 5 -20

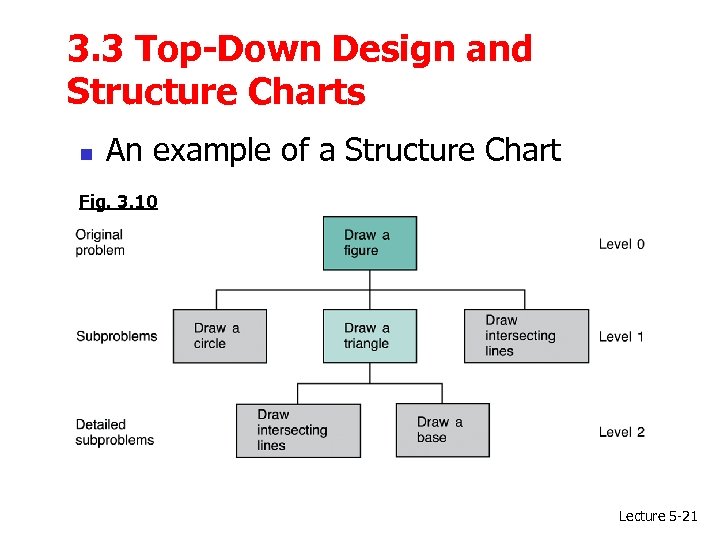3. 3 Top-Down Design and Structure Charts n An example of a Structure Chart Fig. 3. 10 Lecture 5 -21

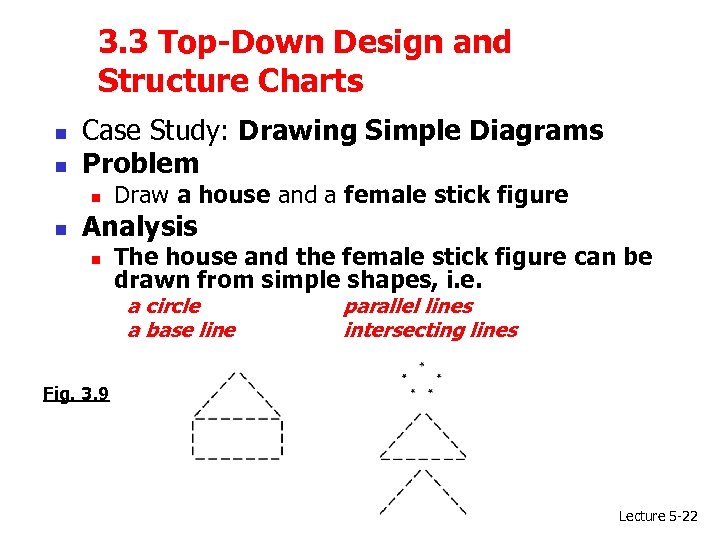3. 3 Top-Down Design and Structure Charts n n Case Study: Drawing Simple Diagrams Problem n n Draw a house and a female stick figure Analysis n The house and the female stick figure can be drawn from simple shapes, i. e. a circle a base line parallel lines intersecting lines Fig. 3. 9 Lecture 5 -22

3. 3 Top-Down Design and Structure Charts n n Case Study: Drawing Simple Diagrams (cont. ) DESIGN n Initial Algorithm 1. 2. 3. n Draw a circle Draw a triangle Draw intersecting lines Algorithm Refinements n Step 2 Refinement n n n 2. 1 Draw intersecting lines 2. 2 Dray a base The structure chart is shown in Fig. 3. 10 Lecture 5 -23

3. 4 Functions without arguments n Functions n n n functions with argument (s) functions without argument Example: The atatement n n n draw_circle(); /*call a function draw_circle with out argument */ This statement call a function draw_circle that implement the algorithm step Draw a circle. Function Call Statement (without argument) SYNTAX: fname(); EXAMPLE: draw_circle(); Interpretation: The function fname is called. after fname has finished execution, the statement that follows the function call will be executed. Lecture 5 -24

Function Prototypes A function must be declared before it can be referenced (called) To declare a function: n n n insert a function prototype before the main function Figure 3. 11 Function Prototypes and Main Function for Stick Figure /* Draws a stick figure */ #include /* function prototypes */ void draw_circle(void); /* Draws a circle */ void draw_intersect(void); /* Draws intersecting lines void draw_base(void); /* Draws a base line void draw_triangle(void); /* Draws a triangle int main(void) { /* Draw a circle. */ draw_circle(); /* Draw a triangle. */ draw_triangle(); /* Draw intersecting lines. */ draw_intersect(); } return (0); */ */ */ Function Prototype (without argument) FORM: ftype fname(void); EXAMPLE: void draw_circle(void); ftype specifies the type of returned value, e. g. , int, double, char, etc. ftype = void means the function does not return a value Lecture argument = void means no argument 5 -25

Function Definitions n Function definitions Function Heading (not ended by ‘; ’ ) Function body enclosed in brackets Return statement (can be eliminated if no value is returned) n n n Figure 3. 23 Function scale /* * Multiplies its first argument by the power of 10 specified * by its second argument. * Pre : x and n are defined and math. h is included. */ double scale(double x, int n) { double scale_factor; /* local variable */ scale_factor = pow(10, n); } return (x * scale_factor); Lecture 5 -26

Figure 3. 14 Program to Draw a Stick Figure /* Draws a stick figure */ #include /* Function prototypes */ void draw_circle(void); void draw_intersect(void); void draw_base(void); void draw_triangle(void); int main(void) { /* Draw a circle. draw_circle(); /* Draws a circle /* Draws intersecting lines /* Draws a base line /* Draws a triangle */ /* Draw a triangle. draw_triangle(); } */ */ */ /* Draw intersecting lines. draw_intersect(); return (0); */ Placement of Functions in a Program /* Draws a circle */ void draw_circle(void) { printf(" * n"); printf(" * * n"); } Lecture 5 -27

Figure 3. 14 Program to Draw a Stick Figure (continue) /* * Draws intersecting lines */ void draw_intersect(void) { printf(" / \ n"); /* Use 2 's to print 1 */ printf(" / \ n"); printf("/ \n"); } /* * Draws a base line */ void draw_base(void) { } printf("-------n"); /* * Draws a triangle */ void draw_triangle(void) { draw_intersect(); draw_base(); } Placement of Functions in a Program Lecture 5 -28