Crystal Nomenclature Weiss parameters Miller indices Axial

Crystal Nomenclature : Weiss parameters Miller indices Axial elements Zones, zone axes, zone symbols

Weiss parameters - (1818 - C. S. Weiss) Weiss parameters give an approximate indication of a face's attitude to the crystallographic axes and also serve as a symbol for this face. Weiss parameters give the relative number of units at which a face cuts each axis. Negative signs indicate that the negative end of an axis is intersected. The reasons to create these parameters were to refer with no ambiguity the different faces of a crystal. To do this, a set of crystallogaphic axes is chosen among the 7 crystal systems recognized which corresponds to the symmetry of the crystal selected.

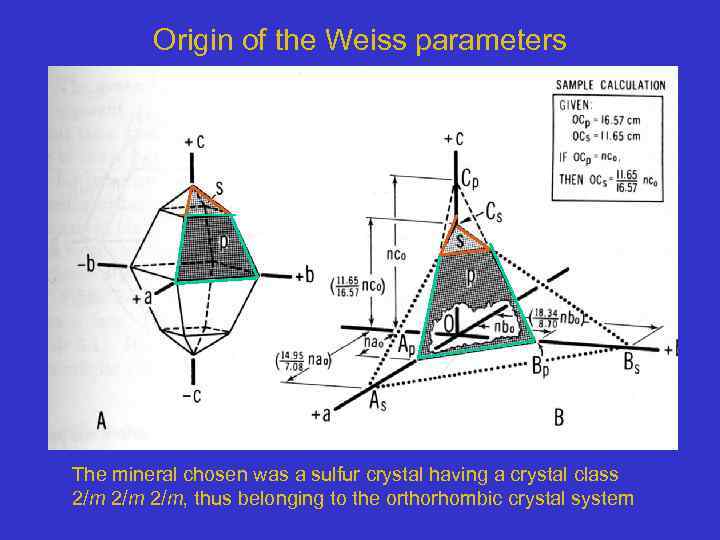Origin of the Weiss parameters The mineral chosen was a sulfur crystal having a crystal class 2/m 2/m, thus belonging to the orthorhombic crystal system

Weiss parameters - How to proceed ? 1) Select a unit face, usually the face having the largest development 2) This face will be served at a reference to measure the other faces of the crystal. It will be the unit face or parametral plane. 3) The lenght of the face intercepts on the crystallographic axes segments may be measured for the two faces. 1) They refer to the a, b and c crystallographic axes 2) 4) Write the ratio of the face intercepts between the face 3) selected and that of the reference face. 4) Initially, Weiss started with the exact lenght of the two 5) face intersepts. Then the reference face was considered 6) to have parameters equal to unity.

About face intercepts The intercepts of a face have no relation to its size, for a face may be moved parallel to itself for any distance without changing the relative values of its intersections with the crystallographic axes. Intercepts measure where a crystal face hits a crystal axis. The location on the axes corresponding to unit lengths is arbitrary and chosen for simplicity and convenience. Axes usually radiate from the center in a right hand rule arrangement. Axes pass through centers or edges.

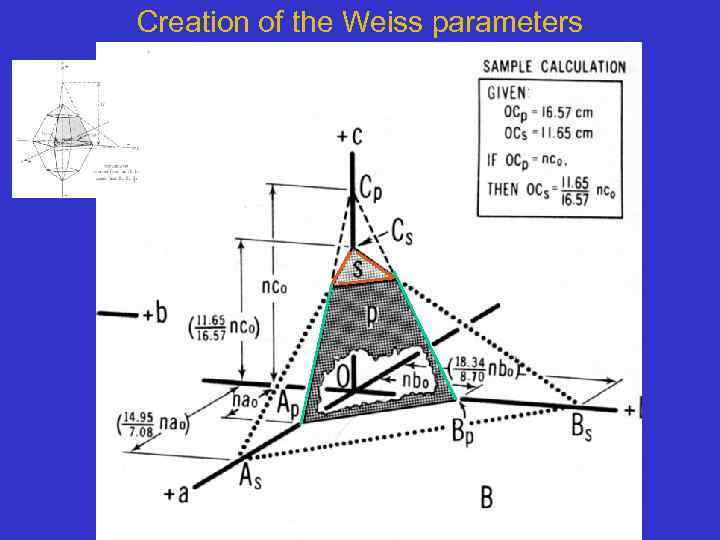Creation of the Weiss parameters

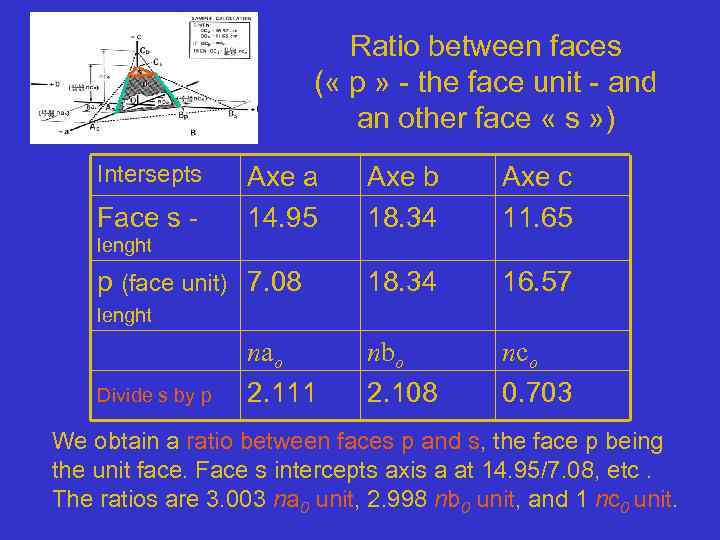Ratio between faces ( « p » - the face unit - and an other face « s » ) Intersepts Face s - Axe a 14. 95 Axe b 18. 34 Axe c 11. 65 18. 34 16. 57 nbo 2. 108 nco 0. 703 lenght p (face unit) 7. 08 lenght nao Divide s by p 2. 111 We obtain a ratio between faces p and s, the face p being the unit face. Face s intercepts axis a at 14. 95/7. 08, etc. The ratios are 3. 003 na 0 unit, 2. 998 nb 0 unit, and 1 nc 0 unit.

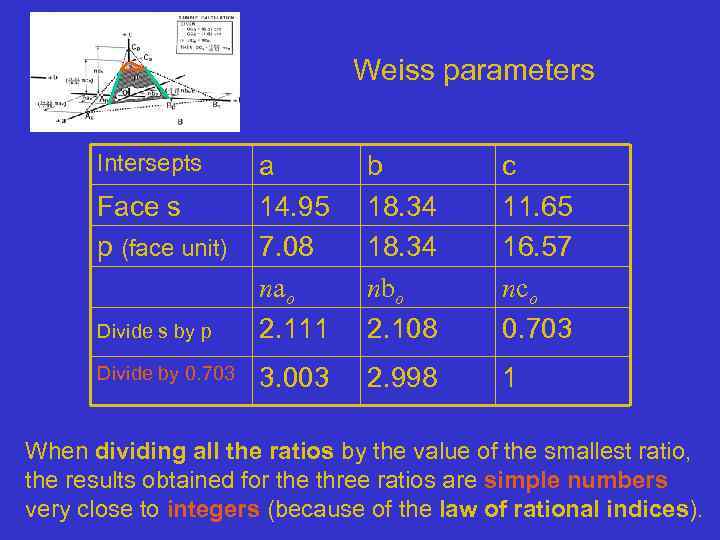Weiss parameters Intersepts Divide s by p a 14. 95 7. 08 nao 2. 111 b 18. 34 nbo 2. 108 c 11. 65 16. 57 nco 0. 703 Divide by 0. 703 3. 003 2. 998 1 Face s p (face unit) When dividing all the ratios by the value of the smallest ratio, the results obtained for the three ratios are simple numbers very close to integers (because of the law of rational indices).

Law of rational indices (Hauy’s law) The division of the cell unit by the parameters of an unknown face always yield to simple rational numbers (simple fractions or simple integers), usually less than 6. Hauy first disclosed the rational nature of the Weiss parameters or Miller indices. This phenomenon is referred as the law of rational indices or Hauy's law. Its validity becomes apparent with the internal structure of minerals, particularly crystal lattices. From : http: //www. tulane. edu/~sanelson/eens 211/axial_ratios_paramaters_miller_indices. htm

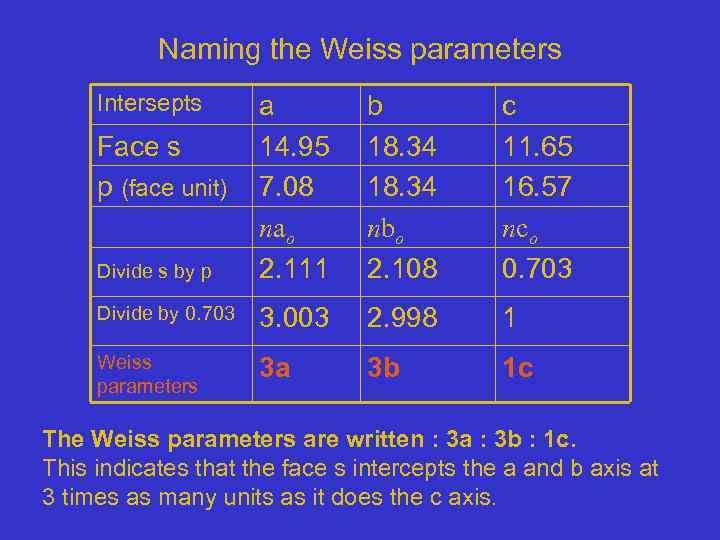Naming the Weiss parameters Intersepts Divide s by p a 14. 95 7. 08 nao 2. 111 b 18. 34 nbo 2. 108 c 11. 65 16. 57 nco 0. 703 Divide by 0. 703 3. 003 2. 998 1 Weiss parameters 3 a 3 b 1 c Face s p (face unit) The Weiss parameters are written : 3 a : 3 b : 1 c. This indicates that the face s intercepts the a and b axis at 3 times as many units as it does the c axis.

Weiss parameters Two important points 1) The intercepts or parameters are relative values, and do not indicate any actual cutting lengths. 2) Since they are relative, a face can be moved parallel to itself without changing its relative intercepts or parameters.

Weiss parameters - 1 face parallel to 2 cristallographic axes If a face is parallel to an axis, it is assumed to intercept this axis at an infinite distance from the origin. The Weiss parameters of the shaded face is : ¥ a : ¥ b : 1 c From : http: //www. tulane. edu/~sanelson/eens 211/axial_ratios_paramaters_miller_indices. htm

Weiss parameters - 1 face parallel to 1 cristallographic axis The Weiss parameters of the shaded face is : a : 1 b : ¥ c From : http: //www. tulane. edu/~sanelson/eens 211/axial_ratios_paramaters_miller_indices. htm

Weiss parameters - 1 crystal face that intersects all 3 cristallographic axes The face is assumed to intersect the a, b, and c crystallographic axes at one unit length on each. Thus, the parameters would be: 1 a : 1 b : 1 c From : http: //www. tulane. edu/~sanelson/eens 211/axial_ratios_paramaters_miller_indices. htm

Miller indices - Nomenclature What are Miller indices ? It’s a new notation of faces proposed by W. H. Miller, from the Cambridge University. The Miller indices are just the inverse of the Weiss Parameters - with the fraction cleared. In addition, the letter denoting the cristallographic axes is omitted, the « : » suppressed and parentheses are added. . If a face is written with Weiss parameters as 1 a : 1 b : c the report of this face with Miller indices becomes: (110)

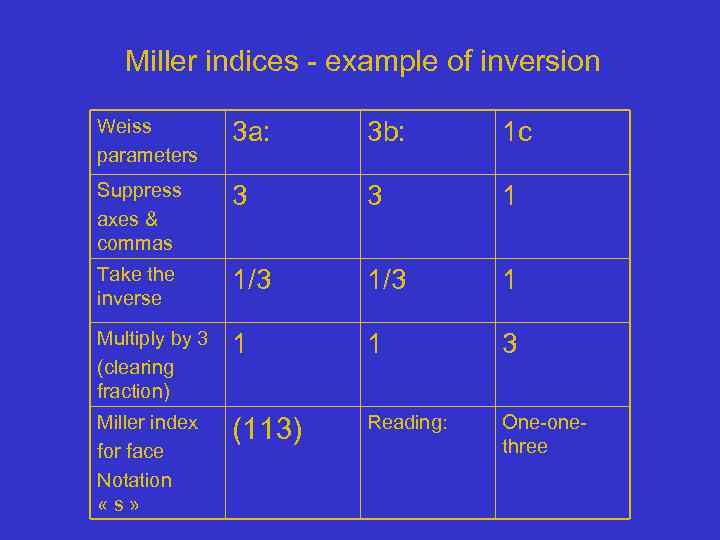Miller indices - example of inversion Weiss parameters 3 a: 3 b: 1 c Suppress axes & commas 3 3 1 Take the inverse 1/3 1 Multiply by 3 (clearing fraction) 1 1 3 Miller index for face Notation « s » (113) Reading: One-onethree

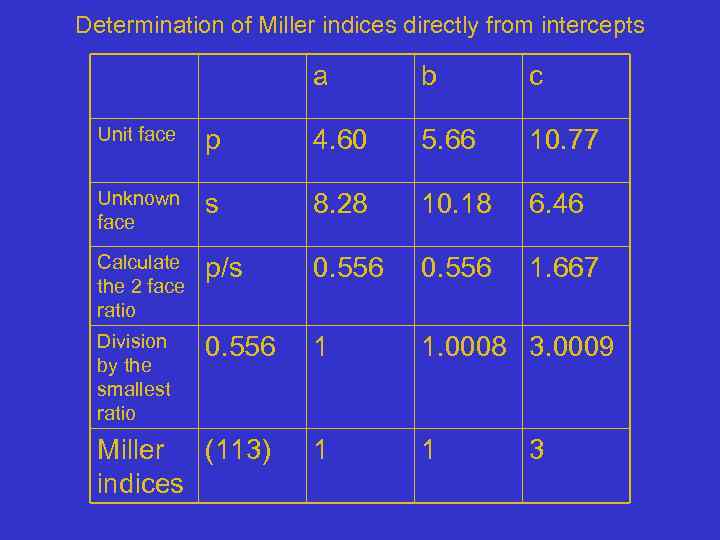Determination of Miller indices directly from intercepts a b c Unit face p 4. 60 5. 66 10. 77 Unknown face s 8. 28 10. 18 6. 46 Calculate the 2 face ratio p/s 0. 556 1. 667 Division by the smallest ratio 0. 556 1 1. 0008 3. 0009 Miller (113) indices 1 1 3

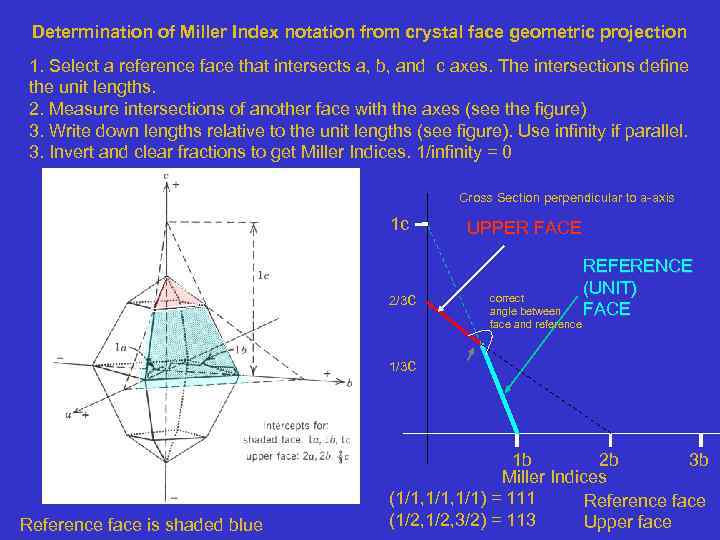Determination of Miller Index notation from crystal face geometric projection 1. Select a reference face that intersects a, b, and c axes. The intersections define the unit lengths. 2. Measure intersections of another face with the axes (see the figure) 3. Write down lengths relative to the unit lengths (see figure). Use infinity if parallel. 3. Invert and clear fractions to get Miller Indices. 1/infinity = 0 Cross Section perpendicular to a-axis 1 c 2/3 c UPPER FACE correct angle between face and reference REFERENCE (UNIT) FACE 1/3 c Reference face is shaded blue 1 b 2 b 3 b Miller Indices (1/1, 1/1) = 111 Reference face (1/2, 3/2) = 113 Upper face

Report of Weiss parameters and Miller indices on crystal - comparison Weiss notation From Bloss, 1994 - New edition - Min. Soc of Amer - Crystallography and Crystal chemistry Miller notation

Examples: finding Miller indices The colored face is parallel to a 1 and a 2, meeting them only at ∞ Problem: find the Miller Index for this face with intercepts ∞a 1, ∞a 2, 1 a 3 1. Invert the indices: Since 1/∞ = 0 and 1/1 = 1 we have 0/1 1/1 2. Clear fractions by multiplying through by 1 (0 0 1)

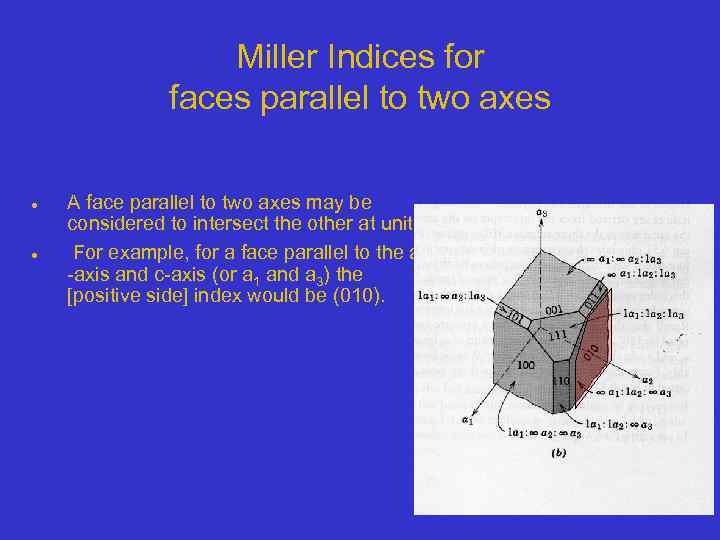Miller Indices for faces parallel to two axes A face parallel to two axes may be considered to intersect the other at unity. For example, for a face parallel to the a -axis and c-axis (or a 1 and a 3) the [positive side] index would be (010).

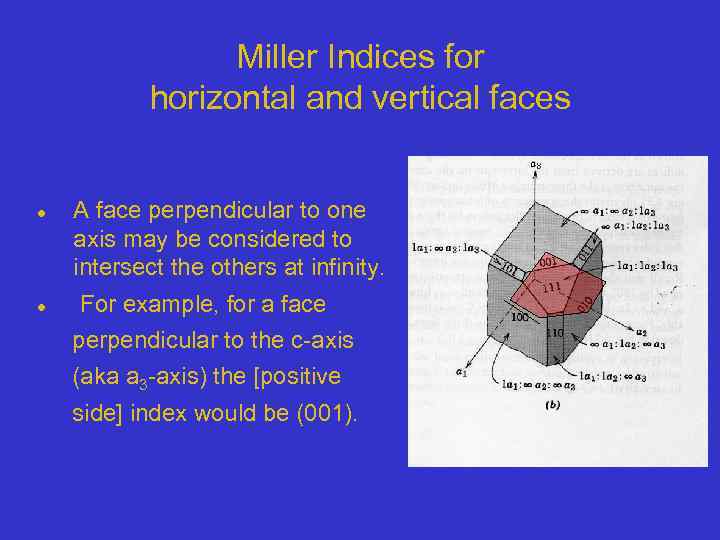Miller Indices for horizontal and vertical faces A face perpendicular to one axis may be considered to intersect the others at infinity. For example, for a face perpendicular to the c-axis (aka a 3 -axis) the [positive side] index would be (001).

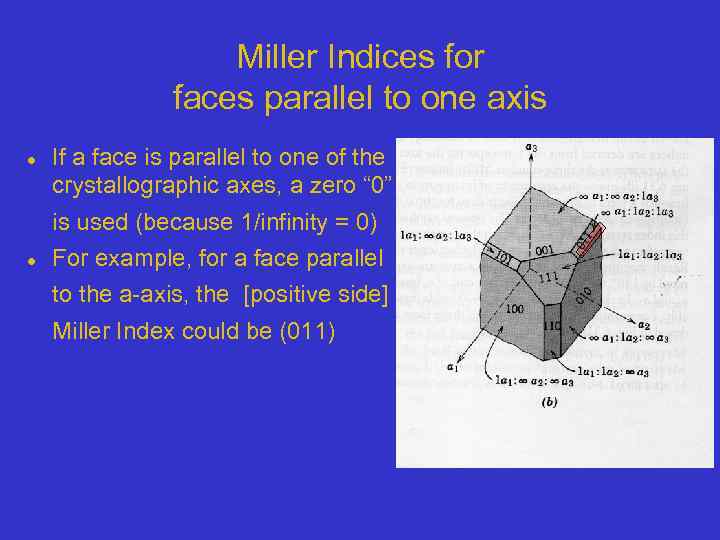Miller Indices for faces parallel to one axis If a face is parallel to one of the crystallographic axes, a zero “ 0” is used (because 1/infinity = 0) For example, for a face parallel to the a-axis, the [positive side] Miller Index could be (011)

Miller Indices: Other Example • The intercepts of the plane are at 0. 5 a, 0. 75 b, and 1. 0 c • Take the reciprocals to get (2, 4/3, 1) • Reduce common factors to get Miller Index of (643)

Faces that intersect axes on their negative side “For faces that intersect negative ends of crystallographic axes, a bar is placed over the appropriate number…. The bar represents the minus sign in a negative number

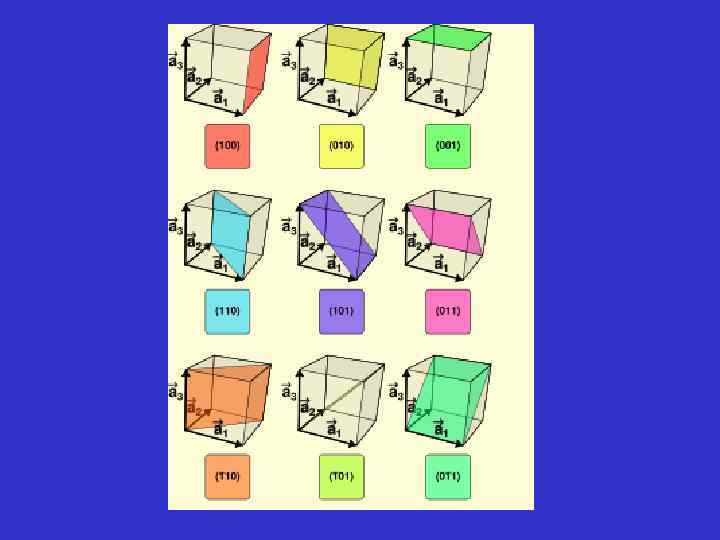
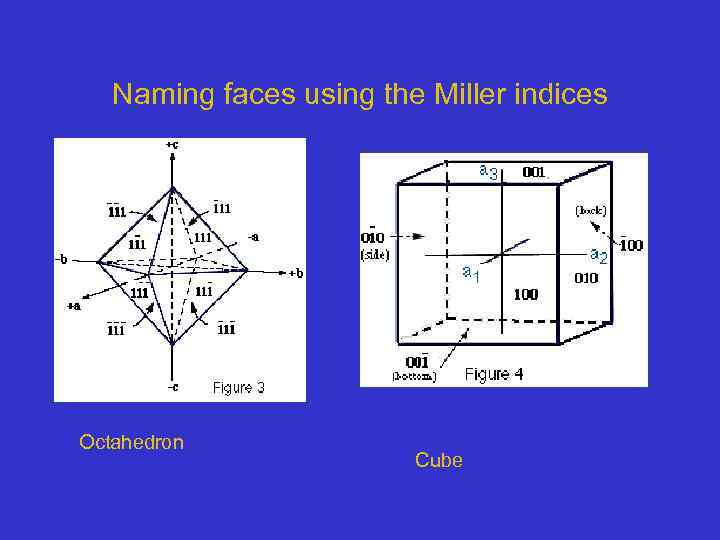Naming faces using the Miller indices Octahedron Cube

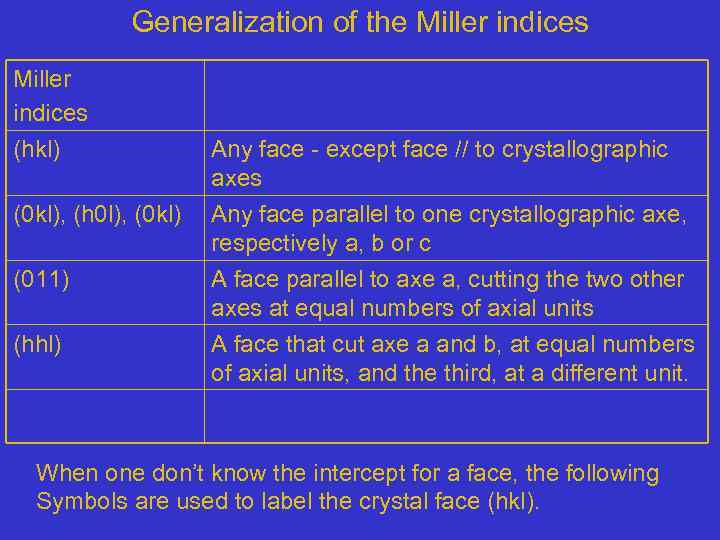Generalization of the Miller indices (hkl) Any face - except face // to crystallographic axes (0 kl), (h 0 l), (0 kl) Any face parallel to one crystallographic axe, respectively a, b or c (011) A face parallel to axe a, cutting the two other axes at equal numbers of axial units A face that cut axe a and b, at equal numbers of axial units, and the third, at a different unit. (hhl) When one don’t know the intercept for a face, the following Symbols are used to label the crystal face (hkl).

Miller - Bravais indices - Hexagonal system Introduction of this system by Auguste Bravais in 1851 due to the existence of four cristallographic axes in the hexagonal system. This set of 4 axes is often called the Bravais axial set and the indices the Miller-Bravais indices as Bravais followed the Miller method. Miller-Bravais 1121 1101 Weiss 2 a 1: 2 a 2: -1 a 3: 1 c 1 a 1: -1 a 2: a 3: 1 c Comments A face cut the positive a 1 and a 2, at twice as many (a 0) units as it cuts the negative axe a 3, and the c axe at the same number of c 0 units as it cuts the a 1 and a 2 axes in a 0 units (hkil)

Miller Bravais Indices Since the hexagonal system has three "a" axes perpendicular to the "c" axis, both the parameters of a face and the Miller indice notation must be modified. The modified parameters and Miller indices must reflect the presence of an additional axis. This modified notation is referred to as Miller-Bravais Indices, with the general notation (hkil). Often called also the Bravais axial set (1851). Bravais has followed the Miller method: The Miller-Bravais method consists of 4 numbers (hkil) cited in order in which they refer to a 1, a 2, a 3 and c axes.

Indicies in the Hexagonal System Miller-Bravais Index Uses all four axes Extra place marker (hkil) “a” Indicies sum to 0 Miller Index Uses three axes index with three place markers (hkl) Convert to Miller. Bravais index by assigning i such that (hkil) sums to 0

Miller - Bravais indices - Hexagonal system (hkil) h + k + i = 0 1121 ----> 1+1 -2=0 1101 ----> 1 -1 = 0

Miller Indices: Example

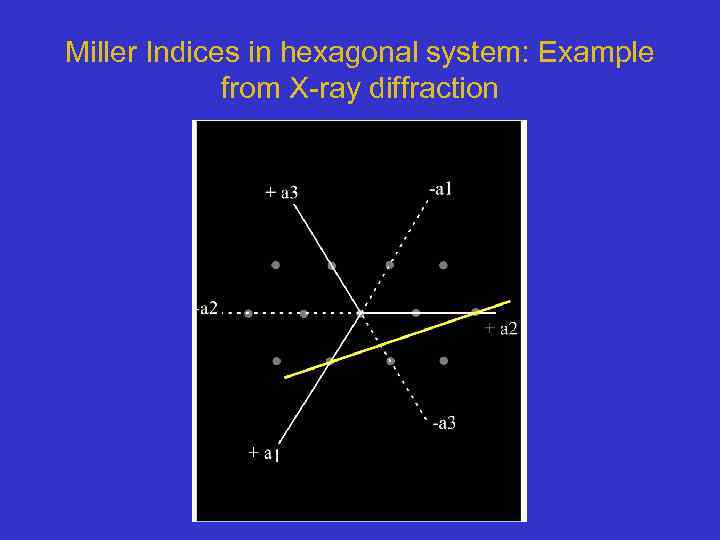Miller Indices in hexagonal system: Example from X-ray diffraction

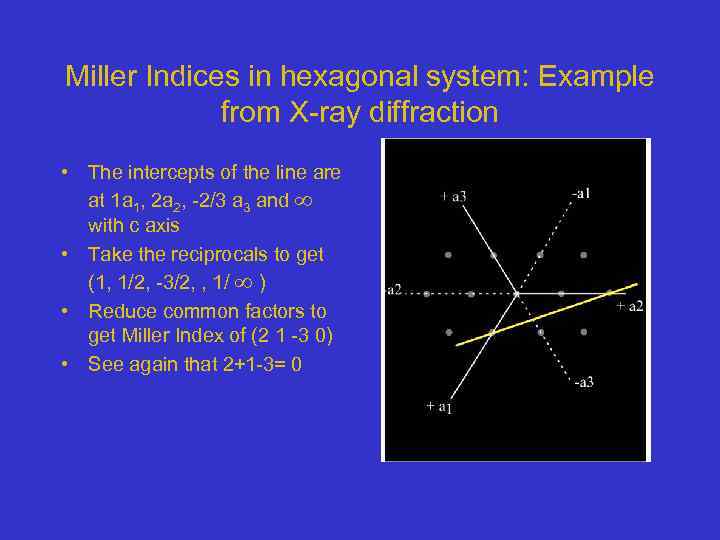Miller Indices in hexagonal system: Example from X-ray diffraction • The intercepts of the line are at 1 a 1, 2 a 2, -2/3 a 3 and with c axis • Take the reciprocals to get (1, 1/2, -3/2, , 1/ ) • Reduce common factors to get Miller Index of (2 1 -3 0) • See again that 2+1 -3= 0

Hexagonal coordinates • Except for (0001) plane, the geometry of this lattice requires both positive and negative terms in the index • A quick check on the correctness of hexagonal indices is that the sum of the first two digits times (-1) should be equal to the third digit.

Axial ratios are defined as the relative lengths of the crystallographic axes. They are normally taken as relative to the length of the b crystallographic axis. Thus, an axial ratio is defined as follows: Axial Ratio = a/b : b/b : c/b Axial Ratio = a/b : 1 : c/b

Axial ratios for the different crystal systems For triclinic, monoclinic and orthorhombic crystals, the lenghts of the crystallographic axes are different. So Axial ratio = a/b: 1 : c/b, other shortened as Axial ratio = a : 1 : c For tetragonal crystals, a and b are equal. So Axial ratio = 1 : c/b, other shortened to 1 : c For isometric crystals, a, b and c are equal. So Axial ratio = 1 : 1, other shortened to 1 For hexagonal crystals, a 1, a 2 and a 3 are equal. So Axial ratio = 1 : 1 : c/a, other shortened to 1 : c

Measurement of axial ratios with X-rays Example - Quartz is hexagonal. a 1 = a 2 = a 3 = 4. 913 A° (Angströms) ; c = 5. 405 A° 1 Angström = 10 -10 meter. The axial ratio is 1 : 1 : (5. 405 / 4. 913) 1 : 1 : 1. 1001 The c axis is 1. 1001 longer than the a axis.

Measurement of axial ratios with X-rays Example - Sulfur is orthorhombic with a≠b≠c. a = 10. 47 A° b = 12. 87 A° c = 24. 39 A° The axial ratio is 10. 47/12. 87 : 12. 87/12. 87 : 24. 39/12. 87 0. 813 : 1. 903 Formely, the axial ratio was determinted by measuring the angles between crystal faces. In 1896, the axial ratio of orthorhombic sulfur was measured with nearly the same value as the one obtained from X-rays measurements.

Why to measure axial ratios in the past ?

Why to measure axial ratios in the past ? Because it was an important mean of identication as Trimetric crystals of differing composition rarely possess identical crystal ratios. This is of course less precise for dimetric crystals as the tetragonal and hexagonals crystals because the axial ratios are expressed with two values only. For the isometric minerals, cubic minerals, the axial ratio is of no significance.

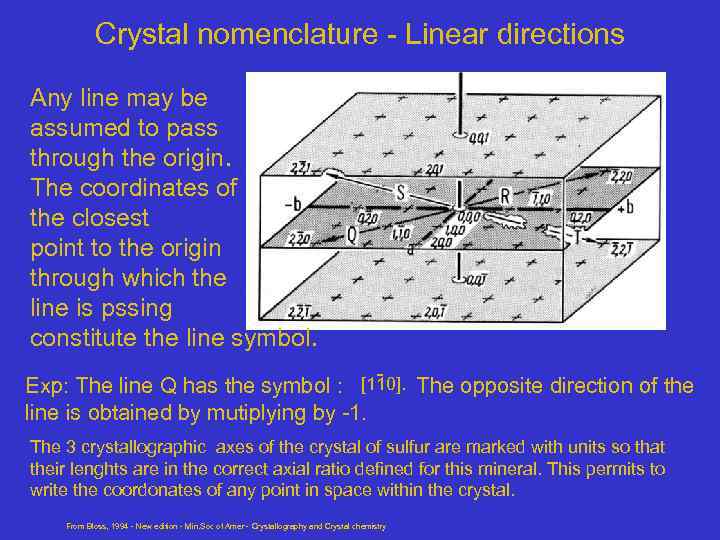Crystal nomenclature - Linear directions Any line may be assumed to pass through the origin. The coordinates of the closest point to the origin through which the line is pssing constitute the line symbol. - [110]. Exp: The line Q has the symbol : The opposite direction of the line is obtained by mutiplying by -1. The 3 crystallographic axes of the crystal of sulfur are marked with units so that their lenghts are in the correct axial ratio defined for this mineral. This permits to write the coordonates of any point in space within the crystal. From Bloss, 1994 - New edition - Min. Soc of Amer - Crystallography and Crystal chemistry

Zone axes and zone symbols A zone axis represents a set of crystal faces parallel to a common line at the intersection of edge faces. Since the edges will all be parallel to a line, we can define the direction of the line using a notation similar to Miller indices with the direction put into brackets [ ]. This notation is often called the zone symbol [uvw]. In crystals, these zone symbols parallel to major face intersection are often parallel to the crystallographic axes. From : http: //www. tulane. edu/~sanelson/eens 211/axial_ratios_paramaters_miller_indices. htm

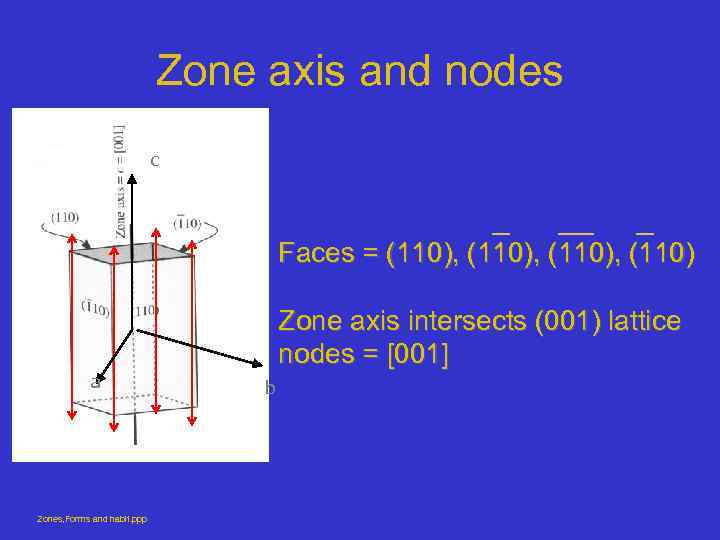Zone axis and nodes c Faces = (110), (110) a Zones, Forms and habit. ppp Zone axis intersects (001) lattice nodes = [001] b

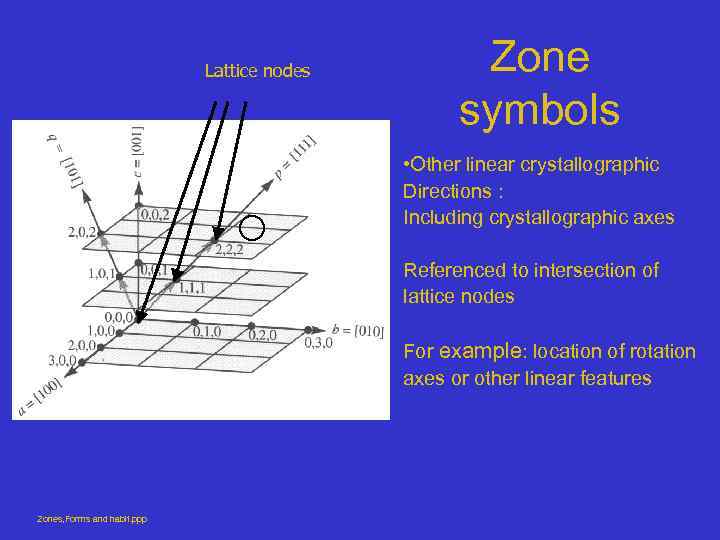Lattice nodes Zone symbols • Other linear crystallographic Directions : Including crystallographic axes Referenced to intersection of lattice nodes For example: location of rotation axes or other linear features Zones, Forms and habit. ppp

Plane, zone axes (100) - Miller index; denote a plane of the crystal structure, and regular repetition of that plane with a particular spacing. In the cubic system, the normal to plane (hkl) is the direction [hkl]. In lower symmetry cases, the normal to (hkl) is not parallel to [hkl]. [100] - Coordinate in square brackets denote a direction vector Other notation : to see later : zone form {100} - Indices in curly brackets or braces denote a family of directions (often plane direction, related by symmetry operations. In the cubic system {100} form would mean a set of the following faces (001), (100), (010) From Bloss, 1994 - New edition - Min. Soc of Amer - Crystallography and Crystal chemistry

Finding the zone symbol of two non parallel faces For a group of faces in the same zone, we can determine the zone symbol for all non-hexagonal minerals by choosing 2 non-parallel faces (hkl) and (pqr). To do so, we write the Miller Index for each face twice, one face directly beneath the other. The first and last numbers in each line are discarded. Then we apply the following formula to determine the indices in the zone symbol. u = k*r - l*q, v = l*p - h*r, and w = h*q - k*p From : http: //www. tulane. edu/~sanelson/eens 211/axial_ratios_paramaters_miller_indices. htm

Determination of zone symbol: example For example, faces (110) and (010) are not parallel to each other. The zone symbol for these faces (and any other faces that lie in the same zone) is determined by writing 110 twice and then immediately below, writing 010 twice. Applying the formula above gives the zone symbol for this zone as [001]. From : http: //www. tulane. edu/~sanelson/eens 211/axial_ratios_paramaters_miller_indices. htm

Crystallographic implications The zone symbol implies a line that is perpendicular to a face having the same index. In other words, [001] is a line perpendicular to the face (001). It can thus be used as a symbol for a line. In this case, the line is the c crystallographic axis. Zone symbols, therefore are often used to denote directions through crystals. Being able to specify directions in crystals is important because many properties of minerals depend on direction. These are called vectorial properties. From : http: //www. tulane. edu/~sanelson/eens 211/axial_ratios_paramaters_miller_indices. htm

Cristallographic relationships in orthorhombic, tetragonal or isometric systems ｷ If h is 0, i. e. (0 kl) is the Miller Index, then the face is parallel to the a crystallographic axis. So, = 0 o or = 180 o ｷ If k is 0 i. e. (h 0 l) is the Miller Index, then the face is parallel to the b crystallographic axis. So, = 90 o or = 270 o ｷ If l is 0, i. e. (hk 0) is the Miller Index, then the face is parallel to the c crystallographic axis. So, = 90 o ｷ If h & k are 0, i. e. (00 l) is the Miller Index, then the face is perpendicular to the c axis So, = 0 o or = 180 o, and is undefined. ｷ If h & l are 0, i. e. (0 k 0) is the Miller Index, then the face is perpendicular to the b axis. So, = 90 o and = 0 o or = 180 o. ｷ If l and k are 0, i. e. (h 00) is the Miller Index, then the face is perpendicular to the a axis. So, = 90 o and = 90 o or = 270 o. From : http: //www. tulane. edu/~sanelson/eens 211/axial_ratios_paramaters_miller_indices. htm

Computing Miller index (hkl) of a face parallel to two given lines (u 1 v 1 w 1) and (u 2 v 2 w 2) This may be done as previously : u 1 v 1 w 1 u 2 v 2 w 2 h = v 1 w 2 - v 2 w 1 k = u 2 w 1 - u 1 w 2 l = u 1 v 2 - u 2 v 1

Test for tautozonality of crystal faces If 3 given planes : (h 1 k 1 l 1), (h 2 k 2 l 2) and (h 3 k 3 l 3) are tautozonal, that is, lying in the same zone, and parallel to the same zone axis, then the determinant formed with their indices must equal 0. h 1 k 1 l 1 h 2 k 2 l 2 = 0 h 3 k 3 l 3 If 3 directions are coplanar, the determinant must be also equal to 0.

Crystallographic calculations Miller Indices (hkl) Axial ratios -. a: 1: c and angles correspond to a Miller Index (hkl) forming angles between crystallographic axes : is the angle between the c axis and the normal to the face is the angle between the b axis and the normal to the face We may calculate the axial ratios, as well as and angles From : http: //www. tulane. edu/~sanelson/eens 211/axial_ratios_paramaters_miller_indices. htm

Cristallographic calculations - Examples (1) Given Miller Indices (hkl) and angles for crystal faces that, in combination, intersect all crystallographic axes, calculate the axial ratios of the mineral. Faces and (110) 90° 45° (011) 70° 0° (110) (011) http: //www. tulane. edu/~sanelson/eens 211/axial_ratios_paramaters_miller_indices. htm

Cristallographic calculations - Examples (1) We can write: tan 45° : 1 b/1 a 1 a/1 b= 1/ tan 45° = 1 So a/b: b/b = 1 : 1

What is the crystal system? We next note that the (011) face intersects the b and c axes only. à Examination of relationships in the plane with b and c. àThe angle is the angle between the pole to the face and axis c ---> The angle exists also, because of similar triangle, between the b axis and the face. tan 70° = 1 c/1 b -----> c: b = 2. 7475 So a : b : c = 1 : 2. 7475 ----> Crystal system ?

It is the tetragonal system We next note that the (011) face Intersects the b and c axes only. àExamination of relationships in the plane with b and c. àThe angle is the angle between the pole to the face and axis c ---> The angle exists also, because of similar triangle, between the b axis and the face. tan 70° = 1 c/1 b -----> c: b = 2. 7475 So a : b : c = 1 : 2. 7475 ----> Tetragonal

Formulas for computation of tan and from its Miller indices (hkl) and from the axial elements

Crystal system - Important points The lengths of the crystallographic axes are controlled by the dimensions of the unit cell upon which the crystal is based. . The angles between the crystallographic axes are controlled by the shape of the unit cell. In addition, the relative lengths of the crystallographic axes control the angular relationships between crystal faces. End !