Скачать презентацию Cryptology LECTURE 2 Cryptology the study of Скачать презентацию Cryptology LECTURE 2 Cryptology the study of

67db160966865939ed0d3f3225d817a3.ppt

  • Количество слайдов: 158

Cryptology LECTURE 2 Cryptology LECTURE 2

Cryptology, the study of cryptosystems can be subdivided into two disciplines: Cryptography cryptanalysis Cryptography Cryptology, the study of cryptosystems can be subdivided into two disciplines: Cryptography cryptanalysis Cryptography : concerns itself with the design of cryptosystems Cryptanalysis: (code breaking) studies the breaking of cryptosystems

History About 1900 BC An Egyptian scribe used non-standard hieroglyphs in an inscription. Julius History About 1900 BC An Egyptian scribe used non-standard hieroglyphs in an inscription. Julius Caesar (100 -44 BC) used a simple substitution with the normal alphabet (just shifting the letters a fixed amount) in government communications

History 1933 -1945 The Enigma machine was not a commercial success but it was History 1933 -1945 The Enigma machine was not a commercial success but it was taken over and improved upon to become the cryptographic workhorse of Nazi Germany. rotor cipher machines used for the encryption and decryption of secret messages. Enigma was invented by German engineer Arthur Scherbius at the end of World War I

History 1976 A design by IBM based on the Lucifer cipher and with changes History 1976 A design by IBM based on the Lucifer cipher and with changes (including both S-box improvements and reduction of key size) by the US NSA, was chosen to be the U. S. Data Encryption Standard.

History 1976 Whitfield Diffie and Martin Hellman published ``New Directions in Cryptography'', introducing the History 1976 Whitfield Diffie and Martin Hellman published ``New Directions in Cryptography'', introducing the idea of public key cryptography

Cryptography Cryptography

Cryptography or Encryption, process of converting messages, information, or data into a form unreadable Cryptography or Encryption, process of converting messages, information, or data into a form unreadable by anyone except the intended recipient. Encrypted data must be deciphered, or decrypted, before it can be read by the recipient.

Cryptography : Requirements two requirements for secure use of symmetric encryption: a strong encryption Cryptography : Requirements two requirements for secure use of symmetric encryption: a strong encryption algorithm a secret key known only to sender / receiver mathematically have: Y = EK(X) X = DK(Y) assume encryption algorithm is known implies a secure channel to distribute key 9

Cryptography : Some Basic Terminology plaintext - original message ciphertext - coded message cipher-algorithm Cryptography : Some Basic Terminology plaintext - original message ciphertext - coded message cipher-algorithm : for transforming plaintext to ciphertext key - info used in cipher known only to sender/receiver encipher (encrypt) - converting plaintext to ciphertext decipher (decrypt) - recovering ciphertext from plaintext 10

Cryptanalysis Cryptanalysis

Cryptanalysis objective to recover key not just message is the art and science of Cryptanalysis objective to recover key not just message is the art and science of analyzing information systems in order to study the hidden aspects of the systems general approaches: ◦ cryptanalytic attack rely on the nature of the algorithm plus perhaps some knowledge of the general characteristics of the plaintext or even some sample plaintext-ciphertext pairs. ◦ Brute-force attack try every possible key on a piece of cipher text until an intelligible translation into plaintext is obtained. 12

Cryptanalytic Attacks ciphertext only knows algorithm & ciphertext known plaintext know/suspect plaintext & ciphertext Cryptanalytic Attacks ciphertext only knows algorithm & ciphertext known plaintext know/suspect plaintext & ciphertext chosen plaintext select plaintext and obtain ciphertext chosen ciphertext select ciphertext and obtain plaintext chosen text select plaintext or ciphertext to en/decrypt 13

Brute Force Search always possible to simply try every key most basic attack, proportional Brute Force Search always possible to simply try every key most basic attack, proportional to key size assume either know / recognise plaintext Key Size (bits) Number of Alternative Keys Time required at 1 decryption/µs Time required at 106 decryptions/µs 32 232 = 4. 3 9 10 231 µs = 35. 8 minutes 2. 15 milliseconds 56 256 = 7. 2 16 10 255 µs = 1142 years 10. 01 hours 128 2128 = 3. 4 38 10 2127 µs years = 5. 4 24 10 5. 4 18 years 10 168 2168 = 3. 7 50 10 2167 µs years = 5. 9 36 10 5. 9 30 years 10 26 characters (permutation) 26! = 4 26 10 2 26 µs = 6. 4 12 10 10 years 6. 4 6 years 10 14

Classic techniques Classic techniques

Cryptography : The main two basic techniques Substitution Transposition 16 Cryptography : The main two basic techniques Substitution Transposition 16

Classical Substitution Ciphers Substitution : where letters of plaintext are replaced by other letters Classical Substitution Ciphers Substitution : where letters of plaintext are replaced by other letters or by numbers or symbols or if plaintext is viewed as a sequence of bits, then substitution involves replacing plaintext bit patterns with cipher text bit patterns 17

Transposition Ciphers Transposition or Permutation ciphers : these hide the message by rearranging the Transposition Ciphers Transposition or Permutation ciphers : these hide the message by rearranging the letter order without altering the actual letters used can recognise these since have the same frequency distribution as the original text. 18

Example for Substitution Example for Substitution

Caesar Cipher earliest known substitution cipher by Julius Caesar first attested use in military Caesar Cipher earliest known substitution cipher by Julius Caesar first attested use in military affairs replaces each letter by 3 rd letter on example: M e e t m e a f t e r t h e t o g a p a r t y P H H W P H D I W H U W K H W R J D S D U W B 20

Caesar Cipher then have Caesar cipher as: c = E(p) = (p + k) Caesar Cipher then have Caesar cipher as: c = E(p) = (p + k) mod (26) p = D(c) = (c – k) mod (26) 21

Caesar Cipher can define transformation as: a b c d e f g h Caesar Cipher can define transformation as: a b c d e f g h i j k l m n o p q r s t u v w x y z D E F G H I J K L M N O P Q R S T U V W X Y Z A B C mathematically give each letter a number a b c d e f g h i j k l m n o p q r s t u v w x y z 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 then have Caesar cipher as: c = E(p) = (p + 3) mod (26) If p= a= 0 , E(a) = (0+3) mod 26 = 3 = D 22

a b c d e f g h i j k l m n a b c d e f g h i j k l m n o p q r s t u v w x y z 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 a 0 b c 1 2 d e 3 4 f 5 g h i 6 7 8 j 9 k l m n o p q r s t u v w x y z 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 23

Caesar Example Let k= 10 Encrypt the following “Hello” 24 Caesar Example Let k= 10 Encrypt the following “Hello” 24

Caesar Example Let k= 10 Encrypt the following “Hello” H E L L O Caesar Example Let k= 10 Encrypt the following “Hello” H E L L O 7 4 11 11 14 17 14 21 21 24 ------------(MOD 26) 17 14 21 24 R O V V Y 25

Caesar Example Let k= 9 Encrypt the following “SUN” 26 Caesar Example Let k= 9 Encrypt the following “SUN” 26

Caesar Example Let k= 9 Encrypt the following “SUN” S U N 18 20 Caesar Example Let k= 9 Encrypt the following “SUN” S U N 18 20 13 27 29 22 ------------(MOD 26) 1 3 22 B D W 27

Caesar Example Let the cipher text = “IFMMP” and k =1 What is the Caesar Example Let the cipher text = “IFMMP” and k =1 What is the plain text? P= (C-1) mod 26 P = Hello 28

Cryptanalysis of Caesar Cipher only have 26 possible ciphers ◦ A maps to A, Cryptanalysis of Caesar Cipher only have 26 possible ciphers ◦ A maps to A, B, . . Z could simply try each in turn a brute force search given ciphertext, just try all shifts of letters do need to recognize when have plaintext eg. break ciphertext "GCUA VQ DTGCM" 29

Example for fun G C U A V Q D T G C M Example for fun G C U A V Q D T G C M A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A B C D E F I J K L M N O p q r s t u v w x O P Q R S T U V W X Y Z A B c d e f g h I j k l m n U V W X Y Z A B C D E F G H I J K l m n o p q r s t P Q R S T U V W X Y Z A B K L M N O P Q R S T U V W X y z a b c d e f g h I j X Y Z A B C D E F g h I j k l m n o p q r s t u v w N O P Q R S T U V W X Y Z A B C D E F G H I J K L M A B C D E F G H I J W X Y Z A B C D E F G H I J K L M 30

Example for fun G C U A V Q D T G C M Example for fun G C U A V Q D T G C M A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A B C D E F I J K L M N O p q r s t u v w x O P Q R S T U V W X Y Z A B c d e f g h I j k l m n U V W X Y Z A B C D E F G H I J K l m n o p q r s t P Q R S T U V W X Y Z A B K L M N O P Q R S T U V W X y z a b c d e f g h I j X Y Z A B C D E F g h I j k l m n o p q r s t u v w N O P Q R S T U V W X Y Z A B C D E F G H I J K L M A B C D E F G H I J W X Y Z A B C D E F G H I J K L M 31

Example of Transposition Ciphers 32 Example of Transposition Ciphers 32

Rail Fence cipher write message letters out diagonally over a number of rows then Rail Fence cipher write message letters out diagonally over a number of rows then read off cipher row by row eg. write message out as: m e m a t r h t g p r y e t e f e t e o a a t giving ciphertext MEMATRHTGPRYETEFETEOAAT 33

MODERN CRYPTOGRAPHIC TECHNIQUES 34 MODERN CRYPTOGRAPHIC TECHNIQUES 34

Modern Cryptographic Techniques Modern cipher system : Symmetric Asymmetric Symmetric cryptography: Stream cipher Block Modern Cryptographic Techniques Modern cipher system : Symmetric Asymmetric Symmetric cryptography: Stream cipher Block cipher 35

Cryptography : Cryptography types or number of Keys Symmetric cipher Asymmetric cipher 36 Cryptography : Cryptography types or number of Keys Symmetric cipher Asymmetric cipher 36

Symmetric Encryption or conventional / private-key / single-key sender and recipient share a common Symmetric Encryption or conventional / private-key / single-key sender and recipient share a common key all classical encryption algorithms are private-key was only type prior to invention of publickey in 1970’s and by far most widely used 37

Symmetric cryptography : ◦ Also called Secret Key Cryptography (SKC): Uses a single Symmetric cryptography : ◦ Also called Secret Key Cryptography (SKC): Uses a single key for both encryption and decryption Plain Text Cipher Text Plain Text

Asymmetric Encryption probably most significant advance in the 3000 year history of cryptography uses Asymmetric Encryption probably most significant advance in the 3000 year history of cryptography uses two keys – a public & a private key asymmetric since parties are not equal uses clever application of number theoretic concepts to function complements rather than replaces private key crypto

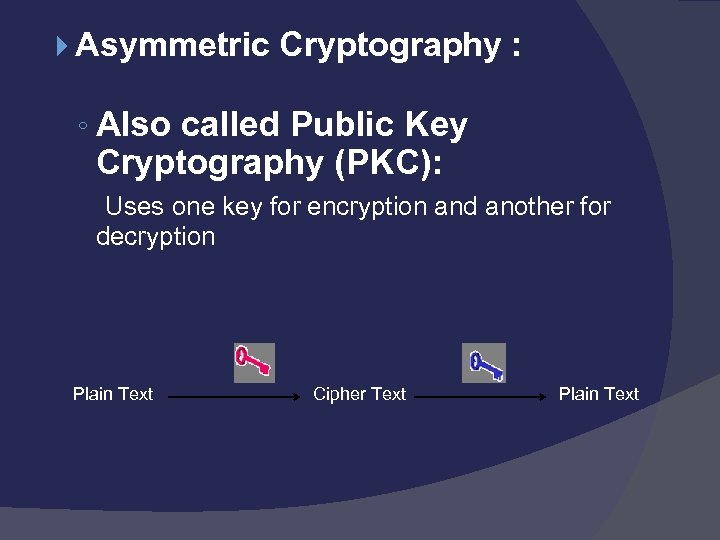Asymmetric Cryptography : ◦ Also called Public Key Cryptography (PKC): Uses one key Asymmetric Cryptography : ◦ Also called Public Key Cryptography (PKC): Uses one key for encryption and another for decryption Plain Text Cipher Text Plain Text

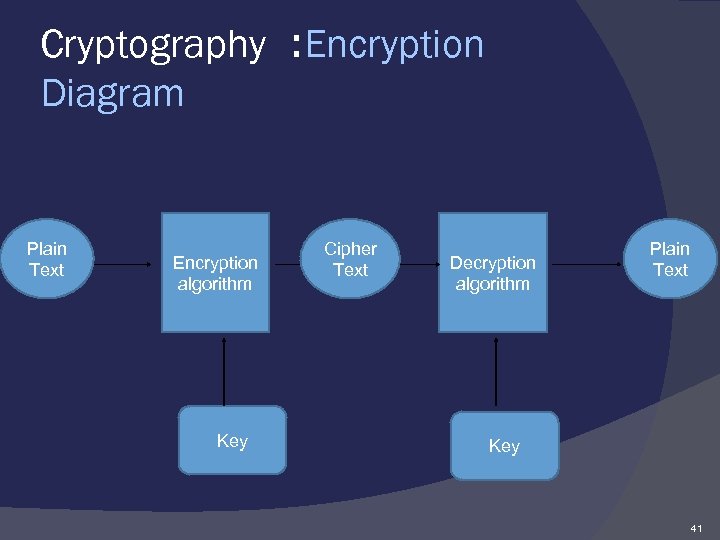Cryptography : Encryption Diagram Plain Text Encryption algorithm Key Cipher Text Decryption algorithm Plain Cryptography : Encryption Diagram Plain Text Encryption algorithm Key Cipher Text Decryption algorithm Plain Text Key 41

Stream ciphers: where plaintext bits are combined with a pseudorandom cipher bit stream (key Stream ciphers: where plaintext bits are combined with a pseudorandom cipher bit stream (key stream), typically by an exclusive-or (xor) operation. In a stream cipher, the plaintext digits are encrypted one at a time, and the transformation of successive digits varies during the encryption. 42

Stream ciphers: - process messages a bit or byte at a time when en/decrypting Stream ciphers: - process messages a bit or byte at a time when en/decrypting 43

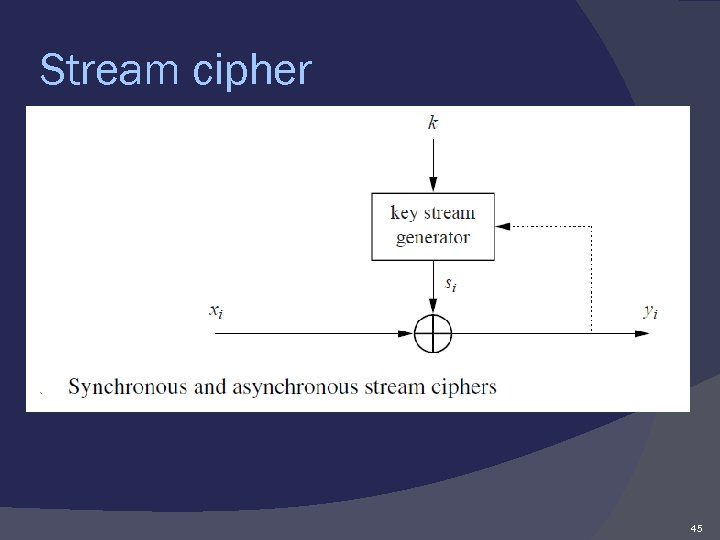
Stream cipher 2 types: Synchronous stream Asynchronous stream Synchronous stream ciphers where the key Stream cipher 2 types: Synchronous stream Asynchronous stream Synchronous stream ciphers where the key stream depends only on the key, Asynchronous stream ones where the key stream also depends on the ciphertext. 44

Stream cipher 45 Stream cipher 45

Stream cipher Definition Stream Cipher Encryption and Decryption The plaintext, the ciphertext and the Stream cipher Definition Stream Cipher Encryption and Decryption The plaintext, the ciphertext and the key stream consist of individual bits, i. e. , xi, yi, si ∈ {0, 1}. Encryption: yi = esi (xi) ≡ xi+si mod 2. Decryption: xi = dsi (yi) ≡ yi+si mod 2. 46

Modern Block Ciphers look at modern block ciphers one of the most widely used Modern Block Ciphers look at modern block ciphers one of the most widely used types of cryptographic algorithms provide secrecy /authentication services focus on DES (Data Encryption Standard) to illustrate block cipher design principles 47

Block cipher scheme : encrypts one block of data at a time using the Block cipher scheme : encrypts one block of data at a time using the same key on each block. • In general, the same plaintext block will always be encrypted to the same cipher text if using the same key in a block cipher whereas the same plaintext will be encrypted to different cipher text in a stream cipher. 48

Block cipher block ciphers: process messages in blocks, each of which is then en/decrypted Block cipher block ciphers: process messages in blocks, each of which is then en/decrypted like a substitution on very big characters 64 -bits or more 49

Block vs Stream Ciphers many current ciphers are block ciphers broader range of applications Block vs Stream Ciphers many current ciphers are block ciphers broader range of applications 50

Block vs Stream Ciphers Block ciphers work a on block / word at a Block vs Stream Ciphers Block ciphers work a on block / word at a time, which is some number of bits. All of these bits have to be available before the block can be processed. Stream ciphers work on a bit or byte of the message at a time, hence process it as a “stream”. Block ciphers are currently better analysed, and seem to have a broader range of applications, hence focus on them. 51

Block mods is self study Block mods is self study

AES AES

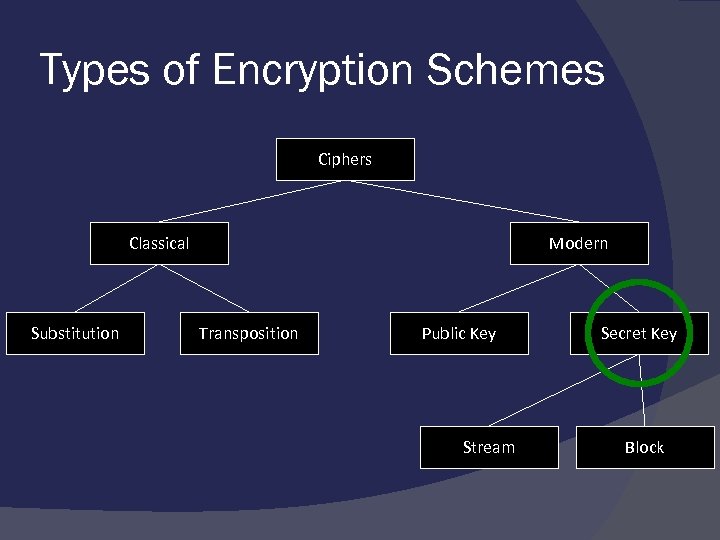Types of Encryption Schemes Ciphers Classical Substitution Modern Transposition Public Key Stream Secret Key Types of Encryption Schemes Ciphers Classical Substitution Modern Transposition Public Key Stream Secret Key Block

History In February 2001, NIST announced that a draft of the Federal Information Processing History In February 2001, NIST announced that a draft of the Federal Information Processing Standard (FIPS) was available for public review and comment. Finally, AES was published as FIPS 197 in the Federal Register in December 2001. 7. 55

History AES is a block cipher with a block length of 128 bits. AES History AES is a block cipher with a block length of 128 bits. AES allows for three different key lengths: 128, 192, or 256 bits. Encryption consists of 10 rounds of processing for 128 -bit keys, 12 rounds for 192 -bit keys, and 14 rounds for 256 bit keys. Except for the last round in each case, all other rounds are identical.

Definitions Byte The basic unit for processing in the AES algorithm is a byte, Definitions Byte The basic unit for processing in the AES algorithm is a byte, a sequence of eight bits treated as a single entity. For example, {01100011} identifies the specific finite field element x 6 + x 5 + x +1.

Definitions Arrays of Bytes Arrays of bytes will be represented in the following form: Definitions Arrays of Bytes Arrays of bytes will be represented in the following form:

Definitions Unlike DES, the decryption algorithm differs substantially from the encryption algorithm. Although, overall, Definitions Unlike DES, the decryption algorithm differs substantially from the encryption algorithm. Although, overall, the same steps are used in encryption and decryption, the order in which the steps are carried out is different, as mentioned previously.

Overview The bytes and the bit ordering within bytes are derived from the 128 Overview The bytes and the bit ordering within bytes are derived from the 128 -bit input sequence as follows: input 0 input 1 input 2 … input 126 input 127 a 0 = {input 0, input 1, …, input 7}; a 1 = {input 8, input 9, …, input 15}; a 15 = {input 120, input 121, …, input 127}.

Overview To appreciate the processing steps used in a single round, it is best Overview To appreciate the processing steps used in a single round, it is best to think of a 128 -bit block as consisting of a 4× 4 matrix of bytes, arranged as follows: The first four byte occupy the first column The 4 x 4 called stat array

7. 1. 4 Data Units. Figure 7. 2 Data units used in AES 7. 7. 1. 4 Data Units. Figure 7. 2 Data units used in AES 7. 62

Example Changing plaintext to state 7. 63 Example Changing plaintext to state 7. 63

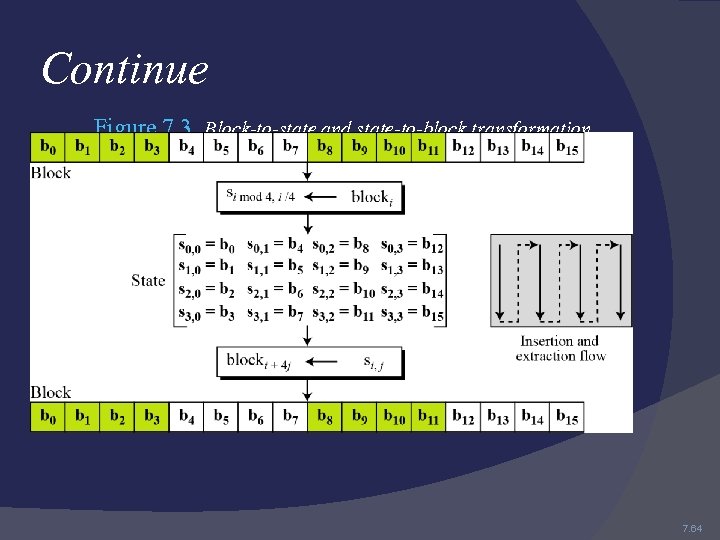Continue Figure 7. 3 Block-to-state and state-to-block transformation 7. 64 Continue Figure 7. 3 Block-to-state and state-to-block transformation 7. 64

Overview AES also has the notion of a word. A word consists of four Overview AES also has the notion of a word. A word consists of four bytes, that is 32 bits. Therefore, each column of the state array is a word, as is each row. Each round of processing works on the input state array and produces an output state array. The output state array produced by the last round is rearranged into a 128 -bit output block.

Overview Assuming a 128 -bit key, the key is also arranged in the form Overview Assuming a 128 -bit key, the key is also arranged in the form of a matrix of 4 × 4 bytes. As with the input block, the first word from the key fills the first column of the matrix, and so on. The four column words of the key matrix are expanded into a schedule of 44 words. Each round consumes four words from the key schedule.

Overview Each round of processing includes one single-byte based substitution step, a row-wise permutation Overview Each round of processing includes one single-byte based substitution step, a row-wise permutation step, a column-wise mixing step, and the addition of the round key. The order in which these four steps are executed is different for encryption and decryption.

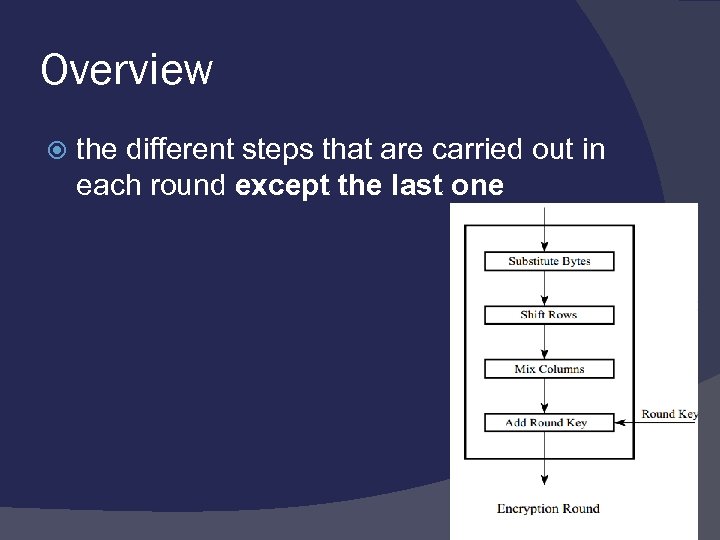Overview the different steps that are carried out in each round except the last Overview the different steps that are carried out in each round except the last one

Watch the film: http: //www. youtube. com/watch? v=mlzxp kd. XP 58 Watch the film: http: //www. youtube. com/watch? v=mlzxp kd. XP 58

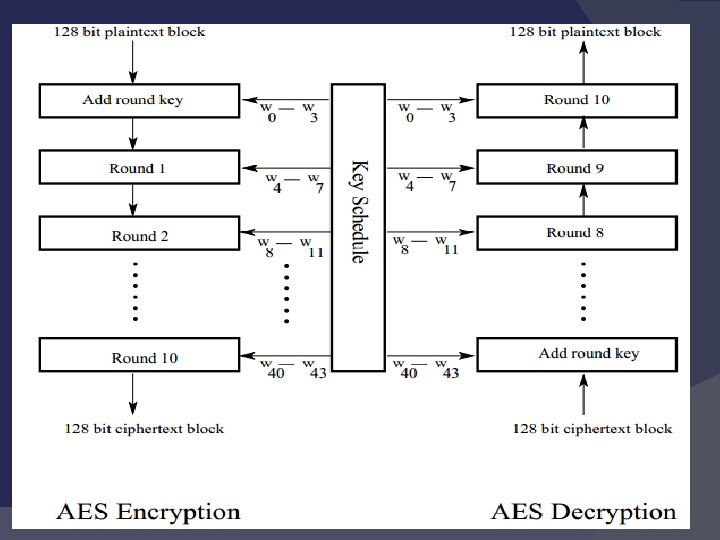
AES: The Advanced Encryption Standard focus particularly on the four steps used in each AES: The Advanced Encryption Standard focus particularly on the four steps used in each round of AES: (1) substitution, (2) shift rows, (3) mix columns, and (4)add round key.

AES: The Advanced Encryption Standard AES: The Advanced Encryption Standard

1 - Sub. Bytes()Transformation 1 - Sub. Bytes()Transformation

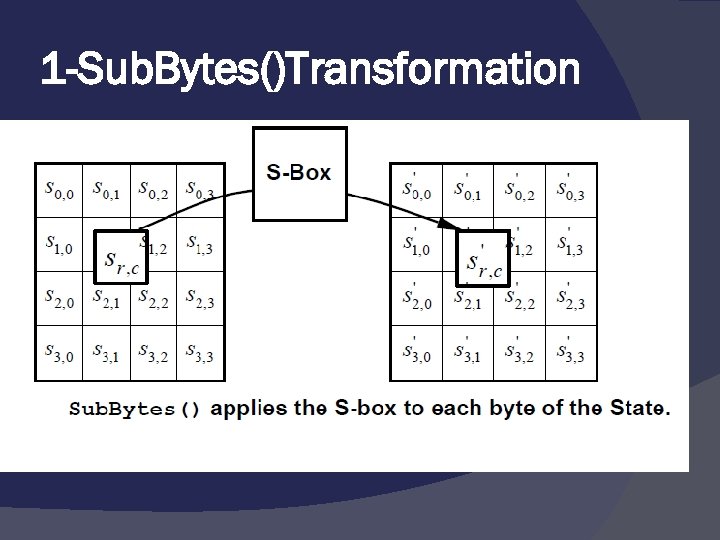
1 - Sub. Bytes()Transformation STEP 1: (called Sub. Bytes for byte-bybyte substitution duringb the 1 - Sub. Bytes()Transformation STEP 1: (called Sub. Bytes for byte-bybyte substitution duringb the forward process) This step consists of using a 16 × 16 lookup table to find a replacement byte for a given byte in the input state array.

1 -Sub. Bytes()Transformation The Sub. Bytes() transformation is a nonlinear byte substitution that operates 1 -Sub. Bytes()Transformation The Sub. Bytes() transformation is a nonlinear byte substitution that operates independently on each byte of the State using a substitution table (S-box).

1 -Sub. Bytes()Transformation 1 -Sub. Bytes()Transformation

1 -Sub. Bytes()Transformation s 1, 1={53}, s’ 1, 1= {ed}. 1 -Sub. Bytes()Transformation s 1, 1={53}, s’ 1, 1= {ed}.

2 - Shift. Rows() Transformation 2 - Shift. Rows() Transformation

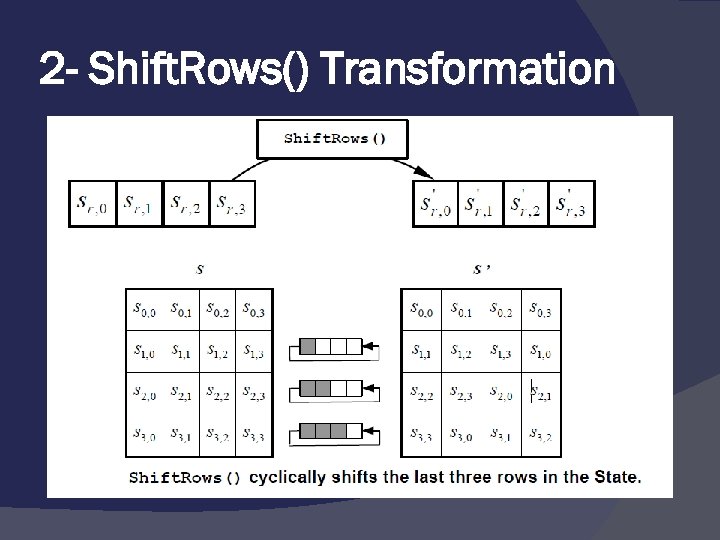
2 - Shift. Rows() Transformation In the Shift. Rows() transformation, the bytes in the 2 - Shift. Rows() Transformation In the Shift. Rows() transformation, the bytes in the last three rows of the State are cyclically shifted over different numbers of bytes (offsets). The first row, r = 0, is not shifted.

2 - Shift. Rows() Transformation 2 - Shift. Rows() Transformation

3 - Mix. Columns() Transformation 3 - Mix. Columns() Transformation

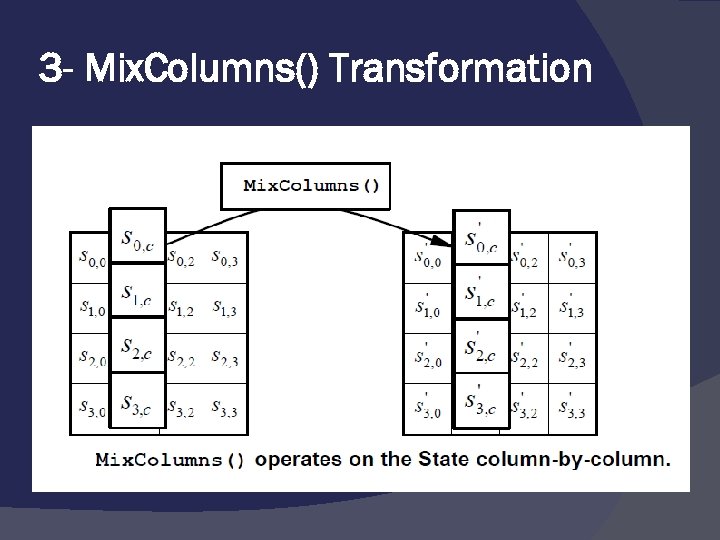
3 - Mix. Columns() Transformation The Mix. Columns() transformation operates on the State column-bycolumn, 3 - Mix. Columns() Transformation The Mix. Columns() transformation operates on the State column-bycolumn, treating each column as a fourterm polynomial :

3 - Mix. Columns() Transformation 3 - Mix. Columns() Transformation

3 - Mix. Columns() Transformation 3 - Mix. Columns() Transformation

4 - Add. Round. Key() Transformation 4 - Add. Round. Key() Transformation

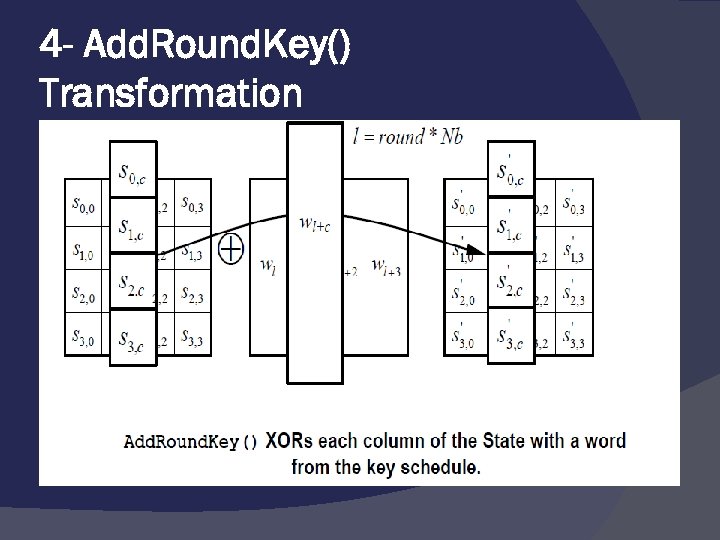
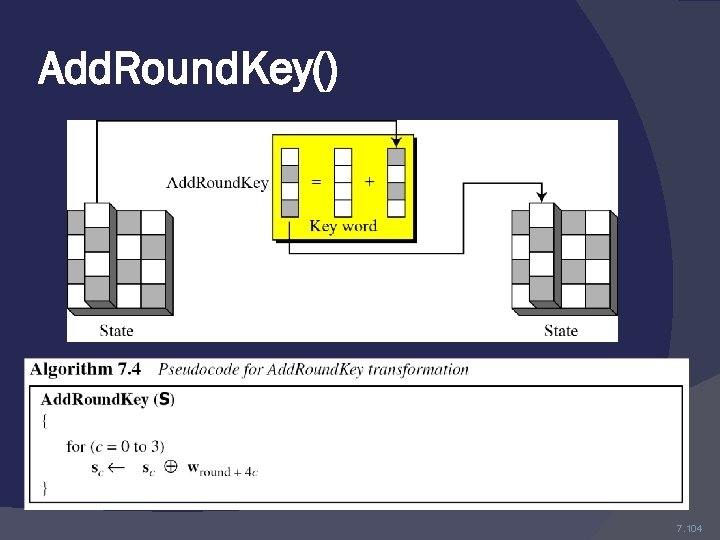
4 - Add. Round. Key() Transformation In the Add. Round. Key() transformation, a Round 4 - Add. Round. Key() Transformation In the Add. Round. Key() transformation, a Round Key is added to the State by a simple bitwise XOR operation.

4 - Add. Round. Key() Transformation 4 - Add. Round. Key() Transformation

Self Study Key Expansion Self Study Key Expansion

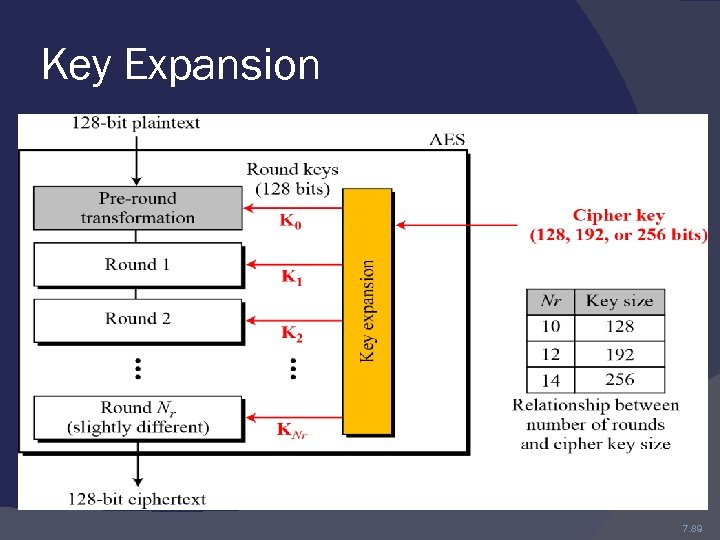Key Expansion 7. 89 Key Expansion 7. 89

Key Expansion The function Rot. Word() takes a word [a 0, a 1, a Key Expansion The function Rot. Word() takes a word [a 0, a 1, a 2, a 3] as input, performs a cyclic permutation, and returns the word [a 1, a 2, a 3, a 0]. Sub. Word() is a function that takes a four-byte input word and applies the Sbox to each of the four bytes to produce an output word.

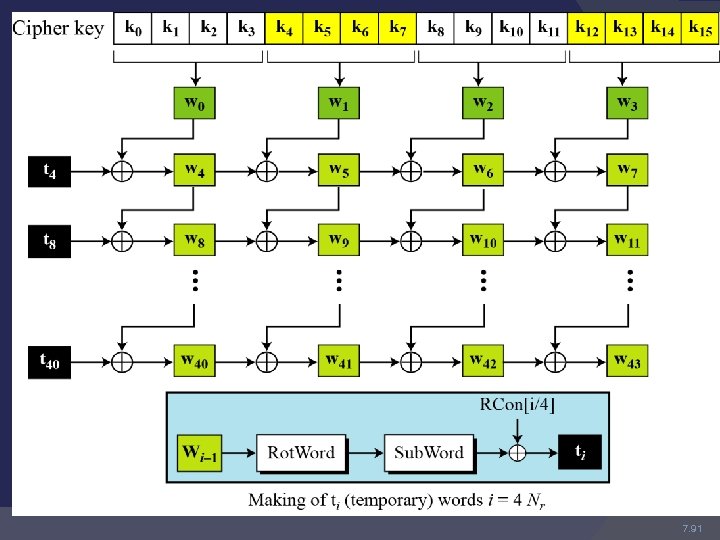7. 91 7. 91

Example Each round key in AES depends on the previous round key. The dependency, Example Each round key in AES depends on the previous round key. The dependency, however, is nonlinear because of Sub. Word transformation. The addition of the round constants also guarantees that each round key will be different from the previous one. The two sets of round keys can be created from two cipher keys that are different only in one bit. 7. 92

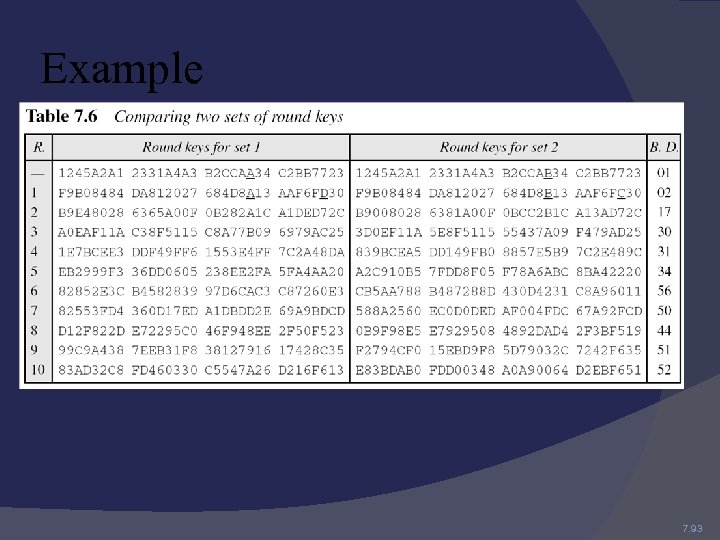Example 7. 93 Example 7. 93

For Reading only Inverse Cipher For Reading only Inverse Cipher

Inverse Cipher The individual transformations used in the Inverse Cipher : Inv. Shift. Rows(), Inverse Cipher The individual transformations used in the Inverse Cipher : Inv. Shift. Rows(), Inv. Sub. Bytes(), Inv. Mix. Columns(), and Add. Round. Key()

Inverse Cipher Inverse Cipher

Inverse Cipher Inv. Shift. Rows(), Inv. Sub. Bytes(), Inv. Mix. Columns Add. Round. Key() Inverse Cipher Inv. Shift. Rows(), Inv. Sub. Bytes(), Inv. Mix. Columns Add. Round. Key()

Inv. Sub. Bytes() Inv. Sub. Bytes()

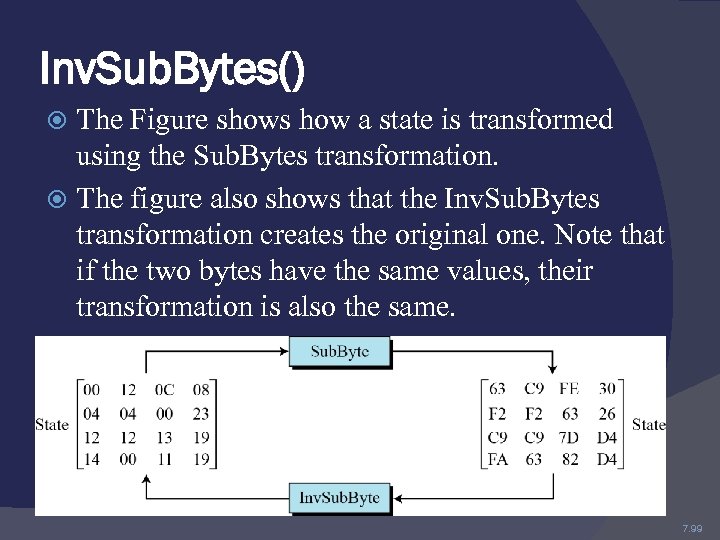Inv. Sub. Bytes() The Figure shows how a state is transformed using the Sub. Inv. Sub. Bytes() The Figure shows how a state is transformed using the Sub. Bytes transformation. The figure also shows that the Inv. Sub. Bytes transformation creates the original one. Note that if the two bytes have the same values, their transformation is also the same. 7. 99

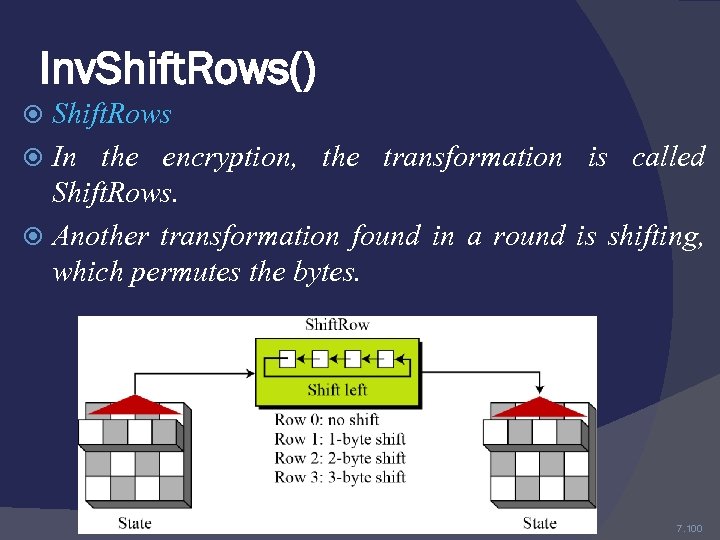Inv. Shift. Rows() Shift. Rows In the encryption, the transformation is called Shift. Rows. Inv. Shift. Rows() Shift. Rows In the encryption, the transformation is called Shift. Rows. Another transformation found in a round is shifting, which permutes the bytes. 7. 100

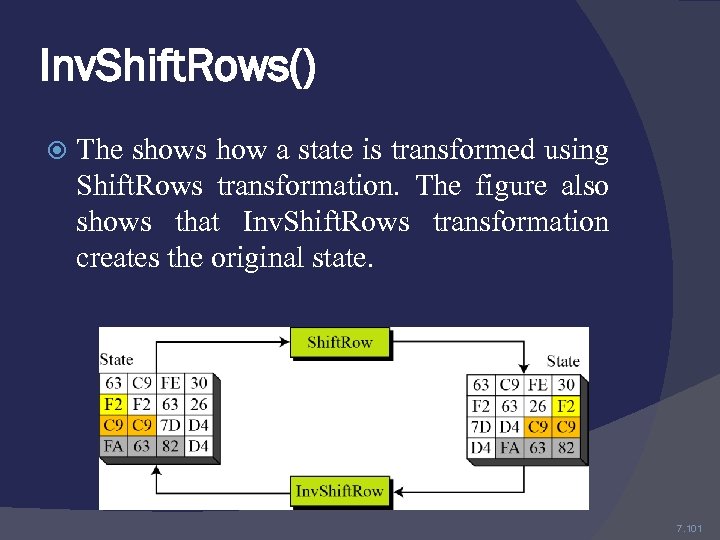Inv. Shift. Rows() The shows how a state is transformed using Shift. Rows transformation. Inv. Shift. Rows() The shows how a state is transformed using Shift. Rows transformation. The figure also shows that Inv. Shift. Rows transformation creates the original state. 7. 101

Inv. Mix. Columns() Inv. Mix. Columns()

Inv. Mix. Columns() The Figure shows how a state is transformed using the Mix. Inv. Mix. Columns() The Figure shows how a state is transformed using the Mix. Columns transformation. The figure also shows that the Inv. Mix. Columns transformation creates the original one. The Mix. Columns transformation in Example 7. 5 7. 103

Add. Round. Key() 7. 104 Add. Round. Key() 7. 104

7. 105 7. 105

Examples In this section, some examples of encryption/ decryption and key generation are given Examples In this section, some examples of encryption/ decryption and key generation are given to emphasize some points discussed in the two previous sections. Example The following shows the ciphertext block created from a plaintext block using a randomly selected cipher key. 7. 106

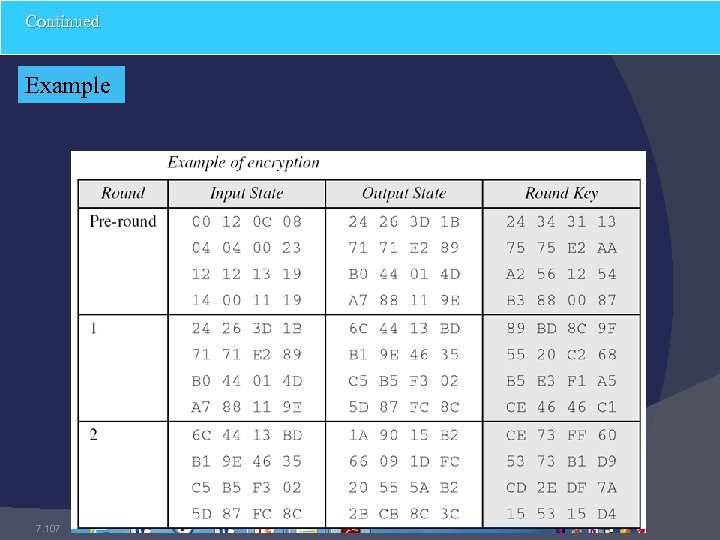Continued Example 7. 107 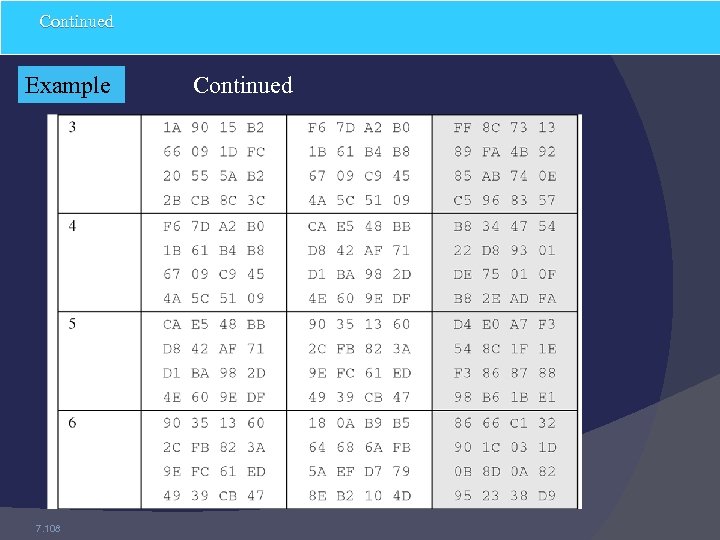Continued Example 7. 107

Continued Example 7. 108 Continued Continued Example 7. 108 Continued

Continued Example 7. 109 Continued 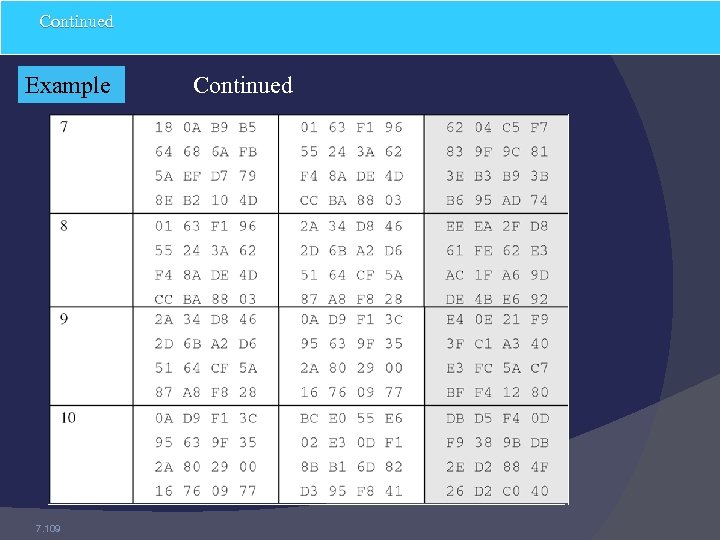Continued Example 7. 109 Continued

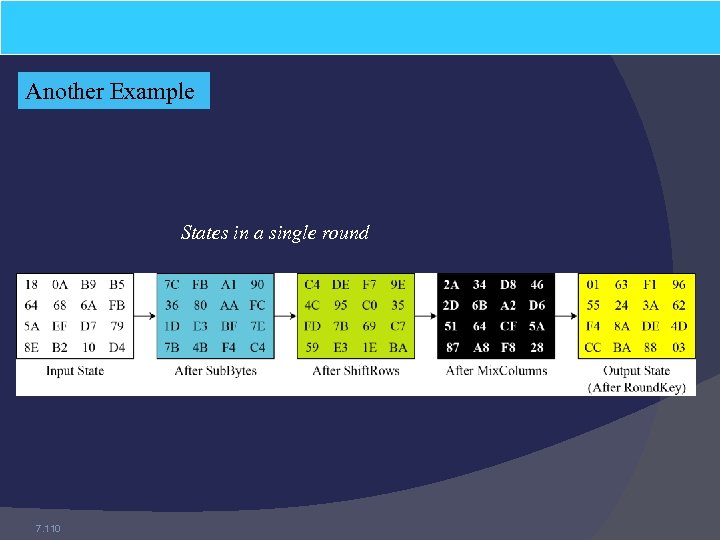Another Example States in a single round 7. 110 Another Example States in a single round 7. 110

Conclusion Rijndael has the symmetric and parallel structure. Gives implementer a lot of flexibility Conclusion Rijndael has the symmetric and parallel structure. Gives implementer a lot of flexibility Have not allowed effective cryptanalytic attacks Rijndael is well adapted to modern processors. Rijndael is suited for Smart cards

ASYMMETRIC CRYPTOGRAPHY ASYMMETRIC CRYPTOGRAPHY

Private-Key Cryptography traditional private/secret/single key cryptography uses one key shared by both sender and Private-Key Cryptography traditional private/secret/single key cryptography uses one key shared by both sender and receiver if this key is disclosed communications are compromised also is symmetric, parties are equal hence does not protect sender from receiver forging a message & claiming is sent by sender

Public-Key Cryptography probably most significant advance in the 3000 year history of cryptography uses Public-Key Cryptography probably most significant advance in the 3000 year history of cryptography uses two keys – a public & a private key asymmetric since parties are not equal uses clever application of number theoretic concepts to function complements rather than replaces private key crypto

Historical Background 1976: W. Diffie and M. E. Hellman proposed the first public-key encryption Historical Background 1976: W. Diffie and M. E. Hellman proposed the first public-key encryption algorithms -- actually an algorithm for public exchange of a secret key. 1978: L. M Adleman, R. L. Rivest and A. Shamir propose the RSA encryption method Currently the most widely used Basis for the spreadsheet used in the lab

Public Key History Some algorithms Diffie-Hellman, 1976, key-exchange based on discrete logs Merkle-Hellman, 1978, Public Key History Some algorithms Diffie-Hellman, 1976, key-exchange based on discrete logs Merkle-Hellman, 1978, based on “knapsack problem” Mc. Eliece, 1978, based on algebraic coding theory RSA, 1978, based on factoring Rabin, 1979, security can be reduced to factoring El. Gamal, 1985, based on discrete logs Blum-Goldwasser, 1985, based on quadratic residues Elliptic curves, 1985, discrete logs over Elliptic curves Chor-Rivest, 1988, based on knapsack problem NTRU, 1996, based on Lattices XTR, 2000, based on discrete logs of a particular field 15 -853 Page 117

Public-Key Cryptography public-key/two-key/asymmetric cryptography involves the use of two keys: a public-key, which may Public-Key Cryptography public-key/two-key/asymmetric cryptography involves the use of two keys: a public-key, which may be known by anybody, and can be used to encrypt messages, and verify signatures a private-key, known only to the recipient, used to decrypt messages, and sign (create) signatures is asymmetric because those who encrypt messages or verify signatures cannot decrypt messages or create signatures

Why Public-Key Cryptography? Compared with symmetric-key encryption, public-key encryption requires more computation and is Why Public-Key Cryptography? Compared with symmetric-key encryption, public-key encryption requires more computation and is therefore not always appropriate for large amounts of data. However, it's possible to use public-key encryption to send a symmetric key, which can then be used to encrypt additional data. 1. Key distribution Secret keys for conventional cryptography Unforgeable public keys (digital certificate) 2. Message authentication Quantum Computing - Daugherity

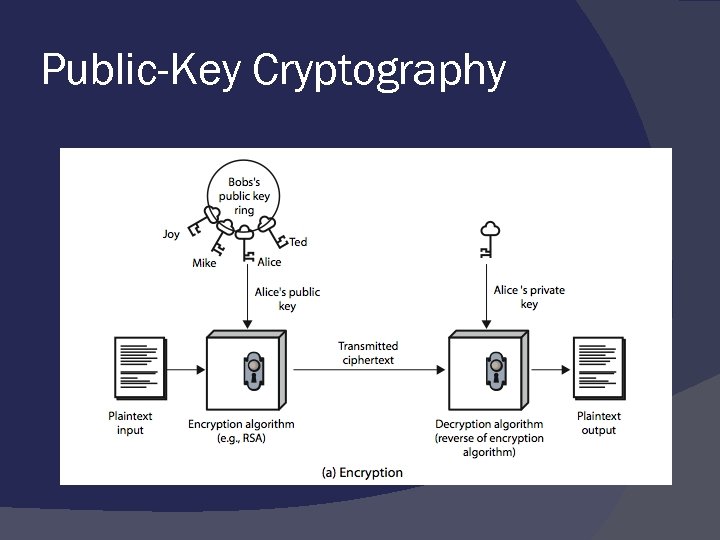Public-Key Cryptography Public-Key Cryptography

Public-Key Characteristics Public-Key algorithms rely on two keys where: it is computationally infeasible to Public-Key Characteristics Public-Key algorithms rely on two keys where: it is computationally infeasible to find decryption key knowing only algorithm & encryption key it is computationally easy to en/decrypt messages when the relevant (en/decrypt) key is known either of the two related keys can be used for encryption, with the other used for decryption (for some algorithms)

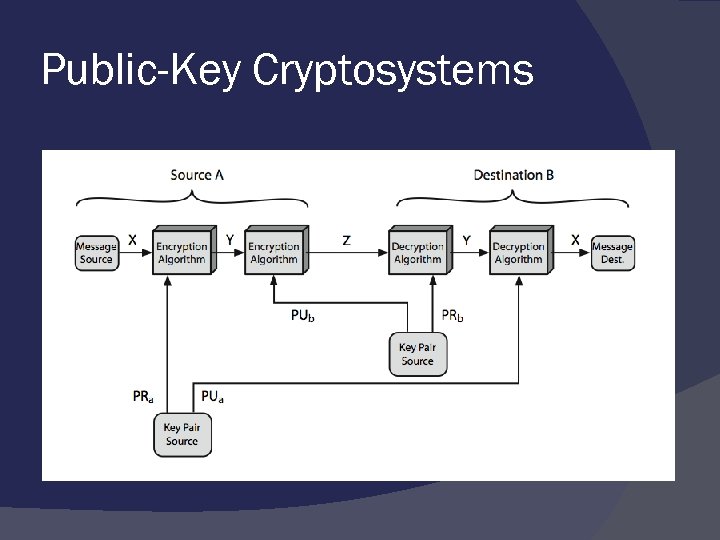Public-Key Cryptosystems Public-Key Cryptosystems

Public-Key Applications Can classify uses into 3 categories: Encryption/decryption (provide secrecy) Digital signatures (provide Public-Key Applications Can classify uses into 3 categories: Encryption/decryption (provide secrecy) Digital signatures (provide authentication) Key exchange (of session keys) some algorithms are suitable for all uses, others are specific to one

RSA by Rivest, Shamir & Adleman of MIT in 1977 best known & widely RSA by Rivest, Shamir & Adleman of MIT in 1977 best known & widely used public-key scheme based on exponentiation in a finite (Galois) field over integers modulo a prime uses large integers (e. g. , 1024 bits) security due to cost of factoring large numbers

MATHEMATICAL BACKGROUND For Reading MATHEMATICAL BACKGROUND For Reading

Prime Numbers prime numbers only have divisors of 1 and self they cannot be Prime Numbers prime numbers only have divisors of 1 and self they cannot be written as a product of other numbers note: 1 is prime, but is generally not of interest eg. 2, 3, 5, 7 are prime, 4, 6, 8, 9, 10 are not prime numbers are central to number theory list of prime number less than 200 is: 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 193 197 199

Prime Factorisation to factor a number n is to write it as a product Prime Factorisation to factor a number n is to write it as a product of other numbers: n=a × b × c note that factoring a number is relatively hard compared to multiplying the factors together to generate the number the prime factorisation of a number n is when its written as a product of primes ﺗﺤﻠﻴﻞ ﺍﻟﻌﺪﺩ ﻟﻌﻨﺎﺻﺮﻩ ﺍﻻﻭﻟﻴﺔ eg. 91=7× 13 ; 3600=24× 32× 52

Relatively Prime Numbers & GCD two numbers a, b are relatively prime if have Relatively Prime Numbers & GCD two numbers a, b are relatively prime if have no common divisors apart from 1 common divisors : ﺍﻟﻘﺎﺳﻢ ﺍﻟﻤﺸﺘﺮﻙ ﺍﻻﻋﻈﻢ eg. 8 & 15 are relatively prime since factors of 8 are 1, 2, 4, 8 and of 15 are 1, 3, 5, 15 and 1 is the only common factor conversely can determine the greatest common divisor by comparing their prime factorizations and using least powers eg. 300=21× 31× 52 18=21× 32 hence GCD(18, 300)=21× 31× 50=6

Fermat's Theorem ap-1 mod p = 1 where p is prime and gcd(a, p)=1 Fermat's Theorem ap-1 mod p = 1 where p is prime and gcd(a, p)=1 also known as Fermat’s Little Theorem useful in public key and primality testing

Fermat's Theorem Example : Let a= 12, p= 7 …. . gcd(12, 7)= 1 Fermat's Theorem Example : Let a= 12, p= 7 …. . gcd(12, 7)= 1 So 12(7 -1) mod 7 = 1 Another example : Let a= 10, p= 3 …. . gcd(10, 3)= 1 So 10(3 -1) mod 3 = 1

Euler Totient Function ø(n) when doing arithmetic modulo n complete set of residues is: Euler Totient Function ø(n) when doing arithmetic modulo n complete set of residues is: 0. . n-1 reduced set of residues is those numbers (residues) which are relatively prime to n eg for n=10, complete set of residues is {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} reduced set of residues is {1, 3, 7, 9} number of elements in reduced set of residues is called the Euler Totient Function ø(n)

Euler Totient Function ø(n) to compute ø(n) need to count number of elements to Euler Totient Function ø(n) to compute ø(n) need to count number of elements to be excluded in general need prime factorization, but for p (p prime) ø(p) = p-1 for p. q (p, q prime) ø(p. q) = (p-1)(q 1) eg. ø(37) = 36 ø(21) = (3– 1)×(7– 1) = 2× 6 = 12

Euler's Theorem a generalisation of Fermat's Theorem aø(n)mod N = 1 where gcd(a, N)=1 Euler's Theorem a generalisation of Fermat's Theorem aø(n)mod N = 1 where gcd(a, N)=1 eg. a=3; n=10; ø(10)=4; hence 34 = 81 = 1 mod 10 a=2; n=11; ø(11)=10; hence 210 = 1024 = 1 mod 11

BACK TO RSA BACK TO RSA

RSA Key Setup each user generates a public/private key pair by: selecting two large RSA Key Setup each user generates a public/private key pair by: selecting two large primes at random : p, q computing their system n=p. q -define ø(n)=(p-1)(q-1) Selecting at random the encryption key e where 1

RSA Example 1. 2. 3. 4. 5. 6. 7. Select primes: p=17 & q=11 RSA Example 1. 2. 3. 4. 5. 6. 7. Select primes: p=17 & q=11 Compute n = pq =17 x 11=187 Compute ø(n)=(p– 1)(q-1)=16 x 10=160 Select e: gcd(e, 160)=1; choose e=7 Determine d: de=1 mod 160 and d < 160 Value is d=23 since 23 x 7=161= 10 x 160+1 Publish public key PU={7, 187} Keep secret private key PR={23, 187}

Another Example Select primes p=11, q=3. n = pq = 11. 3 = 33 Another Example Select primes p=11, q=3. n = pq = 11. 3 = 33 phi = (p-1)(q-1) = 10. 2 = 20 Choose e=3 Check gcd(e, p-1) = gcd(3, 10) = 1 (i. e. 3 and 10 have no common factors except 1), and check gcd(e, q-1) = gcd(3, 2) = 1 therefore gcd(e, phi) = gcd(e, (p-1)(q-1)) = gcd(3, 20) = 1 Compute d such that ed ≡ 1 (mod phi) i. e. compute d = e-1 mod phi = 3 -1 mod 20 i. e. find a value for d such that phi divides (ed-1) i. e. find d such that 20 divides 3 d-1. Simple testing (d = 1, 2, . . . ) gives d = 7 Check: ed-1 = 3. 7 - 1 = 20, which is divisible by phi. Public key = (e, n) = (3, 33) Private key = ( d, n) = (7, 33).

RSA Use in Encryption to encrypt a message M the sender: obtains public key RSA Use in Encryption to encrypt a message M the sender: obtains public key of recipient PU={e, n} computes: C = Me mod n, where 0≤M

RSA Example - En/Decryption sample RSA encryption/decryption is: given message M = 88 1. RSA Example - En/Decryption sample RSA encryption/decryption is: given message M = 88 1. Publish public key PU={7, 187} 2. Keep secret private key PR={23, 187} encryption: C = 887 mod 187 = 11 decryption: M = 1123 mod 187 = 88

Assignments 1. Perform encryption and decryption using RSA algorithm, as in Figure 1, for Assignments 1. Perform encryption and decryption using RSA algorithm, as in Figure 1, for the following: ① p = 3; q = 11, e = 7; M = 5 ② p = 5; q = 11, e = 3; M = 9 Encryption Plaintext 88 2. 88 7 mod 187 = 11 Decryption Ciphertext 11 11 23 mod 187 = 88 KU = 7, 187 KR = 23 , 187 Figure 1. Example of RSA Algorithm Plaintext 88 In a public-key system using RSA, you intercept the ciphertext C = 10 sent to a user whose public key is e = 5, n = 35. What is the plaintext M?

RSA Key Generation users of RSA must: determine two primes at random - p, RSA Key Generation users of RSA must: determine two primes at random - p, q select either e or d and compute the other primes p, q must not be easily derived from modulus n=p. q means must be sufficiently large typically guess and use probabilistic test exponents e, d are inverses, so use Inverse algorithm to compute the other

How to compute d Find d such that : 1 ≡ ( d. e How to compute d Find d such that : 1 ≡ ( d. e mod m ) 1 = Km + de Using the extended Euclid Algorithm

Extended Euclid’s Algorithm Extend the algorithm to compute the integer coefficients x and y Extended Euclid’s Algorithm Extend the algorithm to compute the integer coefficients x and y such that d = gcd(a, b) = ax + by Extended-Euclid(a, b) 1. if b = 0 then return (a, 1, 0) 2. (d’ , x’ , y’ ) ← Extended-Euclid(b, a mod b) 3. (d, x, y) ← (d’ , y’ , x’− [a/b]y’ ) 4. return (d, x, y)

Example Example

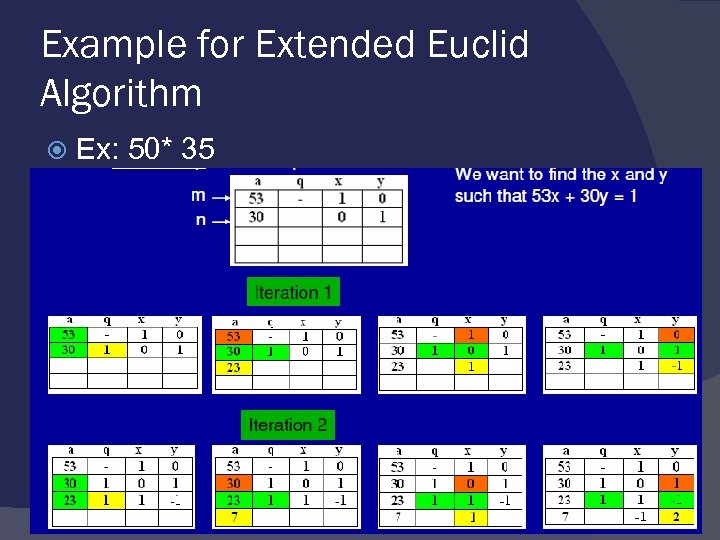Example for Extended Euclid Algorithm Ex: 50* 35 Example for Extended Euclid Algorithm Ex: 50* 35

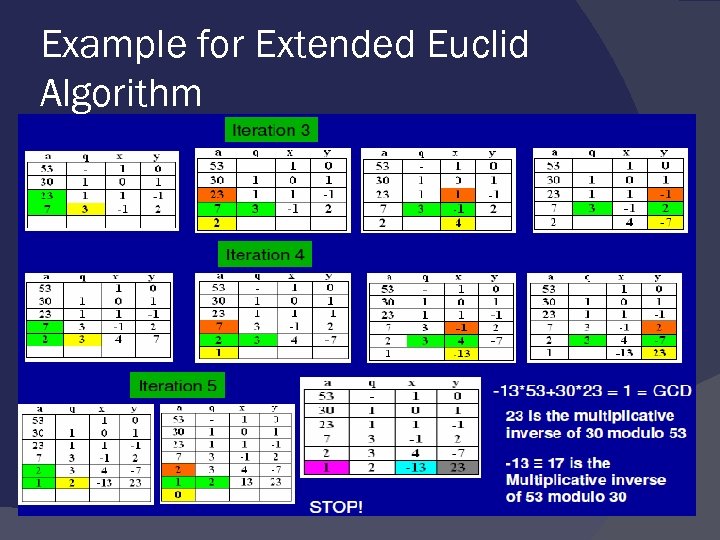Example for Extended Euclid Algorithm Example for Extended Euclid Algorithm

Example : self Let p =11 , q=3 Let e= 3 Calculate d Example : self Let p =11 , q=3 Let e= 3 Calculate d

The results n =p. q= 33 Q(n)= (p-1)(q-1)= 20 d. e mod Q(n) = The results n =p. q= 33 Q(n)= (p-1)(q-1)= 20 d. e mod Q(n) = 1 d= 7

Why RSA Works because of Euler's Theorem: aø(n)mod n = 1 where gcd(a, n)=1 Why RSA Works because of Euler's Theorem: aø(n)mod n = 1 where gcd(a, n)=1 in RSA have: n=p. q ø(n)=(p-1)(q-1) carefully chose e & d to be inverses mod ø(n) hence e. d=1+k. ø(n) for some k hence : Cd = Me. d = M 1+k. ø(n) = M 1. (Mø(n))k = M 1. (1)k = M 1 = M mod n

Efficient Encryption uses exponentiation to power e Hence if e small, this will be Efficient Encryption uses exponentiation to power e Hence if e small, this will be faster often choose e=65537 (216 -1) also see choices of e=3 or e=17 But if e too small (eg e=3) can attack using Chinese remainder theorem & 3 messages with different moduli

Efficient Decryption uses exponentiation to power d this is likely large, insecure if not Efficient Decryption uses exponentiation to power d this is likely large, insecure if not can use the Chinese Remainder Theorem (CRT) to compute mod p & q separately. then combine to get desired answer

Exponentiation can use the Square and Multiply Algorithm a fast, efficient algorithm for exponentiation Exponentiation can use the Square and Multiply Algorithm a fast, efficient algorithm for exponentiation concept is based on repeatedly squaring base and multiplying in the ones that are needed to compute the result look at binary representation of exponent only takes O(log 2 n) multiples for number n eg. 75 = 74. 71 = 3. 7 = 10 mod 11 eg. 3129 = 3128. 31 = 5. 3 = 4 mod 11

Exponentiation The algorithm for computing ab mod n The b integer is expressed as Exponentiation The algorithm for computing ab mod n The b integer is expressed as as binary number : bk , bk-1 , …, b 0

Example Get 7 5 mod 11= ? ? ab mod n as in th Example Get 7 5 mod 11= ? ? ab mod n as in th algorithm 1 0 1 So b= 5 101 b 2 b 1 b 0 k Ask? n= 11 a= 7 c d b(k) The final result is = 10 0 1 2 0 1 Yes b 2 = 1 7 1 1 2 5 No

Example Get 10 3 mod 60= ? ? ab mod n as in th Example Get 10 3 mod 60= ? ? ab mod n as in th algorithm 1 1 So b= 3 11 b 0 2 k Ask? c n= 60 a= 10 d b(k) The final result is = 40 0 1 1 0 1 Yes b 1 = 1 10 1 0 2 40 Yes b 0 = 3 40

RSA Security three approaches to attacking RSA: brute force key search (infeasible given size RSA Security three approaches to attacking RSA: brute force key search (infeasible given size of numbers) mathematical attacks (based on difficulty of computing ø(N), by factoring modulus N) timing attacks (on running of decryption)

Summary have considered: prime numbers Fermat’s and Euler’s Theorems Primality Testing Chinese Remainder Theorem Summary have considered: prime numbers Fermat’s and Euler’s Theorems Primality Testing Chinese Remainder Theorem Discrete Logarithms principles of public-key cryptography RSA algorithm, implementation, security

Second Question Summarize AES algorithm using the given example “video” Summarize RSA algorithm for Second Question Summarize AES algorithm using the given example “video” Summarize RSA algorithm for discuss it at the next lecture