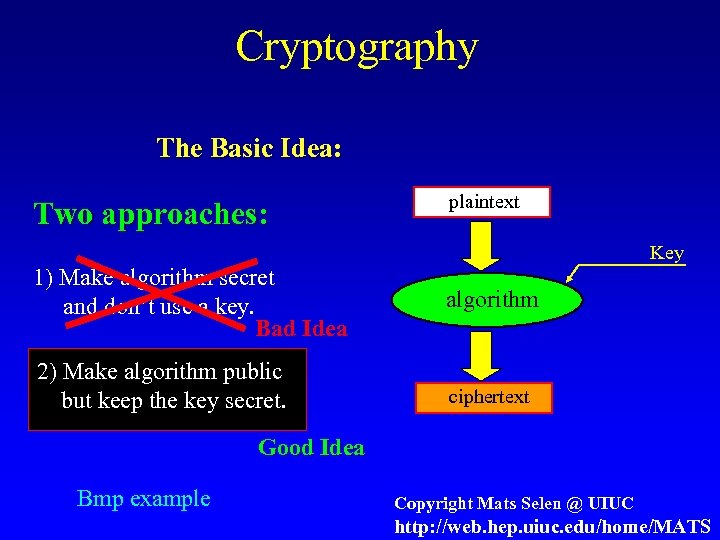
Cryptography The Basic Idea: Two approaches: plaintext Key 1) Make algorithm secret and don’t use a key. Bad Idea 2) Make algorithm public but keep the key secret. algorithm ciphertext Good Idea Bmp example Copyright Mats Selen @ UIUC http: //web. hep. uiuc. edu/home/MATS
Suppose we have an algorithm that takes a block of plaintext and converts it into a block of ciphertext using an N bit key. Suppose that changing any single bit in the key completely changes the ciphertext. We could only break this by trying all 2 N possible keys. If N = 128, the time required is way beyond the age of the universe. DES (Digital Encryption Standard) plaintext block f ciphertext block N bit Key
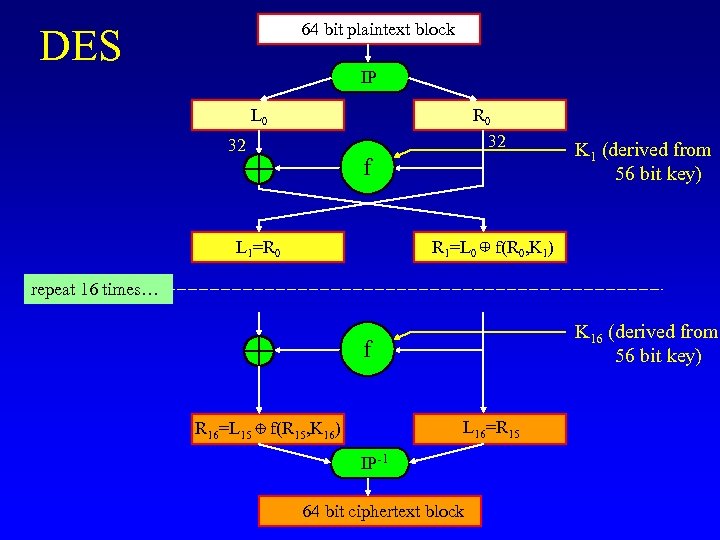
64 bit plaintext block DES IP L 0 R 0 32 32 f L 1=R 0 K 1 (derived from 56 bit key) R 1=L 0 + f(R 0, K 1) repeat 16 times… K 16 (derived from 56 bit key) f L 16=R 15 R 16=L 15 + f(R 15, K 16) IP-1 64 bit ciphertext block
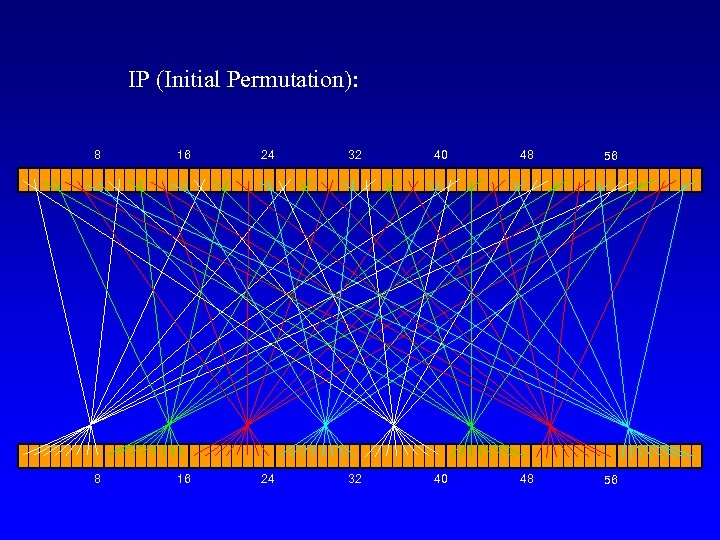
IP (Initial Permutation): 8 16 24 32 40 48 56
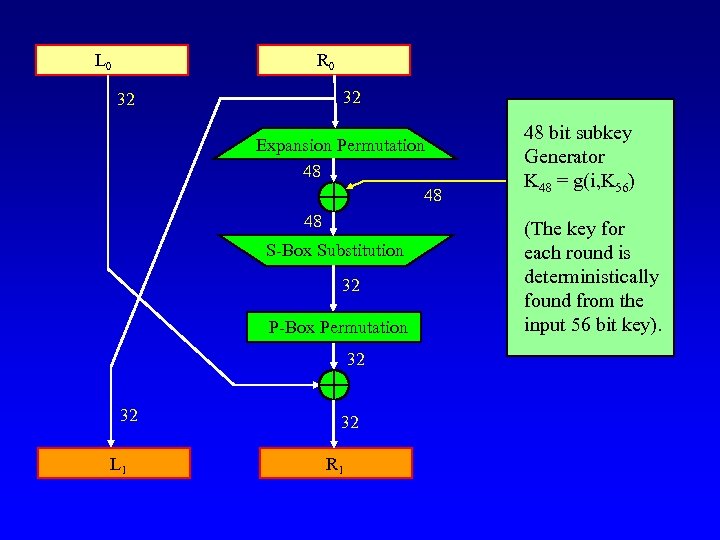
L 0 R 0 32 32 Expansion Permutation 48 48 48 S-Box Substitution 32 P-Box Permutation 32 32 L 1 32 R 1 48 bit subkey Generator K 48 = g(i, K 56) (The key for each round is deterministically found from the input 56 bit key).
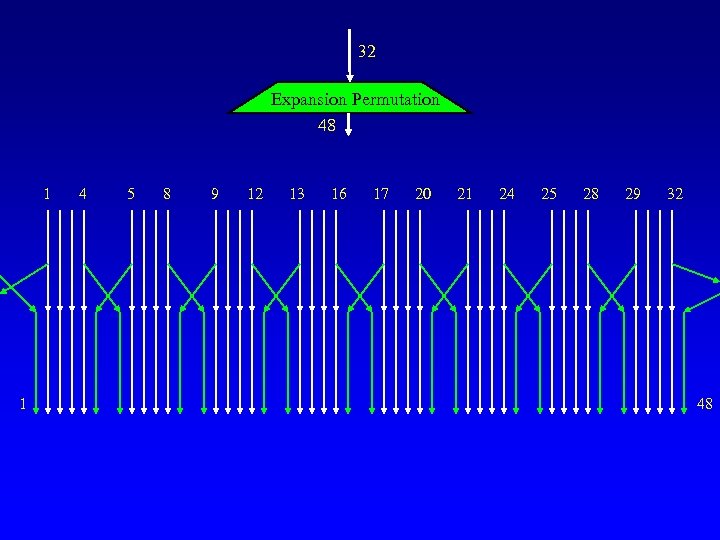
32 Expansion Permutation 48 1 1 4 5 8 9 12 13 16 17 20 21 24 25 28 29 32 48
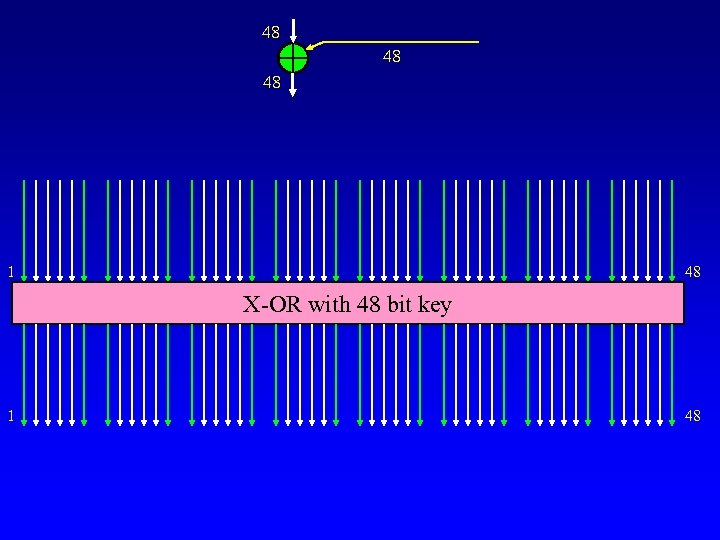
48 48 48 1 48 X-OR with 48 bit key 1 48
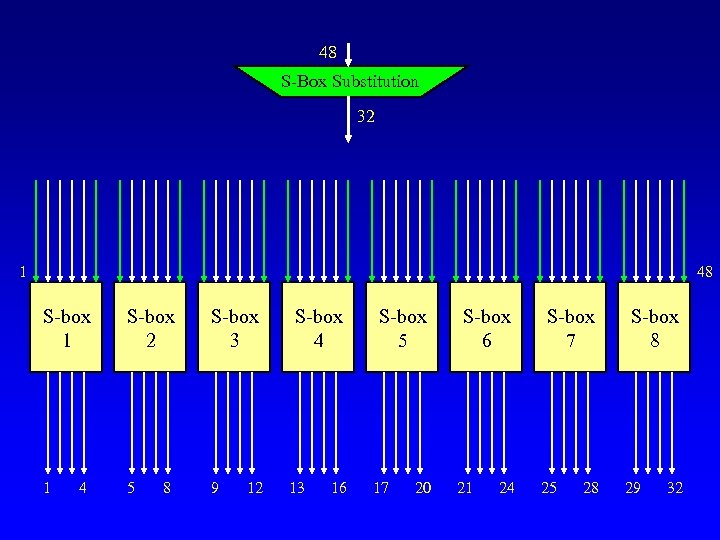
48 S-Box Substitution 32 1 48 S-box 1 S-box 2 S-box 3 1 5 9 4 8 12 S-box 4 13 16 S-box 5 17 20 S-box 6 21 24 S-box 7 25 28 S-box 8 29 32
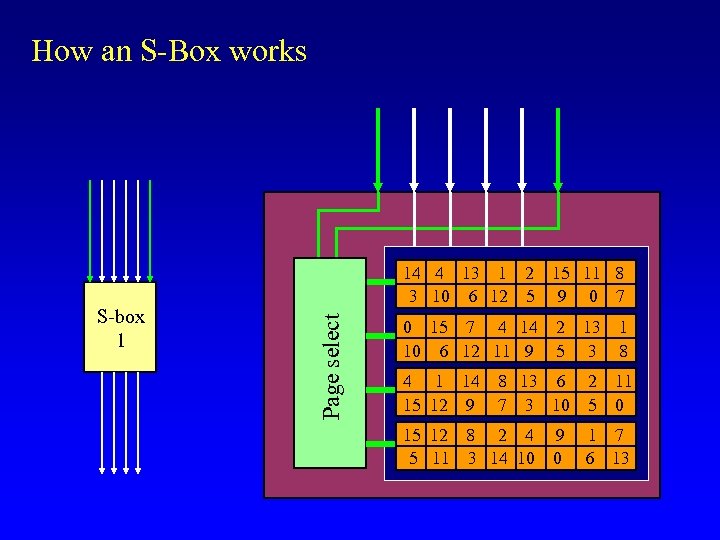
How an S-Box works Page select S-box 1 14 4 13 1 2 15 11 8 3 10 6 12 5 9 0 7 0 15 7 4 14 10 6 12 11 9 4 1 14 15 12 9 2 5 13 3 1 8 8 13 6 7 3 10 2 5 11 0 15 12 8 2 4 5 11 3 14 10 9 0 1 7 6 13
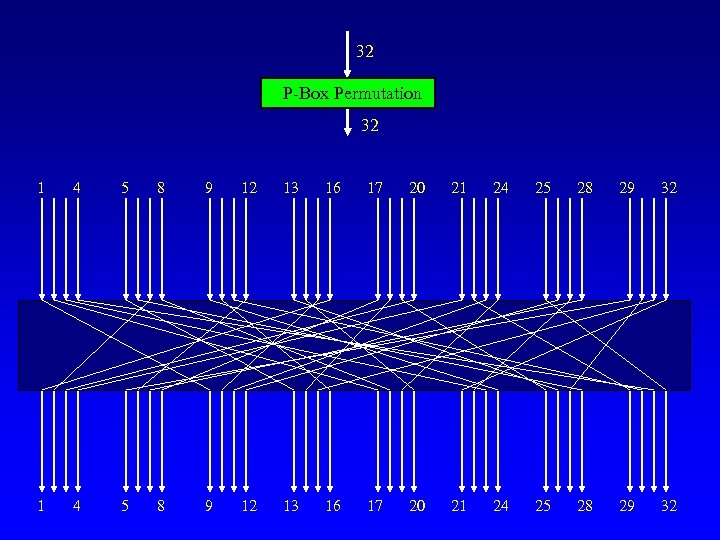
32 P-Box Permutation 32 1 4 5 8 9 12 13 16 17 20 21 24 25 28 29 32
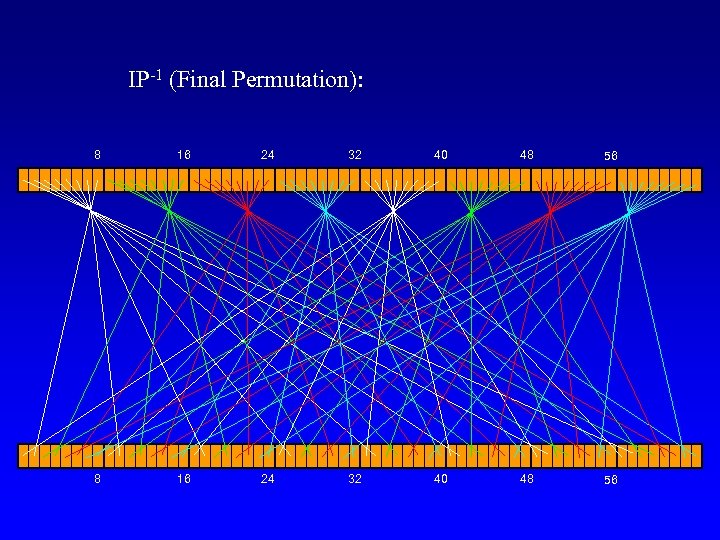
IP-1 (Final Permutation): 8 16 24 32 40 48 56
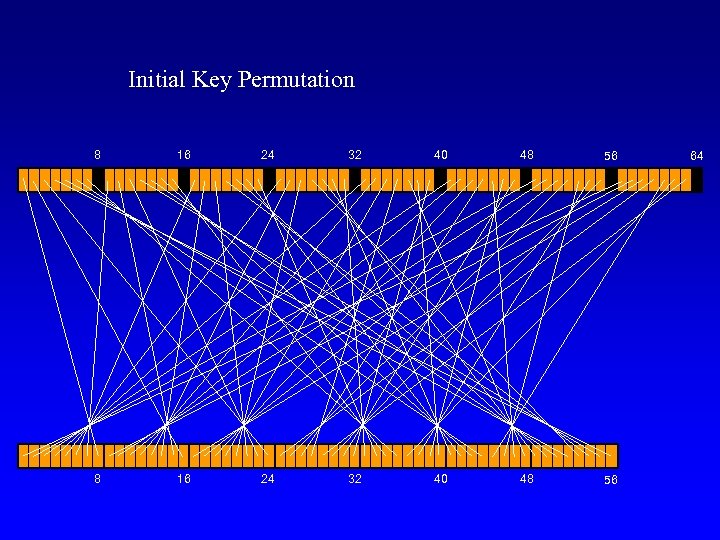
Initial Key Permutation 8 16 24 32 40 48 56 64
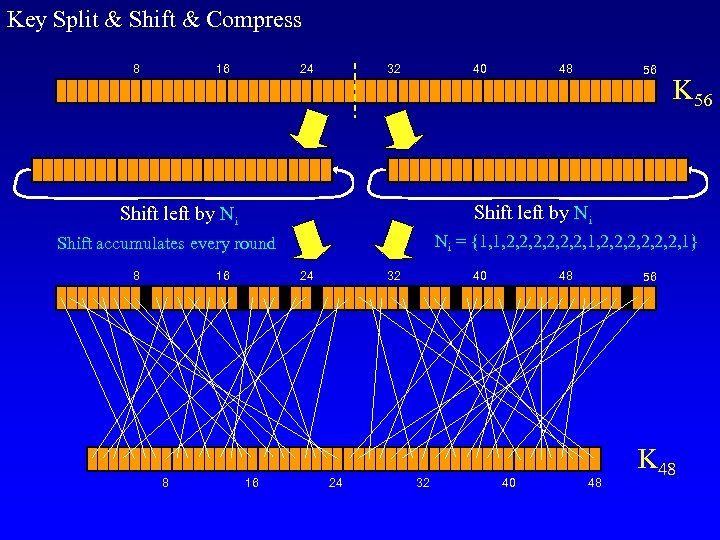
Key Split & Shift & Compress 8 16 24 32 40 K 56 Ni = {1, 1, 2, 2, 2, 1} Shift accumulates every round 16 8 56 Shift left by Ni 8 48 24 16 32 24 40 32 48 40 56 48 K 48
Public Key Cryptography: RSA (Rivest, Shamnir, Adleman: 1977) IDEA: Alice has a “public” encryption key that everyone knows, and a “private” decryption key that only she knows. Bob looks up her public key, encrypts his message, and sends it to her. She decrypts it with her private key. 1) 2) 3) 4) Pick two large prime numbers p and q. These are secret. Calculate n = pq Pick another number e such that e and (p-1)(q-1) are relatively prime. The numbers n and e make up your public key. Publish them! 5) Calculate d such that ed = 1 mod (p-1)(q-1) {i. e. d = e-1 mod (p-1)(q-1) } 6) The number d is your private key. Encrypt message m via c = me mod n Decrypt the ciphertext c via m = cd mod n example This is what happens when you buy a book from Amazon. com
Скачать презентацию Cryptography The Basic Idea Two approaches plaintext Key
9b848bf75f9e061bfe14e8b9f0dbf5c9.ppt