Cryptography Mathematical Foundations Algorithms and Protocols Klaus Köhler

Cryptography Mathematical Foundations, Algorithms, and Protocols Klaus Köhler Munich University of Applied Sciences Fachhochschule München E-Mail: k. koehler@informatik. fh-muenchen. de Home Page: http: //www. cs. fhm. de/~koehler pgp key fingerprint: 8 F 2 A 16 D 9 6 A BF 2 B F 6 77 C 2 39 82 1 F D 3 69 F 4 X. 509 Certificate: http: //www. trustcenter. de/cgi-bin/Search. cgi Jan/Feb 2002 Cryptography

Contents • Requirements of IT-Security • Overview of Symmetric and Asymmetric Ciphers • Classical Ciphers • Stream Ciphers • Block Ciphers • Asymmetric Ciphers • Random Number Generators • Prime Number Generators • Hash Functions with mathematical foundations interspersed Not contained: Information Theory, Cryptanalysis Klaus Köhler Cryptography

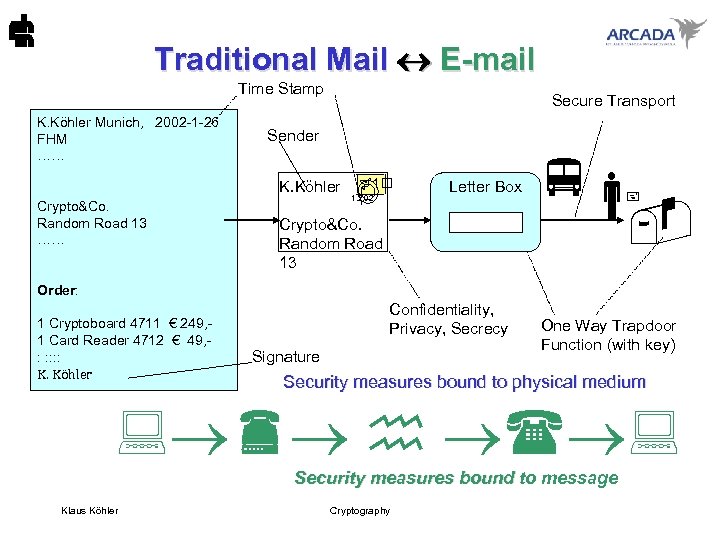Traditional Mail E-mail Time Stamp K. Köhler Munich, 2002 -1 -26 FHM …… Secure Transport Sender K. Köhler Crypto&Co. Random Road 13 …… 1 1. 2. 02 Letter Box Crypto&Co. Random Road 13 Order: 1 Cryptoboard 4711 € 249, 1 Card Reader 4712 € 49, : : : K. Köhler Confidentiality, Privacy, Secrecy Signature One Way Trapdoor Function (with key) Security measures bound to physical medium Security measures bound to message Klaus Köhler Cryptography

Goals of Cryptography • Privacy, Secrecy, Confidentiality Only intended receiver shall be able to read data. envelope • Integrity Receiver can check if transmitted data have been modified. untampered envelope • Authenticity Receiver can check that data were generated by sender. known handwriting, style, voice • Liability (Non-repudiation) The receiver can proof that the data came from the sender. signature Klaus Köhler Cryptography

Goals of IT-Security Jerome Saltzer and Michael Schroeder • Privacy. A socially defined ability of an individual or organization to determine whether, when, and to whom personal or organizational information is to be released. • Security. Techniques that control who may use or modify the computer or the information within it. • Protection. The security techniques that control the access of executing programs to stored information. • Integrity. Techniques that control the reliability of information storage and computing service despite accidental failure of individual components and programs. • Reliability. A system is reliable if failures do not seriously impair its satisfactory operation. Klaus Köhler Cryptography

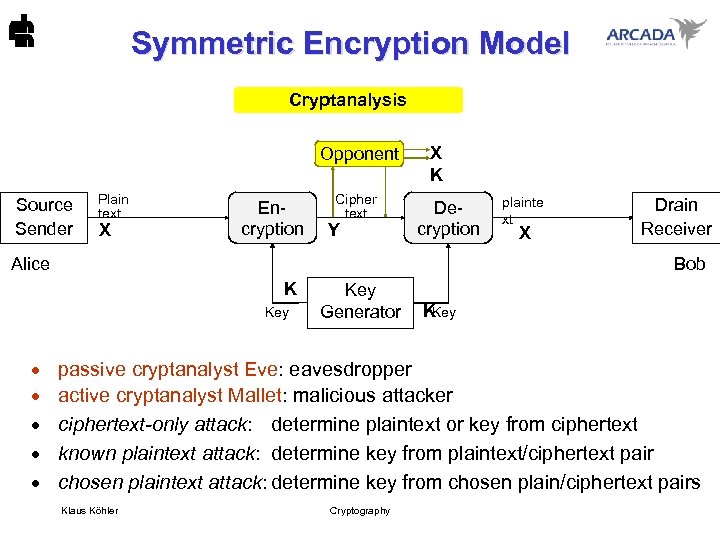Symmetric Encryption Model Cryptanalysis Opponent Source Sender Plain text X Encryption Cipher text Y X K Decryption Alice X Drain Receiver Bob K Key · · · plainte xt Key Generator K Key passive cryptanalyst Eve: eavesdropper active cryptanalyst Mallet: malicious attacker ciphertext-only attack: determine plaintext or key from ciphertext known plaintext attack: determine key from plaintext/ciphertext pair chosen plaintext attack: determine key from chosen plain/ciphertext pairs Klaus Köhler Cryptography

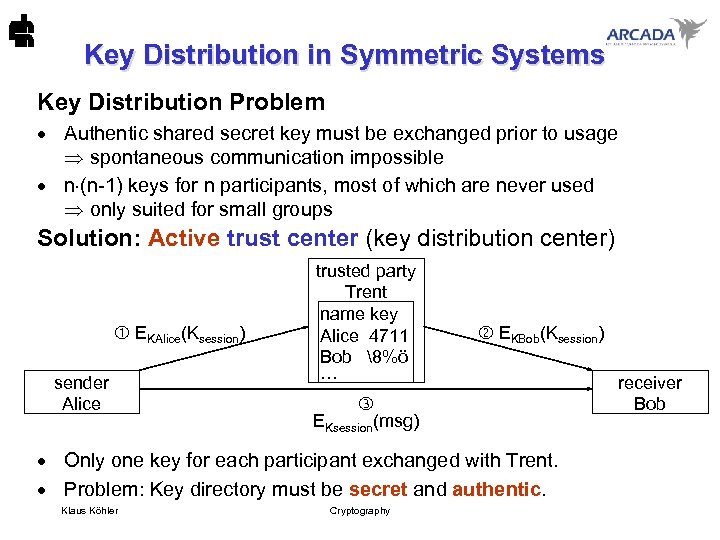Key Distribution in Symmetric Systems Key Distribution Problem · Authentic shared secret key must be exchanged prior to usage spontaneous communication impossible · n (n-1) keys for n participants, most of which are never used only suited for small groups Solution: Active trust center (key distribution center) EKAlice(Ksession) sender Alice trusted party Trent name key Alice 4711 Bob 8%ö ··· EKsession(msg) EKBob(Ksession) · Only one key for each participant exchanged with Trent. · Problem: Key directory must be secret and authentic. Klaus Köhler Cryptography receiver Bob

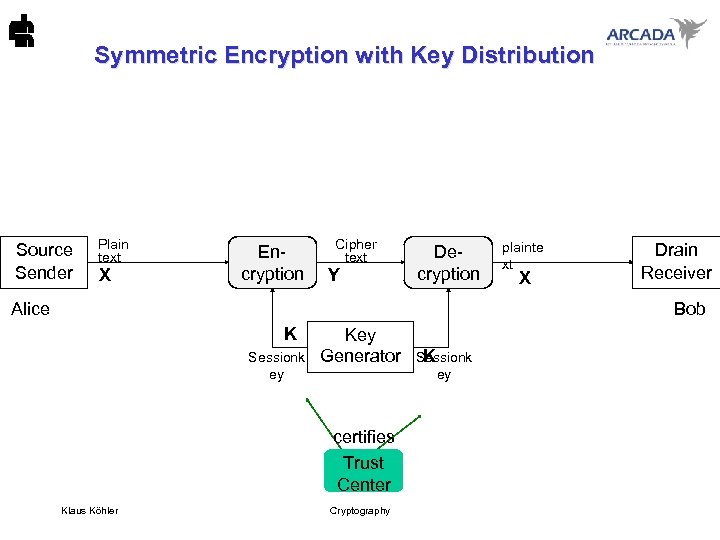Symmetric Encryption with Key Distribution Source Sender Plain text X Encryption Cipher text Y Decryption Alice plainte xt X Drain Receiver Bob K Sessionk ey Key Generator ey certifies Trust Center Klaus Köhler K Sessionk Cryptography

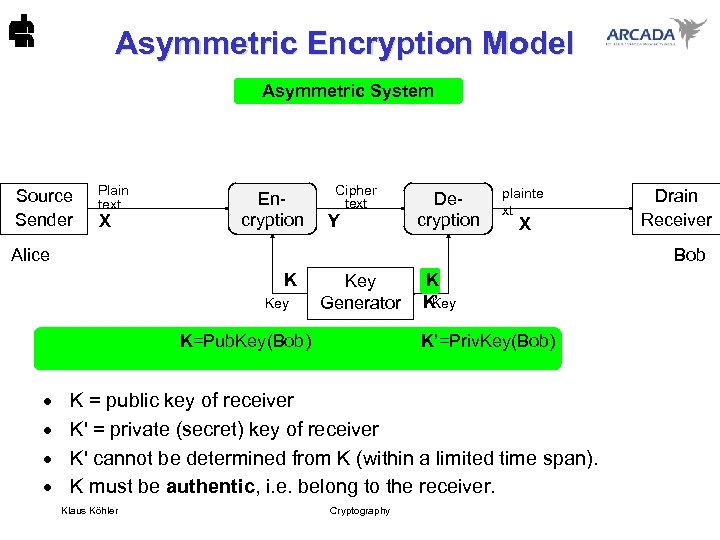Asymmetric Encryption Model Asymmetric System Source Sender Plain text X Encryption Cipher text Y Decryption plainte xt X Alice Bob K Key Generator K K K’ Key K=Pub. Key(Bob) K’=Priv. Key(Bob) · · Drain Receiver K = public key of receiver K' = private (secret) key of receiver K' cannot be determined from K (within a limited time span). K must be authentic, i. e. belong to the receiver. Klaus Köhler Cryptography

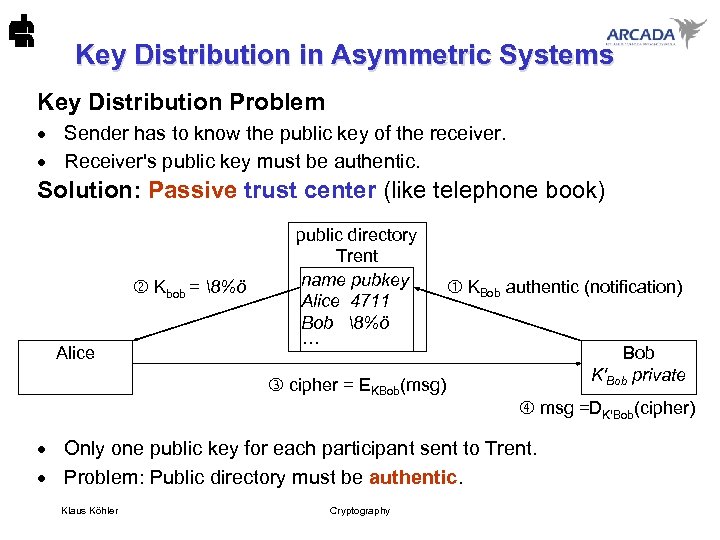Key Distribution in Asymmetric Systems Key Distribution Problem · Sender has to know the public key of the receiver. · Receiver's public key must be authentic. Solution: Passive trust center (like telephone book) Kbob = 8%ö Alice public directory Trent name pubkey Alice 4711 Bob 8%ö ··· KBob authentic (notification) Bob K'Bob private cipher = EKBob(msg) msg =DK'Bob(cipher) · Only one public key for each participant sent to Trent. · Problem: Public directory must be authentic. Klaus Köhler Cryptography

Authentication in Symmetric Systems Prerequisite: Sender and receiver share a secret key · Message redundant: like encryption Bob Alice DK(cipher) sensible? cipher = EK(msg) · Message not redundant, e. g. compressed file: insert redundancy Bob Alice Problems: (msg, cipher) (msg, sighash) sighash = EK(H(msg)) msg = DK(cipher) ? H(msg) = DK(sighash) ? 1. Alice and Bob must trust each other as both can generate the same messages no proof of origin, no non-repudiation, no liability 2. Twice as much data transferred Solutions: 1. Complicated protocol involving a trusted arbiter 2. Replace cipher with sighash = EK(H(msg)) using a hash function H that compresses msg to a short, fixed length fingerprint H(msg). Klaus Köhler Cryptography

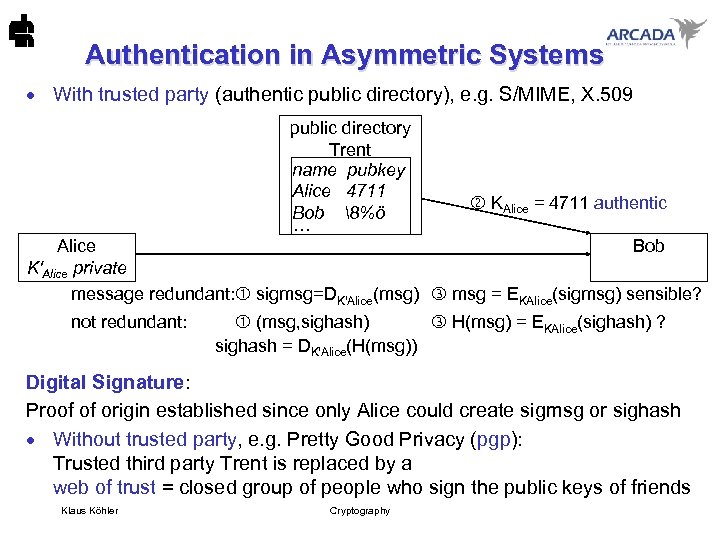Authentication in Asymmetric Systems · With trusted party (authentic public directory), e. g. S/MIME, X. 509 public directory Trent name pubkey Alice 4711 Bob 8%ö ··· KAlice = 4711 authentic Alice Bob K'Alice private message redundant: sigmsg=DK'Alice(msg) msg = EKAlice(sigmsg) sensible? not redundant: (msg, sighash) H(msg) = EKAlice(sighash) ? sighash = DK'Alice(H(msg)) Digital Signature: Proof of origin established since only Alice could create sigmsg or sighash · Without trusted party, e. g. Pretty Good Privacy (pgp): Trusted third party Trent is replaced by a web of trust = closed group of people who sign the public keys of friends Klaus Köhler Cryptography

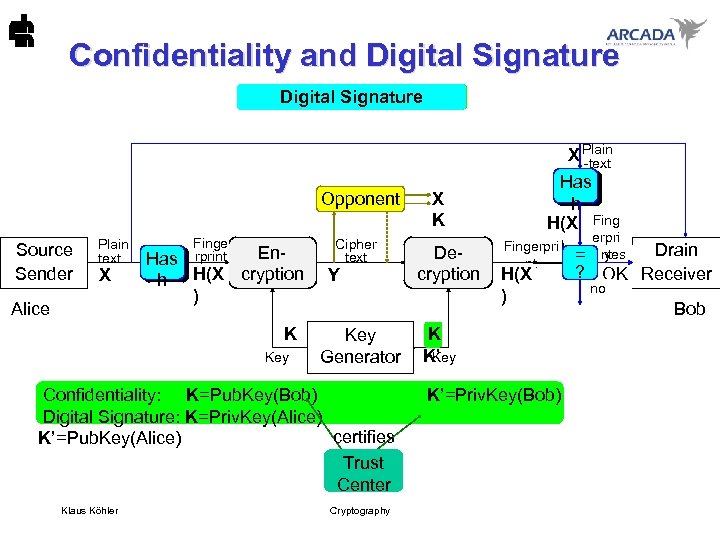Confidentiality and Digital Signature Asymmetric System cryptanalysis X Plain -text Opponent Source Sender Plain text X Alice Finge rprint En. Has h H(X cryption ) K Key Cipher text Y Key Generator X K Decryption Has h H(X Fing erpri Fingerpri plainte ) Drain yes = nt xt nt ? OK Receiver H(X X no ) Bob K K’ Key Confidentiality: K=Pub. Key(Bob) K’=Priv. Key(Bob) Digital Signature: K=Priv. Key(Alice) certifies K’=Pub. Key(Alice) Trust Center Klaus Köhler Cryptography

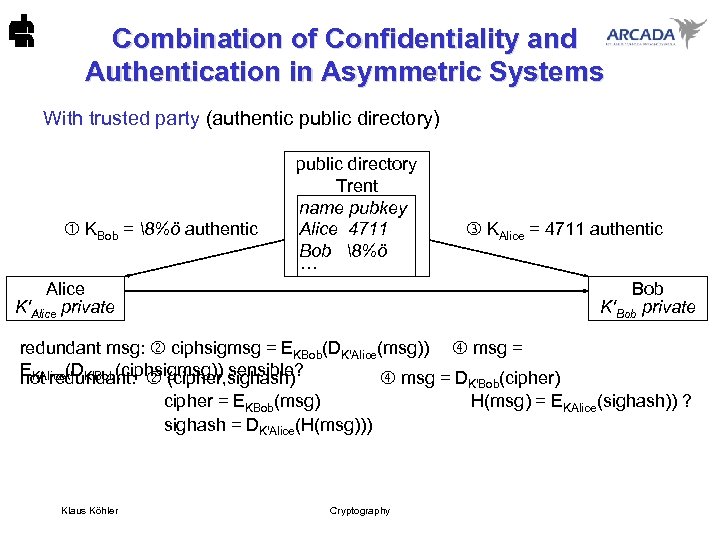Combination of Confidentiality and Authentication in Asymmetric Systems With trusted party (authentic public directory) KBob = 8%ö authentic Alice K'Alice private public directory Trent name pubkey Alice 4711 Bob 8%ö ··· KAlice = 4711 authentic Bob K'Bob private redundant msg: ciphsigmsg = EKBob(DK'Alice(msg)) msg = EKAlice(DK'Bob(ciphsigmsg)) sensible? not redundant: (cipher, sighash) msg = D (cipher) K'Bob cipher = EKBob(msg) sighash = DK'Alice(H(msg))) Klaus Köhler Cryptography H(msg) = EKAlice(sighash)) ?

Combination of Symmetric and Asymmetric Systems Symmetric crypto systems · are about 1000 times faster than asymmetric · suffer from key distribution problems · are less suited for authentication, in particular digital signatures Use symmetric systems for · bulk data encryption with session keys Use asymmetric systems for · key distribution, e. g. session key agreement or encryption · digital signatures Hashing is even faster than symmetric encryption Apply hash functions before digitally signing a message Klaus Köhler Cryptography

Cryptographic Building Blocks • Symmetric Ciphers (bulk data encryption) – Block ciphers – Stream ciphers • Asymmetric Ciphers – encryption of small quantities, e. g. symmetric keys (confidentiality) – digital signatures • Random Generators – Key generation (asymmetric, symmetric) – Authentication, e. g. challenges and nonces • Prime Number Generators (for asymmetric ciphers) • Hash Functions – fixed, e. g. MD 5, SHA-1, RIPE-MD – keyed (often a combination of block and stream ciphers) Klaus Köhler Cryptography

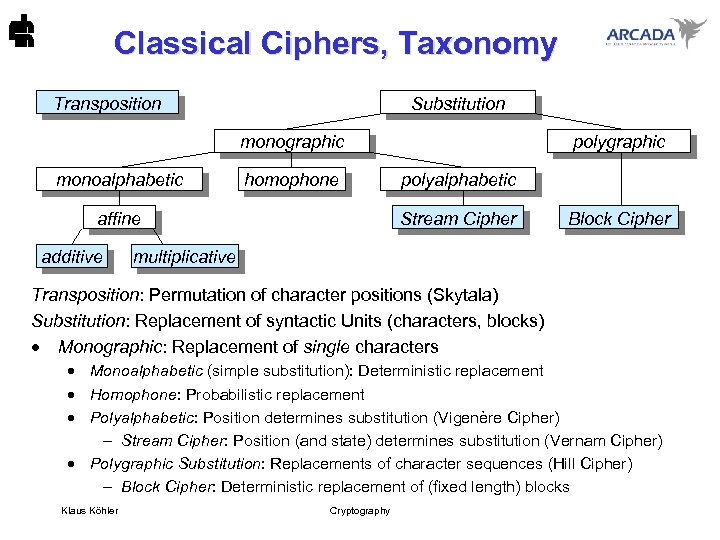Classical Ciphers, Taxonomy Transposition Substitution monographic monoalphabetic homophone affine additive polygraphic polyalphabetic Stream Cipher Block Cipher multiplicative Transposition: Permutation of character positions (Skytala) Substitution: Replacement of syntactic Units (characters, blocks) · Monographic: Replacement of single characters · Monoalphabetic (simple substitution): Deterministic replacement · Homophone: Probabilistic replacement · Polyalphabetic: Position determines substitution (Vigenère Cipher) - Stream Cipher: Position (and state) determines substitution (Vernam Cipher) · Polygraphic Substitution: Replacements of character sequences (Hill Cipher) - Block Cipher: Deterministic replacement of (fixed length) blocks Klaus Köhler Cryptography

Transposition Ciphers A O F S P A R T A T S T A S R H K A O P T E Y L F A A Skytala: • • • wind parchment tape around a roll write plaintext in a row and read it column by column, i. e. unwind tape key k = |rows| = diameter • Positions of letters changed Ciphertext contains the same letters with the same frequencies • Bigrams, e. g. "th", are separated by k letters distance = key Diffusion = breaking local dependencies Transposition Cipher = block cipher EK: Xm Xm, EK(a 0 am-1) = a (0) a (m-1) Plaintext = ciphertext alphabet = X (block size m = matrix size = whole text) Permutation Sm of the positions {0, . . . , m-1} Klaus Köhler Cryptography

Additive Substitution Ciphers Cesar Cipher: • Replace each letter by the letter k=3 positions away in the alphabet A D, B E, . . . , W Z, X A, Y B, Z C • Example: SECRET VHFUHW Properties • Replace letters (not positions) plaintext letters appear with the same frequencies as their substitutes in the ciphertext • plaintext pairs (bigrams), triples, etc. appear with the same frequencies as their corresponding substitutes in the ciphertext • Example (ciphertext frequencies): H: 2, U: 1, . . . probably E H k=3 Additive Cipher EK: X X, Ek(a) = (a + k) mod n (with encoding A 0, B 1, . . . ) Plaintext = ciphertext alphabet = X = {0, . . . , n-1} Key k Z= {0, . . . , n-1} small key space enables brute force attack Klaus Köhler Cryptography

Multiplicative Substitution Ciphers Multiplicative Cipher EK: X X, Ek(a) = a·k mod n Plaintext = ciphertext alphabet = X = {0, . . . , n-1}, Not all keys k {0, . . . , n-1} are valid, since EK must be invertible (injective) Example: X = {0, . . . , 25}, n=26, k=13, • • A 0 Ek(0) = 0· 13 mod 26 = 0 A C 2 Ek(2) = 2· 13 mod 26 = 0 A not injective decryption impossible Proposition: EK: X X, Ek(a) = a·k mod n is invertible n and k are relatively prime i. e. gcd(n, k) = 1 The inverse key k-1 mod n can be determined by the extended Euclidean algorithm. Example: n=26 • encryption k = 9: SECRET 18 4 2 17 4 19 6 10 18 23 10 15 GKSXKP • decryption k-1=3 since 9· 3 mod 26 = 1 Klaus Köhler Cryptography

Excursion: Modular Arithmetic n= {0, 1, . . . , n-1} with addition a+b = a+b mod n is a commutative group, i. e. the following axioms hold for all a, b, c n – – – a+b n (a+b)+c = a+(b+c) a+b = b+a 0+a = a (n-a)+a = 0 (closed) (associative) (commutative) (neutral element) (inverse element: n-a is inverse to a) l n= {0, 1, . . . , n-1} with multiplication a · b = a·b mod n is a commutative semigroup with neutral element, i. e. the following axioms hold for all a, b, c n – a · b n (closed) – (a · b) · c = a · (b · c) (associative) – a · b = b · a (commutative) – 1 · a = a (neutral element) The inverse element need not exist, e. g. 2 26 is not invertible, but 9 is: 9 -1=3 because 9 · 3 = 27 mod 26 = 1 = neutral element. Klaus Köhler Cryptography

Excursion: Modular Arithmetic, cont. Definition a, b are called relatively prime, if gcd(a, b) = 1. Euclidean Algorithm (for determining the greatest common divisor) • Idea: gcd(a, b) = gcd(b, a-b) and hence gcd(a, b) = gcd(b, a mod b) apply this transformation iteratively until b=0 obtaining gcd(a, 0) = a • Example: gcd(26, 9) = gcd(9, 26 mod 9) = gcd(9, 8) = gcd(8, 9 mod 8) = gcd(8, 1) = gcd(1, 8 mod 1) = gcd(1, 0) = 1 int gcd(int a, int b) { // Euclidean Algorithm for integers int g = a, q = b, r; while(q!=0) { // Invariant: gcd(a, b) = gcd(g, q) && q != 0; Variant: |q| r = g%q; // gcd(a, b) = gcd(g, q) = gcd(q, g%q) = gcd(q, r) g = q; // |r|<|q|=|g| q = r; // gcd(a, b) = gcd(g, q) |q|<|qold| } // q = 0 and gcd(a, b) = gcd(g, q) // i. e. gcd(a, b) = gcd(g, 0) = g return g; } Klaus Köhler Cryptography

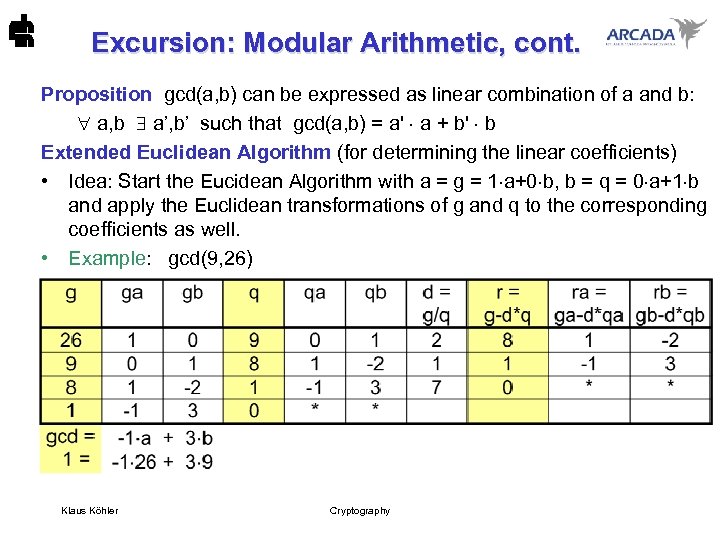Excursion: Modular Arithmetic, cont. Proposition gcd(a, b) can be expressed as linear combination of a and b: a, b a’, b’ such that gcd(a, b) = a' a + b' b Extended Euclidean Algorithm (for determining the linear coefficients) • Idea: Start the Eucidean Algorithm with a = g = 1 a+0 b, b = q = 0 a+1 b and apply the Euclidean transformations of g and q to the corresponding coefficients as well. • Example: gcd(9, 26) Klaus Köhler Cryptography

Excursion: Extended Euclidean Algorithm int gcd. Ext(int a, int b, int& ga, int& gb) { int g, q, qa, qb, d, r, ra, rb; // auxiliary variables g = a; ga = 1; gb = 0; // g = ga * a + gb * b q = b; qa = 0; qb = 1; // q = qa * a + qb * b while(q!=0) { // Variant: |q| // Invariant: g = ga * a + gb * b // q = qa * a + qb * b // q != 0 and gcd(a, b) = gcd(g, q) d = g/q; r = g%q; // r = remainder of division of g by q // = g - d * q // gcd(a, b) = gcd(g, q) = gcd(q, g%q) = gcd(q, r) ra = ga - d * qa; rb = gb - d * qb; // r = ra * a + rb * b g = q; ga = qa; gb = qb; // g = ga * a + gb * b q = r; // gcd(a, b) = gcd(g, q) qa = ra; qb = rb; // q = qa * a + qb * b } // q = 0 and gcd(a, b) = gcd(g, q) , g = ga * a + gb * b // i. e. gcd(a, b) = gcd(g, 0) = ga * a + gb * b return g; } Klaus Köhler Cryptography

Excursion: Modular Arithmetic, cont. Corollary 1 • a n : = {0, 1, . . . , n-1} with multiplication modulo n is invertible a and n are relatively prime, i. e. gcd(a, n) = 1 • a-1 can be determined by the extended Euclidean algorithm Corollary 2 • n* : = {a n| a invertible} = {a n| gcd(a, n)=1} with multiplication modulo n is a group. • n* = n{0} = {1, . . . , n-1} n is prime. Euler's Totient Function • For n Euler's phi-Funktion (n) counts the natural numbers i < n relatively prime to n: (n) = |{i | 0 < i < n, gcd(i, n) = 1}| • (n) gives the number of invertible elements of n: (n) = | n*| • n = p prim (p) = p-1 • n = p 2, p prim (p 2) = p (p-1) • n = p q, p, q prim, p q (p q) = (p-1) (q-1) Klaus Köhler Cryptography

Excursion: Rings and Fields • is a commutative ring, i. e. the following axioms hold for all a, b, c – is a commutative group with respect to addition – is a commutative semigroup with respect to multiplication – (a+b) · c = a·c + b·c (distributive) • n= {0, 1, . . . , n-1} with modular addition and multiplication is a commutative ring, too. • is a Euclidean ring, i. e. division is almost possible: – a, b , a 0 q, r , so that b = q a + r and r = 0 or |r| < |a| • n is not euclidean. • For primes p p is a Galois field, i. e. – p is a commutative ring with respect to addition and multiplication – p* = p{0} = {1, . . . , n-1} is a group with respect to multiplication (If n =p·q is not prime, p 1 and q 1 are not invertible, since p·q = n = 0 n) • is not a field, since the only multiplicatively invertible elements of are 1 and -1. Klaus Köhler Cryptography

Excursion: Rings and Fields, cont. Definition of substructures: U < S A subset U of an algebraic structure (group / ring / field) S is called a substructure (subgroup / subring / subfield) if it is a group / ring / field with respect to the operations of the superstructure S. Examples of substructures • Subgroup: 2 < with respect to addition The multiplicative group 5* = {1, 2, 3, 4} has the subgroups {1}, {1, 4}, 5*. • Subring: 2 < with respect to addition and multiplication The ring 6 = {0, 1, 2, 3, 4, 5} has the proper subrings {0}, {0, 3}, {0, 2, 4}. • Subfield: < with respect to addition and multiplication Order of structures: |U| |S| • The number of elements of a algebraic structure S is called its order |S|. • The order of a substructure U of a finite algebraic structure S is a divisor of the order of S: |U| |S| Klaus Köhler Cryptography

Excursion: Rings and Fields, cont. Construction of finite fields (Galois fields) The field p was constructed from the Euclidean ring , addition + and multiplication · being defined modulo a prime p. Theorem Let R be an Euclidean ring and p R a prime element (p is not invertible and has no proper divisors). Then R with addition + and multiplication · modulo p is a field R/p·R. (Abbreviation: p : = /p· ) Proof parallels the proof of p being a field. Corollary • Let F be a field and p(x) a prime polynomial (irreducible) of the ring of polynomial F[x]. Then F[x]/p(x)·F[x] is a field. In particular • q[x]/p(x)· q is a field, if q is prime in and p(x) is prime in q[x]. Proof: Polynomial division in F[x] yields a residue of smaller degree. Hence, F[x] is Euclidean. Inverse elements are determined by the extended Euclidean algorithm. Klaus Köhler Cryptography

Excursion: Rings and Fields, cont. Example • q = 2 is prime and p(x) = x 3 + x 2 + 1 q[x] is irreducible. Therefore, 2[x]/p(x)· 2 is a field. • Elements can be reduced modulo p(x) 8 polynomials of degree < 3: 0, 1, x, x+1, x 2+1, x 2+x+1 • Powers of x: x, x 2, x 3 = x 2 + 1, x 4 = x 2+x+1, x 5 = x+1, x 6 = x 2+x, x 7 = 1 The multiplicative group of q[x]/p(x)· q is generated by x. Klaus Köhler Cryptography

Excursion: Rings and Fields, cont. Theorem 1 The only finite fields (up to isomorphism) are q and q[x]/p(x)· q, where q is prime in and p(x) is prime in q[x]. 2 The multiplicative group of a finite field is cyclic, i. e. generated by a primitive element. 3 The prime field q is a subfield of q[x]/p(x)· q. 4 q[x]/p(x)· q is a vector space over its prime field q. 5 q[x]/p(x)· q has qn, n = degree(p(x)) elements: | q[x]/p(x)· q| = qn. 6 For every prime q and every degree n there exist irreducible polynomials p(x) in q[x]. 7 For every prime power qn there is exactly one field with qn elements (up to isomorphism). Proof: For 1, 2, and 6 see any algebra book. The other proofs are left as exercises. Klaus Köhler Cryptography

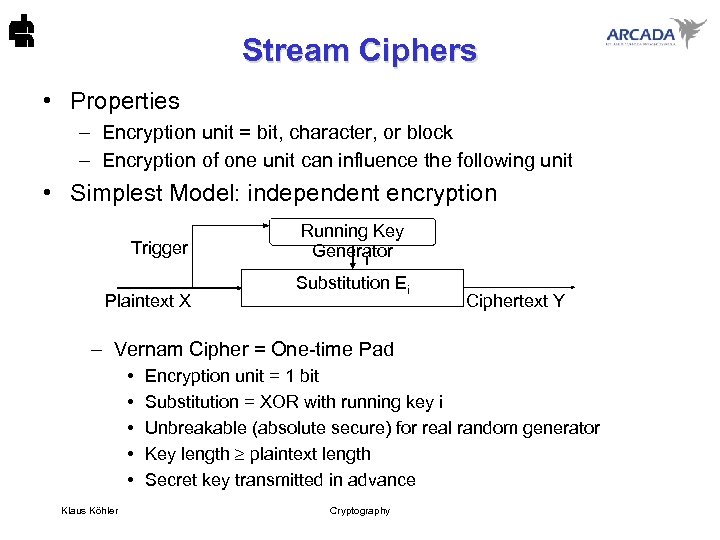Stream Ciphers • Properties – Encryption unit = bit, character, or block – Encryption of one unit can influence the following unit • Simplest Model: independent encryption Trigger Plaintext X Running Key Generator i Substitution Ei Ciphertext Y – Vernam Cipher = One-time Pad • • • Klaus Köhler Encryption unit = 1 bit Substitution = XOR with running key i Unbreakable (absolute secure) for real random generator Key length plaintext length Secret key transmitted in advance Cryptography

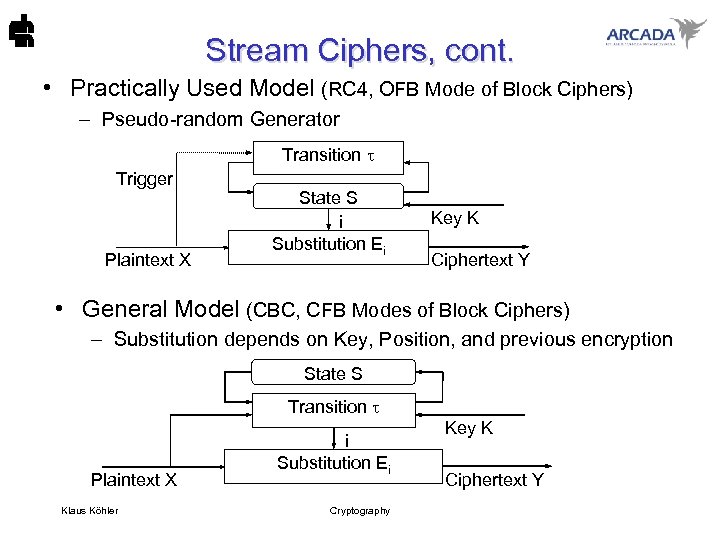Stream Ciphers, cont. • Practically Used Model (RC 4, OFB Mode of Block Ciphers) – Pseudo-random Generator Transition Trigger Plaintext X State S i Substitution Ei Key K Ciphertext Y • General Model (CBC, CFB Modes of Block Ciphers) – Substitution depends on Key, Position, and previous encryption State S Transition Plaintext X Klaus Köhler i Substitution Ei Cryptography Key K Ciphertext Y

Symmetric Block Ciphers Design Principles • Desirable properties: – confusion: hide statistical particularities goal: equally distributed cipher text (for each key) – diffusion: break up local dependencies goal: completeness (every ciphertext bit depends on each plaintext bit) – avalanche effect: 1 bit change in plaintext swaps half of ciphertext bits – non-linearity: no ciphertext bit is linearly dependent on the plaintext equal distribution but long delay, more waste • Key length: big more security but big effort (time and space) • Encryption/Decryption similarity: • Block length: big – (almost) same algorithm for encryption and decryption Klaus Köhler Cryptography

Symmetric Block Ciphers, cont. Efficiency • lookup table efficient (time) but too big (space) • pure calculation inefficient (time) but small (space) compromise: combine efficient building blocks that operate on smaller partial blocks Building blocks • (involutary) permutations of positions (transpositions) • (involutary) substitutions • (incompatible) group operations (diffusion) (confusion) Resulting cipher: (cascaded) product cipher with several rounds (IDEA) Klaus Köhler Cryptography

Advanced Encryption Standard (AES) History • 1997: National Institute of Standards and Technology (NIST) called for a successor of DES. The proposed AES-algorithms should be – unclassified, – publicly disclosed – available royalty-free, worldwide. The algorithm must implement – symmetric key cryptography as a block cipher and (at a minimum) support block sizes of 128 -bits and key sizes of 128 -, 192 -, and 256 -bits. • 1998: NIST announced a group of fifteen AES candidate algorithms • 1999: NIST selected five algorithms after in depth analysis conducted by the global cryptographic community on the candidate algorithms: MARS (IBM), RC 6 (RSA), Twofish (Counterpane), Rijndael, Serpent • 2000: NIST proposed Rijndael for the AES • 2001: approval of the Federal Information Processing Standard (FIPS) for the Advanced Encryption Standard Klaus Köhler Cryptography

Rijndael (V. Rijmen, J. Daemon, University of Leuven) Rijndael Features • Key length Nk, , block length Nb: 32 N, N = 4, . . . , 8, (128, 160, 192, 224, 256) independently chosen • Block represented as state S = 4 Nb-byte matrix • r = max(Nb, Nk)+6 rounds • Rounds transform state S through – – x Byte. Sub: parallel byte operations: confusion by non-linear substitution Shift. Row: parallel row operations: diffusion through linear operation Mix. Column: parallel column operations: diffusion through linear operation Add. Round. Key: matrix operation (XOR with key): dependency of key Byte Shift Mix Sub Row Colm K 0 K . . . Byte Shift Mix Sub Row Colm K 1 Kr-1 Key-Schedule Algorithm Klaus Köhler Byte Shift Sub Row Cryptography y Kr

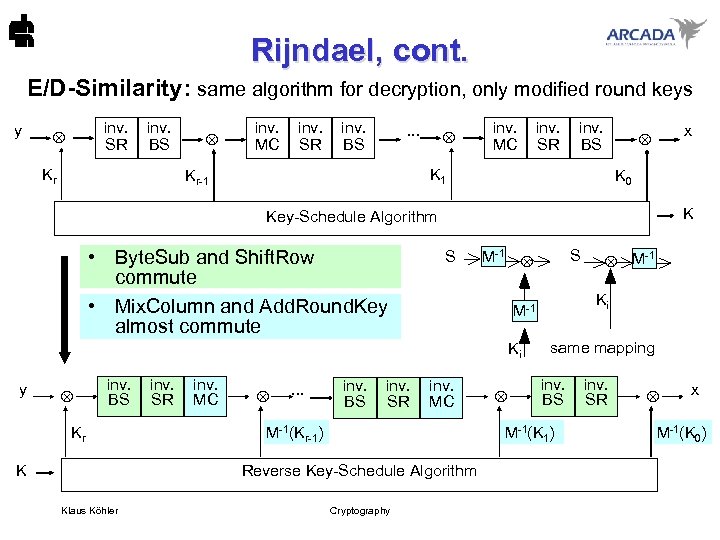Rijndael, cont. E/D-Similarity: same algorithm for decryption, only modified round keys y inv. SR Kr inv. BS inv. MC inv. SR inv. BS . . . inv. MC inv. SR inv. BS K 1 Kr-1 x K 0 K Key-Schedule Algorithm • Byte. Sub and Shift. Row commute • Mix. Column and Add. Round. Key almost commute S M-1 inv. BS SR MC Kr . . . inv. BS SR MC M-1(Kr-1) Klaus Köhler same mapping inv. BS SR M-1(K 1) Reverse Key-Schedule Algorithm K Cryptography -1 M Ki M-1 Ki y S x M-1(K 0)

Basic Rijndael Operations Add. Round. Key • XOR of state S and round key Ki Shift. Row • row 1 fixed • row 2 -4 cyclic shift by 1 to 4 positions depending on the block length Nb Byte. Sub • combination of – affine mapping of the vector space GF(28) over its prime field GF(2)= 2 – inverse mapping in the field GF(28) Mix. Column • linear transformation of the vector space GF(28)4 induced by a polynomial multiplication Klaus Köhler Cryptography

Rijndael Key Scheduling Purpose: derive round keys from the cipher key x Byte Shift Mix Sub Row Colm K 0 K . . . Byte Shift Mix Sub Row Colm K 1 Byte Shift Sub Row y Kr-1 Kr Key-Schedule Algorithm • r+1 keys K 0, . . . , Kr for r rounds necessary: (r+1) · Nb 32 bit words • cipher key is expanded to an "expanded key" of that size (or more) recursion formula (for Nk 6, slightly different for Nk > 6): – Wi = Wi-Nk Wi-1 if Nk is no divisor of i – Wi = Wi-Nk (BS(SR(Wi-1)) RC[i/Nk] if Nk is a divisor of i BS = Byte. Sub, SR = Shift. Row 1 Byte, RC = (xi-1, 0016, 0016), xi-1 in GF(28), i. e. calculated modulo p(x) = x 8+x 4+x 3+x+1 • round keys are taken from the expanded key in the order of rounds Klaus Köhler Cryptography

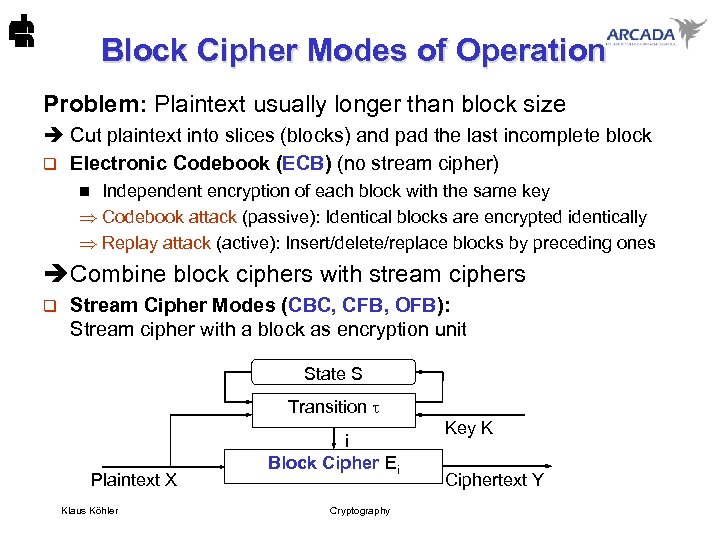Block Cipher Modes of Operation Problem: Plaintext usually longer than block size è Cut plaintext into slices (blocks) and pad the last incomplete block q Electronic Codebook (ECB) (no stream cipher) Independent encryption of each block with the same key Codebook attack (passive): Identical blocks are encrypted identically Replay attack (active): Insert/delete/replace blocks by preceding ones n è Combine block ciphers with stream ciphers q Stream Cipher Modes (CBC, CFB, OFB): Stream cipher with a block as encryption unit State S Transition Plaintext X Klaus Köhler i Block Cipher Ei Cryptography Key K Ciphertext Y

Block Cipher Modes of Operation Assessment Criteria 1 2 3 4 5 6 7 Propagation of transmission errors (change bits) Synchronisation errors (delete or insert bits) Code expansion Effective key size Cryptanalysis, security Application areas Effective encryption rate (compared with ECB) Klaus Köhler Cryptography

Electronic Codebook (ECB) Assessment 1 Propagation of transmission errors (change bits) whole block corrupted, succeeding blocks unchanged 2 Synchronisation errors (delete or insert bits) all succeeding blocks corrupted 3 Code expansion last block expansion due to padding can be avoided (ciphertext stealing) 4 Effective key size = key size 5 Cryptanalysis, security poor security, codebook analysis for redundant plaintexts (e. g. English) 6 Application areas random access of single blocks, e. g. data bases 7 Effective encryption rate (compared with ECB) 1 Klaus Köhler Cryptography

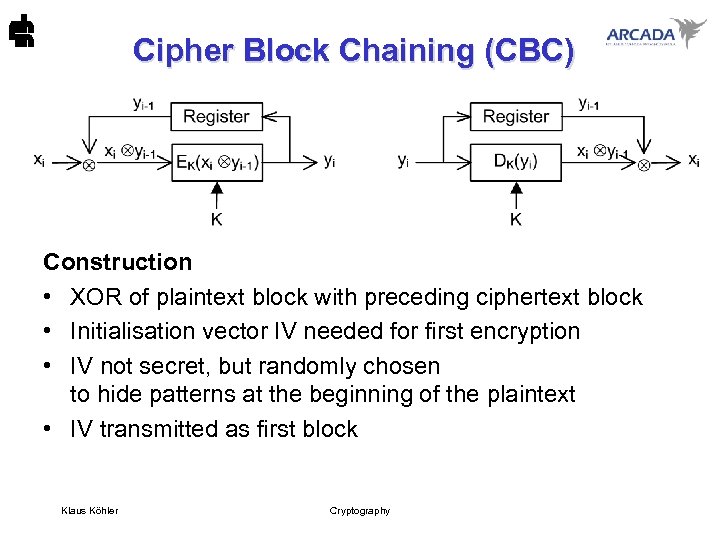Cipher Block Chaining (CBC) Construction • XOR of plaintext block with preceding ciphertext block • Initialisation vector IV needed for first encryption • IV not secret, but randomly chosen to hide patterns at the beginning of the plaintext • IV transmitted as first block Klaus Köhler Cryptography

Cipher Block Chaining (CBC), cont. Assessment 1 Propagation of transmission errors (change bits) block and next blocks corrupted, succeeding blocks unchanged 2 Synchronisation errors (delete or insert bits) all succeeding blocks corrupted 3 Code expansion last block expansion due to padding can be avoided (ciphertext stealing) 4 Effective key size = key size 5 Cryptanalysis, security plaintext patterns hidden, no codebook analysis, no statistical analysis 6 Application areas encryption of long texts (archives) when random access is not essential, cope with synchronisation errors through transmission protocols 7 Effective encryption rate (compared with ECB) 1 Klaus Köhler Cryptography

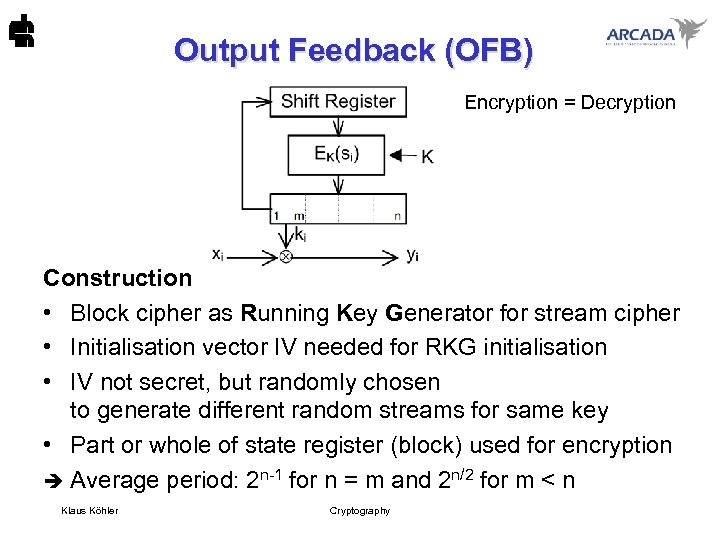Output Feedback (OFB) Encryption = Decryption Construction • Block cipher as Running Key Generator for stream cipher • Initialisation vector IV needed for RKG initialisation • IV not secret, but randomly chosen to generate different random streams for same key • Part or whole of state register (block) used for encryption è Average period: 2 n-1 for n = m and 2 n/2 for m < n Klaus Köhler Cryptography

Output Feedback (OFB), cont. Assessment 1 Propagation of transmission errors (change bits) no error propagation at all 2 Synchronisation errors (delete or insert bits) all succeeding blocks corrupted 3 Code expansion none 4 Effective key size = key size 5 Cryptanalysis, security plaintext patterns hidden, no codebook analysis, no statistical analysis, short period 2 n/2 sometimes insufficient, no error propagation active manipulations may remain undetected 6 Application areas online transactions without delay or error propagation cope with manipulation problems through error detecting protocols 7 Effective encryption rate (compared with ECB) m/n if only m bits out of n (= block length) are used for encryption Klaus Köhler Cryptography

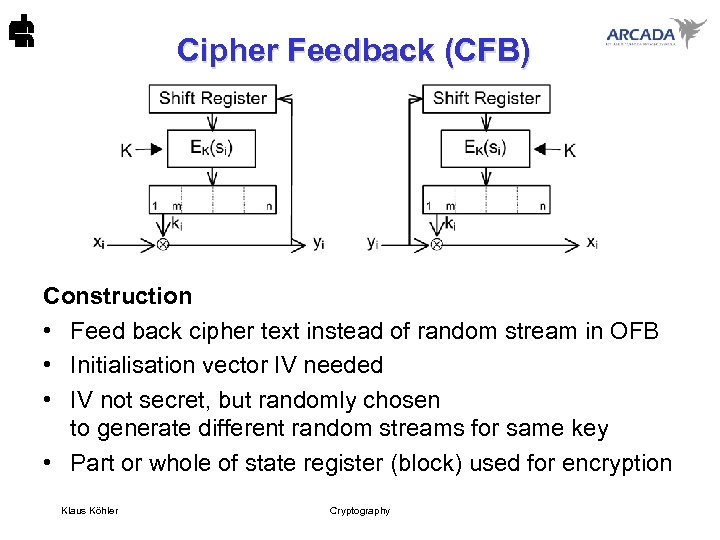Cipher Feedback (CFB) Construction • Feed back cipher text instead of random stream in OFB • Initialisation vector IV needed • IV not secret, but randomly chosen to generate different random streams for same key • Part or whole of state register (block) used for encryption Klaus Köhler Cryptography

Cipher Feedback (CFB), cont. Evaluation 1 Propagation of transmission errors (change bits) affected block and n/m-1 succeeding blocks (of length m) corrupted 2 Synchronisation errors (delete or insert bits) erroneous blocks as long as shift register is corrupted completely self-synchronising for m=1 3 Code expansion none 4 Effective key size = key size 5 Cryptanalysis, security plaintext patterns hidden, no codebook analysis, no statistical analysis, error propagation active manipulations can be detected 6 Application areas online transactions without delay but detection of manipulations 7 Effective encryption rate (compared with ECB) m/n if only m bits out of n (= block length) are used for encryption Klaus Köhler Cryptography

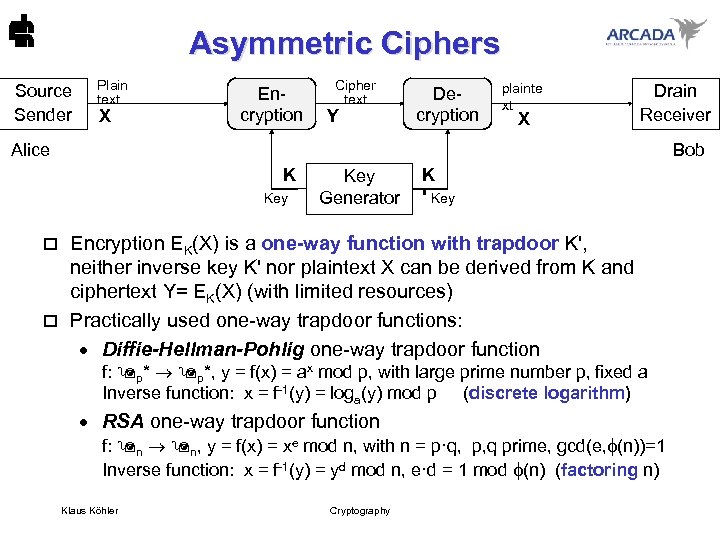Asymmetric Ciphers Source Sender Plain text X Encryption Cipher text Y Decryption plainte xt X Drain Receiver Alice Bob K Key Generator K ' Key Encryption EK(X) is a one-way function with trapdoor K', neither inverse key K' nor plaintext X can be derived from K and ciphertext Y= EK(X) (with limited resources) o Practically used one-way trapdoor functions: · Diffie-Hellman-Pohlig one-way trapdoor function o f: p*, y = f(x) = ax mod p, with large prime number p, fixed a Inverse function: x = f-1(y) = loga(y) mod p (discrete logarithm) · RSA one-way trapdoor function f: n n, y = f(x) = xe mod n, with n = p·q, p, q prime, gcd(e, (n))=1 Inverse function: x = f-1(y) = yd mod n, e·d = 1 mod (n) (factoring n) Klaus Köhler Cryptography

Diffie-Hellman one-way function f: p*, y = f(k) = ak mod p, with large prime number p, fixed a • Fast computation with Square-and-Multiply algorithm • Idea: k = (bn-1, . . . , b 1, b 0)2 = bn-1 2 n-1+. . . +b 1 2+b 0 (binary representation) • Algorithm: Iteratively apply formula • Example: a 13 = a a 12 = a (a 2)6 = a ((a 2)2)3 = a a 13 = a a 12 = a a 1 (a 12)1 = a a 1 (a 2)1 = a a 1 a 20 z : = 1; z : = z a; z : = z a 1; z : = z a 2 1; Klaus Köhler Cryptography

Square-and-Multiply /** Square-and-multiply algorithm for integral power calculation a^k, k>=0 */ long power(long a, int k) { // a and z from any multiplicative group long z = 1; // power = z * a^k while (k > 0) { // Variant: k; // Invariant: power = z * a^k if (k%2 == 0) { // k is even k /= 2; a *= a; // power = z * a^k } else { // k is odd k--; z *= a; // power = z * a^k } } return z; // k = 0 ==> power = z * a^k=z } • Time complexity: O(log(k)) for worst case and best case k even (bit = 0): 1 mult=square (a*=a), 1 shift (k/=2), ½k k odd (bit = 1): 1 mult=square (z*=a), 1 bit and (k--), k even loop: 1 step for each bit=1 + 1 step for each bit: max 2· log 2(k) steps • Space complexity: O(1) = constant, independent of k Klaus Köhler Cryptography

Diffie-Hellman Public Key-Distribution System Establish a shared secret (e. g. a symmetric key ) using insecure communication channels. o Solve the key distribution problem for symmetric keys. o No Public Key Cryptosystem! o o Protocol: Agree upon a common large prime p and a primitive element g of p Each member A chooses a private random number x. A and sends y. A=g. XA as public information to a (passive) trust center. From the public key y. B=g. XB of the partner B calculate the shared secret K : = y. BXA = (g. XB)XA = (g. XA)XB = y. AXB Trent y. A=gx. A 1. y. B Alice 2. K= y. Bx. A Y=EK(M) Klaus Köhler y. B=gx. B 4. y. A 3. Y Cryptography Bob 5. K= y. Ax. B M=DK(Y)

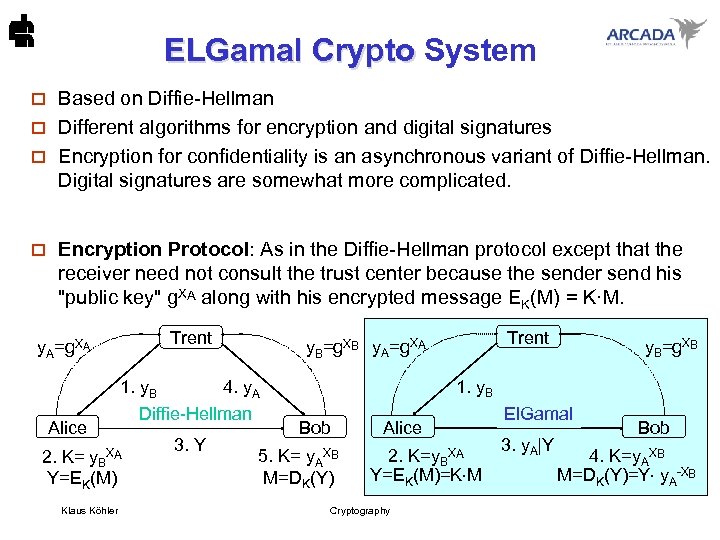ELGamal Crypto System ELGamal Crypto Based on Diffie-Hellman o Different algorithms for encryption and digital signatures o Encryption for confidentiality is an asynchronous variant of Diffie-Hellman. Digital signatures are somewhat more complicated. o o Encryption Protocol: As in the Diffie-Hellman protocol except that the receiver need not consult the trust center because the sender send his "public key" g. XA along with his encrypted message EK(M) = K·M. Trent y. A=g. XA Alice 1. y. B 4. y. A Diffie-Hellman 2. K= y. BXA Y=EK(M) Klaus Köhler 3. Y Trent y. B=g. XB y. A=g. XA y. B=g. XB 1. y. B Bob 5. K= y. AXB M=DK(Y) Alice 2. K=y. BXA Y=EK(M)=K M Cryptography El. Gamal 3. y. A|Y Bob 4. K=y. AXB M=DK(Y)=Y y. A-XB

Digital Signature Algorithm (DSA) Based on El. Gamal signatures o More efficient than El. Gamal signatures because o operations are performed in a smaller group (time complexity) o only 2· 160 bit for digital signature (space complexity) o Hash function SHA-1 used (160 bit) o No legal or patent restrictions o Used in pgp (version 6 and beyond) o Klaus Köhler Cryptography

Elliptic Curve Cryptography (ECC) Based on El. Gamal o El. Gamal uses only multiplicative group p* any group will do if o · multiplication is fast (and therefore, rising to the nth power, too) · inverse operation (logarithm) is hard. o Elliptic Curves are points P = (x, y) p p with · y 2 = x 3+a x+b, 4 a 3+27 b 2 0 mod p (with suitable a, b p) · multiplication defined by P 3 = P 1 P 2 = (x 3, y 3) with · neutral element (not representable as point) · inverse element P-1 = (x, p-y) of P = (x, y). ECC needs smaller keys (160 bit) than RSA (1024 bit) o ECC best suited for smart cards o Klaus Köhler Cryptography

RSA o Public Key Cryptosystem Confidentiality o Authenticity including digital signatures o o Key generation for messages encoded as natural numbers M < m = 2 l Each member: Secretly choose two large primes p and q and calculate n : = p q > m (public) m Choose e < (n)=(p-1)·(q-1), so that gcd(e, (n)) = 1, e. g. e = 3 or e = 216+1 m Determine d < (n), so that e d = 1 mod (n) (extended Euclidean algorithm) m (n, e) is the public key, d is the private key m Encrypt message M: o Decrypt message C = Ee(M): o Sign message M: o Verify message C = De(M): o Klaus Köhler Ee(M) = Me mod n, Dd(C) = Cd mod n, Dd(M) = Md mod n, Ee(C) = Ce mod n, Cryptography e = receiver's public key d = receiver's private key d = sender's private key e = sender's public key

Security of RSA Known-Plaintext Attack = Chosen-Plaintext Attack Determination of the private key d from plaintext M = Cd mod n and ciphertext C = Ee(M) ciphertext is a discrete logarithm problem. o Ciphertext-only Attacks o Message-dependent attacks: Deriving m M from e, n and C = Ee(M) = Me mod n is tantamount to determining the eth root modulo n. This problem is equivalent to factoring n. m d from e, n and C = Ee(M) = Me mod n seems to be just as hard as the m Message-independent attack: Deriving d from e and n is assumed to be equivalent to factoring n. o Factoring a large composite number n = p·q is a classical hard problem. Best (known) algorithms have time complexity m Klaus Köhler Cryptography

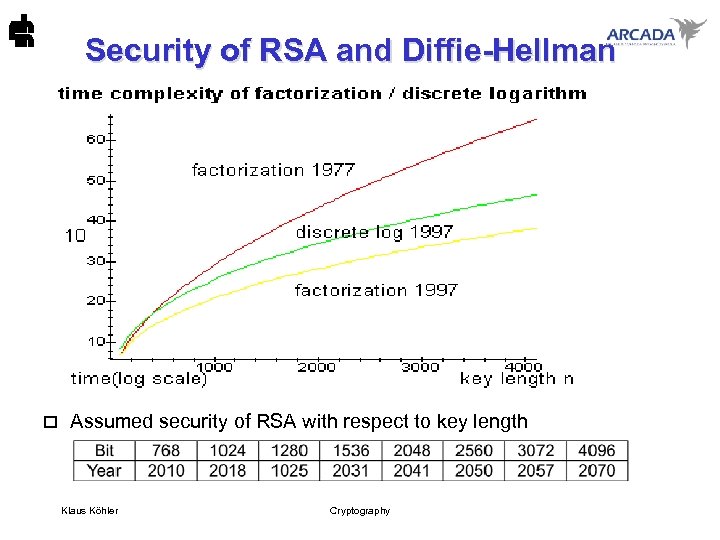Security of RSA and Diffie-Hellman o Assumed security of RSA with respect to key length Klaus Köhler Cryptography

Random Number Generators • Use – Key generation (asymmetric, symmetric) – Authentication, e. g. challenge and response – Nonces in key distribution schemes to prevent replay attacks • Requirements – Randomness: • Uniform distribution of the values in the sequence (single numbers and subsequences of any length) • Independence of the sequence values of each other – Unpredictability of successive members of the sequence Klaus Köhler Cryptography

Types of Random Number Generators • Physical noise generators (stochastic) – ionising radiation events – leaky capacitors • Pseudorandom Number Generators (deterministic) – linear congruential method (easy to break) si=c·si-1+d mod p, p prime – linear feedback shift registers (good statistics, easy to break) sj = -c 1 sj-1 - c 2 sj-2 -. . . - cl sj-l mod p – nonlinear feedback shift registers (still insecure) filters, stop-and-go generators • Cryptographical Random Number Generators – block cipher based (good statistics, secure, complex) – based on public key cryptography (equally secure) Klaus Köhler Cryptography

Linear Congruential Method si=c·si-1+d mod p, p prime • c=1: si=si-1+d mod p linear sequence predictable • d=0: si=c·si-1 mod p, s 0 0, c primitive, i. e. c : ={1, c, c 2, c 3, . . . , cp-2}= p*={1, 2, . . . , p-1} {s 0, s 1=c·s 0, s 2= c 2·s 0, . . . , sp-2= cp-2·s 0} = c ·s 0 = p* Examples: p=23 -1=7, c=2 c : ={1, 2, 4} not primitive c=5 c : ={1, 5, 4, 6, 2, 3} primitive (1 of ( (p))=2) s 0=2: c ·s 0 = {2, 3, 1, 5, 4, 6} = p* random p=231 -1 is prime, c=75 is primitive: used in IBM 360 Klaus Köhler Cryptography

Linear Feedback Shift Registers sj = -c 1 sj-1 - c 2 sj-2 -. . . - cl sj-l mod p, p prime • maximum period pl-1 c(x) primitiv, i. e. the multiplicative group of the Galois field p[x]/c(x) p[x] is generated by the coset of x • Example: p=2, c(x) = x 3 + x 2 + 1 is irreducible and primitive: x = {x, x 2, x 3=x 2+1, x 4=x 2+x+1, x 5=x+1, x 6=x 2+x, x 7=1}, generated sequence with period 23 -1=7: 1011100. . . • can be broken, if a subsequence of 2·l elements is known Klaus Köhler Cryptography

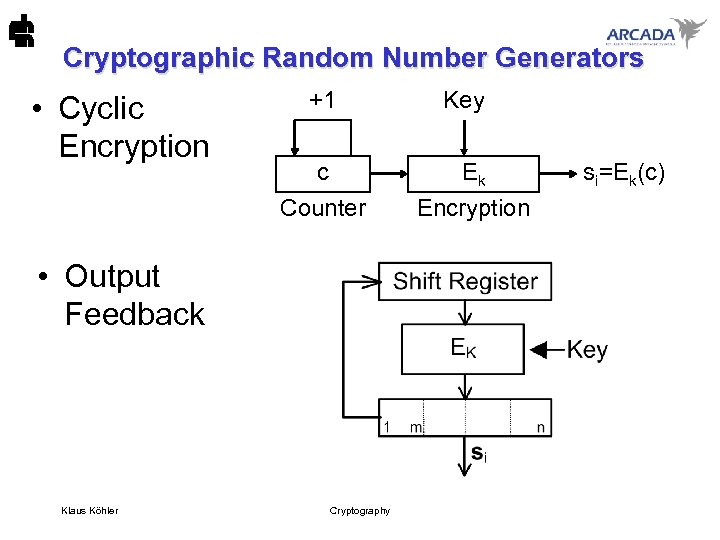Cryptographic Random Number Generators • Cyclic Encryption +1 c Counter • Output Feedback Klaus Köhler Cryptography Key Ek Encryption si=Ek(c)

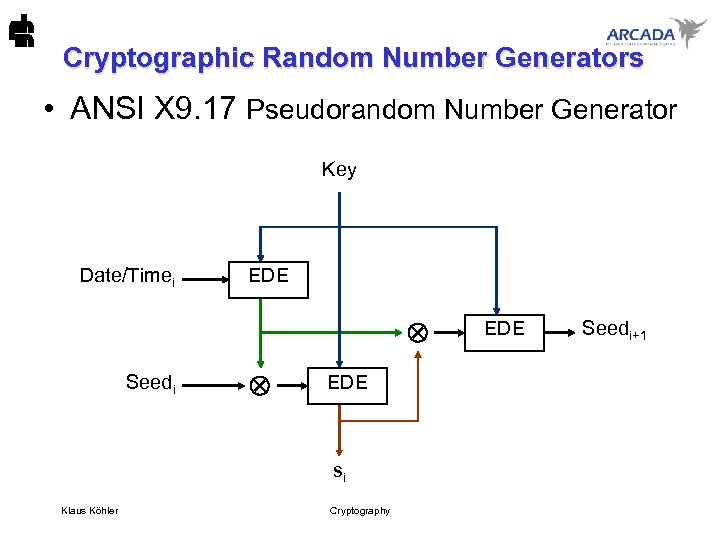Cryptographic Random Number Generators • ANSI X 9. 17 Pseudorandom Number Generator Key Date/Timei EDE Seedi EDE si Klaus Köhler Cryptography EDE Seedi+1

Prime Number Generators o n/ln(n) prime numbers < n P(n is prime) ln(n) for a randomly chosen n only few tries necessary to catch a prime o Algorithm: choose a random number p of appropriate size test if p is prime repeat until p is prime Prime number tests o deterministic: assure primality, but time consuming, e. g. factoring o probabilistic: assure primality with a given probability (almost 1) o Algorithm: repeat n times (certainty 1 -2 n) o (probabilistic) test with a random witness if p may be prime return false if p is definitely not prime return true p prime: single test (witness) never fails (never signals "not prime") p composite: witness signals "not prime" with probability > 0. 5 Klaus Köhler Cryptography

Prime Number Tests o Lehmann p prime p is a field (p) = | p*| = p-1 ap-1 mod p = 1 for a 0 p composite ap-1 mod p need not be 1 for a 0, but P(a | ap-1 mod p 1) 0. 5 for p composite l Algorithm: choose a random number a < p return ap-1 mod p == 1 o Rabin-Miller p odd prime p-1 can easily be decomposed: p-1 = 2 b·m 1 = ap-1 mod p = ap-1 = (am)2 b = (···(am)2)···)2 mod p (am)2 i mod p = 1 p may be prime Use Lehmanns test, but avoid to calculate ap-1 if already (am)2 i mod p = 1 l Algorithm Klaus Köhler choose a random number a < p z = am; i = 0 while z 1 and i < b (invariant: ap-1 = z 2 b-i) z = z 2; i = i+1 yes z 1 no p is not prime p may be prime Cryptography

Hash Functions o Requirements Compression map a arbitrary-length input m on a fixed-length output h = H(m) that should depend on every input bit (typical length: 128 or 160 bit) o Equal distribution of the hash values o Avalanche effect One bit change in the message swaps half of the hash value bits (on average). o One-way o Given m, it is easy to compute h = H(m). o Given h, it is hard to compute an m' such that H(m') = h o o Collision-resistant (stronger requirement than one-way) o o It is hard to find two random messages m and m' such that H(m) = H(M'). Examples MD 5 (128 bit) o SHA-1 (160 bit) o Klaus Köhler Cryptography

Hash Functions, cont. o Compression principle Cut message M into fixed-length blocks Mi o Apply a one-way function o hi+1 = f(Mi, hi) Mi hi one-way function f hi+1 with an initial value h 0 that contains the message length (MD strengthening) n times. The last hi is the hash value of the entire message. o Hypothesis (not proved) The (iterated) variable-length hash function is secure if the fixed-length one-way function f is secure o One-way function several rounds with o non-linear operations o Klaus Köhler Cryptography

Message Authentication Code (MAC) o Key-dependent one-way hash function often in combination with symmetric encryption o Message Authentication of files between users o Proof that a file has not been changed, for example by a virus o o Example Klaus Köhler Cryptography