Cryptography in the Bounded-Quantum-Storage Model Christian Schaffner BRICS

Cryptography in the Bounded-Quantum-Storage Model Christian Schaffner BRICS, University of Aarhus Ph. D Defense Friday, April 27 th 2007

Agenda p Motivation, p Classical Bit Commitment (BC) Protocol for BC p Quantum Effects p Quantum Protocol for BC p Conclusion 2 / 38

Alice & Bob *!¤ Alice Bob 3 / 38

Divorce Problems *!¤ Alice who gets the house? Bob 4 / 38

Coin-Flipping over the Telephone [Blum 82] Alice It’s tails, I get the house! Bad Bob 5 / 38

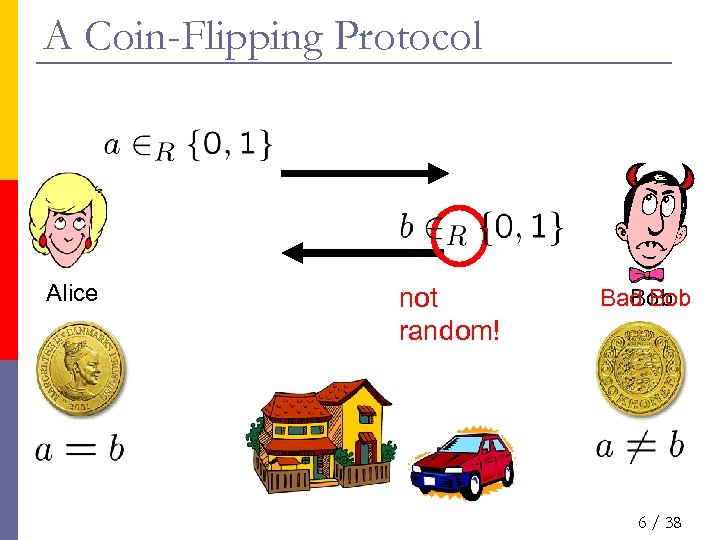
A Coin-Flipping Protocol Alice not random! Bad Bob 6 / 38

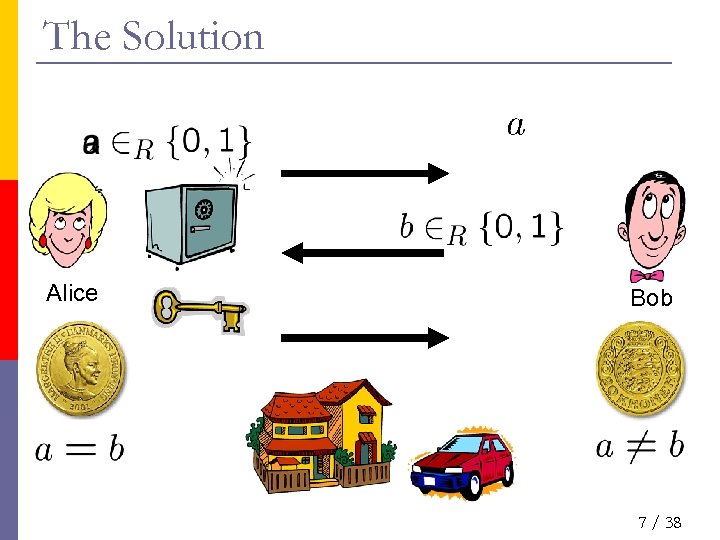
The Solution Alice Bob 7 / 38

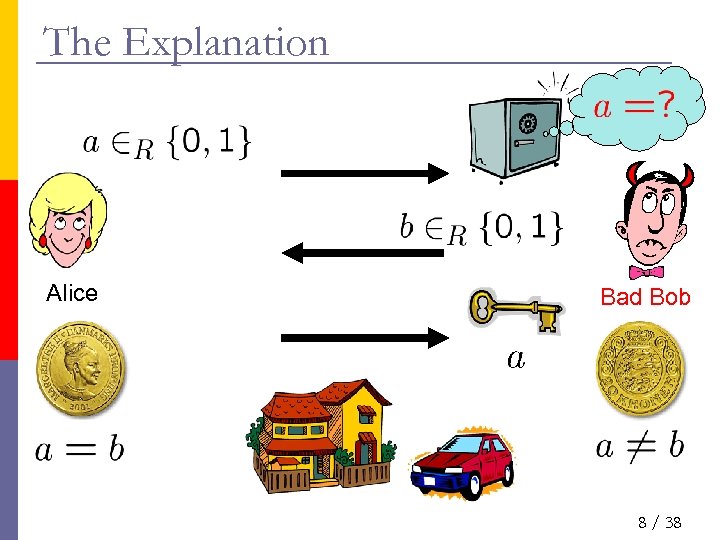
The Explanation Alice Bad Bob 8 / 38

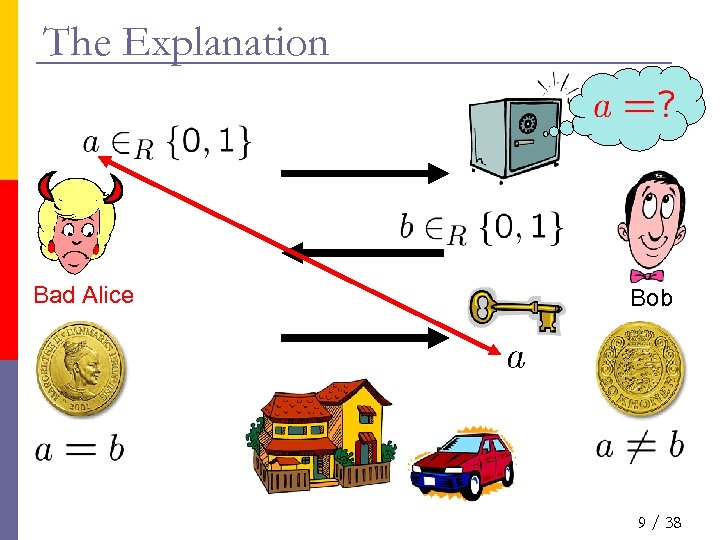
The Explanation Bad Alice Bob 9 / 38

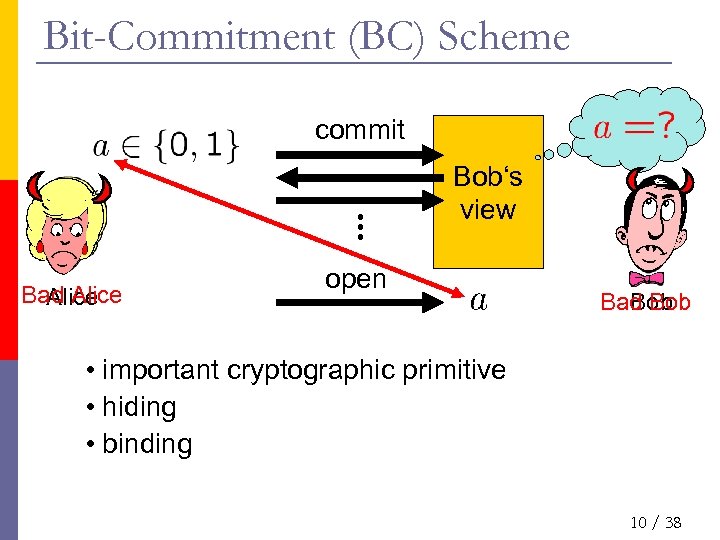
Bit-Commitment (BC) Scheme commit Bob‘s view Bad Alice open Bad Bob • important cryptographic primitive • hiding • binding 10 / 38

Agenda üMotivation, Bit Commitment (BC) p Classical Protocol for BC p Quantum Effects p Quantum Protocol for BC p Conclusion 11 / 38

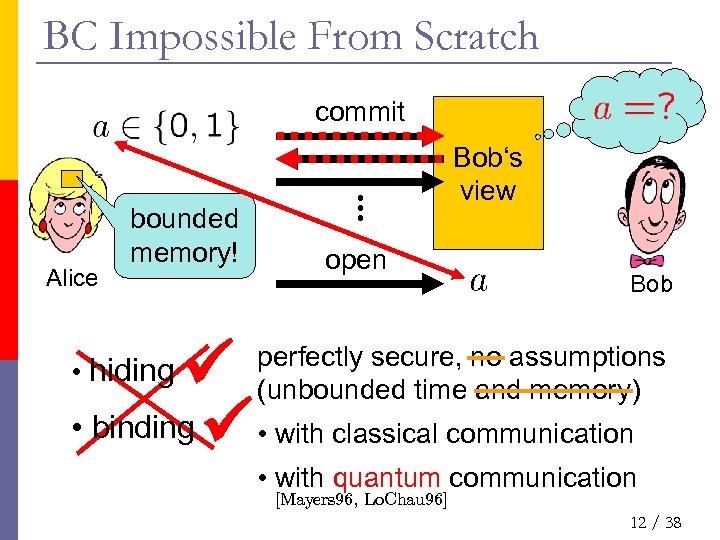
BC Impossible From Scratch commit Alice bounded memory! Bob‘s view open Bob • binding • with classical communication • hiding perfectly secure, no assumptions (unbounded time and memory) • with quantum communication [Mayers 96, Lo. Chau 96] 12 / 38

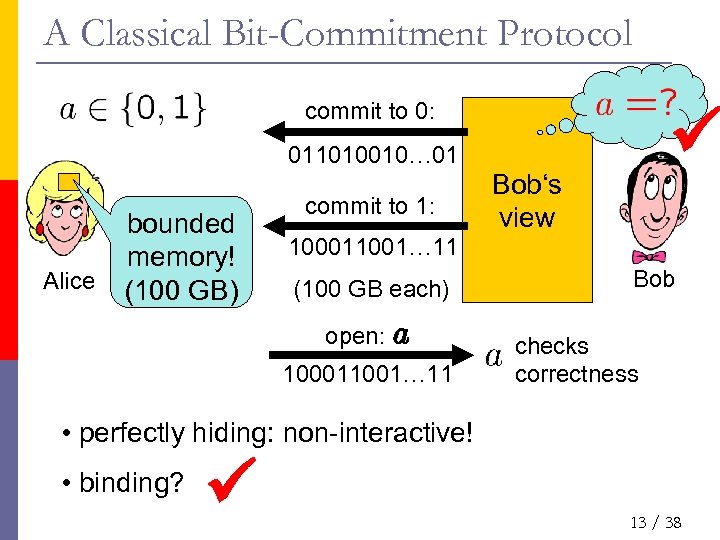
A Classical Bit-Commitment Protocol commit to 0: 011010010… 01 Alice bounded memory! (100 GB) commit to 1: Bob‘s view 100011001… 11 (100 GB each) open: a 100011001… 11 Bob checks correctness • perfectly hiding: non-interactive! • binding? 13 / 38

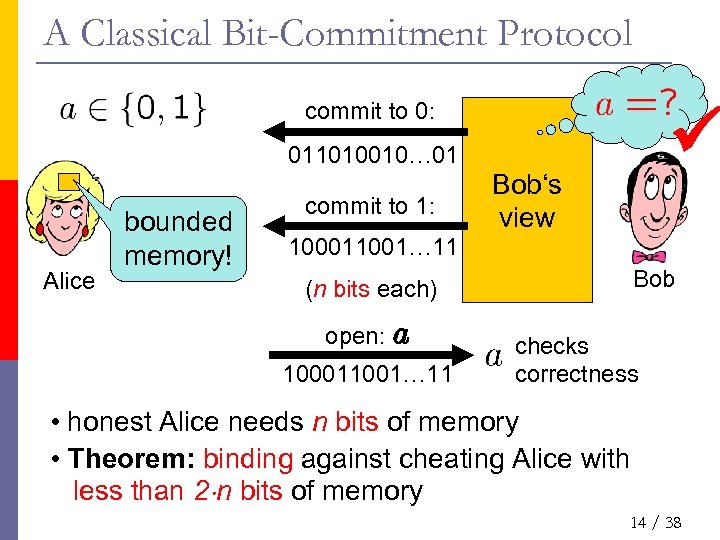
A Classical Bit-Commitment Protocol commit to 0: 011010010… 01 Alice bounded memory! commit to 1: Bob‘s view 100011001… 11 Bob (n bits each) open: a 100011001… 11 checks correctness • honest Alice needs n bits of memory • Theorem: binding against cheating Alice with less than 2¢n bits of memory 14 / 38

A Classical Bit-Commitment Protocol commit to 0: • unrealistic assumption: 011010010… 01 difficult to store classical bits Bob‘s Alice bounded memory! commit to 1: view • 100011001… 11 honest player’s only twice the memory is required to break Bob (n bits each) protocol open: a 100011001… 11 checks correctness • honest Alice needs n bits of memory • Theorem: binding against cheating Alice with less than 2¢n bits of memory 15 / 38

A Quantum Bit-Commitment Protocol Alice bounded quantum bounded memory! commit to 0: n quantum bits 011010010… 01 commit to 1: Bob‘s view 100011001… 11 Bob (n bits each) open: a 100011001… 11 checks correctness • honest Alice needs n bits of memory • Theorem: binding against cheating Alice with less than 2¢n bits of memory 16 / 38

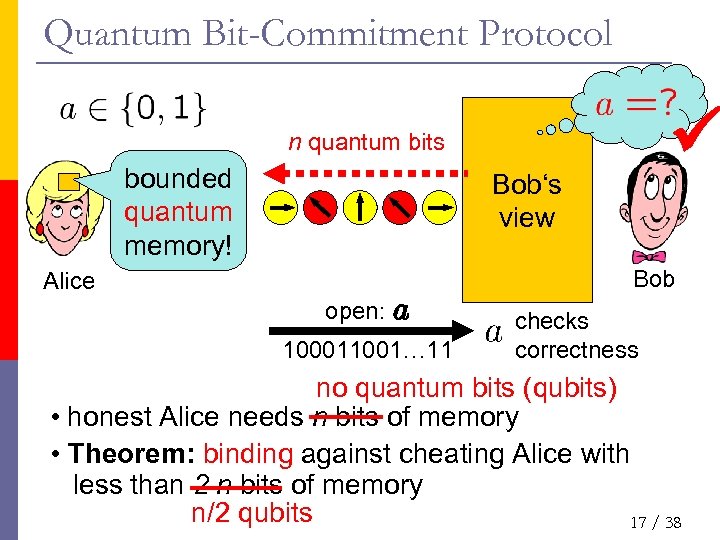
Quantum Bit-Commitment Protocol n quantum bits bounded quantum memory! Bob‘s view Bob Alice open: a 100011001… 11 checks correctness no quantum bits (qubits) • honest Alice needs n bits of memory • Theorem: binding against cheating Alice with less than 2¢n bits of memory n/2 qubits 17 / 38

Agenda üMotivation, Bit Commitment (BC) üClassical Protocol for BC p Quantum Effects p Quantum Protocol for BC p Conclusion 18 / 38

Quantum Bit: Ce. g. Polarization of Light qubit as unit vector in 2 19 / 38

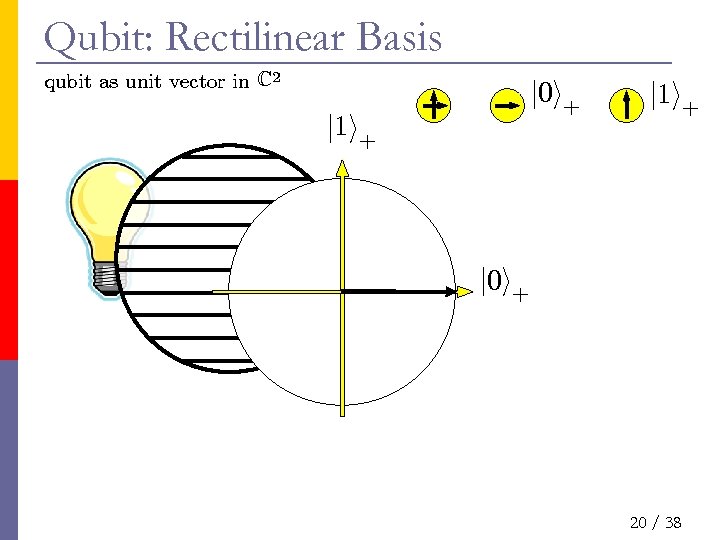
Qubit: Rectilinear Basis qubit as unit vector in C 2 j 0 i+ j 1 i+ j 0 i+ 20 / 38

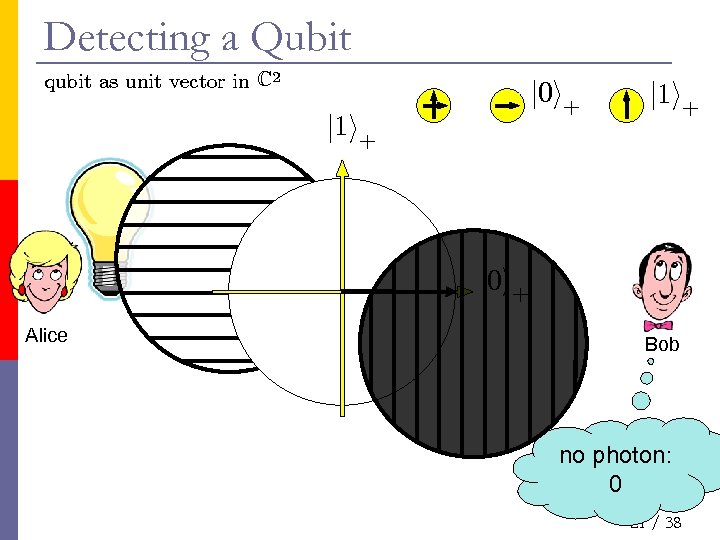
Detecting a Qubit qubit as unit vector in C 2 j 0 i+ j 1 i+ j 0 i+ Alice Bob no photon: 0 21 / 38

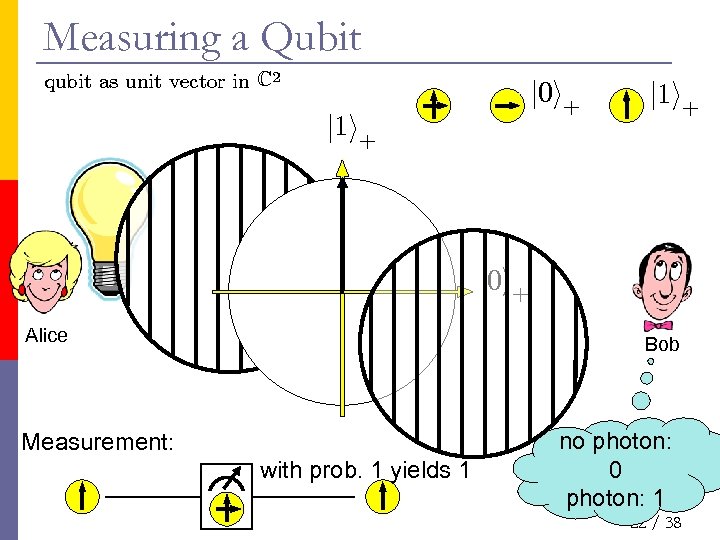
Measuring a Qubit qubit as unit vector in C 2 j 0 i+ j 1 i+ j 0 i+ Alice Bob Measurement: with prob. 1 yields 1 no photon: 0 photon: 1 22 / 38

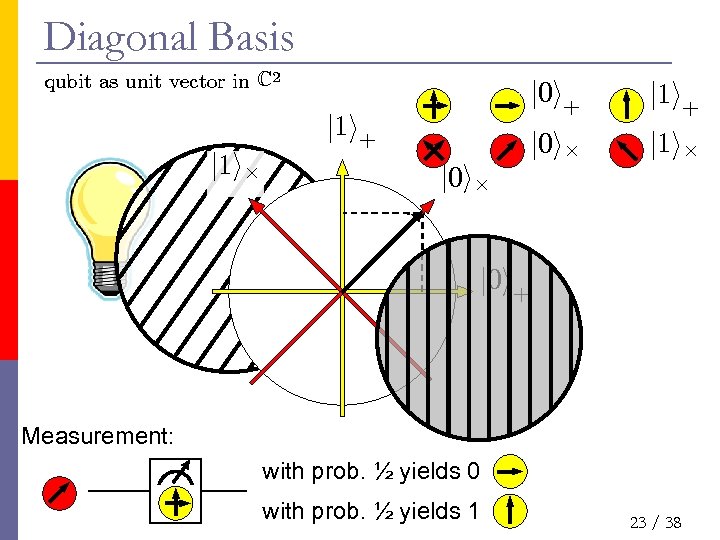
Diagonal Basis qubit as unit vector in C 2 j 0 i+ j 1 i£ j 0 i£ j 1 i+ j 0 i£ j 1 i£ j 0 i+ Measurement: with prob. ½ yields 0 with prob. ½ yields 1 23 / 38

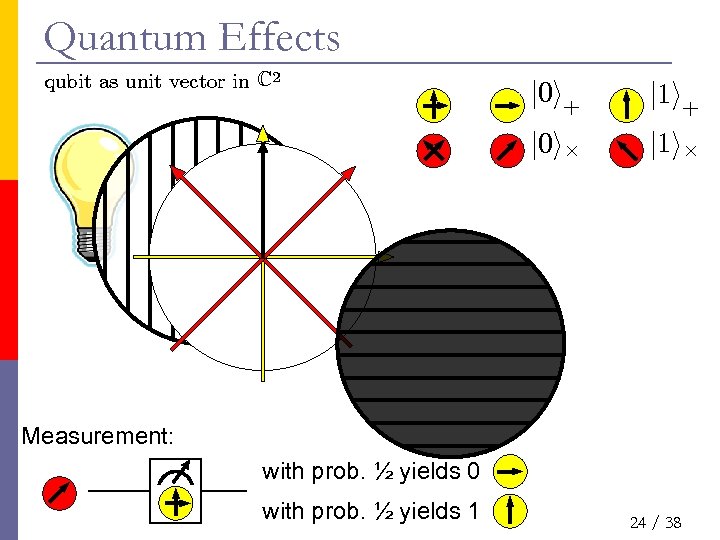
Quantum Effects qubit as unit vector in C 2 j 0 i+ j 1 i+ j 0 i£ j 1 i£ Measurement: with prob. ½ yields 0 with prob. ½ yields 1 24 / 38

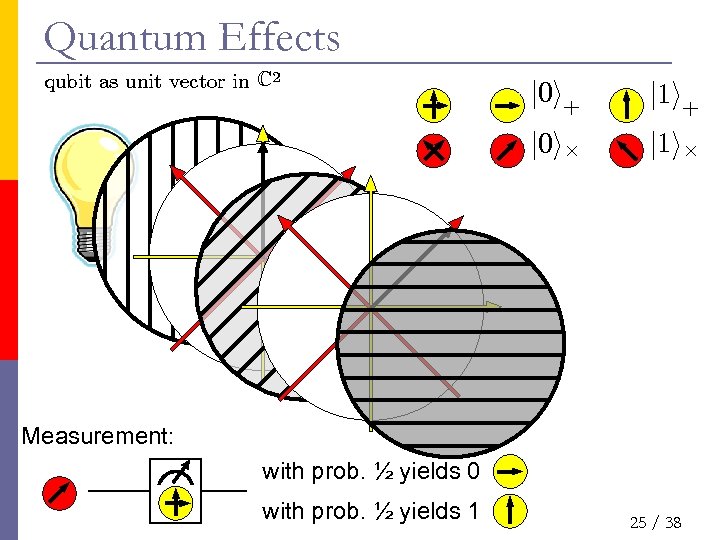
Quantum Effects qubit as unit vector in C 2 j 0 i+ j 1 i+ j 0 i£ j 1 i£ Measurement: with prob. ½ yields 0 with prob. ½ yields 1 25 / 38

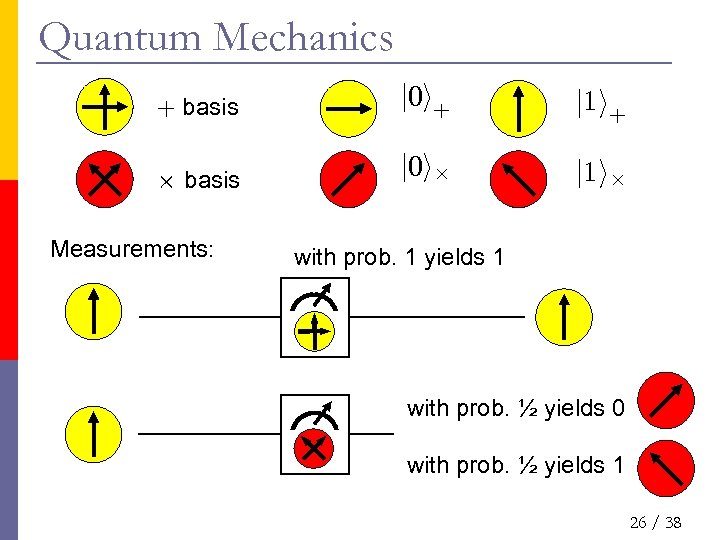
Quantum Mechanics + basis j 0 i+ j 1 i+ £ basis j 0 i£ j 1 i£ Measurements: with prob. 1 yields 1 with prob. ½ yields 0 with prob. ½ yields 1 26 / 38

Agenda üMotivation, Bit Commitment (BC) üClassical Protocol for BC üQuantum Effects p Quantum Protocol for BC p Conclusion 27 / 38

Quantum Bit-Commitment Protocol picks at random: n quantum bits 0 1 1 1 0 bounded quantum memory! 28 / 38

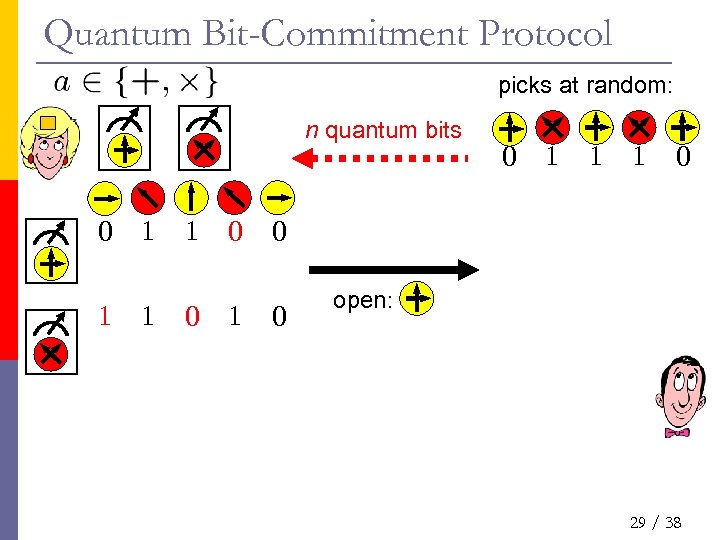
Quantum Bit-Commitment Protocol picks at random: n quantum bits 0 1 1 0 0 1 1 1 0 0 0 1 0 open: 29 / 38

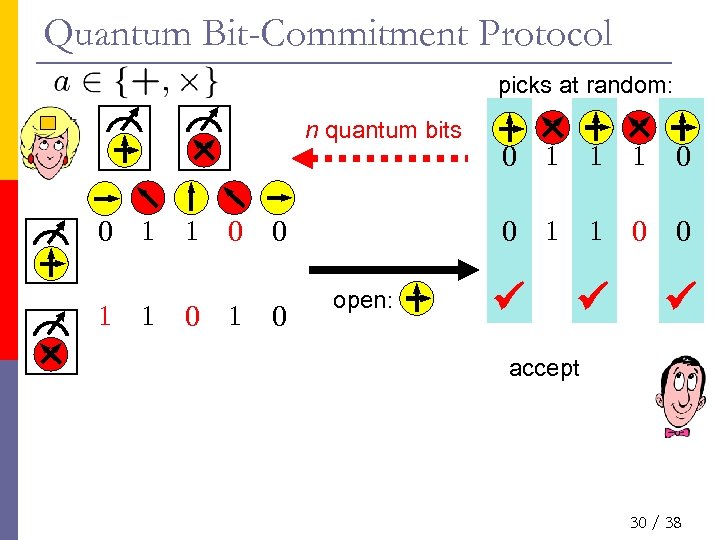
Quantum Bit-Commitment Protocol picks at random: n quantum bits 0 1 1 0 1 0 open: 1 1 1 0 0 0 1 1 0 0 accept 30 / 38

Quantum Bit-Commitment Protocol picks at random: n quantum bits 0 1 1 1 0 0 0 1 1 0 open: accept • measurement upon reception • honest players need no quantum memory 31 / 38

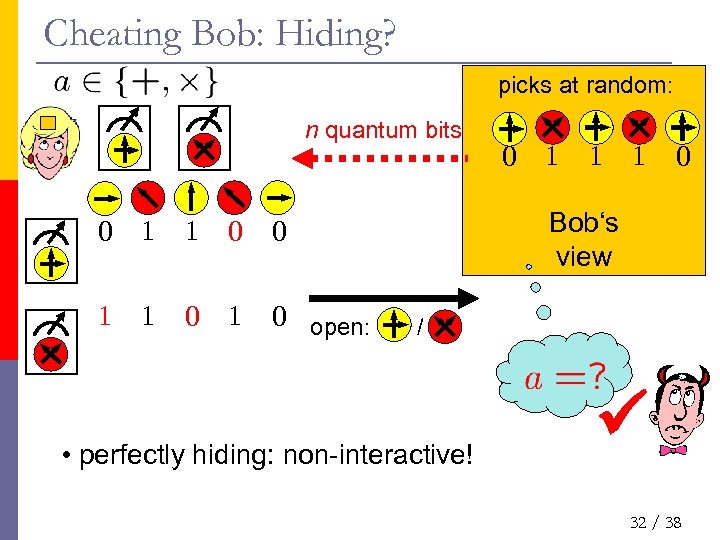
Cheating Bob: Hiding? picks at random: n quantum bits 0 1 1 1 0 open: 1 1 1 0 Bob‘s view 0 0 1 0 / • perfectly hiding: non-interactive! 32 / 38

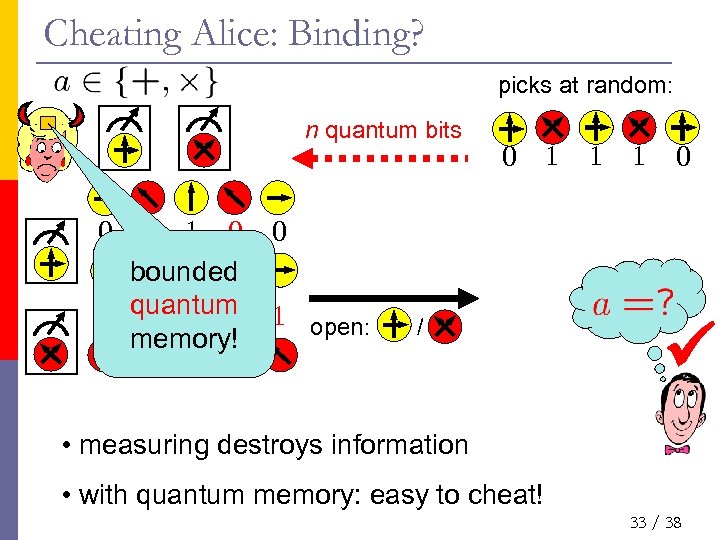
Cheating Alice: Binding? picks at random: n quantum bits 1 1 0 0 bounded 1 quantum 1 open: 0 1 0 memory! 0 1 1 1 0 0 / • measuring destroys information • with quantum memory: easy to cheat! 33 / 38

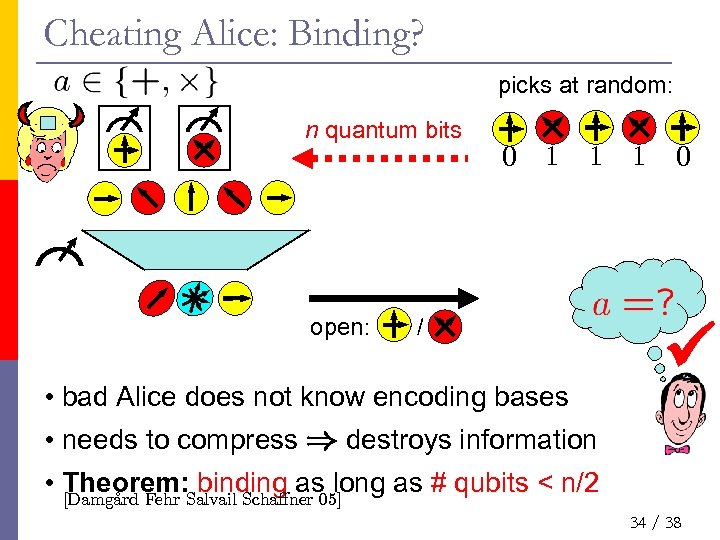
Cheating Alice: Binding? picks at random: n quantum bits open: 0 1 1 / • bad Alice does not know encoding bases 1 0 • needs to compress ) destroys information • Theorem: Salvail Scha®ner 05] binding as long as # qubits < n/2 ard [Damgº Fehr 34 / 38

Agenda üMotivation, Bit Commitment (BC) üClassical Protocol for BC üQuantum Effects üQuantum Protocol for BC p Conclusion 35 / 38

Summary • Motivation: § Coin-Flipping over Telephone § Bit Commitment (BC) • protocol for BC: perfectly hiding, binding for memory-bounded Alice • classical: unpractical assumptions • Bounded-Quantum-Storage Model: § showed quantum effects § BC: better parameters, practical! 36 / 38

QUSEP Project: Bob Alice 37 / 38

The End *!¤ bounded quantum memory! Alice Bob bounded quantum memory! 38 / 38