Cryptographic methods for privacy aware computing applications

Cryptographic methods for privacy aware computing: applications

Outline o o Review: three basic methods Two applications n n Distributed decision tree with horizontally partitioned data Distributed k-means with vertically partitioned data

Three basic methods o o o 1 -out-K Oblivious Transfer Random share Homomorphic encryption * Cost is the major concern

Two example protocols o The basic idea is n n Do not release original data Exchange intermediate result o Applying the three basic methods to securely combine them

Building decision trees over horizontally partitioned data o o o Horizontally partitioned data Entropy-based information gain Major ideas in the protocol

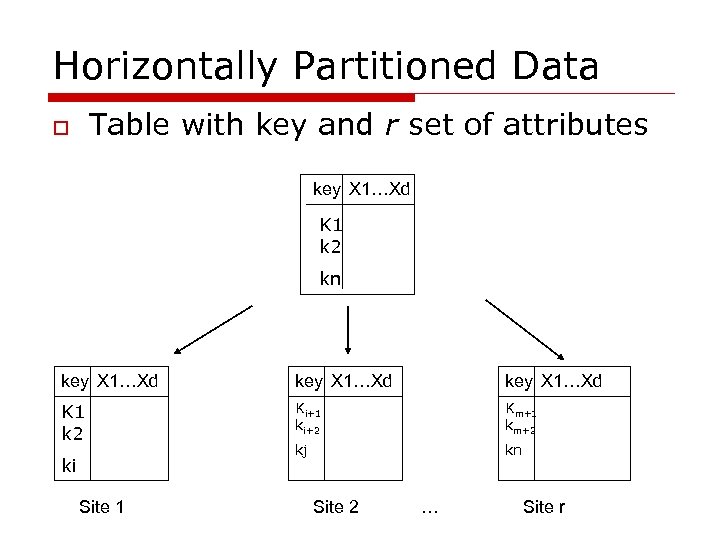Horizontally Partitioned Data Table with key and r set of attributes o key X 1…Xd K 1 k 2 kn key X 1…Xd K 1 k 2 Ki+1 ki+2 Km+1 km+2 kj kn ki Site 1 Site 2 … Site r

Review decision tree algorithm (ID 3 algorithm) o Find the cut that maximizes gain n n certain attribute Ai, sorted v 1…vn Certain value in the attribute o o Ai For categorical data we use Ai=vi For numerical data we use Ai

Key points o Calculating entropy Ai label v 1 v 2 l 1 l 2 vn ln cut The key is calculating x log x, where x is the sum of values from the two parties P 1 and P 2 , i. e. , x 1 and x 2, respectively -decomposed to several steps -Each step each party knows only a random share of the result

steps Step 1: compute shares for w 1 +w 2= (x 1+x 2)ln(x 1+x 2) * a major protocol is used to compute ln(x 1+x 2) Step 2: for a condition (Ai, vi), find the random shares for E(S), E(S 1) and E(S 2) respectively. Step 3: repeat step 1&2 to all possible (Ai, vi) pairs Step 4: a circuit gate to determine which (Ai, vi) pair results in maximum gain. x 1 w 11 w 21 x 2 w 12 w 22 … … (Ai, vi) with Maximum gain

2. K-means over vertically partitioned data o o o Vertically partitioned data Normal K-means algorithm Applying secure sum and secure comparison among multi-sites in the secure distributed algorithm

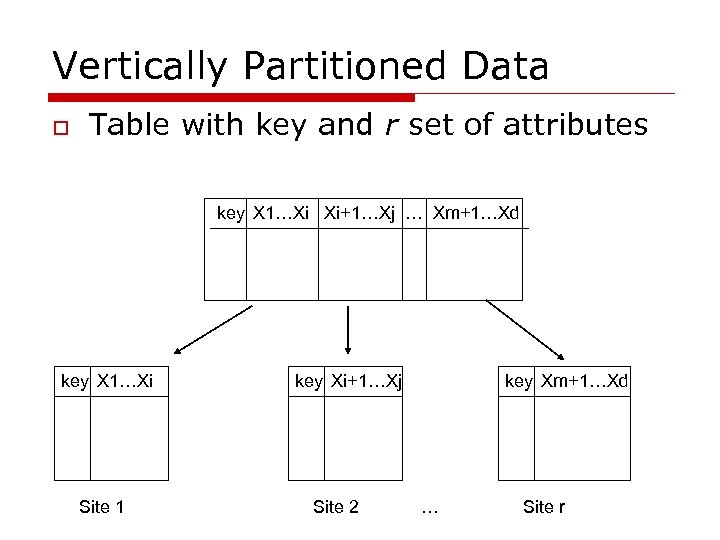Vertically Partitioned Data o Table with key and r set of attributes key X 1…Xi Xi+1…Xj … Xm+1…Xd key X 1…Xi Site 1 key Xi+1…Xj Site 2 key Xm+1…Xd … Site r

Motivation o Naïve approach: send all data to a trusted site and do k-mean clustering there n n o Costly Trusted third party? Preferable: distributed privacy preserving k-means

Basic K-means algorithm o 4 main steps: step 1. Randomly select k initial cluster centers (k means) repeat step 2. Assign any point i to its closest cluster center step 3. Recalculate the k means with the new point assignment Until step 4. the k means do not change

Distributed k-means o Why k-means can be done over vertically partitioned data n n n All of the 4 steps are decomposable ! The most costly part (step 2 and 3) can be done locally We will focus on the step 2 (Assign any point i to its closest cluster center)

step 1 o All sites share the index of the initial random k records as the centroids µ 11 … µ 1 i+1 … µ 1 j µ 1 m …µ 1 d µk µk 1 … µki+1 … µkj µkm … µkd Site 1 Site 2 … Site r

Step 2: o Assign any point x to its closest cluster center 1. Calculate distance of point X (X 1, X 2, … Xd) to each cluster center µk -- each distance calculation is decomposable! d 2 = [(X 1 - µk 1)2 +… (Xi- µki)2] + [(Xi+1 - µki+1)2 +… (Xj- µkj)2] + … Partial distances: d 1 Site 1 + d 2 +… site 2 For each X, each site has a k-element vector that is the result for the partial distance to the k centroids, notated as Xi 2. Compare the k full distances to find the minimum one

Privacy concerns for step 2 o Some concerns: n n o Partial distances d 1, d 2 … may breach privacy (the Xi and µki ) – need to hide it distance of a point to each cluster may breach privacy – need hide it Basic ideas to ensure security n n Disguise the partial distances Compare distances so that only the comparison result is learned Permute the order of clusters so the real meaning of the comparison results is unknown. Need 3 non-colluding sites (P 1, P 2, Pr)

Secure Computing of Step 2 o Stage 1: prepare for secure sum of partial distances n n p 1 generate V 1+V 2 + …Vr = 0, Vi is random k-element vector, used to hide the partial distance for site i Use “Homomorphic encryption” to do randomization: Ei(Xi)Ei(Vi) = Ei(Xi+Vi) o Stage 2: calculate secure sum for r-1 parties n n P 1, P 3, P 4… Pr-1 send their perturbed and permuted partial distances to Pr Pr sums up the r-1 partial distances (including its own part)

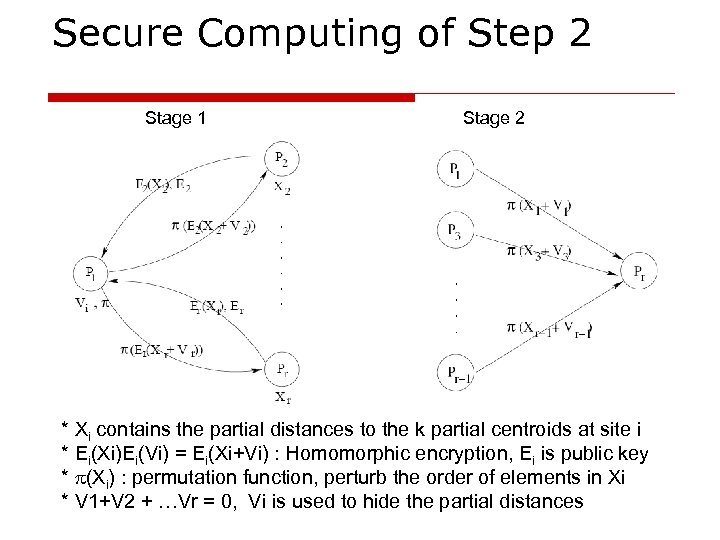Secure Computing of Step 2 Stage 1 Stage 2 * Xi contains the partial distances to the k partial centroids at site i * Ei(Xi)Ei(Vi) = Ei(Xi+Vi) : Homomorphic encryption, Ei is public key * (Xi) : permutation function, perturb the order of elements in Xi * V 1+V 2 + …Vr = 0, Vi is used to hide the partial distances

o Stage 3: secure_add_and_compare to find the minimum distance n Involves only Pr and P 2 K-1 comparisons: n o Use a standard Secure Multiparty Computation protocol to find the result Stage 4: n n n the index of minimum distance (permuted cluster id) is sent back to P 1 knows the permutation function thus knows the original cluster id. P 1 broadcasts the cluster id to all parties.

Step 3: can also be done locally o Update partial means µi locally according to the new cluster assignments. Cluster labels Cluster 2 X 11 … X 1 i+1 … X 1 j X 1 m …X 1 d Cluster k X 21 … X 2 i Cluster k Xn 1 … Xni+1 … Xnj Xnm … Xnd Site 1 Site 2 … Site r

Extra communication cost o O(nrk) n n n o n : # of records r: # of parties k: # of means Also depends on # of iterations

Conclusion o o It is appealing to have cryptographic privacy preserving protocols The cost is the major concern n It can be reduced using novel algorithms