93cb07978a463b0c293669f5164ebca0.ppt
- Количество слайдов: 95

Creating a science base to support new directions in computer science John Hopcroft Cornell University Ithaca, New York CAS May 24, 2010

Time of change § The information age is a fundamental revolution that is changing all aspects of our lives. § Those individuals and nations who recognize this change and position themselves for the future will benefit enormously. CAS May 24, 2010

Drivers of change § § Merging of computing and communications Data available in digital form Networked devices and sensors Computers becoming ubiquitous CAS May 24, 2010

Internet search engines are changing n When was Einstein born? Einstein was born at Ulm, in Wurttemberg, Germany, on March 14, 1879. List of relevant web pages CAS May 24, 2010

CAS May 24, 2010

Internet queries will be different § § § Which car should I buy? What are the key papers in Theoretical Computer Science? Construct an annotated bibliography on graph theory. Where should I go to college? How did the field of CS develop? CAS May 24, 2010

Which car should I buy? n Search engine response: Which criteria below are important to you? § § § Fuel economy Crash safety Reliability Performance Etc. CAS May 24, 2010
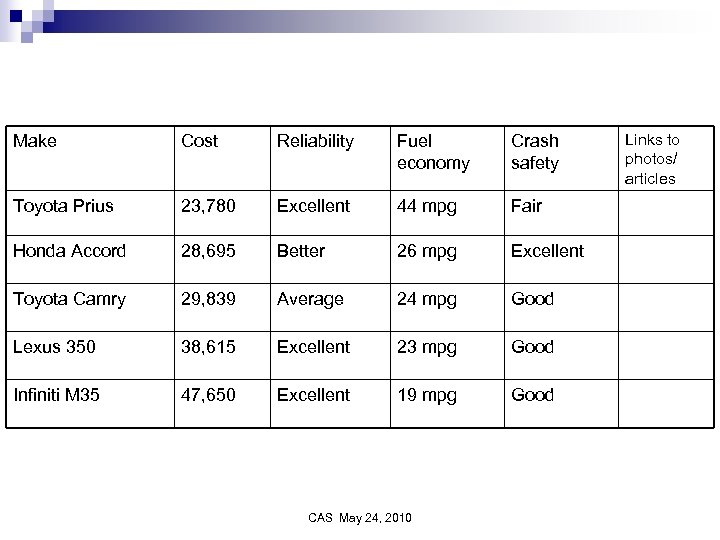
Make Cost Reliability Fuel economy Crash safety Toyota Prius 23, 780 Excellent 44 mpg Fair Honda Accord 28, 695 Better 26 mpg Excellent Toyota Camry 29, 839 Average 24 mpg Good Lexus 350 38, 615 Excellent 23 mpg Good Infiniti M 35 47, 650 Excellent 19 mpg Good CAS May 24, 2010 Links to photos/ articles

CAS May 24, 2010

2010 Toyota Camry - Auto Shows Toyota sneaks the new Camry into the Detroit Auto Show. Usually, redesigns and facelifts of cars as significant as the hotselling Toyota Camry are accompanied by a commensurate amount of fanfare. So we were surprised when, right about the time that we were walking by the Toyota booth, a chirp of our Blackberries brought us the press release announcing that the facelifted 2010 Toyota Camry and Camry Hybrid mid-sized sedans were appearing at the 2009 NAIAS in Detroit. We’d have hardly noticed if they hadn’t told us—the headlamps are slightly larger, the grilles on the gas and hybrid models go their own way, and taillamps become primarily LED. Wheels are also new, but overall, the resemblance to the Corolla is downright uncanny. Let’s hear it for brand consistency! Four-cylinder Camrys get Toyota’s new 2. 5 -liter four-cylinder with a boost in horsepower to 169 for LE and XLE grades, 179 for the Camry SE, all of which are available with six-speed manual or automatic transmissions. Camry V-6 and Hybrid models are relatively unchanged under the skin. Inside, changes are likewise minimal: the options list has been shaken up a bit, but the only visible change on any Camry model is the Hybrid’s new gauge cluster and softer seat fabrics. Pricing will be announced closer to the time it goes on sale this March. CAS May 24, 2010 Toyota Camry ·› Overview ·› Specifications ·› Price with Options ·› Get a Free Quote News & Reviews · 2010 Toyota Camry - Auto Shows Top Competitors ·Chevrolet Malibu ·Ford Fusion ·Honda Accord sedan

Which are the key papers in Theoretical Computer Science? n n n n Hartmanis and Stearns, “On the computational complexity of algorithms” Blum, “A machine-independent theory of the complexity of recursive functions” Cook, “The complexity of theorem proving procedures” Karp, “Reducibility among combinatorial problems” Garey and Johnson, “Computers and Intractability: A Guide to the Theory of NP-Completeness” Yao, “Theory and Applications of Trapdoor Functions” Shafi Goldwasser, Silvio Micali, Charles Rackoff , “The Knowledge Complexity of Interactive Proof Systems” Sanjeev Arora, Carsten Lund, Rajeev Motwani, Madhu Sudan, and Mario Szegedy, “Proof Verification and the Hardness of Approximation Problems” CAS May 24, 2010
CAS May 24, 2010
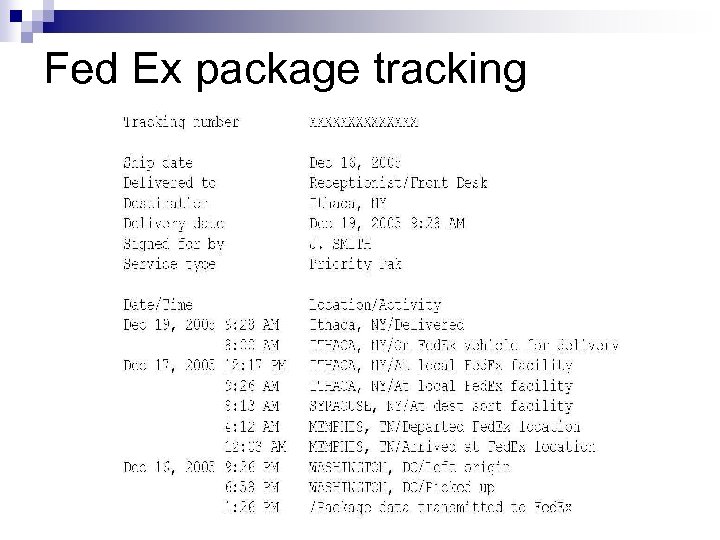
Fed Ex package tracking CAS May 24, 2010
CAS May 24, 2010
CAS May 24, 2010

CAS May 24, 2010
CAS May 24, 2010
CAS May 24, 2010
Pan Map Zoom Out Zoom In Zoom Map Click: Regional Radar Show Severe Total Precipitation Storm Tracks Animate Map NEXRAD Radar Binghamton, Base Reflectivity 0. 50 Degree Elevation Range 124 NMI — » A d v a n c e d R a d a r Map of All US Radar Sites T y p e s C L I C CAS May 24, 2010
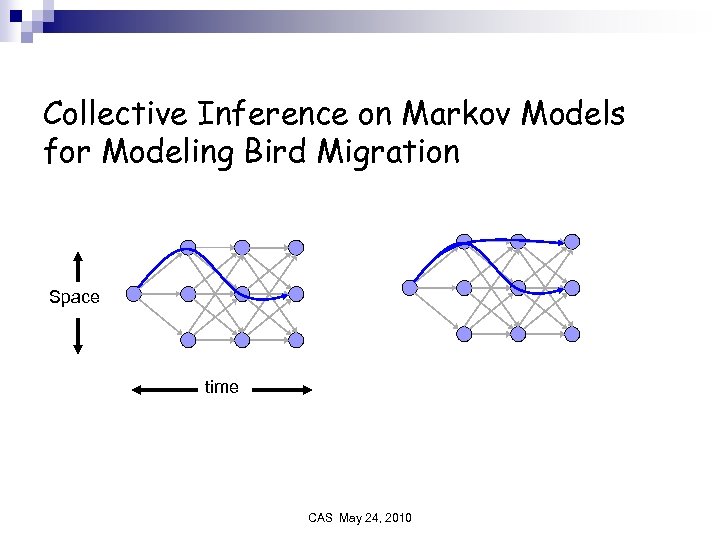
Collective Inference on Markov Models for Modeling Bird Migration Space time CAS May 24, 2010
Daniel Sheldon, M. A. Saleh Elmohamed, Dexter Kozen CAS May 24, 2010

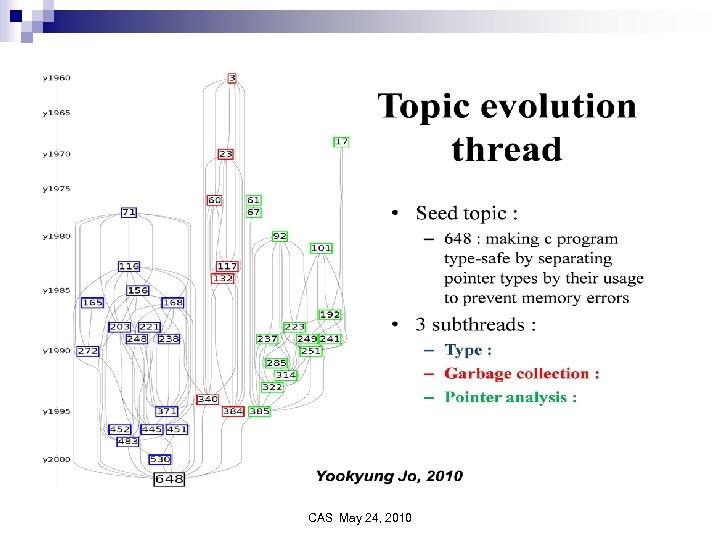
Science base to support activities Track flow of ideas in scientific literature n Track evolution of communities in social networks n Extract information from unstructured data sources. n CAS May 24, 2010

Tracking the flow of ideas in scientific literature Yookyung Jo CAS May 24, 2010
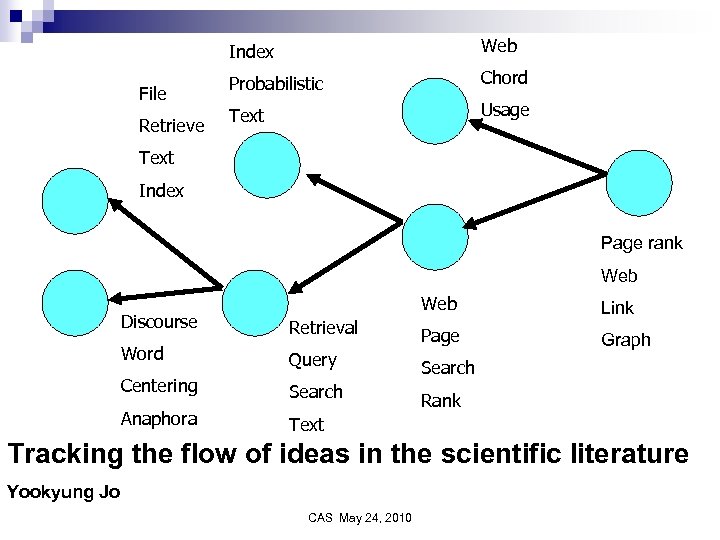
Index File Retrieve Web Probabilistic Chord Text Usage Text Index Page rank Web Link Graph Discourse Retrieval Word Page Query Centering Search Anaphora Rank Text Tracking the flow of ideas in the scientific literature Yookyung Jo CAS May 24, 2010

Original papers CAS May 24, 2010

Original papers cleaned up CAS May 24, 2010

Referenced papers CAS May 24, 2010
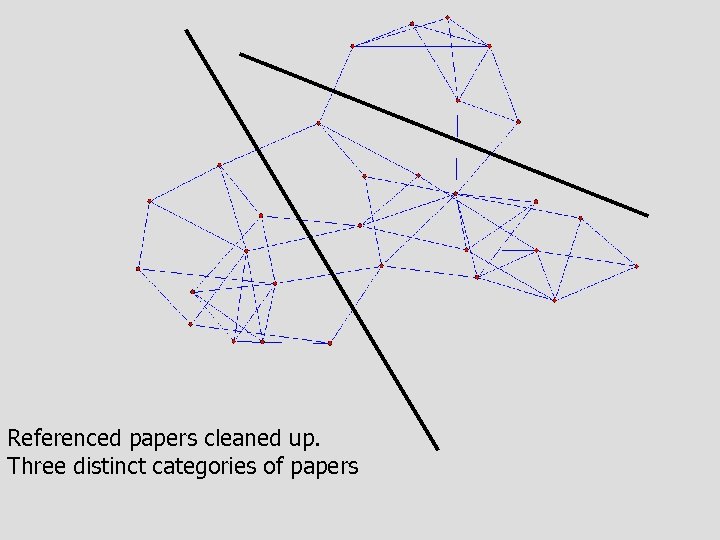
Referenced papers cleaned up. Three distinct categories of papers CAS May 24, 2010
CAS May 24, 2010

Tracking communities in social networks Liaoruo Wang CAS May 24, 2010

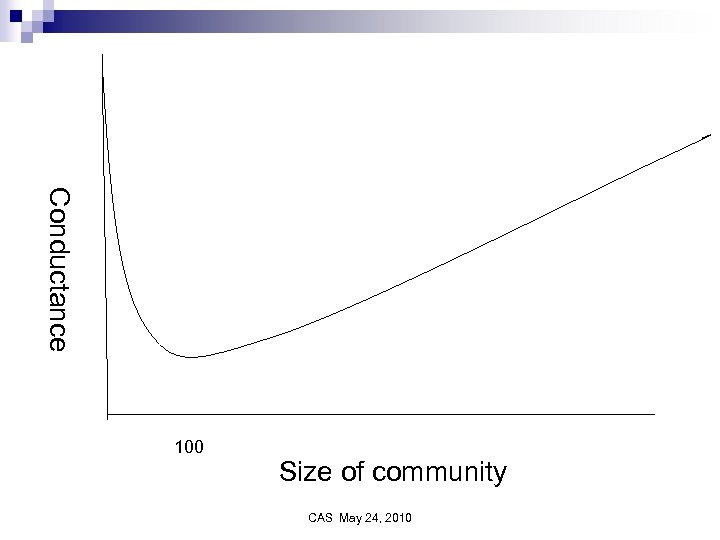
“Statistical Properties of Community Structure in Large Social and Information Networks”, Jure Leskovec; Kevin Lang; Anirban Dasgupta; Michael Mahoney n Studied over 70 large sparse real-world networks. n Best communities approximately size 100 to 150. CAS May 24, 2010

Our most striking finding is that in nearly every network dataset we examined, we observe tight but almost trivial communities at very small scales, and at larger size scales, the best possible communities gradually "blend in" with the rest of the network and thus become less "community-like. " CAS May 24, 2010
Conductance 100 Size of community CAS May 24, 2010

Giant component CAS May 24, 2010
Whisker: A component with v vertices connected by edges CAS May 24, 2010
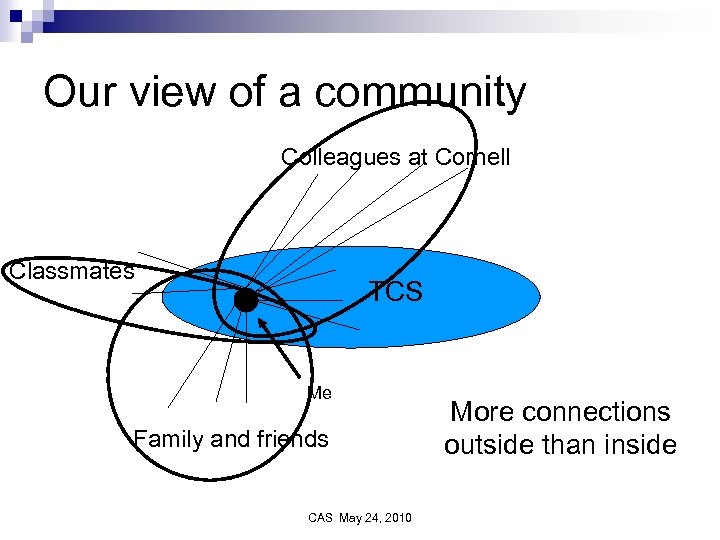
Our view of a community Colleagues at Cornell Classmates TCS Me Family and friends CAS May 24, 2010 More connections outside than inside

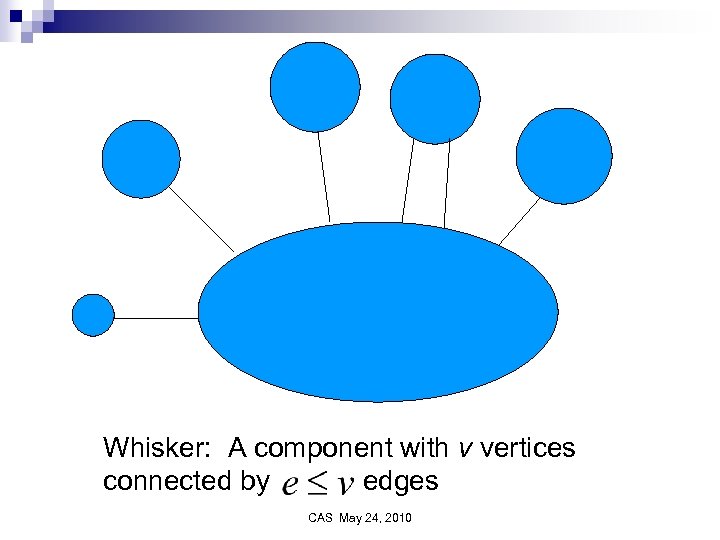
Core Should we remove all whiskers and search for communities in core? CAS May 24, 2010

Should we remove whiskers? Does there exist a core in social networks? Yes n Experimentally it appears at p=1/n in G(n, p) model n Is the core unique? Yes and No n In G(n, p) model should we require that a whisker have only a finite number of edges connecting it to the core? n Laura Wang CAS May 24, 2010

Algorithms How do you find the core? n Are there communities in the core of social networks? n CAS May 24, 2010

How do we find whiskers? NP-complete if graph has a whisker n There exists graphs with whiskers for which neither the union of two whiskers nor the intersection of two whiskers is a whisker n CAS May 24, 2010
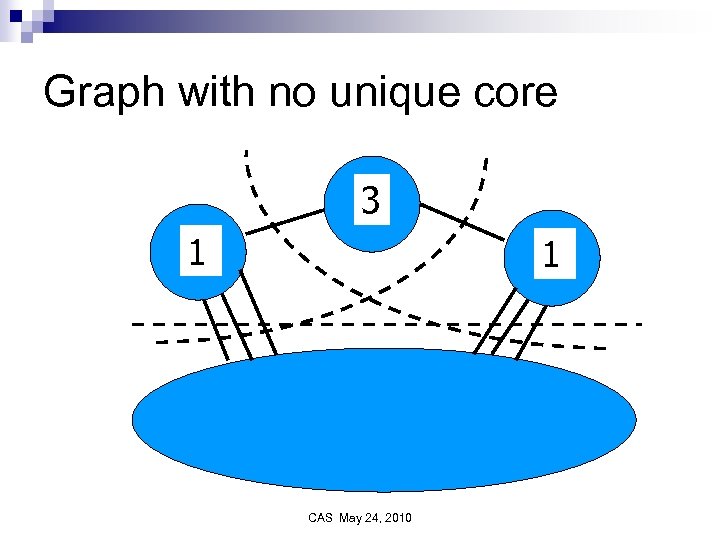
Graph with no unique core 3 1 1 CAS May 24, 2010

Graph with no unique core 1 CAS May 24, 2010

n. What is a community? n. How do you find them? CAS May 24, 2010

Communities § § Conductance Can we compress graph? § § Rosvall and Bergstrom, “An informatiotheoretic framework for resolving community structure in complex networks” Hypothesis testing § Yookyung Jo CAS May 24, 2010
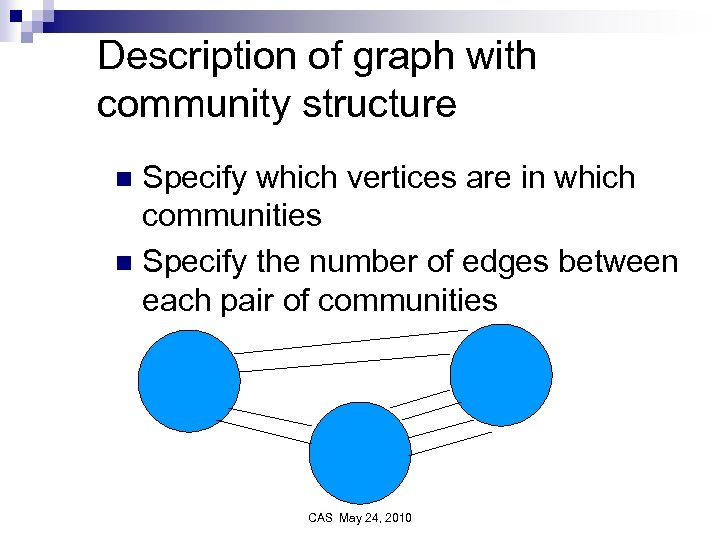
Description of graph with community structure Specify which vertices are in which communities n Specify the number of edges between each pair of communities n CAS May 24, 2010

Information necessary to specify graph given community structure n n n m=number of communities ni=number of vertices in ith community lij number of edges between ith and jth communities n CAS May 24, 2010

Description of graph consists of description of community structure plus specification of graph given structure. n Specify community for each edge and the number of edges between each community n n Can this method be used to specify more complex community structure where communities overlap? CAS May 24, 2010

Hypothesis testing Null hypothesis: All edges generated with some probability p 0 n Hypothesis: Edges in communities generated with probability p 1, other edges with probability p 0. n CAS May 24, 2010

Massively overlapping communities Are there a small number of massively overlapping communities that share a common core? n Are there massively overlapping communities in which one can move from one community to a totally disjoint community? n CAS May 24, 2010
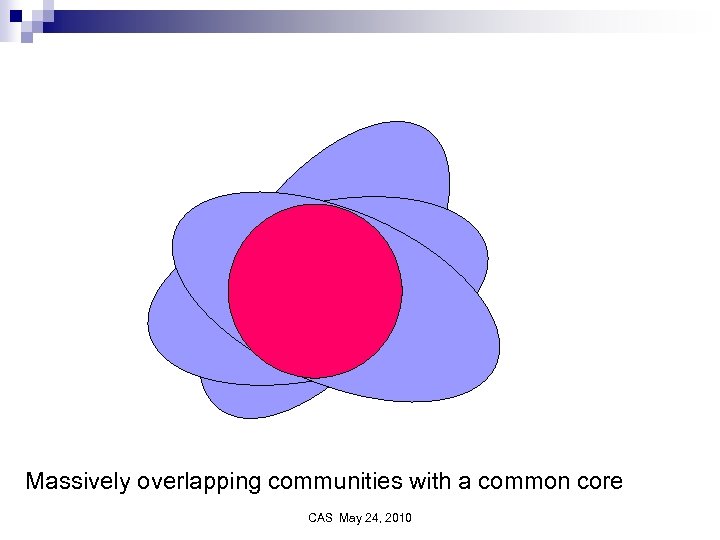
Massively overlapping communities with a common core CAS May 24, 2010

Massively overlapping communities CAS May 24, 2010

Clustering Social networks Mishra, Schreiber, Stanton, and Tarjan Each member of community is connected to a beta fraction of community n No member outside the community is connected to more than an alpha fraction of the community n Some connectivity constraint n CAS May 24, 2010

In sparse graphs How do you find alpha – beta communities? n What if each person in the community is connected to more members outside the community then inside? n CAS May 24, 2010

Transmission paths for viruses, flow of ideas, or influence Sucheta Soundarajan CAS May 24, 2010
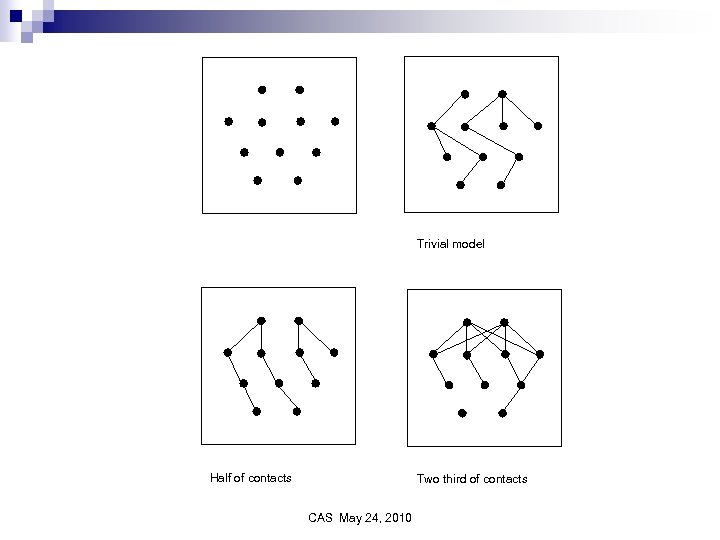
Trivial model Half of contacts Two third of contacts CAS May 24, 2010
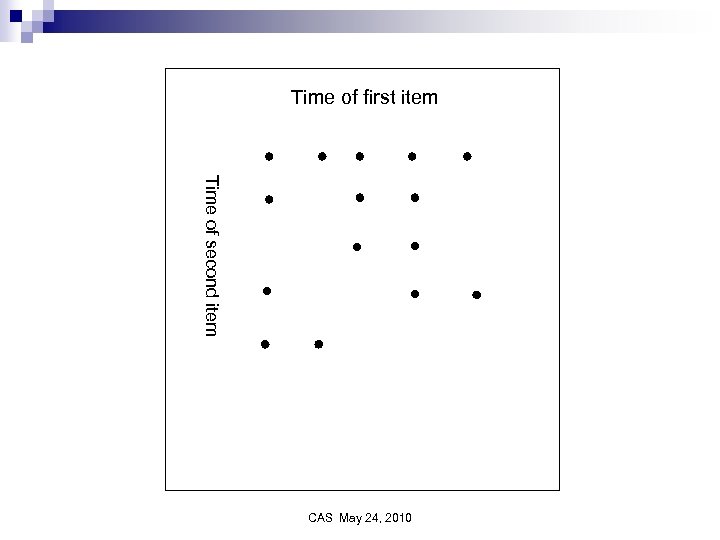
Time of first item Time of second item CAS May 24, 2010

Theory to support new directions § § § Large graphs Spectral analysis High dimensions and dimension reduction Clustering Collaborative filtering Extracting signal from noise CAS May 24, 2010

Theory of Large Graphs § § Large graphs with billions of vertices Exact edges present not critical Invariant to small changes in definition Must be able to prove basic theorems CAS May 24, 2010
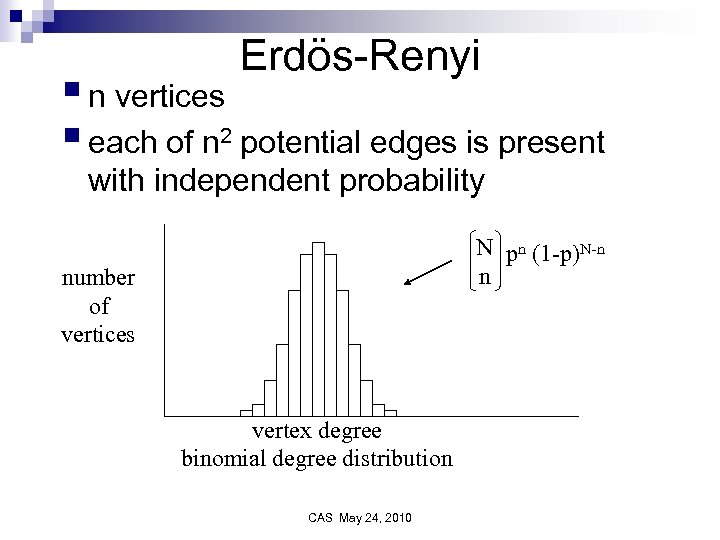
Erdös-Renyi § n vertices § each of n 2 potential edges is present with independent probability N pn (1 -p)N-n n number of vertices vertex degree binomial degree distribution CAS May 24, 2010
CAS May 24, 2010

Generative models for graphs § Vertices and edges added at each unit of time § Rule to determine where to place edges § Uniform probability § Preferential attachment - gives rise to power law degree distributions CAS May 24, 2010
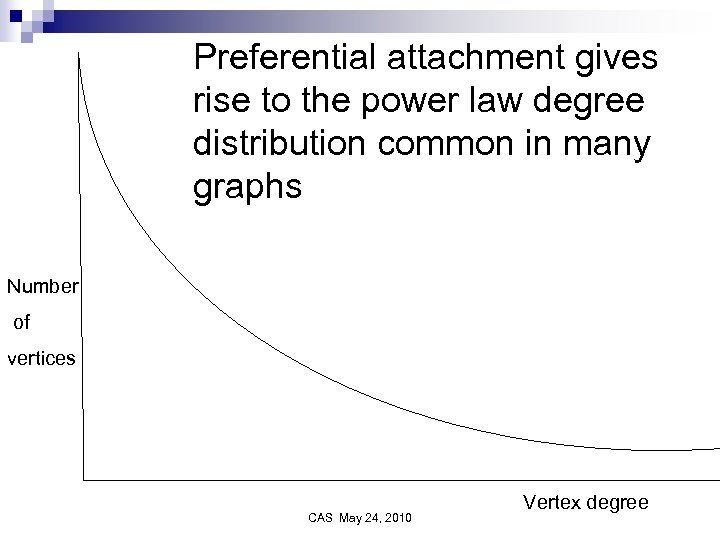
Preferential attachment gives rise to the power law degree distribution common in many graphs Number of vertices CAS May 24, 2010 Vertex degree
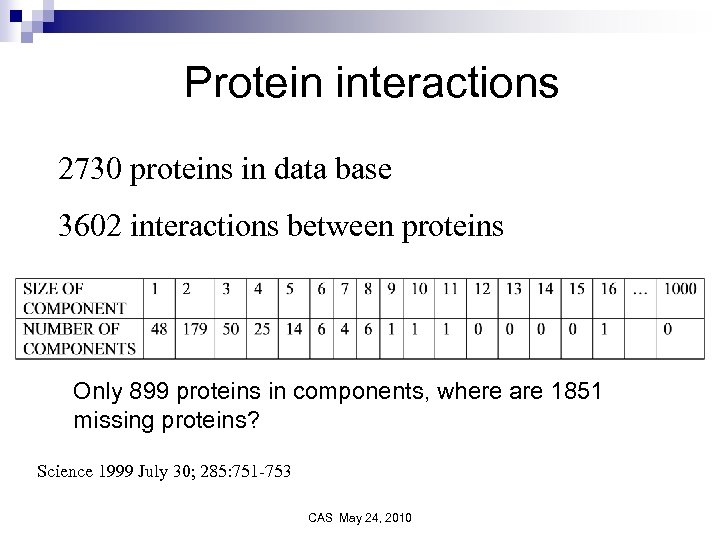
Protein interactions 2730 proteins in data base 3602 interactions between proteins Only 899 proteins in components, where are 1851 missing proteins? Science 1999 July 30; 285: 751 -753 CAS May 24, 2010
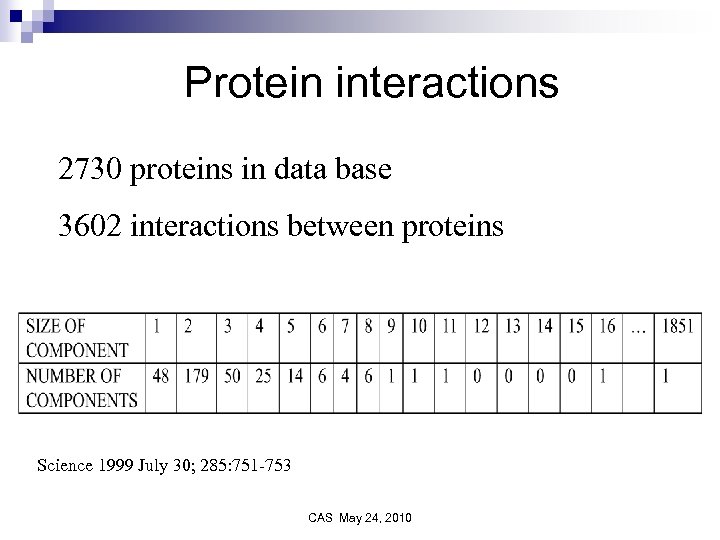
Protein interactions 2730 proteins in data base 3602 interactions between proteins Science 1999 July 30; 285: 751 -753 CAS May 24, 2010

Giant Component 1. Create n isolated vertices 2. Add Edges randomly one by one 3. Compute number of connected components CAS May 24, 2010
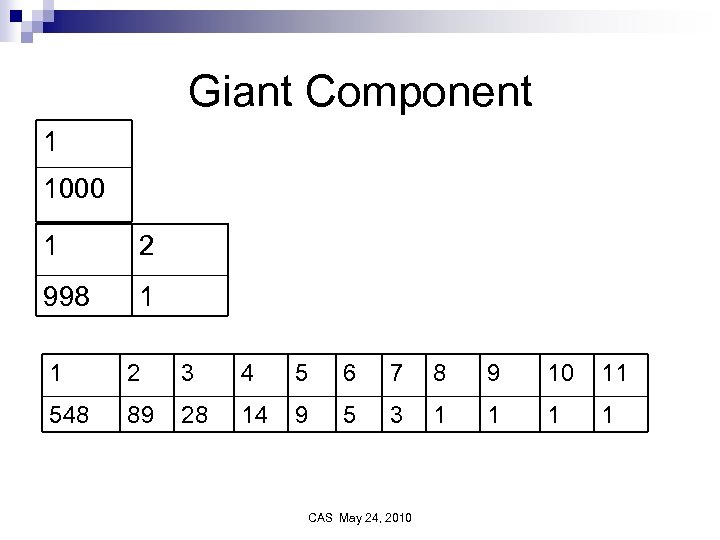
Giant Component 1 1000 1 2 998 1 1 2 3 4 5 6 7 8 9 10 11 548 89 28 14 9 5 3 1 1 CAS May 24, 2010

Giant Component 1 367 2 70 3 24 4 12 5 9 6 3 7 2 8 2 9 2 10 2 12 1 13 2 14 2 20 1 55 1 101 1 CAS May 24, 2010
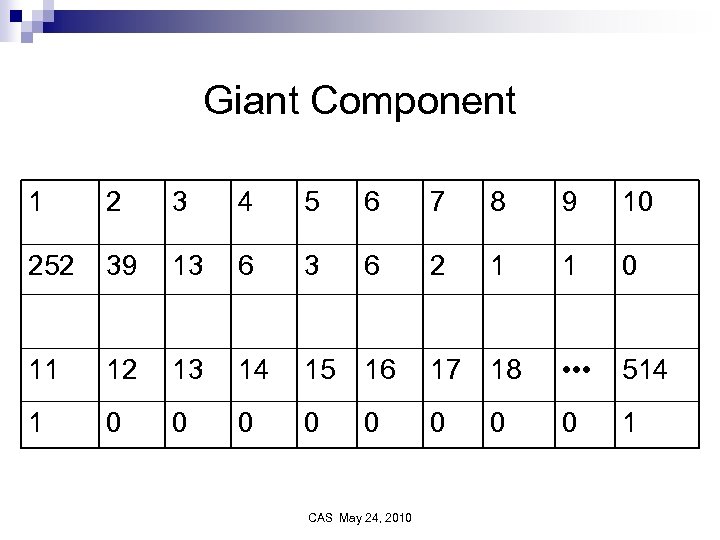
Giant Component 1 2 3 4 5 6 7 8 9 10 252 39 13 6 2 1 1 0 11 12 13 14 15 16 17 18 • • • 514 1 0 0 0 0 1 CAS May 24, 2010

Science base n What do we mean by science base? § Example: High dimensions CAS May 24, 2010
High dimension is fundamentally different from 2 or 3 dimensional space CAS May 24, 2010

High dimensional data is inherently unstable n Given n random points in d dimensional space essentially all n 2 distances are equal. n CAS May 24, 2010

High Dimensions Intuition from two and three dimensions not valid for high dimension Volume of cube is one in all dimensions Volume of sphere goes to zero CAS May 24, 2010
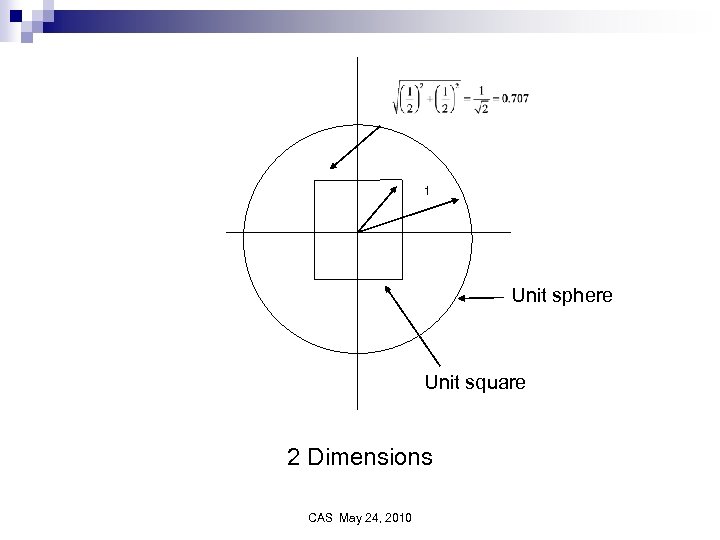
1 Unit sphere Unit square 2 Dimensions CAS May 24, 2010

4 Dimensions CAS May 24, 2010

1 d Dimensions CAS May 24, 2010

Almost all area of the unit cube is outside the unit sphere CAS May 24, 2010
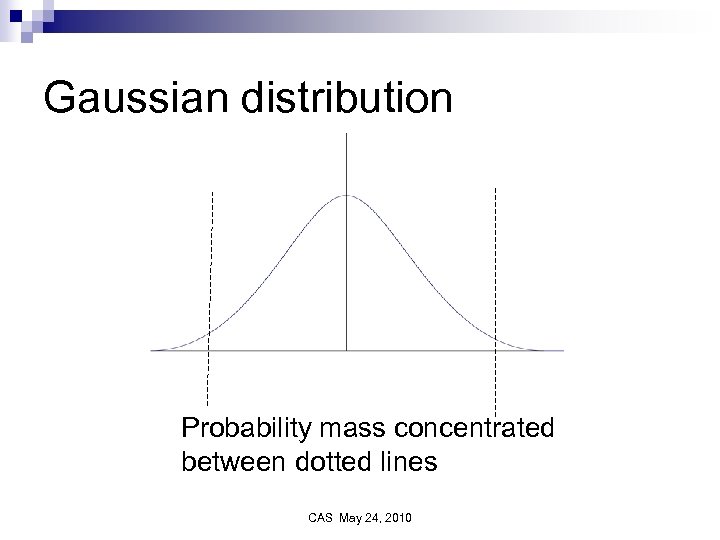
Gaussian distribution Probability mass concentrated between dotted lines CAS May 24, 2010

Gaussian in high dimensions CAS May 24, 2010

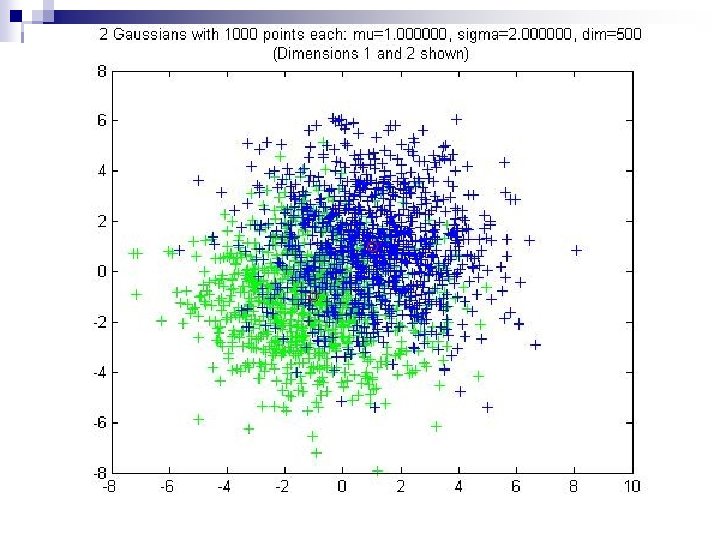
Two Gaussians CAS May 24, 2010
CAS May 24, 2010

Distance between two random points from same Gaussian § Points on thin annulus of radius § Approximate by sphere of radius § Average distance between two points is (Place one pt at N. Pole other at random. Almost surely second point near the equator. ) CAS May 24, 2010

CAS May 24, 2010
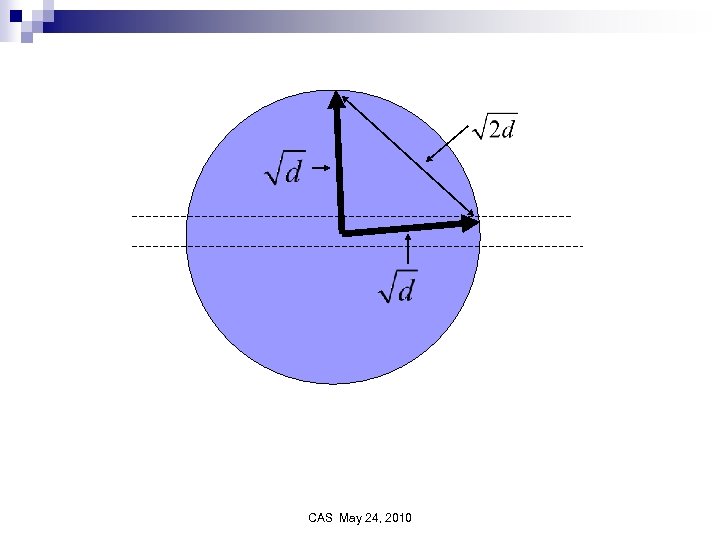
CAS May 24, 2010
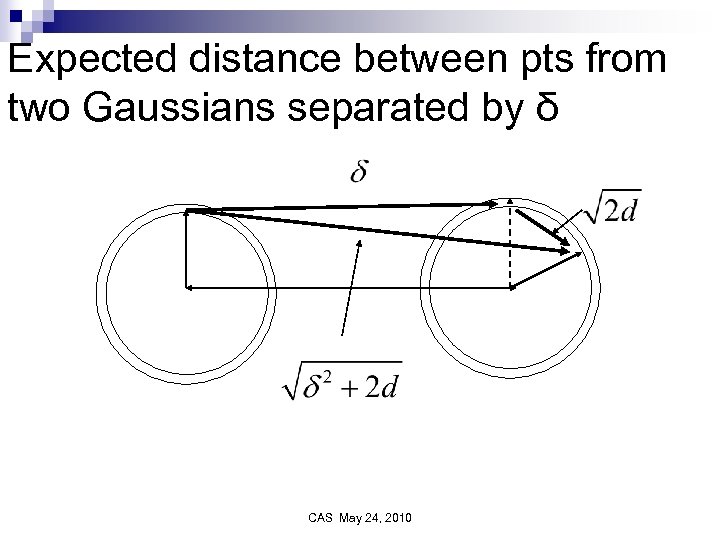
Expected distance between pts from two Gaussians separated by δ CAS May 24, 2010

Can separate points from two Gaussians if CAS May 24, 2010

Dimension reduction Project points onto subspace containing centers of Gaussians n Reduce dimension from d to k, the number of Gaussians n CAS May 24, 2010
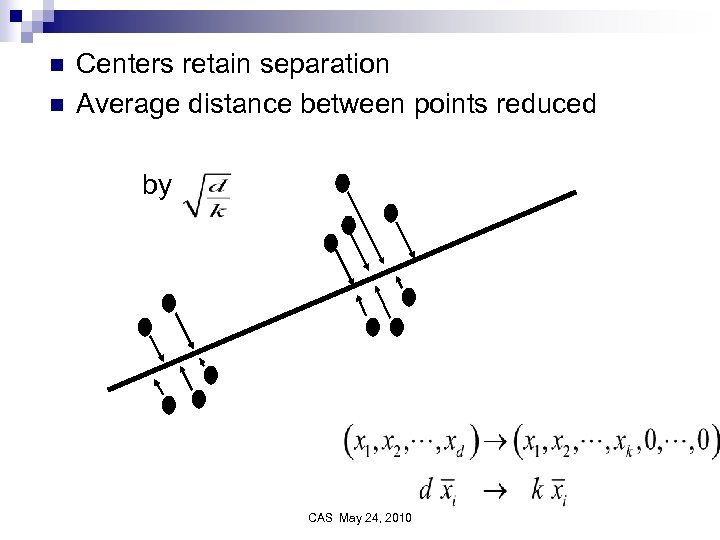
n n Centers retain separation Average distance between points reduced by CAS May 24, 2010

Can separate Gaussians provided > some constant involving k and γ independent of the dimension CAS May 24, 2010

Finding centers of Gaussians First singular vector v 1 minimizes the perpendicular distance to points CAS May 24, 2010

Gaussian The first singular vector goes through center of Gaussian and minimizes distance to points CAS May 24, 2010

Best k-dimensional space for Gaussian is any space containing the line through the center of the Gaussian CAS May 24, 2010
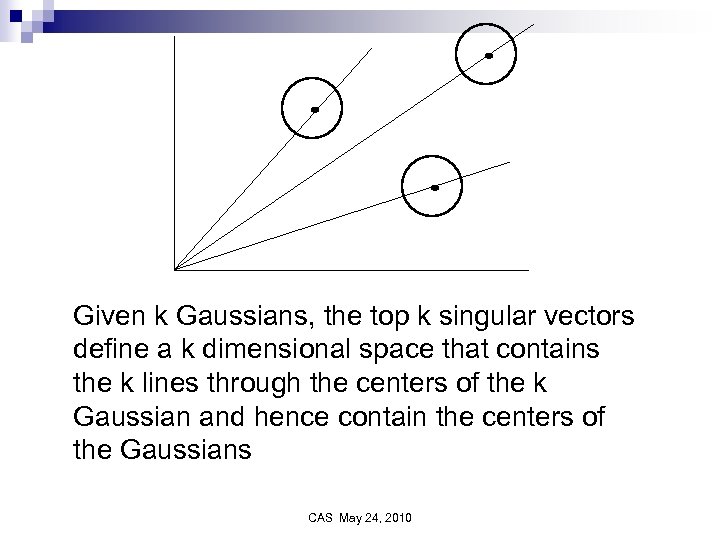
Given k Gaussians, the top k singular vectors define a k dimensional space that contains the k lines through the centers of the k Gaussian and hence contain the centers of the Gaussians CAS May 24, 2010

n We have just seen what a science base for high dimensional data might look like. n What other areas do we need to develop a science base for? CAS May 24, 2010

§ Ranking is important Restaurants, movies, books, web pages § Multi billion dollar industry § § Collaborative filtering § § When a customer buys a product what else is he likely to buy Dimension reduction Extracting information from large data sources Social networks CAS May 24, 2010

Conclusions § We are in an exciting time of change. § Information technology is a big driver of that change. § The computer science theory needs to be developed to support this information age. CAS May 24, 2010
93cb07978a463b0c293669f5164ebca0.ppt