6591f1a3d9f655543d107b209a7fba58.ppt
- Количество слайдов: 44

CPE/CSC 481: Knowledge-Based Systems Dr. Franz J. Kurfess Computer Science Department Cal Poly © 2002 Franz J. Kurfess Introduction 1

Course Overview u Introduction u Knowledge u Semantic Nets, Frames, Logic u Reasoning u with Uncertainty Probability, Bayesian Decision Making u Expert u and Inference Predicate Logic, Inference Methods, Resolution u Reasoning u Representation System Design u CLIPS u Overview Concepts, Notation, Usage u Pattern u Matching Variables, Functions, Expressions, Constraints u Expert System Implementation u Salience, Rete Algorithm u Expert System Examples u Conclusions and Outlook ES Life Cycle © 2002 Franz J. Kurfess Introduction 2

Overview Reasoning and Uncertainty u Motivation u Dempster-Shafer u Objectives u u Sources of Uncertainty and Inexactness in Reasoning u u u Incorrect and Incomplete Knowledge Ambiguities Belief and Disbelief u Probability u Certainty Factors u Approximate u Theory Reasoning Fuzzy Logic u Important Concepts and Terms u Chapter Summary Theory Bayesian Networks © 2002 Franz J. Kurfess Introduction 3

Logistics u u Introductions Course Materials u u textbooks (see below) lecture notes u u u handouts Web page u u u Power. Point Slides will be available on my Web page http: //www. csc. calpoly. edu/~fkurfess Term Project Lab and Homework Assignments Exams Grading © 2002 Franz J. Kurfess Introduction 4

Bridge-In © 2002 Franz J. Kurfess Introduction 5

Pre-Test © 2002 Franz J. Kurfess Introduction 6

Motivation © 2002 Franz J. Kurfess Introduction 7

Objectives © 2002 Franz J. Kurfess Introduction 8

Introductions u reasoning under uncertainty and with inexact knowledge u heuristics u u ways to mimic heuristic knowledge processing methods used by experts u empirical u u associations experiential reasoning based on limited observations u probabilities u u objective (frequency counting) subjective (human experience ) u reproducibility u will observations deliver the same results when repeated © 2002 Franz J. Kurfess Introduction 10

Dealing with Uncertainty u expressiveness u u can concepts used by humans be represented adequately? can the confidence of experts in their decisions be expressed? u comprehensibility u u representation of uncertainty utilization in reasoning methods u correctness u u u probabilities relevance ranking long inference chains u computational u complexity feasibility of calculations for practical purposes © 2002 Franz J. Kurfess Introduction 11

Sources of Uncertainty u data u missing data, unreliable, ambiguous, imprecise representation, inconsistent, subjective, derived from defaults, … u expert u u inconsistency between different experts plausibility v u “best guess” of experts quality v v u knowledge causal knowledge v deep understanding statistical associations v observations scope v only current domain? © 2002 Franz J. Kurfess Introduction 12

Sources of Uncertainty (cont. ) u knowledge representation u restricted model of the real system u limited expressiveness of the representation mechanism u inference process u deductive v the derived result is formally correct, but wrong in the real system u inductive v new conclusions are not well-founded u unsound © 2002 Franz J. Kurfess reasoning methods Introduction 13

Uncertainty in Individual Rules u individual rules u errors domain errors v representation errors v inappropriate application of the rules v u likelihood of evidence for each premise v for the conclusion v combination of evidence from multiple premises v © 2002 Franz J. Kurfess Introduction 14

Uncertainty and Multiple Rules u conflict resolution v if multiple rules are applicable, which one is selected v explicit priorities, provided by domain experts v implicit priorities derived from rule properties » specificity of patterns, ordering of patterns creation time of rules, most recent usage, … u compatibility u u contradictions between rules subsumption v u u u one rule is a more general version of another one redundancy missing rules data fusion v integration of data from multiple sources © 2002 Franz J. Kurfess Introduction 15

Basics of Probability Theory u mathematical u sample space set X = {x 1, x 2, …, xn} v v u approach for processing uncertain information collection of all possible events can be discrete or continuous probability number P(xi) likelihood of an event xi to occur v v v non-negative value in [0, 1] total probability of the sample space is 1 for mutually exclusive events, the probability for at least one of them is the sum of their individual probabilities experimental probability v based on the frequency of events subjective probability v based on expert assessment © 2002 Franz J. Kurfess Introduction 16

Compound Probabilities u describes u do independent events not affect each other in any way u joint probability of two independent events A and B P(A B) = n(A B) / n(s) = P(A) * P (B) where n(S) is the number of elements in S u union probability of two independent events A and B P(A B) = P(A) + P(B) - P(A B) =P(A) + P(B) - P(A) * P (B) v where © 2002 Franz J. Kurfess n(S) is the number of elements in S Introduction 17

Conditional Probabilities u describes u affect dependent events each other in some way u conditional probability of event a given that event B has already occurred P(A|B) = P(A B) / P(B) © 2002 Franz J. Kurfess Introduction 18

Advantages and Problems of Probabilities u advantages u formal foundation u reflection of reality (a posteriori) u problems u may v be inappropriate the future is not always similar to the past u inexact v or incorrect especially for subjective probabilities u knowledge © 2002 Franz J. Kurfess may be represented implicitly Introduction 19

Bayesian Approaches u derive the probability of a cause given a symptom u has gained importance recently due to advances in efficiency u more computational power available u better methods u especially useful in diagnostic systems u medicine, u inverse computer help systems or a posteriori probability u inverse to conditional probability of an earlier event given that a later one occurred © 2002 Franz J. Kurfess Introduction 20

Bayes’ Rule for Single Event u single hypothesis H, single event E P(H|E) = (P(E|H) * P(H)) / P(E) or u P(H|E) = (P(E|H) * P(H) / (P(E|H) * P(H) + P(E| H) * P( H) ) © 2002 Franz J. Kurfess Introduction 21

Bayes’ Rule for Multiple Events u multiple hypotheses Hi, multiple events E 1, …, Ei, …, En P(Hi|E 1, E 2, …, En) = (P(E 1, E 2, …, En|Hi) * P(Hi)) / P(E 1, E 2, …, En) or u P(Hi|E 1, E 2, …, En) = (P(E 1|Hi) * P(E 2|Hi) * …* P(En|Hi) * P(Hi)) / k P(E 1|Hk) * P(E 2|Hk) * … * P(En|Hk) * P(Hk) with independent pieces of evidence Ei © 2002 Franz J. Kurfess Introduction 22

Advantages and Problems of Bayesian Reasoning u advantages u u sound theoretical foundation well-defined semantics for decision making u problems u requires large amounts of probability data v u u u sufficient sample sizes subjective evidence may not be reliable independence of evidences assumption often not valid relationship between hypothesis and evidence is reduced to a number explanations for the user difficult high computational overhead © 2002 Franz J. Kurfess Introduction 23

Dempster-Shafer Theory u mathematical theory of evidence u notations u frame v power set of the set of possible conclusions u mass v u of discernment FD probability function m assigns a value from [0, 1] to every item in the frame of discernment mass probability m(A) v portion of the total mass probability that is assigned to an element A of FD © 2002 Franz J. Kurfess Introduction 24

Belief and Certainty u belief Bel(A) in a subset A u sum of the mass probabilities of all the proper subsets of A u likelihood that one of its members is the conclusion u plausibility u maximum u certainty Pl(A) belief of A Cer(A) u interval [Bel(A), Pl(A)] u expresses the range of belief © 2002 Franz J. Kurfess Introduction 25

Combination of Mass Probabilities m 2 (C) = X Y=C m 1(X) * m 2(Y) / 1 - X Y=C m 1(X) * m 2(Y) where X, Y are hypothesis subsets and C is their intersection u m 1 © 2002 Franz J. Kurfess Introduction 26

Advantages and Problems of Dempster-Shafer u advantages u clear, rigorous foundation u ability oto express confidence through intervals v certainty about certainty u problems u non-intuitive determination of mass probability u very high computational overhead u may produce counterintuitive results due to normalization u usability somewhat unclear © 2002 Franz J. Kurfess Introduction 27

Certainty Factors u shares some foundations with Dempster-Shafer theory, but more practical u denotes the belief in a hypothesis H given that some pieces of evidence are observed u no statements about the belief is no evidence is present u in contrast to Bayes’ method © 2002 Franz J. Kurfess Introduction 28

Belief and Disbelief u measure of belief u degree to which hypothesis H is supported by evidence E u MB(H, E) = 1 IF P(H) =1 (P(H|E) - P(H)) / (1 - P(H)) otherwise u measure of disbelief u degree to which doubt in hypothesis H is supported by evidence E u MB(H, E) = 1 IF P(H) =0 (P(H) - P(H|E)) / P(H)) otherwise © 2002 Franz J. Kurfess Introduction 29

Certainty Factor u certainty factor CF u ranges between -1 (denial of the hypothesis H) and 1 (confirmation of H) u CF = (MB - MD) / (1 - min (MD, MB)) u combining antecedent evidence u use of premises with less than absolute confidence E 1 E 2 = min(CF(H, E 1), CF(H, E 2)) v E 1 E 2 = max(CF(H, E 1), CF(H, E 2)) v E = CF(H, E) v © 2002 Franz J. Kurfess Introduction 30

Combining Certainty Factors u certainty factors that support the same conclusion u several rules can lead to the same conclusion u applied incrementally as new evidence becomes available u Cfrev(CFold, CFnew) = u CFold + CFnew(1 - CFold) if both > 0 u CFold + CFnew(1 + CFold) if both < 0 u CFold + CFnew / (1 - min(|CFold|, |CFnew|)) if one < 0 © 2002 Franz J. Kurfess Introduction 31

Advantages and Problems of Certainty Factors u Advantages u u simplementation reasonable modeling of human experts’ belief v u u expression of belief and disbelief successful applications for certain problem classes evidence relatively easy to gather v no statistical base required u Problems u partially ad hoc approach v theoretical foundation through Dempster-Shafer theory was developed later combination of non-independent evidence unsatisfactory u new knowledge may require changes in the certainty factors of existing knowledge u certainty factors can become the opposite of conditional probabilities for certain cases u not suitable for long inference chains © 2002 Franz J. Kurfess u Introduction 32

Fuzzy Logic u approach to a formal treatment of uncertainty u relies on quantifying and reasoning through natural language u uses linguistic variables to describe concepts with vague values v tall, large, small, heavy, . . . © 2002 Franz J. Kurfess Introduction 33

Get Fuzzy © 2002 Franz J. Kurfess Introduction 34

Fuzzy Set u categorization u described v of elements xi into a set S through a membership function m(s) associates each element xi with a degree of membership in S u possibility measure Poss{x S} u degree to which an individual element x is a potential member in the fuzzy set S u possibility refers to allowed values u probability expresses expected occurrences of events u combination of multiple premises Poss(A B) = min(Poss(A), Poss(B)) v Poss(A B) = max(Poss(A), Poss(B)) v © 2002 Franz J. Kurfess Introduction 35
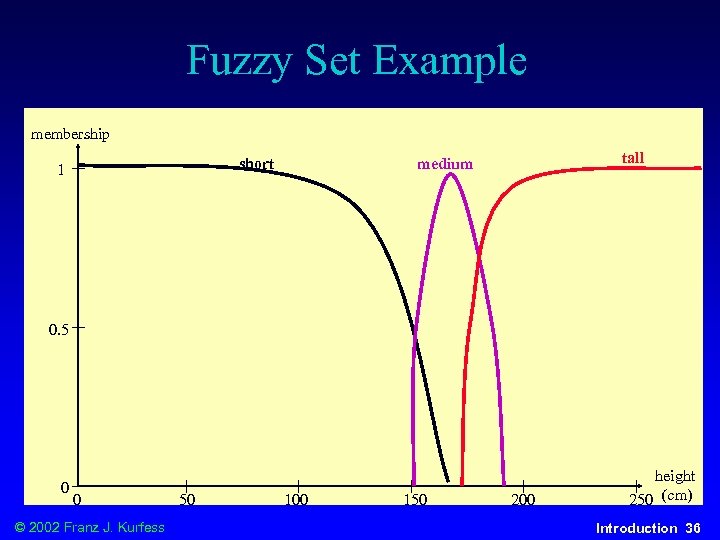
Fuzzy Set Example membership short 1 tall medium 0. 5 0 0 © 2002 Franz J. Kurfess 50 100 150 200 height 250 (cm) Introduction 36
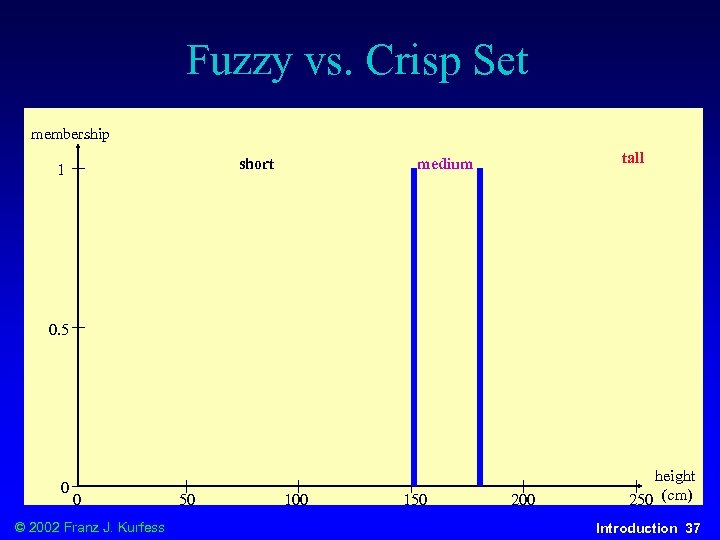
Fuzzy vs. Crisp Set membership short 1 tall medium 0. 5 0 0 © 2002 Franz J. Kurfess 50 100 150 200 height 250 (cm) Introduction 37

Fuzzy Inference Methods u how to combine evidence across rules u Poss(B|A) v = min(1, (1 - Poss(A)+ Poss(B))) implication according to Max-Min inference u also Max-Product inference and other rules u formal foundation through Lukasiewicz logic v extension of binary logic to infinite-valued logic © 2002 Franz J. Kurfess Introduction 38

Example Fuzzy Reasoning © 2002 Franz J. Kurfess Introduction 39

Advantages and Problems of Fuzzy Logic u advantages u general theory of uncertainty u wide applicability, many practical applications u natural use of vague and imprecise concepts v helpful for commonsense reasoning, explanation u problems u membership functions can be difficult to find u multiple ways for combining evidence u problems with long inference chains © 2002 Franz J. Kurfess Introduction 40

Post-Test © 2002 Franz J. Kurfess Introduction 41
![Use of References u [Giarratano & Riley 1998] u [Russell & Norvig 1995] u Use of References u [Giarratano & Riley 1998] u [Russell & Norvig 1995] u](https://present5.com/presentation/6591f1a3d9f655543d107b209a7fba58/image-41.jpg)
Use of References u [Giarratano & Riley 1998] u [Russell & Norvig 1995] u [Jackson 1999] u [Durkin 1994] [Giarratano & Riley 1998] © 2002 Franz J. Kurfess Introduction 43

Important Concepts and Terms u u u u agent automated reasoning belief network cognitive science computer science hidden Markov model intelligence knowledge representation linguistics Lisp logic machine learning microworlds © 2002 Franz J. Kurfess u u u u natural language processing neural network predicate logic propositional logic rational agent rationality Turing test Introduction 44

Summary Chapter-Topic © 2002 Franz J. Kurfess Introduction 45

© 2002 Franz J. Kurfess Introduction 46
6591f1a3d9f655543d107b209a7fba58.ppt