Course outline 1 Introduction 2 Theoretical background Biochemistry molecular

Course outline 1 Introduction 2 Theoretical background Biochemistry/molecular biology 3 Theoretical background computer science 4 History of the field 5 Splicing systems 6 P systems 7 Hairpins 8 Detection techniques 9 Micro technology introduction 10 Microchips and fluidics 11 Self assembly 12 Regulatory networks 13 Molecular motors 14 DNA nanowires 15 Protein computers 16 DNA computing - summery 17 Presentation of essay and discussion

More serious

Tom Head – splicing systems 4 There is a solid theoretical foundation for splicing as an operation on formal languages. 4 In biochemical terms, procedures based on splicing may have some advantages, since the DNA is used mostly in its double stranded form, and thus many problems of unintentional annealing may be avoided. 4 The basic model is a single tube, containing an initial population of ds. DNA, several restriction enzymes, and a ligase. Mathematically this is represented as a set of strings (the initial language), a set of cutting operations, and a set of pasting operations. 4 It has been proved to a Universal Turing Machine.

Tom Head – splicing systems These are the techniques that are common in the microbiologist's lab and can be used to program a molecular computer. DNA can be: 4 synthezise desired strands can be created 4 separate strands can be sorted and separated by length 4

Tom Head – splicing systems 8 Initial set (finite or infinite) double-stranded DNA molecules consists of 8 Specific classes of enzymatic activities considered -those of restriction enzymes 8 Recombinant behavior modeled and associated sets analyzed by new formalism called Splicing Systems 8 Attention focused on effect of sets of restriction enzymes and a ligase that allow DNA molecules to be cleaved and Re-associated to produce further molecules.

Splicing systems Circular DNA and Splicing Systems DNA molecules exist not only in linear forms but also in circular forms.

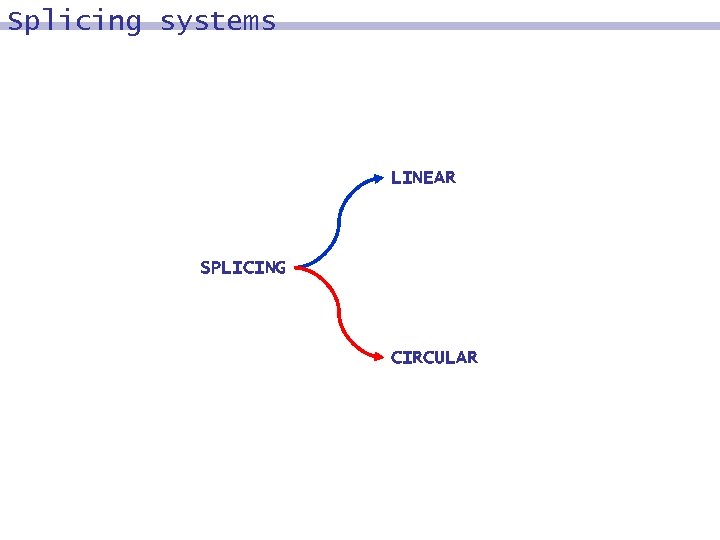
Splicing systems LINEAR SPLICING CIRCULAR

Linear splicing

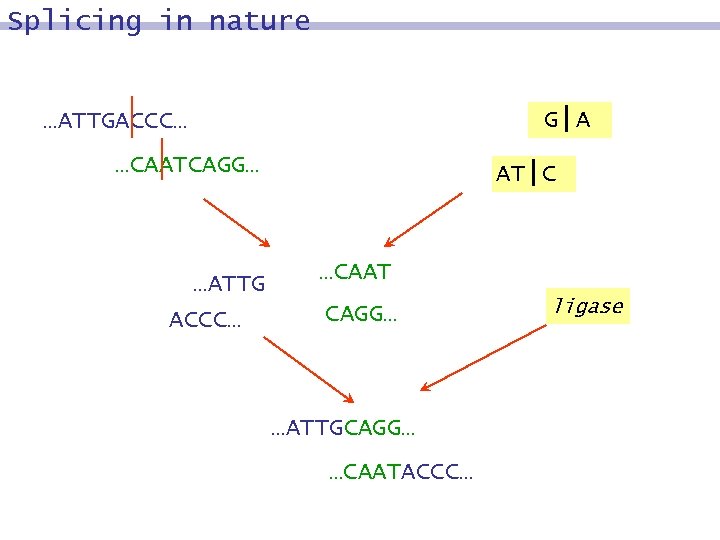
Splicing in nature G|A …ATTGACCC… …CAATCAGG… …ATTG ACCC… AT|C …CAAT CAGG… …ATTGCAGG… …CAATACCC… ligase

Splicing in DNA computing V r alphabet = (x, y) u 1 u 2 u 3 u 4 r (z, splicing rule x, y, z, w V* w) x = x 1 u 1 u 2 x 2 y = y 1 u 3 u 4 y 2 u 1, u 2, u 3, u 4 V* x 1 u 1 u 4 y 2 = z r y 1 u 3 u 2 x 2 = w x 1, x 2, y 1, y 2 V*

Extended H-system = (V, T, A, R) V alphabet T V terminal alphabet A V* set of strings R splicing rules L( ) = *(A) T* if A, R FIN then L( ) REG … with permitting context u 1 C 1 u 3 if u 2 u 4 C 2 A, R FIN then R L( ) RE C 1, C 2 V*

Rotation h 1 abs 1 ct 1 h 1 bs 1 c. At 1 h 1 a bs 1 ct 1 h. Abs 1 c t 1 1 h. A At. A h 1 a At. A h. A bs 1 c. At. A 2 h 1 bs 1 c. At 1 h 1 bs 1 c. A t. A h. Aa t 1 3 1 2 h 1 a {s 1} h. A At. A t 1 h 1 a At. A {h. A, s 1} 3 h 1 at 1 h. Aat. A 4 3 4 h. A {s 1, t. A} h 1 at 1 t. A h. Aa t 1 {h 1, s 1}

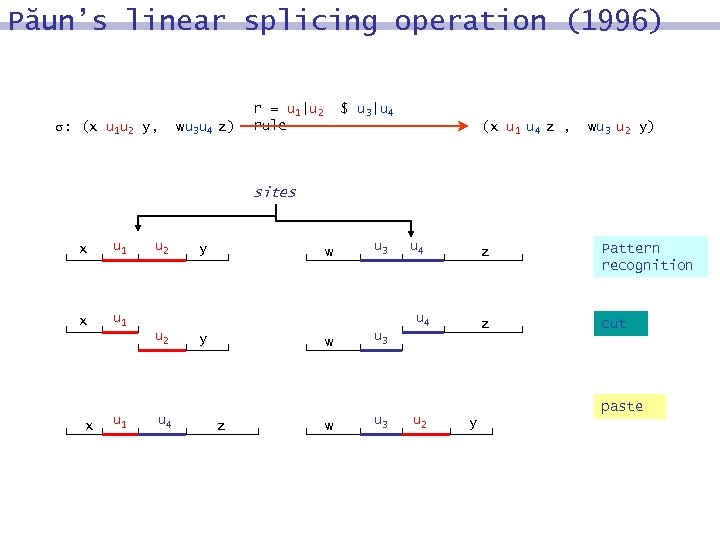
Păun’s linear splicing operation (1996) : (x u 1 u 2 y, wu 3 u 4 z) r = u 1|u 2 rule $ u 3|u 4 (x u 1 u 4 z , wu 3 u 2 y) sites x u 1 x u 2 u 1 w u 3 u 4 z u 4 y w z w u 3 u 2 Pattern recognition z u 4 u 2 x y cut paste y

Circular splicing

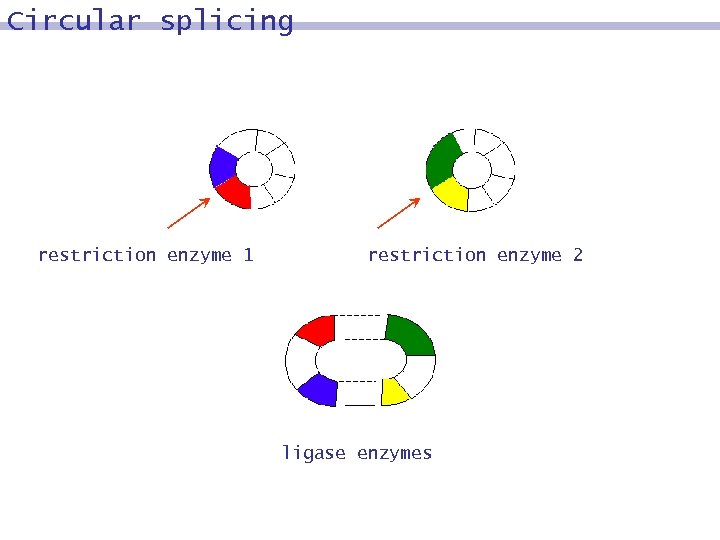
Circular splicing restriction enzyme 1 restriction enzyme 2 ligase enzymes

Circular languages Conjugacy relation on A* w, w A*, Example w ~ w w = xy, w = yx abaa, baaa, aaab, aaba Ao = A* o = set of all circular words ow = [w]o , w A* are conjugates

Circular languages Circular language A* A* C Ao set of equivalence classes o L Cir(L) = {ow | w L} L C (circularization of L) (A linearization of C, i. e. Cir(L)=C ) {w A*| ow C}= Lin(C) (Full linearization of C) C

Circular languages Definition FAo ={ C Ao | L A*, Cir(L) = C, L FA, FA Chomsky hierarchy} Theorem [Head, Păun, Pixton] C Rego Lin (C) Reg

Circular splicing systems (A= finite alphabet, I Ao initial language) Păun’s definition SCPA = (A, I, R) ohu 1 u 2 , u 2 hu 1 oku R 3 u 4 Ao u 4 ku 3 A* | A* $ A* | A* r = u 1 | u 2 ou 2 hu 1 rules $ u 3 | u 4 R u 4 ku 3

Circular splicing systems Definition A circular splicing language C(SCPA) (i. e. a circular language generated by a splicing system SCPA) is the smallest circular language containing I and closed under the application of the rules in R.

Other splicing systems I Ao initial language) (A= finite alphabet, Head’s definition SCH = (A, I, T) ohpxq , T A* A* Ao okuxv (p, x, q ), (u, x, v) T ohpx vkux q hpx triples vkux q Pixton’s definition SCPI = (A, I, R) o h , h o R h A* A* Ao h rules ( , ; ), ( , ; ) R oh h

Problem Characterize C(Reg, Fin) FAo C(Fin, Fin) class of circular languages C= C(SCPA) generated by SCPA with I and R both finite sets.

Problem Theorem [Păun 96] F {Rego, CFo, REo} R +add. hyp. (symmetry, reflexivity, self-splicing) C(F, Fin) F Theorem [Pixton 95 -96] F {Rego, CFo, REo} R Fin+add. hyp. (symmetry, reflexivity) C(Rego, Fin) Rego, C(F, Reg) F

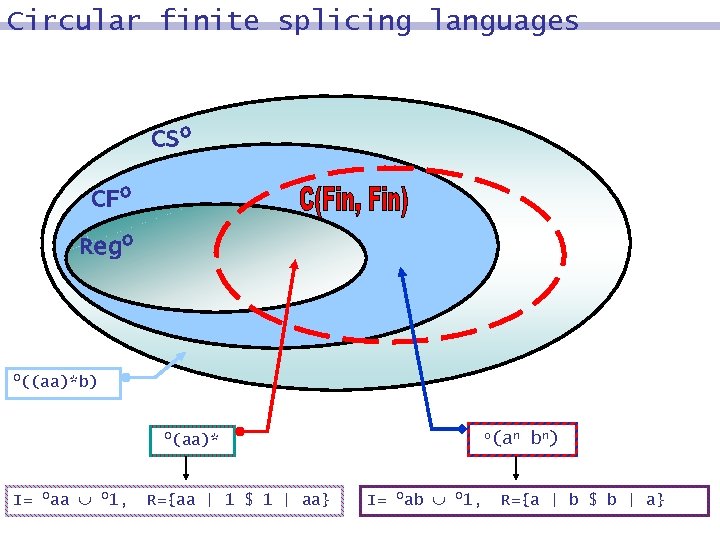
Circular finite splicing languages CSo CFo Rego o((aa)*b) o(aa)* I= oaa o 1, R={aa | 1 $ 1 | aa} o(an I= oab o 1, bn) R={a | b $ b | a}

Circular automata

Finite automata for circular languages J. Kari and L. Kari Context-free Recombinations, words, sequences, languages where computer science, biology and linguistics meet, C. Martin-Vide, V. Mitrana (Eds. ). Kluwer, the Netherlands.

Finite automata for circular languages Definition 8 Finite automaton A, circular language K-accepted by A, L( A )o. K , all words wo such that A has a cycle labeled by w 8 K–Acceptance Circular/linear language accepted by a finite automaton A, defined as L(A) o. L(A), L(A) linear language accepted by automaton A defined in the usual way Definition A circular/linear language L * o is regular if there is a finite automaton A that accepts the circular and linear parts of L, i. e. that accepts L * and L o

P-acceptance The following definition is equivalent to a definition given by Pixton: the circular language accepted by a finite automaton is a set of all words that label a loop containing at least one initial and one final state. Definition Given a finite automaton A, the circular language accepted by A, L(A)o. P is the set of all words ow such that A has a cycle labeled by w that contains at least one final state.

H-acceptance The circular languages accepted by finite automaton by the following definition coincide with the regular circular languages introduced by Head. Given a finite automation A, the circular language accepted by A, L( A )o. H is the set of all words ow such that w = u v and v u L( A ) Pixton has shown that if in addition we assume that the family of languages is closed under repetition (i. e. , wn is in the language whenever w is) H – acceptance and P – Acceptance are equivalent

K-acceptance Advantages of K-acceptance The same automaton accepts both the linear and circular components of the language

Counting problem

Sources T. Head, Circular Suggestions for DNA Computing, in: Pattern Formation in Biology, Vision and Dynamics, Eds. A. Carbone, M Gromov and P. Prusinkiewicz, World Scientific, Singapore , 2000, pp. 325 -335. J. Kari, A Cryptosystem Based on Propositional Logic, in: Machines, Languages and Complexity, 5 th International Meeting of Young Computer Scientists, Czeckoslovakia, Nov. 14 -18, 1988, Eds. J. Dassow and J. Kelemen, LNCS 381, Springer, 1989, pp. 210 -219. Rani Siromoney, Bireswar Das, DNA Algorithm for Breaking a Propositional Logic Based Cryptosystem, Bulletin of the EATCS, Number 79, February 2003, pp. 170 -176.

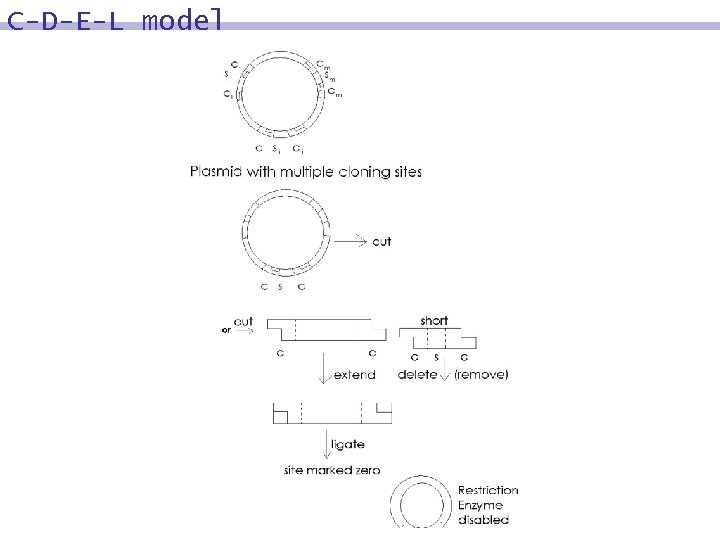
C-D-E-L model Introducing CUT-DELETE-EXPAND-LIGATE (C-D-E-L) model Combine features in Divide-Delete-Drop (D-D-D) (Leiden) and CUT-EXPAND-LIGATE (C-E-L) (Binghamton) to form CUT-DELETEEXPAND-LIGATE (C-D-E-L) model This enables us to get an aqueous solution to 3 SAT which is a counting problem and known to be in IP. 3 SAT Defined as follows: Instance: F a propositional formula of form F = C 1 C 2 …Cm where Ci are clauses and i = 1, 2, …, m. Each Ci is of the form ( li 1 li 2 li 3) where li j , j = 1, 2, 3 are literals from the set of variables {x 1 , x 2 , … , xn} Question What is the number of truth assignments that satisfy F?

Data register molecule Standard double stranded commercially available. DNA cloning plasmid are A plasmid is a circular molecule approximately 3 kb. It contains a sub-segment, MCS (multiple cloning site) of approximately 175 base pairs that can be removed using a pair of restriction enzyme sites that flank the segment. The MCS contains pair-wise disjoint sites at which restriction enzymes act such that each produces a 5’ overhang.

C-D-E-L model In C-D-E-L, a segment of the plasmid used is of the form …c 1 s 1 c 1…c 2 s 2 c 2…cnsnncn… Where ci are called sites, such that no other subsequence of plasmid matches with this sequence and si are called stations and i=1, …, n In D-D-D, lengths of stations are required to be the same However in C-D-E-L, lengths of stations all different which is fundamental in solving #3 SAT Bio-molecular operations used in C-D-E-L are similar to the operations in C-E-L

Design x 1 , … , xn x 1 , … , xn si si ci ci vi vn+j the variables in F, their negations station associated with xi station associatd with si site associated with station length of station associated xj , j=1, …, n si si with xi, i=1, …, n with literal Choose stations in such a way that the sequence [ v 1 , … , v 2 n ] satisfies the property k vi < vk+1 , k = 1, … , 2 n-1 i=1 i. e. an Super-increasing (Easy) Knapsack Sequence From sum, sub-sequence efficiently recovered.

Solution 8 Solution in Cn is analyzed by gel separation 8 If more than one solution is present, they will be of different lengths, thus will form separate bands 8 By counting number of bands we count the number of satisfying assignments. 8 Furthermore, from lengths of satisfying assignment , exact assignment is read. 8 This can be done since stations have lengths from easy knapsack sequence any subsequence of an easy knapsack sequence has different sum from the sums of other subsequences.

C-D-E-L model

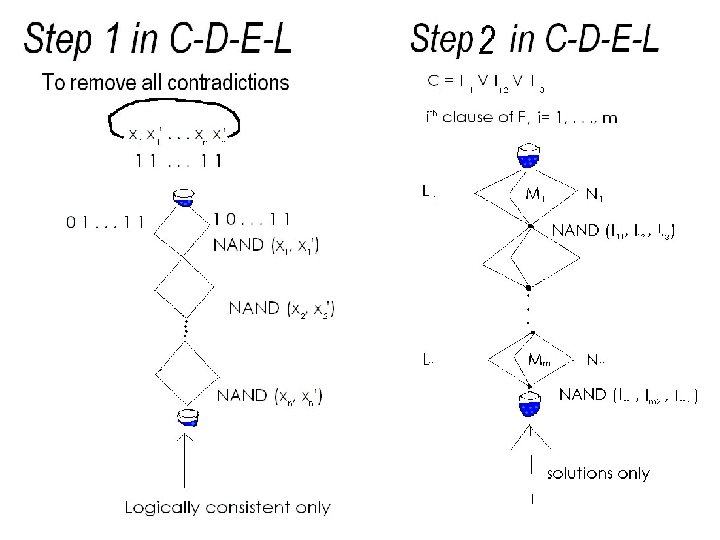
Solution Thus solution to 3–SAT viz. finding the number of satisfying assignments is effectively done. Moreover, reading the truth assignments is a great advantage to break the cryptosystem based on propositional logic

Advantage over previous method of attack 8 In the cryptanalytic attack proposed earlier, modifying D-D-D, it was required to execute the DNA algorithm for each bit in the crypto-text 8 But in the present method proposed, using C-D-E-L (combining features of C-C-C and C-E-L ) apply 3 -SAT on P and read any satisfying assignment from the final solution 8 This gives an equivalent public key, which amounts to breaking the cryptosystem

Splicing systems so far 8 H-system 8 Lipton[94 -95 a-95 b] Formalization and generalization of Adleman’s approach to other NP-complete problems. Ex H-system Circular H-system Sticker system P-system 8 8

Splicing systems so far For computational strength 8 Turing Equivalence Expansion 8 8 Finiteness & Regularity More Operator Formalization To confirm homogeneity 8 HPP solving & AGL

Molecular application

Operations of DNA molecules 8 8 8 Separating and fusing DNA strands Lengthening of DNA Shortening DNA Cutting DNA Multiplying DNA

Separating and fusing DNA strands Denaturation 8 separating 8 8 the single strands without breaking them weaker hydrogen than phosphodiester bonding heat DNA (85° - 90° C) Renaturation 8 slowly cooling down 8 annealing of matching, separated strands

Enzymes Machinery for Nucleotide Manipulation 8 Enzymes are proteins that catalyze 8 8 8 chemical reactions. Enzymes are very specific. Enzymes speed up chemical reactions extremely efficiently (speedup: 1012) Nature has created a multitude of enzymes that are useful in processing DNA.

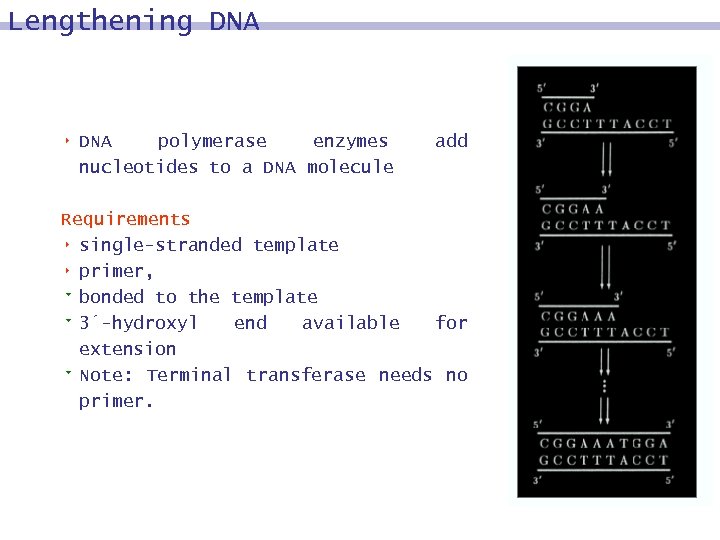
Lengthening DNA 8 DNA polymerase enzymes nucleotides to a DNA molecule add Requirements 8 single-stranded template 8 primer, 9 bonded to the template 9 3´-hydroxyl end available for extension 9 Note: Terminal transferase needs no primer.

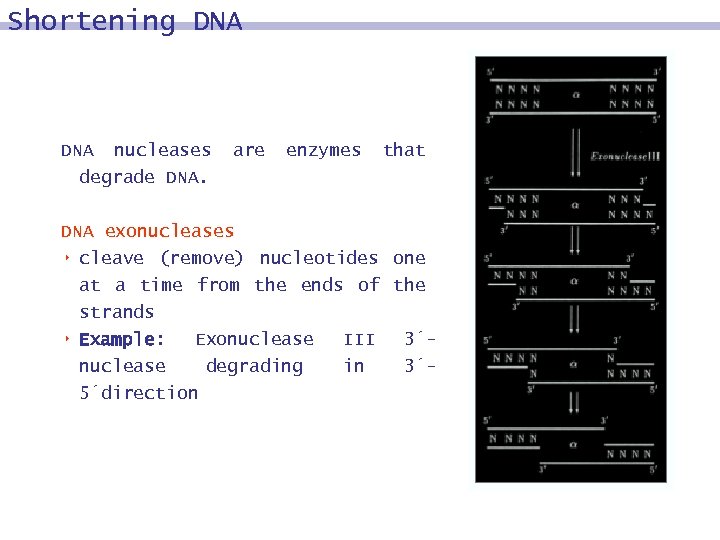
Shortening DNA nucleases degrade DNA. are enzymes that DNA exonucleases 8 cleave (remove) nucleotides one at a time from the ends of the strands 8 Example: Exonuclease III 3´nuclease degrading in 3´ 5´direction

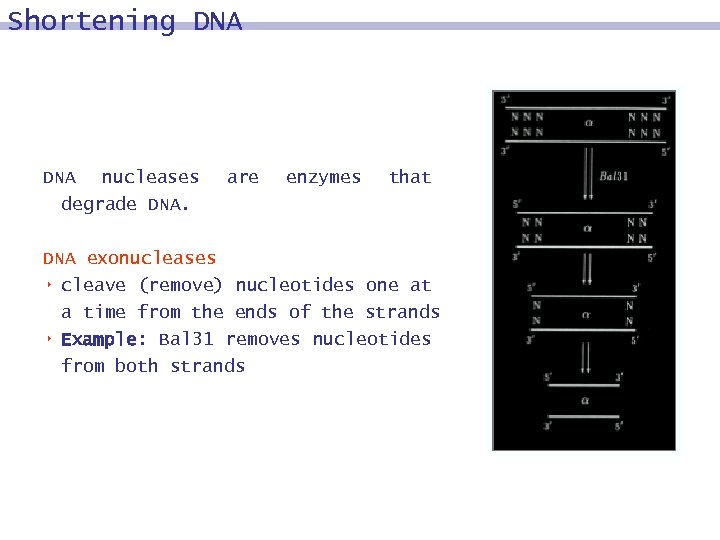
Shortening DNA nucleases degrade DNA. are enzymes that DNA exonucleases 8 cleave (remove) nucleotides one at a time from the ends of the strands 8 Example: Bal 31 removes nucleotides from both strands

Cutting DNA nucleases are enzymes that degrade DNA endonucleases 8 destroy internal phosphodiester bonds 8 Example: S 1 cuts only single strands or within single strand sections Restriction endonucleases 8 much more specific 8 cut only double strands 8 at a specific set of sites (Eco. RI)

Multiplying DNA 8 8 8 Amplification of a „small“ amount of a specific DNA fragment, lost in a huge amount of other pieces. „Needle in a haystack“ Solution: PCR = Polymerase Chain Reaction devised by Karl Mullis in 1985 Nobel Prize a very efficient molecular copy machine

PCR - initialisation Start with containing a the solution following ingredients: 8 the target DNA molecule 8 primers (synthetic oligonucleotides), complementary to the terminal sections 8 polymerase, heat resistant nucleotides

PCR – denaturation 8 Solution heated close to boiling temperature. 8 Hydrogen bonds between the double strands are separated into single strand molecules.

PCR - priming 8 The solution is cooled down (to about 55° C). 8 Primers anneal to their complementary borders.

PCR - extension 8 The solution is heated again (to about 72° C). 8 Polymerase will extend the primers, using nucleotides available in the solution. 8 Two complete strands of the target DNA molecule are produced.

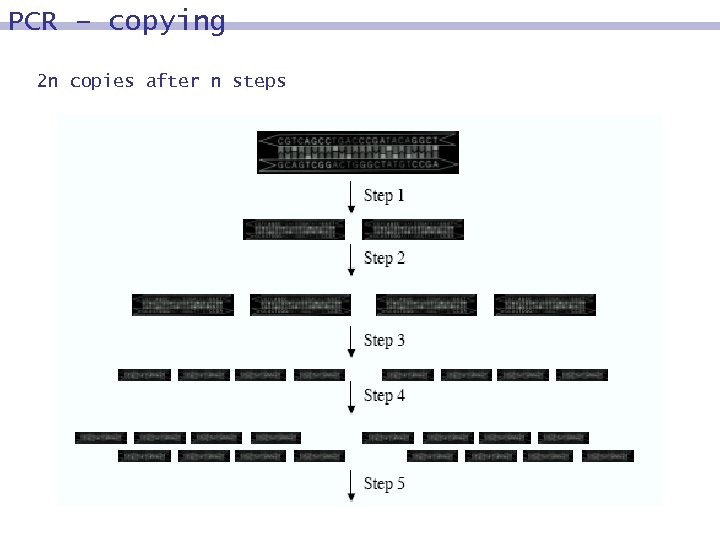
PCR – copying 2 n copies after n steps

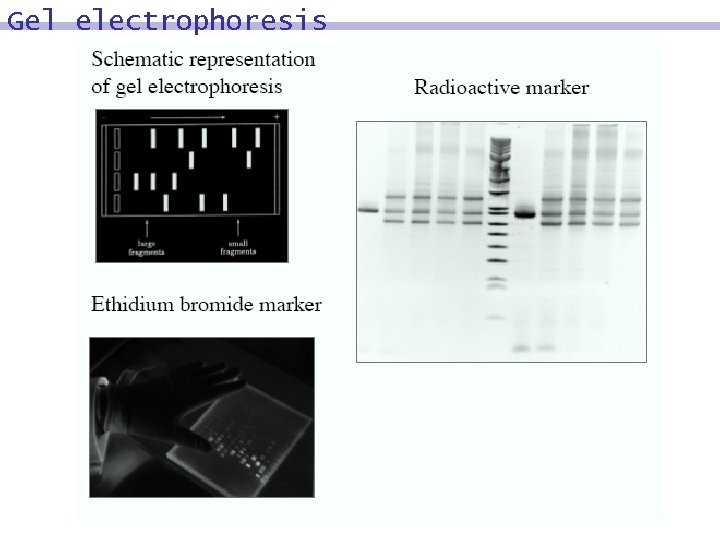
Gel electrophoresis Measuring the Length of DNA Molecules 8 DNA molecules are negatively charged. 8 Placed in an electric field, they will move towards the positive electrode. 8 The negative charge is proportional to the length of the DNA molecule. 8 The force needed to move proportional to its length. 8 A gel makes the molecules move at different speeds. 8 DNA molecules are invisible, and must be marked (ethidium bromide, radioactive) the molecule is

Gel electrophoresis

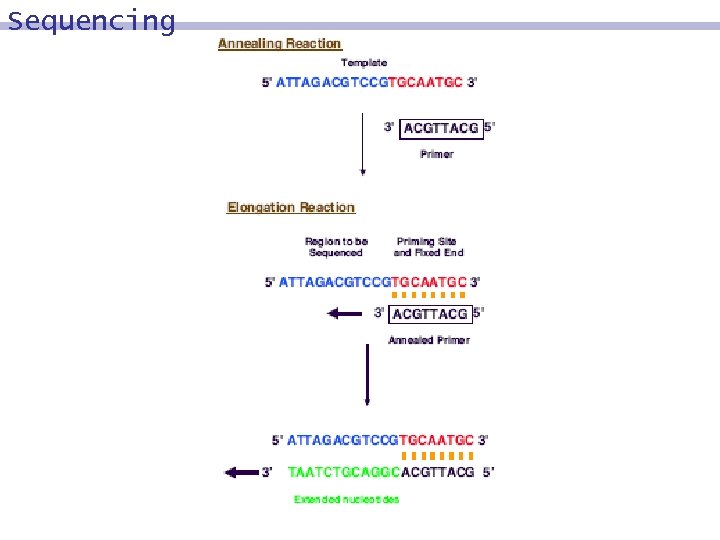
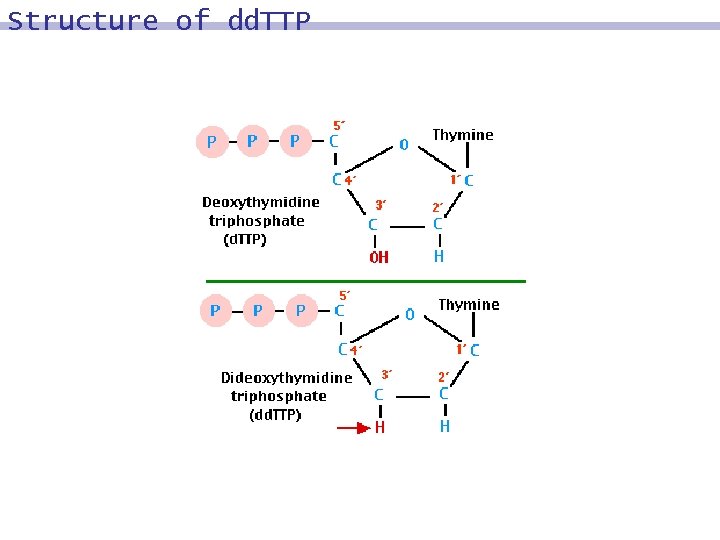
Sequencing 8 reading the exact sequence of comprising a given DNA molecule nucleotides based on 9 the polymerase action of extending a primed single stranded template 9 nucleotide analogues 9 chemically modified e. g. , replace 3´-hydroxyl group (3´-OH) by 3´-hydrogen atom (3´-H) 8 9 dideoxynucleotides: - dd. A, dd. T, dd. C, dd. G 9 Sanger method, dideoxy enzymatic method

Sequencing Objective 8 We want to sequence a single stranded molecule a. Preparation 8 We extend a at the 3´ end by a short (20 bp) sequence g, which will act as the W-C complement for the primer compl(g). l Usually, the primer is labelled (radioactively, or marked fluorescently) 8 This results in a molecule b´= 3´- ga. 5' ATTAGACGTCCGTGCAATGC 3' 3'ACGTTACG 5'

Sequencing

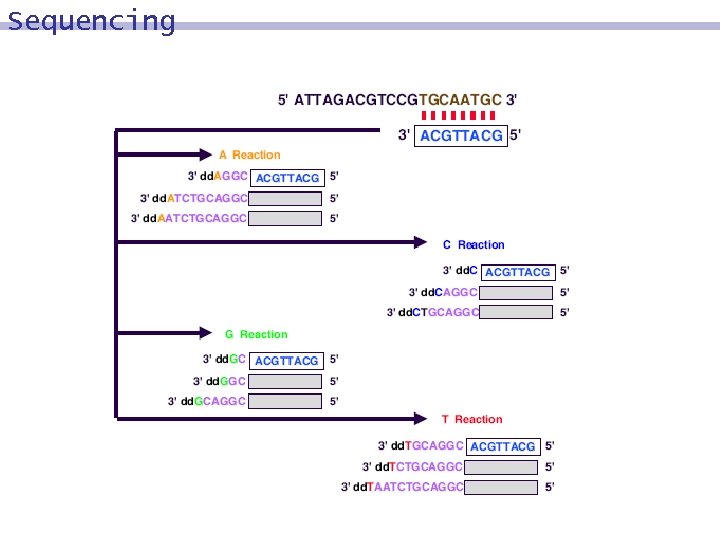
Sequencing 4 tubes are prepared 8 Tube A, Tube T, Tube C, Tube G 8 Each of them contains 9 b molecules 9 primers, compl(g) 9 polymerase 9 nucleotides A, T, C, and G. 9 Tube A contains a limited amount of dd. A. 9 Tube T contains a limited amount of dd. T. 9 Tube C contains a limited amount of dd. C. 9 Tube G contains a limited amount of dd. G.

Structure of dd. TTP

Termination with dd. TTP

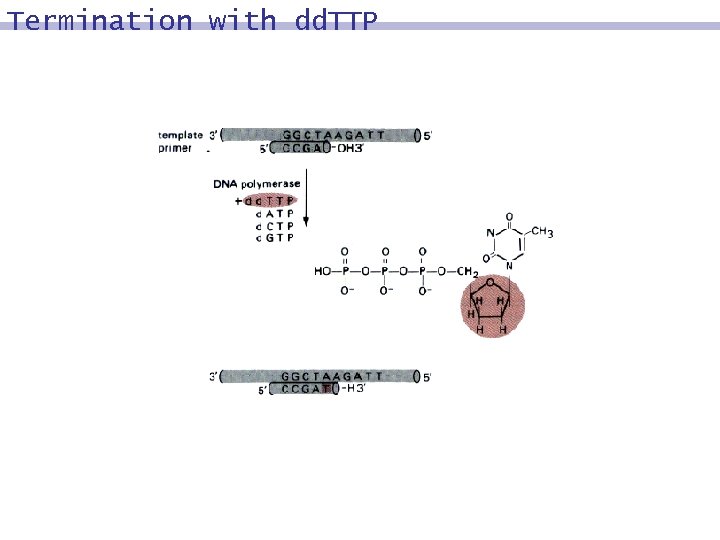
Sequencing Reaction in Tube A 8 The polymerase enzyme extends the primer of b´, using the nucleotides present in Tube A: dd. A, A, T, C, G. using only A, T, C, G: 9 b´ is extended to the full duplex. 8 using dd. A rather than A: 9 complementing will end at the position of the dd. A nucleotide. 8

Sequencing

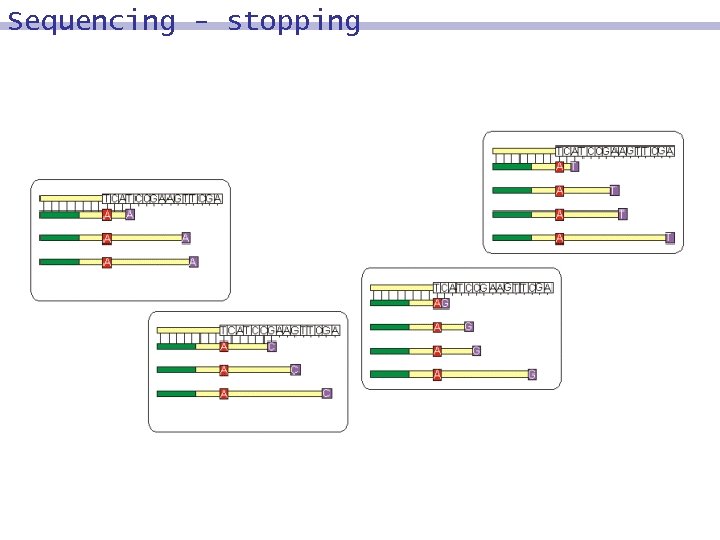
Sequencing - stopping

Sequencing -results Tube A 8 GCCTGCAGATTA 8 CGGACGTCTAA Tube C 8 GCCTGCAGATTA 8 CGGACGTC Tube T 8 GCCTGCAGATTA 8 CGGACGTCTAAT Tube G 8 GCCTGCAGATTA 8 CGGACG

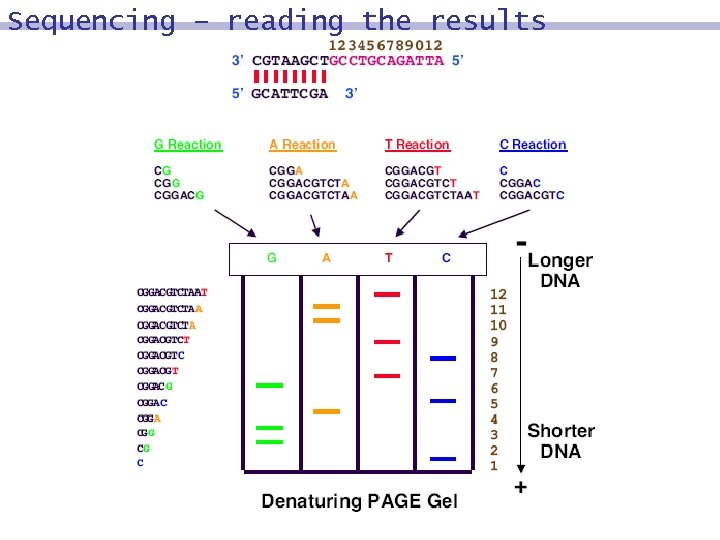
Sequencing – reading the results