Course Director Ø Ø Dónal Leech Room C

Course Director Ø Ø Dónal Leech Room C 205 (in Physical Chemistry) E-mail: donal. leech@nuigalway. ie Phone: 493563 (from outside), ext 3563 (internal phones) Web-site: http: //www. nuigalway. ie/chemistry/staff/donal_leech/teaching. html 1

Second Year Chemistry • 1 st semester: Organic • 1 st semester: Physical (2008 -2009) • December exams • 2 nd: Analytical & Environmental • 2 nd: Inorganic • Summer exams • Physical: 4 lecturers Þ ~8 topics • Dónal Leech: two topics • Thermodynamics • Gases, Laws 2

Course Outline • • • 8 topics, 2 per Lecturer 3 Lectures per topic Exam: 2 hour, answer 4 questions • 1 Q per topic, 2 Q per section (Lecturer) • Must attempt one Q per section • See past papers • http: //www. nuigalway. ie/chemistry/exam_papers. html 3

Introduction Energetics and Equilibria What makes reactions “go”! This area of science is called THERMODYNAMICS Thermodynamics is expressed in a mathematical language BUT Don’t, initially anyway, get bogged down in the detail of the equations: try to picture the physical principle expressed in the equations We will develop ideas leading to one important Law, and explore practical applications along the way The Second Law of Thermodynamics 4

Lecture Resources 6 lectures leading to two exam questions • Main Text: “Elements of Physical Chemistry” Atkins & de Paula, 4 th Edition (Desk reserve) http: //www. oup. com/uk/orc/bin/9780199271832/ OTHERS. “Physical Chemistry” Atkins & de Paula, 7 th Edition or any other PChem textbook These notes available on NUI Galway web pages at http: //www. nuigalway. ie/chemistry/courses. html See also excellent lecture notes from James Keeler, Cambridge, although topics are treated in a different running order than here. 5

Course Structure Ø Ø Ø 6 Revision of gases Energy, heat and expansion work 1 st Law of thermodynamics Thermochemistry and phase diagrams Entropy 2 nd Law of thermodynamics

Revision States of Matter (bulk) Gas: fluid form that fills container Liquid: fluid form with well-defined surface, fills bottom of container (in gravitational field) Solid: retains its own inherent shape Difference between these states related to freedom of particles (molecules) to move past each other. We describe the macroscopic physical state of matter under conditions of volume, pressure, temperature and amount present. 7

Units of some properties • Mass, m: quantity of matter in kg (Pt-Ir sample near Paris)=1000 g • Volume, V: space occupied in m 3= 1000 L • Force, F: mass × acceleration in newtons (N=kg m s-2) • Work, w: F × distance (N m = joule, J), form of ENERGY (capacity to do work) • Pressure, p: F/area (N m-2 = pascal, Pa) • Temperature, T: determines in which direction energy will flow (higher to lower), reported in K (= θ °C + 273. 15) • Amount, n: mole (number of atoms in exactly 12 g carbon-12) • Avogadro’s number, NA = 6. 022 × 1023 mol-1 • 8 Nb of atoms = n × NA • Molar mass, M: mass per mole of substance (g/mol), M = m / n

Pressure (revision) Ø Ø Ø Pressure is the force that acts on a given area (P=F/A). Gravity on earth exerts a pressure on the atmosphere: atmospheric pressure. We can evaluate this by calculating the force due to acceleration (by gravity) of a 1 m 2 column of air extending through the atmosphere (this has a mass of ~10, 000 kg). This unit is a newton (N) This unit is a pascal (Pa) 9

Units of Pressure S. I. unit of pressure is the N/m 2, given the name pascal (Pa). A related unit is the bar (1 x 105 Pa) used because atmospheric pressure is ~ 1 x 105 Pa (100 k. Pa, or 1 bar). Torricelli (a student of Galileo) was the first to recognise that the atmosphere had weight, and measured pressure using a barometer Standard atmospheric pressure was thus defined as the pressure sufficient to support a mercury column of 760 mm (units of mm. Hg, or torr). Another popular unit was thus introduced to simplify things, the atmosphere (atm = 760 mm. Hg). 10

To be presented in Lecture Come to the lecture to see what is on this slide! 11

Ideal Gas Law • Can specify state of sample by giving V, P, T and n. • These are however interdependent Equation of state of low-pressure gas is known (from combination of Boyle’s, Charles’s Laws and Avogadro’s principle) PV = n. RT R = 8. 314 J K-1 mol-1 (= NAk) (or L k. Pa K-1 mol-1 or m 3 Pa K-1 mol-1) 12

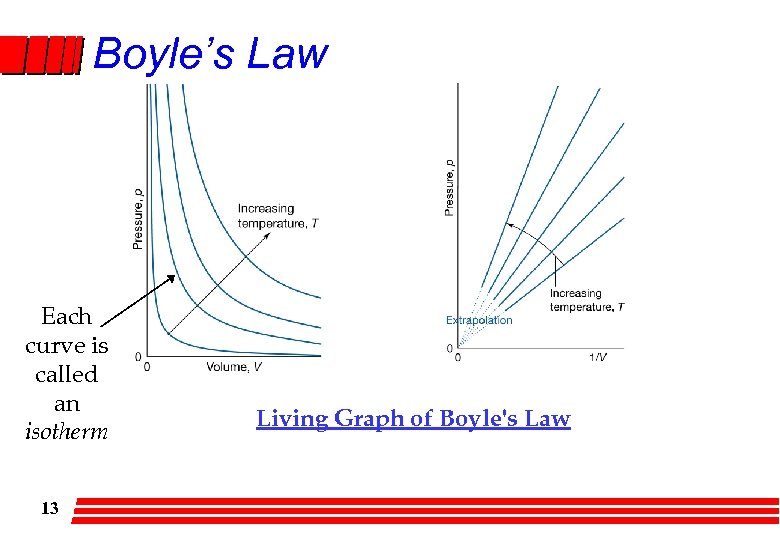Boyle’s Law Each curve is called an isotherm 13 Living Graph of Boyle's Law

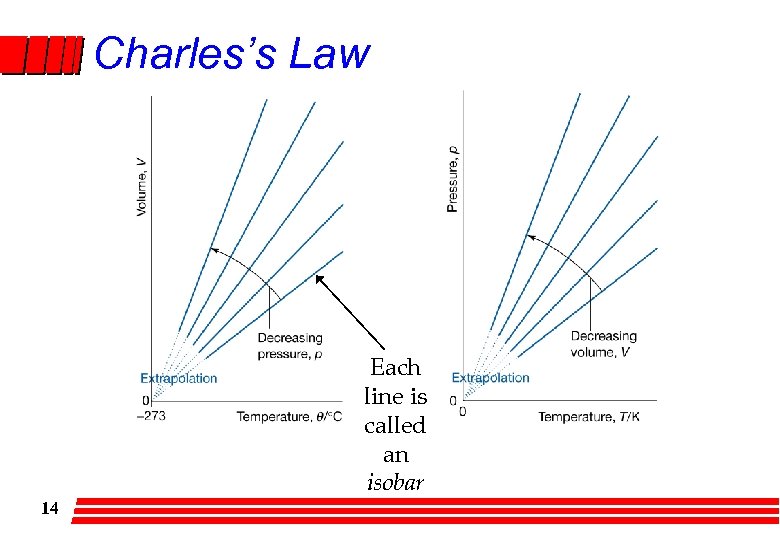Charles’s Law Each line is called an isobar 14

Avogadro principle • At a given T and p, equal volumes of gases contain the same number of molecules, Vm = V/n • Table below presents the molar volumes of selected gases at standard ambient temperature (298. 15 K) and pressure (1 bar) 22. 414 L/mol 15

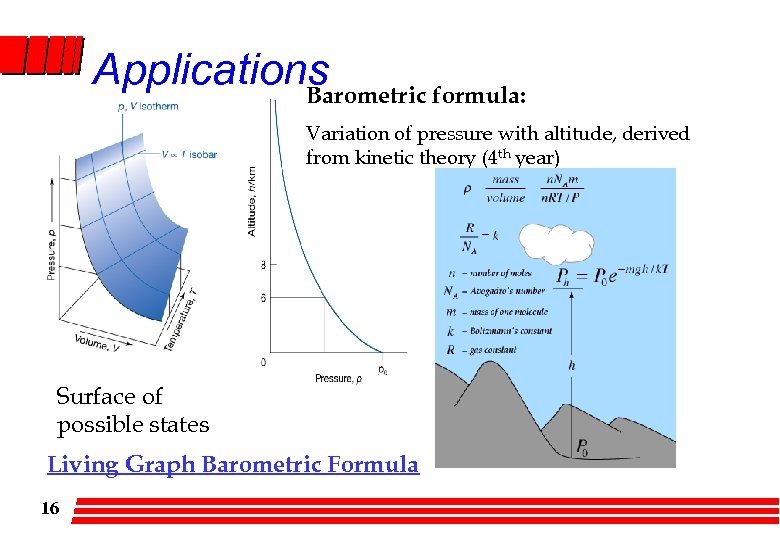Applications Barometric formula: Variation of pressure with altitude, derived from kinetic theory (4 th year) Surface of possible states Living Graph Barometric Formula 16

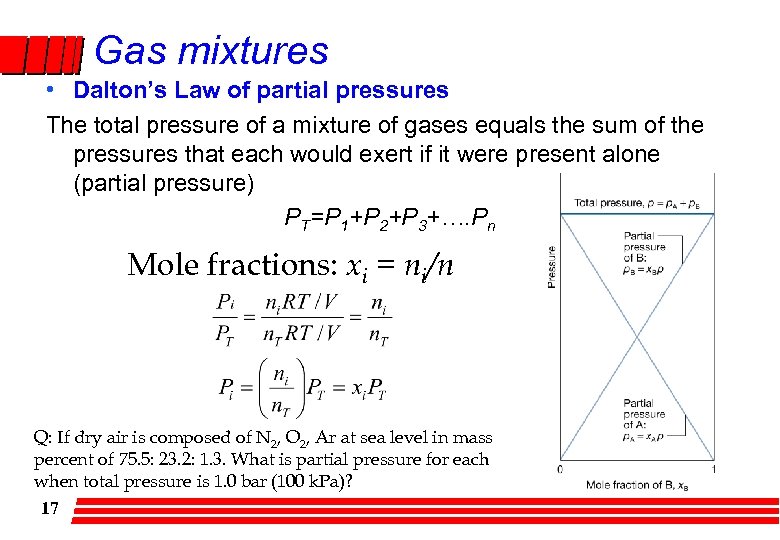Gas mixtures • Dalton’s Law of partial pressures The total pressure of a mixture of gases equals the sum of the pressures that each would exert if it were present alone (partial pressure) PT=P 1+P 2+P 3+…. Pn Mole fractions: xi = ni/n Q: If dry air is composed of N 2, O 2, Ar at sea level in mass percent of 75. 5: 23. 2: 1. 3. What is partial pressure for each when total pressure is 1. 0 bar (100 k. Pa)? 17

Problem solved Come to the lecture to see what is on this slide! 18

Kinetic model of gases Ø Based on 3 assumptions Ø Molecules are in ceaseless random motion Ø Size of molecules is negligible Ø Molecules do not interact Can derive: (see further information 1. 1 in textbook) Where c is the root-mean-squared (rms) speed 19

Kinetic Molecular Theory Ø 20 Compare KMT to Ideal Gas Law

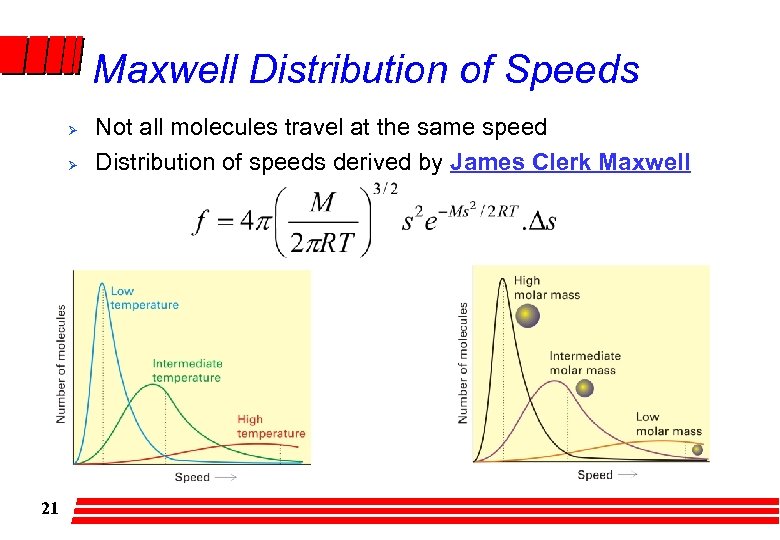Maxwell Distribution of Speeds Ø Ø 21 Not all molecules travel at the same speed Distribution of speeds derived by James Clerk Maxwell

Diffusion and Effusion Thomas Graham proposed a Law (1883) to summarize experimental observations on effusion Rate of Effusion 1/√M Relative rates of effusion 22

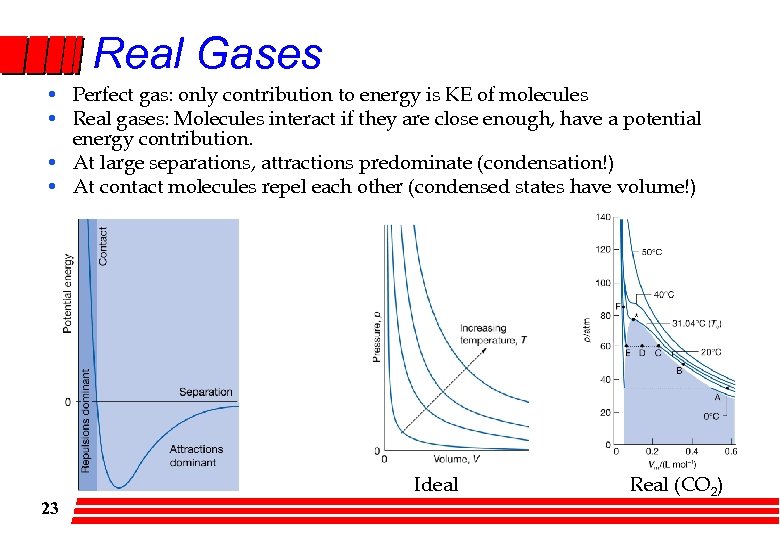Real Gases • Perfect gas: only contribution to energy is KE of molecules • Real gases: Molecules interact if they are close enough, have a potential energy contribution. • At large separations, attractions predominate (condensation!) • At contact molecules repel each other (condensed states have volume!) Ideal 23 Real (CO 2)

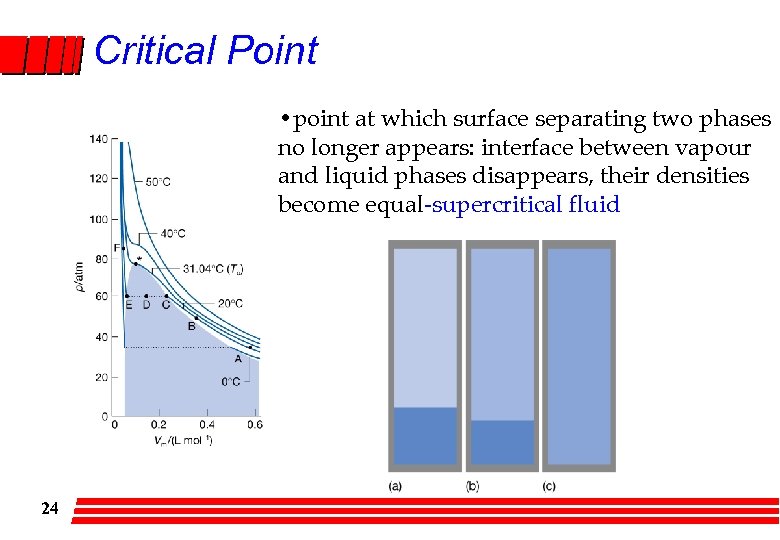Critical Point • point at which surface separating two phases no longer appears: interface between vapour and liquid phases disappears, their densities become equal-supercritical fluid 24

Critical Temperatures Gas cannot be condensed to a liquid above Tc Vapour: gaseous phase below Tc Gas: gaseous phase above Tc 25

Come to the lecture to see what is on this slide! 26

Virial Coefficients and Boyle Temperature • Virial coefficients depend upon T • T at which Z 0 is called the Boyle Temperature (most like perfect gas) • p. Vm = RTB Although the virial equation of state is the most reliable, it does not provide much insight into the behaviour of gases Johannes van der Waals (Dutch physicist) proposed in 1873 an alternate approximate equation of state 27

Van der Waals equation of state • Actual volume reduced in proportion to number of molecules present (repulsions) • Attractive forces reduce frequency of collisions and their strength • Parameters depend on the gas, but are taken to be independent of T. • a is large when attractions are large, b scales in proportion to molecular size (note units) 28

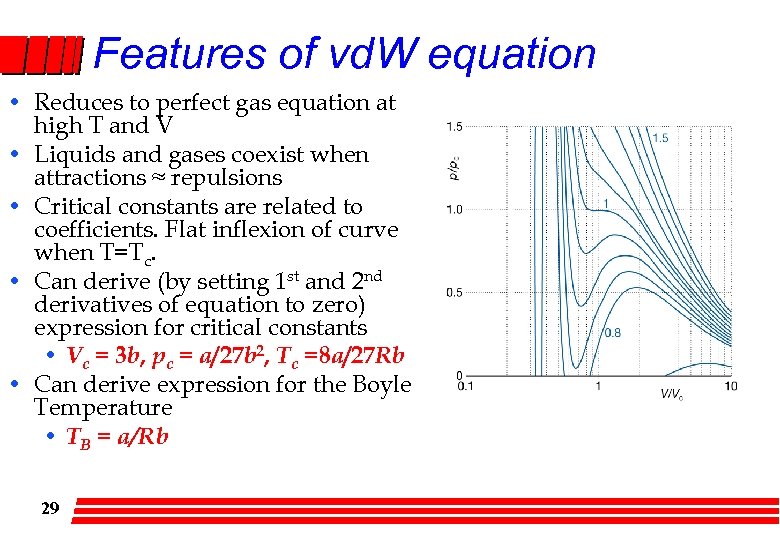Features of vd. W equation • Reduces to perfect gas equation at high T and V • Liquids and gases coexist when attractions ≈ repulsions • Critical constants are related to coefficients. Flat inflexion of curve when T=Tc. • Can derive (by setting 1 st and 2 nd derivatives of equation to zero) expression for critical constants • Vc = 3 b, pc = a/27 b 2, Tc =8 a/27 Rb • Can derive expression for the Boyle Temperature • TB = a/Rb 29

Derivation Come to the lecture to see what is on this slide! 30

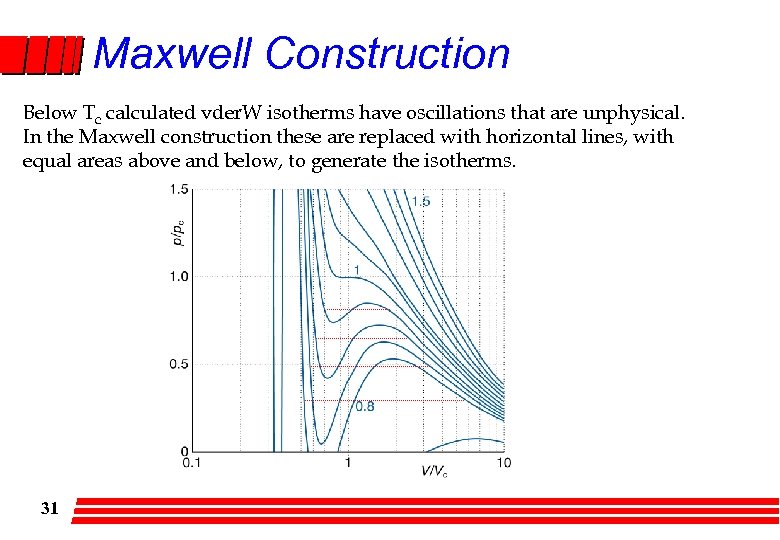Maxwell Construction Below Tc calculated vder. W isotherms have oscillations that are unphysical. In the Maxwell construction these are replaced with horizontal lines, with equal areas above and below, to generate the isotherms. 31

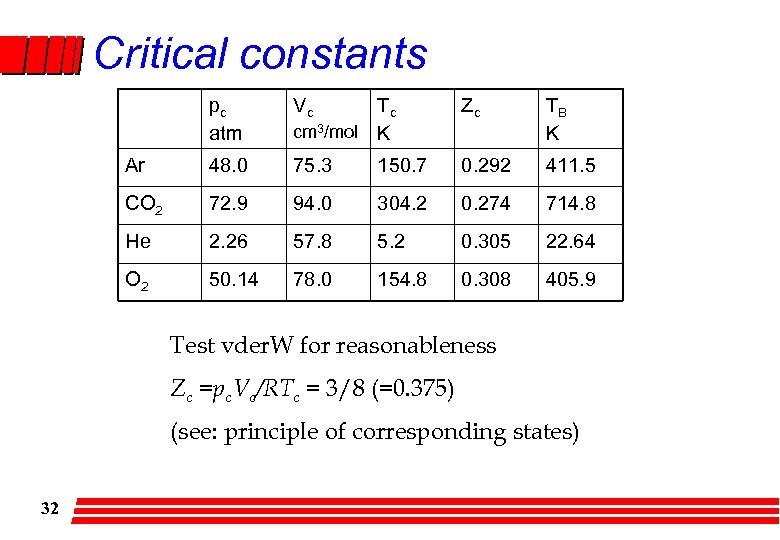Critical constants pc atm Vc Tc cm 3/mol K Zc TB K Ar 48. 0 75. 3 150. 7 0. 292 411. 5 CO 2 72. 9 94. 0 304. 2 0. 274 714. 8 He 2. 26 57. 8 5. 2 0. 305 22. 64 O 2 50. 14 78. 0 154. 8 0. 308 405. 9 Test vder. W for reasonableness Zc =pc. Vc/RTc = 3/8 (=0. 375) (see: principle of corresponding states) 32

Liquefaction-Irish Links! • Refrigeration developed by Carl von Linde in 19 th Century, in response to a request from Guinness in Dublin for a new cooling technique. • Based upon the fact that gases cool as they expand: Joule-Thomson effect (William Thomson, later Lord Kelvin, born in Belfast), The Linde refrigerator combines the JT process with a counter-flow heat exchanger. The gas is re-circulated and it cools on expansion through the throttle. The cooled gas cools the highpressure gas, which cools still further as it expands. Eventually liquefied gas drips from the throttle. 33

Summary l Simplest state of matter is that of a gas • We can assemble an equation of state for an idealised gas from experimental results (Boyle, Charles, Avogadro) • Kinetic Molecular Theory can help explain the molecular basis for these Laws • Real gases differ from ideal gases because of intermolecular interactions. 34